线性代数知识点总结之行列式
本章知识图解:
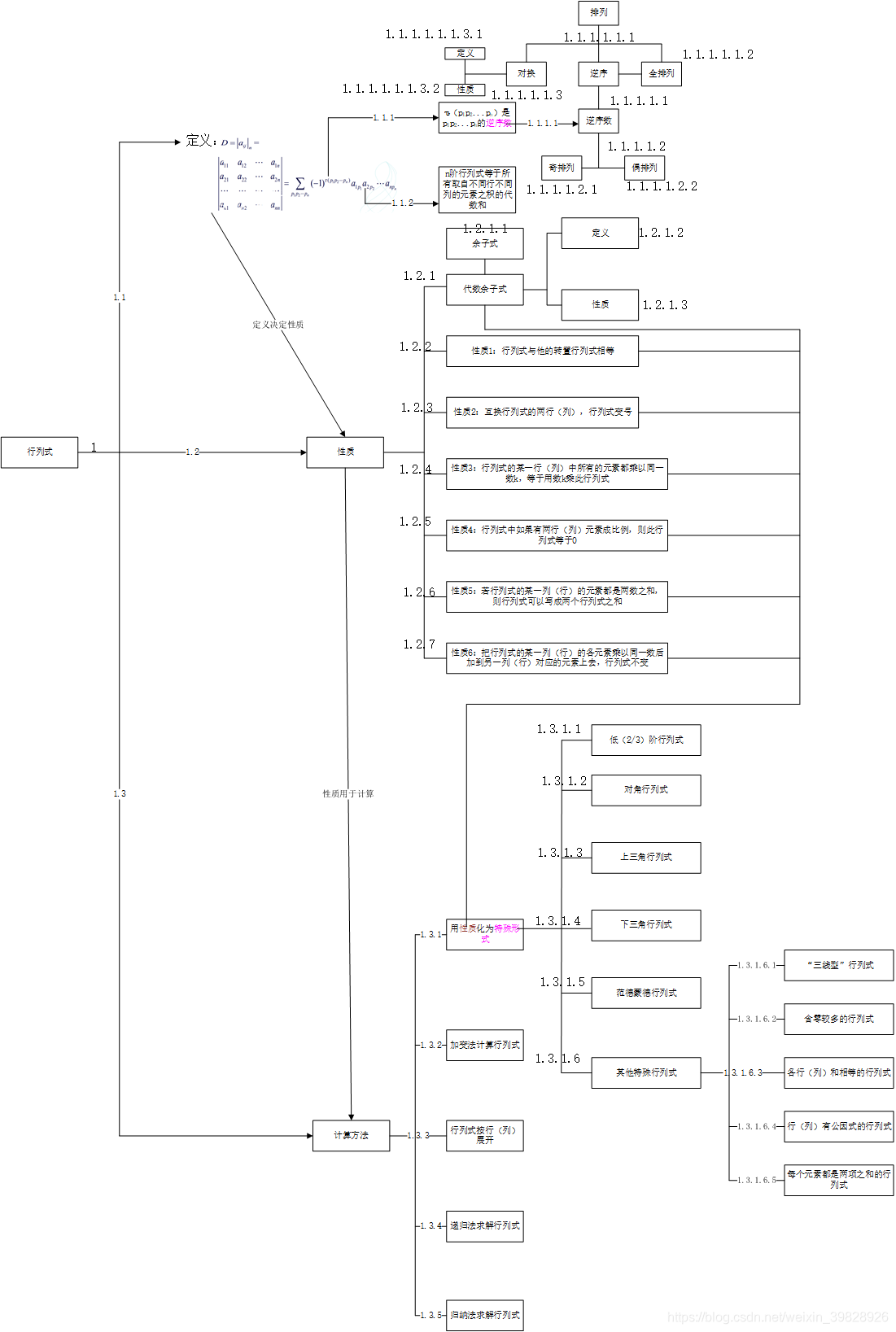
对图解的初级补充与完善
1.1.1.1.1.1.排列:一般地,从n个不同元素中取出m(m≤n)个元素,按照一定的顺序排成一列,叫做从n个元素中取出m个元素的一个排列(permutation);
1.1.1.1.1.2.全排列:n个不同的元素排成一列称为n个元素的全排列。即在排列的定义中m=n的情况就是全排列;
1.1.1.1.1.3.1.对换的定义:在排列中将任意两个元素对换,其余不动,称为对换;
1.1.1.1.1.3.2.对换的性质:①、一个排列中的任意两个元素对换,排列的逆序数改变奇偶性;②、奇排列变成标准排列(标准排列就是按照从小到达的顺序排成的一列)的对换次数为奇数,偶排列变成标准排列的对换次数为偶数;
1.1.1.1.1.逆序:排列中的某两个元素的先后次序与标准次序(某种规则规定的次序)不同,就说有一个逆序;
1.1.1.1.逆序数:①定义:一个排列a,b,c,d,…中所有的逆序的综合称为这个排列的逆序数,记作τ(a,b,c,d,...)\tau(a,b,c,d,...)τ(a,b,c,d,...);②τ\tauτ为奇数,称为奇排列,τ\tauτ为偶数,称为偶排列;③逆序数公式:(1)τ(a,b,c,d,...)=b前面比b大的数的个数+c前面比c大的个数+...\tau(a,b,c,d,...)=b前面比b大的数的个数+c前面比c大的个数+...τ(a,b,c,d,...)=b前面比b大的数的个数+c前面比c大的个数+...;
(2)τ(a,b,c,d,...)=b后面比b小的数的个数+c后面比c小的个数+...\tau(a,b,c,d,...)=b后面比b小的数的个数+c后面比c小的个数+...τ(a,b,c,d,...)=b后面比b小的数的个数+c后面比c小的个数+...
1.2.1.1.余子式的定义:在n阶行列式中,把ai,j所在的第i行第j列划去后,留下的n-1阶行列式称为ai,j的余子式,记作Mi,j;
1.2.1.2.代数余子式的定义:ai,j的代数余子式Ai,j=(-1)i+jMi,j;
1.2.1.3.代数余子式的性质:∑k=1nakiAkj=Dδij=D,当i=j;=0,当i≠j\sum_{k=1}^na_{ki}A_{kj}=D\delta_{ij}=D,当i=j;=0,当i≠j∑k=1nakiAkj=Dδij=D,当i=j;=0,当i̸=j∑k=1naikAjk=Dδij\sum_{k=1}^na_{ik}A_{jk}=D\delta_{ij}∑k=1naikAjk=Dδij也有相同的结论;
对图解的补充与完善的下一步任务
想要让知识之间彻底的融会贯通,单凭这一个图解是远远不够的。需要从思维的想明白两个问题:
- 定义是如何决定性质的:搞清楚这一点才能真的懂得每一个性质的由来,才能真的理解每一个性质,而不是单单靠记忆;
- 性质是怎么应用到计算中的:行列式的理解重点在于性质,而应用的重点在于计算。将性质应用到计算中才能发挥性质的作用。
另外,本章另外一个重点就是计算行列式。这个专题要放到我的“线性代数习题总结之行列式”这一篇中讲解。
所以,就此篇文章需要日后完善的重点就是以性质为思考核心的知识串联。








 本文深入解析线性代数中行列式的关键概念,包括排列、全排列、对换、逆序及逆序数等基础理论,并详细阐述余子式与代数余子式的定义及其性质,旨在帮助读者透彻理解并灵活运用行列式计算。
本文深入解析线性代数中行列式的关键概念,包括排列、全排列、对换、逆序及逆序数等基础理论,并详细阐述余子式与代数余子式的定义及其性质,旨在帮助读者透彻理解并灵活运用行列式计算。
















 2575
2575

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








