回溯法经典例题--求解图的m着色问题--C语言

问题描述：

        给定无向连通图G和m种不同的颜色，用这些颜色为图G的个顶点着色，每个顶点一种颜色。如果有一种着色法使G中每条边的两个顶点不同颜色，则称这个图是m可着色的。图的m着色问题是对于给定图G和m种颜色，找出所有不同的着色法。

求解：

        给无向图上色且相邻顶点不能上同样的色，把它看作m叉树后，类似于红黑树。

        

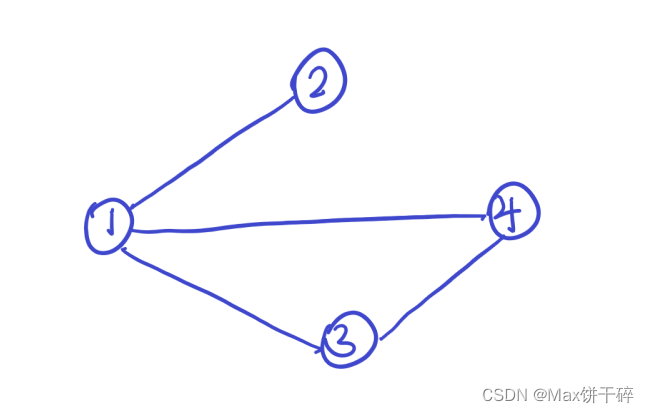
        我们把颜色用数字代替。有多少种颜色，每个节点就有多少个孩子，每一层对应当前节点选择上的色.

        当到达叶子节点时，表示所有节点已经按照要求选好了颜色，也就是出口。

         

 

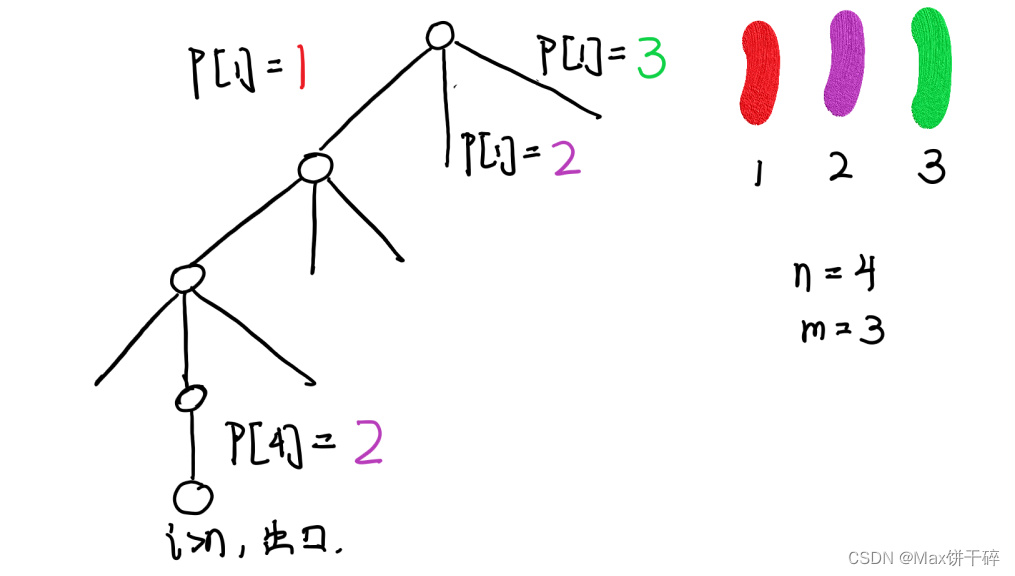
代码：

        g是图的邻接矩阵，p存储i节点涂的颜色代号，n为节点个数，i为当前递归节点，m颜色数量

#include<stdio.h>
#include<iostream>
using namespace std;
#define max 10
int num = 0;
bool paintable(int g[max][max], int p[max], int n,int i) {
	for (int j = 1; j <= n; j++) {
		if (g[i][j] == 1 && p[i] == p[j])
			return false;
	}
	return true;
}
void dfs(int g[max][max],int p[max], int n, int m,int i) {
	if (i > n) {
		num++;
	}
	else {
		for (int j = 1; j <= m; j++) {
			p[i] = j;
			if (paintable(g, p, n, i))
				dfs(g, p, n, m, i + 1);
			p[i] = 0;
		}
	}
}
int main() {
	int n = 4;
	int m = 3;
	int g[max][max];
	int paint[max];
	memset(paint, 0, sizeof(paint));
	memset(g, 0, sizeof(g));
	g[1][2] = 1;g[1][3] = 1;g[1][4] = 1;
	g[2][1] = 1;
	g[3][1] = 1; g[3][4] = 1;
	g[4][1] = 1; g[4][3] = 1;
	dfs(g, paint, n, m, 1);
	cout << num;
	return 0;
}