回溯法经典例题--n皇后问题--C语言

问题描述：

        在n*n的棋盘上尽可能多的放置皇后棋子，但棋子之间不能同行、不能同列、也不能同对角线，请给出可能的放法。

求解：

        根据要求每行一个，那么就让行数i成为递归的自增参数。

        不能同行并且不能同对角线作为剪枝条件。

        首先设计递归函数。

        chess【】【】为棋盘，起始为0，放入棋子后为1，n为棋盘大小，i为当前递归的行数。出口为i==n，即所有行均遍历完毕。否则就遍历当前行的所有列，挨个放皇后，并且每次放之前都要判断当前位置符合要求。

        如果当前的放置方法会让后面几行无法放置皇后，那么就回溯，让chess【i】【j】=0；

void queen(int chess[max][max],int n,int i) {
	if (i == n)
		dis(n, chess);
	for (int j = 0; j < n; j++) {
		if (place(chess, n, i, j)) {
			chess[i][j] = 1;
			queen(chess, n, i + 1);
			chess[i][j] = 0;
			continue;
		}
	}
}

        其次是判断可放置函数place（）。

        主要判断两点，一是不同列，二是不同行。

        不同列：遍历当前递归行之前的所有行，找到所有皇后位置判断y！=j。

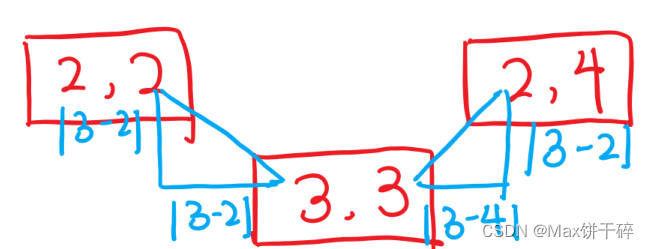
        不同对角线：即（x，y）与之前放置的皇后（i，j）构成等腰直角三角形，|x-i|==|y-j|，边长相等。

 

bool place(int chess[max][max], int n, int x, int y) {
	for (int i = 0; i < x; i++) {
		int j = 0;
		while (chess[i][j] != 1)
			j++;
		if (j == y||abs(i-x)==abs(j-y))
			return false;
	}
	return true;
}

代码：

        

#include<stdio.h>
#include<iostream>
using namespace std;
#define max 10
void dis(int n, int chess[max][max]) {
	for (int i = 0; i < n; i++) {
		for (int j = 0; j < n; j++)
			cout << chess[i][j] << " ";
		cout << endl;
	}
	cout << endl;
}
bool place(int chess[max][max], int n, int x, int y) {
	for (int i = 0; i < x; i++) {
		int j = 0;
		while (chess[i][j] != 1)
			j++;
		if (j == y||abs(i-x)==abs(j-y))
			return false;
	}
	return true;
}
void queen(int chess[max][max],int n,int i) {
	if (i == n)
		dis(n, chess);
	for (int j = 0; j < n; j++) {
		if (place(chess, n, i, j)) {
			chess[i][j] = 1;
			queen(chess, n, i + 1);
			chess[i][j] = 0;
			continue;
		}
	}
}

int main() {
	int chess[max][max];
	memset(chess, 0, sizeof(chess));
	int n = 5;
	queen(chess, n, 0);
	return 0;
}