大规模 MIMO 检测的近似消息传递 (AMP)附matlab代码

最新推荐文章于 2025-12-10 11:08:55 发布

原创最新推荐文章于 2025-12-10 11:08:55 发布 · 81 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#matlab #开发语言

文章介绍了在多用户下行通信系统中，如何使用混合VectorPerturbation(VP)预编码和LatticeReduction(LR)技术提高性能。通过零强迫(ZF)或逐次干扰消除(SIC)的简单预编码，结合LR后信号空间的特性，为近似消息传递(AMP)算法的应用铺平道路，进一步提升任何次优预编码器的性能。研究表明，AMP算法对数据符号在整数中且晶格基不独立同分布的晶格解码问题有益。数值结果验证了低复杂度的AMP算法能显著改善LR辅助预编码的符号错误率性能。

✅作者简介：热爱科研的Matlab仿真开发者，修心和技术同步精进，matlab项目合作可私信。

🍎个人主页：Matlab科研工作室

🍊个人信条：格物致知。

更多Matlab仿真内容点击👇

智能优化算法神经网络预测雷达通信无线传感器电力系统

信号处理图像处理路径规划元胞自动机无人机

⛄ 内容介绍

Vector perturbation (VP) precoding is a promising technique for multiuser communication systems operating in the downlink. In this work, we introduce a hybrid framework to improve the performance of lattice reduction (LR) aided precoding in VP. First, we perform a simple precoding using zero forcing (ZF) or successive interference cancellation (SIC) based on a reduced lattice basis. Since the signal space after LR-ZF or LR-SIC precoding can be shown to be bounded to a small range, then along with sufficient orthogonality of the lattice basis guaranteed by LR, they collectively pave the way for the subsequent application of an approximate message passing (AMP) algorithm, which further boosts the performance of any suboptimal precoder. Our work shows that the AMP algorithm can be beneficial for a lattice decoding problem whose data symbols lie in integers and entries of the lattice basis may not be i.i.d. Gaussian. Numerical results confirm that the low-complexity AMP algorithm can improve the symbol error rate performance of LR-aided precoding significantly.

⛄ 部分代码

clc;clear all;close all;

linestyles = cellstr(char('-','--','-.','--'));

SetColors=lines(10);

Markers=['o','x','+','*'];

legendbox={'MMSE','MMSE-AMPT', 'MMSE-AMPG'};

n=32;% # of users

m=64;% # of received antennas; m is much larger than n in massive mimo

SNR_range=[0:4:16]; % the tested range of SNR

count=0;

algorithms=[1:1:3];

for SNR=SNR_range

for monte=1:4e3 % the number of MonteCarlo simulations

H=randn(m,n); %channel matrix

A=7;% size of constellations

u=1*randi([-A,A],n,1);% symbols in users

sigmas2=A*(A+1)/3; % theoretical signal power;

sigma2=sigmas2/((10^(SNR/10))); % noise power

y=H*u+sqrt(sigma2)*randn(m,1); %the received signal

for j=algorithms

switch j

case 1 % MMSE

xhat=round(pinv([H;sigma2/sigmas2*eye(n)])*[y;zeros(n,1)]);

x_mmse=xhat;

case 2 % MMSE-AMPT

yp=y-H*x_mmse; %yp is the difference vector

xhat=x_mmse+AMPT(yp,H,.5,.5); % AMP with ternery priors

case 3 % MMSE-AMPG

yp=y-H*x_mmse;

xhat=x_mmse+AMPG(yp,H,sigmas2/20,.5);% AMP with Gaussian priors;the signal power is unknown

end

uhat=max(min(xhat,A*ones(n,1)),-A*ones(n,1));%estimated symbols

ser(j,monte)=sum(u~=uhat)/n; % symbol error rate

end

count=count+1;

SER(:,count)=mean(ser,2);

end

figure(1)

for j=algorithms

semilogy(SNR_range,SER(j,:),[linestyles{j} Markers(j)],'Color',SetColors(j,:),'Linewidth',2);

hold on;

grid on;

end

hold off;

h=legend(legendbox(algorithms));

xlabel('SNR/dB');ylabel('SER');

⛄ 运行结果

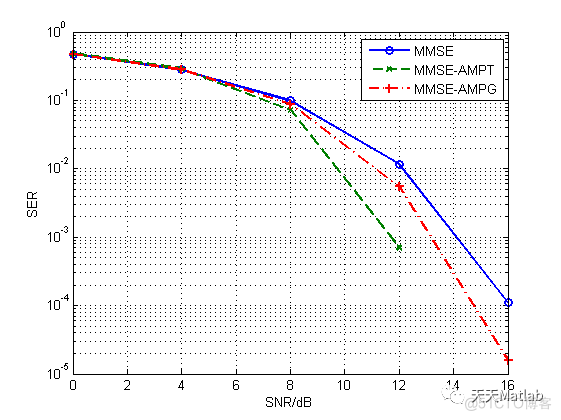
大规模 MIMO 检测的近似消息传递 (AMP)附matlab代码_ci

⛄ 参考文献

[1] Lyu S , Ling C . Hybrid Vector Perturbation Precoding: The Blessing of Approximate Message Passing[J]. IEEE Transactions on Signal Processing, 2017, PP:1-1.