【卡尔曼滤波跟踪】跟踪以恒定或变化速度移动的物体（Matlab实现）-优快云博客

本文链接：https://blog.youkuaiyun.com/Matlab88888/article/details/138672263

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

💥1 概述

卡尔曼滤波是一种用于估计系统状态的强大技术，特别适用于跟踪移动物体的位置和速度。当跟踪物体时，通常需要考虑噪声和不确定性，而卡尔曼滤波能够有效地处理这些问题。首先，需要建立物体运动的动态系统模型。对于跟踪以恒定速度移动的物体，可以使用简单的线性模型描述其运动。对于跟踪以变化速度移动的物体，可能需要更复杂的非线性模型。确定如何通过传感器测量来观测物体的状态。这通常包括将传感器测量转换为状态向量的测量值，并考虑传感器误差和噪声。预测步骤：基于系统模型，使用上一个时刻的状态估计来预测下一个时刻的状态。更新步骤：利用测量值对预测的状态进行修正，以获得更准确的状态估计。在更新步骤中，卡尔曼滤波考虑了预测和测量之间的不确定性，并通过加权平均的方式来融合两者。可以使用卡尔曼滤波有效地跟踪以恒定或变化速度移动的物体，并在存在噪声和不确定性的情况下提供准确的状态估计。

📚2 运行结果

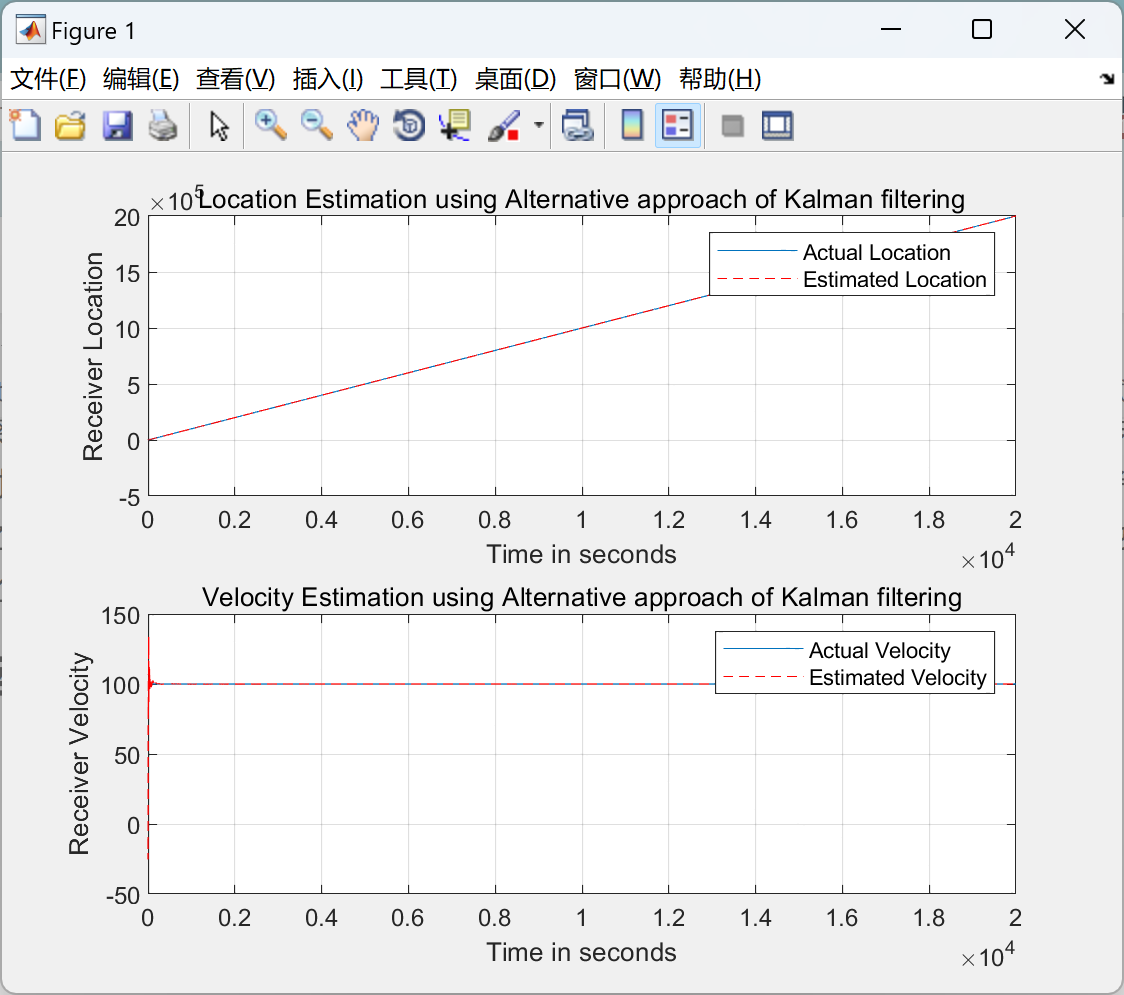
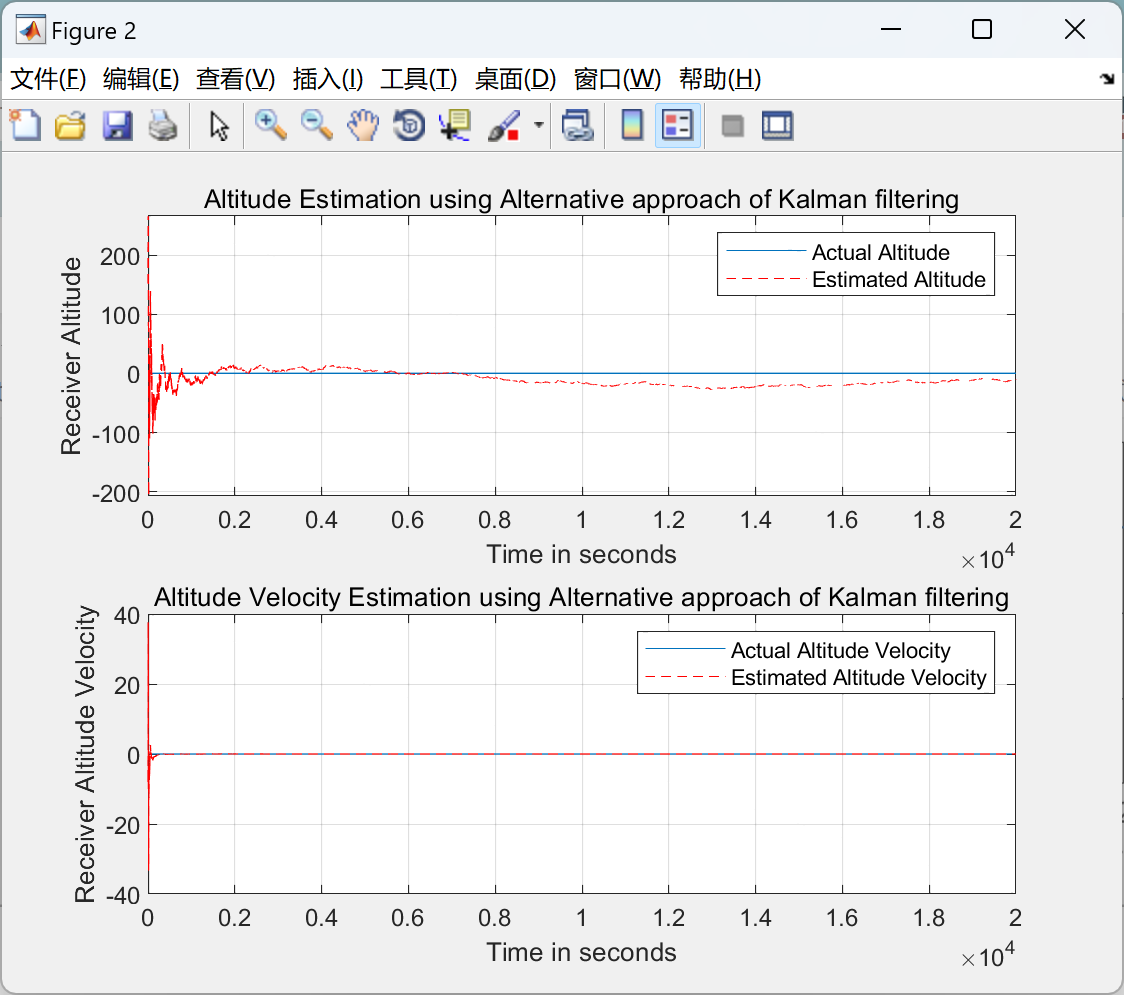
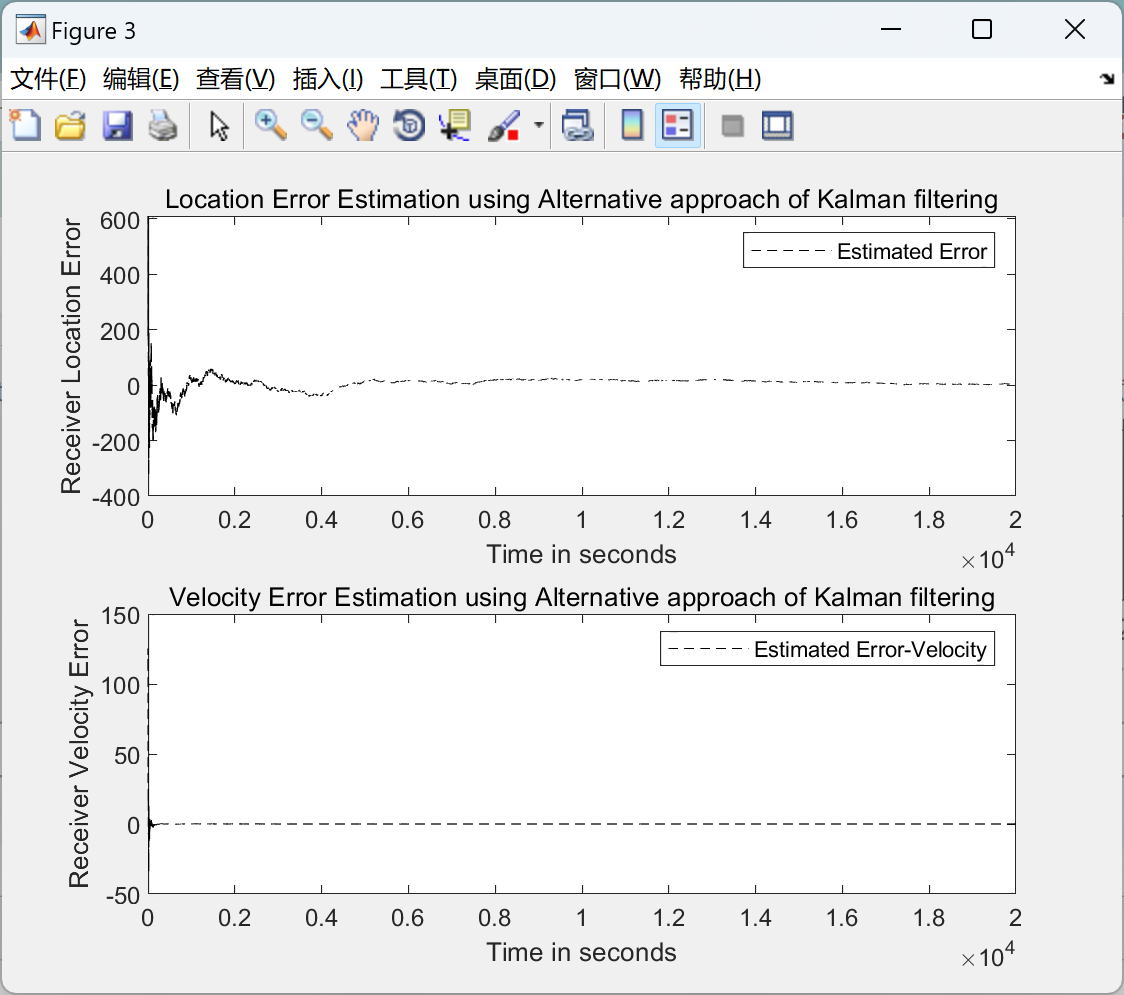
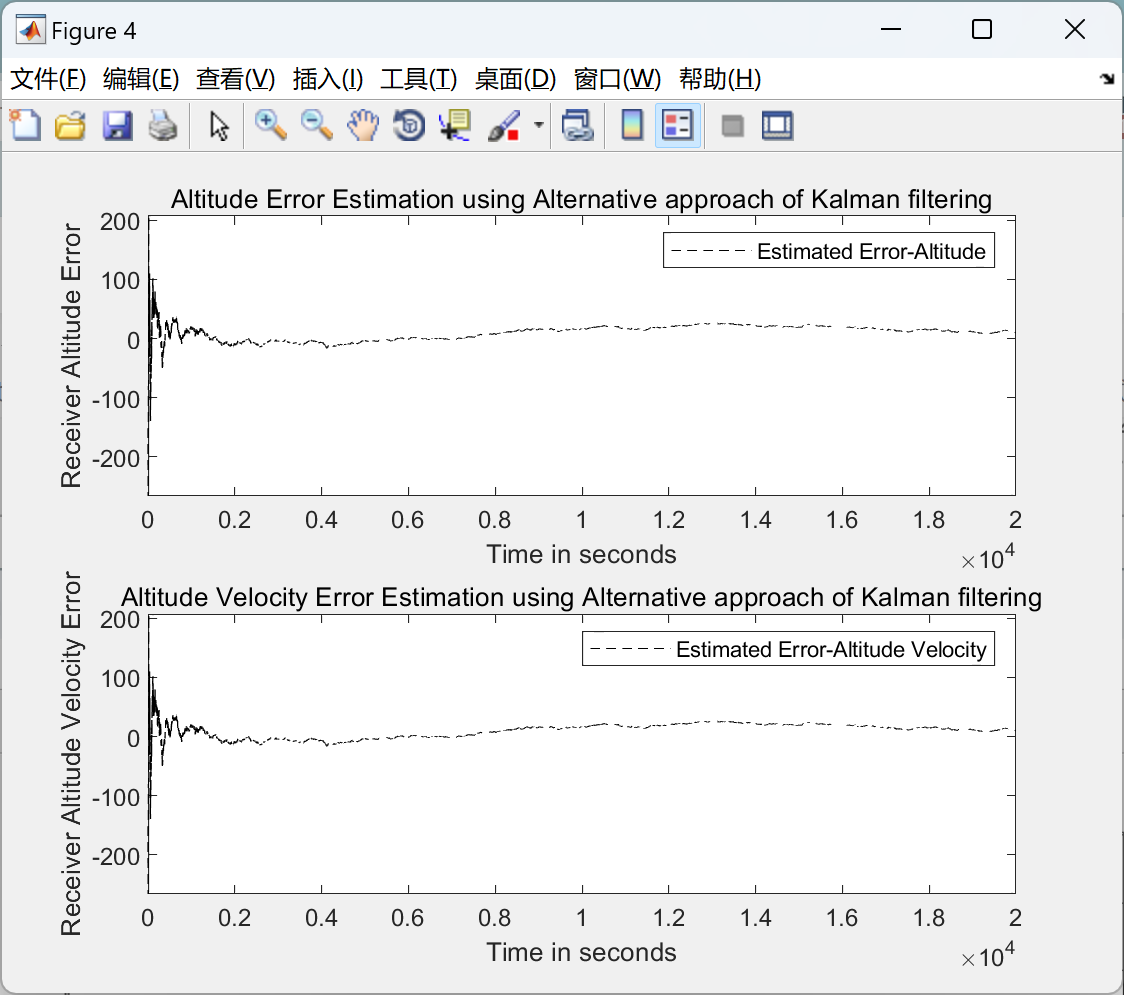
主函数部分代码：

SIGNOISE=300.; 
X=0.;
Y=0.; 
XH=1000.; 
YH=2000.; 
XDH=0.; 
YDH=0.; 
XR1=1000000.; 
YR1=20000.*3280.; 
XR2=50000000.; 
YR2=20000.*3280.; 
ORDER=4; TS=1.; 
TF=20000.; 
PHIS=0.; 
T=0.; 
S=0.; 
H=.01; 
PHI=zeros(ORDER,ORDER); 
P=zeros(ORDER,ORDER); 
IDNP=eye(ORDER); 
Q=zeros(ORDER,ORDER); 
P(1,1)=1000.^2; 
P(2,2)=100.^2; 
P(3,3)=2000.^2; 
P(4,4)=100.^2; 
RMAT(1,1)=SIGNOISE^2; 
RMAT(1,2)=0.; 
RMAT(2,1)=0.; 
RMAT(2,2)=SIGNOISE^2; 
TS2=TS*TS; 
TS3=TS2*TS;
Q(1,1)=PHIS*TS3/3.; 
Q(1,2)=PHIS*TS2/2.; 
Q(2,1)=Q(1,2); 
Q(2,2)=PHIS*TS; 
Q(3,3)=PHIS*TS3/3.; 
Q(3,4)=PHIS*TS2/2.; 
Q(4,3)=Q(3,4); 
Q(4,4)=PHIS*TS; 
count=0; 
while T<=TF
    XR1OLD=XR1; 
    XR2OLD=XR2; 
    XOLD=X; 
    YOLD=Y; 
    XR1D=-14600.; 
    XR2D=-14600.; 
    XD=100.; 
    YD=0.; 
    XR1=XR1+H*XR1D; 
    XR2=XR2+H*XR2D; 
    X=X+H*XD; 
    Y=Y+H*YD; 
    T=T+H; 
    XR1D=-14600.; 
    XR2D=-14600.; 
    XD=100.; 
    YD=0.;