💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
⛳️赠与读者
👨💻做科研,涉及到一个深在的思想系统,需要科研者逻辑缜密,踏实认真,但是不能只是努力,很多时候借力比努力更重要,然后还要有仰望星空的创新点和启发点。当哲学课上老师问你什么是科学,什么是电的时候,不要觉得这些问题搞笑。哲学是科学之母,哲学就是追究终极问题,寻找那些不言自明只有小孩子会问的但是你却回答不出来的问题。建议读者按目录次序逐一浏览,免得骤然跌入幽暗的迷宫找不到来时的路,它不足为你揭示全部问题的答案,但若能让人胸中升起一朵朵疑云,也未尝不会酿成晚霞斑斓的别一番景致,万一它居然给你带来了一场精神世界的苦雨,那就借机洗刷一下原来存放在那儿的“躺平”上的尘埃吧。
或许,雨过云收,神驰的天地更清朗.......🔎🔎🔎
💥1 概述
同步相量是以标准时间信号作为采样过程的基准,通过对采样数据计算而得到的相量,同步相量测量信息包含每个测量量值的幅值和相角以及相应的时间标签。数据采集与监视控制系统(Supervisory Control And Data Acquisition,SCADA)是以计算机为基础的电力自动化监控系统,其运用领域涵盖了电力、冶金、石油、化工等,SCADA在过去的电力系统监视中应用最为广泛,技术发展最为成熟。
新一代电网通过以同步相量测量技术为基础的广域测量系统来检测和控制系统的状态。同步相量测量技术的核心是相量估计算法的设计,即算法的估计精度将直接影响到的应用效果。本次大作业旨在运用信号与系统课程所学知识,对所给电压信号进行频谱分析,并设计算法计算信号的同步向量,主要包含两个部分:幅值计算、相位计算。
需要指出的是,同步向量的幅值为有效值,相位为余弦函数表示下的相位。

详细报告讲解见第4部分。
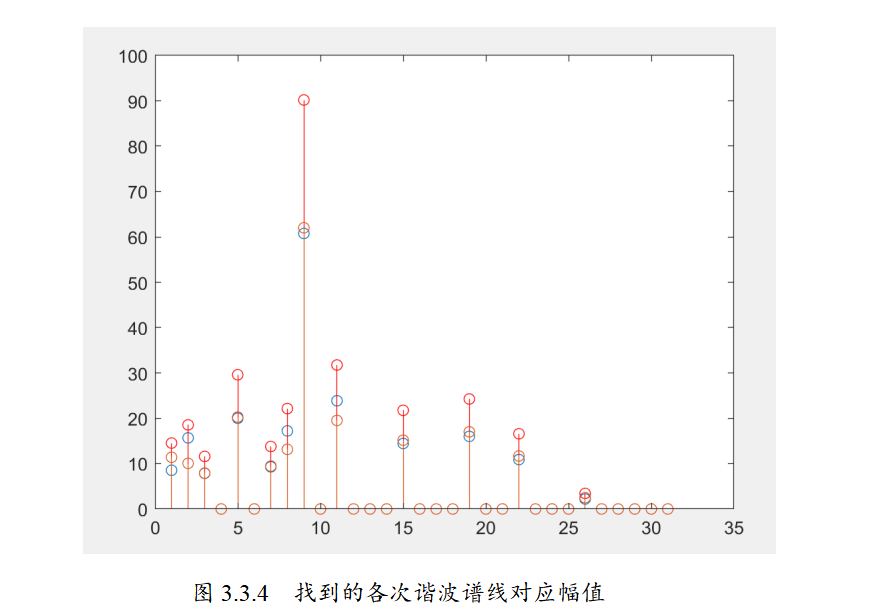
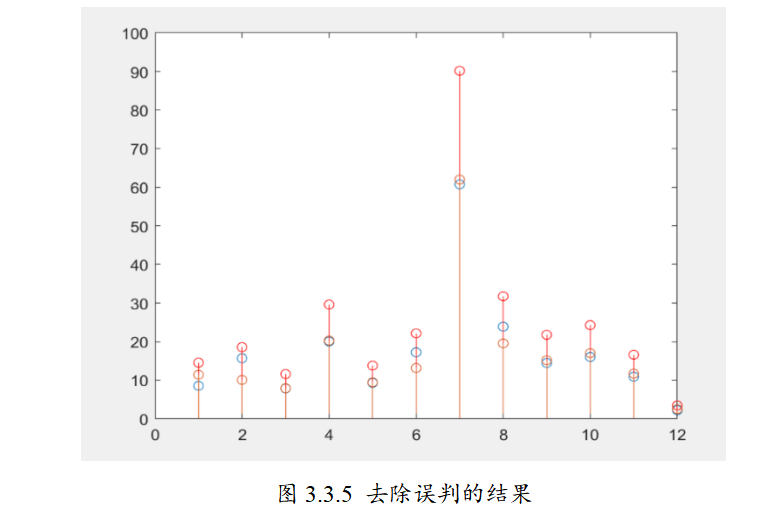
对于实际的信号,实际上直接使用必做的程序就可以实现分析,因为程序具有一定的通用性,所以只要稍微调节一下判断误判的阈值就可以实现谐波分析。通过观察,我们发现实际信号的频谱中基本上不含有直流分量,所以也就不需要像选做一那样减去白色频谱进行修正。
对于窗口的选择,我们目前使用了Blackman Harris窗和hamming窗并且使用差值方法进行了修正,这在一定程度上提高了分析的精度。
结果如下图所示。
| 频率成分 | 频率 | 幅值(有效值) |
| 基波频率 | 49.98494 | 59.90183 |
| 2次谐波 | 99.92123 | 0.021707 |
| 3次谐波 | 150.0042 | 0.033451 |
| 4次谐波 | 199.9507 | 0.034666 |
| 5次谐波 | 249.9206 | 0.995032 |
| 6次谐波 | 299.9011 | 0.036796 |
| 7次谐波 | 349.8984 | 0.078450 |
| 11次谐波 | 549.8625 | 0.014618 |
| 13次谐波 | 649.7971 | 0.062858 |
| 15次谐波 | 749.7748 | 0.007414 |
| 17次谐波 | 849.7505 | 0.019783 |
| 19次谐波 | 949.6638 | 0.015713 |
| 21次谐波 | 1049.679 | 0.008713 |
| 25次谐波 | 1249.702 | 0.008675 |
| 30次谐波 | 1449.559 | 0.011964 |
| 31次谐波 | 1549.535 | 0.008167 |
1. 快速傅里叶变换(FFT)在同步相量计算中的应用
1.1 基本原理与计算优化
FFT是离散傅里叶变换(DFT)的高效算法,通过蝶形运算分解大点数DFT为小规模计算,将复杂度从O(N2)O(N2)降至O(NlogN)O(NlogN)。其核心包括:
- 时间抽取法(DIT)与频率抽取法(DIF) :适用于序列长度N=2mN=2m的分解。
- 原位计算与码位倒序:减少存储需求,提升实时性。
- 硬件加速:基于DSP(如TMS320LF2407)或GPU/CUDA实现并行计算,满足实时性要求。
1.2 电力系统同步相量计算实现
-
基波与谐波分离:FFT将非正弦周期信号分解为基波和谐波分量,计算电压/电流相量(幅值、相位)。
-
加窗修正:电力信号常存在频率偏移(ΔfΔf),导致频谱泄漏和栅栏效应。需加窗(如汉宁窗)并插值修正,公式为:
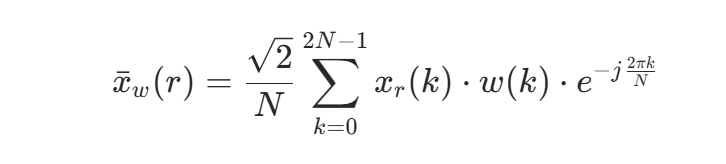
其中w(k)为窗函数系数,修正后相位误差可稳定在0.00001∘
-
案例:配电网PMU中,采用汉宁窗FFT插值算法,相位误差<0.1°,满足高精度同步相量测量要求。
2. 窗函数法的技术特点与电力系统应用
2.1 窗函数的选择与性能指标
-
核心目标:抑制频谱泄漏和栅栏效应,提升谐波分析精度。
-
关键参数:
- 主瓣宽度:决定频率分辨率(越窄越好)。
- 旁瓣衰减:决定抗干扰能力(越高越好)。
-
常用窗函数对比:
窗函数类型 幅度误差(%) 相位误差(°) 频率误差(Hz) Blackman窗 2.51×10−5 5.72×10−4 2.91×10−6 Hanning窗 1.20×10−5 3.45×10−4 1.87×10−6 Nuttall窗 0.98×10−5 2.76×10−4 1.52×10−6 SPMC互卷积窗 0.31×10−5 0.89×10−4 0.47×10−6

2.2 电力系统应用案例
- 谐波检测:改进Gauss窗设计的FIR滤波器,有效提升电网谐波分析准确性。
- 同步相量测量:
- 汉宁窗:在配电网PMU中实现无偏相量计算,抑制谐波/间谐波干扰。
- 自卷积窗(如Hanning自相乘窗):进一步降低频谱泄漏,应用于高压输电网谐波分析。
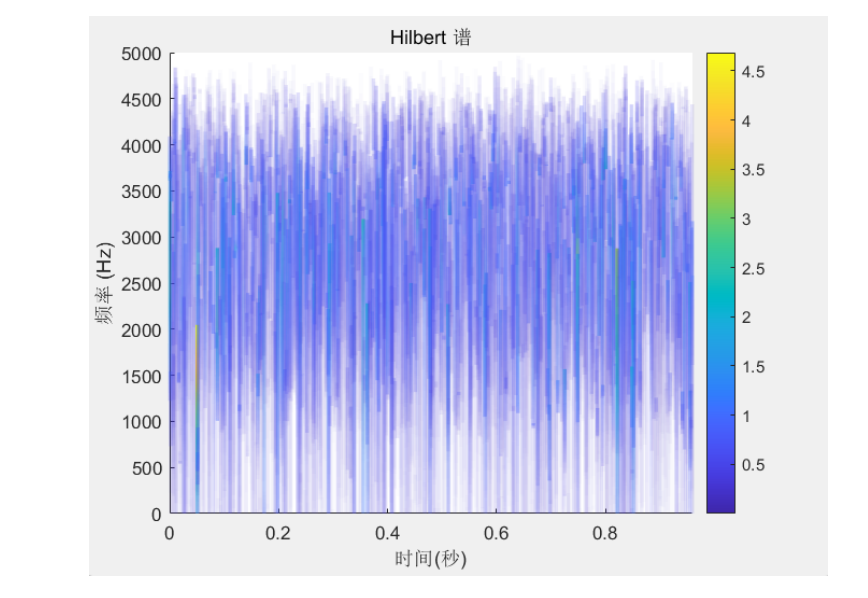
3. 希尔伯特-黄变换(HHT)在非平稳信号分析中的优势
3.1 核心机制:经验模态分解(EMD)与Hilbert谱
-
EMD自适应分解:将信号分解为固有模态函数(IMF),满足条件:
- 极值点与过零点数量相差≤1;
- 局部包络均值为零。
-
Hilbert时频谱:对每个IMF进行Hilbert变换,获得瞬时频率和幅值,公式为:

其中ai(t)和ωi(t)为瞬时幅值与频率。
3.2 非平稳信号分析优势
- 自适应性强:无需预设基函数,适合非线性、非稳态信号(如故障暂态信号)。
- 高时频分辨率:突破Heisenberg测不准原理限制,精准捕捉突变特征(如短路电流)。
- 工程应用案例:
- 风电系统故障诊断:HHT成功识别风机轴承故障特征频带(0.5–1.5 kHz)。
- 脑电信号去噪:改进HHT算法有效分离高噪声背景下的生理信号。
4. 小波变换的多分辨率分析与同步相量提取
4.1 多分辨率特性
- 变尺度分析:
- 低频段:宽时间窗 → 高频率分辨率(分析基波相量)。
- 高频段:窄时间窗 → 高时间分辨率(捕捉暂态谐波)。
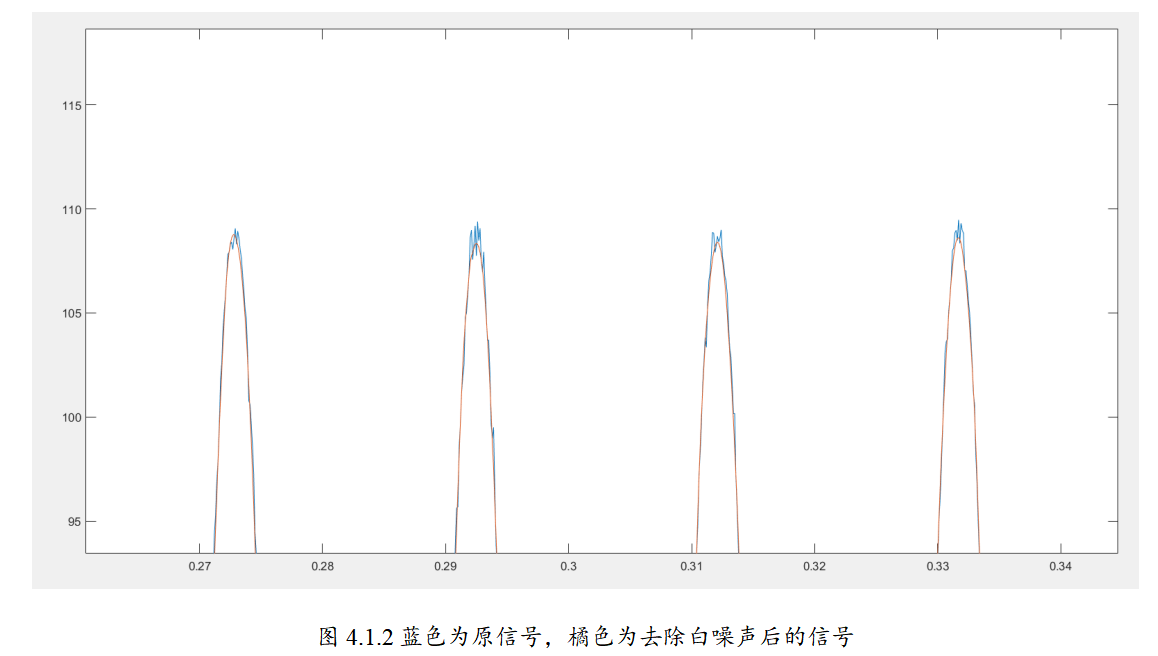
- 去噪能力:小波系数稀疏分布(低熵性),通过阈值法抑制白噪声。
4.2 同步相量提取中的应用
- 动态相量跟踪:利用小波多尺度分解,分离频率时变信号的基波分量。
- 高精度时频表征:
- SETPWT(同步提取三参数小波变换) :调节小波基参数匹配地震子波信号,提升储层含气性检测精度。
- 配电网信号处理:小波去噪后结合FFT,提高谐波测量鲁棒性。
5. 实际应用案例对比
| 技术 | 应用场景 | 典型案例 |
|---|---|---|
| FFT+窗函数 | 谐波分析、PMU同步相量测量 | 汉宁窗FFT在配电网PMU实现0.05°相位精度;Blackman-Harris窗用于高压谐波检测。 |
| HHT | 非平稳故障诊断 | 风电系统轴承故障特征提取;内燃机敲缸故障频带分析(0.5–1.5 kHz)。 |
| 小波变换 | 暂态信号处理、去噪 | SETPWT算法提升地震信号时频分辨率;配电网白噪声抑制。 |
6. 技术挑战与发展趋势
- FFT与窗函数:需解决频率快速波动时的实时跟踪问题,结合自适应滤波提升鲁棒性。
- HHT:EMD存在模态混叠,需发展改进算法(如切线平均点优化包络拟合)。
- 小波变换:需平衡计算复杂度与精度,GPU加速或成未来方向。
- 融合应用:如“小波预处理+HHT分解”处理复杂暂态信号,或“窗函数FFT+小波去噪”提升PMU精度。
结论:FFT与窗函数法因其高效性和成熟度,仍是电力系统同步相量计算的主流;HHT和小波变换在非平稳信号处理中展现独特优势,尤其在故障诊断与高噪声环境下。未来技术发展将聚焦算法融合与硬件加速,以满足智能电网对高精度动态监测的需求。
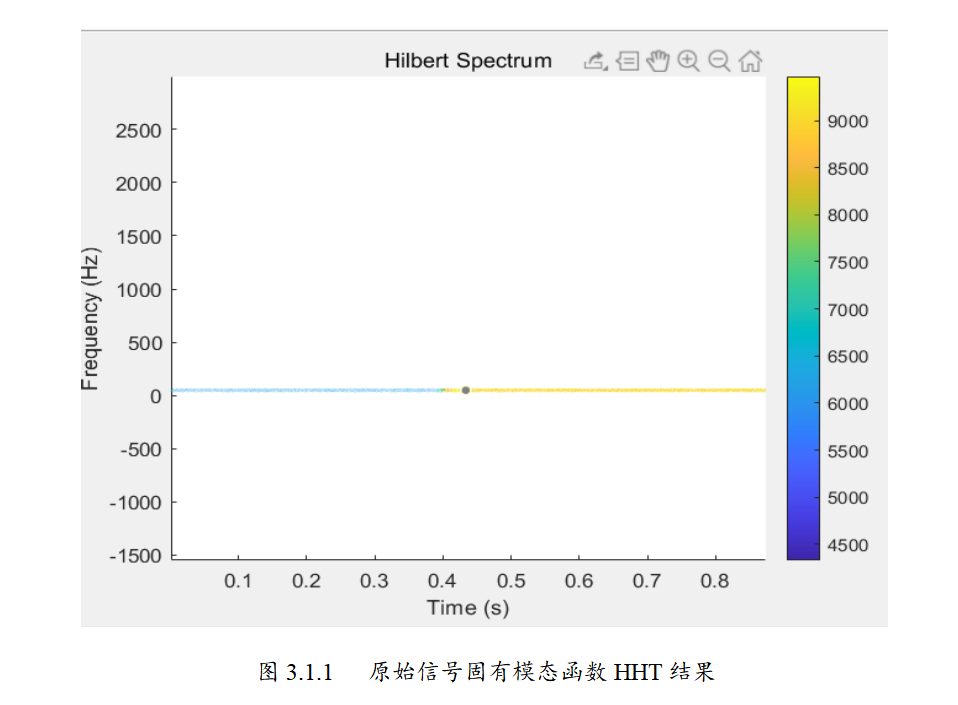
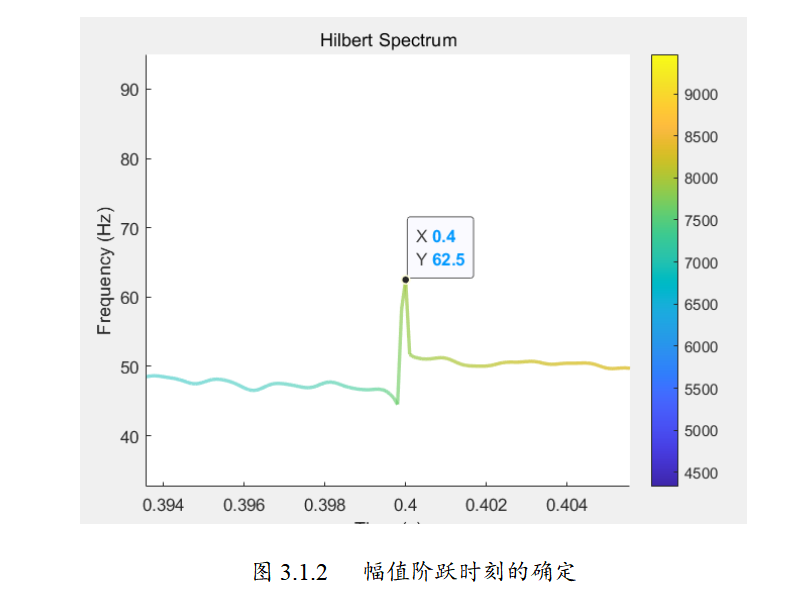
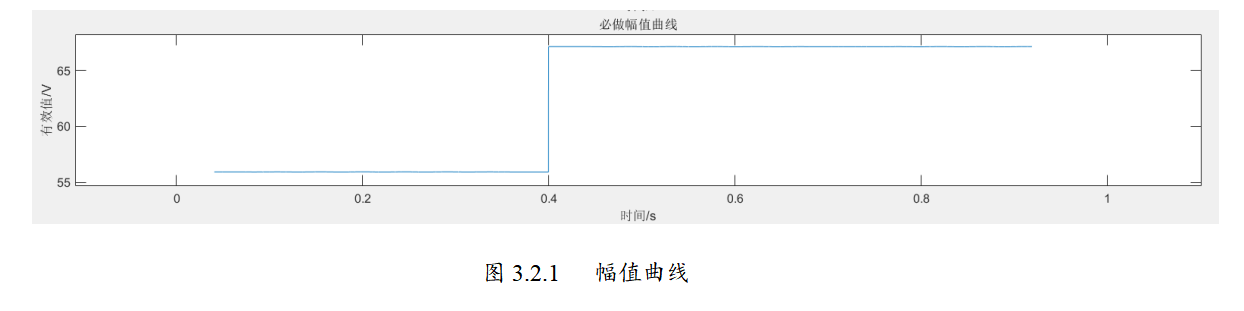
📚2 运行结果
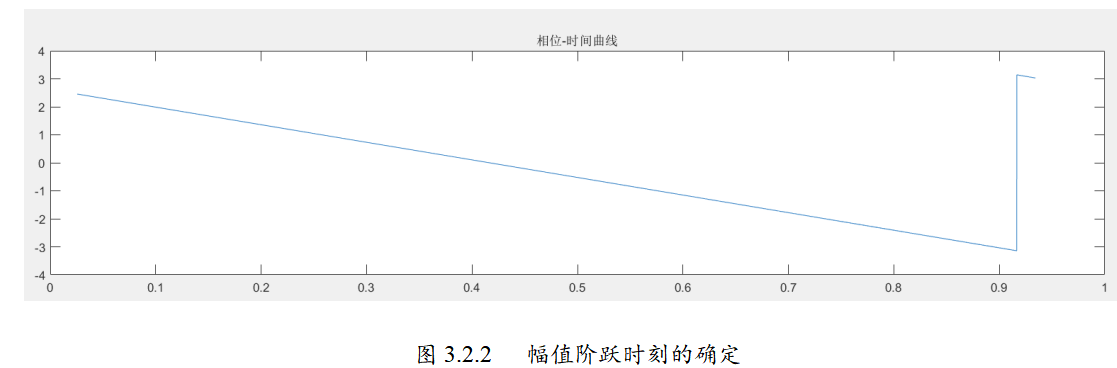
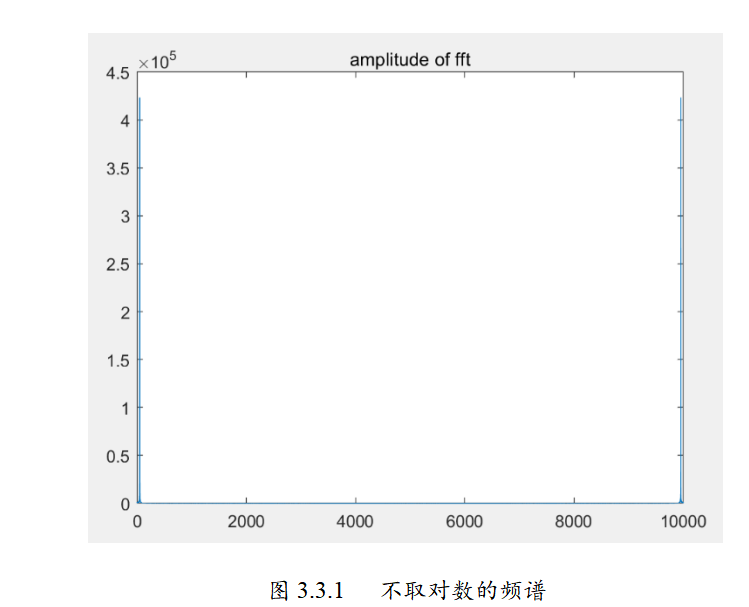
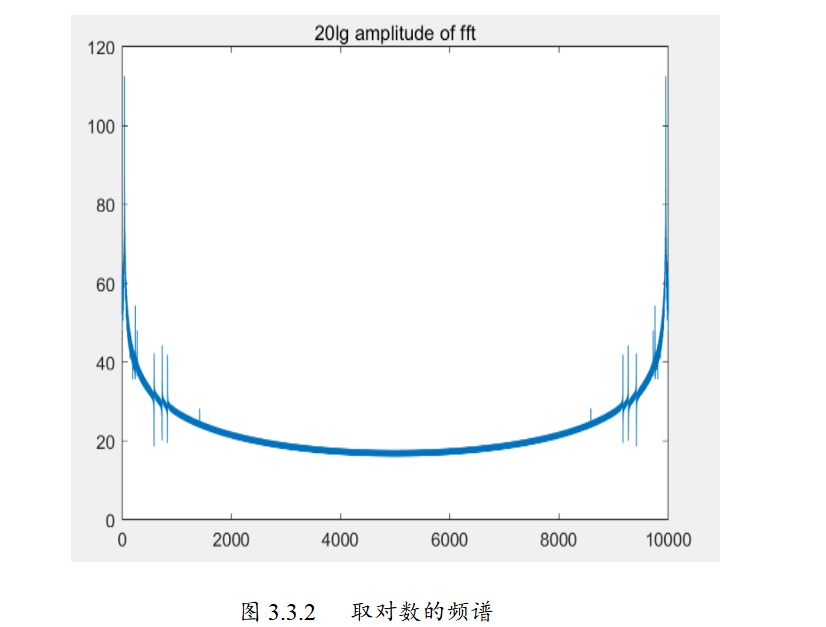
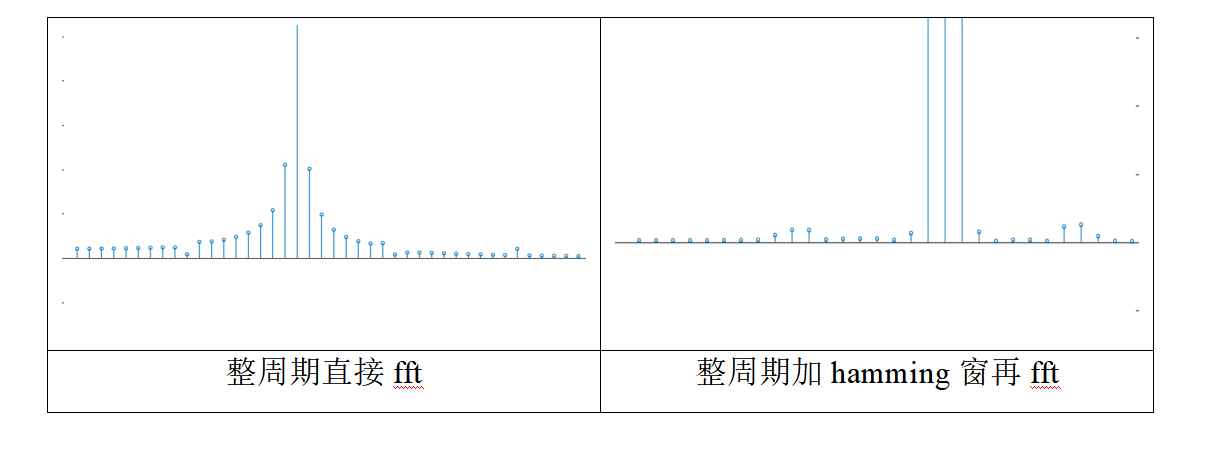
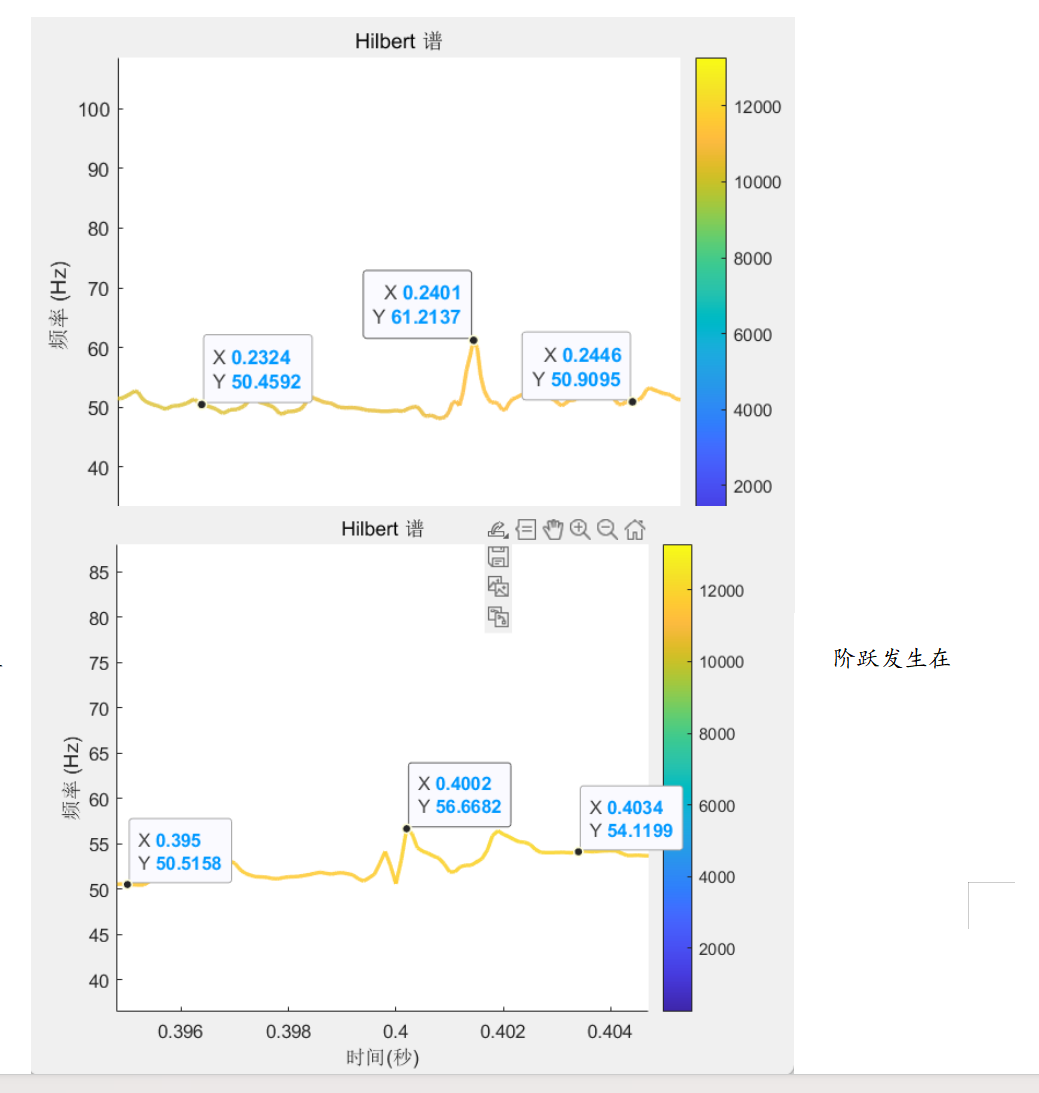
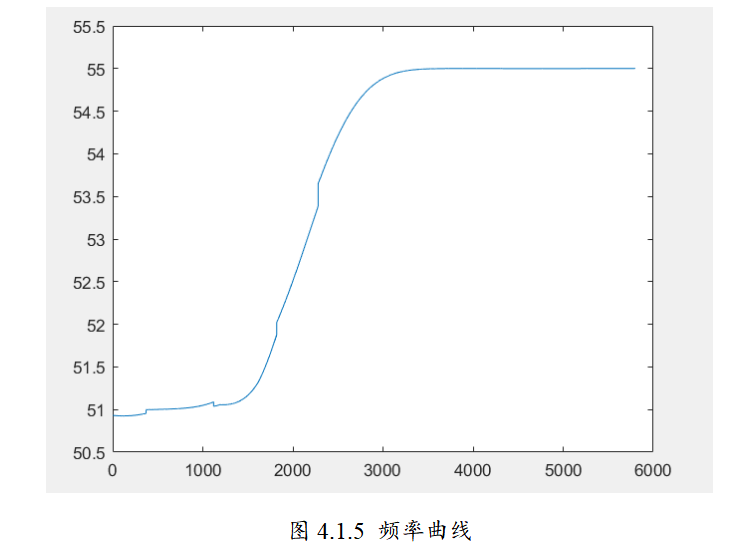
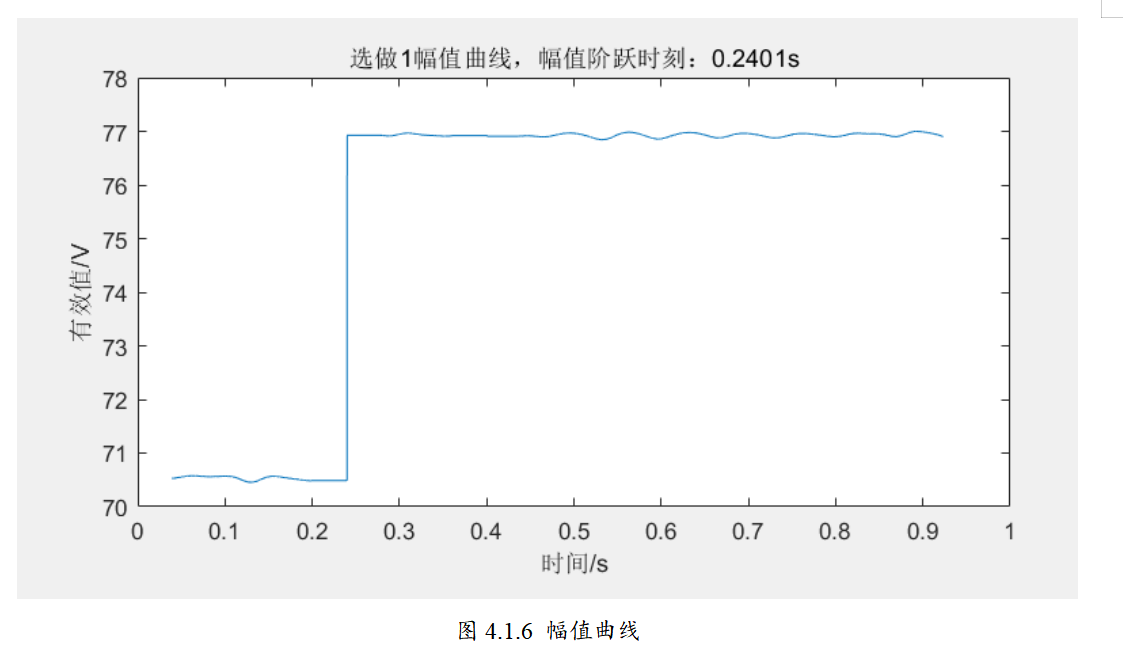
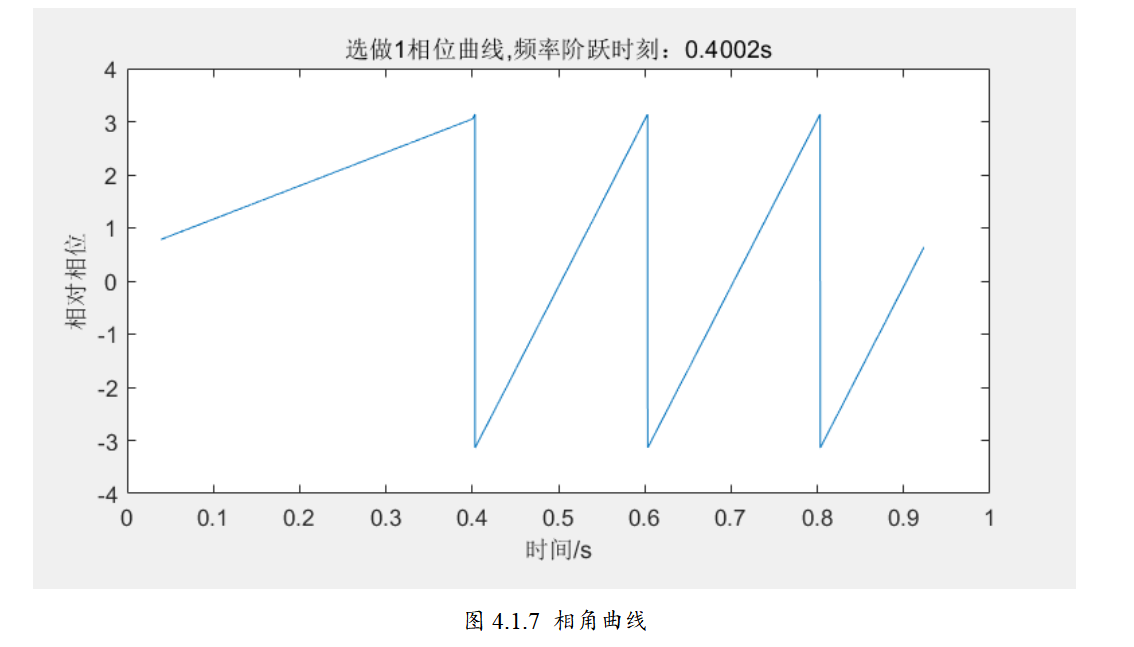
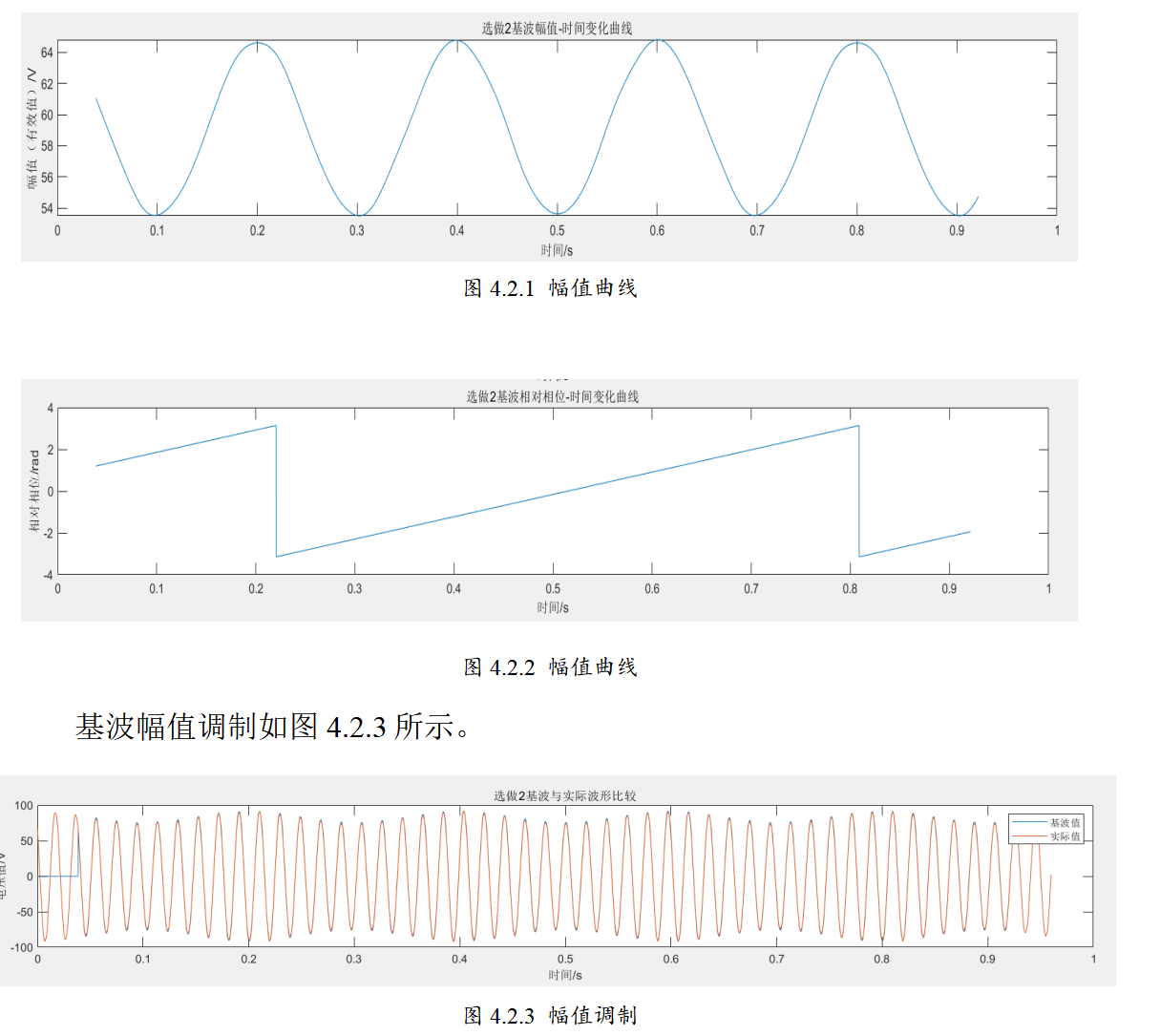
🎉3 参考文献
文章中一些内容引自网络,会注明出处或引用为参考文献,难免有未尽之处,如有不妥,请随时联系删除。
[1]邢海潼,卢梁宇宸,杨旻,电力系统同步相量计算
[2] 王光荣.基于Hilbert变换的信号包络提取方法研究[J].中国科技信息,2012(01):87-88.
[3] 徐佳雄,张明,王阳,程郴,何顺帆.基于改进希尔伯特黄变换的电能质量扰动定位与分类 [J/OL].现代电力:1-8[2021-06-30].https://doi.org/10.19725/j.cnki.1007-2322.2020.0179
[4]文莉,刘正士,葛运建.小波去噪的几种方法[J].合肥工业大学学报(自然科学版),2002(02):167-172.
[5]崔璨,袁英才.窗函数在信号处理中的应用[J].北京印刷学院学报,2014,22(04):71-74+77.DOI:10.19461/j.cnki.1004-8626.2014.04.021.
[6]周西峰,赵蓉,郭前岗.Blackman-Harris窗的插值FFT谐波分析与应用[J].电测与仪表,2014,51(11):81-85.




















 358
358

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








