洛谷 3216 [HNOI2011]数学作业题解（矩阵快速幂）

最新推荐文章于 2021-09-25 14:31:13 发布

原创最新推荐文章于 2021-09-25 14:31:13 发布 · 215 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#题解

洛谷专栏收录该内容

75 篇文章

订阅专栏

本博客介绍如何使用矩阵快速幂解决求1到n连写模m的问题。通过分析123456...n模m的规律，构建矩阵进行转移，并处理指数b的变化，最终给出代码实现。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

原链接
洛谷: 点我QωQ
bzoj：点我QωQ

题意简述

求 $1234567891011121314151617181920\cdots n$ （即 $1$ 到 $n$ 连在一起） $m o d$ $m$ 的值。

数据

输入

第一行两个正整数 $n, m$ ， $n<=10^18$ ， $m<=10^9$

输出

如题意简述。

样例

输入
13 13
输出
4

解释

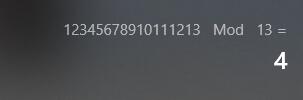
12345678910111213 % 13 = 4

思路

我们会发现，设 $f (n)$ 为 $123456789101112\cdots n\%m$ ，那么 $f(n)=f(n-1)\times 10^b+n$ ，其中 $b$ 是 $n$ 的十进制位长度。我们发现它关系到几个数: $f (n - 1), n, 1$ （先写一个 $1$ 上来，万一过会缺常数呢。。。）。设计出这样的矩阵：
$\times\begin{bmatrix} f(n-1)\\ n-1\\ 1\\ \end{bmatrix}= \begin{bmatrix} f(n-1)\times10^b+(n-1)+1\\ (n-1)+1\\ 1 \end{bmatrix}$
先凑 $S$ 的第一行。根据矩阵的乘法法则，应该是有三个数，设为 $a, b, c$ 。那么应该满足：
$af(n-1)+b(n-1)+c=f(n-1)\times10^b+(n-1)+1$ ，（我就说会缺常数吧。。。所以才多放一个 $1$ 在这里）显然看出一个解
$\begin{cases} a=10^b\\ b=1\\ c=1\\ \end{cases}$
这就凑出了第一行
$\begin{bmatrix} 10^b & 1 & 1 \end{bmatrix}$
用类似的方法，珂以凑出转移矩阵 $S =$
$\begin{bmatrix} 10^b & 1 & 1\\ 0 & 1 & 1\\ 0 & 0 & 1\\ \end{bmatrix}$
但是我们会发现这个 $b$ 特别讨厌：它会随着 $n$ 的增长而变化。那怎么办呢？打到矩阵里？反正我不会。。。（ $b$ 并不是乘上去的，而是作为指数的，所以没法弄）。但是这个 $b$ 增长的很慢，因为 $n<=10^18$ ， $b$ 一共才 $18$ 个取值，那就分块求一下然后合并即可。也没多慢。

代码:

#include<bits/stdc++.h>
using namespace std;
namespace Flandle_Scarlet
{
    #define int long long
    int n,m;
    class Matrix//矩阵(方阵)类
    {
        #define N 5
        private:
            int a[N][N];
        public:
            int n;//矩阵大小
            //初始化部分
            Matrix()
            {
                memset(a,0,sizeof(a));
                n=0;
            }
            Matrix(int _n)
            {
                memset(a,0,sizeof(a));
                n=_n;
            }
            Matrix(int _n,int _x)
            {_x%=m;
                n=_n;
                for(int i=0;i<N;++i)
                {
                    for(int j=0;j<N;++j)
                    {
                        a[i][j]=_x;
                    }
                }
            }

            //取值部分
            int* operator[](int i)
            {
                return *(a+i);
            }

            //设值部分
            void Set(int x)
            {x%=m;
                for(int i=0;i<N;++i)
                {
                    for(int j=0;j<N;++j)
                    {
                        a[i][j]=x;
                    }
                }
            }
            void Identity()
            {
                memset(a,0,sizeof(a));
                for(int i=0;i<N;++i)
                {
                    a[i][i]=1;
                }
            }
            #undef N //5
    };
    Matrix operator*(Matrix x,Matrix y)//矩阵乘法
    {
        Matrix ans(x.n,0);
        int n=ans.n;
        for(int i=1;i<=n;++i)
        {
            for(int j=1;j<=n;++j)
            {
                for(int k=1;k<=n;++k)
                {
                    ans[i][j]+=x[i][k]*y[k][j];
                    ans[i][j]%=m;
                }
            }
        }
        return ans;
    }
    Matrix operator^(Matrix x,int p)//矩阵快速幂
    {
        Matrix ans(x.n,1);
        ans.Identity();
        while(p)
        {
            if (p&1) ans=ans*x;
            x=x*x,p>>=1;
        }
        return ans;
    }

    Matrix ans;
    void calc(int now,int p)//现在的底数是now(就是上面讲的10^b的值)，要算p次方
    {
        Matrix TransMatrix(3,0);//TransMatrix就是S矩阵
        TransMatrix[1][1]=now%m;
        TransMatrix[1][2]=TransMatrix[1][3]=TransMatrix[2][2]=TransMatrix[2][3]=TransMatrix[3][3]=1;

        ans=(TransMatrix^p)*ans;
    }
    void Solve()
    {
        ans.n=3;
        ans.Identity();
        int r=10;
        while(r<=n) calc(r,r-(r/10)),r*=10;
        //r=10^b
        //有b-1个十进制位的自然数应该有10^b-10^(b-1)个,即r-r/10个
        //分块即珂
        calc(r,n-r/10+1);//最后乘上剩余部分
        printf("%lld\n",ans[1][3]);
    }
    void Main()
    {
        if (0)
        {
            freopen("","r",stdin);
            freopen("","w",stdout);
        }
        scanf("%lld%lld",&n,&m);
        Solve();
    }
    #undef int //long long
};
main()
{
    Flandle_Scarlet::Main();
    return 0;
}