洛谷 3140 (USACO2016Dec金组 T2 Circular Barn Revisited) 题解

最新推荐文章于 2025-05-21 22:51:00 发布

原创最新推荐文章于 2025-05-21 22:51:00 发布 · 313 阅读

1 ·

CC 4.0 BY-SA版权

文章标签：

#题解

洛谷专栏收录该内容

75 篇文章

订阅专栏

该博客介绍了USACO2016Dec金组的一道题目，题号为3140。博主详细解析了题意，描述了在环形排列的点上放置源并分配牛的策略，以使总代价达到最小。数据部分展示了输入输出格式。博主提出使用动态规划（DP）解决此问题，初始状态设置以及如何断环成链的方法。博客还提及存在O(n^3k)的时间复杂度解决方案，并提到了更优的O(n^2k)斜率优化策略，但表示自己并未掌握。

题意简述

在一个 $n (n < = 100)$ 个点的环中放置 $k (k < = 7)$ 个源，这 $k$ 个源中每个都珂以按顺时针方向跑出去一些牛，假设这一个源在 $x$ ，跑出去的牛要到 $y$ ，则每头牛代价都是 $∣ x - y ∣$ 。合理分配，使得总代价最少，并且满足顺时针第 $i$ 个点上有 $r_i$ 头牛。

数据

输入
6 2
2
5
4
2
6
2
输出
14

解释

把管辖点放在 $2, 5$ 号点上，然后如图所示分配。

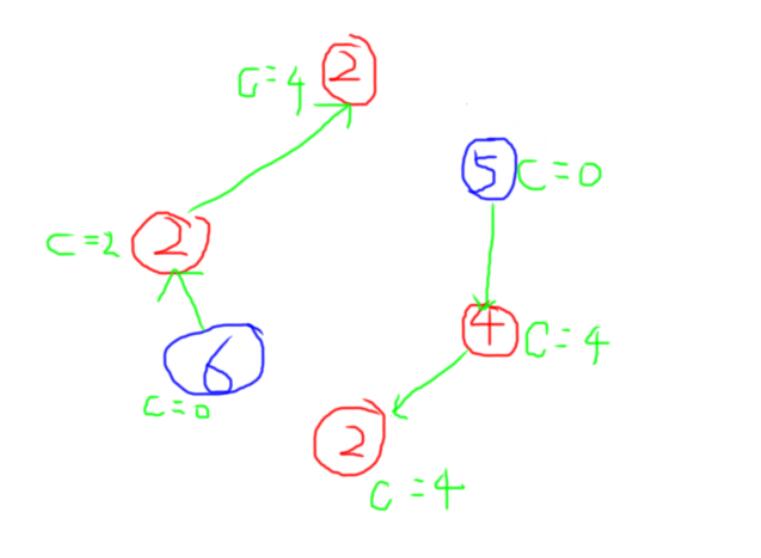
思路

很明显 $D P$ 。由于是顺时针，所以我们是向后考虑。 $d p [i] [k k]$ 表示到点 $i$ ，放 $k k$ （为了防止和给定的 $k$ 重名）个源，的最小代价。如何断环成链。。。只要每次初始化一下 $D P$ 数组，然后用 $r o t a t e ()$ 函数把第一个放到最后面，循环 $n$ 次，就珂以了。

然后一个显然的事实：因为要求最小，所以初始值要设置成 $0 x 3 f$ ，但是 $d p [n + 1] [0] = 0$ ，这个边界别忘了。（忘了样例都过不去）。 $d p [i] [k k]$ 的时候，只要去前面找一个后继节点 $p (p > i)$ ，表示我们在 $p$ 这个位置放了一个源，然后只要暴力统计距离和，然后用 $d p [p] [k k - 1] + s u m$ (就是刚刚求出来的那个距离和) 的值更新 $d p [i] [k k]$ 的值。然后只要求每次滚动时 $d p [1] [k]$ 的最小值即可。

这个是 $O(n^3k)$ 的，对于本题足够了。但是也有 $O(n^2k)$ 的斜率优化做法，~~我不会~~。

代码：

#include<bits/stdc++.h>
#define INF 0x3f3f3f3f3f3f3f3fll
#define int long long
#define N 110
using namespace std;

int n,k;
int r[N];

void Input()
{
    scanf("%lld%lld",&n,&k);
    for(int i=1;i<=n;++i)
    {
        scanf("%lld",&r[i]);
    }
}

int dp[N][8];
void upmin(int &x,int y)//用y更新x的最小值
{
    x=min(x,y);
}
void DP()
{
    int ans=INF;
    for(int i=1;i<=n;++i)
    {
        memset(dp,0x3f,sizeof(dp));
        dp[n+1][0]=0;//边界别忘了

        for(int kk=1;kk<=k;++kk)
        {
            for(int j=1;j<=n;++j)
            {
                int sum=0;
                for(int p=j+1;p<=n+1;++p)
                {
                    sum+=r[p-1]*(p-j-1);
                    upmin(dp[j][kk],dp[p][kk-1]+sum);//状态转移方程
                }
            }
        }
        upmin(ans,dp[1][k]);//ans取dp[1][k]中的最小值
        rotate(r+1,r+2,r+n+1);
    }
    printf("%lld\n",ans);
}

main()
{
    if (0)
    {
        freopen("cbarn2.in","r",stdin);
        freopen("cbarn2.out","w",stdout);
    }
    Input();
    DP();
    return 0;
}