Day 17 常见聚类算法

最新推荐文章于 2025-11-24 15:27:14 发布

原创最新推荐文章于 2025-11-24 15:27:14 发布 · 798 阅读

24 ·

CC 4.0 BY-SA版权

文章标签：

#聚类 #机器学习 #python

Python打卡训练营专栏收录该内容

52 篇文章

订阅专栏

@浙大疏锦行

今日任务：

聚类的指标
聚类常见算法：kmeans聚类、dbscan聚类、层次聚类
三种算法对应的流程
对心脏病数据集进行聚类。

与回归、分类问题不同，聚类属于无监督算法，也就是只有特征而没有标签。聚类常用来发现数据中的模式，并对每一个聚类特征进行可视化操作，以此得到新的特征（赋予实际含义）。

聚类评估指标

对于聚类算法，有三种常见的评估指标：轮廓系数、CH指数及DB指数。

轮廓系数（Silhouette Score）

用于衡量一个样本点与其所属簇的匹配程度，即该样本是否位于其“应该属于”的簇中。

核心思想（对于任意一个样本i）：

凝聚度：该样本与同簇内所有其它样本的平均距离 a(i)，a(i)越小，说明该样本应该被分到这个簇。
分离度：该样本与其它某个簇所有样本的平均距离中的最小值 b(i)，这个最近的簇被称为该样本的“邻近簇”。b(i) 越小，说明该样本越有可能属于这个邻近簇。
轮廓系数： $s(i) = \frac{b(i)-a(i)}{max\left \{ a(i),b(i) \right \}}$ ，取值范围[-1,1]。若s(i)≈1，说明 a(i)≪b(i)，样本 i 的凝聚度远小于分离度，意味着该样本被分配到了非常合适的簇中。s(i)≈0，说明 a(i)≈b(i)，簇内距离和簇间距离差不多，该样本处于两个簇的边界上，分配不明确。s(i)≈−1，说明 a(i)≫b(i)，样本 i 到其他簇的距离比到本簇的距离还近，说明该样本很可能被分配到了错误的簇中。
最终得分：将所有样本的轮廓系数求平均，得到整个数据集的平均轮廓系数，用于评估整体聚类质量。
选择轮廓系数最高的 `k` 值作为最佳簇数量

CH指数（Calinski-Harabasz Index）

CH指数，又称方差比标准，通过簇间离散度与簇内离散度的比值来衡量聚类效果。

核心思想：

簇内离散度小：同一个簇内的点尽可能紧凑。
簇间离散度大：不同簇之间的点尽可能分离。
CH指数： $CH\left ( k \right ) = \frac{\frac{B_{k}}{k-1}}{\frac{W_{k}}{n-k}}$ 。CH指数越大，说明簇间离散度大，簇内离散度小，聚类效果好。
选择 CH 指数最高的 `k` 值作为最佳簇数量

DB指数（Davies-Bouldin Index）

计算任意两个不同簇之间的平均“相似度”。这里的“相似度”是一个不好的东西，我们希望它越小越好。

核心思想：

首先，计算每个簇 $C_{i}$ 内所有样本到其质心的平均距离，记为 $S_{i}$ ，这代表了簇 ii 的散度。
然后，计算簇 i 和簇 j 的质心之间的距离，记为 $d_{ij}$ 。
定义簇 i 和簇 j 之间的“相似度” $R_{ij}$ 为：

$R_{ij} = \frac{S_{i}+S_{j}}{d_{ij}}$

这个公式很直观：分子（两个簇的散度之和）越大，说明两个簇自身越分散；分母（簇间距离）越小，说明两个簇靠得越近。因此， $R_{ij}$ 越大，说明这两个簇的区分度越差。

对于每个簇 ii，找到与之最“相似”（即 $R_{ij}$ 最大）的那个簇 j（j≠i），记为Di
最后，DB指数是所有 Di的平均值：
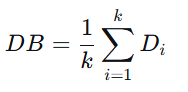
选择 DB 指数最低的 `k` 值作为最佳簇数量。

下面是三种指标的对比，实际中需要结合多个指标来综合判断聚类质量：

指标	核心思想	评估标准	优点	缺点
轮廓系数	衡量每个样本点与自身簇和其他簇的关系	越大越好，范围[-1,1]	直观，对样本点有解释性	计算成本高，对非凸簇效果差
CH指数	簇间方差与簇内方差的比值	越大越好	计算快，对凸形簇效果好	对簇大小敏感，对非凸簇效果差
DB指数	任意两簇之间的平均“相似度”	越小越好	计算简单，定义清晰	依赖于质心距离，对非球形簇效果差

KMeans聚类

K-Means是一个以距离（欧几里得距离）为尺度，通过迭代的分配和更新步骤，将数据划分为指定数量 kk 个簇的聚类算法。

原理

将数据集中的 n 个样本点划分为 k 个簇，使得同一个簇内的样本点彼此非常相似（紧凑），而不同簇之间的样本点尽可能不相似（分离）。KMeans算法是一个迭代过程，包括两个核心步骤：分配和更新。

具体而言：

随机选择 `k` 个样本点作为初始质心（簇中心）。
计算每个样本点到各个质心的距离，将样本点分配到距离最近的质心所在的簇。
更新每个簇的质心为该簇内所有样本点的均值。
重复步骤 2 和 3，直到质心不再变化或达到最大迭代次数为止。

肘部法

由于使用KMeans算法时，需要预先设定k值，但是如何确定一个好的k值，可以通过"肘部法则"解决。

计算步骤：

运行K-Means：对一系列不同的 k 值（例如，从 k=1 到 k=10），分别运行K-Means算法。
计算WCSS：对于每一个 k 值，计算并记录其对应的WCSS（簇内平方和）。
绘制曲线图：以 k 值为横坐标，以对应的WCSS值为纵坐标，绘制一条曲线。
寻找“肘点”：观察绘制的曲线，找到一个点，在这个点之后，WCSS的下降速度突然由快变慢。这个形状看起来像人的手臂和手肘，该点即为“肘点”。
“肘点”对应的 k 值就是推荐的聚类数量。

那么具体怎么看图确定，最佳的k值呢？需要综合考虑：

肘部法则图：找下降速率变慢的拐点
轮廓系数图：找局部最高点
CH指数图：找局部最高点
DB指数图：找局部最低点

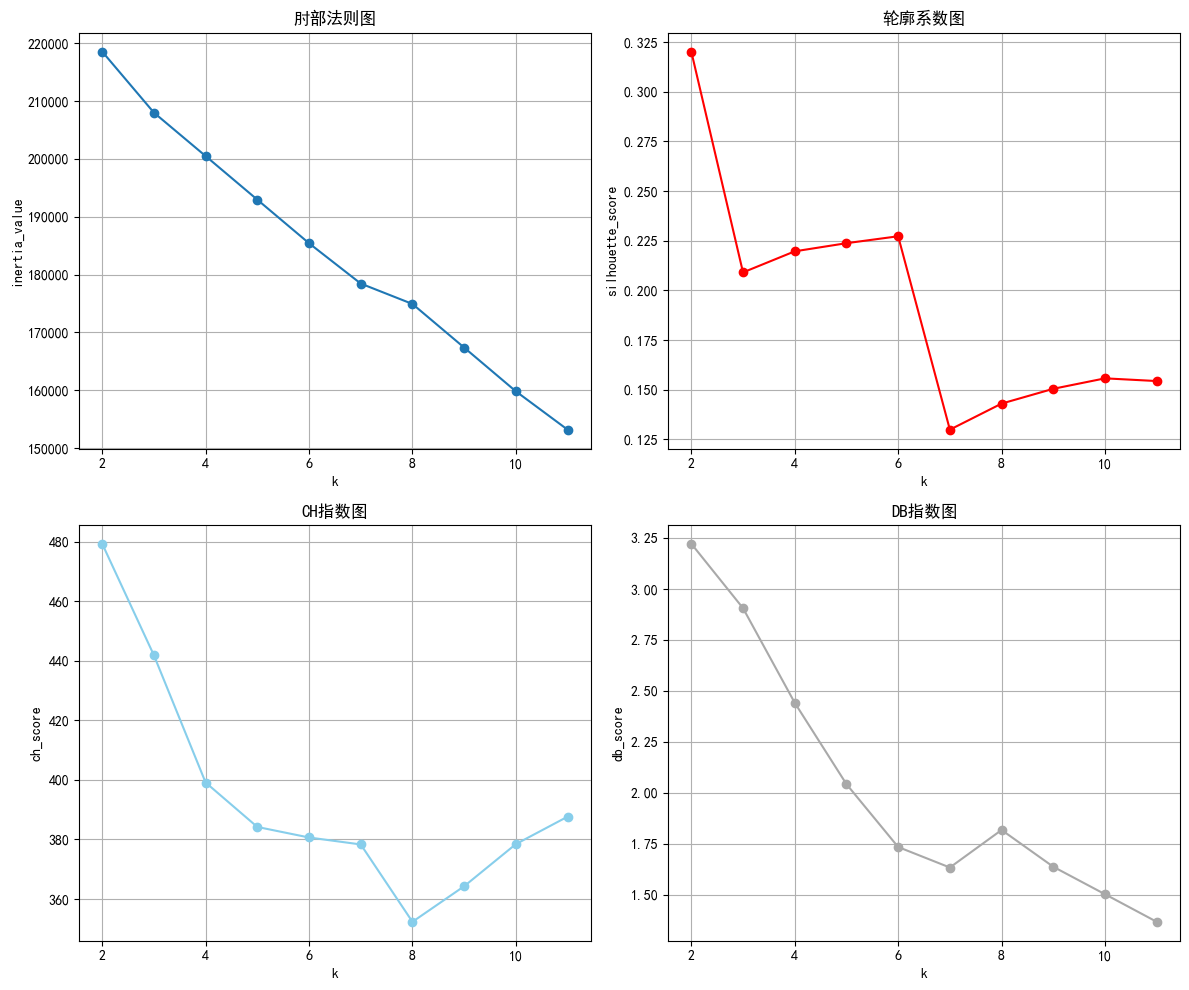
为什么选择局部最优的点？因为比如簇间差异，分得越细越好，但是k太细了没价值，所以要有取舍。

接下来说明KMeans算法的流程：

准备工作：不同k值的序列；存放惯性值、轮廓系数、CH指数及DB指数的空列表
循环遍历：实例化、训练后得到分类标签，得到每个k值下的相应的评估指标
可视化：绘制k值与惯性值、轮廓系数、CH指数、DB指数的图
综合考虑，选择最佳的k
利用最佳的k值重新训练模型进行聚类
PCA降维可视化：降维到2D，将聚类结果可视化

#评估不同k下的指标
k_values = range(2,12)
inertia_score = []
silhouette_scores = []
ch_scores = []
db_scores = []

#循环遍历
for i in k_values:
    kmeans = KMeans(n_clusters=i,random_state=42)
    kmeans_labels = kmeans.fit_predict(X_scaled)
    #惯性，肘部法则
    inertia_score.append(kmeans.inertia_) 
    #轮廓系数
    silhouette = silhouette_score(X=X_scaled,labels=kmeans_labels)
    silhouette_scores.append(silhouette)
    #CH指数
    ch = calinski_harabasz_score(X=X_scaled,labels=kmeans_labels)
    ch_scores.append(ch)
    #DB指数
    db = davies_bouldin_score(X=X_scaled,labels=kmeans_labels)
    db_scores.append(db)

#可视化
plt.figure(figsize=(12,10))

#子图的绘制方法
plt.subplot(2,2,1) #绘制2行2列中的第一个子图
plt.plot(k_values,inertia_score,marker='o')
plt.title('肘部法则图')
plt.xlabel('k')
plt.ylabel('inertia_value')
plt.grid(True) #显示网格

plt.subplot(2,2,2) #绘制2行2列中的第二个子图
plt.plot(k_values,silhouette_scores,marker='o',color='red')
plt.title('轮廓系数图')
plt.xlabel('k')
plt.ylabel('silhouette_score')
plt.grid(True)

plt.subplot(2,2,3) #绘制2行2列中的第三个子图
plt.plot(k_values,ch_scores,marker='o',color='skyblue')
plt.title('CH指数图')
plt.xlabel('k')
plt.ylabel('ch_score')
plt.grid(True)

plt.subplot(2,2,4) #绘制2行2列中的第四个子图
plt.plot(k_values,db_scores,marker='o',color='darkgrey')
plt.title('DB指数图')
plt.xlabel('k')
plt.ylabel('db_score')
plt.grid(True)

plt.tight_layout()
plt.show()

#PCA降维可视化
select_k = 6

#训练
kmeans = KMeans(n_clusters=select_k,random_state=42)
k_labels = kmeans.fit_predict(X_scaled)

#PCA降维到2D
pca = PCA(n_components=2) #实例化
x_pca = pca.fit_transform(X_scaled) #训练

#可视化
plt.figure(figsize=(8,6))
sns.scatterplot(x=x_pca[:,0],y=x_pca[:,1],hue=k_labels, palette='viridis')
plt.title(f'KMeans Clustering with k={select_k} (PCA Visualization)')
plt.xlabel('PCA Component 1')
plt.ylabel('PCA Component 2')
plt.show()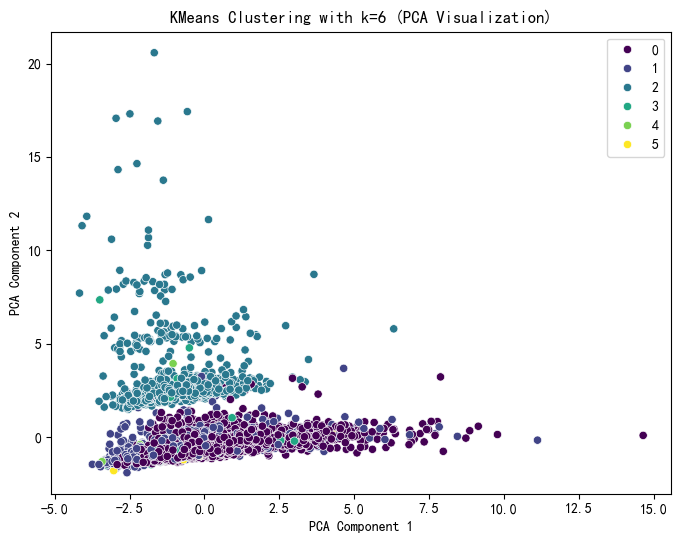

优缺点

KMeans算法的优点是简单高效、适用性强以及易于解释。缺点是需预先指定k值、对初始质心和噪声、异常值敏感以及不适合非球形簇。

DBSCAN聚类

DBSCAN（Density-Based Spatial Clustering of Applications with Noise）是一种基于密度的聚类算法。

相关概念，两个关键参数和三种类型的点：

eps，邻域半径；通过k距离图确定，拐点
min_samples，核心点所需的最小邻居数；小数据集，一般取4，大数据集，一般为数据维度的2倍
核心点、边界点、噪声点
正整数代表不同的聚类，-1代表噪声点

关于DBSCAN的工作流程：

随机选择未访问的点
查找eps邻域内的所有点
判断是否为核心点
如果是核心点，扩展形成聚类
重复直到所有点被访问

# 评估不同 eps 和 min_samples 下的指标
# eps这个参数表示邻域的半径，min_samples表示一个点被认为是核心点所需的最小样本数。
# min_samples这个参数表示一个核心点所需的最小样本数。

eps_range = np.arange(0.3, 0.8, 0.1)  # 测试 eps 从 0.3 到 0.7
min_samples_range = range(3, 8)  # 测试 min_samples 从 3 到 7
results = []

for eps in eps_range:
    for min_samples in min_samples_range:
        dbscan = DBSCAN(eps=eps, min_samples=min_samples)
        dbscan_labels = dbscan.fit_predict(X_scaled)
        # 计算簇的数量（排除噪声点 -1）
        n_clusters = len(np.unique(dbscan_labels)) - (1 if -1 in dbscan_labels else 0)
        # 计算噪声点数量
        n_noise = list(dbscan_labels).count(-1)
        # 只有当簇数量大于 1 且有有效簇时才计算评估指标
        if n_clusters > 1:
            # 排除噪声点后计算评估指标
            mask = dbscan_labels != -1
            if mask.sum() > 0:  # 确保有非噪声点
                silhouette = silhouette_score(X_scaled[mask], dbscan_labels[mask])
                ch = calinski_harabasz_score(X_scaled[mask], dbscan_labels[mask])
                db = davies_bouldin_score(X_scaled[mask], dbscan_labels[mask])
                results.append({
                    'eps': eps,
                    'min_samples': min_samples,
                    'n_clusters': n_clusters,
                    'n_noise': n_noise,
                    'silhouette': silhouette,
                    'ch_score': ch,
                    'db_score': db
                })
                print(f"eps={eps:.1f}, min_samples={min_samples}, 簇数: {n_clusters}, 噪声点: {n_noise}, "
                      f"轮廓系数: {silhouette:.3f}, CH 指数: {ch:.2f}, DB 指数: {db:.3f}")
        else:
            print(f"eps={eps:.1f}, min_samples={min_samples}, 簇数: {n_clusters}, 噪声点: {n_noise}, 无法计算评估指标")

# 将结果转为 DataFrame 以便可视化和选择参数
results_df = pd.DataFrame(results)

在上面的代码中，要注意以下几点：

使用循环遍历的方法确定参数
簇的实际数量的计算：需要排除噪声点（-1），np.unique()
有效簇大于1时计算评估指标：这里使用了布尔掩码（mask = dbscan_labels != -1）。布尔掩码就是一个由 True 和 False 组成的数组，用来标记哪些元素满足某个条件。使用布尔掩码可以完成对元素的筛选，例如X_scaled[mask]（得到非噪声数据）

最佳参数可视化：

# 绘制评估指标图，增加点论文中的工作量
plt.figure(figsize=(15, 10))
# 轮廓系数图
plt.subplot(2, 2, 1)
for min_samples in min_samples_range:
    subset = results_df[results_df['min_samples'] == min_samples] # 
    plt.plot(subset['eps'], subset['silhouette'], marker='o', label=f'min_samples={min_samples}')
plt.title('轮廓系数确定最优参数（越大越好）')
plt.xlabel('eps')
plt.ylabel('轮廓系数')
plt.legend()
plt.grid(True)

# CH 指数图
plt.subplot(2, 2, 2)
for min_samples in min_samples_range:
    subset = results_df[results_df['min_samples'] == min_samples] # results_df[results_df['min_samples'] == min_samples]  #
    plt.plot(subset['eps'], subset['ch_score'], marker='o', label=f'min_samples={min_samples}')
plt.title('Calinski-Harabasz 指数确定最优参数（越大越好）')
plt.xlabel('eps')
plt.ylabel('CH 指数')
plt.legend()
plt.grid(True)

# DB 指数图
plt.subplot(2, 2, 3)
for min_samples in min_samples_range:
    subset = results_df[results_df['min_samples'] == min_samples]
    plt.plot(subset['eps'], subset['db_score'], marker='o', label=f'min_samples={min_samples}')
plt.title('Davies-Bouldin 指数确定最优参数（越小越好）')
plt.xlabel('eps')
plt.ylabel('DB 指数')
plt.legend()
plt.grid(True)

# 簇数量图
plt.subplot(2, 2, 4)
for min_samples in min_samples_range:
    subset = results_df[results_df['min_samples'] == min_samples]
    plt.plot(subset['eps'], subset['n_clusters'], marker='o', label=f'min_samples={min_samples}')
plt.title('簇数量变化')
plt.xlabel('eps')
plt.ylabel('簇数量')
plt.legend()
plt.grid(True)

plt.tight_layout()
plt.show()

得到最佳参数后，与KMeans类似使用PCA降维到2D将聚类结果可视化。

#PCA降维可视化
#最佳参数
selected_eps = 0.6
selected_min_samples = 6

#训练
dbscan = DBSCAN(eps = selected_eps,min_samples=selected_min_sampls)
db_labels = dbscan.fit_predict(X_scaled)

#PCA降维到2D
pca = PCA(n_components=2) #实例化
x_pca = pca.fit_transform(X_scaled) #训练

#可视化
plt.figure(figsize=(8,6))
sns.scatterplot(x=x_pca[:,0],y=x_pca[:,1],hue=db_labels, palette='viridis')
plt.title(f'DBSCAN Clustering with k={select_k} (PCA Visualization)')
plt.xlabel('PCA Component 1')
plt.ylabel('PCA Component 2')
plt.show()

层次聚类

层次聚类是一种通过层层分解或层层聚合来构建聚类层次结构的算法。与K-Means需要预先指定聚类数量不同，层次聚类会生成一个完整的聚类树（树状图）。

包括两种主要方法：

凝聚式层次聚类（Agglomerative）：自底向上。从每个点作为一个聚类开始，逐步合并最相似的聚类。
分裂式层次聚类（Divisive）：自顶向下。从所有点作为一个聚类开始，逐步分裂成更小的聚类。

这里使用的是凝聚式层次聚类，确定最佳初始簇的数量的流程与KMeans类似。即给定范围，遍历，使用评估指标评估，可视化，综合考虑选择最佳。

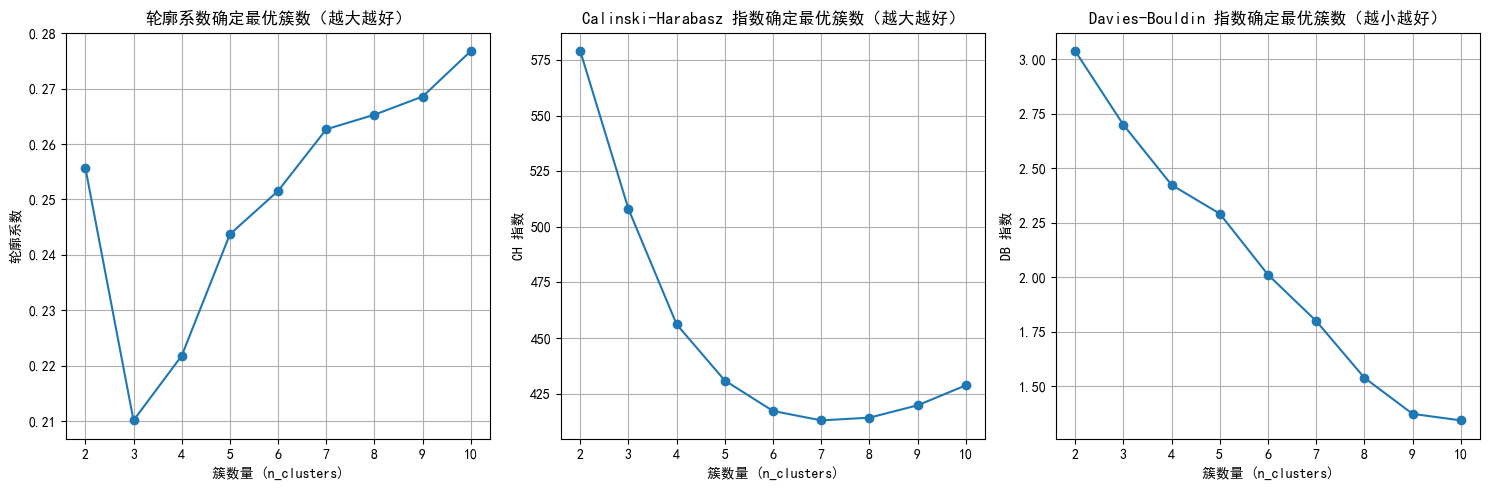
同样地，使用PCA降维可视化聚类结果：

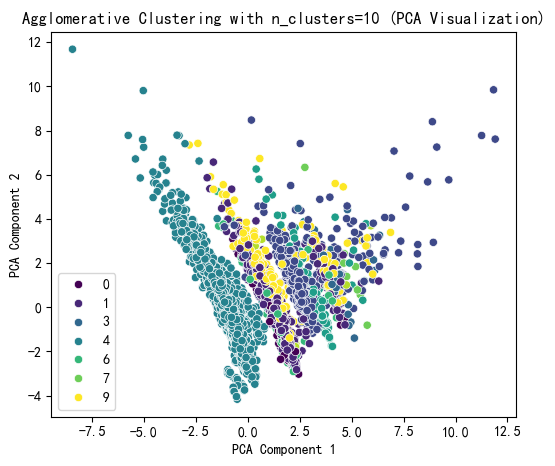
下面是三种聚类算法的对比：

算法	优点	缺点
K-Means	• 计算速度快 • 适合大数据集 • 结果相对稳定	• 需要指定K值 • 对初始值敏感 • 只能发现球形聚类 • 对噪声敏感
DBSCAN	• 不需要指定K值 • 能发现任意形状 • 对噪声鲁棒 • 能识别异常点	• 对参数敏感 • 密度不均匀时效果差 • 高维数据效果下降
层次聚类	• 不需要指定K值 • 结果可解释性强 • 提供层次信息 • 对数据分布无假设	• 计算复杂度高 • 对噪声敏感 • 合并决策不可逆 • 不适合大数据集

作业：心脏病数据集聚类

import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

# 设置中文字体（解决中文显示问题）
plt.rcParams['font.sans-serif'] = ['SimHei']  # Windows系统常用黑体字体
plt.rcParams['axes.unicode_minus'] = False    # 正常显示负号
#读取数据
data = pd.read_csv(r'heart.csv')
data.head() #读取前5行

#对于多分类特征进行独热编码
continous_features = ['age','trestbps','chol','thalach','oldpeak']
discrete_features = ['sex','cp','fbs','restecg','exang','slope','thal']
multi_features = ['cp','restecg','slope','thal']
data = pd.get_dummies(data=data,columns=multi_features,prefix=multi_features) #返回的是新的dataframe+编码列
data.head()

#对连续特征进行标准化
from sklearn.preprocessing import StandardScaler
standard_scaler = StandardScaler() #实例化
data[continous_features] = standard_scaler.fit_transform(data[continous_features])
data[continous_features].head()

#标签和特征
X = data.drop(['target'],axis=1)
y = data['target']

from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(X,y,train_size=0.7,random_state=42)

import numpy as np
from sklearn.cluster import KMeans, DBSCAN, AgglomerativeClustering
from sklearn.decomposition import PCA
from sklearn.metrics import silhouette_score,calinski_harabasz_score,davies_bouldin_score

#评估不同k下的指标
k_values = range(2,12)
inertia_score = []
silhouette_scores = []
ch_scores = []
db_scores = []

#循环遍历
for i in k_values:
    kmeans = KMeans(n_clusters=i,random_state=42)
    kmeans_labels = kmeans.fit_predict(X)
    #惯性，肘部法则
    inertia_score.append(kmeans.inertia_) 
    #轮廓系数
    silhouette = silhouette_score(X=X,labels=kmeans_labels)
    silhouette_scores.append(silhouette)
    #CH指数
    ch = calinski_harabasz_score(X=X,labels=kmeans_labels)
    ch_scores.append(ch)
    #DB指数
    db = davies_bouldin_score(X=X,labels=kmeans_labels)
    db_scores.append(db)

#可视化
plt.figure(figsize=(12,10))

#子图的绘制方法
plt.subplot(2,2,1) #绘制2行2列中的第一个子图
plt.plot(k_values,inertia_score,marker='o')
plt.title('肘部法则图')
plt.xlabel('k')
plt.ylabel('inertia_value')
plt.grid(True) #显示网格

plt.subplot(2,2,2) #绘制2行2列中的第二个子图
plt.plot(k_values,silhouette_scores,marker='o',color='red')
plt.title('轮廓系数图')
plt.xlabel('k')
plt.ylabel('silhouette_score')
plt.grid(True)

plt.subplot(2,2,3) #绘制2行2列中的第三个子图
plt.plot(k_values,ch_scores,marker='o',color='skyblue')
plt.title('CH指数图')
plt.xlabel('k')
plt.ylabel('ch_score')
plt.grid(True)

plt.subplot(2,2,4) #绘制2行2列中的第四个子图
plt.plot(k_values,db_scores,marker='o',color='darkgrey')
plt.title('DB指数图')
plt.xlabel('k')
plt.ylabel('db_score')
plt.grid(True)

plt.tight_layout()
plt.show()

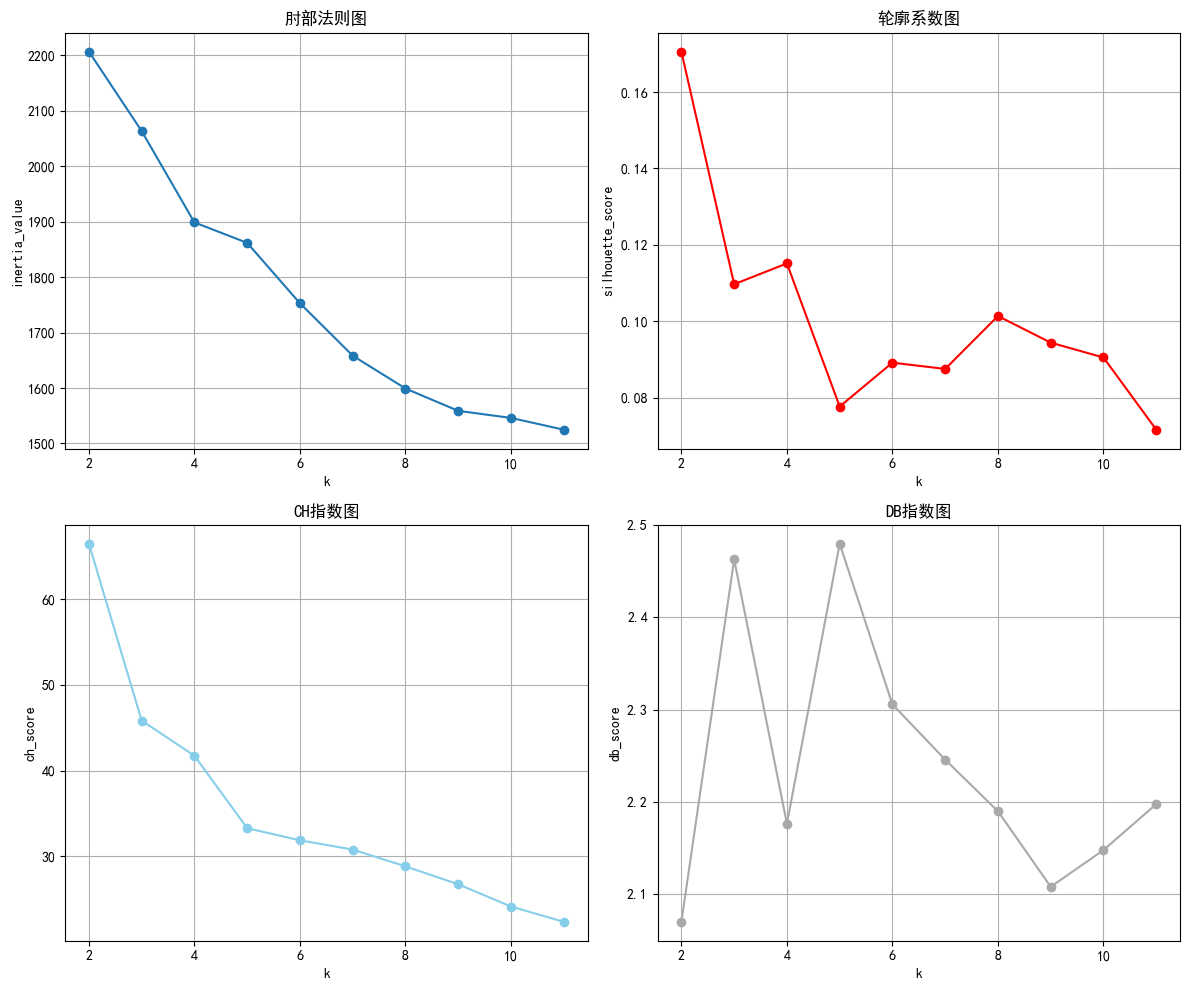
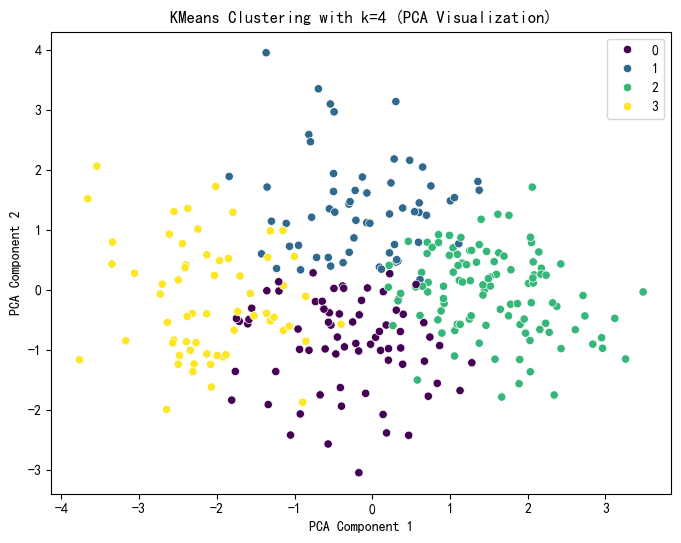
#PCA降维可视化
select_k = 4

#训练
kmeans = KMeans(n_clusters=select_k,random_state=42)
k_labels = kmeans.fit_predict(X)

#PCA降维到2D
pca = PCA(n_components=2) #实例化
x_pca = pca.fit_transform(X) #训练

#可视化
plt.figure(figsize=(8,6))
sns.scatterplot(x=x_pca[:,0],y=x_pca[:,1],hue=k_labels, palette='viridis')
plt.title(f'KMeans Clustering with k={select_k} (PCA Visualization)')
plt.xlabel('PCA Component 1')
plt.ylabel('PCA Component 2')
plt.show()