Day 18 推断聚类后簇的类型

最新推荐文章于 2025-11-24 19:50:57 发布

原创最新推荐文章于 2025-11-24 19:50:57 发布 · 639 阅读

24 ·

CC 4.0 BY-SA版权

文章标签：

#聚类 #机器学习 #python

Python打卡训练营专栏收录该内容

51 篇文章

订阅专栏

@浙大疏锦行

今日任务：

推断簇含义的2个思路：先选特征和后选特征
通过可视化图形借助ai定义簇的含义
通过精度判断特征工程价值
参考示例代码对心脏病数据集采取类似操作，并且评估特征工程后模型效果有无提升。

在Day 17 的学习中，了解了三种聚类算法的使用。但是如果仅得到聚类后的结果而不赋予实际含义，那么聚类将毫无意义。聚类回答了“是什么”的问题，而给聚类标签赋予实际意义则解决“为什么”的问题。

在赋予实际意义之前，需要有特定的特征，但是这个特征如何确定？

目前常用的思路有两种，分别是目标明确的设计型聚类和探索驱动的解释型聚类：

设计型：在聚类之前，根据背景知识选定研究目标，进而确定选取的特征，用来确定簇含义。
解释型：聚类前不知道目的，尝试用探索的方式找到一些现象。因而选择使用全部特征进行聚类后，再将某特征聚类后得到的簇类别作为标签y，其余特征作为x，通过重要性排序得到关键特征，再赋予其含义。

在实际使用的过程中，可以将两种思路相结合：先采取思路二进行全面的筛选与探索，然后利用思路一进行深入的设计。

下面通过信贷数据集，进行思路2的实操。

KMeans聚类

将经过预处理的数据（注意标准化），对所有特征进行KMeans算法聚类（确定最佳k值）

#标准化数据
from sklearn.preprocessing import StandardScaler
standard_scacler = StandardScaler()
X_scaled = standard_scacler.fit_transform(X)
#划分数据集
from sklearn.model_selection import train_test_split
X = data.drop(['Credit Default'], axis=1)  # 特征，axis=1表示按列删除
y = data['Credit Default'] # 标签
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)  # 80%训练集，20%测试集

from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score,calinski_harabasz_score,davies_bouldin_score
from sklearn.decomposition import PCA

#最佳k值的确定
k_range = range(2,11) #定义k的取值范围
inertia_scores = []
silhouette_scores = []
ch_scores = []
db_scores = []

for k in k_range:
    kmeans = KMeans(n_clusters=k,random_state=42) #实例化
    k_labels = kmeans.fit_predict(X_scaled) #训练
    #计算评估指标
    inertia = kmeans.inertia_ #惯性值
    silhouette = silhouette_score(X_scaled,k_labels)
    ch_score = calinski_harabasz_score(X_scaled,k_labels)
    db_score = davies_bouldin_score(X_scaled,k_labels)
    #添加
    inertia_scores.append(inertia) 
    silhouette_scores.append(silhouette)
    ch_scores.append(ch_score)
    db_scores.append(db_score)
    #打印参数
    print(f'k={k},惯性:{inertia:.2f}, 轮廓系数:{silhouette:.2f}, CH指数:{ch_score:.2f}, DB指数:{db_score:.2f}')


#可视化
plt.figure(figsize=(12,10))

#k与惯性
plt.subplot(2,2,1)
plt.plot(k_range,inertia_scores,marker='o')
plt.title('肘部法则')
plt.xlabel('k')
plt.ylabel('inertia_score')
plt.grid(True)

# 轮廓系数图
plt.subplot(2, 2, 2)
plt.plot(k_range, silhouette_scores, marker='o', color='orange')
plt.title('轮廓系数确定最优聚类数 k（越大越好）')
plt.xlabel('聚类数 (k)')
plt.ylabel('轮廓系数')
plt.grid(True)

# CH 指数图
plt.subplot(2, 2, 3)
plt.plot(k_range, ch_scores, marker='o', color='green')
plt.title('Calinski-Harabasz 指数确定最优聚类数 k（越大越好）')
plt.xlabel('聚类数 (k)')
plt.ylabel('CH 指数')
plt.grid(True)

# DB 指数图
plt.subplot(2, 2, 4)
plt.plot(k_range, db_scores, marker='o', color='red')
plt.title('Davies-Bouldin 指数确定最优聚类数 k（越小越好）')
plt.xlabel('聚类数 (k)')
plt.ylabel('DB 指数')
plt.grid(True)

plt.tight_layout()
plt.show()

#根据最佳的k值进行训练，并使用PCA降维可视化
selected_k = 3 #此处便于后续分析，选择数值3，实际不是最佳值
#建模训练
kmeans = KMeans(n_clusters=selected_k,random_state=42)
k_labels = kmeans.fit_predict(X_scaled)
X['Kmeans_clusters'] = k_labels #将聚类结果添加入原始数据
#PCA降维到2D
pca = PCA(n_components=2) 
x_pca = pca.fit_transform(X_scaled)
#可视化
sns.scatterplot(x=x_pca[:,0],y=x_pca[:,1],hue=k_labels,palette='viridis')
plt.xlabel('pca_component_1')
plt.ylabel('pca_component_2')
plt.show()

建模训练与特征筛选

将聚类后的簇类别作为标签y，剩余特征作为x。然后选择模型进行训练，借助shap库进行特征重要性的排序。

#特征筛选
#特征与标签划分
x1 = X.drop(columns=['Kmeans_clusters'],axis=1)
y1 = X['Kmeans_clusters']
from sklearn.ensemble import RandomForestClassifier
rf_model = RandomForestClassifier(random_state=42) #实例化
rf_model.fit(x1,y1) #训练

import shap
explainer = shap.TreeExplainer(model=rf_model) #初始化解释器
shap_values = explainer.shap_values(X=x1) #计算shap值

#绘图
shap.initjs()#初始化JavaScript可视化功能，确保后续可视化图表正常工作
shap.summary_plot(shap_values[:,:,0],x1,plot_type='bar',show=False)
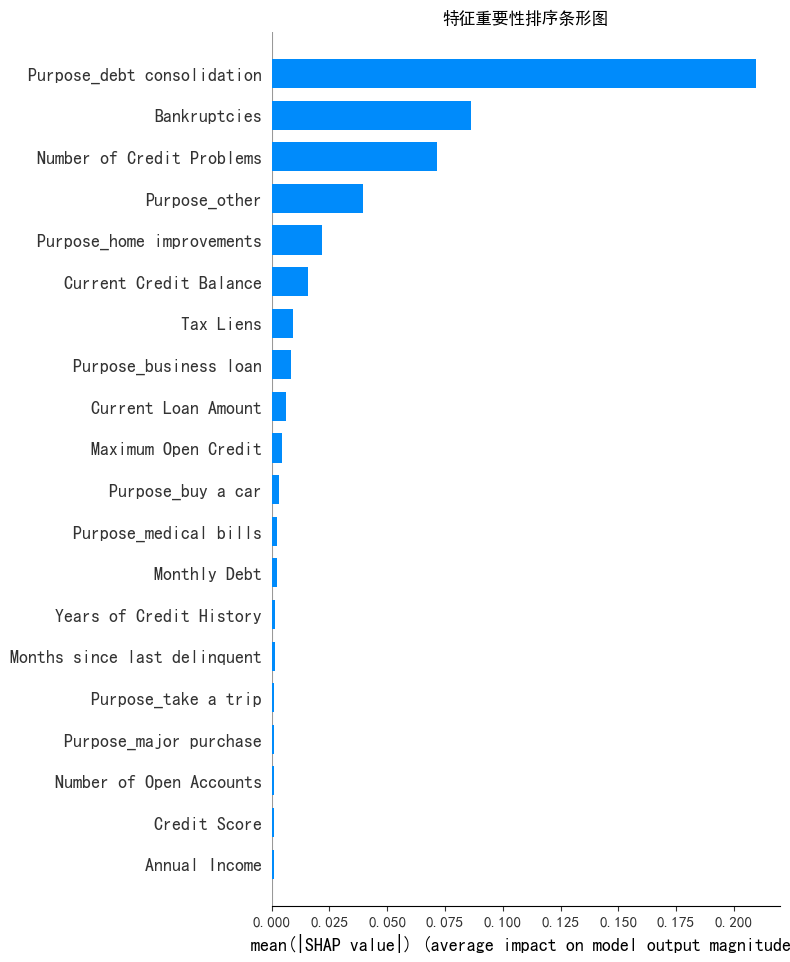
plt.title('特征重要性排序条形图')
plt.show()

通过特征重要性条形图可以发现，前几个特征的shap值较高。为方便后续画图，选取前4个特征。这里判断了这几个特征的数据类型，可能是为了后续可视化特征分布的图形选择。

#特征的数据类型判断
selected_features = ['Purpose_debt consolidation','Bankruptcies','Number of Credit Problems','Purpose_other']
#判断特征为离散型还是连续型
for i in selected_features:
    unique_counts = X[i].nunique() # 唯一值指的是在某一列或某个特征中，不重复出现的值
    print(f'{i}有{unique_counts}个变量') # 连续型变量通常有很多唯一值，而离散型变量的唯一值较少
    if unique_counts < 10: # 这里 10 是一个经验阈值，可以根据实际情况调整
        print(f'{i}为离散特征')
    else:
        print(f'{i}为连续特征')

可视化与含义赋予

找到关键特征后，需要将每个簇别对应的特征分布展示出来，从而分析其中的特点，得到对应的“用户画像”。

具体而言，先筛选出不同簇的DataFrame，然后分别绘制对应的特征分布图即可。

#提取不同的簇别
x_cluster0 = X[X['Kmeans_clusters']==0]
x_cluster1 = X[X['Kmeans_clusters']==1]
x_cluster2 = X[X['Kmeans_clusters']==2]

#可视化簇别
#簇别0
fig,axes = plt.subplots(2,2,figsize=(12,10))
axes = axes.flatten()

for index,value in enumerate(selected_features):
    sns.histplot(x_cluster0[value],ax=axes[index],bins=20)#使用countplot,由于float型，导致跑得很慢
    axes[index].set_xlabel(f'{value}')
    axes[index].set_title(f'The Countplot of {value}')

plt.tight_layout()
plt.show()

#可视化簇别
#簇别1
fig,axes = plt.subplots(2,2,figsize=(12,10))
axes = axes.flatten()

for index,value in enumerate(selected_features):
    sns.histplot(x_cluster1[value],ax=axes[index],bins=20)#使用countplot,由于float型，导致跑得很慢
    axes[index].set_xlabel(f'{value}')
    axes[index].set_title(f'The Countplot of {value}')

plt.tight_layout()
plt.show()

#可视化簇别
#簇别2
fig,axes = plt.subplots(2,2,figsize=(12,10))
axes = axes.flatten()

for index,value in enumerate(selected_features):
    sns.histplot(x_cluster2[value],ax=axes[index],bins=20)#使用countplot,由于float型，导致跑得很慢
    axes[index].set_xlabel(f'{value}')
    axes[index].set_title(f'The Countplot of {value}')

plt.tight_layout()
plt.show()

完成可视化操作后，就需要对图进行分析，无论是借助自己的相关知识还是AI辅助分析，最终基本上可以得到不同簇别的特点，从而构建新的标签。后续只需按照之前的步骤进行处理（独热编码），建模训练，对比特征提取前后的效果，看模型的精度是否有所提高。

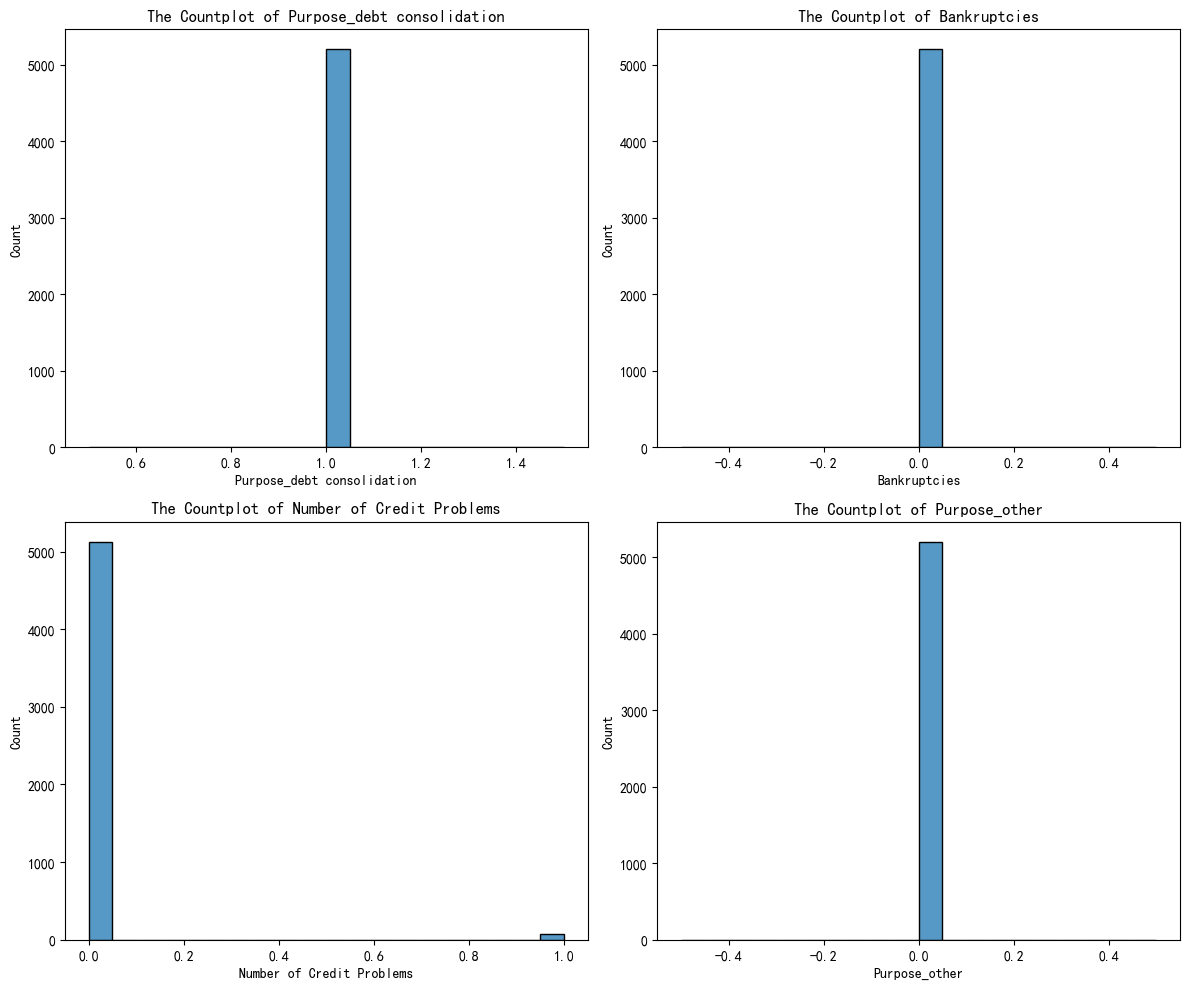
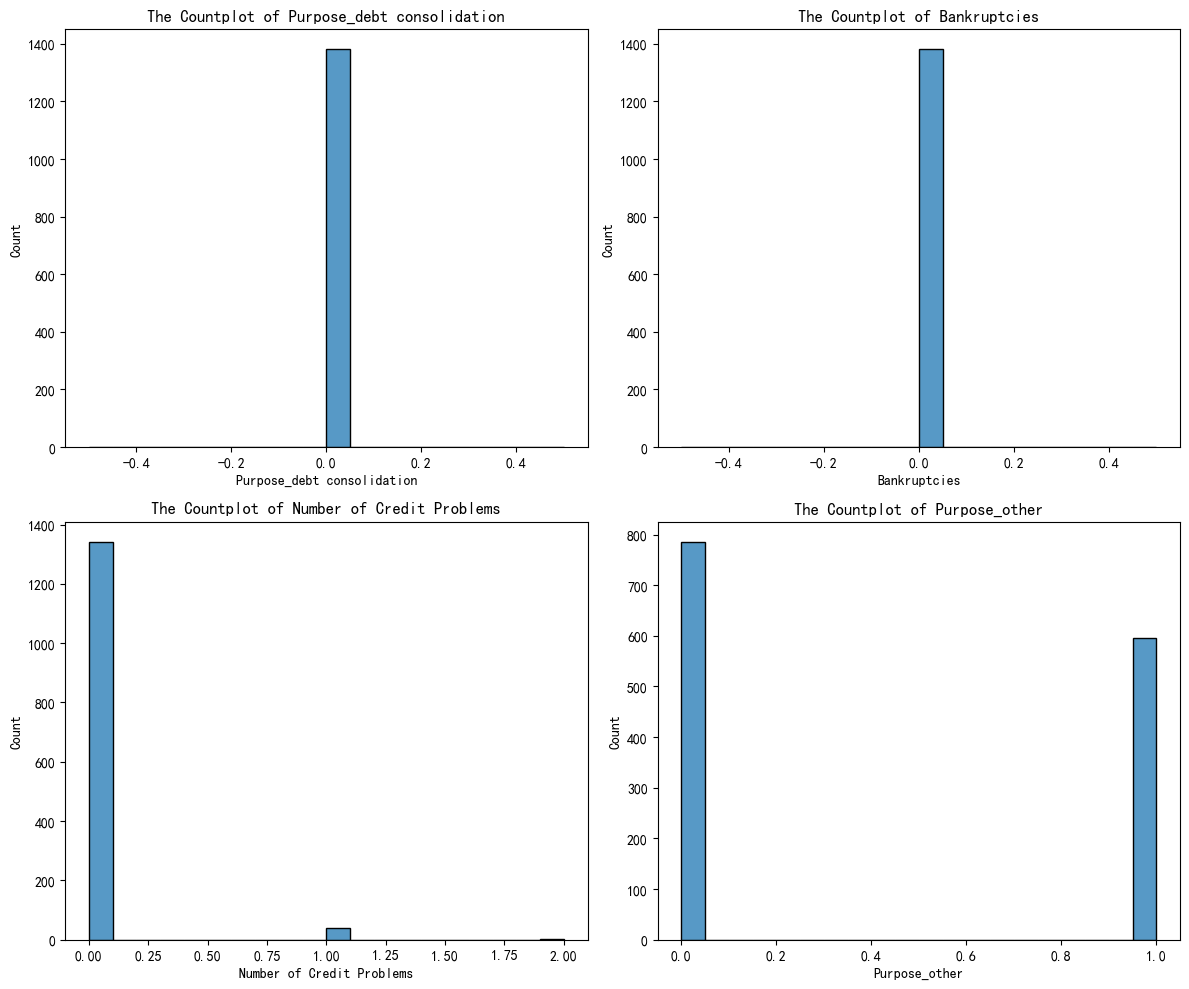
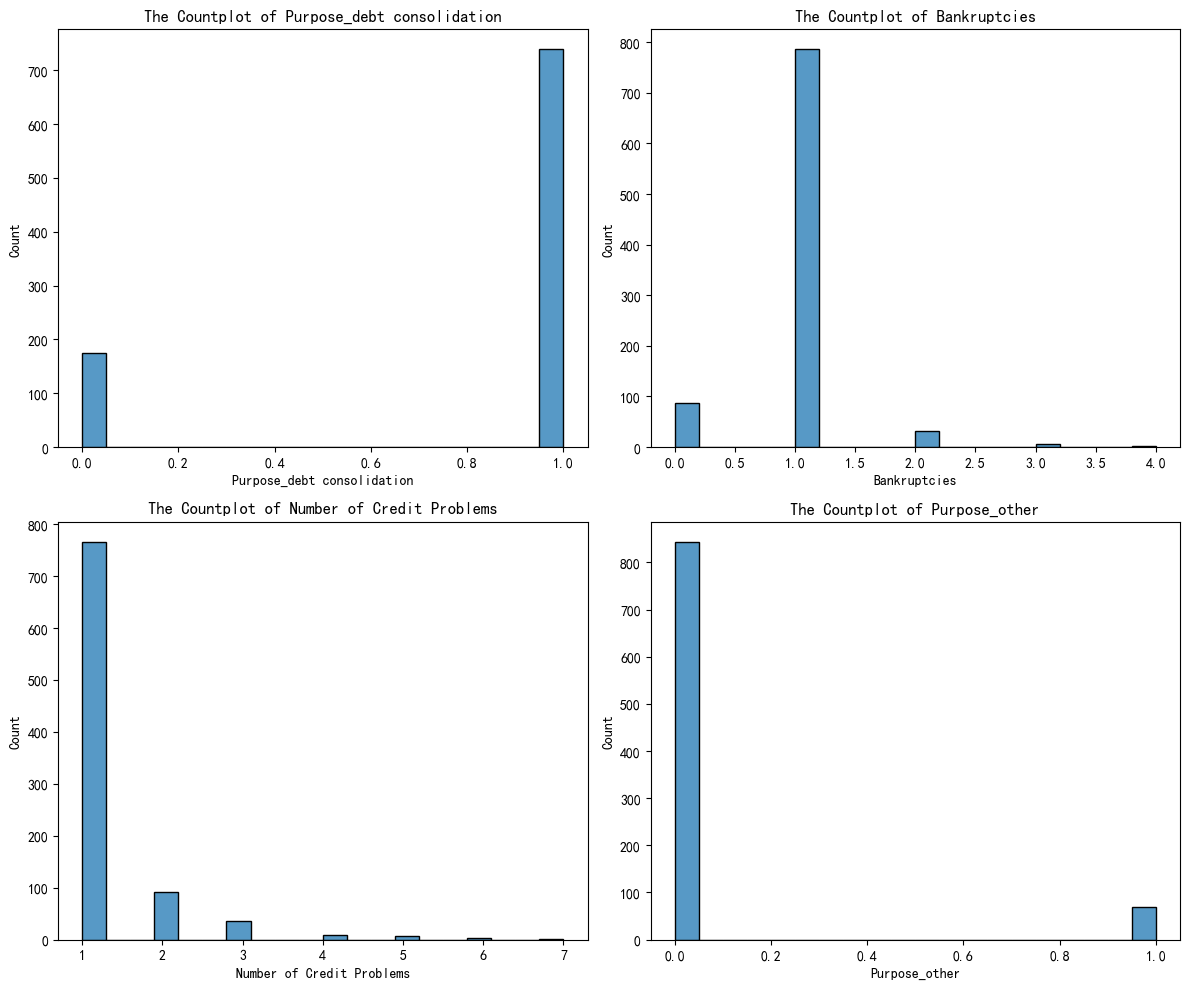
下面分别是簇别0，簇别1及簇别2的特征分布图

下面是借助AI分析得到的簇别含义的定义：

簇	主要特征	风险等级	客户画像	建议策略
0	债务整合 + 1次破产 + 多信用问题	高风险	财务困难、曾破产、需重组	审慎放贷，加强贷后监控，考虑更高利率或担保
1	其他用途 + 无破产 + 无信用问题	低风险	收入稳定、信用良好、消费驱动	可放宽审批，推荐长期产品
2	债务整合 + 无破产 + 无信用问题	低风险	信用优秀、主动优化债务	可优先授信，提供优惠利率或自动化服务

作业：心脏病数据集练习

针对心脏病数据集，练习上面的操作流程。

数据预处理与KMeans聚类，day17已练习过。只说明今日的内容。

#特征筛选
#特征与标签划分
x1 = X.drop(columns=['KMeans_clusters'],axis=1)
y1 = X['KMeans_clusters']
from sklearn.ensemble import RandomForestClassifier
rf_model = RandomForestClassifier(random_state=42) #实例化
rf_model.fit(x1,y1) #训练
import shap
explainer = shap.TreeExplainer(model=rf_model) #初始化解释器
shap_values = explainer.shap_values(X=x1) #计算shap值
#绘图
shap.initjs()#初始化JavaScript可视化功能，确保后续可视化图表正常工作
shap.summary_plot(shap_values[:,:,0],x1,plot_type='bar',show=False)
plt.title('特征重要性排序条形图')
plt.show()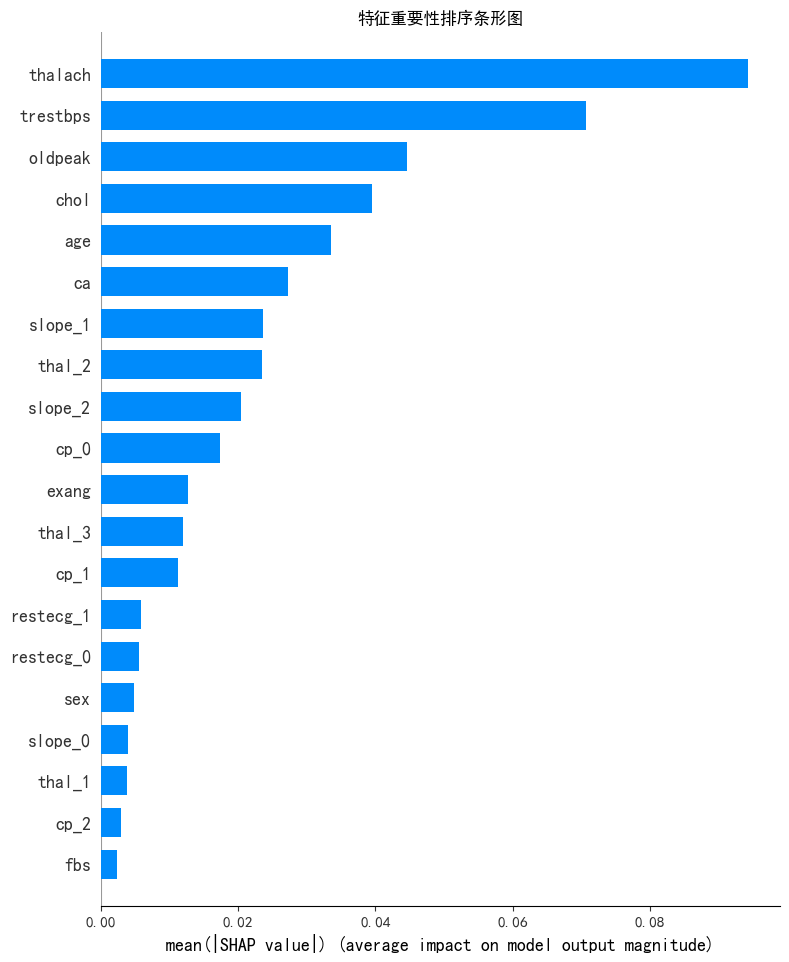

#特征的数据类型判断
selected_features = ['thalach','trestbps','oldpeak','chol']
#判断特征为离散型还是连续型
for i in selected_features:
    unique_counts = X[i].nunique() # 唯一值指的是在某一列或某个特征中，不重复出现的值
    print(f'{i}有{unique_counts}个变量') # 连续型变量通常有很多唯一值，而离散型变量的唯一值较少
    if unique_counts < 10: # 这里 10 是一个经验阈值，可以根据实际情况调整
        print(f'{i}为离散特征')
    else:
        print(f'{i}为连续特征')

#提取不同的簇别
x_cluster0 = X[X['KMeans_clusters']==0]
x_cluster1 = X[X['KMeans_clusters']==1]
x_cluster2 = X[X['KMeans_clusters']==2]
x_cluster3 = X[X['KMeans_clusters']==3]

#可视化簇别
#簇别0
fig,axes = plt.subplots(2,2,figsize=(12,10))
axes = axes.flatten()

for index,value in enumerate(selected_features):
    sns.histplot(x_cluster0[value],ax=axes[index],bins=20)#连续特征
    axes[index].set_xlabel(f'{value}')
    axes[index].set_title(f'The Countplot of {value}')

plt.tight_layout()
plt.show()

剩下的几个簇别，绘图类似，最后得到下面四个图：

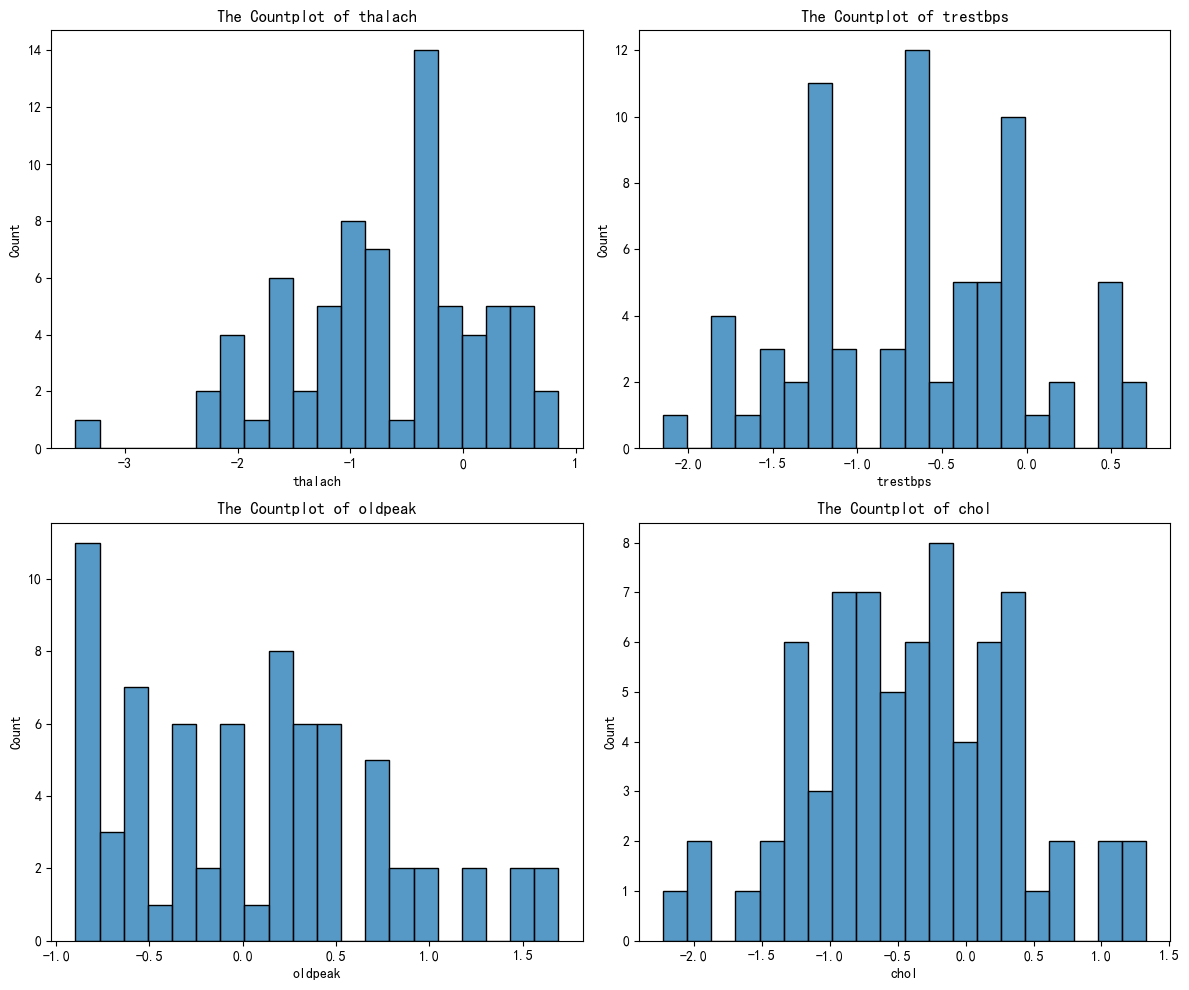
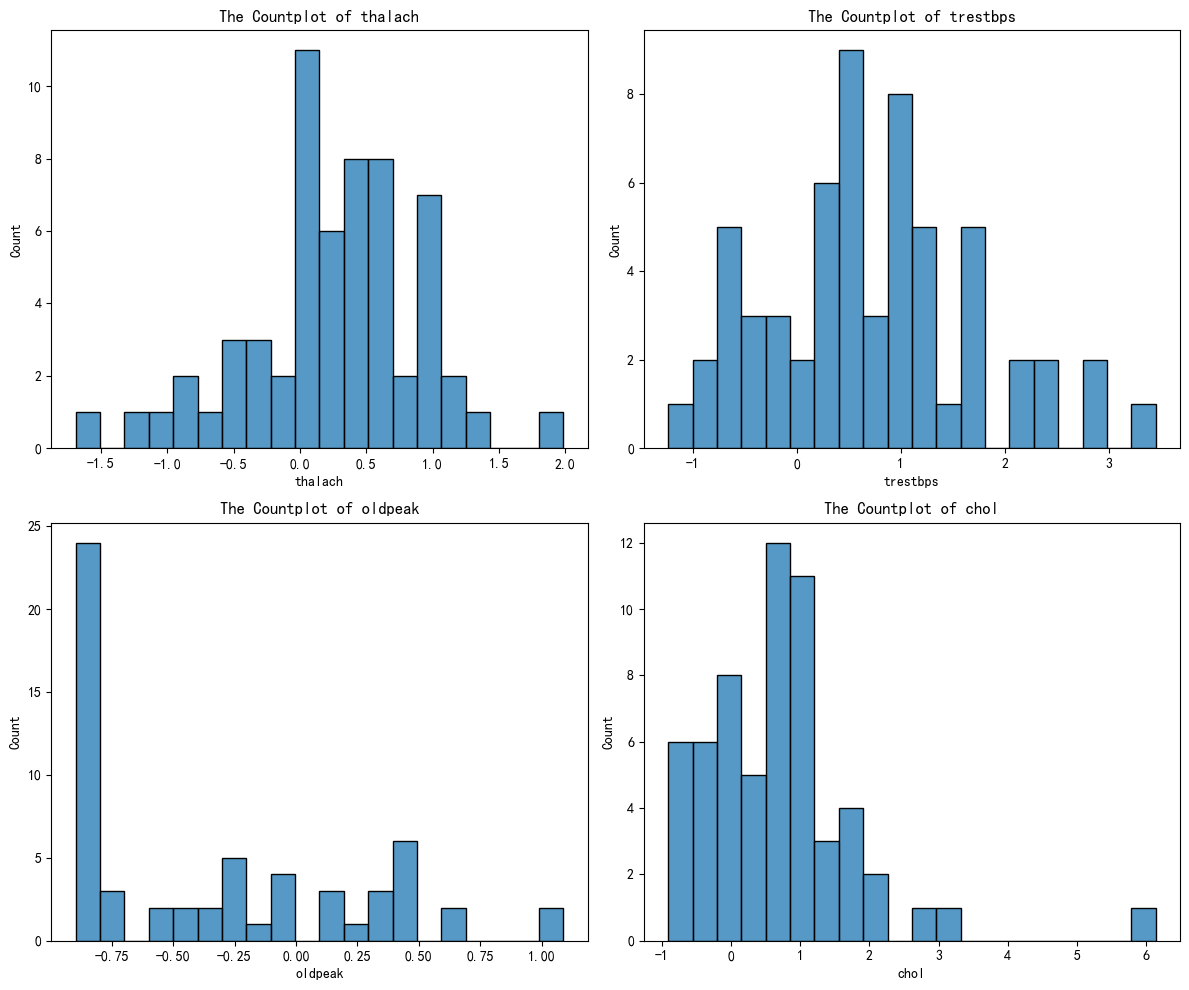
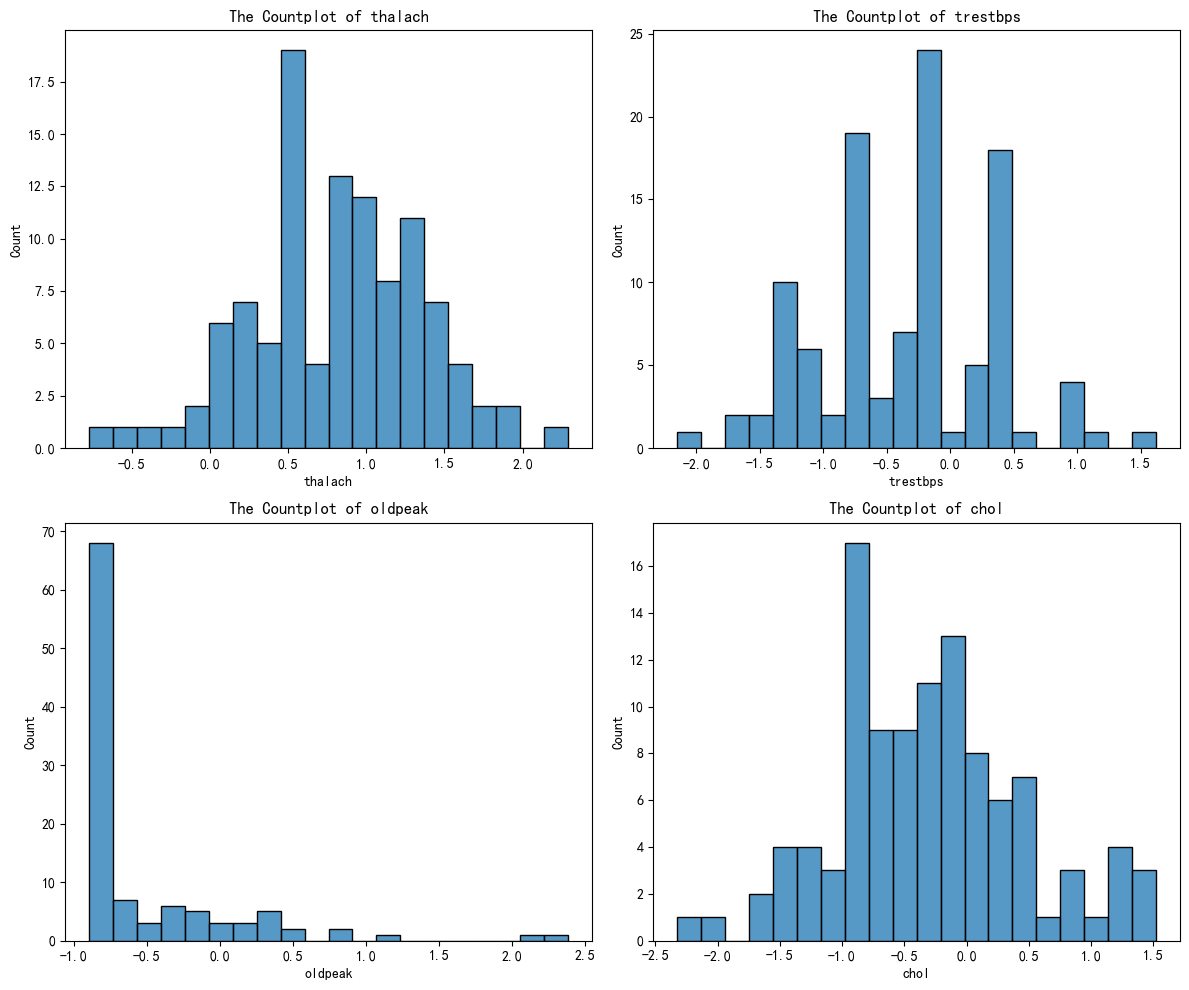
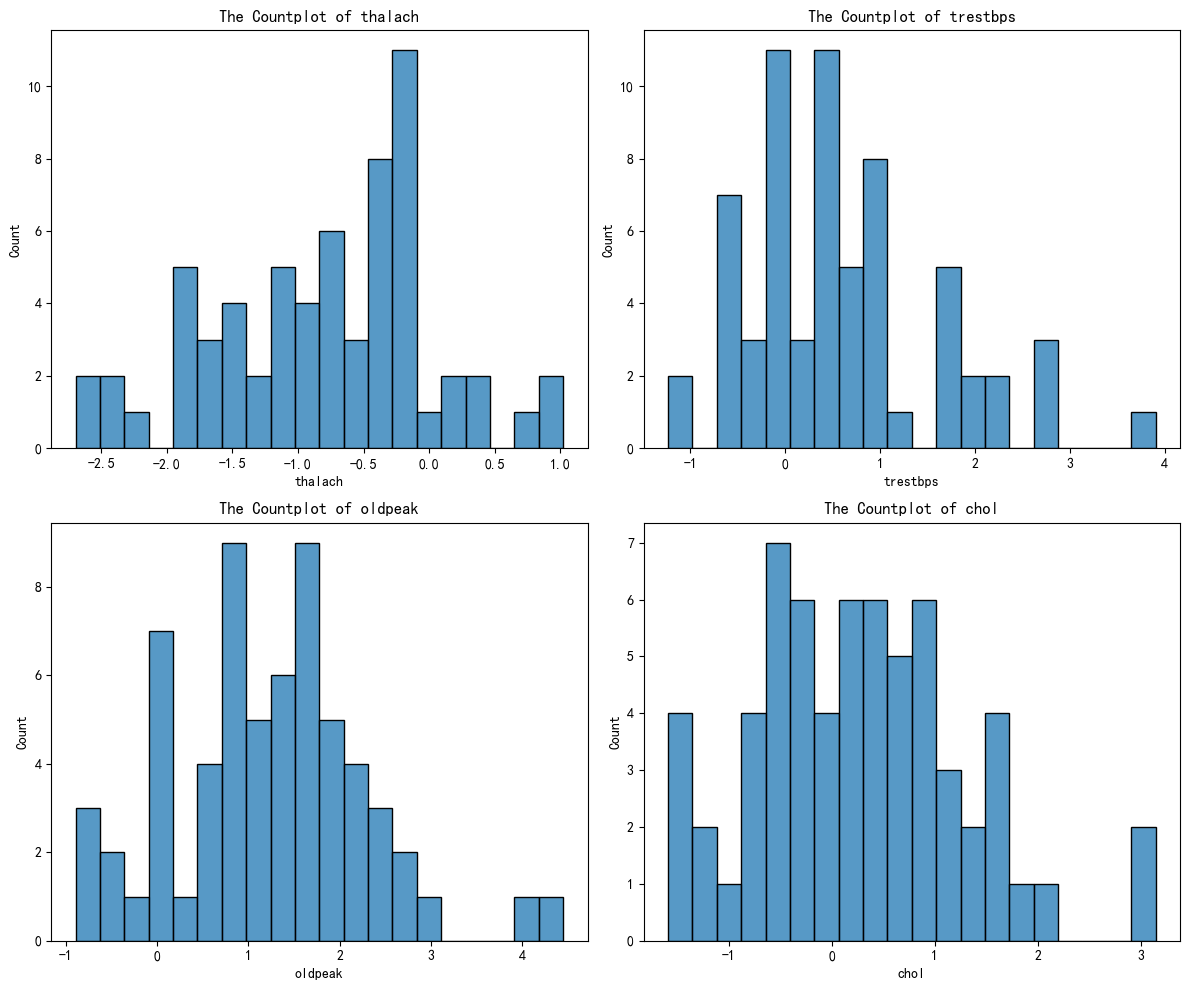
通过AI分析后得到下面的结果：

簇	thalach	trestbps	oldpeak	chol	临床画像	风险等级
0	偏低	正常	轻微缺血	正常	轻度心功能不全	中等
1	正常偏高	偏高	无缺血	偏高	高血压+高血脂	中高
2	显著偏高	正常偏低	无缺血	正常	心血管健康	低
3	偏低	偏高	显著缺血	偏高	多重风险+心肌缺血	高