MIT18.06学习笔记 - Lecture 4: Factorization into A = LU

这个系列文章是我重温Gilbert老爷子的线性代数在线课程的学习笔记。
Course Name：MIT 18.06 Linear Algebra
Text Book: Introduction to Linear Algebra
章节内容: 2.6

---

课程提纲
1. Factorization $A=LU$
2. Explanation: why $A = LU$

课程重点

Factorization $A=LU$

Many key ideas of linear algebra, when we look at them closely, are really factorizations of a matrix. The first and most important factorization in practice comes from elimination: $A=LU$, where factors $L$ and $U$ are triangular matrices.
The entries of $L$ are exactly the multipliers $l_{ij}$ - which multiplied the pivot row $j$ when it was subtracted from row $i$:

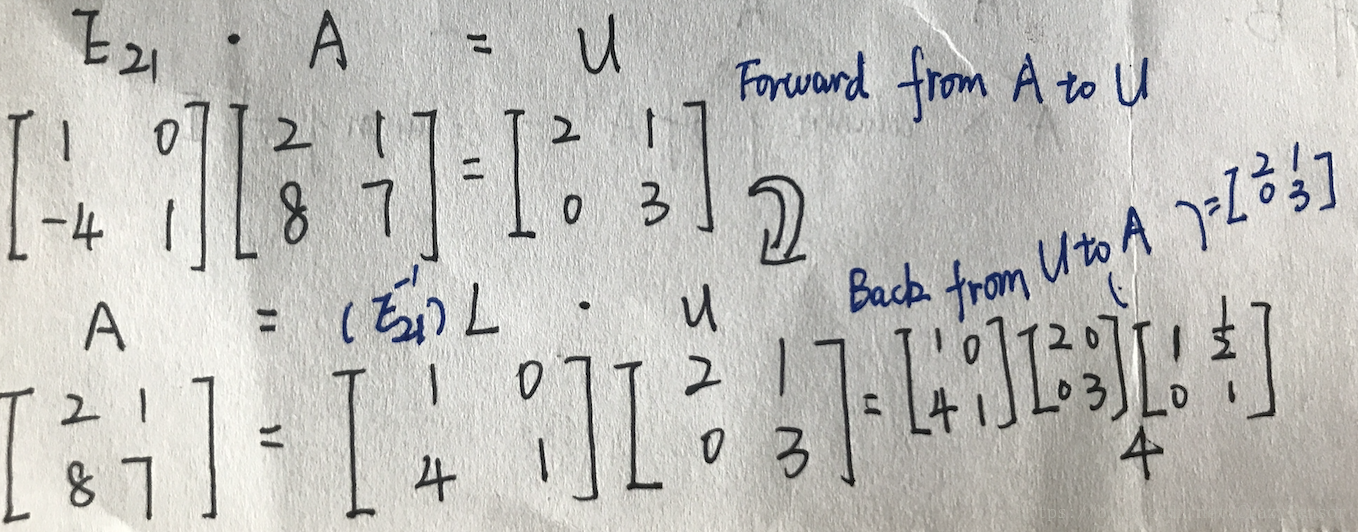
$A = LU$ ($A=LDU$) is elimination without row exchanges. The upper triangular $U$ has the pivots on its diagonal. The lower triangular $L$ has all 1’s on its diagonal. The multipliers are below the diagonal of $L$. If no row exchanges, each multiplier $l_{ij}$ goes directly into its $i$, $j$ position into $L$.

Assume no row exchanges, when can we predict zeros in $L$ and $U$:

• When a row of $A$ starts with zeros, so does that row of $L$.
• When a column of $A$ starts with zeros, so does that column of $U$.
  

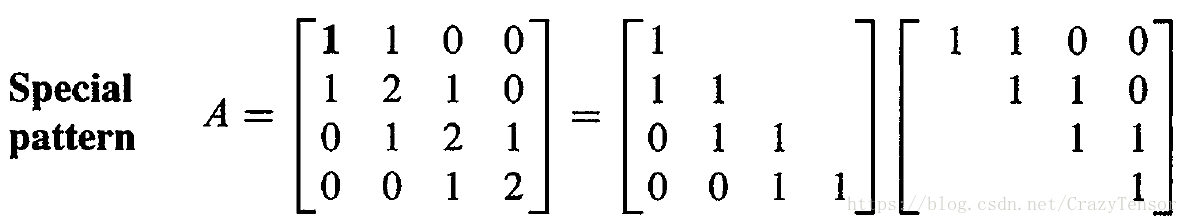
Explanation: why $A = LU$

When computing row of $U$, we subtract multiples of earlier rows of $U$ (not rows of $A$!):

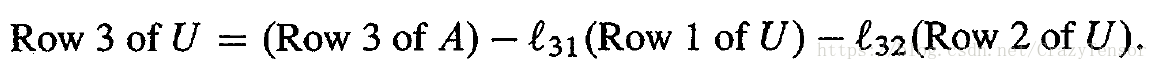
Rewrite this equation to see that the row $[l_{31}\ l_{32}\ 1]$ is multiplying $U$:

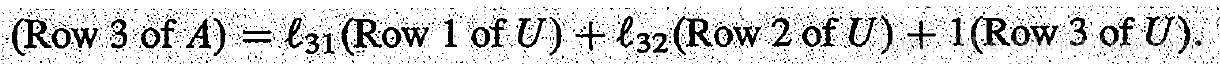
This is exactly row 3 of $A=LU$. That row of $L$ holds $l_{31}, l_{32}, 1$.

Better balance: Divide $U$ by a diagonal matrix $D$ that contains the pivots:

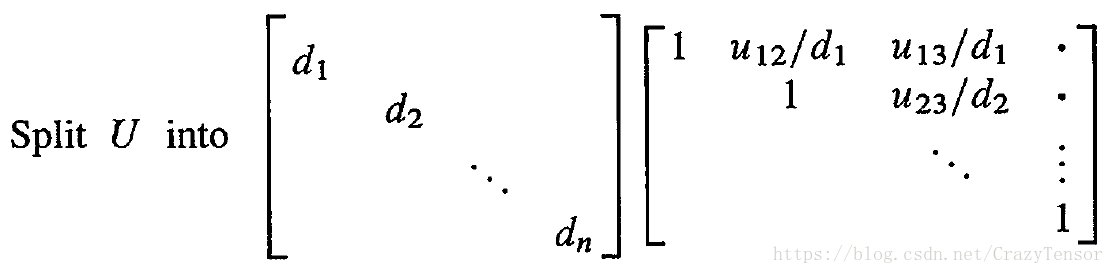
The triangular factorization can be written $A=LU$ or $A=LDU$.