前言
机器人学的机器人正运动学、逆运动学分析等是机器人设计与控制的基础,本文主要是对正运动学的知识框架进行总结,以便后续用到随时查阅。在《机器人学》专栏中,还补充了运动副、刚体位姿描述等知识也是本文的一部分学习基础,如读者朋友需要可以自行查阅。
机器人运动学是从几何角度去描述机器人位置、速度及加速度等特性,不考虑产生运动的力和力矩。运动学建模方法主要有几何建模法、D-H建模法等,其中D-H建模法具有较强适用性,而几何建模一般适用于结构简单的机器人(比如平面机器人),笔记重点讲解D-H建模法描述机器人正运动学。
1. 连杆参数
机器人运动实际就是各个连杆依靠关节将运动传递下去,为了进行运动学建模,首先要做的就是对连杆的参数进行描述:
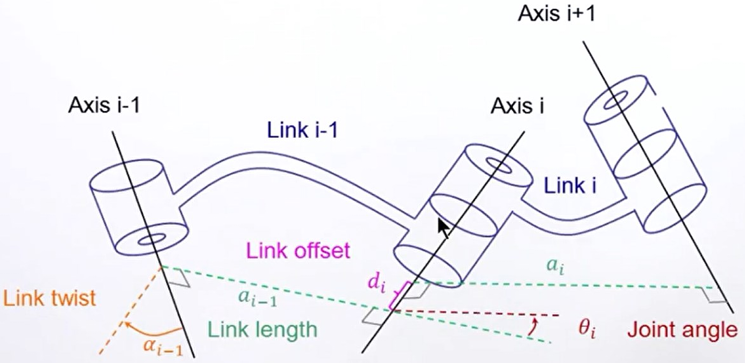
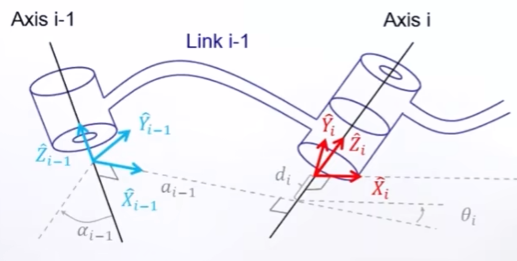
①由于结构设计不同,关节间的杆形状不同,那么如何定义连杆长度呢?对于上图的连杆,将同时垂直于两个关节轴线的这条线段
称为连杆长度。
②但只有一个连杆长度参数,不足以定义连杆特征。所以将关节与
轴向夹角
称为扭转角。
如上图所示,如果只有连杆长度与扭转角两个参数,是没有办法准确描述多杆串联的特征的,因此引入了下面两个参数:
③对于连杆与连杆
,两者的连杆长度的偏置,也就是沿着两者公共关节
轴向来看,
与
之间的距离
。
④除了长度以外,再有一个角度才能确定两者的关系。引入了两个连杆之间的关节角,也就是沿着
轴向看,
与
之间的夹角。
2. 连杆坐标系
所以这样如果对于移动关节,那么只有偏置是一个变量;而对于转动关节其关节角
,是唯一的变量。下面为了更加清楚描述连杆的参数与关系,在关节上建立坐标系:
· 转动或移动转轴的方向为;
· 沿着连杆长度方向建立关节的
;垂直于xz平面建立
。
(右手法则:右手拇指指向Z,食指指向X,中指就是Y)
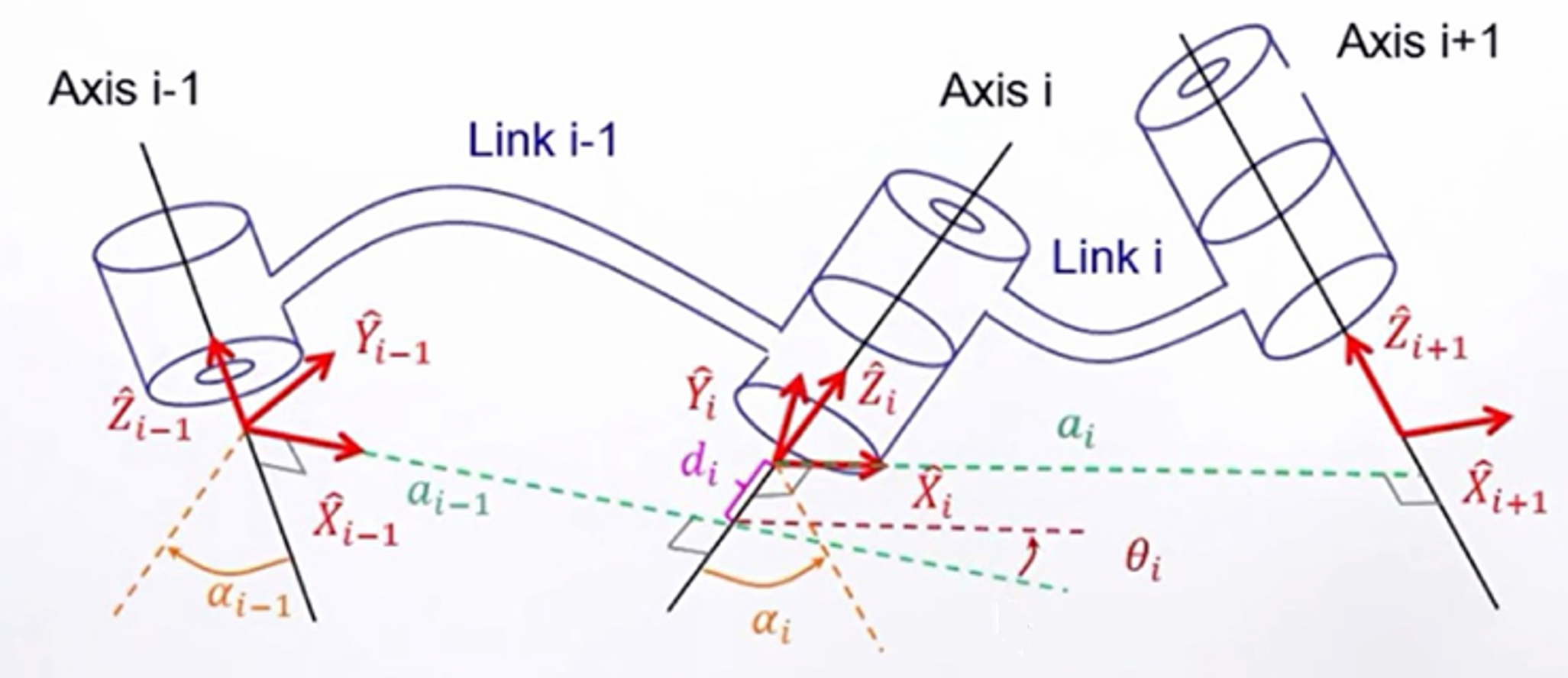
注:
①对于首杆0,约定选择轴沿着关节轴1的方向,也就是使得关节0与1的坐标系重合。
②类似地,对于最后一个连杆,约定其关节沿着上一关节
的方向。宗旨就是使尽量多参数为零,简化运动学方程。
3. 首尾杆的描述
①首杆
在机器人中特殊的有首杆与尾杆,像下图中所示0杆就是首杆,并且是固定的。这里让连杆0与连杆1的坐标系重合,那么对于它的描述就是:
,
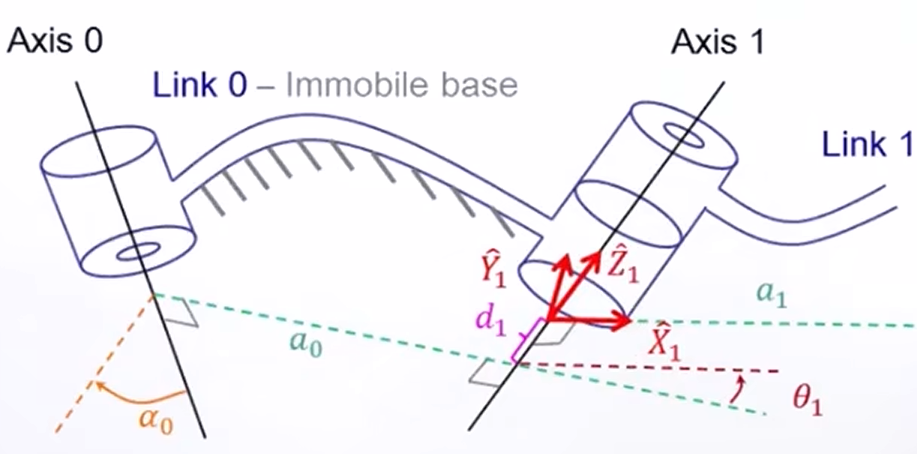
对于转动关节:就是关节变量,同时习惯约定
,这里取
为连杆1的零位;
对于移动关节:就是唯一变量,同时习惯约定
,这里取
为连杆1的零位。
②末杆
最后一根连杆n和前一个连杆n-1选择与
同向,所以这里:
,
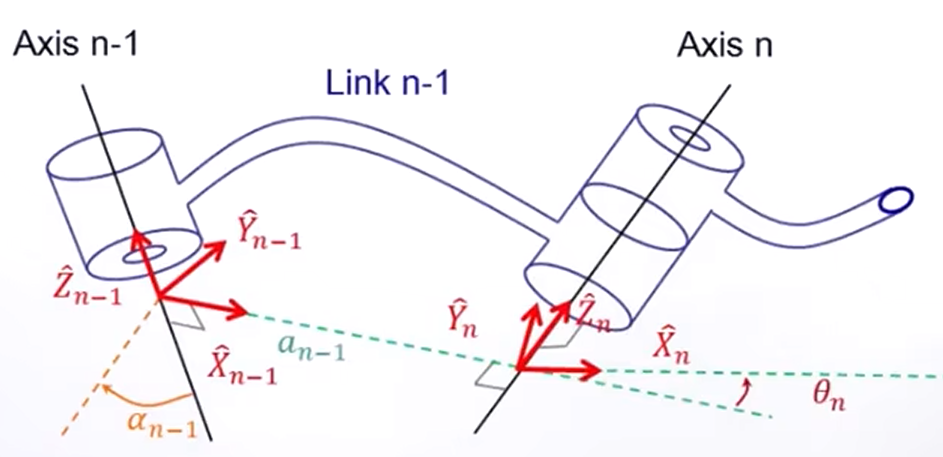
对于转动关节:就是关节变量,同时约定
,这里取
为连杆n的零位;
对于移动关节:就是唯一变量,同时约定
,这里取
为连杆n的零位。
4. 连杆变换与正向运动学方程
1)连杆变换
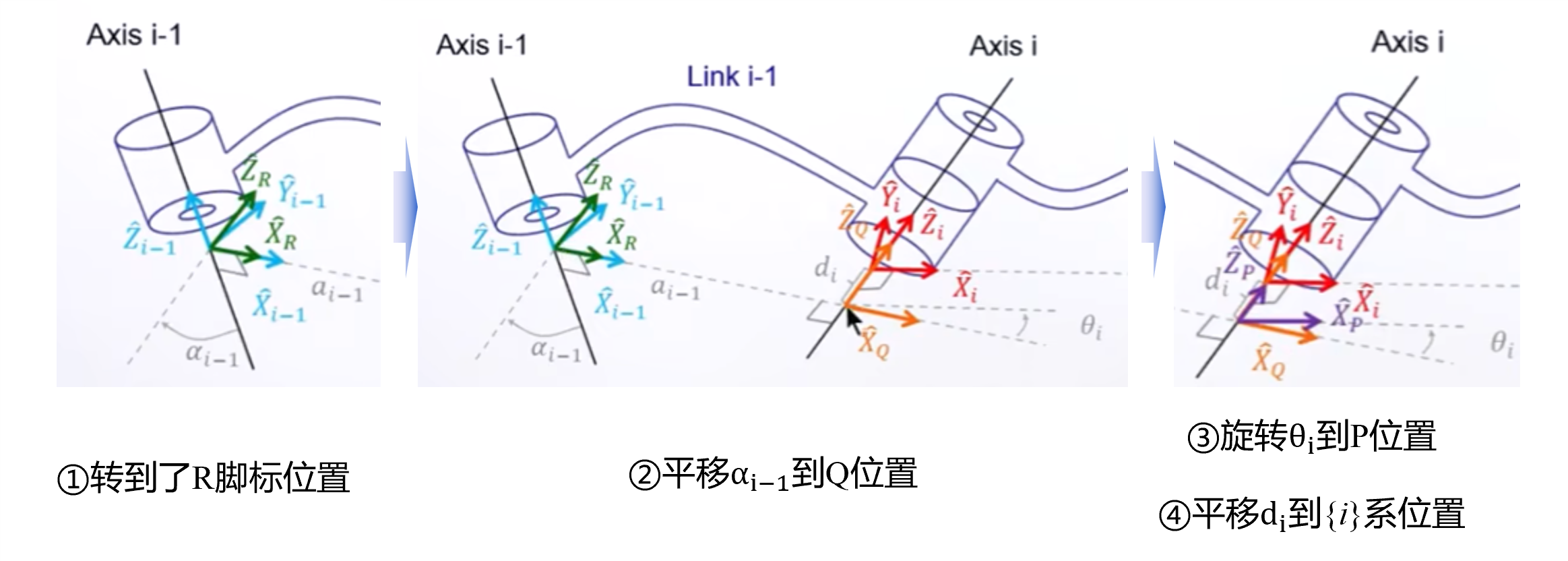
前面已经建立了两个杆件分别的坐标系,但是相邻的杆件坐标系有什么关系呢?这就是我们连杆变换要讨论的内容。如果我们已知在系中的一点P,那我们可以通过
这个式子反推到P点在
系中的表达,那我们如何通过上面讲的四个参数得到这个齐次变换矩阵呢?
相邻的两连杆变换可以看作,坐标系就是系
经过以下变换得到的:

结合下图可以进一步理解这一变换过程:
2)建立正向运动学方程
由于子变换都是相对于动坐标系描述的(因为此为一般情况),相乘顺序按着“从左向右”的原则,即齐次变换矩阵:

有了上面的描述,那就很容易得到一个连续的串联手臂变换矩阵,也就是系对于
系的关系:
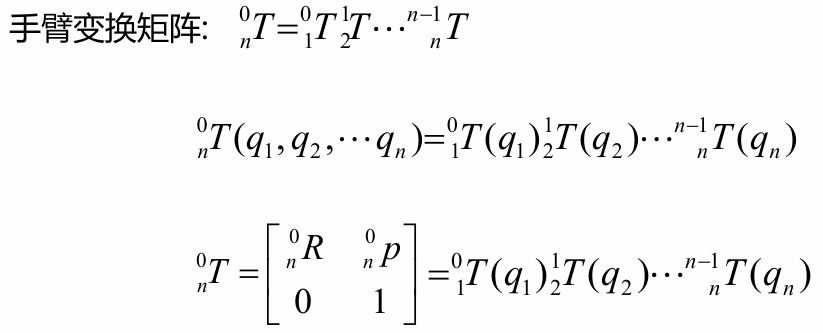
上式即为正向运动学方程,表示末端连杆的位姿与关节变量之间的联系。
3)建立D-H参数表
对于一个机器人将连杆参数形成一个D-H参数表的过程,其实就是将上面讲到的四个参数列写出来。步骤主要是:

例子
下面我们举几个例子来进一步理解连杆参数与D-H参数表:
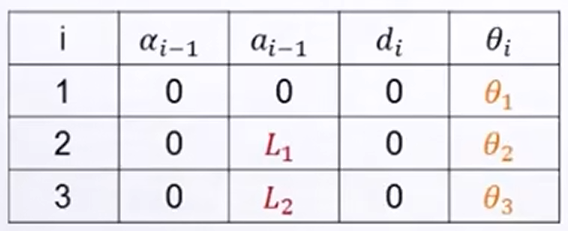
①对于平面RRR机器人,建立其连杆坐标系并列写D-H参数表
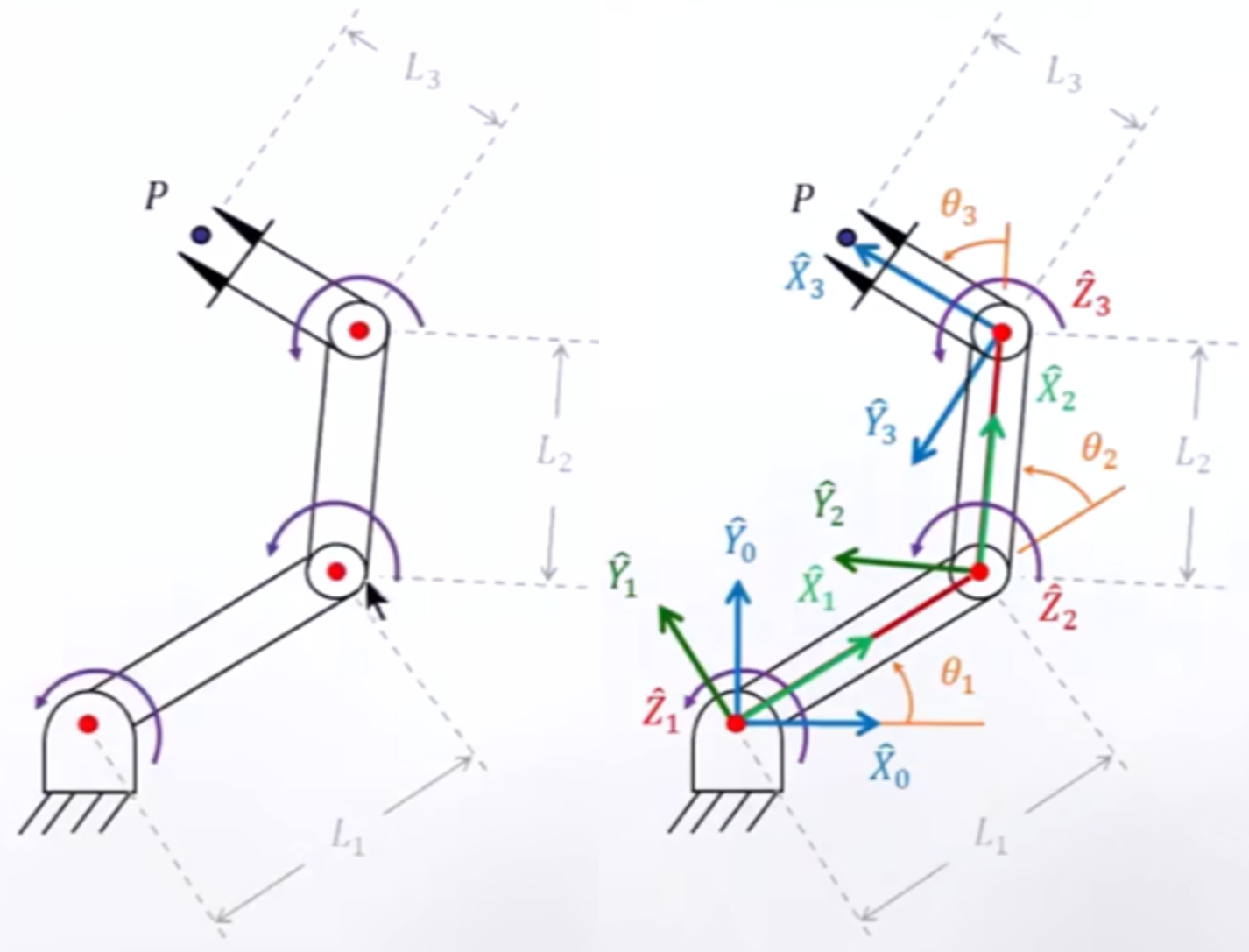
a. 上面左图就是机构的简图,然后从下到上依次为0~3号杆(0为基座。
b. 建立坐标系,如上右图,首先在基座建立Z轴向外,X轴水平的坐标系;其次1号系也建立在基座与杆1的旋转关节处,Z冲外,X沿着杆方向;2、3杆也是一样道理建立坐标系。
c. 根据定义确定连杆参数与关节的参数,最终填写D-H参数表。(这里判断参数方法,可以看小结中的结论,更为简单易懂)
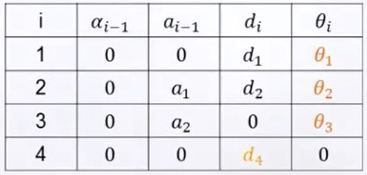
② 下面是一个空间SCARA机器人,建立其连杆坐标系并列写D-H参数表
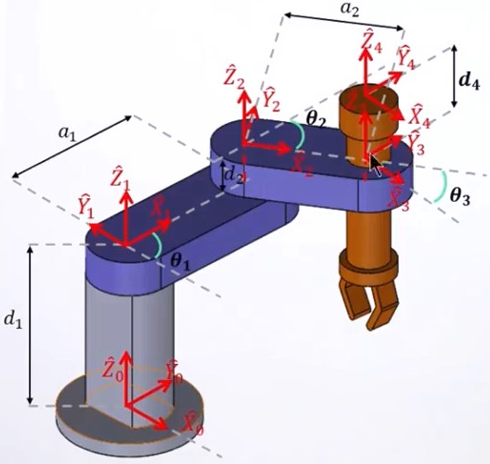
a. 与平面机器人类似,也是先定义杆号;
b. 确定xyz轴:Z轴都是沿着轴向,注意到了第4个关节时除了转动还有一个移动,所以建立4系主要是为了看相对于3系的移动;X轴沿着连杆的方向
c. 列写所有关节参数:由于所有Z轴平行,所以都为0;由于杆连接处有一定厚度,所以存在
;注意最后一个坐标系与3坐标系实际只有距离关系,故
。
小结
①连杆参数
描述连杆参数主要有4个,分别为:

注:以xx方向看,是对着箭头来看,如果对于
来讲是向逆时针的方向,那就是正的角度。
②连杆坐标系
对于关节,沿其轴向为
, 沿
方向为关节
的
;垂直于xz平面建立
(右手定则)。建系的主要宗旨就是使尽量多参数为零,简化运动学方程。
③连杆变换与正运动学方程
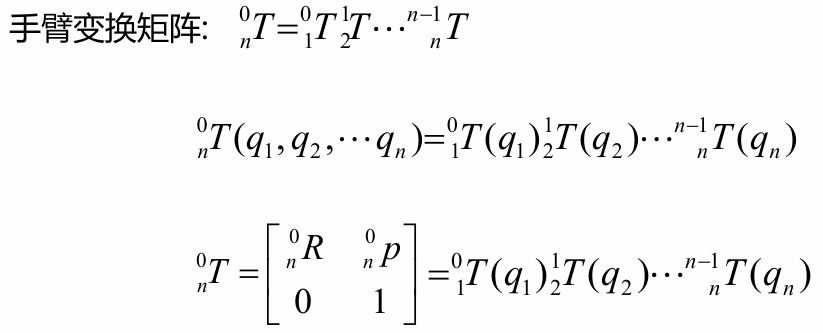
声明,本文的主要学习资料有:
1. 机器人运动学——林沛群老师课程
3. 《机器人学 建模、控制与视觉》 熊有伦院士
本文主要以学习为目的,会不断将所学总结更新,如有不足还望不吝赐教。





















 5087
5087

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








