齐次变换与齐次变换矩阵的计算

前言

上一篇文章中，讲到了刚体位姿描述与坐标变换，最终得到了坐标变换的一般形式：，也就是任一点坐标系下的都能描述到极基坐标系当中去。但是可以发现这一个坐标变换被拆为一个矩阵相乘和一个矩阵相加的形式，那么能否将这些操作合并呢？本文就将这一问题进行总结。

1. 齐次变换

齐次变换要求矩阵维数一致，所以与一般形式中点(3*1列向量)不同，其中加入了第四个分量1，变成了4*1的列向量，称为点的齐次坐标：

所以将一般形式进行齐次变换的形式是：

或表示为矩阵相乘形式：

式中：与均为4*1的列向量，与一般形式中的维数不同。这两个4*1的列矢量就称为点的齐次坐标。

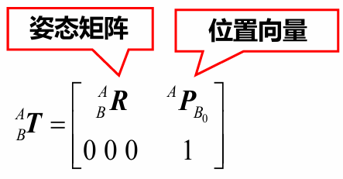
2. 齐次变换矩阵

上述进行齐次变换之后，可以发现一个有加法的矩阵变为了两个矩阵相乘的形式，所以齐次变换矩阵就是：

其特点是一个4*4的矩阵，最后一行的元素为，这样一来就综合的表示了平移变换与旋转变换的复合。

齐次变换矩阵的三个物理意义：

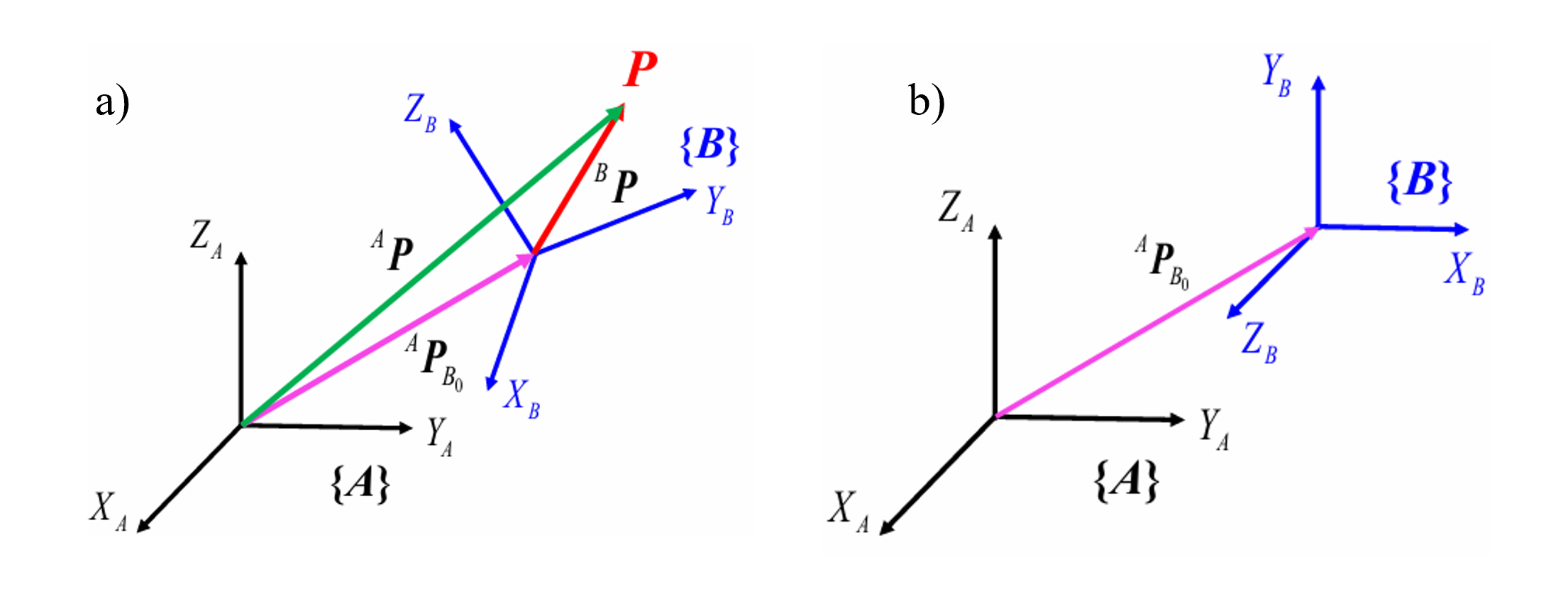
①坐标变换

可以作为两个坐标系间的坐标变换矩阵：

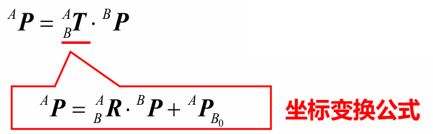
②坐标系的描述

齐次变换矩阵描述了坐标系相对于的位置与姿态：

比如对于下面的旋转矩阵（姿态对应了上面的图b）:

分析可以得到第四列矢量为，也就是系原点位置相对于系来讲xyz坐标为（-1,3,2）。分析前三列姿态矩阵可以得到：

③运动算子

描述了某个刚体的运动情况：

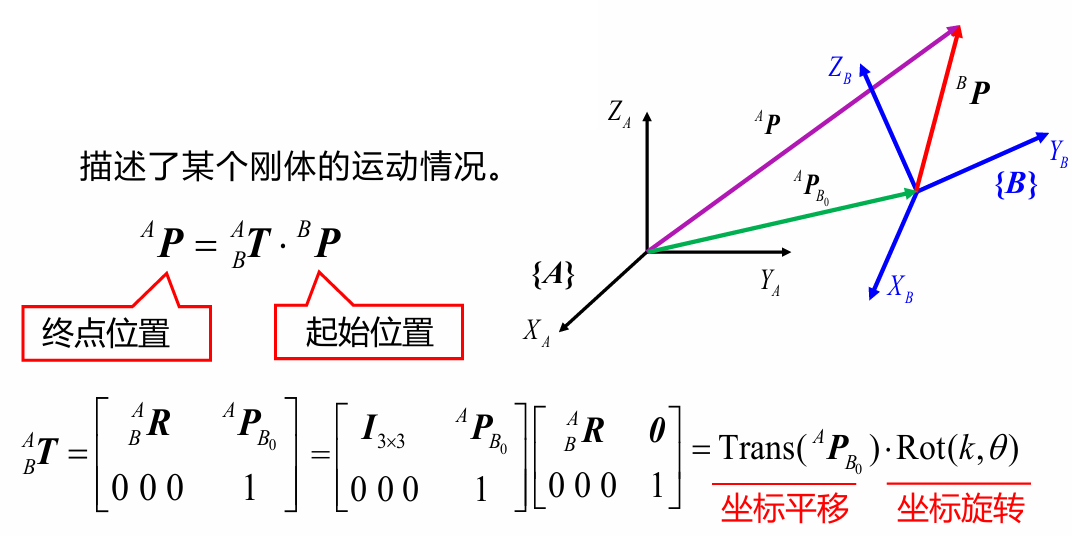
也就是说旋转矩阵与起始位置相乘后，让原来的点发生了某种平移与旋转运动，从而最终到达了终点位置。

3. 齐次变换矩阵的计算

可以看到其实前面讲到的是一个刚体在两个不同坐标系下的变换，但是实际上的系统更为复杂，那么如何描述多个坐标系间的坐标变换呢？

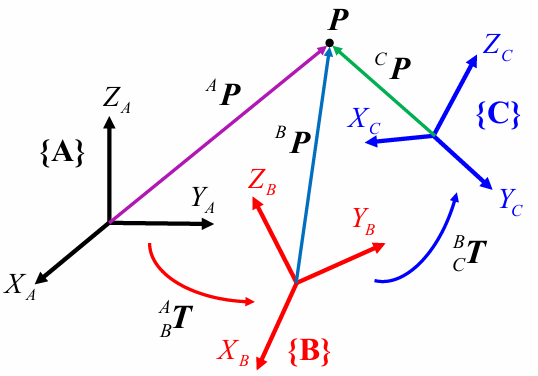
如果有三个坐标系分别为，，，通过我们上面的分析，可以知道，间的齐次变换矩阵为；，之间的齐次变换矩阵为。

如果任意给出了一点P，那么P点在三个坐标系中的描述一定均不相同，但是两两之间的齐次变换公式可以写出：

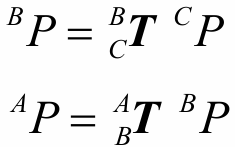
如果将上面的式子带入下面可以发现：

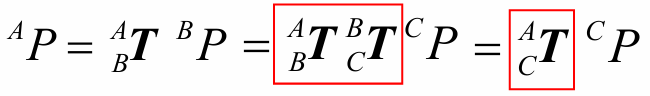
似乎P点在与之间的描述也用一个齐次变换解决了，而这个齐次变换矩阵就是与矩阵的乘积。因此利用齐次变换矩阵相乘，能够描述多个坐标系之间的变换关系。

4. 齐次变换矩阵相乘的物理意义

①齐次变换矩阵相乘能够实现坐标系描述之间的变换：

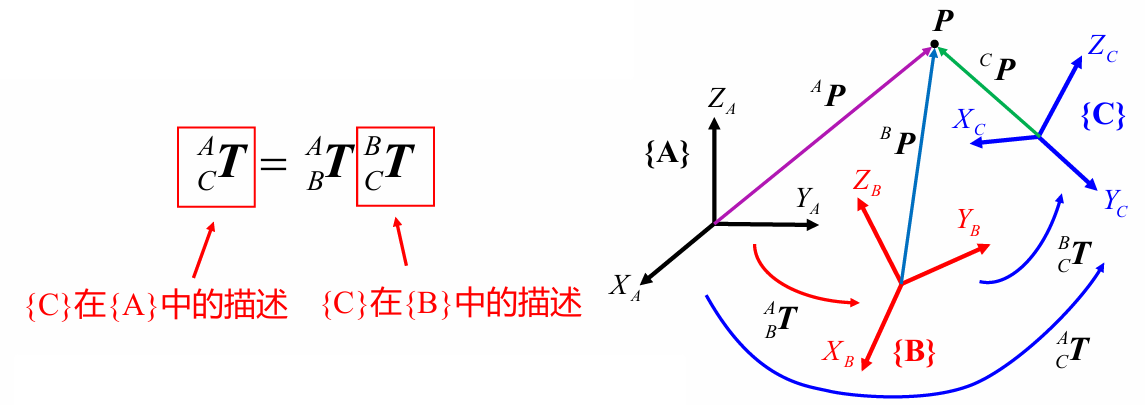
②相对固定坐标系先后发生的若干运动的合成：

假设最开始，，三个坐标系完全重合，那么可以将齐次变换矩阵相乘进行拆分：

第一步就是系先相对于（因为重合，其实也是）进行一个齐次变换；然后让与同时相对于进行一个齐次变换。注意相乘的顺序是从右向左的。

为更清楚理解，下面举个例子：

例①

答：可以看出其实是三次连续的绕固定坐标系的运动，那么我们可以分开写这三个齐次变换矩阵，然后再连续相乘：

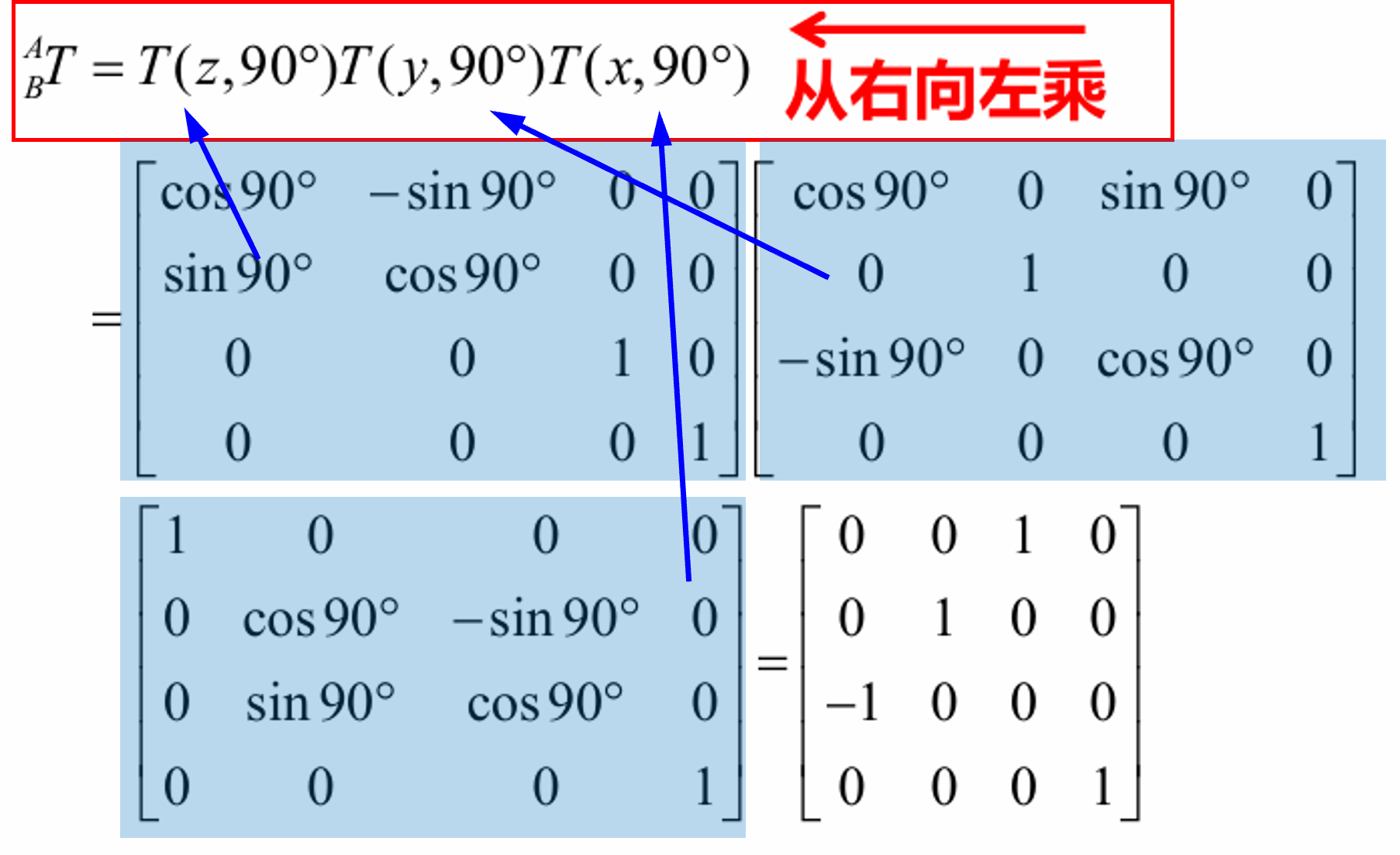
注意列写齐次变换矩阵可以按着从右向左先写出来，但是最后计算一定要按照矩阵相乘的运算规则进行计算~

例②

答：可以看出其实是三次连续的绕动坐标系的运动，那么我们可以分开写这三个齐次变换矩阵，然后再连续相乘（特别注意，由于是绕着动坐标系，这里列写顺序变为从左向右）

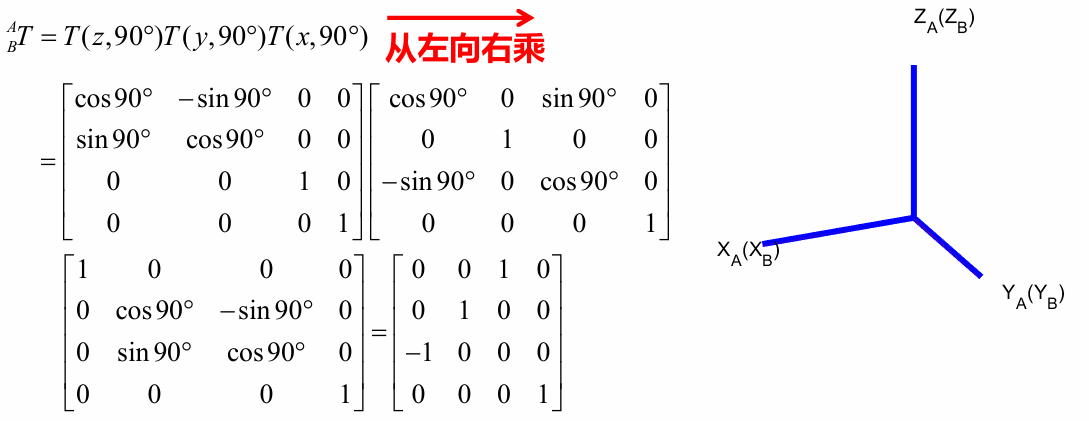
5. 齐次变换矩阵中的逆变换

已知相对于的描述为，如何求解相对于的描述呢？下面是最直接的方法，就是通过矩阵求逆来得到：

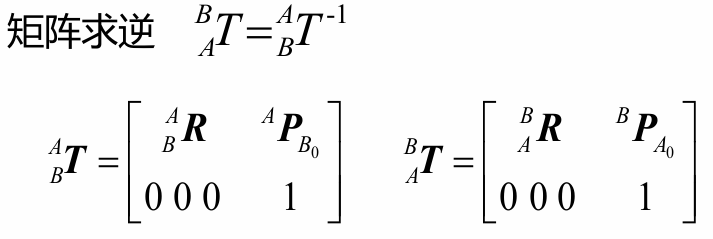
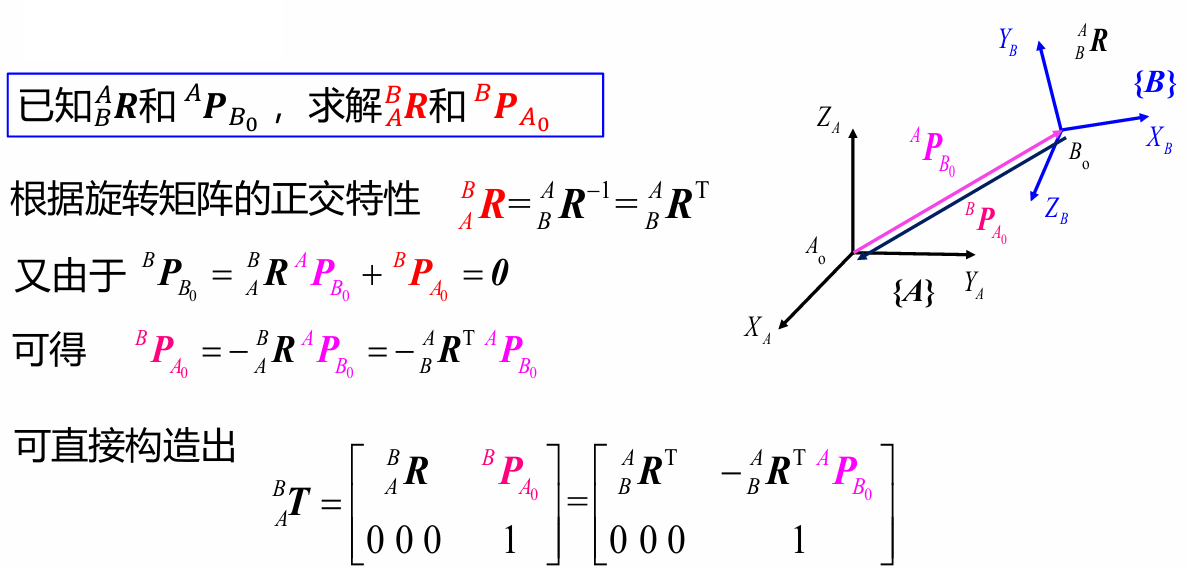
但是矩阵求逆过于繁琐，那我们从定义出发，由于是由与组成，那么问题就变为了已知了与去求与：

总结

---

声明：本文以学习燕山大学-机器人技术课程资料和熊有伦院士《机器人学 建模、控制与视觉》一书所写，主要用于共同学习~