动态规划，记忆搜索，uva1629,切蛋糕

先给链接：https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=4504

大意就是切n*m蛋糕，有k樱桃，只能横着竖着切，要求每一块蛋糕上恰好有一个樱桃，且割线总长最小。

Sample Input
3 4 3

1 2

2 3

3 2

Sample Output
Case 1: 5

/*自己写切的时候炸了，还是大佬厉害，膜拜膜拜*/

这题第一个难点就是区域的划分记录，用数组D[r][c][w][h]来记录（以（r,c）点为区域左上坐标，r为点所在宽度，c为点所在长度，不能与x,y坐标弄混，w为区域的宽度，h为此区域的长度）此区域最短切割的最小长度。题目给的n是行，是长度，m是列，是宽度，读入的时候注意。

再要用数组Chery[r][c][w][h]记录区域的樱桃总数，从而保证每个切分出的蛋糕恰好有一个樱桃。

第二个难点就是划分区域时长度，宽度和坐标的关系。

先看区域求樱桃和：

int CR_Cnt(int r,int c,int w,int h){//区域[r,c,w,h]之间的所有樱桃数 
	int& ans = Chery[r][c][w][h];
	if(ans != -1) return ans;
	
	if(w>1)
	return ans = CR_Cnt(r,c,1,h) + CR_Cnt(r,c+1,w-1,h);//行数大于1，r,c点对应行的樱桃数+ 下一行（宽度-1，长度不变） 
	return ans = CR_Cnt(r,c,1,1) + CR_Cnt(r+1,c,1,h-1);//这时行数只能为1，列数先为一再往后移； 
}

如果行数w>1,无法找到点坐标的樱桃，而是分出当前行，那么我切出了当前行（r,c,1,h），再加上另一部分，此时的剩下的部分的纵坐标由于被切了一行，所以要往下移一位，他的宽度对应减一。

当切到了最后宽度为1的时候，开始以1为单位切长度，分为当前坐标长度[r,c,1,1]和剩余区域长度[r+1,c,1,h-1]。

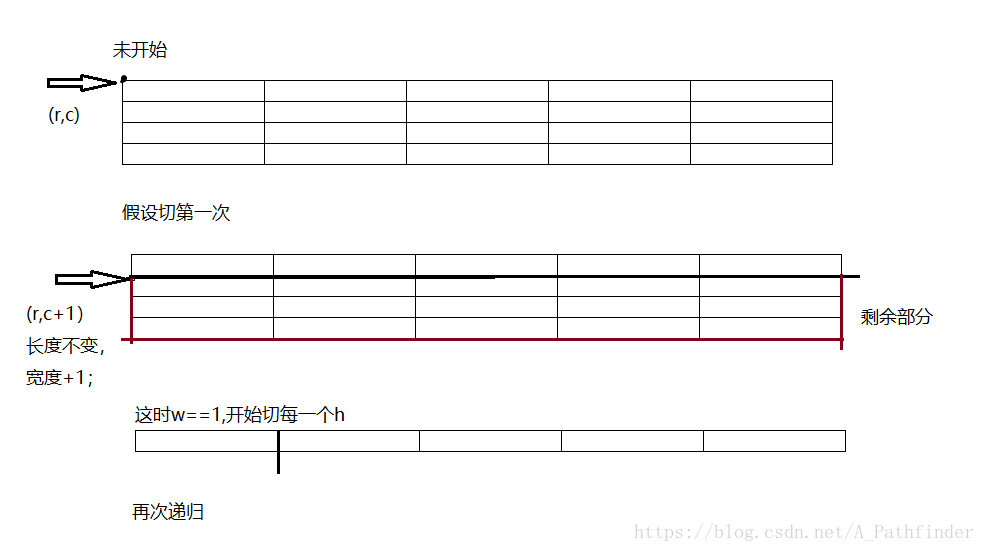
再来就是遍历横切和竖切，坐标，区域变化和以上类似；

分割线：

---

#include<bits/stdc++.h>
using namespace std;

const int maxn = 20 +1; 
int n,m,k,D[maxn][maxn][maxn][maxn],Chery[maxn][maxn][maxn][maxn];

int CR_Cnt(int r,int c,int w,int h){//区域[r,c,w,h]之间的所有樱桃数 
	int& ans = Chery[r][c][w][h];
	if(ans != -1) return ans;
	
	if(w>1)
	return ans = CR_Cnt(r,c,1,h) + CR_Cnt(r,c+1,w-1,h);//行数大于1，r,c点对应行的樱桃数+ 下一行（宽度-1，长度不变） 
	return ans = CR_Cnt(r,c,1,1) + CR_Cnt(r+1,c,1,h-1);//当行数为1，长度切割，再往后移； 
}

int dp(int r,int c,const int W,const int H){
	int& ans = D[r][c][W][H];
	if(ans != -1) return ans;
	if(CR_Cnt(r,c,W,H)==1 ) return ans = 0; //如果只有此区域内只有一个樱桃，不划分。 
	
	auto updateans = [&](int a){ //这里是c++11 带的匿名函数，引用追踪 a为 W+dp(r+h,c,W,H-h) + dp(r,c,W,h))，不习惯可以用我注释的那段。 
		if(ans == -1) ans = a;
		else ans =min(ans,a);
	};
	
	for(int h = 1;h < H; ++h)//横向切割 
	if(CR_Cnt(r,c,W,h) >= 1 && CR_Cnt(r,c,W,H-h) >= 1) //可以继续切割的条件是当前行樱桃数目大于1，且剩余部分樱桃数目大于1； 
	updateans(W+dp(r+h,c,W,H-h) + dp(r,c,W,h));
	/*if(ans == -1) ans =  W+dp(r+h,c,W,H-h) + dp(r,c,W,h); 
	else ans = min(ans,W+dp(r+h,c,W,H-h) + dp(r,c,W,h));*/
	
	for(int w = 1;w < W; ++w)//竖向切割
	if(CR_Cnt(r,c,W-w,H) >= 1 && CR_Cnt(r,c,w,H) >=1)
		updateans(H + dp(r,c+w,W-w,H) + dp(r,c,w,H));
	
	return ans;
}

int main(){
	for(int kase = 1,r,c;scanf("%d%d%d",&n,&m,&k) == 3;kase++){//读入 
		memset(D,-1,sizeof(D));
		memset(Chery,-1,sizeof(Chery));
		for(int i = 0;i < n; ++i)
		for(int j = 0;j < m; ++j)
		Chery[i][j][1][1] = 0;
		for(int i = 0;i < k; ++i){
			scanf("%d%d",&r,&c);
			Chery[r-1][c-1][1][1] = 1;//有k个樱桃，记录它们具体位置，由于数组从0开始，题目-1。 
		}
		printf("Case %d: %d\n",kase,dp(0,0,m,n));//dp(0,0,m,n)起始0，0，这里的宽度是m,长度是n 
	}
	return 0;
}

最后：

programming is the most fun you can have with your clothes on.