在上一篇提到,因为R和T是定义在一个乘法运算的群上,他们对加法是不封闭的,导致在对其进行求导时会不成立。在引入了李代数这个映射后,那么接下来就是我们感兴趣的对一个旋转矩阵R左乘另外一个旋转矩阵对应到李代数上是什么样的。
一. BCH公式与近似形式
当我们计算两个旋转矩阵相乘时,可以转换为其对应的两个李代数指数映射的形式,即
两个矩阵指数相乘结果可以由BCH(Backer-Campbell-Hausdorff) 公式给出
其中表示A和B所在群的运算。根据该公式可以发现把乘法转换到一个无穷个李括号组成的加法运算上。而当
和
其中有一项是很小量(其实就是在SLAM中机器人每次运动很小,对应的旋转矩阵和转换矩阵就很小)的时候,那么这个公式的近似表达是:
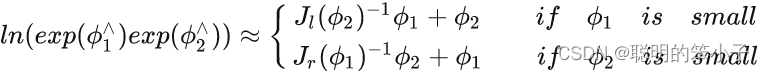
这说明当其中一项(比如)是小量的时候,结果可以近似成另一项(
)加上一个
。SLAM14讲书中给出了
表达式:
而的逆表达式为
其中和
分别表示旋转向量
对应的旋转角度和旋转轴。而当
较小时,有
至此,当旋转矩阵R发生一次微小旋转R时,在正交群上进行计算应该是
,而这个计算映射到李代数上则变成上面表示出来的加法了:
而当在李代数上进行加法时,根据上面的公式可以反推出以下公式:
所以我们就找到了一个用加法表示在机器人位姿不断变化的情况下的位姿表示,这就为后面求导做好了铺垫。
二. 李代数求导
现在返回最初使用李代数的初衷,我们需要使用它来对一个特殊正交群进行求导,以此达到我们想要求解最优化问题的目的。
假设某个时刻机器人的位姿为,此时机器人观测到一个landmark记作P,产生了观测量
,那么就有
其中W为噪声,所以观测值和观测模型推导出的观测值之间存在误差。那么此时的机器人的最优估计就可以表示为
,其中n表示landmark的总数量。
很明显这是个最小化误差函数的问题,一般的求解思路就是求导,令导数等于零,得到最优解下对应的T。但这里的问题就是对一个关于转换矩阵T函数不能直接求导,因为它对加法并不收敛。所以这时就需要转换到李代数进行求导。
这里举了一个简单的例子来引入李代数求导。考虑空间中的一个点p,经过一次旋转R后,此时的坐标为Rp,那么对Rp对R的求导形式不严谨的表示为。但是由于特殊正交群对加法不封闭,所以这个式子在李代数上的表示就变为了:
。
接下来根据导数的定义就有:

其中第二行是BCH公式的线性近似,第三行是泰勒展开后舍去高阶项的近似,第四第五行是将反对称符号看做两个向量的叉积(这点很容易证明),交换之后变号。于是我们得到了旋转后的点对于李代数的导数。
鉴于这个方法需要求解,计算过程会很复杂,一般会使用扰动模型来避开它。
对R进行一次扰动,就等于是在R左乘一个
,而李代数角度就等于两个李代数的指数映射相乘。以左扰动为例,假设左扰动
对应的李代数为
,对其求导为:

这里的第一步没有太理解,但是看了另一个博主的推导感觉更合理一点:
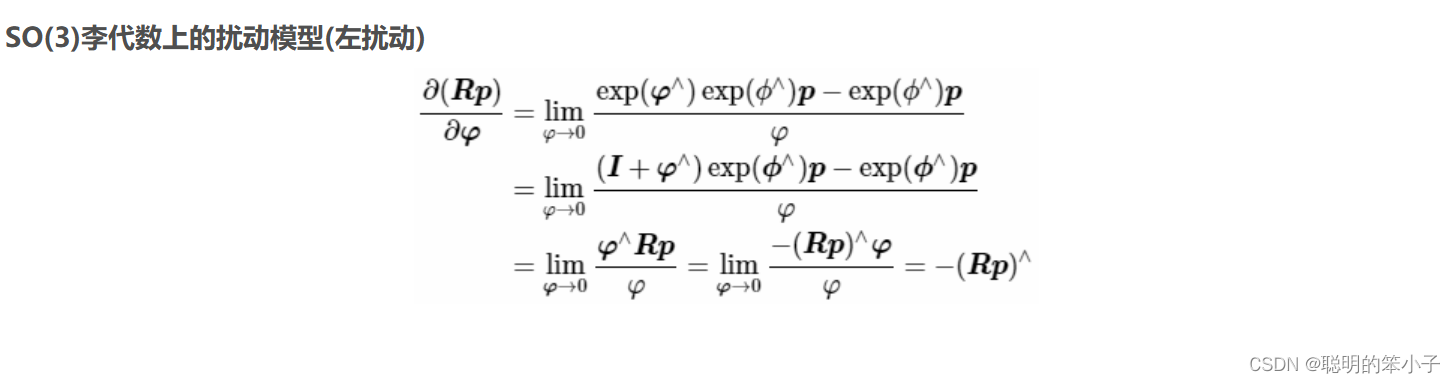
第一步等式相当于是左乘一个扰动相当于其对应的李代数指数映射相乘,然后因为扰动趋近于0,扰动李代数的指数映射就可以近似为单位矩阵(相当于1)加上本身的李代数对应的反对称矩阵相加。这样第三步就可以约掉相同项并得到最后的结果。
本文引用:
[1]. 高翔,张涛, “视觉SLAM十四讲”, slambook/ch6/g2o_curve_fitting/main.cpp at master · gaoxiang12/slambook · GitHub
[2]. 李狗嗨,"如何通俗地解释李群和李代数的关系?",如何通俗地解释李群和李代数的关系? - 知乎
[3]. skycrygg,“李代数求导与扰动模型”,李代数求导与扰动模型_skycrygg的博客-优快云博客





 文章介绍了在SLAM(SimultaneousLocalizationAndMapping)中,如何利用李代数解决旋转矩阵不封闭于加法运算的问题。通过BCH公式和近似表达,当旋转矩阵发生微小变化时,可以用李代数的加法来表示。文章进一步讨论了李代数在求导中的作用,特别是在对旋转矩阵求导时,如何通过扰动模型简化计算过程,以求解最优化问题。
文章介绍了在SLAM(SimultaneousLocalizationAndMapping)中,如何利用李代数解决旋转矩阵不封闭于加法运算的问题。通过BCH公式和近似表达,当旋转矩阵发生微小变化时,可以用李代数的加法来表示。文章进一步讨论了李代数在求导中的作用,特别是在对旋转矩阵求导时,如何通过扰动模型简化计算过程,以求解最优化问题。
















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








