VSLAM(8)：后端---Pose Graph优化和Factor Graph优化

原创

已于 2023-07-30 20:38:26 修改 · 1.3k 阅读

7 ·

CC 4.0 BY-SA版权

文章标签：

#计算机视觉 #人工智能

于 2023-07-25 19:17:36 首次发布

本文详细介绍了SLAM后端优化中的两种关键方法：位姿图（PoseGraph）优化和因子图优化。位姿图优化通过去掉特征点，仅保留位姿节点，以提高实时性和减少计算负担；因子图则利用贝叶斯网络和概率论，通过因子节点表示变量间的约束，实现更通用的优化。文章还提供了g2o和gtsam库在实际代码中的应用示例。

前一章主要介绍了BA图优化的后端方法，这种方法可以同时优化相机位姿和路标点位置。这里的路标点其实就是特征点，往往数量巨大，对存储和计算都会带来巨大的负担，并且会不断累加，导致在大场景下无法实时化。

特征点的数量远大于位姿节点的数量，一个关键帧的特征点往往会有几百个关键帧。对于BA优化的方法，即使利用稀疏性，达到实时也只能有几万个点。那么为了解决实时性的问题，可以适当丢弃一些历史数据，想Sliding Window（滑动窗口法）；或则直接选择不对路标点进行优化，只保留位姿之间的约束条件，使用Pose Graph。

一，位姿图

1.1 Pose Graph的意义

BA优化的主要计算压力来自于对特征点的优化，因为随着特征点的不断增加，计算效率就会不断降低。实际上，在经过数次观测后，那些收敛的特征点，空间位置估计就会在某一个值附近保持不动；而发散的外点通常就看不到了。所以可不可以假设一个特征点，经过几次优化后就可以不再考虑，只把他们看作位姿估计的约束，而不再去对他的位置进行优化。

那如果考虑算法更快，完全不去考虑路标点的优化，只管轨迹优化呢？构建一个只有轨迹而没有特征点的图优化，节点为各个时刻的位姿，节点之间的边为由相邻两帧之间的特征匹配的结果作为初值。与BA优化不同的是，一旦初始估计完成后，就不再去考虑优化特征点位置，而只关心所有的相机位姿之间的联系。过程如下所示：

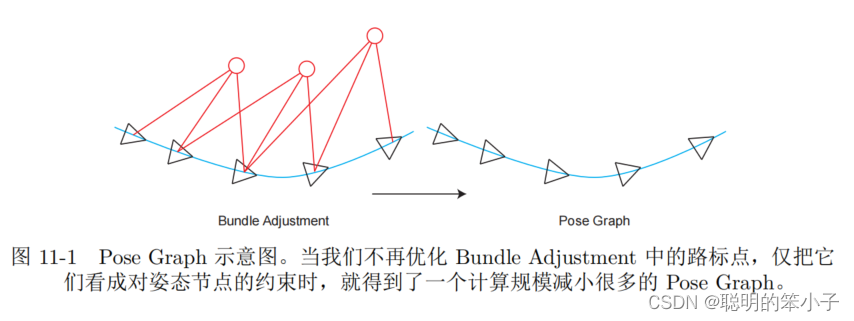
在Pose Graph问题中，每个节点就是相机此时的位姿，用它的李代数（ $\xi _1 , \dots , \xi _n$ ）表示；图的边就是根据相邻帧估计的位姿节点之间相对运动，这个估计结果可能来自直接发或则特征点法。在实际的SLAM框架中，也可能会有其他的约束条件，比如来自闭环检测的约束。这个运动在李代数上的定义为：

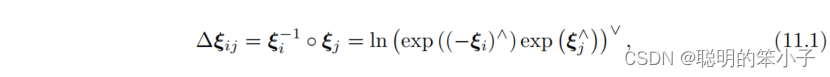
而按照李群的写法为：

就像之前在视觉里程计中说的1，这个估计本身就会存在误差，所以等式不会精确的成立。所以可以设最小二乘误差，利用优化方法求解最优值。误差 $e_{ij}$ 可以定义为：

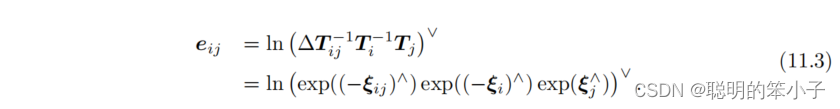
可以看到误差定义式子中 $\Delta T^{-1}_{ij}$ 和 $\xi _{ij}$ 代表相邻帧估计结果,即相对位姿，可以通过IMU,lidar或则是camera传感器，使用一定的算法得到，例如ego-emotion，scan-registration，ICP等，是已知量，而待优化量则是前后两个时刻的相机位姿 $\xi _i$ 和 $\xi _j$ ，因此对这两项求导来得到雅可比矩阵。按照李代数的求导方式，分别给 $\xi _i$ 和 $\xi _j$ 各一个左扰动： $\delta \xi _i$ 和 $\delta \xi _j$ ，于是误差变为：

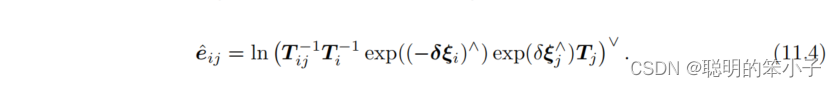
如果想利用BCH公式来近似的话，需要将中间的两个扰动项移到式子左边或则右边。这里使用下面的伴随性质：

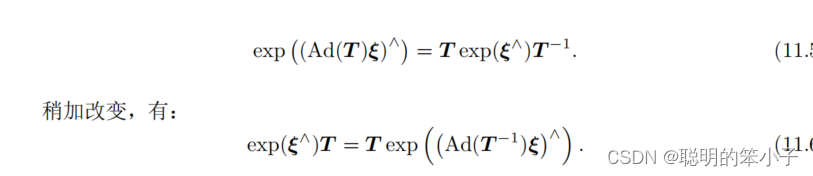
就有：

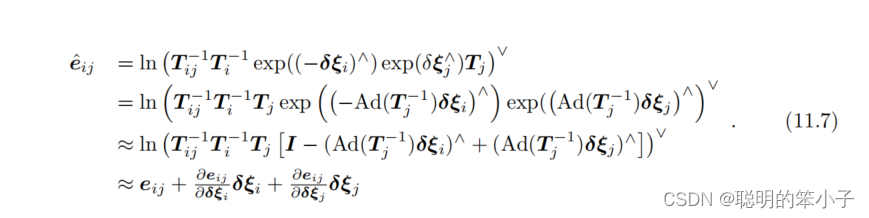
因此，按照李代数上的求导法则，对 $T_i$ 的雅可比矩阵就是：

对 $T_j$ 的雅可比矩阵就是：

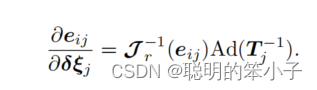
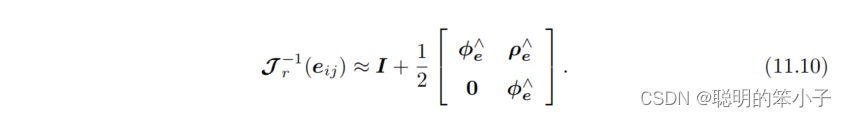
得到雅可比矩阵后，剩下就是定义目标函数，使用图优化的方法求解。总体目标函数为：

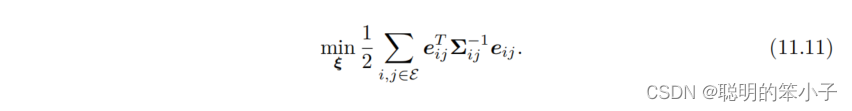
其中 $\Sigma _{i,j} ^{-1}$ 代表节点i和j之间的信息矩阵（information matrix），信息矩阵用来代表边的不确定度，信息矩阵越大代表这条边在优化的过程中越重要。

Pose Gragh的优势：求解问题存在稀疏性，可以加快求解速度，并且对于初始状态的变化较为鲁棒。

Pose Gragh的缺点：对外点(outliers，亲切一点就是错的离谱的结果)不具有鲁棒性，另外，优化估计Rotation的过程是一个非凸优化问题，容易造成导致局部最优问题，且不保证全局最优问题。

重磅论文精读！SLAM中姿态估计的图优化方法比较_问题_约束_Pose (sohu.com)这个文章了使用不同框架，在相同的而数据集（INTEL, MIT两个数据集）上求解Pose Graph问题的对比。

1.2 Pose Graph代码实践

这里给了一个带噪声的球形位姿图，使用g2o_viewer查看如下左图所示，是由g2o的create sphere函数创造的。而经过Pose Graph优化后的结果就左图所示。

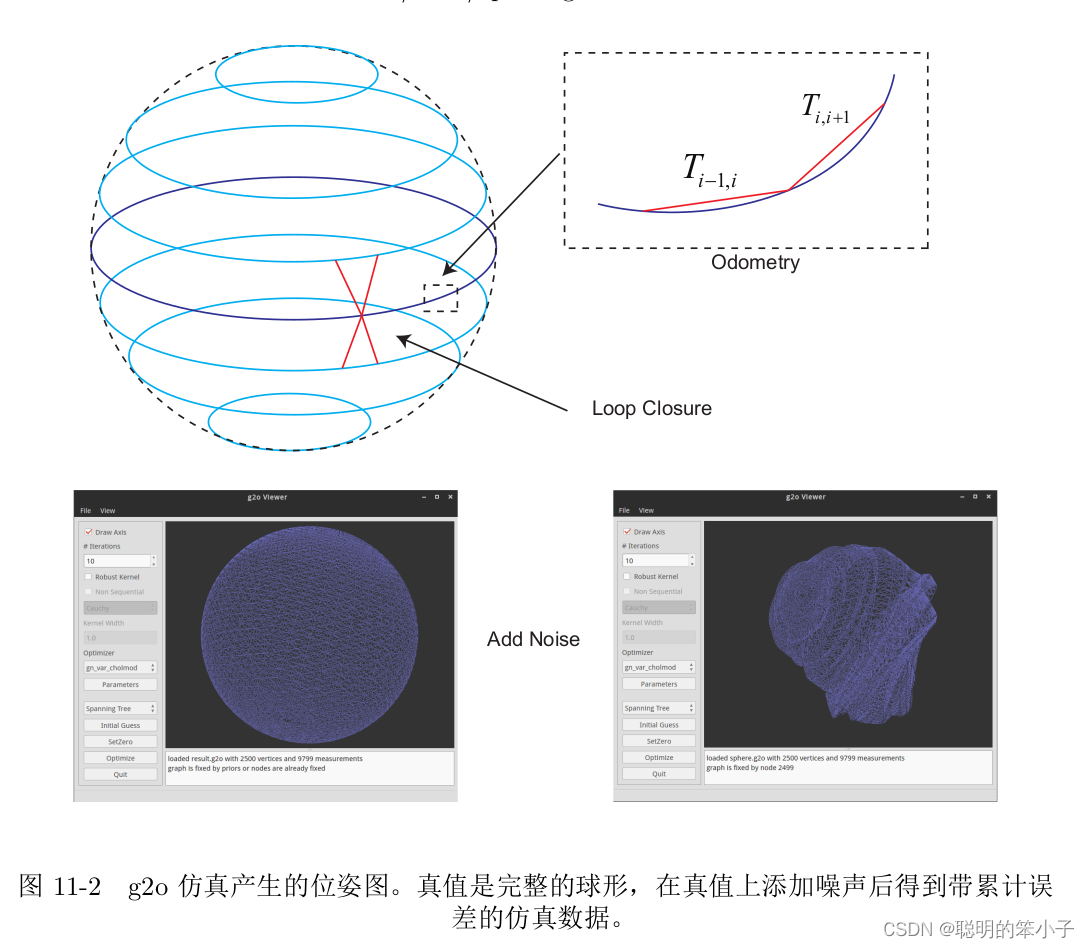
位姿图优化的代码使用了g2o库自带的SE3和自己定义的SE3来实现。因为g2o自带的默认旋转向量以四元数的形式表示。代码分别如下：

#include <iostream>
#include <fstream>
#include <string>

#include <g2o/types/slam3d/types_slam3d.h>
#include <g2o/core/block_solver.h>
#include <g2o/core/optimization_algorithm_levenberg.h>
#include <g2o/core/optimization_algorithm_gauss_newton.h>
#include <g2o/solvers/dense/linear_solver_dense.h>
#include <g2o/solvers/cholmod/linear_solver_cholmod.h>
using namespace std;

/************************************************
 * 本程序演示如何用g2o solver进行位姿图优化
 * sphere.g2o是人工生成的一个Pose graph，我们来优化它。
 * 尽管可以直接通过load函数