李群和李代数是SLAM中在优化时用到的两个数学概念。在看高翔博士SLAM14讲的时候对这一部分学的是一知半解,只是知道李代数是为了更好的求解最小二乘问题中转移矩阵的求导问题引入的。后来看了一些网上大佬的解释,感觉有了更深入的了解,所以写下来记录下自己的理解。
一. 李群
1.1 群
首先是群的定义,在高博的书中对于群的定义是:
群(Group)是一种集合(G),加上一种运算(·)组成的结构。他满足的条件如下:
- 封闭性:对于所有G中a, b,运算a·b的结果也在G中
- 结合律:对于所有G中的a, b和c,等式 (a·b)·c = a· (b·c)成立
- 幺元:存在G中的一个元素e,使得对于所有G中的元素a,总有等式e·a = a·e = a 成立
- 逆元:对于每个G中的a,存在G中的一个元素b使得总有a·b = b·a = e,此处e为单位
快速记忆的方法就是“凤姐咬你”。我对于群的理解就是对于一个集合,在其内部进行一种运算,该运算满足以上条件,就称该集合和运算构成一个群。而在对于SLAM问题来说,不论是旋转矩阵还是齐次变换矩阵,他们是一种特殊的集合,满足一定的性质。并且对于乘法*,上面四条关于群的性质是满足的。所以称三维旋转矩阵R构成了特殊的正交群SO(3),而三维变换矩阵构成了特殊的欧式群SE(3)。
但是需要注意的是,不论R还是T,他们对于加法是不满足上诉条件的,故称他们对加法不封闭。而这个就是我们需要引入李代数的主要原因,后面会讲到。
1.2 李群
那什么是李群。李群其实就是连续的群。
对谁连续?对于SO(3)和SE(3),他们是对时间连续的,所以他们也是李群的一种。
二. 李代数
2.1 李代数的引出
首先对于一个旋转矩阵R。它随着时间变化而变化,那么可以记为R(t)。根据旋转矩阵的定义,有
对两边求导,可以得到
整理得
可以看出,是一个反对称矩阵。根据反对称矩阵的性质,会有一个向量对之对应。对于反对对称矩阵
,我们将它对应的向量记作
。那么就可以找到一个向量
,使得
因为对来说存在
。所以对等式两边同时右乘R(t)得
于是,对R(t)的求导就变成了对R(t)左乘一个反对称矩阵。
假设t0 = 0 和 R(t0) = I。 那么在t0 = 0 处进行一阶泰勒展开:
故称在
原点附近的正切空间上 (没有太理解,后面更新)
设,那么就有
求解这个一次微分方程就可以得到R(t)关于t的表达式
到此,我们找到了旋转矩阵和一个向量之间的转换关系,两者之间存在一个指数映射的关系。而这个
其实就是后面引出的旋转矩阵
对应的李代数
。
2.2 李代数so(3)
首先是给出李代数的定义。
李代数有一个集合V,一个数域F和一个二元运算[·]组成。其中二元运算记作李括号。根群的定义相似,它也有四个性质需要满足:
- 封闭性
- 双线性
- 自反性
- 雅可比等价
李代数是为了研究李群和微分流形之类的几何对象而引入的。每个李群都有与之对应的李代数,李代数描述了李群的局部性质。
对于上诉的,对应的是一个三维的向量,记作
,并且对应一个反对称矩阵
。
在此定义下,两个向量和
对应的李括号运算为
其中是表示将反对称矩阵转换回向量的符号
于是此时定义了so(3)的李代数形式如下:
而so(3)的指数映射就是SO(3)。
2.2 李代数se(3)
那么SO(3)找到对应的映射,SE(3)(即转换矩阵T对应的李群,欧式正交群)也应该有对应的映射。这里跟SLAM14讲书上一样,没有数学证明直接给出公式。
se(3)的定义如下:
其中对应的是平移向量。而对应的李括号的运算定义如下:
三. 指数映射
3.1 so(3)上的指数映射
在2.1的末尾,引出了,而公式的右边是一个矩阵的指数形式,成为指数映射
根据矩阵指数映射的性质,任意矩阵的指数映射可以写成一个泰勒展开,但是只有在收敛的情况下才会有结果,其结果仍是一个矩阵。
所以,对于矩阵就有
是一个三维向量,对于三维向量,可以由一个模长和一个单位方向向量来表示,即
并且对于有如下的性质:
这里套用书中的推导:
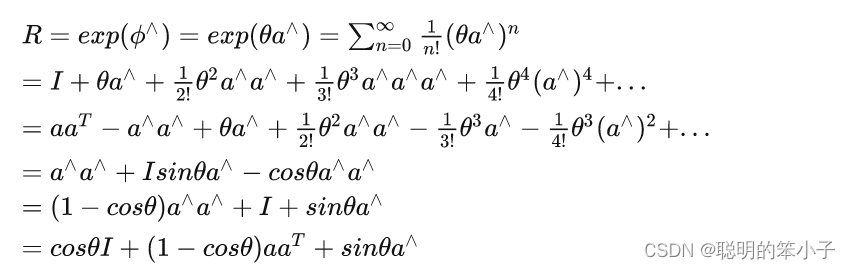
可以发现,最后的结果与之前旋转向量到旋转矩阵的转换公式(即罗斯里格斯公式)一样。这就说明了so(3)正是旋转向量组成的空间,而指数映射正是罗斯里格斯公式。
反之,在SO(3)中定义so(3)的映射就是对数映射
3.2 se(3)上的指数映射
se(3)的指数映射定义如下:
简写为:
其中对应旋转矩阵,而
对应平移向量
四. 总结
至此,介绍完李群和李代数以及他们在旋转矩阵和转换矩阵中转换证明,我们可以得到一个结论:
在SO(3)上进行的操作,可以等价到so(3)的指数映射上。这也就意味着当我们需要在SO(3)进行加法运算时,可以转换到so(3)的指数映射上进行。
至于为什么需要使用到加法,这就涉及对旋转矩阵求导,回放下一篇文章。
本文引用:
[1] 高翔,张涛, “视觉SLAM十四讲”, https://github.com/gaoxiang12/slambook/blob/master/ch6/g2o_curve_fitting/main.cpp
[2] 菠萝包包包, “李群和李代数 —— 名字听起来很猛其实也没那么复杂”,李群和李代数 —— 名字听起来很猛其实也没那么复杂 - 知乎
[3] 李狗嗨,"如何通俗地解释李群和李代数的关系?",如何通俗地解释李群和李代数的关系? - 知乎





 文章介绍了李群和李代数在SLAM中的应用,特别是如何解决旋转矩阵和变换矩阵的优化问题。李群如SO(3)和SE(3)分别对应三维旋转和平移,而李代数so(3)和se(3)则用于描述这些群的局部性质。通过指数映射和对数映射,可以在李代数上进行加法运算,解决了群运算中的非封闭性问题,简化了计算过程。
文章介绍了李群和李代数在SLAM中的应用,特别是如何解决旋转矩阵和变换矩阵的优化问题。李群如SO(3)和SE(3)分别对应三维旋转和平移,而李代数so(3)和se(3)则用于描述这些群的局部性质。通过指数映射和对数映射,可以在李代数上进行加法运算,解决了群运算中的非封闭性问题,简化了计算过程。
















 3472
3472

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








