题目描述
给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ,同时还满足 nums[i] + nums[j] + nums[k] == 0 。请你返回所有和为 0 且不重复的三元组。
注意:答案中不可以包含重复的三元组。
示例 1:
输入:nums = [-1,0,1,2,-1,-4]
输出:[[-1,-1,2],[-1,0,1]]
解释:
nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。
nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。
nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。
不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。
注意,输出的顺序和三元组的顺序并不重要。
示例 2:
输入:nums = [0,1,1]
输出:[]
解释:唯一可能的三元组和不为 0 。
示例 3:
输入:nums = [0,0,0]
输出:[[0,0,0]]
解释:唯一可能的三元组和为 0 。
提示:
3 <= nums.length <= 3000
-105 <= nums[i] <= 105
思考(暴力三重循环)
暴力解法,三重循环分别枚举 i,j,k,但是要注意去重。首先给数组排序,这是为了把相同的元素放到一起。然后每个循环开始都执行类似这样的语句if (j !== i + 1 && nums[j] === nums[j-1]),这是判断如果当前遍历的元素不是当前循环开始的第一个,那么判断前一个元素是否和当前元素相同,如果相同就跳过不使用,这样保证了每个重复元素都是使用第一个出现的。整个时间复杂度是O(n3)O(n^3)O(n3),不满足题目要求的规模3<=nums.length<=30003 <= nums.length <= 30003<=nums.length<=3000,需要优化。
代码
/**
* @param {number[]} nums
* @return {number[][]}
*/
var threeSum = function(nums) {
const ans = [];
nums.sort((a,b) => a-b);
const len = nums.length;
for (let i = 0; i < len-2; i++) {
if (i !== 0 && nums[i] === nums[i-1]) continue; // 去重
for (let j = i + 1; j < len-1; j++) {
if (j !== i + 1 && nums[j] === nums[j-1]) continue; // 去重
for (let k = j + 1; k < len; k++) {
if (k !== j + 1 && nums[k] === nums[k-1]) continue; // 去重
if (nums[i] + nums[j] + nums[k] === 0) {
ans.push([nums[i], nums[j], nums[k]]);
}
}
}
}
return ans;
};
思考二(双指针)
三个数,i<j<ki < j < ki<j<k,数组从小到大排序后,枚举第一个数 nums[i],后面两个数位于第一个数后面的单调递增的开区间 (i,nums.length)(i, nums.length)(i,nums.length),可以用相向双指针快速找到满足条件 sum = nums[i] + nums[j] + nums[k] = 0。当 sum < 0 时表示 nums[j] + nums[k] 值偏小,应该 j++,让较小的数变大;当 sum > 0 时,k–,让较大的数变小;sum == 0 时,得到一个解,此时,j++,k–,排除计算过的数,寻求新的解。
- 为什么不会漏掉解?
假设存在一组有效解(i, j0, k0)(i < j0 < k0),我们需要证明双指针遍历过程中一定会遇到j0和k0。
- 初始时
j = i+1,k = n-1,显然j ≤ j0且k ≥ k0(因为j0在i右侧,k0在数组中间)。 - 若当前
j < j0:- 此时
k可能大于k0(因为初始k是最右侧)。由于nums[j] ≤ nums[j0]且nums[k] ≥ nums[k0],则nums[j] + nums[k] ≥ nums[j0] + nums[k0](目标和)。 - 若总和偏大(
>0),会左移k直到k = k0;若总和刚好等于目标,则直接找到解。
- 此时
- 若当前
k > k0:- 此时
j可能小于j0。由于nums[j] ≤ nums[j0]且nums[k] ≥ nums[k0],若总和偏小(<0),会右移j直到j = j0。
- 此时
通过上述过程,双指针会逐步逼近 j0 和 k0,最终必然会遍历到这组解。
- 去重
- 外层循环依然通过
if (i > 0 && nums[i] === nums[i-1]) continue;这种方式去重。 - 双指针循环中在找到一组解后要循环判断当前元素和下一个元素是否重复,重复继续移动指针。
- 为什么在 sum ≠ 0 的情况下不用去重?因为非解状态(sum ≠ 0)下,重复元素不影响结果唯一性,即使指针在几个重复元素上移动,但由于不是有效解,无关紧要。去重的目的是避免相同的三元组被重复记录。
- 外层循环依然通过
代码
/**
* @param {number[]} nums
* @return {number[][]}
*/
var threeSum = function(nums) {
const ans = [];
nums.sort((a,b) => a-b);
const len = nums.length;
for (let i = 0; i < len-2; i++) {
if (nums[i] > 0) break; // 升序排序的数组,如果当前nums[i] > 0,三数之和一定大于0,剪枝
if (i > 0 && nums[i] === nums[i-1]) continue; // 去重:保证连续重复的数字只用第一个
let j = i + 1, k = len - 1;
while (j < k) {
const sum = nums[i] + nums[j] + nums[k];
if (sum === 0) {
ans.push([nums[i], nums[j], nums[k]]);
while (j < k && nums[j] === nums[j+1]) j++; // 去重:保证连续重复的数字只用第一个
while (j < k && nums[k] === nums[k-1]) k--; // 去重:保证连续重复的数字只用最后一个
j++;
k--;
} else if (sum < 0) {
j++;
} else {
k--;
}
}
}
return ans;
};
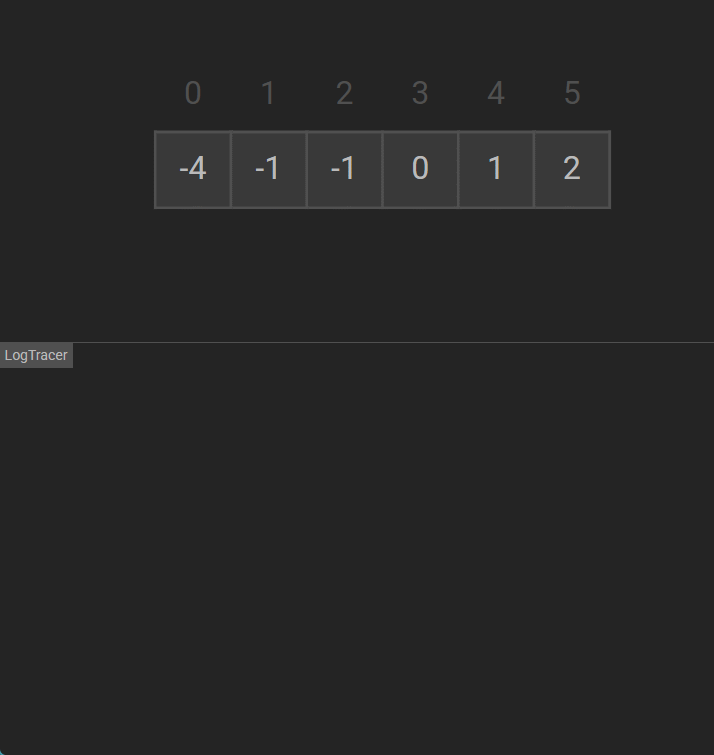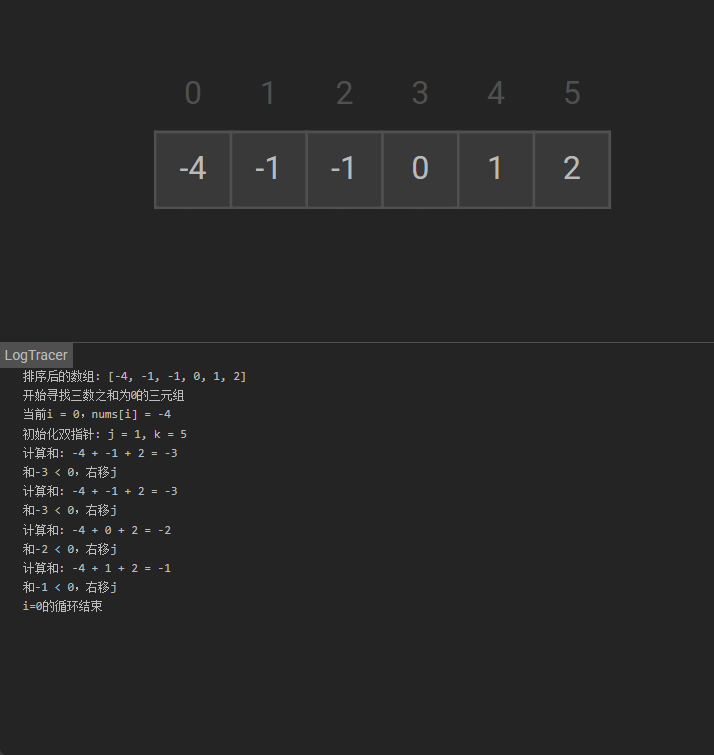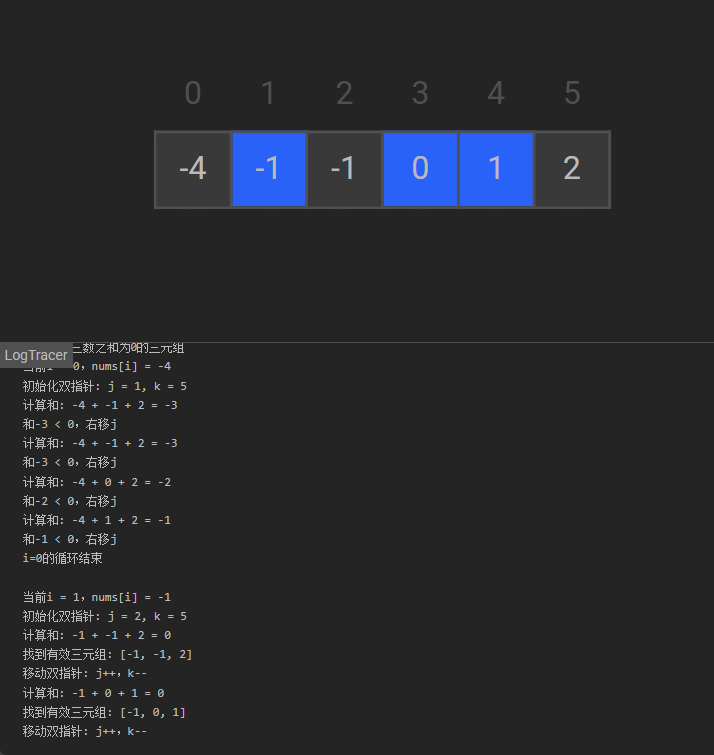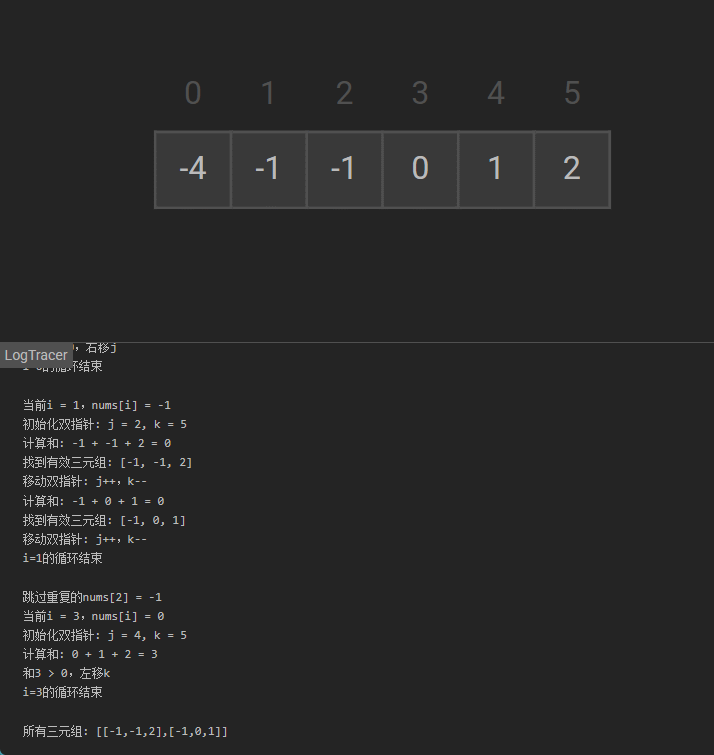
可视化





















 1008
1008

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








