【LeetCode热题100道笔记+动画】单词拆分

题目描述

给你一个字符串 s 和一个字符串列表 wordDict 作为字典。如果可以利用字典中出现的一个或多个单词拼接出 s 则返回 true。

注意：不要求字典中出现的单词全部都使用，并且字典中的单词可以重复使用。

示例 1：
输入: s = “leetcode”, wordDict = [“leet”, “code”]
输出: true
解释: 返回 true 因为 “leetcode” 可以由 “leet” 和 “code” 拼接成。

示例 2：
输入: s = “applepenapple”, wordDict = [“apple”, “pen”]
输出: true
解释: 返回 true 因为 “applepenapple” 可以由 “apple” “pen” “apple” 拼接成。
注意，你可以重复使用字典中的单词。

示例 3：
输入: s = “catsandog”, wordDict = [“cats”, “dog”, “sand”, “and”, “cat”]
输出: false

提示：

• 1 <= s.length <= 300
• 1 <= wordDict.length <= 1000
• 1 <= wordDict[i].length <= 20
• s 和 wordDict[i] 仅由小写英文字母组成
• wordDict 中的所有字符串 互不相同

思考

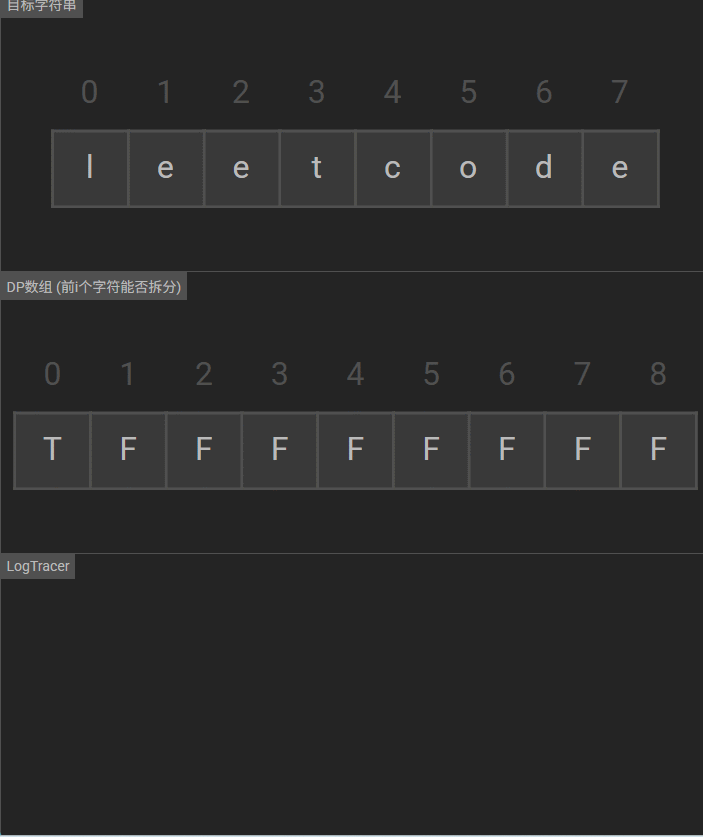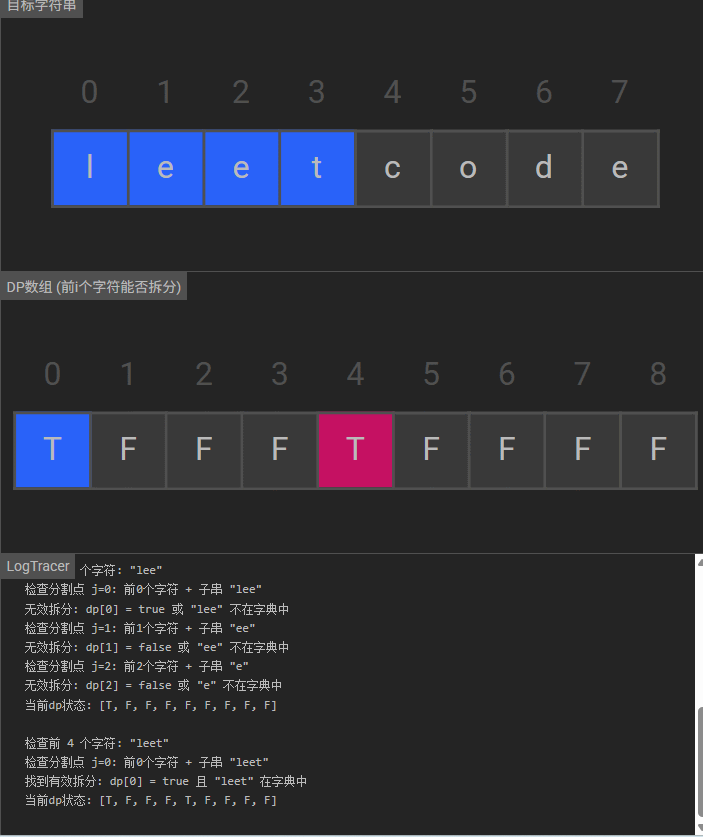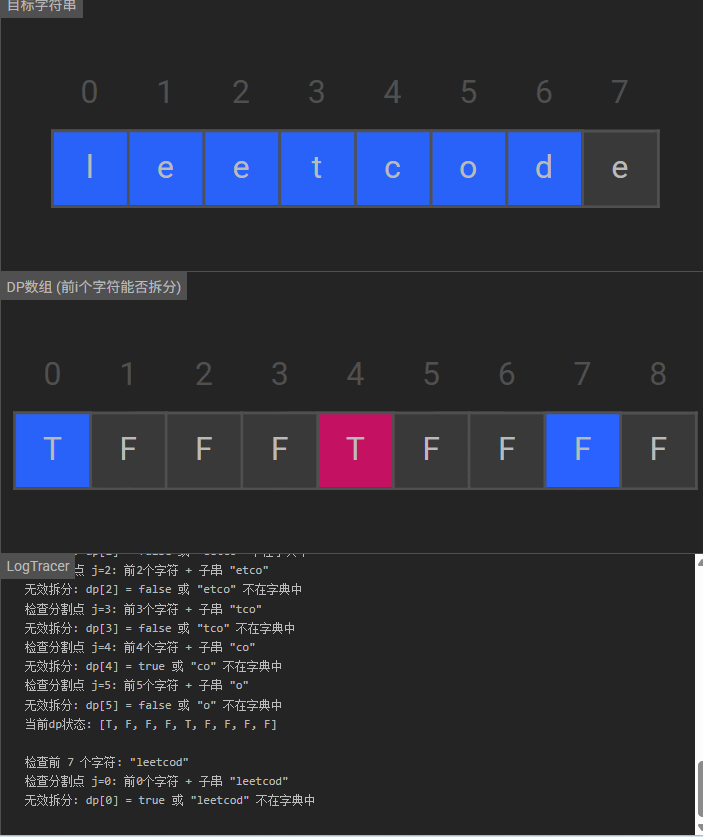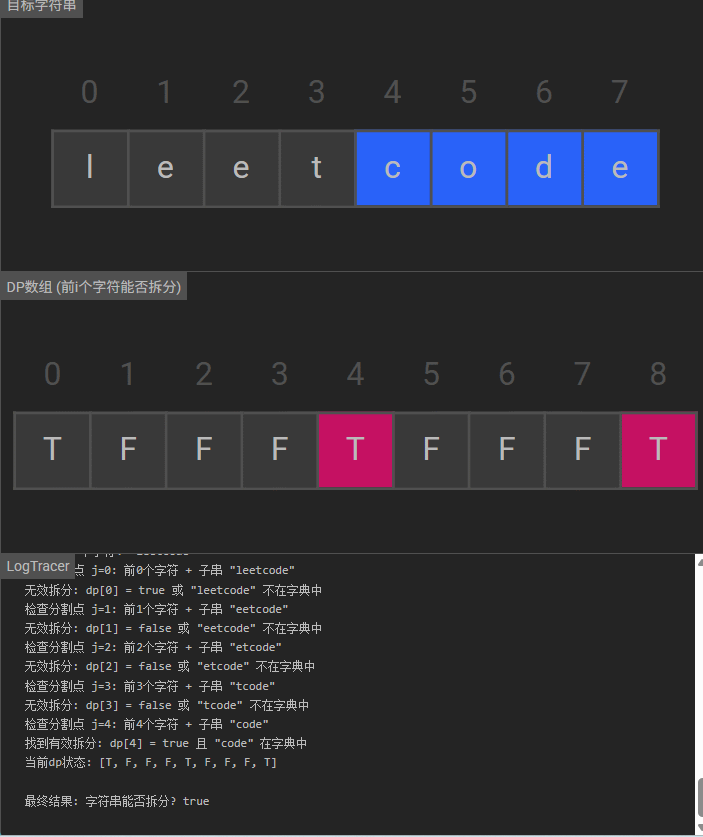
动态规划解法通过状态追踪字符串前缀的可分割性：

• dp[i] 表示字符串 s 的前 i 个字符（s[0..i-1]）能否被分割为字典中的单词组合
• 核心逻辑：枚举分割点，若前缀可分割且剩余子串在字典中，则当前前缀可分割

算法过程

1. 初始化：

   • dp 数组长度为 n+1（n 为字符串长度），dp[0] = true（空字符串可被分割）
   • 其余 dp[i] 初始为 false

2. 状态更新：

   • 遍历所有前缀长度 i（从 1 到 n）：
     • 枚举分割点 j（从 0 到 i-1）：
       • 若 dp[j] 为 true（前 j 个字符可分割），且子串 s[j..i-1] 在字典中：
         • 标记 dp[i] = true 并跳出循环（找到有效分割）

3. 返回结果：dp[n] 表示整个字符串能否被分割

时间复杂度

• 时间复杂度：O(n² × m)，n 为字符串长度（两层循环），m 为子串平均长度（includes 方法和 substring 操作）
• 空间复杂度：O(n)，需存储长度为 n+1 的 dp 数组 。

代码

/**
 * @param {string} s
 * @param {string[]} wordDict
 * @return {boolean}
 */
var wordBreak = function(s, wordDict) {
    const n = s.length;
    const dp = Array(n+1).fill(false);
    dp[0] = true;

    for (let i = 1; i <= n; i++) {
        for (let j = 0; j < i; j++) {
            if (dp[j] && wordDict.includes(s.substring(j, i))) {
                dp[i] = true;
                break;
            }
        }
    }
    
    return dp[n];
};

可视化