题目描述
给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
示例 1:
输入:nums = [1,5,11,5]
输出:true
解释:数组可以分割成 [1, 5, 5] 和 [11] 。
示例 2:
输入:nums = [1,2,3,5]
输出:false
解释:数组不能分割成两个元素和相等的子集。
提示:
- 1 <= nums.length <= 200
- 1 <= nums[i] <= 100
思考
0-1背包问题的变形应用:将问题转化为"能否从数组中选取部分元素,使其和等于数组总和的一半"。通过动态规划求解,利用滚动数组优化空间复杂度。
算法过程
- 计算数组总和,若为奇数直接返回false(无法分割为两个等和子集)
- 定义目标容量
volume = sum / 2,问题转化为"能否装满容量为volume的背包" - 初始化dp数组:
dp[j]表示能否组成和为j的子集,dp[0] = true(空子集) - 遍历每个元素v:
- 从大到小遍历容量j(避免重复使用同一元素)
- 状态转移:
dp[j] = dp[j] || dp[j - v](不选v或选v)
- 最终返回
dp[volume](能否组成目标和)
时间复杂度
- 时间复杂度:O(n×volume),n为数组长度,volume为总和的一半
- 空间复杂度:O(volume),使用滚动数组优化,仅需一维数组存储状态
该方法通过动态规划高效解决子集分割问题,将0-1背包思想巧妙应用于子集和判断场景。
代码
/**
* @param {number[]} nums
* @return {boolean}
*/
var canPartition = function(nums) {
const sum = nums.reduce((a, b) => a + b, 0);
if (sum % 2 !== 0) return false; // 和为奇数时无法分割
const volume = sum / 2;
// dp[j]表示能否组成和为j的子集
const dp = Array(volume + 1).fill(false); // 数组长度应为volume + 1
dp[0] = true; // 基础情况:和为0可以通过空子集实现
for (let v of nums) {
// 从大到小遍历,避免重复使用同一个元素
for (let j = volume; j >= v; j--) {
// 状态转移:如果j-v可以组成,那么j也可以组成
dp[j] = dp[j] || dp[j - v];
}
}
return dp[volume];
};
可视化
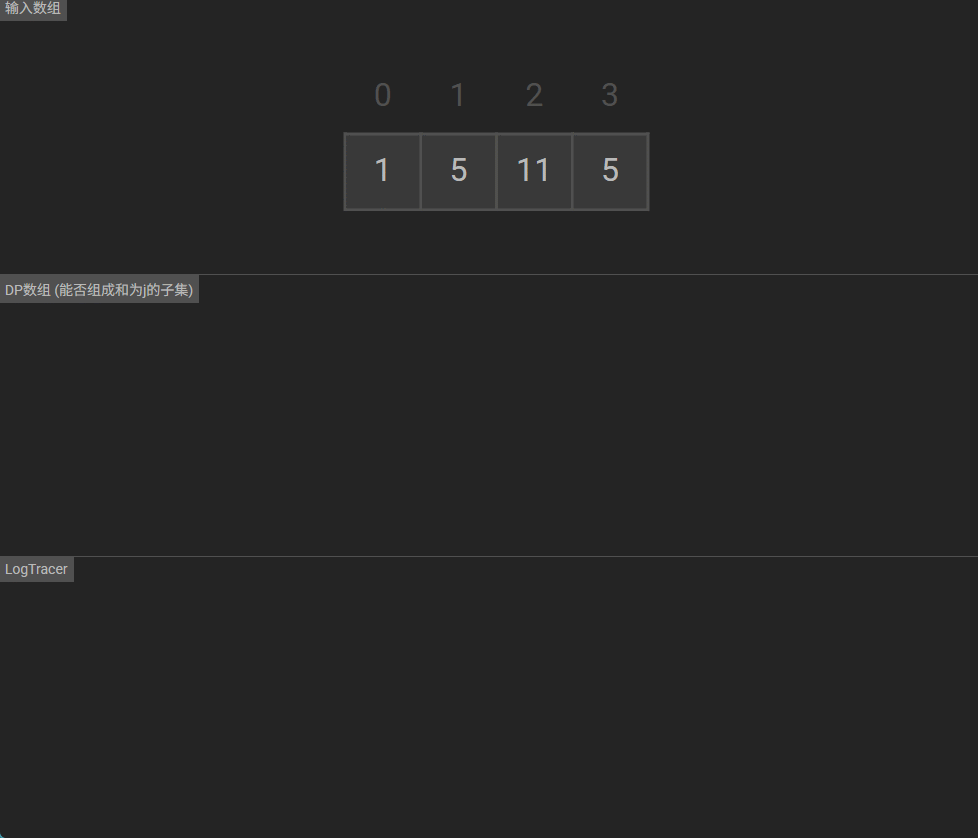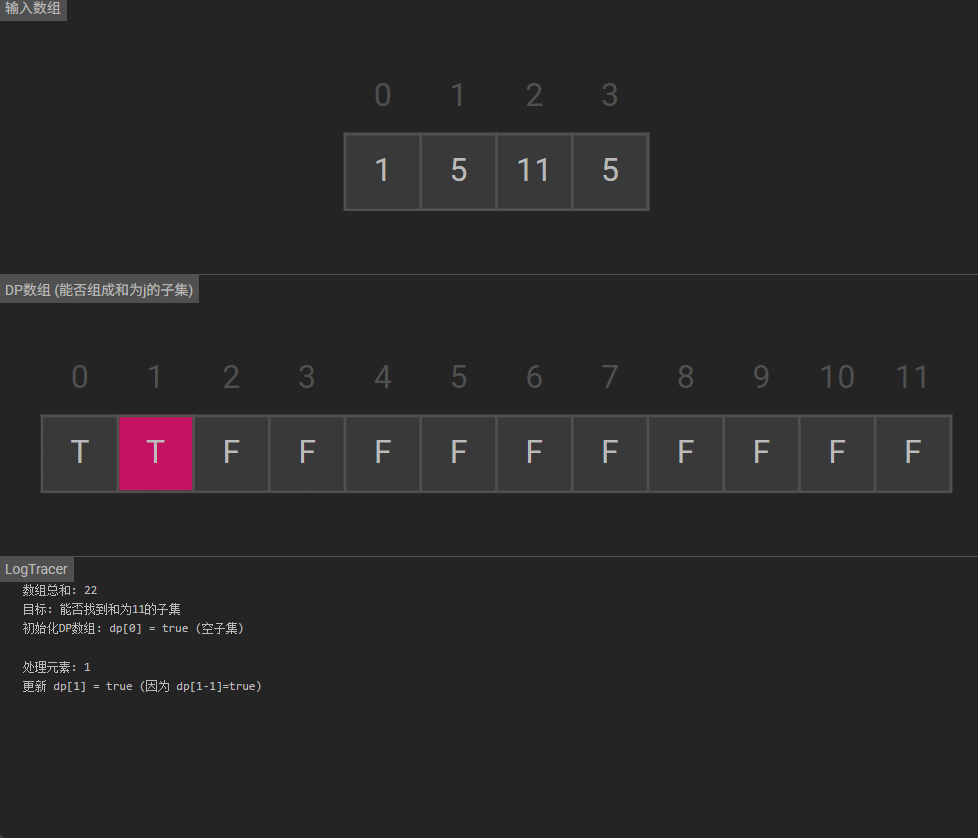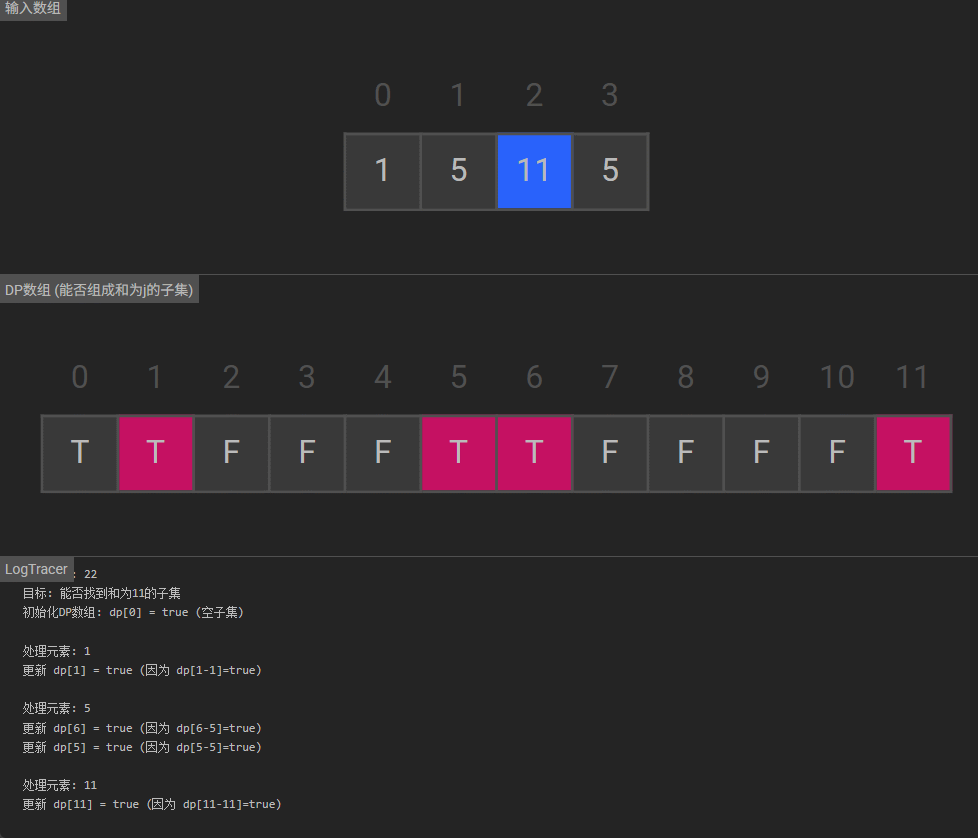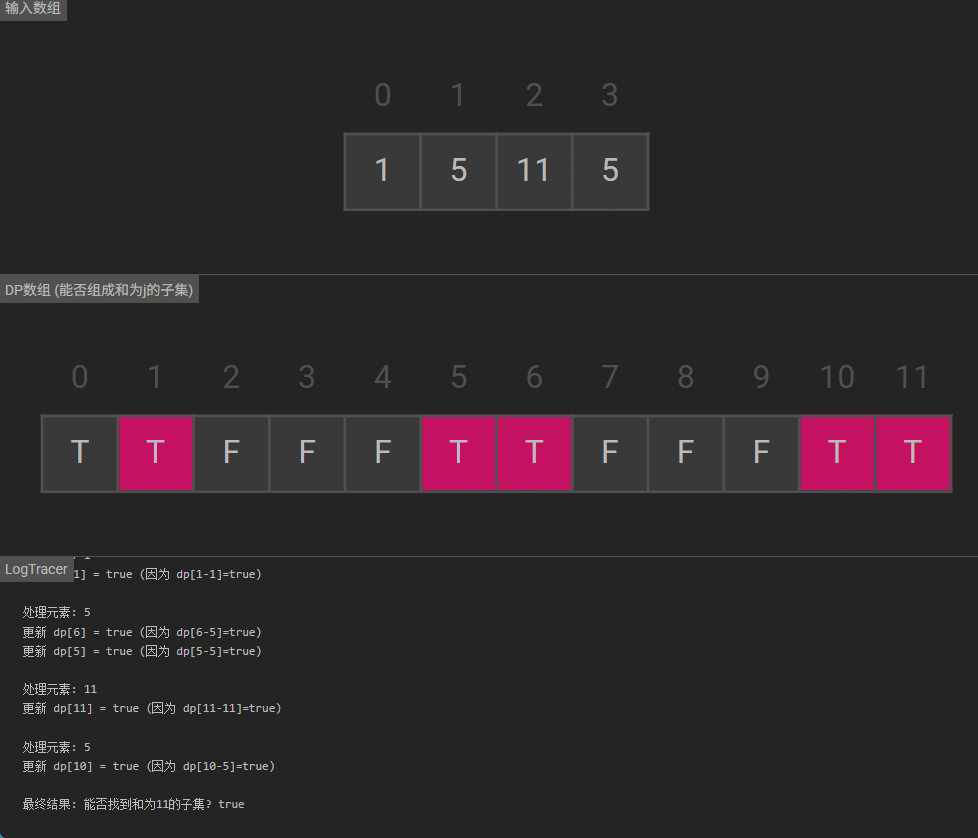






















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








