【LeetCode热题100道笔记+动画】盛最多水的容器

题目描述

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。
找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。
说明：你不能倾斜容器。

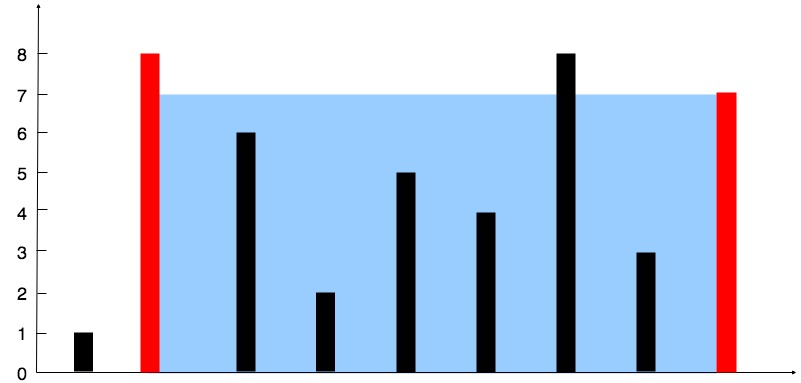
示例 1：
输入：[1,8,6,2,5,4,8,3,7]
输出：49
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例 2：
输入：height = [1,1]
输出：1

提示：
n == height.length
2 <= n <= 105
0 <= height[i] <= 104

思考

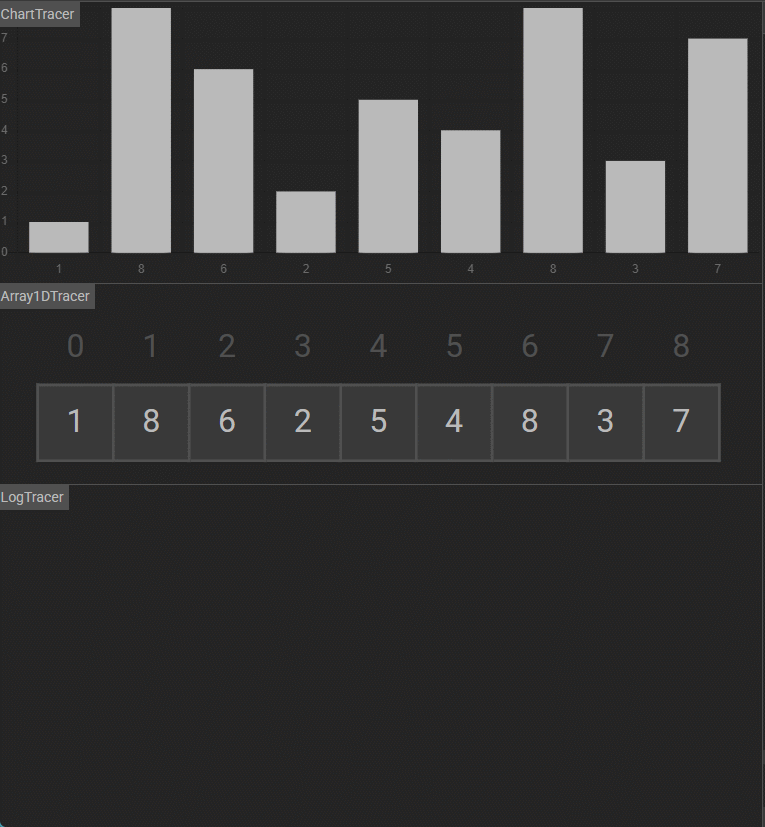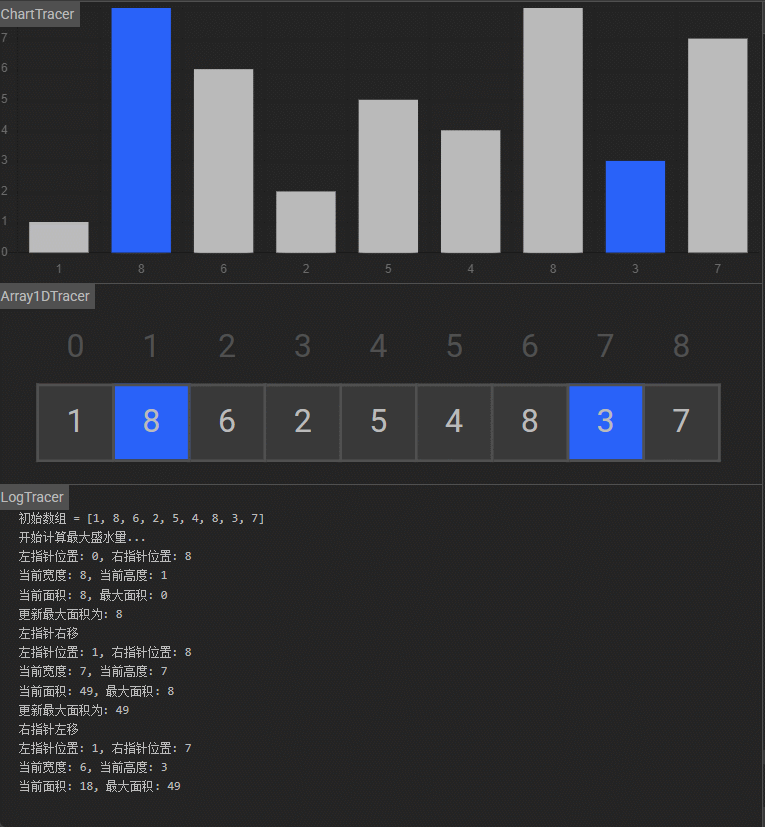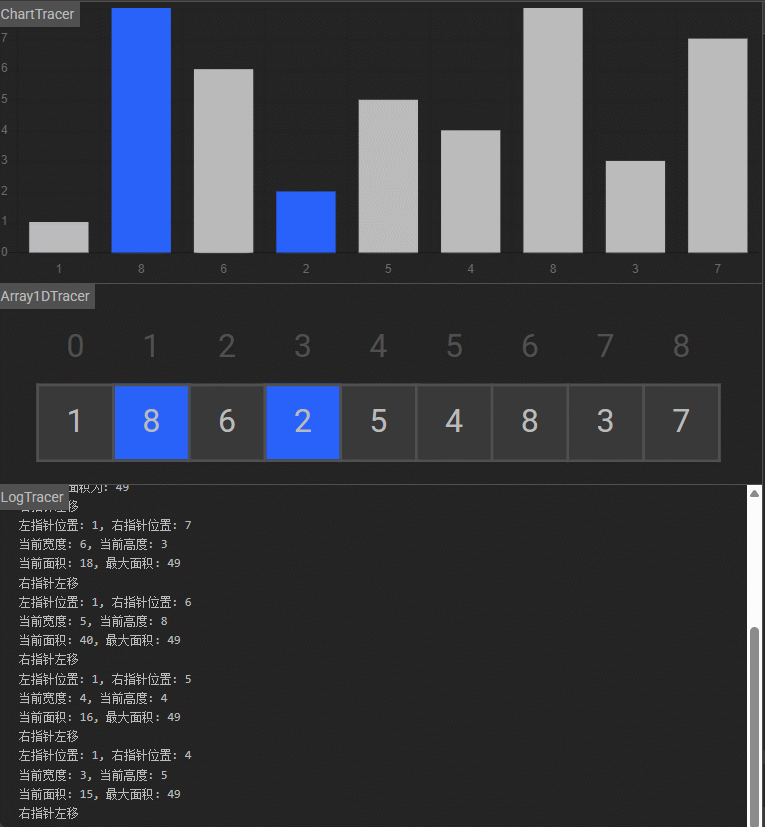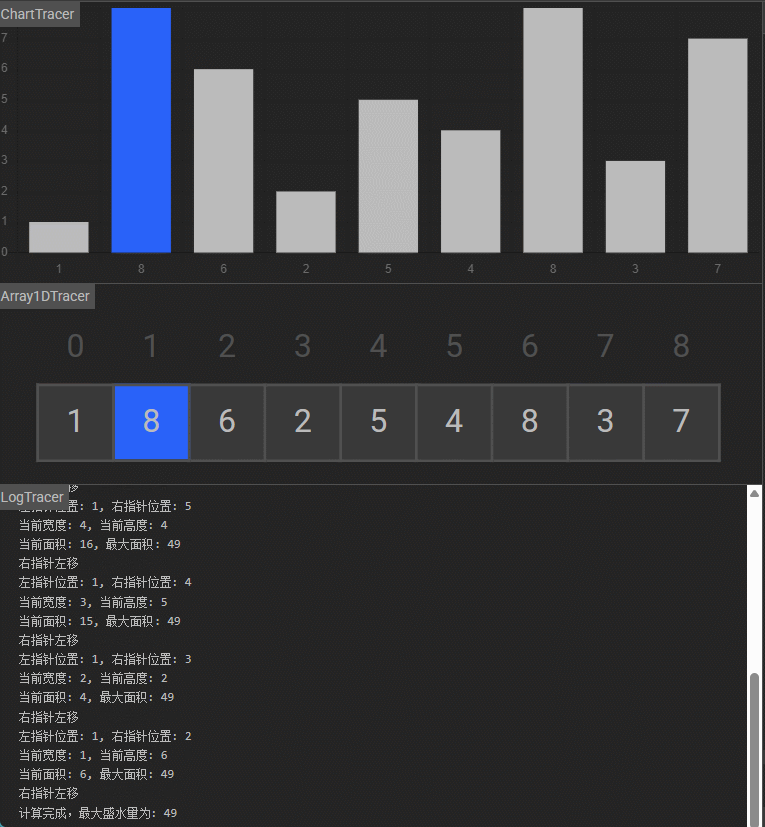
相向双指针+贪心，矩形宽度每次递减的同时尽量移动指针使最小的高度条增大。开始时左右指针分别为 l = 0 和 r = height.length-1 位置，此时盛水矩形宽度是 r -l，此时无论 l++ 还是 r--， 矩形宽度必然都减小，如果希望矩形面积变大，只能寄希望于高度条 height[l] 或 height[r] 变大，由于实际矩形的高度取两者中较小的 $min(height[l],height[r])$，所以肯定是把较小的高度条更新为较大的才可能使整个矩形面积增大。再反过来证明，如果我更新指向高度较大的指针，此时假如移动后指针指向更大的高度条了，但是由于矩形高度由两侧较小的高度决定，因此即使较大的高度变得更大，仍然会使用较小的那个高度，所以移动指向较大高度的指针不可能让矩形面积变大。这其实类似木桶原理，我要让木桶装更多水应该加长它的短板。相向双指针遍历了整个数组一遍，每次移动指针更新当前矩形面积，更新全局最大矩形面积， 时间复杂度 $O(n)$，空间复杂度$O(1)$。

算法过程

1. 初始化：左指针 l 指向数组起始位置（0），右指针 r 指向数组末尾（height.length - 1），最大面积 ans 初始化为0。
2. 计算当前面积：根据两指针位置，计算当前容器容量（(r - l) * min(height[l], height[r])），并更新最大面积 ans。
3. 移动指针：若左指针高度小于右指针高度（height[l] < height[r]），则右移左指针（l++）；否则左移右指针（r--）（核心逻辑：移动较矮的一侧，才可能提升容器高度）。
4. 终止条件：当左右指针相遇（l >= r）时，循环结束，返回最大面积 ans。

代码

/**
 * @param {number[]} height
 * @return {number}
 */
var maxArea = function(height) {
    let l = 0, r = height.length-1;
    let ans = 0;
    while (l < r) {
        const area = (r - l) * Math.min(height[l], height[r]);
        ans = Math.max(ans, area);
        if (height[l] < height[r]) {
            l++;
        } else {
            r--;
        }
    }
    return ans;
};

可视化