题目描述
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。
计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。
你可以认为每种硬币的数量是无限的。
示例 1:
输入:coins = [1, 2, 5], amount = 11
输出:3
解释:11 = 5 + 5 + 1
示例 2:
输入:coins = [2], amount = 3
输出:-1
示例 3:
输入:coins = [1], amount = 0
输出:0
提示:
- 1<=coins.length<=121 <= coins.length <= 121<=coins.length<=12
- 1<=coins[i]<=231−11 <= coins[i] <= 231 - 11<=coins[i]<=231−1
- 0<=amount<=1040 <= amount <= 10^40<=amount<=104
思考
完全背包问题的应用:将硬币面值视为物品,金额金额视为背包容量,求解求“装满容量为amount的背包所需最少物品数量”。通过动态规划求解,允许物品重复选择(硬币可多次使用)。
算法过程
-
初始化:
dp[i]表示装满金额i所需的最少硬币数- 初始化
dp数组为Infinity(表示初始状态下无法装满) - 特例:
dp[0] = 0(金额为0时无需任何硬币)
-
状态更新:
- 遍历所有金额
i(从1到amount):- 遍历每个硬币面值
coins[j]:- 若
i >= coins[j](当前硬币可使用),则dp[i] = min(dp[i], dp[i - coins[j]] + 1)(取“不使用当前硬币”和“使用当前硬币(基于i - coins[j]的解加1)”中的最小值)
- 若
- 遍历每个硬币面值
- 遍历所有金额
-
结果判断:
- 若
dp[amount]仍为Infinity,返回-1(无法凑成该金额) - 否则返回
dp[amount](最少硬币数)
- 若
时间复杂度
- 时间复杂度:O(amount × n),
amount为目标金额,n为硬币种类数(两层循环) - 空间复杂度:O(amount),需存储长度为
amount + 1的dp数组
该方法通过完全背包的正向遍历逻辑(允许重复使用硬币),高效求解最少硬币数量,利用 Infinity 巧妙标记不可达状态。
代码
/**
* @param {number[]} coins
* @param {number} amount
* @return {number}
*/
var coinChange = function(coins, amount) {
const dp = Array(amount+1).fill(Infinity);
dp[0] = 0;
for (let i = 1 ; i <= amount; i++) {
for (j = 0; j < coins.length; j++) {
if (i >= coins[j]) {
dp[i] = Math.min(dp[i], dp[i-coins[j]] + 1);
}
}
}
return dp[amount] === Infinity ? -1: dp[amount];
};
可视化
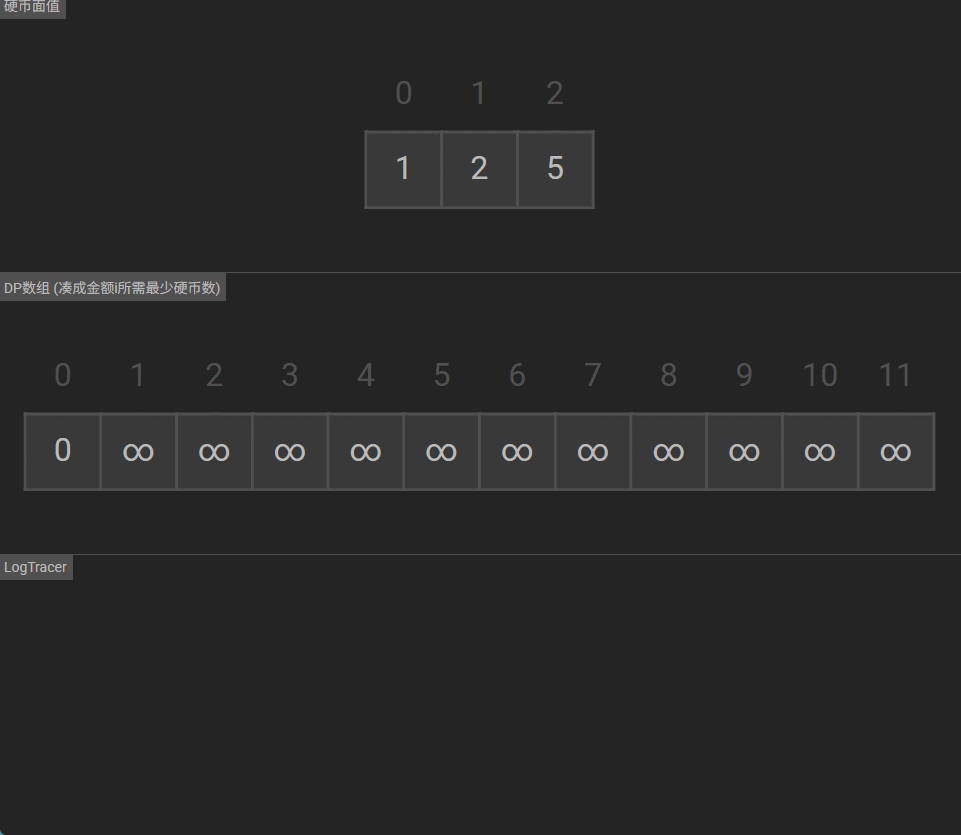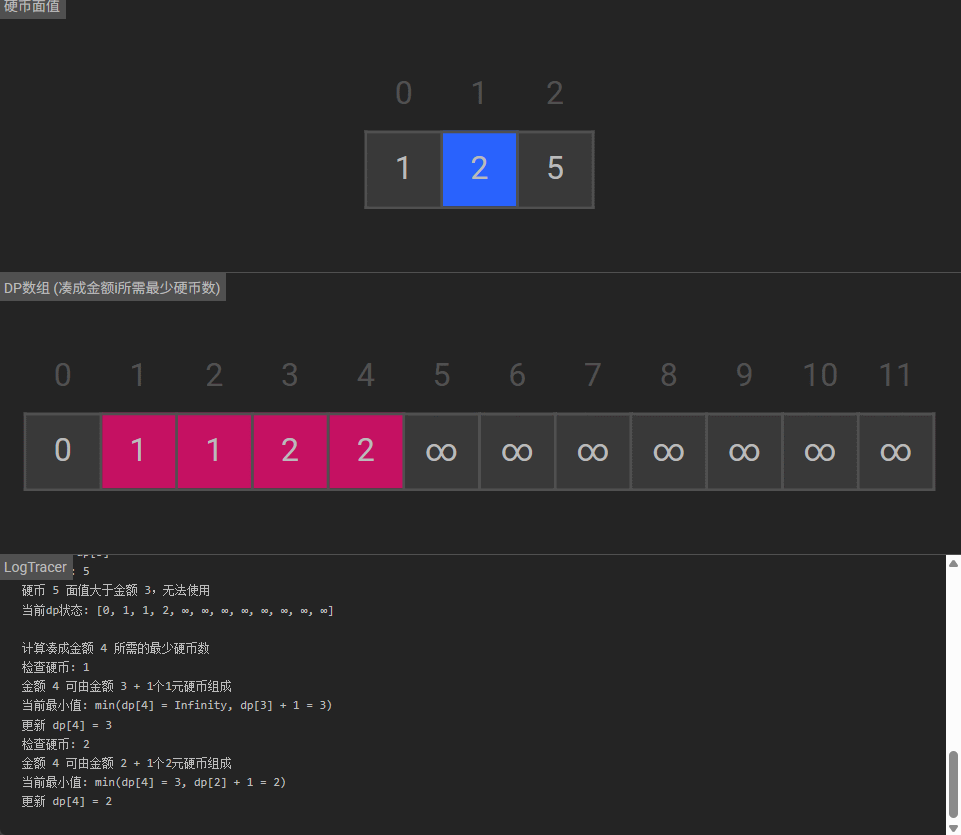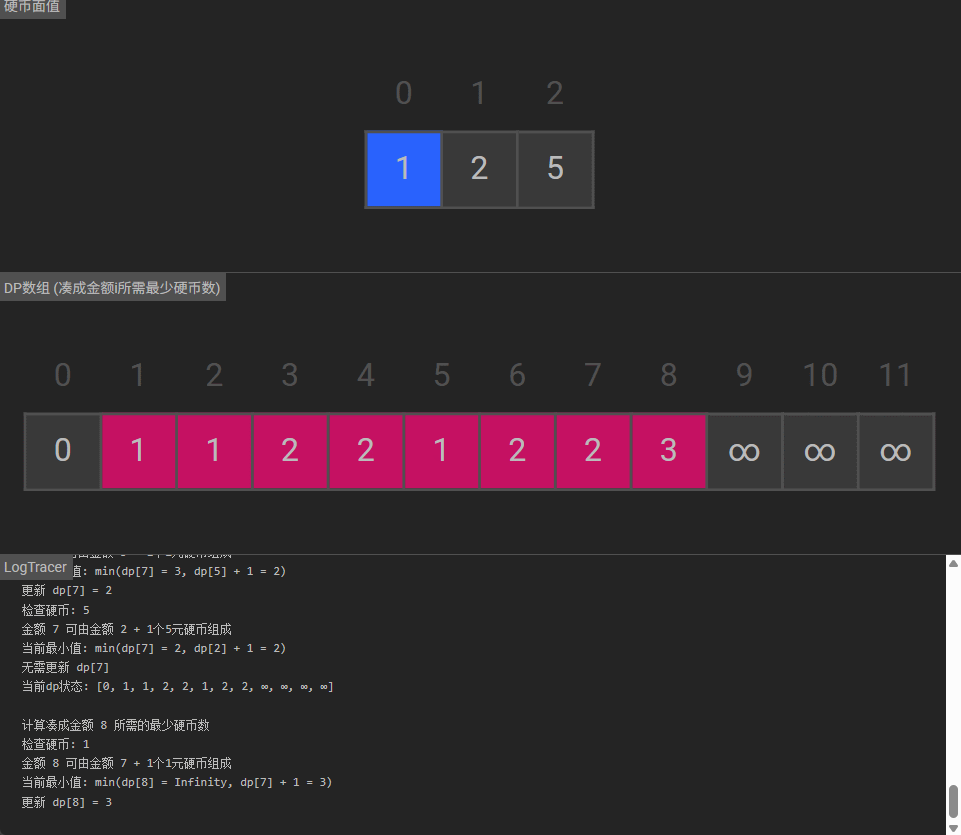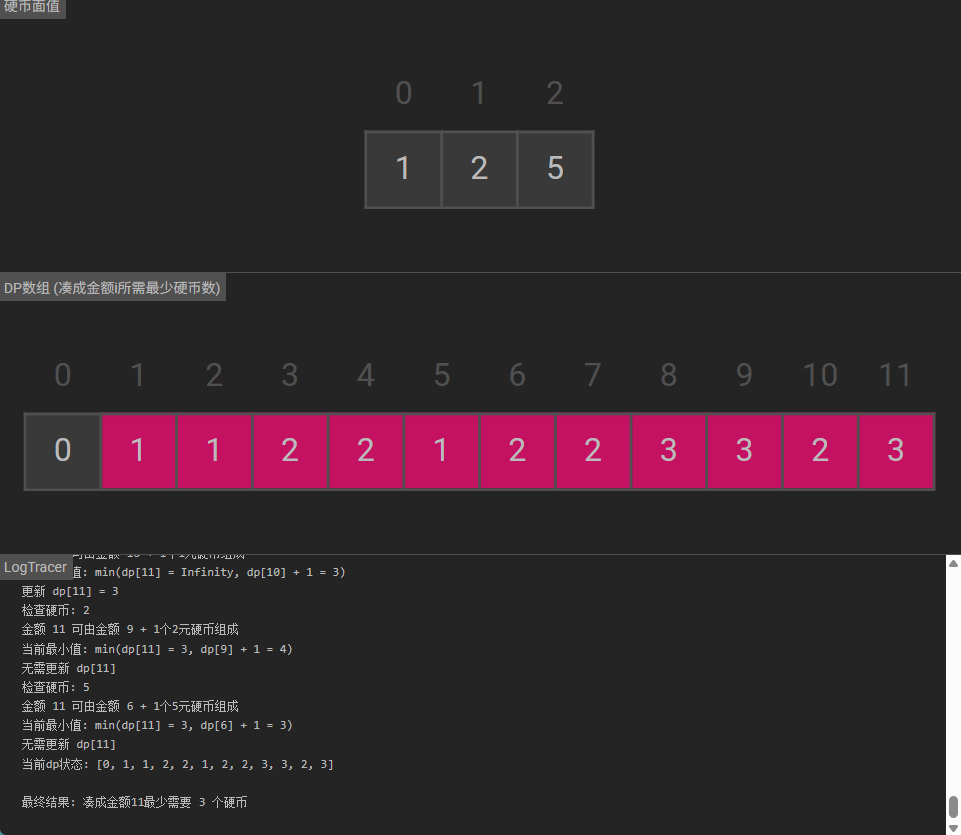





















 1119
1119

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








