【LeetCode热题100道笔记+动画】最小覆盖子串

题目描述

给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串，则返回空字符串 “” 。

注意：
对于 t 中重复字符，我们寻找的子字符串中该字符数量必须不少于 t 中该字符数量。
如果 s 中存在这样的子串，我们保证它是唯一的答案。

示例 1：
输入：s = “ADOBECODEBANC”, t = “ABC”
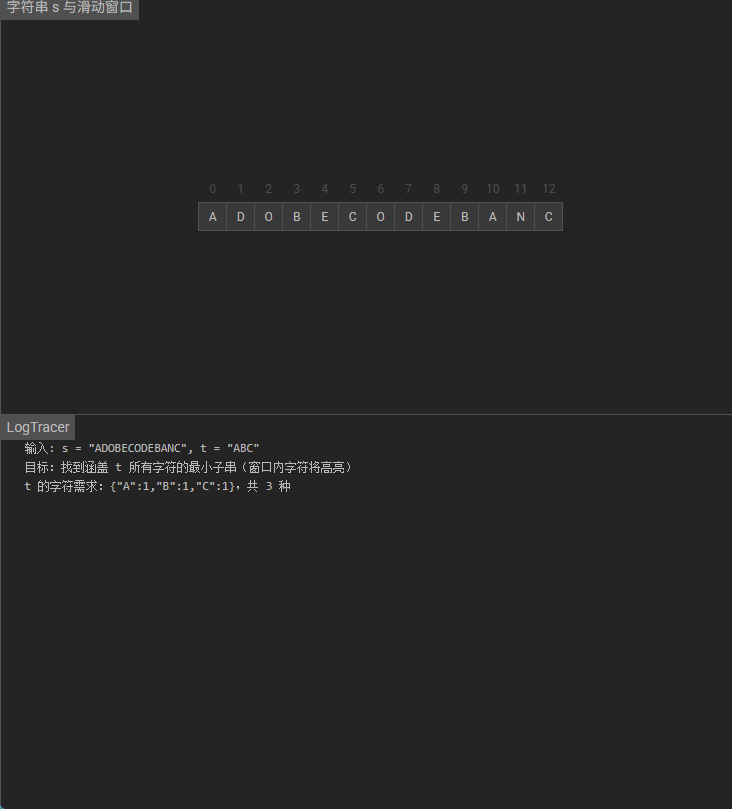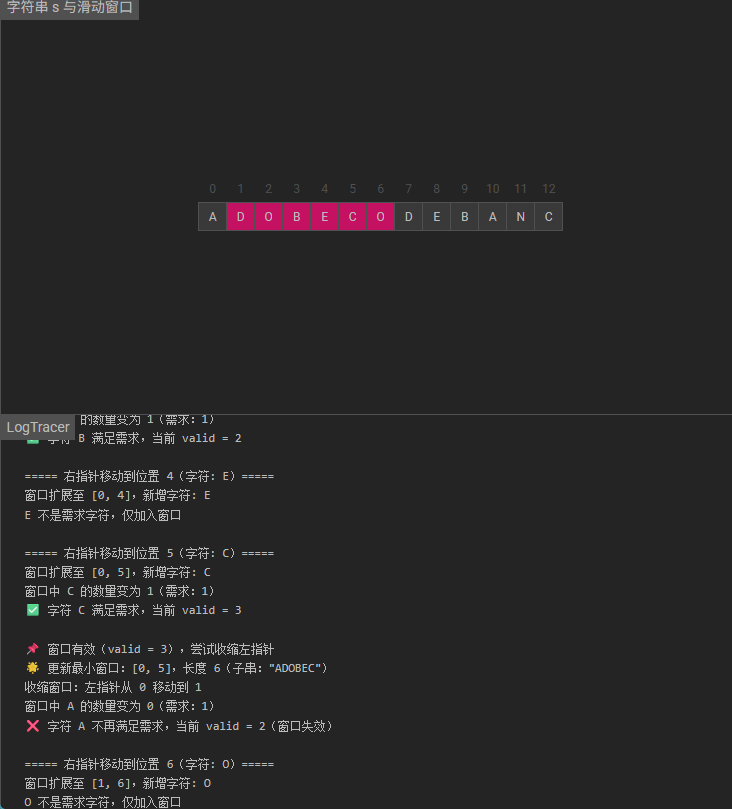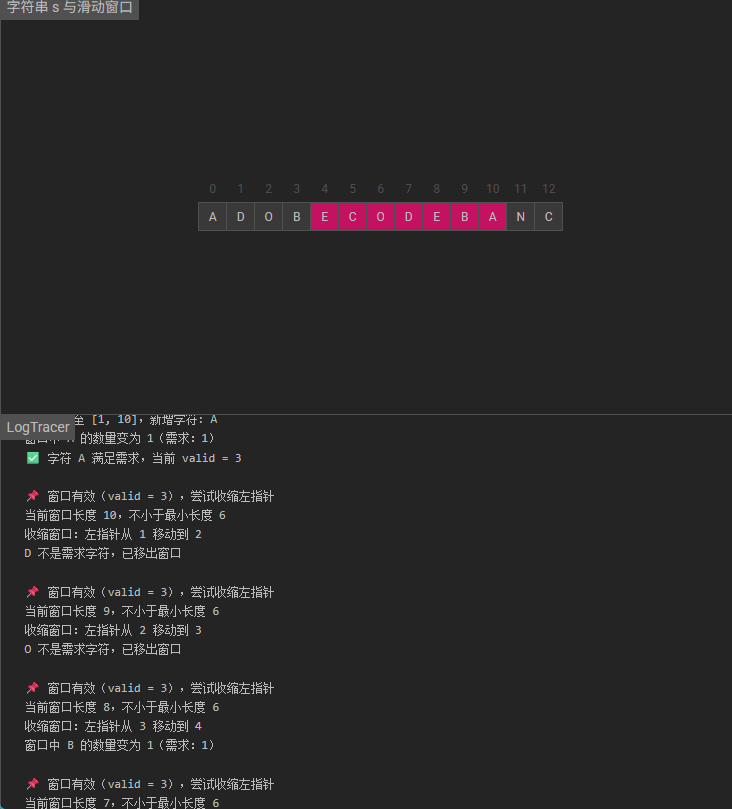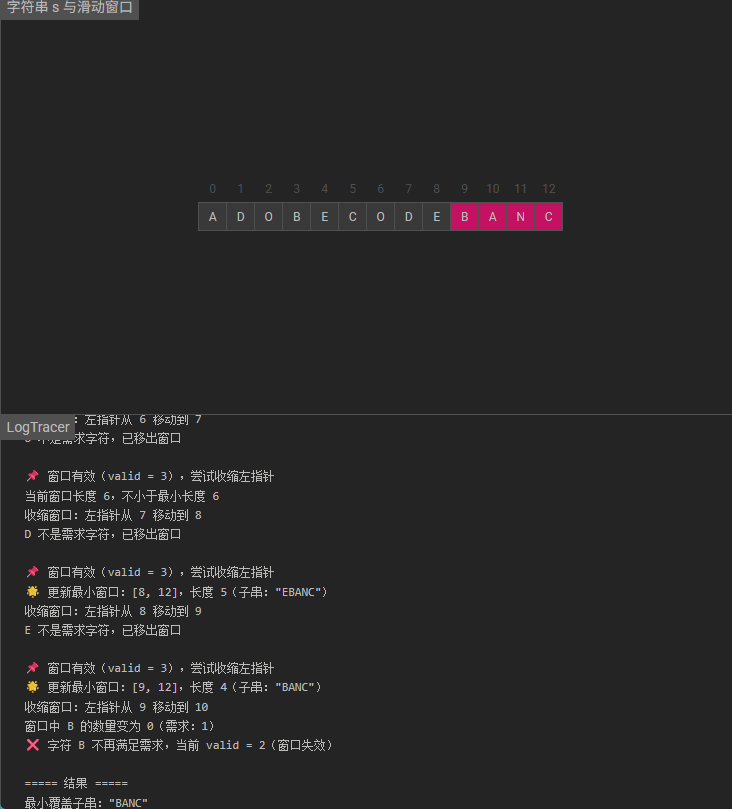
输出：“BANC”
解释：最小覆盖子串 “BANC” 包含来自字符串 t 的 ‘A’、‘B’ 和 ‘C’。

示例 2：
输入：s = “a”, t = “a”
输出：“a”
解释：整个字符串 s 是最小覆盖子串。

示例 3:
输入: s = “a”, t = “aa”
输出: “”
解释: t 中两个字符 ‘a’ 均应包含在 s 的子串中，
因此没有符合条件的子字符串，返回空字符串。

提示：
m == s.length
n == t.length
1 <= m, n <= 105
s 和 t 由英文字母组成

进阶：你能设计一个在 o(m+n) 时间内解决此问题的算法吗？

思考

滑动窗口求解，难点1在于怎么统计窗口中的字符种类和数量和 t 中的字符相同。一般需要用两个哈希表进行统计；难点2在于什么时候收缩窗口（右移左指针），很容易混乱。

算法过程

1. 初始化需求：

   • 遍历 t 构建 need 哈希表，记录每个字符的需求量（如 t="ABC" 对应 {A:1, B:1, C:1}）；
   • 记录 t 的字符种类数 needSize（用于判断窗口是否有效）。

2. 扩展右指针（扩大窗口）：

   • 右指针 r 从 0 遍历 s，将当前字符 s[r] 加入窗口；
   • 若 s[r] 是 need 中的字符，更新 win 中该字符的数量；
   • 当 win 中该字符的数量等于 need 中的需求量时，valid 加 1（表示该字符种类满足需求）。

3. 收缩左指针（缩小窗口）：

   • 当 valid === needSize（窗口有效）时，尝试收缩左指针 l 以寻找更小的有效窗口；
   • 计算当前窗口长度 r-l+1，若小于已知最小长度 minLen，更新 minLen 和起始位置 start；
   • 若左指针字符 s[l] 是 need 中的字符，更新 win 中该字符的数量；若数量从满足需求变为不满足（win[c] < need[c]），valid 减 1（窗口失效）；
   • 左指针 l 右移，继续收缩直至窗口失效。

4. 返回结果：

   • 遍历结束后，若 minLen 仍为初始值（无穷大），返回空串；否则返回 s 中从 start 开始、长度为 minLen 的子串。

代码

/**
 * @param {string} s
 * @param {string} t
 * @return {string}
 */
var minWindow = function(s, t) {
    const len = t.length;
    let need = new Map();
   
    for (let c of t) {
        need.set(c, (need.get(c) || 0) + 1); // 统计参考子串中各个字符的需求量
    }
    let needSize = need.size; // 需要的字符种类总数

    let win = new Map(); // 记录窗口中每种字符数量
    let l = 0, valid = 0, minLen = Infinity, start = 0;
    for (let r = 0; r < s.length; r++) {
        let c = s[r];
        if (need.has(c)) {
            win.set(c, (win.get(c) || 0) + 1);
            if (win.get(c) === need.get(c)) { // 满足一种字符数量要求
                valid++;
            }
        }

        while (valid === needSize) { // 当所有字符满足需求时尝试收缩左指针
            if (minLen > r - l + 1) {
                start = l;
                minLen = r - l + 1;
            }

            if (need.has(s[l])) {
               if (win.get(s[l]) === need.get(s[l])) {
                  valid--;
               }
               win.set(s[l], win.get(s[l])-1);
            }
            l++;
        }
    }

    return minLen === Infinity ? "" : s.substr(start, minLen);   
};

可视化