1. 二叉搜索树
1.1. 概念
二叉搜索树: 左子树上所有节点值均小于根值, 右子树所有节点值均大于根值的特殊二叉树.
1.2. 增删改查
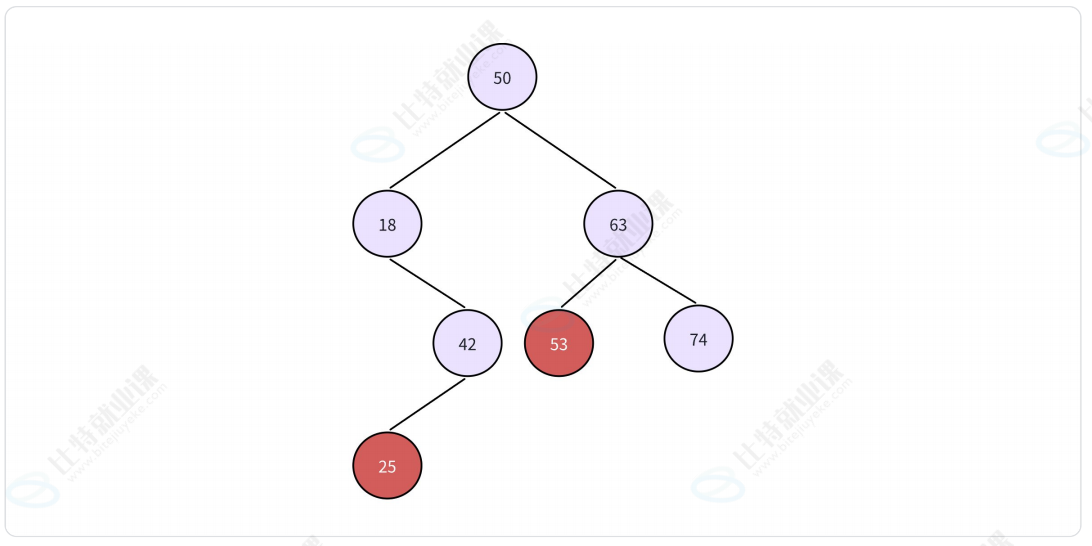
- 如果删除的是二叉树的叶子节点 -> 直接删除
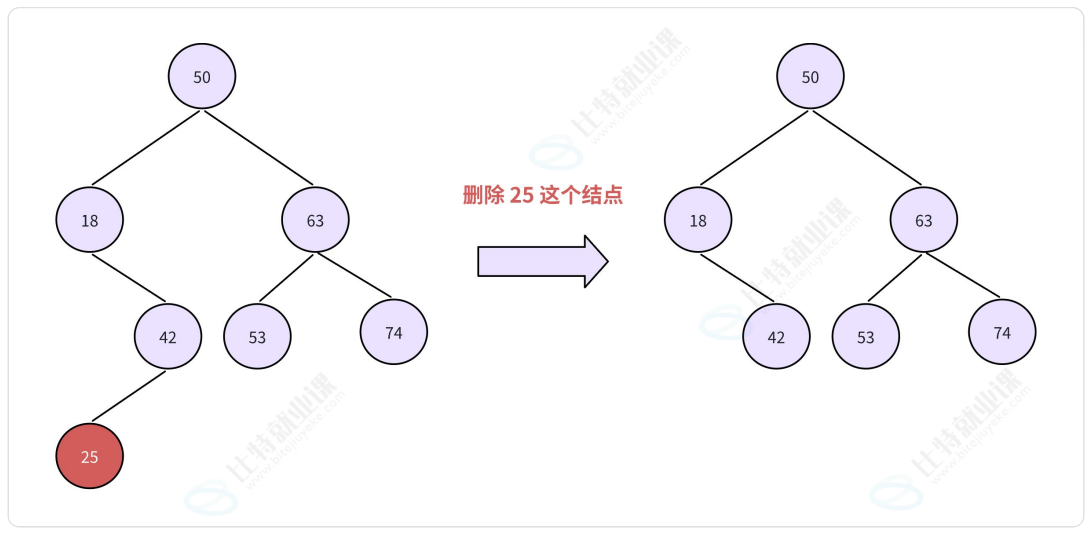
- 若被删除结点只有一颗左子树或右子树,则让的子树成为父结点的子树,替代的位置 -> 把孩子托付给父节点即可.
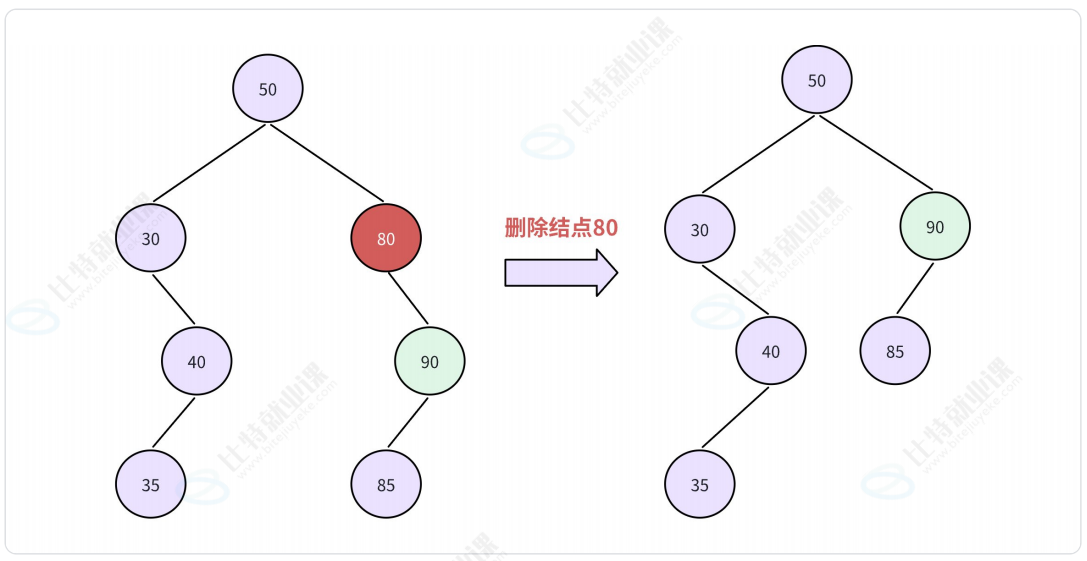
- 若结点x既有左子树,又有右子树。
-
- 令 x 的
直接后继替代,然后从二叉搜索树中删去这个直接后继;注: 后继是指中序的下一个节点 或 右子树最左节点 - 令 x 的
直接前驱替代,然后从二叉搜索树中删去这个直接前驱。注: 前驱是指中序的上一个节点 或 左子树最右节点
- 令 x 的
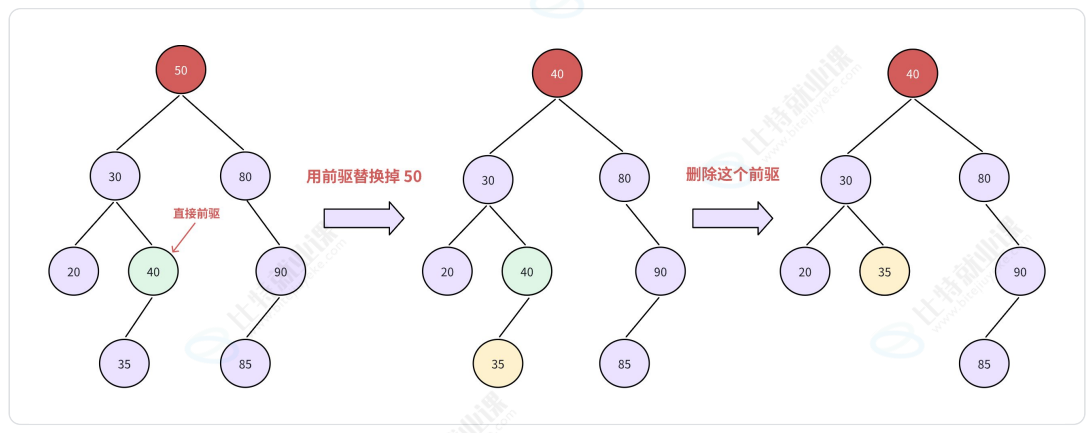
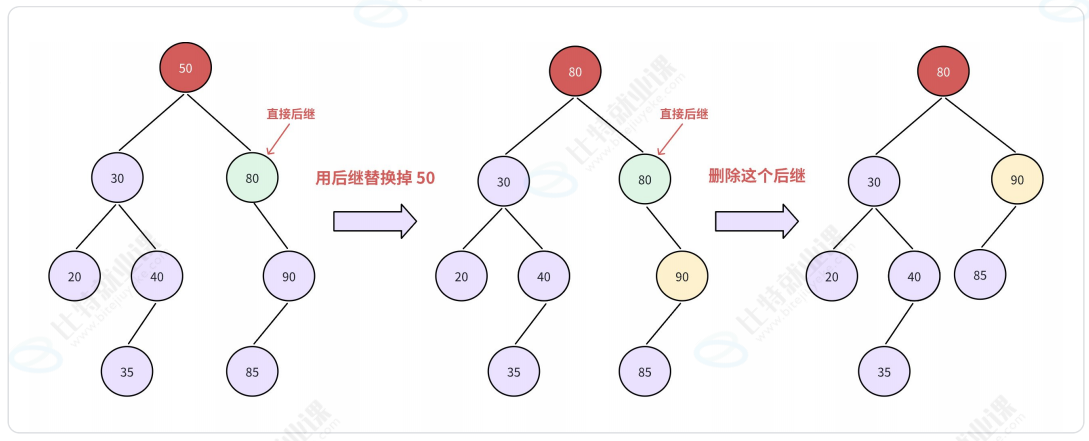
问题: 一般二叉搜索树高度依赖建树序列, 在有序情况下, 搜索效率直接退化为链表.
2. 平衡二叉树(AVL树)
2.1. AVL树
平衡二叉树(AVL树): 左右子树高度差不超过1的二叉搜索树.
平衡因子: 为了刻画一棵树是否满足平衡条件的参考值, 平衡树 b ∈ { 1, 0, -1}
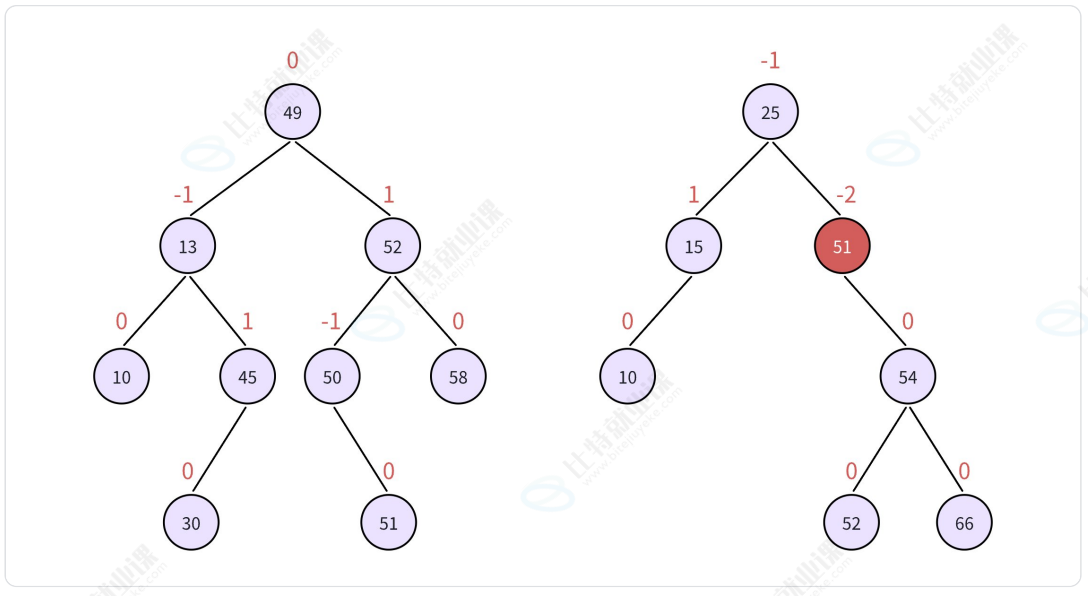
最小不平衡树: 新插入节点 与 最近的b ∉ { 1, 0, -1}的根 所构成的子树
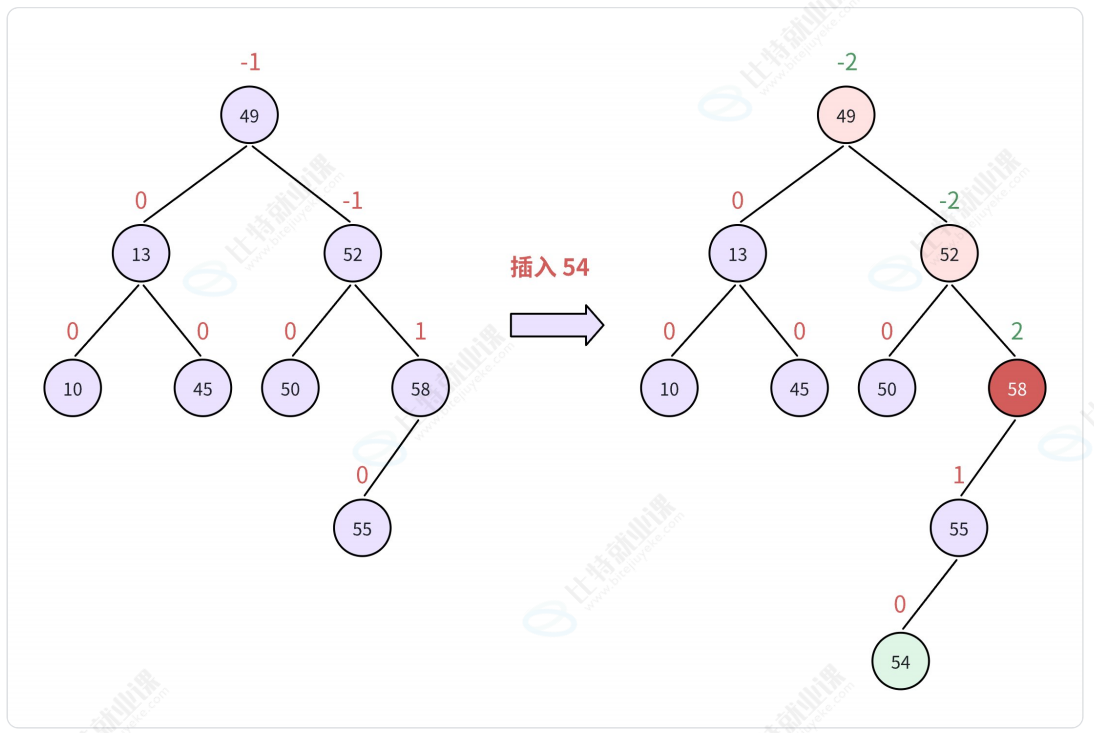
2.2. AVL的旋转
2.2.1. LL型-右单旋
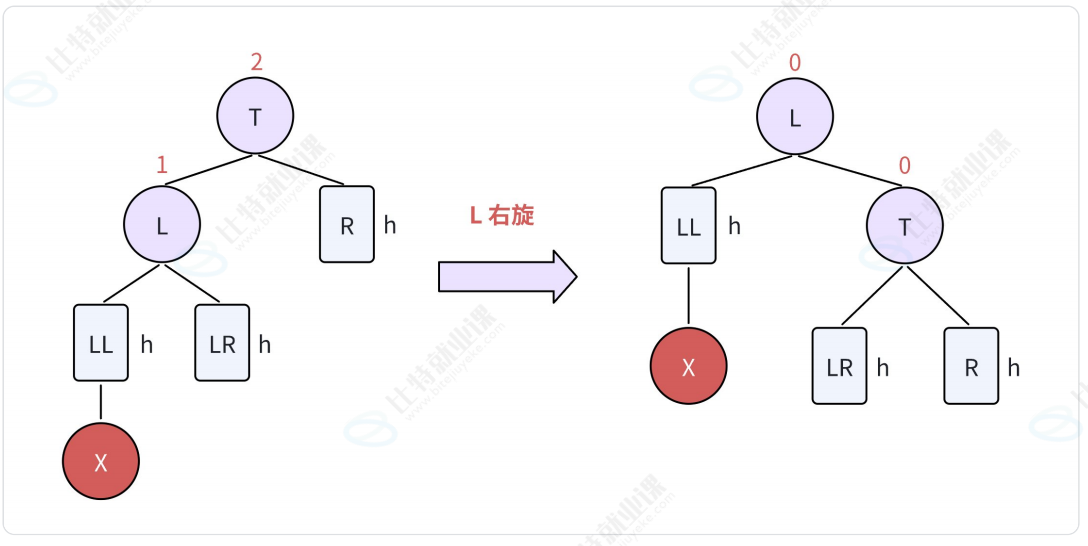
LL表示:新结点由于插入在T结点的左孩子(L)的左子树(LL)中,从而导致失衡。
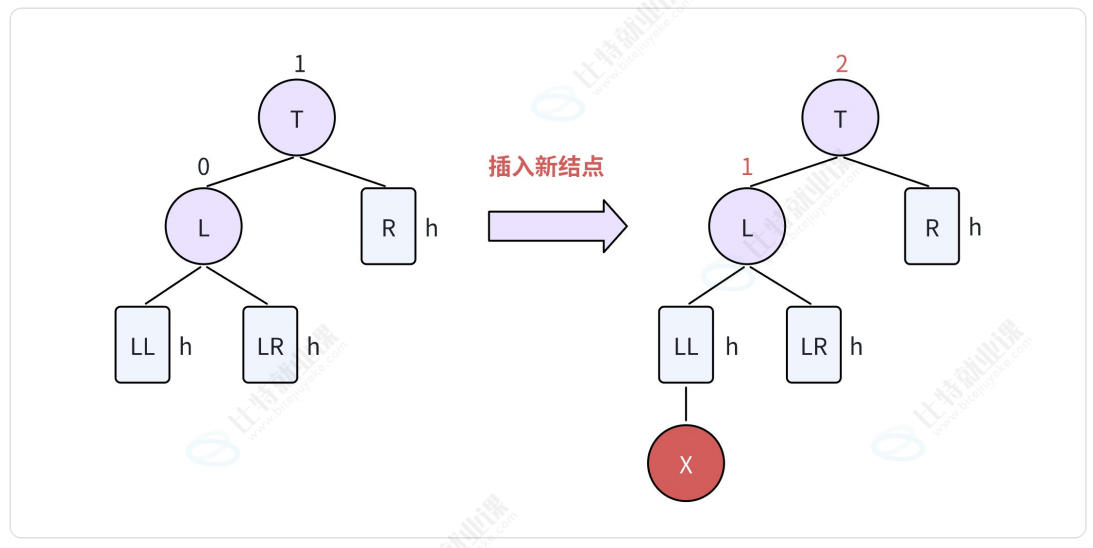
- 将结点L向右上旋转代替结点T作为根结点;
- 将节点T向右下旋转作为结点L的右子树的根结点;
- 结点L的原右子树(LR)则作为结点T的左子树。
2.2.2. RR型-左单旋
RR表示:新结点由于插入在T结点的右孩子(R)的右子树(RR)中,从而导致失衡。
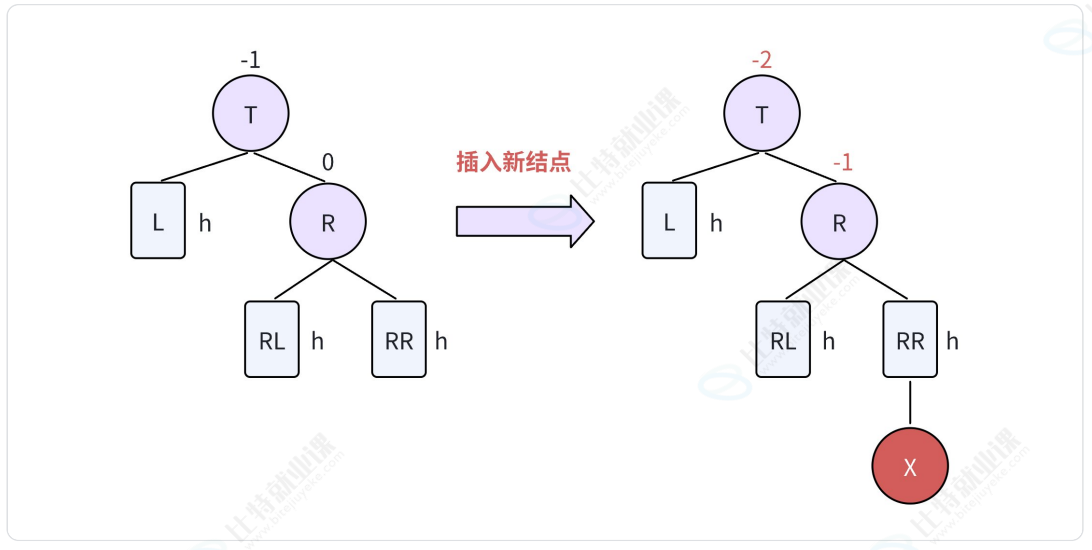
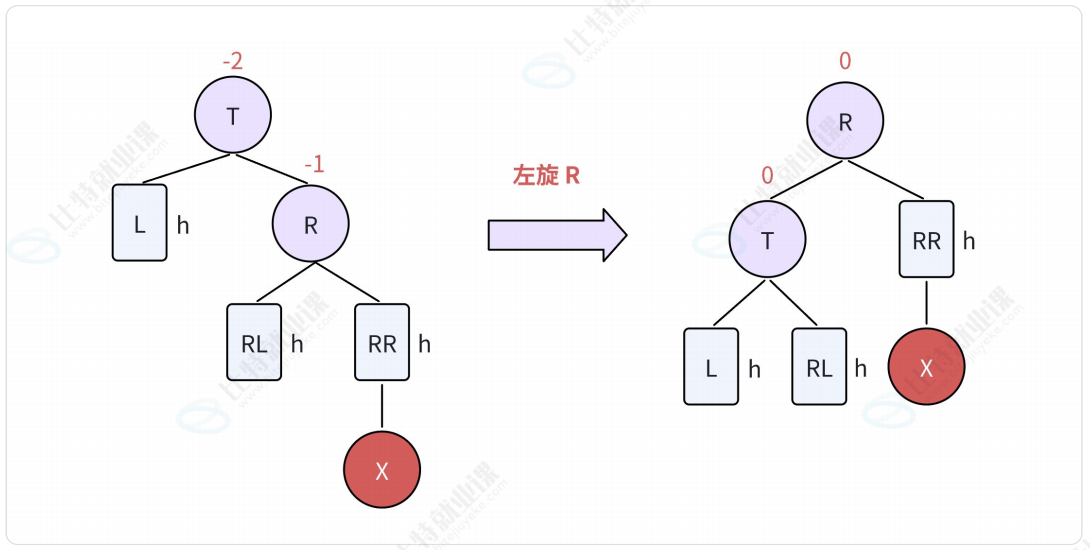
- 将结点R向左上旋转代替结点T作为根结点;
- 将节点T向左下旋转作为结点R的左子树的根结点;
- 结点R的原左子树(RL)则作为结点T的右子树。
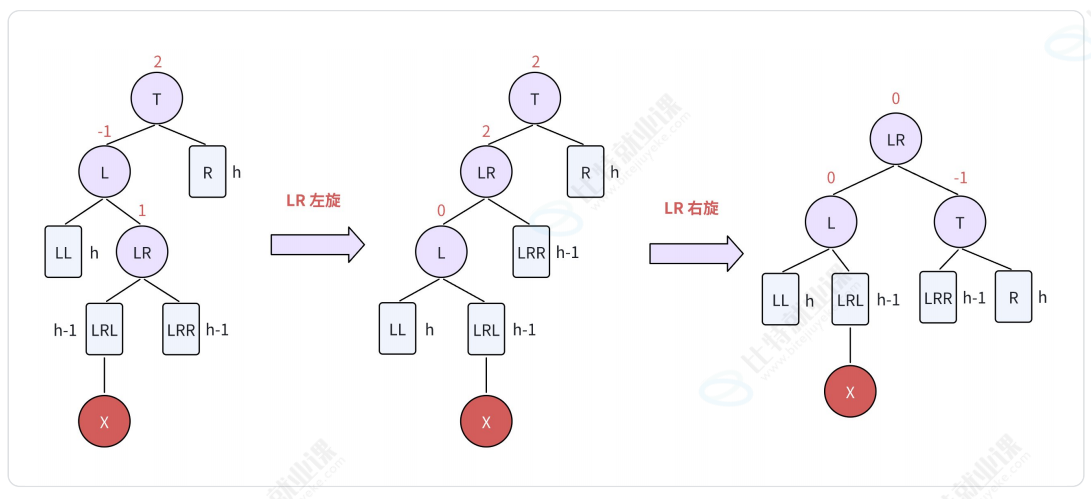
2.2.3. LR型-左右双旋
LR表示:新结点由于插入在T结点的左孩子(L)的右子树(LR)中,从而导致失衡。
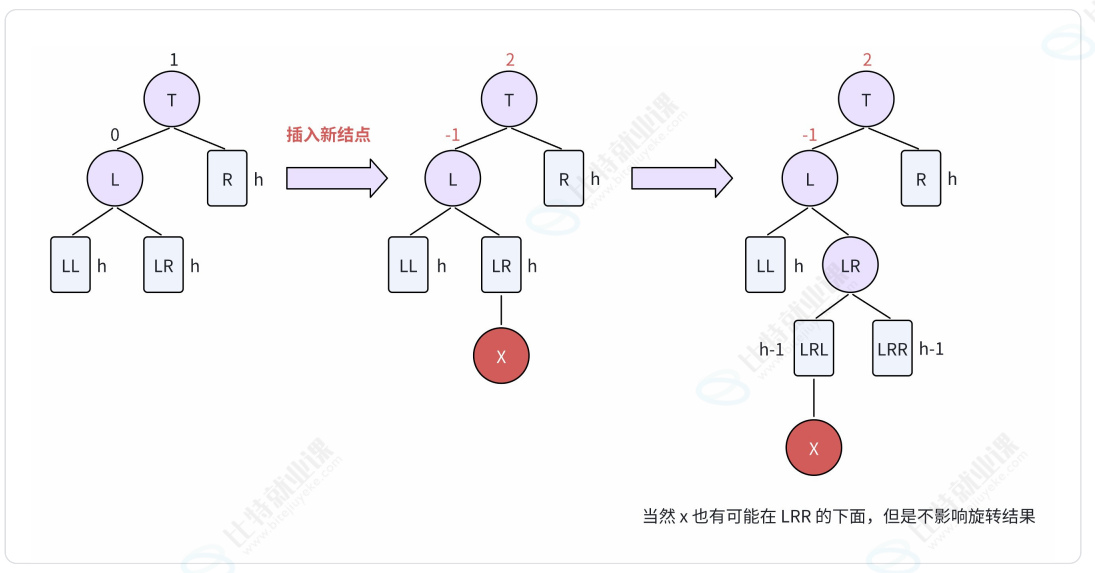
将 LR左旋:
- 将结点LR向左上旋转代替结点L作为根结点;
- 将节点L向左下旋转作为结点LR的左子树的根结点;
- 结点LR的原左子树(LRL)则作为结点L的右子树。
将LR右旋:
- 将结点LR向右上旋转代替结点T作为根结点;
- 将节点T向右下旋转作为结点LR的右子树的根结点;
- 结点LR的原右子树(LRR)则作为结点T的左子树。
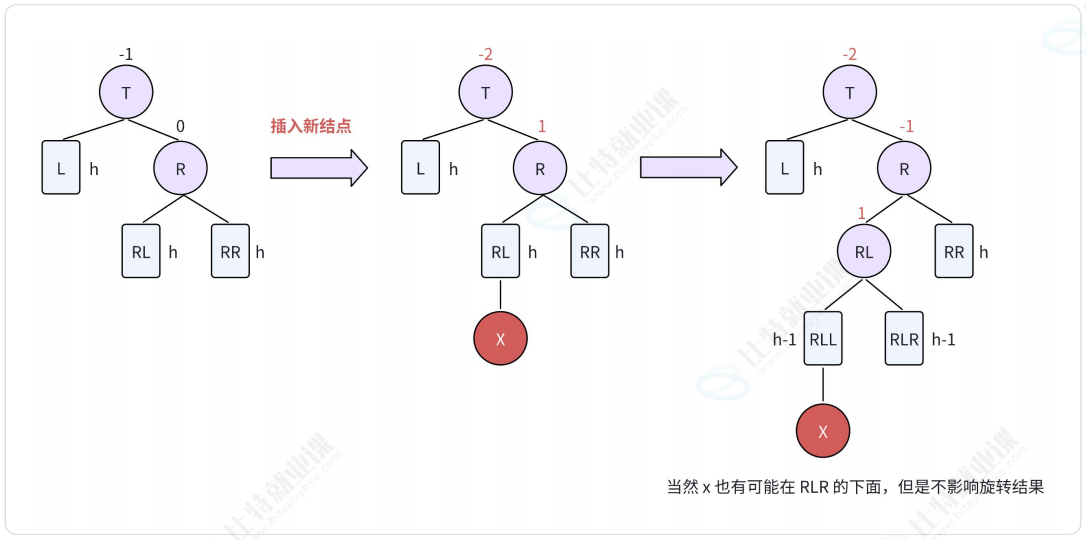
2.2.4. RL型-右左双旋
RL表示:新结点由于插入在T结点的右孩子(R)的左子树(RL)中,从而导致失衡。
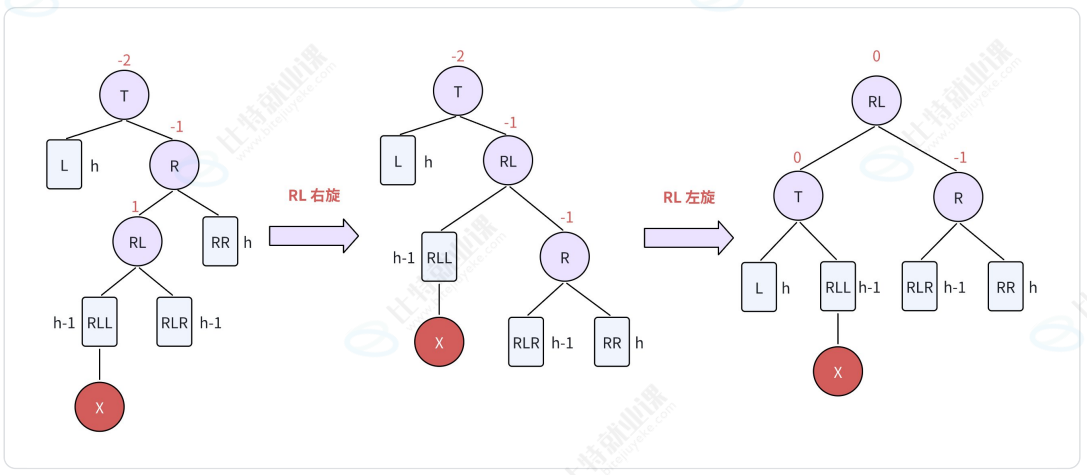
将 RL右旋:
- 将结点RL向右上旋转代替结点R作为根结点;
- 将节点R向右下旋转作为结点RL的右子树的根结点;
- 结点RL的原右子树(RLR)则作为结点R的右子树。
将RL左旋:
- 将结点RL向左上旋转代替结点T作为根结点;
- 将节点T向左下旋转作为结点RL的左子树的根结点;
- 结点RL的原左子树(RLL)则作为结点T的右子树。
2.3. AVL树的删除
- 根据二叉搜索树中的规则删除节点
- 找到最小不平衡树, 然后进行旋转使得这棵树平衡
- 继续向上搜索祖先节点是否还有不平衡点, 重复1~2步骤
3. 红黑树
3.1. 概念
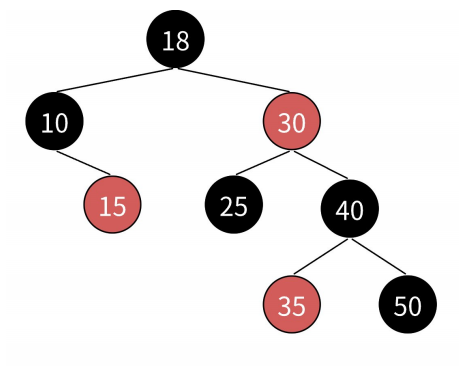
红黑树: 每条路径(包括null节点)差值不超过两倍的近似平衡的二叉树.
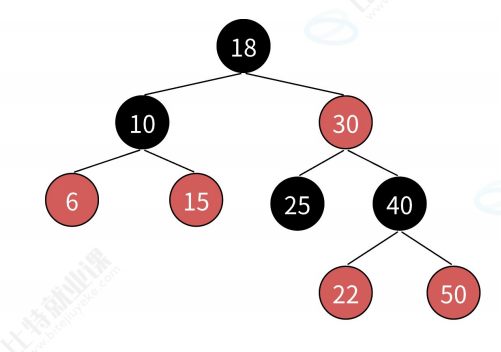
3.2. 规则
- 非红即黑: 每个结点要么是红色要么是黑色;
- 两端均黑: 根节点和叶子结点(这里的叶子结点不是常规意义上的叶子结点,而是空结点,如下图中的NIL)是黑色的;
- 红不相连: 如果一个结点是红色的,则它的两个孩子结点必须是黑色的,也就是说任意一条路径不会有连续的红色结点;
- 黑数相同: 对于任意一个结点,从该结点到其所有叶子的路径上,均包含相同数量的黑色结点。
3.3. 性质
- 从根结点到叶结点的最长路径不大于最短路径的2倍。
- 有 n 个结点的红黑树,高度 h ≤ 2log2(n +1), 也就是说查找时间复杂度为O(logN)
3.4. 插入
- 情况一:插入的是根节点
这是第一次插入结点,直接将结点的颜色变成黑色即可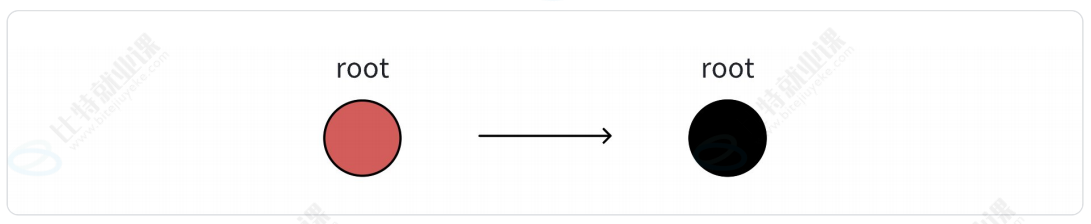
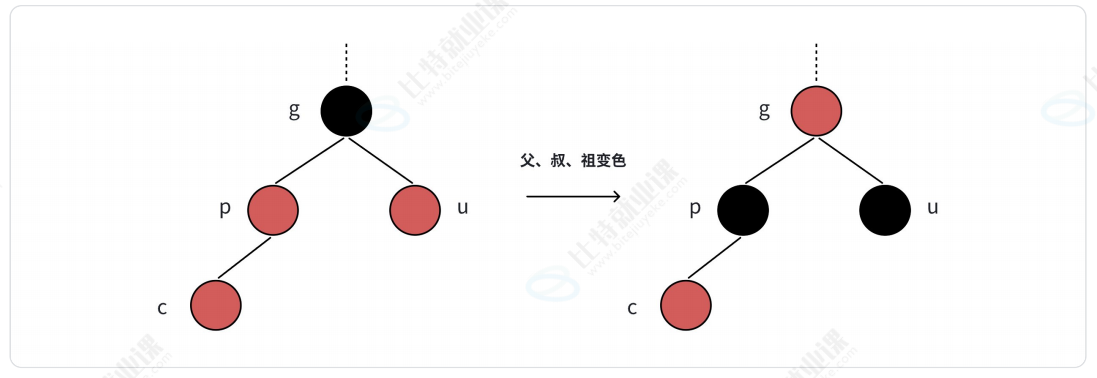
- 情况二:叔叔是红色
父亲、叔叔和爷爷同时变色,然后将爷爷看做新插入的结点,继续向上判断。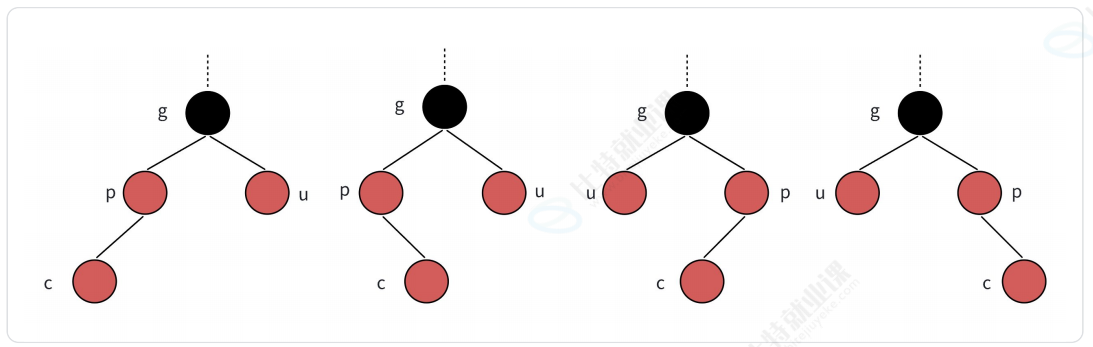
- 情况三:叔叔是黑色
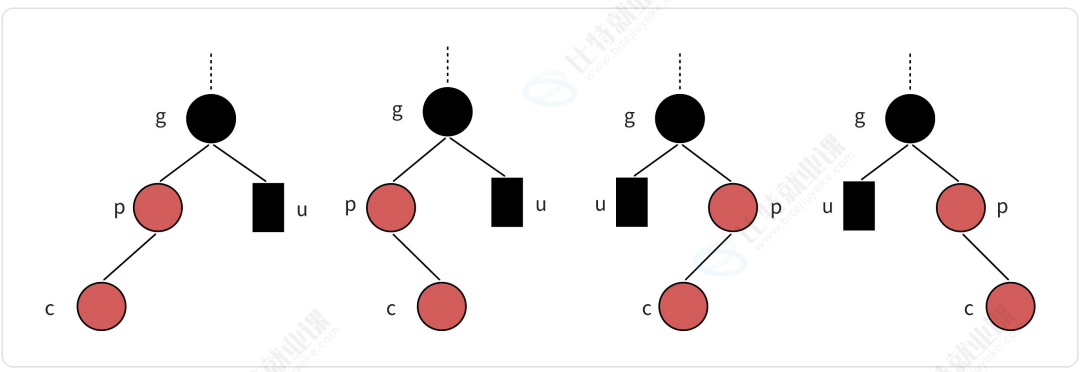
-
- LL型(新结点是爷爷的左孩子的左孩子): 右单旋+父爷变色
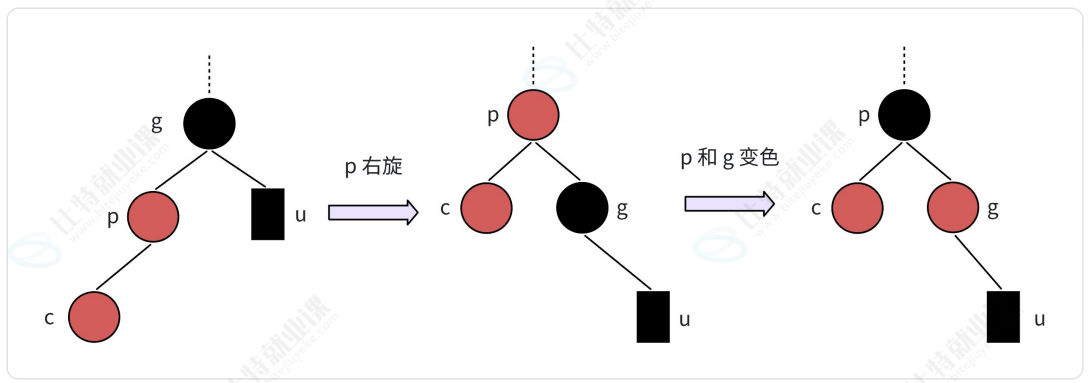
- RR型(新结点是爷爷的右孩子的右孩子)-左单旋+父爷变色
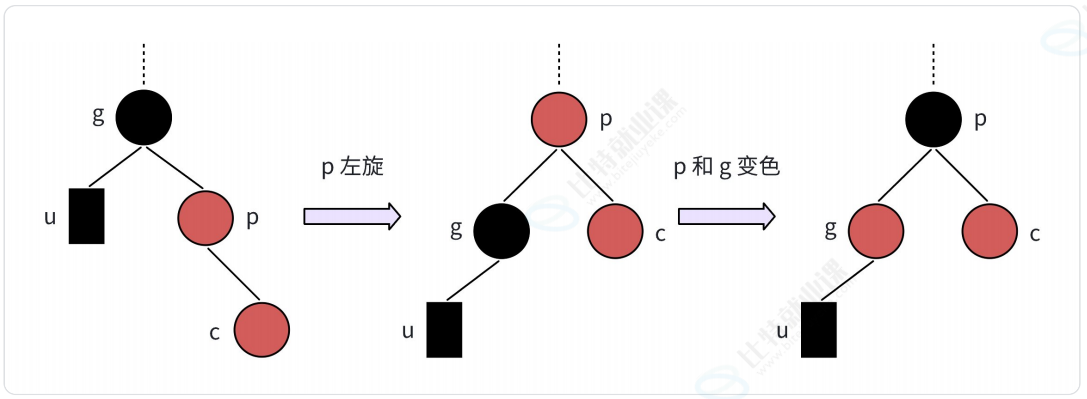
- LR型(新结点是爷爷的左孩子的右孩子)-左右双旋+儿爷变色
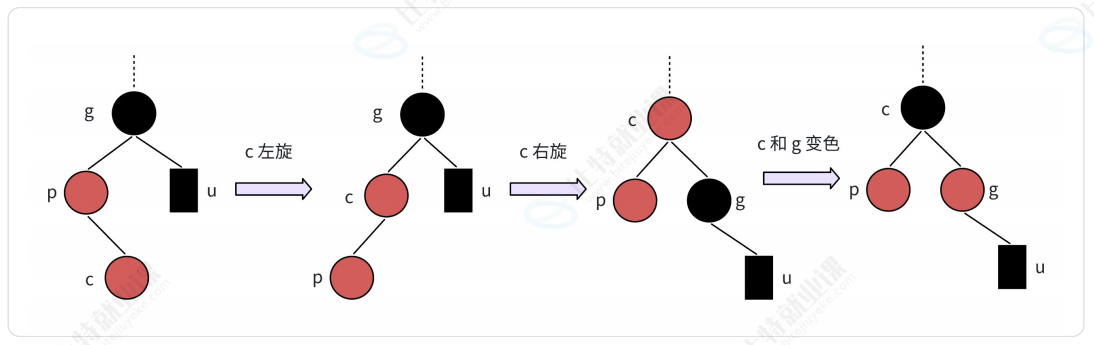
- RL型(新结点是爷爷的右孩子的左孩子)-右左双旋+儿爷变色
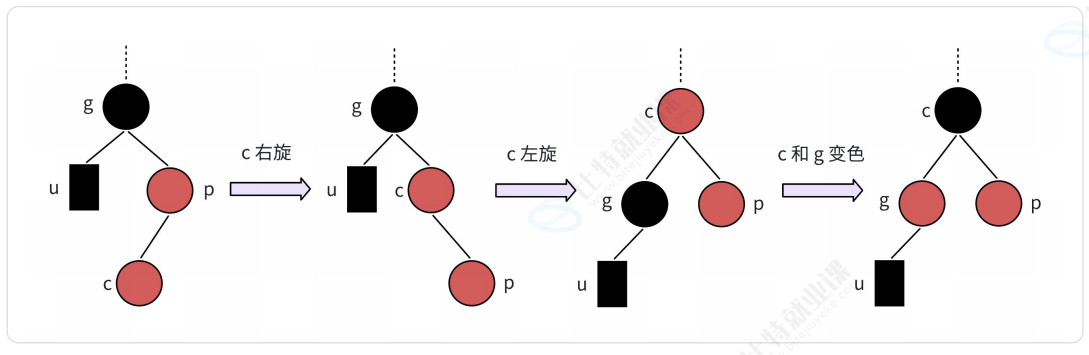
- LL型(新结点是爷爷的左孩子的左孩子): 右单旋+父爷变色
4. STL -- set/mutilset 与 map/mutilmap
- set: 底层红黑树实现, 存储的是
k值, 不允许存储相同值 - mutilset: 底层红黑树实现, 存储的是
k值, 允许存储相同值
#include <iostream>
#include <set>
using namespace std;
int a[] = {10, 60, 20, 70, 80, 30, 90, 40, 100, 50};
int main()
{
set<int> mp;
// 插入
for(auto x : a)
{
mp.insert(x);
}
// 遍历 set,最终的结果应该是有序的
for(auto x : mp)
{
cout << x << " ";
}
cout << endl;
// if(mp.count(1)) cout << "1" << endl;
// if(mp.count(99)) cout << "99" << endl;
// if(mp.count(30)) cout << "30" << endl;
// if(mp.count(10)) cout << "10" << endl;
// mp.erase(30);
// mp.erase(10);
// if(mp.count(30)) cout << "30" << endl;
// else cout << "no:30" << endl;
// if(mp.count(10)) cout << "10" << endl;
// else cout << "no:10" << endl;
auto x = mp.lower_bound(20);
auto y = mp.upper_bound(20);
cout << *x << " " << *y << endl;
return 0;
}- map: 底层红黑树实现, 存储的是
<k,v>值, 不允许存储相同值 - mutilmap: 底层红黑树实现, 存储的是
<k,v>值, 允许存储相同值
#include <iostream>
#include <map>
using namespace std;
void print(map<string, int>& mp)
{
for(auto& p : mp)
{
cout << p.first << " " << p.second << endl;
}
}
// 统计一堆字符串中,每一个字符串出现的次数
void fun()
{
string s;
map<string, int> mp; // <字符串,字符串出现的次数>
for(int i = 1; i <= 10; i++)
{
cin >> s;
mp[s]++; // 体现了 operator 的强大
}
print(mp);
}
int main()
{
fun();
// map<string, int> mp;
// // 插入
// mp.insert({"张三", 1});
// mp.insert({"李四", 2});
// mp.insert({"王五", 3});
// // print(mp);
// // operator[] 可以让 map 像数组一样使用
// cout << mp["张三"] << endl;
// mp["张三"] = 110;
// cout << mp["张三"] << endl;
// // 注意事项:operator[] 有可能会向 map 中插入本不想插入的元素
// // [] 里面的内容如果不存在 map 中,会先插入,然后再拿值
// // 插入的时候:第一个关键字就是 [] 里面的内容,第二个关键字是一个默认值
// if(mp.count("赵六") && mp["赵六"] == 4) cout << "yes" << endl;
// else cout << "no" << endl;
// // 删除
// mp.erase("张三");
// print(mp);
return 0;
}- Lower_bound:大于等于x的最小元素,返回的是迭代器。时间复杂度:: O(log M)
- upper_bound:大于x的最小元素,返回的是迭代器。时间复杂度:O(log M)
5. 算法习题
5.1. P2786 英语1(eng1)- 英语作文
用map统计词频
#include <iostream>
#include <map>
using namespace std;
typedef long long LL;
int n, p;
map<string, int> mp; // <高级词汇,含金量>
// 判断 ch 是否合法
bool check(char ch)
{
if((ch >= '0' && ch <= '9') || (ch >= 'a' && ch <= 'z') || (ch >= 'A' && ch <= 'Z'))
{
return true;
}
else return false;
}
int main()
{
cin >> n >> p;
for(int i = 1; i <= n; i++)
{
string s; int x;
cin >> s >> x;
mp[s] = x;
}
LL ret = 0;
char ch; // 一个字符一个字符读
string t = "";
while(scanf("%c", &ch) != EOF)
{
if(check(ch)) t += ch;
else
{
// 读到分隔符
ret = (ret + mp[t]) % p;
t = "";
}
}
cout << ret << endl;
return 0;
}5.2. P2234 [HNOI2002] 营业额统计
用set找>=x的min值 和 <x的max值
#include <iostream>
#include <set>
using namespace std;
const int INF = 1e7 + 10;
int n;
set<int> mp; // 存储 i 天之前的营业额
int main()
{
cin >> n;
int ret; cin >> ret;
mp.insert(ret);
// 左右护法 - 防止越界访问
mp.insert(-INF); mp.insert(INF);
for(int i = 2; i <= n; i++)
{
int x; cin >> x;
// 找出距离 x 最近的那一个
auto it = mp.lower_bound(x);
auto tmp = it;
tmp--;
if(*it == x) continue;
ret += min(abs(*tmp - x), abs(*it - x));
mp.insert(x);
}
cout << ret << endl;
return 0;
}5.3. P5250 【深基17.例5】木材仓库
用set找>=x的min值 和 <x的max值
#include <iostream>
#include <set>
using namespace std;
typedef long long LL;
const LL INF = 1e10 + 10;
set<LL> mp;
int main()
{
int q; cin >> q;
// 左右护法 - 处理边界情况
mp.insert(-INF); mp.insert(INF);
while(q--)
{
LL op, len; cin >> op >> len;
if(op == 1) // 进货
{
if(mp.count(len)) cout << "Already Exist" << endl;
else mp.insert(len);
}
else // 出货
{
if(mp.size() == 2)
{
cout << "Empty" << endl;
}
else
{
// 找到距离 len 最近的那一个
auto it = mp.lower_bound(len);
auto tmp = it;
tmp--;
if(abs(*tmp - len) <= abs(*it - len))
{
cout << *tmp << endl;
mp.erase(tmp); // 别忘了删除
}
else
{
cout << *it << endl;
mp.erase(it);
}
}
}
}
return 0;
}























 812
812

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








