近期学习总结：数学，计数，多项式

转载大佬的总结，顺便写一些心得，便于以后经常复习（大佬写得太详尽，我就不写了 ）

附上一个大佬的总结zjp-shadow

关于数学和计数

1. 生成函数，计数

关于DAG计数 from yyb
大体思路是推式子，然后化成相应生成函数的形式，用生成函数直接卷积，再求对应项系数
注意推式子的时候要注意边界下标，如果常数项在卷积的时候没有是要补上的

指数型生成函数表示排列，用于区分物品或者带标号的计数
普通生成函数表示组合，一般指数表示物品个数（体积），而方案数一般是选几个（线性的）

这篇总结文尾有很多相应的叙述 from yyb

这类题非常有意思，但是思路也非常广。我现在对生成函数的理解远不够深入，并且计数的技巧也不行，还要多做这类题和总结方法来提高！

生成函数要注意什么时候加常数项。边界必须想清楚。看卷积完后是否漏掉常数项

update
学习了[汪乐平的冬令营讲义](file:///C:/Users/z1318/OneDrive/ACM/slides/2019/%E7%94%9F%E6%88%90%E5%87%BD%E6%95%B0%EF%BC%8C%E5%A4%9A%E9%A1%B9%E5%BC%8F%E7%AE%97%E6%B3%95%E4%B8%8E%E5%9B%BE%E7%9A%84%E8%AE%A1%E6%95%B0.pdf)
推式子应该把方案数直接对应到生成函数，然后把递推式用生成函数的卷积表示。
同求导和积分补齐项，不用像以前用多个生成函数表示
**联通和不连通可以用exp和ln表示：

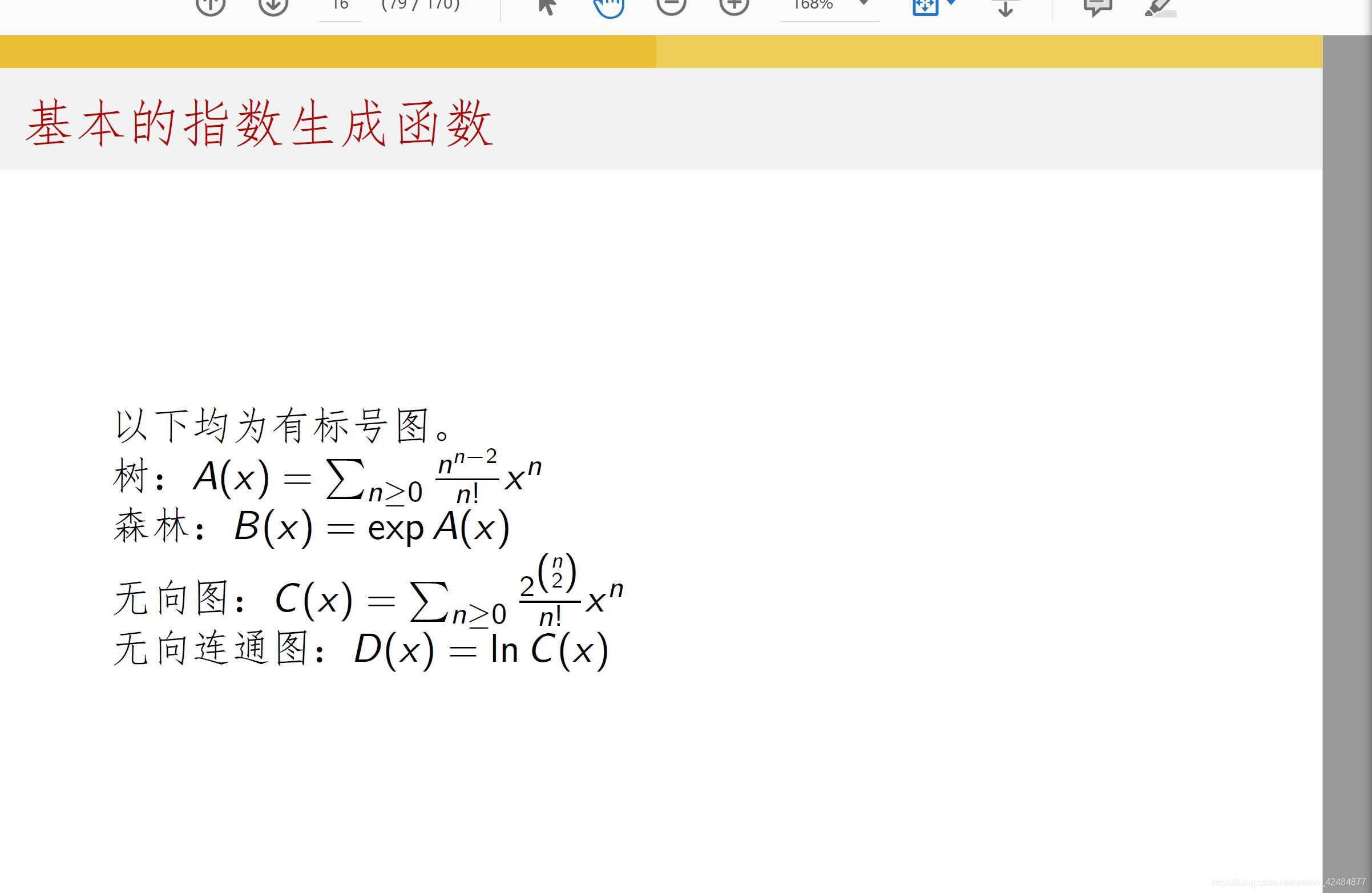
经典模板题【CF438E】The Child and Binary Tree（多项式运算，生成函数）

2. 多项式各种技巧：求逆，取对数，开方，exp，取模和除法。。。

完完全全的模板题

这是一篇非常好的博客。特别是把所有多项式操作都用泰勒展开推导，以后就不用再死记，也不用担心推错了！from yyb

FFT用来加速运算：比如字符串匹配或者其他下标满足卷积形式的运算

**如果下标是乘起来则可以把下标取对数（如果没有原根就对模数质因数分解，然后高维FFT），就变成加法形式 **例如H. Epic Convolution

有些式子看似很难求，利用取对数或者变换的技巧（主要是取对数）。构造出相应系数，在对数意义下变成系数相加，再exp回来
洛谷 P4705 玩游戏 非常经典的多项式构造技巧

取对数积分的时候要把分母化成生成函数无穷集数形式
经常利用已知多项式，变换出位置多项式。如ln(A(x)) = B(x)，有可能取A(x)好求，也有可能B(x)好求，总之要灵活的推式子，多尝试！

多项式求模还有直接快速幂的一种，当求x^m的第n项，n是1e9的时候

多项式快速幂可以DFT到点积对点积直接快速幂，但是如果是循环卷积就必须老老实实IDFT回来，取模加到对应项后再快速幂（比如这道题：bzoj 3992序列统计）

多项式复合逆

没有搞懂为什么，姑且背下公式
拉格朗日反演
求复合逆的一项。
里面第二道例题还没有懂

多项式多点求值和快速插值from miskcoo

有些时候多项式次数已知，但是要求某个点的值（这给点很大），无法求解，可以带入小点求值，然后插值出多项式再求值
这里有一道例题，虽然有dp的做法，但是这个思路可以运用codeforces 995 F

FFT优化卷积运算

FFT还有一大用处就是优化卷积，加速运算，用在匹配上，或者快速求解推出的式子

优化字符串匹配：把匹配拆成字符平方相减，带通配符成个系数，然后拆开分别计算。但是两个串都有通配符就很麻烦（要6次FFT）

[LOJ6436][PKUSC2018]神仙的游戏
这道题利用border的性质，简化了运算，好题！

3.组合计数 我的小结：反演，容斥，组合计数