CSP-J-2020-优秀的拆分多种解法

题目描述

一般来说，一个正整数可以拆分成若干个正整数的和。

例如，1=1，10=1+2+3+4 等。对于正整数 n 的一种特定拆分，我们称它为“优秀的”，当且仅当在这种拆分下，n 被分解为了若干个不同的 2 的正整数次幂。注意，一个数 x 能被表示成 2 的正整数次幂，当且仅当 x 能通过正整数个 2 相乘在一起得到。

例如，

 是一个优秀的拆分。但是， 就不是一个优秀的拆分，因为 1 不是 2 的正整数次幂。

现在，给定正整数 n，你需要判断这个数的所有拆分中，是否存在优秀的拆分。若存在，请你给出具体的拆分方案。

输入

输入只有一行，一个整数 n，代表需要判断的数。

输出

如果这个数的所有拆分中，存在优秀的拆分。那么，你需要从大到小输出这个拆分中的每一个数，相邻两个数之间用一个空格隔开。可以证明，在规定了拆分数字的顺序后，该拆分方案是唯一的。

若不存在优秀的拆分，输出 -1。

样例 1

样例输入 1

6

样例输出 1

4 2

解释

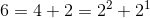
 是一个优秀的拆分。注意，6=2+2+2 不是一个优秀的拆分，因为拆分成的 3 个数不满足每个数互不相同。

 

样例 2

样例输入 2

7

样例输出 2

-1

数据规模

• 对于 20% 的数据，n≤10。
• 对于另外 20% 的数据，保证 n 为奇数。
• 对于另外 20% 的数据，保证 n 为 2 的正整数次幂。
• 对于 80% 的数据，n≤1024。
• 对于 100% 的数据，

  

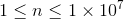
思路

      读者可以发现一个规律，对于一个数N，如果它是一个大于1的偶数，它一定满足一个优秀的拆分。

     对于一个数的合法的优秀的拆分，会发现可以从大到小进行枚举即可，这就变成了位运算。当然如果你没有发现的话，就乖乖使用DFS

AC代码（位运算未优化）

#include<iostream>
using namespace std;
unsigned long long n;
int main(){
	cin>>n;
	if(n%2==1 || n<2){
		cout<<"-1";
		return 0;
	}
	else{
		for(unsigned long long i=1<<30;i>0;i>>=1){
			if(i<=n){
				n=n-i;
				cout<<i<<" ";
			}
			if(n==0)break;
		}
	}
	return 0;
}

AC代码（位运算优化）

#include<cstdio>
signed main(){
	int n;
	scanf("%d",&n);
	if(n%2==1 || n<2){
		putchar('-');
		putchar('1');
		return 0;
	}
	int i=2;
	while(i*2<=n)i<<=1;
	while(n!=0){
		if(i<=n){
			n=n-i;
		    printf("%d ",i);
		}
		i>>=1;
	}
	return 0;
}

呵呵，考试的时候我却很不正经地使用了DFS，没错我就是那个很乖的人，但幸好数据规模不大。

DFS Code Here

#include<cstdio>
int ans[100];
int n,tot=0;
int dfs(int start){
	for(int i=start;i<=n;i=i*2){
		if(i==n){
		    printf("%d ",i);           //倒序输出
			for(int j=tot;j>0;j--){
				printf("%d ",ans[j]);   
			}
			return 0;
		}
		else if(i<=n){
			n=n-i;
			ans[++tot]=i;        
			dfs(i*2);
			tot--;                    //还原
			n=n+i;
		}
		else 
		    return 0;
	}
}
int main(){
	scanf("%d",&n);
	if(n%2==1 || n<2){
		printf("-1");
		return 0;
	}
	else 
	    dfs(2);
	return 0;
}

谢谢大家的支持