C++求一元二次方程方程的根（C++的精确度问题）

利用C++求一元二次方程的根，不能单纯地依靠数学原理，否则会得出错误的结果！

---

先看一道例题：

1058：求一元二次方程

时间限制: 1000 ms         内存限制: 65536 KB
提交数: 102128     通过数: 18399

【题目描述】

利用公式x1=−b+b2−4ac√2a，x2=−b−b2−4ac，求一元二次方程ax2+bx+c=0的根，其中a不等于0。结果要求精确到小数点后5位。

【输入】

输入一行，包含三个浮点数a,b,c（它们之间以一个空格分开），分别表示方程ax2+bx+c=0的系数。

【输出】

输出一行，表示方程的解。

若两个实根相等，则输出形式为x1=x2=；

若两个实根不等，在满足根小者在前的原则，则输出形式为：x1=  x2=

若无实根输出“No answer!”。

所有输出部分要求精确到小数点后5位，数字、符号之间没有空格。

【输入样例】

-15.97 19.69 12.02

【输出样例】

x1=-0.44781;x2=1.68075

题目高速路：

一元二次方程http://ybt.ssoier.cn:8088/problem_show.php?pid=1058

一般的思路：

Code

#include<iostream>
#include<iomanip>
#include<cmath>
using namespace std;
main()
{
	double a,b,c,r;
	cin>>a>>b>>c;
	r=b*b-4*a*c;
	cout<<fixed<<setprecision(5);
	if(r==0)
	    cout<<"x1=x2="<<-b/(2*a);
	else if(r<0)
	    cout<<"No answer!";
	else 
	    cout<<"x1="<<(-b+sqrt(r))/(2*a)<<';x2='<<(-b-sqrt(r))/(2*a);
}

这不用我多说吧，先求,根据的大小判断根的情况，计算输出即可。

咋一看没问题呀，我们看一下测评结果：

 呵呵，不对。

哪里错了呢！

---

先告诉你答案，问题出现在我们对的符号判断上，我们先上一个测试代码 

TEST Code

#include<cstdio>
int main(){
	double a,b,c;
	scanf("%lf %lf %lf",&a,&b,&c);
	double res=b*b-4.0*a*c;
	printf("%lf",res);
	return 0;
}

输入输出结果如图所示：

 

 为什么会这样呢，不应该是0吗？

解释：

首先你要明白输入的是两个十进制的数，计算机首先要转换成2进制。我们看0.3，对于十进制转换成二进制的方法都会吧，不会百度！请看运算过程：

0.3*2=0.6

0.6*2=1.2

0.2*2=0.4

0.4*2=0.8

0.8*2=1.6

0.6*2=1.2

............

有没有发现这是一个循环啊，根本算不尽，那么计算机就必须取近似值。这就是说明了一点：

浮点数不能用==比较大小，他们很多情况下并不和原值相等，我们尽量用   > and < 

---

那么的大小如何判断呢？题目要求精确到小数点后5位，那么好了，我们只要保证前5位的正确即可。

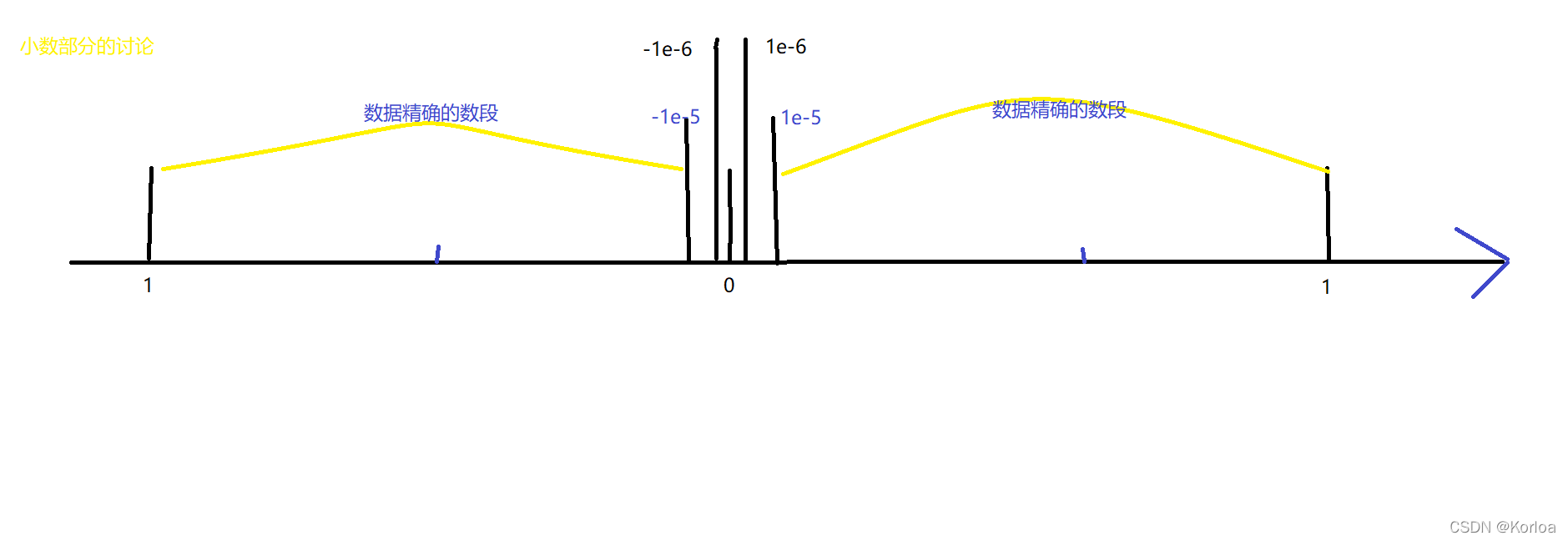
考虑情况:

>0时，也就意味着保留小数点5位，最小为0.00001                近似认为>0.000001

<0时，也就意味着保留小数点5位，最小为-0.00001                近似认为<-0.000001 

=0时，也就意味着保留小数点5为，在-0.00001~0.00001之间

                                                                                              近似认为 -0.000001< <0.000001

完美避免了等号！也保证了精确度

注解：<

1.你选取的近似值，即上面的0.000001，也可以换成其他的数，只要保证前面的情况不出现例外。当然如果你对精确度有更高的要求，可以设成0.000000001，随你便咯！请根据实际要求

2.1e-6=0.000001

   1e+6=1000000

     Tip：还是不放心你不会科学计数法，会当我废话

>

给张图理解理解：

AC code

#include<iostream>
#include<cmath>
#include<cstdio>
using namespace std;
int main(){

	double a,b,c,delta;
	const double precision=1e-6;//小数精度。 
	double x1,x2;
	cin>>a>>b>>c;
	delta=b*b-4*a*c;
	if(delta<-precision)
		cout<<"No answer!\n";
	else if(fabs(delta)<precision){
		//认为等于0，浮点数，无法做相等比较。 
		x1=x2=-b/(2*a);
		printf("x1=x2=%.5lf",x1); 
	}else{
		//delta>0
		delta=sqrt(delta);
		x1=(-b+delta)/(2*a);
		x2=(-b-delta)/(2*a);
		if(x1>x2){
			a=x1;
			x1=x2;
			x2=a;
		}
		printf("x1=%.5lf;x2=%.5lf",x1,x2);
	}
		
	
	

return 0;
}

测评结果：

 End~~~

写作多是一件美差，谢谢支持！