分支界定算法实践(三) 精确求解TSP

TSP问题是非常经典的NP难问题，问题描述很简单，但是求解难度却很大。首先还是给出TSP的数学描述：

• 图$G(V,E)$是一个无向简单图，集合$V$包含了顶点$1,2,...,n$，集合$E$包含了所有边$e(i,j),i,j\in V$. 每条边$e(i,j)$都有对应的权重$w_{ij}\ge 0$. 需要找到一个边集合$T\subset E$，其包含的边构成了图的最短路径，最短路径的长度可以定义为${\sum }_{(i,j)\in T}{w}_{ij}$，图上的每对顶点$s,t\in V$都存在只属于$T$的边来相通，并且每个顶点都只有两个属于$T$的边被确定

一般会把TSP问题用01变量或者置换队列来进行数学描述, 如果是01变量的表述形式，通用的分支界定算法也可以求解，不过我们可以使用一些更加特异化的分支界定算法，更具效率，本文就介绍其中一种

分支界定是一种求精确解的算法，如果TSP的顶点数太多，无论多高明的分支界定算法也无能为力，所以它只适用于规模较小的情况。分支界定算法只是一种算法框架，要应用该算法，需要首先从整体上确定算法中的三个主要成分的实现手段，然后具体细化所有的算法步骤。这三个算法主要成分是：

• 分支策略：我们需要决定如何对父结点进行分支，也就是添加新约束来产生子问题结点；
• 定界策略：在每个问题结点上，需要求解当前约束下的问题下界，同时整个算法也维护一个问题上界，如果该问题的下界大于上界，那么该结点可以进行剪枝；
• 分支结点选择：对于多个可以进行分支的结点，我们也需要用一种选择策略选取结点进行分支

下面我们具体分析. 首先需要确定的是如何表述TSP问题和约束，也就是决策变量是哪个。这里我们明确决策变量是所有边的状态，如果边$e_{ij}=1$，表示该边在路径上(included edge)；如果$e_{ij}=0$，表示该边不在路径上(excluded edge)，这样求解TSP的过程可以看作是从图中选取边来构成一条最短的路径。

确定分支策略。每一次产生子问题，就是在父问题的图中选择一条尚未确定状态的边来设定状态，加入路径或者排除出路径。在根节点，所有的边都没有确定状态，随着分支过程的进行，越来越多的边的状态被确定，最终达到一些可行解。在选择边的具体实现上，有两种方式：

• 按照字典序选边(Lexicographic Order, LG)。这是比较简单直接的方式，例如在当前结点，边$e_{1,2}$被加入路径，对其进行分支，那么按照字典序就选择边$e_{1,3}$，如果边$e_{1,3}$已经被确定了状态，那就继续看边$e_{1,4}$，以此类推
• 按照边长升序选择(Increasing Length, IL)。就是说选择剩余未明确边中最小长度的边，这种选取方式基于思想是选取更小的边加入路径，更有可能较早地找到最短路径

而在通过分支加入新的边约束之后，一些额外的边状态检查和确定工作也需要被执行，来达到一种类似"约束传播"的效果，减小搜索空间：

• 如果某个顶点上除了两条相邻边，都被排除出了路径，那么这两条边肯定要被加入路径
• 如果某个顶点上已经有两条加入路径的相邻边，那么所有其他的相邻边都要被排除出路径
• 对于一条未确定状态的边，如果把它加入路径会导致子回路产生，那么这条边一定要被排除出路径

接着确定定界策略。全局上界很明显就是当前的最短路径，每次找到一个更短的全路径，就用这个值更新上界；而在每个子问题结点上，如何计算下界是需要着重讨论的。在分支界定算法中，在每个结点上的最优解的目标值是肯定不会比下界更小的，在TSP问题中，下界就是当前结点对应的图中最短路径所能达到的理论最小值(所谓理论，就是除了已经确定好的边，其他未确定状态边可以任意设定状态)。同样我们也有两种计算下界的方法：

• 简单下界(Simple lower bound, SB)。对每个顶点$i$，假设$(a_i,i)$和$(b_i,i)$是顶点$i$的两个相邻边，这两条边要么是已经明确在路径中的，要么是未确定状态边中最短的，那么下界就是所有顶点的这两条边长的总和：
  $$L=\frac{1}{2}\sum _{i=1}^n{w}_{a_{i}i}+w_{b_{i}i}$$
• 1-tree下界(OT)。1-tree是最小生成树的变体，首先生成树指的是指一个连通图的子图，它含有图中全部$n$个顶点，但只有足以构成一棵树的$n-1$条边，如果生成树中再添加一条边，则必定成环；所有生成树中边权重和最小的叫最小生成树(MST)，下图是生成树和最短生成树的示意图：
  
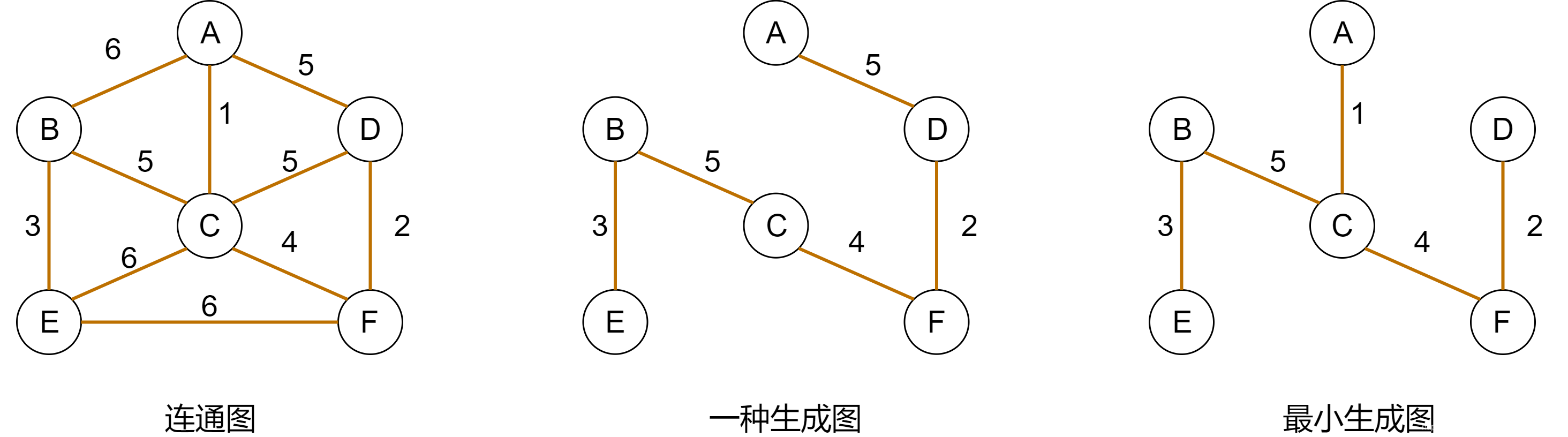
  在最小生成图的基础上，我们这样定义1-tree：图$G(V,E)$是全连接无向图，1-tree是指顶点{ 2,...,n}\{2,...,n\}{ 2,...,n}加上顶点1及顶点1两条相邻边构成的生成树，总权重最小的1-tree则是最小1-tree。最小1-tree可以通过顶点{ 2,...,n}\{2,...,n\}{ 2,...,n}的MST加上顶点1的两条最短边构成，下图是一个最小1-tree的示意图
  

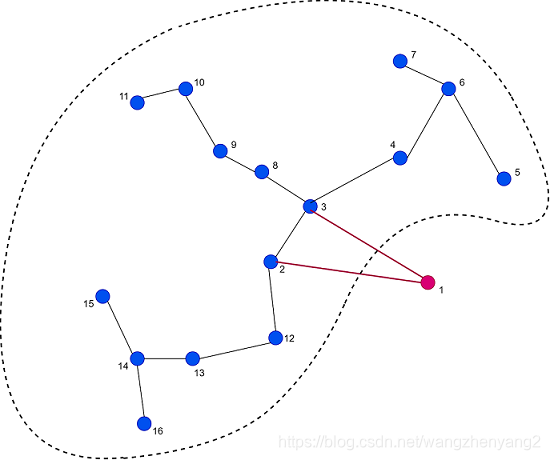
回到TSP问题，可以用最小1-tree的值来作为下界值，1-tree里的顶点1就是TSP的起点。

最后是分支结点的选择。我们对于最小化问题，一般都会采取更小下界优先的原则，也就是先选下界更小的结点来分支，因为这样找到一个更短路径的可能性更大一些，也就意味着尽可能早的更新全局上界，这样后续分支时也更可能剪枝，提升算法速度。对TSP问题，我们采用同样的策略。

下面用python代码实现一个TSP实例，采用IL+SB策略组合的分支界定算法。首先给出一个距离矩阵作为问题实例，这是一个numpy二维数组，尺寸是14X14，也就是14个顶点：

size=14
costs=np.array([ [0