分配问题(Assignment Problem)很常见,例如给多个开发者安排开发任务,一个开发者只能分配到一个任务,一个任务也只能由一个人完成,不同的人对不同的任务有不同的完成时间,那么如何进行安排使得总的开发时间最短就是一个典型的分配问题。如果说传输问题是一类特殊的线性规划问题(传输问题定义),那么分配问题则是一类特殊的传输问题,如果我们把传输问题中所有Supplier和Demander的供应量或需求量都降到1,那么这就变成了一个分配问题
既然分配问题属于传输问题,那么Stepping-Stone算法或者Modified Distribution算法当然也可以直接应用于分配问题,但是我们可以想象一下,对于一个 n × n n\times n n×n的分配问题,它任何一个可行解的矩阵形式都是只有n个1,而迭代中非退化的条件是1的数量等于 n × n − 1 n\times n-1 n×n−1,这意味着每次迭代计算都要处理退化情况,所以直接应用传输问题的算法效率非常低。文本介绍处理分配问题常用的一种算法,一般称之为匈牙利算法(Hungarian Algorithm),不过实际上匈牙利算法的原始版本并非处理传输问题,下面介绍的其实是Harold W.Kuhn和James Munkre在此基础上提出的,所以严格说应该叫Kuhn-Munkre算法
算法主流程
先举个案例来方便描述:我们就假设有A,B,C,D四个开发任务,1,2,3,4四个开发者,各个开发者对开发任务的评估时间(单位: 分钟)可以用下面的cost矩阵来描述
| Task \ Person | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| A | 210 | 90 | 180 | 160 |
| B | 100 | 70 | 130 | 200 |
| C | 175 | 105 | 140 | 170 |
| D | 80 | 65 | 105 | 120 |
分配(A,1),(B,2),(C,3),(D,4)就是一种可行解,表述成矩阵形式:
| Assign | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| A | 1 | 0 | 0 | 0 |
| B | 0 | 1 | 0 | 0 |
| C | 0 | 0 | 1 | 0 |
| D | 0 | 0 | 0 | 1 |
对于上面的cost矩阵,我们通过观察可以发现,对某一个行或者某一列统一减去某个值(例如下表中将第一行统一减去10),其实并不影响问题的描述,也就是说通过行或列的减值操作,得到新的cost矩阵,在它上面计算的结果和原始的cost矩阵是一样的
| Task \ Person | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| A | 210-10=200 | 90-10=80 | 180-10=170 | 160-10=150 |
| B | 100 | 70 | 130 | 200 |
| C | 175 | 105 | 140 | 170 |
| D | 80 | 65 | 105 | 120 |
再考虑,如果某个开发者对一个task的评估时间是零,那么我们当然优先给他分配这个任务;如果每个开发者都有一个互不相同的评估时间是零的task,那么这种分配就是最优的,因为总时间是零。
结合这两个特点,我们可以想到,对各行各列,都减去那一行或列的最小值,这样就可以转化到一个包含多个零的cost矩阵,如果这个cost矩阵中存在没有行列冲突的4个零,那么我们就已经找到了最优解,例如下面的形式,分配(A,1),(C,2),(B,3),(D,4)就是最优分配
| Task \ Person | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| A | 0 | 80 | 170 | 150 |
| B | 100 | 70 | 0 | 200 |
| C | 175 | 0 | 140 | 170 |
| D | 80 | 65 | 105 | 0 |
所以算法的第一步就是进行行列的减法操作,先将每一行减去该行的最小值,再将每一列减去该列的最小值,这样就可以产生多个零:
行减(Row Reduction):
| Task \ Person | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| A | 120 | 0 | 90 | 70 |
| B | 30 | 0 | 60 | 130 |
| C | 70 | 0 | 35 | 65 |
| D | 15 | 0 | 40 | 55 |
列减(Column Reduction):
| Task \ Person | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| A | 105 | 0 | 55 | 15 |
| B | 15 | 0 | 25 | 75 |
| C | 55 | 0 | 0 | 10 |
| D | 0 | 0 | 5 | 0 |
现在我们需要评估一下当前的cost矩阵,是否存在互相独立的4个零,所谓互相独立,指它们中任意两个既不在同一行也不在同一列;如何评估呢,我们在cost矩阵上划线,可以是在行上也可以在列上,用最少的线来覆盖到所有的零,如果刚好是4条,那么就存在相互独立的4个零;如果小于4条,则不存在,这是一个可以数学证明的推论,我们直接接受这个设定。在上面这个cost矩阵中,我们发现只用3条线就可以覆盖到所有的零

这也就意味着,我们找不到相互独立的四个零,当前不存在一个cost为零的最优解;怎么办呢,一个自然的想法就是在划线外的区域产生更多的零,这样划出的线可能达到4条了;那么怎么只对划线外的单元格进行减值操作呢,注意行减或列减操作必须是整行或整列,不能对单个单元格,但是我们可以组合行减和列减达到目的:先对所有非划线行的单元进行减值操作:

然后对所有在划线列上的单元进行加值操作:

这样的最终效果就是对所有划线外的单元减去
h
h
h,对划线的交点单元加上
h
h
h,而这个
h
h
h我们可以取划线外单元格的最小值,即10,所以,减值的结果变成:
| Task \ Person | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| A | 95 | 0 | 55 | 5 |
| B | 5 | 0 | 25 | 65 |
| C | 45 | 0 | 0 | 0 |
| D | 0 | 10 | 15 | 0 |
再来评估,发现仍然只能用3条线来覆盖,我们还没找到最优解:

继续对矩阵进行减值操作,得到:
| Task \ Person | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| A | 90 | 0 | 50 | 0 |
| B | 0 | 0 | 20 | 60 |
| C | 45 | 5 | 0 | 0 |
| D | 0 | 15 | 15 | 0 |
现在我们发现已经存在四个独立的零了:(B,1),(A,2),(C,3),(D,4),这就是最优的分配方案
因此,Kuhn-Munkre算法的步骤就是上面描述的过程:
- Row Reduction: 对cost矩阵的每一行,减去该行的最小值
- Column Reduction: 对每一列,减去该列的最小值
- 评估: 在cost矩阵上找出能覆盖所有零的最少数量的划线,如果划线数等于cost矩阵的边长n,那么已经存在最佳分配,退出算法;如果小于n,则继续4
- 设 h h h是所有不在划线中的单元的最小值,将所有不在划线中的单元减去 h h h,对划线的交点单元则加上 h h h
- 重复3,4
你可能会对步骤4有疑问,会不会步骤4一直产生不了最优解,导致算法陷入死循环呢? 其实步骤4的计算方式决定了算法一定会在有限步数内终止,证明如下:
- 设 α \alpha α是步骤4中的减数,集合 I I I是行覆盖线集, J J J是列覆盖线集,在步骤4中,我们是先从 n ( n − ∣ I ∣ ) n(n-|I|) n(n−∣I∣)个单元中减 α \alpha α,然后给 n ∣ J ∣ n|J| n∣J∣个单元加上 α \alpha α,所以总的变化量是 α n ∣ J ∣ − α n ( n − ∣ I ∣ ) = α n ( ∣ I ∣ + ∣ J ∣ − n ) \alpha n|J|-\alpha n(n-|I|)=\alpha n(|I|+|J|-n) αn∣J∣−αn(n−∣I∣)=αn(∣I∣+∣J∣−n),而 ∣ I ∣ + ∣ J ∣ − n |I|+|J|-n ∣I∣+∣J∣−n是小于零的,所以总的变化量恒定为负,如果一直进行步骤4,cost矩阵的总和只会一直减小,也就意味着零的出现只会增多,算法一定会停止
对于算法的复杂度,研究者进行了详细的数学推导,证明该算法的复杂度是 n 3 n^3 n3,对比暴力搜索的 n ! n! n!,该算法的效率非常高
如何划线
算法的主体并不复杂,但是关键的划线步骤并没有描述细节,在上面的例子中,我们可以直观地找到最少数量的划线,但是怎么用一个算法来描述却并不简单,从复杂度上看,划线子算法要比主算法更难操作和理解,下面我结合一个例子来描述这个子算法
假设当前的cost矩阵为:
| Task \ Person | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| A | 105 | 0 | 55 | 15 |
| B | 0 | 0 | 25 | 75 |
| C | 35 | 0 | 0 | 0 |
| D | 0 | 0 | 0 | 15 |
- 遍历cost矩阵中的每个零,如果在该零所属的行或列中不存在标 ∗ * ∗的零,那么就给它标上 ∗ * ∗;划出所有包含标 ∗ * ∗零的列 (标 ∗ * ∗零意味着相互独立,通过这个操作是初步找出了一些独立的零)
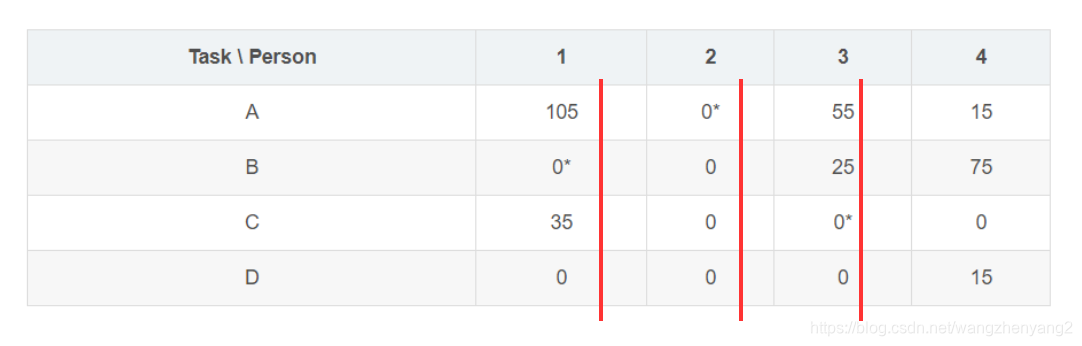
- 遍历每个未被线覆盖到的零,首先标上^,然后看它所在的行,如果该行有标 ∗ * ∗的零,对该行划线,同时移掉该行标 ∗ * ∗零所在列的线;如果该行没有标 ∗ * ∗零,则执行步骤3;重复步骤2,直到所有零都被线覆盖,退出子算法
根据步骤2的描述,首先找到单元格C4,对其标^,划下该行,移掉列2:
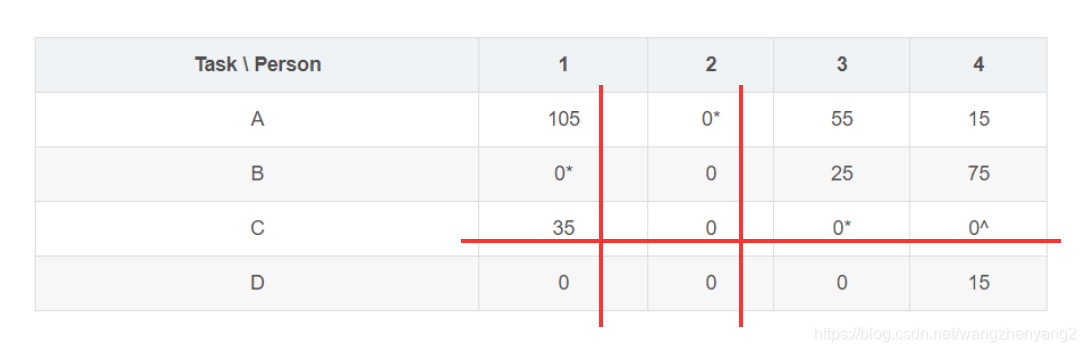
经过这个操作,单元格D3变成了一个未被覆盖的零,并且该行没有标
∗
*
∗的零,所以需要进行步骤3的操作
- 构造由标^和标 ∗ * ∗零组成的序列:定义 Z 0 Z_0 Z0是最新的那个标^零, Z 1 Z_1 Z1是 Z 0 Z_0 Z0所在列中的标 ∗ * ∗零, Z 2 Z_2 Z2是 Z 1 Z_1 Z1所在行中的标^零,以此类推,直到遇到用 Z 2 k Z_{2k} Z2k表示的标^零,它所在列中不存在标 ∗ * ∗零. 对于这个序列上的零,我们移除掉所有标 ∗ * ∗零的 ∗ * ∗号,把标^零改为标 ∗ * ∗;注意到这个序列的首末两个零都是标^的,经过这个"反转"操作,标 ∗ * ∗零的数量多了一个;清空所有的^标记,清空覆盖线,划出所有包含标 ∗ * ∗零的列,回到步骤2
对于我们的例子,从单元格D3出发,我们可以找到序列
{
Z
D
3
,
Z
C
3
,
Z
C
4
}
\{Z_{D3}, Z_{C3}, Z_{C4} \}
{ZD3,ZC3,ZC4}
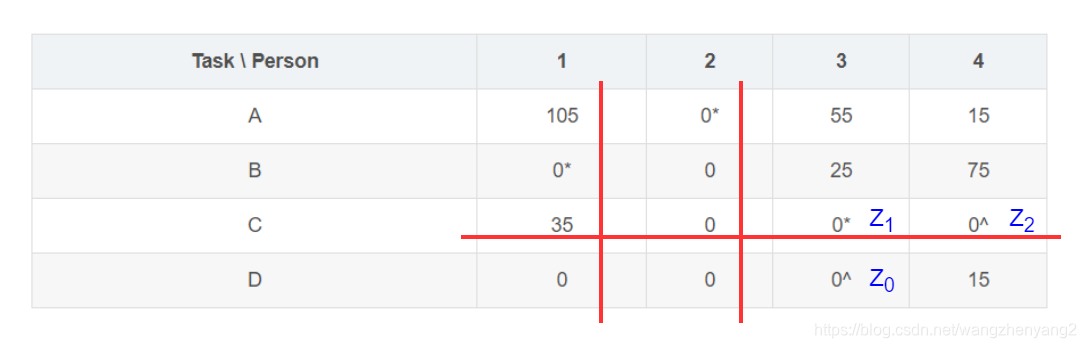
"翻转"一下序列中的零:
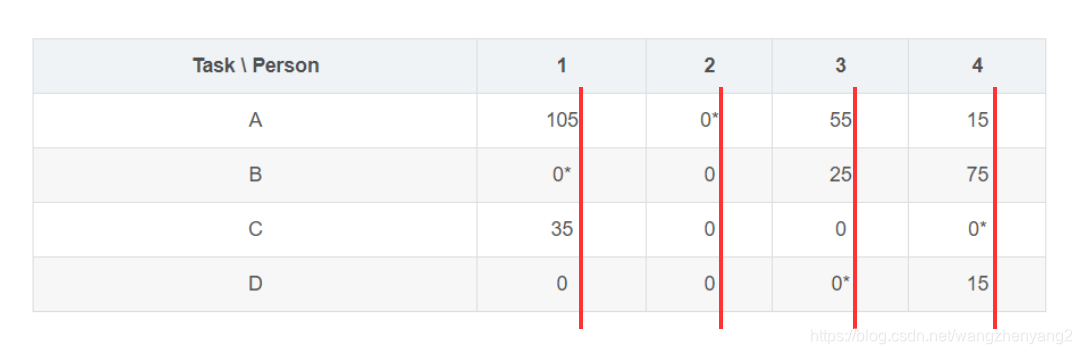
现在可以看到已经没有未被覆盖的零了,而且划线数刚好是4,所以其实这个cost矩阵里已经包含了一个最优解。这个子算法一方面是在搜索划线,另一方面其实也是在找相互独立的最大数量的零,即标注
∗
*
∗号的单元格
非平衡处理
上面的例子里开发者的数量和task数量相等,所以这是一个平衡分配问题,和传输问题一样,非平衡的情况更为多见,不过非平衡问题只需要在算法计算前对cost矩阵进行虚拟行或列的扩充就行了。
例如添加一个Task E,因为开发者只有4个,A到E的5个Task中必定有一个会空出来不被任何开发者领取,所以可以给cost矩阵添加一个cost为零的虚拟列,这对算法的计算没有任何影响
| Task \ Person | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| A | 210 | 90 | 180 | 160 | 0 |
| B | 100 | 70 | 130 | 200 | 0 |
| C | 175 | 105 | 140 | 170 | 0 |
| D | 80 | 65 | 105 | 120 | 0 |
| E | 95 | 115 | 120 | 100 | 0 |
类似的,如果是开发者数量更多,则添加cost为零的虚拟行
代码实现
最后我写了一份python代码来实现上述的算法过程
定义了一个AdjacencyMatrixHungarian类(之所以用AdjacencyMatrix,是因为该算法可以看成是邻接矩阵形式的Hungarian算法),它的输入参数就是一个cost矩阵,在初始化时,判断是否需要进行非平衡处理;calculate方法是算法的主流程,而findMinCoverLines方法是划线搜索子算法的实现,该方法相对复杂,尤其是搜索翻转序列时会调用findAugmentSequence的方法,该方法采用递归的手段来搜索序列
import numpy as np
class AdjacencyMatrixHungarian:
def __init__(self, costEdges):
self.costEdges=costEdges
if costEdges.shape[0]!=costEdges.shape[1]:
self.handleUnbalance()
self.n=self.costEdges.shape[0]
def handleUnbalance(self):
m=self.costEdges.shape[0]
n=self.costEdges.shape[1]
if(m<n):
dummy_row=np.zeros((1,n))
self.costEdges=np.vstack((self.costEdges,dummy_row))
elif(m>n):
dummy_column=np.zeros((m,1))
self.costEdges=np.hstack((self.costEdges,dummy_column))
def calculate(self):
self.rowReduction()
self.columnReduction()
print("Cost matrix after row and column reduction")
print(self.costEdges)
(coverRows,coverColumns,independentZeros)=self.findMinCoverLines()
n1=len(coverRows)+len(coverColumns)
while n1!=self.n:
print("Haven't reach optimal, start iterate reduction")
self.costEdges=self.iterateReduction(coverRows,coverColumns)
print("Cost matrix after iterate reduction")
print(self.costEdges)
(coverRows,coverColumns,independentZeros)=self.findMinCoverLines()
n1=len(coverRows)+len(coverColumns)
return independentZeros
def rowReduction(self):
for i in range(self.n):
minValue=self.costEdges[i].min()
for j in range(self.n):
self.costEdges[i,j]=self.costEdges[i,j]-minValue
def columnReduction(self):
for j in range(self.n):
minValue=self.costEdges[:,j].min()
for i in range(self.n):
self.costEdges[i,j]=self.costEdges[i,j]-minValue
def iterateReduction(self, coverRows, coverColumns):
minValue=float('inf')
for i in range(self.n):
for j in range(self.n):
if i in coverRows or j in coverColumns:
continue
if self.costEdges[i,j]<minValue:
minValue=self.costEdges[i,j]
for i in range(self.n):
if i in coverRows:
continue
for j in range(self.n):
self.costEdges[i,j]-=minValue
for j in range(self.n):
if j in coverColumns:
for i in range(self.n):
self.costEdges[i,j]+=minValue
return self.costEdges
def findMinCoverLines(self):
starMarks=np.zeros((self.n,self.n))
primeMarks=np.zeros((self.n,self.n))
coverRows=[]
coverColumns=[]
for i in range(self.n):
for j in range(self.n):
if self.costEdges[i,j]!=0:
continue
existStarZeroThisRow=False
for k in range(self.n):
if starMarks[i,k]==1:
existStarZeroThisRow=True
break
existStarZeroThisColumn=False
for l in range(self.n):
if starMarks[l,j]==1:
existStarZeroThisColumn=True
break
if not existStarZeroThisRow and not existStarZeroThisColumn:
starMarks[i,j]=1
coverColumns.append(j)
while True:
uncoverZeroCounter=0
for i in range(self.n):
for j in range(self.n):
if self.costEdges[i,j]!=0:
continue
if i in coverRows or j in coverColumns:
continue
uncoverZeroCounter+=1
primeMarks[i,j]=1
noStarZeroThisRow=True
for k in range(self.n):
if starMarks[i,k]==1:
coverColumns.remove(k)
coverRows.append(i)
noStarZeroThisRow=False
break
if not noStarZeroThisRow:
continue
else:
sequence=self.findAugmentSequence(starMarks, primeMarks, [(i,j)])
for k in range(len(sequence)):
if k%2==0:
primeMarks[sequence[k][0],sequence[k][1]]=0
starMarks[sequence[k][0],sequence[k][1]]=1
else:
starMarks[sequence[k][0],sequence[k][1]]=0
primeMarks[:,:]=0
coverRows=[]
coverColumns=[]
for j in range(self.n):
for i in range(self.n):
if starMarks[i,j]==1:
coverColumns.append(j)
continue
if uncoverZeroCounter==0:
break
independentZeros=[]
for i in range(self.n):
for j in range(self.n):
if starMarks[i,j]==1:
independentZeros.append((i,j))
return (coverRows,coverColumns,independentZeros)
def findAugmentSequence(self, starMarks, primeMarks, sequence):
if primeMarks[sequence[-1][0],sequence[-1][1]]==1:
for i in range(self.n):
if starMarks[i,sequence[-1][1]]==1:
sequence.append((i,sequence[-1][1]))
return self.findAugmentSequence(starMarks,primeMarks,sequence)
return sequence
elif starMarks[sequence[-1][0],sequence[-1][1]]==1:
for j in range(self.n):
if primeMarks[sequence[-1][0],j]==1:
sequence.append((sequence[-1][0],j))
return self.findAugmentSequence(starMarks,primeMarks,sequence)
return sequence
用下面的代码进行测试:
import numpy as np
from AdjacencyMatrixHungarian import AdjacencyMatrixHungarian
costEdges=np.array([
[210, 90, 180, 160],
[100, 70, 130, 200],
[175, 105,140, 170],
[80, 65, 105, 120]
])
algorithm=AdjacencyMatrixHungarian(costEdges)
result=algorithm.calculate()
print("Optimal result")
print(result)
结果:
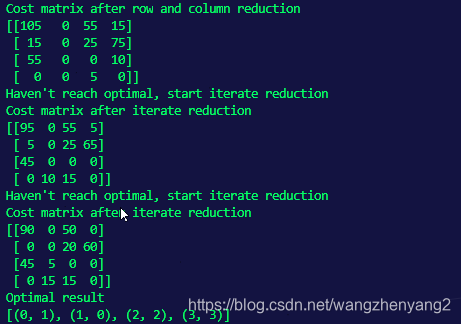





 本文详细介绍了Kuhn-Munkres算法,用于解决分配问题,如最短开发时间分配。通过行和列减法操作,寻找最优解。文章包括算法流程、划线方法、非平衡处理及Python代码实现。
本文详细介绍了Kuhn-Munkres算法,用于解决分配问题,如最短开发时间分配。通过行和列减法操作,寻找最优解。文章包括算法流程、划线方法、非平衡处理及Python代码实现。
















 3874
3874










