长链剖分详细讲解

前言

本来想随便写一点长剖细节就算了，但是发现长剖好的讲解很少。

长链剖分

节点x有若干个儿子，经过其中一个儿子y可以走到以x为根的子树中深度最深的节点。则称y为x的深儿子，其他儿子是浅儿子。
由深儿子组成的一条链叫做长链。
如果节点x没有儿子，则它自己单独构成一条长链。

长链的性质

总长度

所有长链的总链长相加为n。

性质二

任何一个节点x的k级祖先所在的长链的链长都≥k

复杂度

从任意一个节点出发，跳长链直到根节点，最多跳根号次。
这是由于：每跳到另一个长链，新链的链长至少比旧链的链长+1，那么最坏情况下链长是1、2、3、…，这样，跳根号步，总链长就到达了n，也就必然到达了根节点。

链顶和链底

链顶没什么性质。
链底必然是叶子节点。

长链剖分优化动态规划

设f[u][x]表示节点u向下x步的节点数量。
暴力求解复杂度是O(n²)，而且会爆空间。

长链剖分可以优化于深度相关的计算，我们考虑模仿DSU on Tree（树上启发式合并）的思路，O(1)继承深儿子，暴力浅儿子。
这样复杂度是O(n)的，证明一会再说吧。

先说一下实现：
设f[x]表示当前节点向下走x步的节点数量。
我们考虑直接让同一条链上的节点共用f数组，这样可以O(1)继承，具体来说：

我们开辟一片内存：

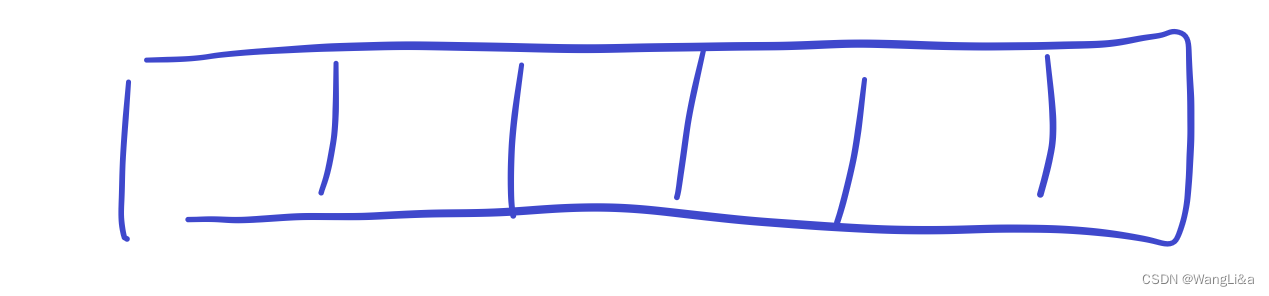
那么父亲的f数组在这里：

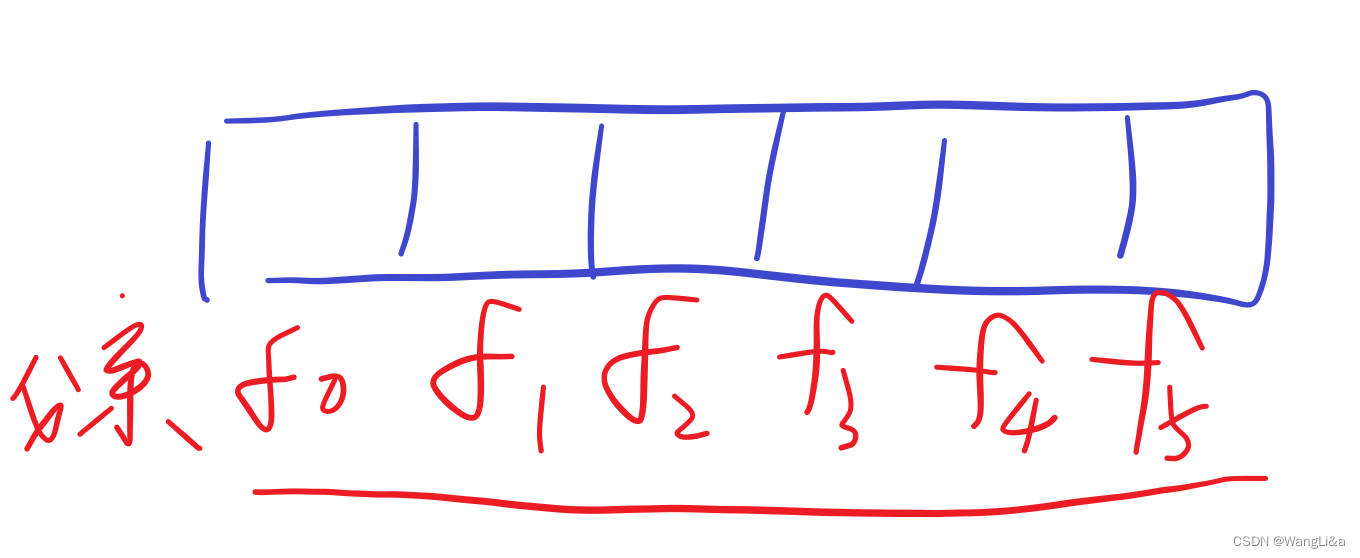
儿子的f数组在这里：

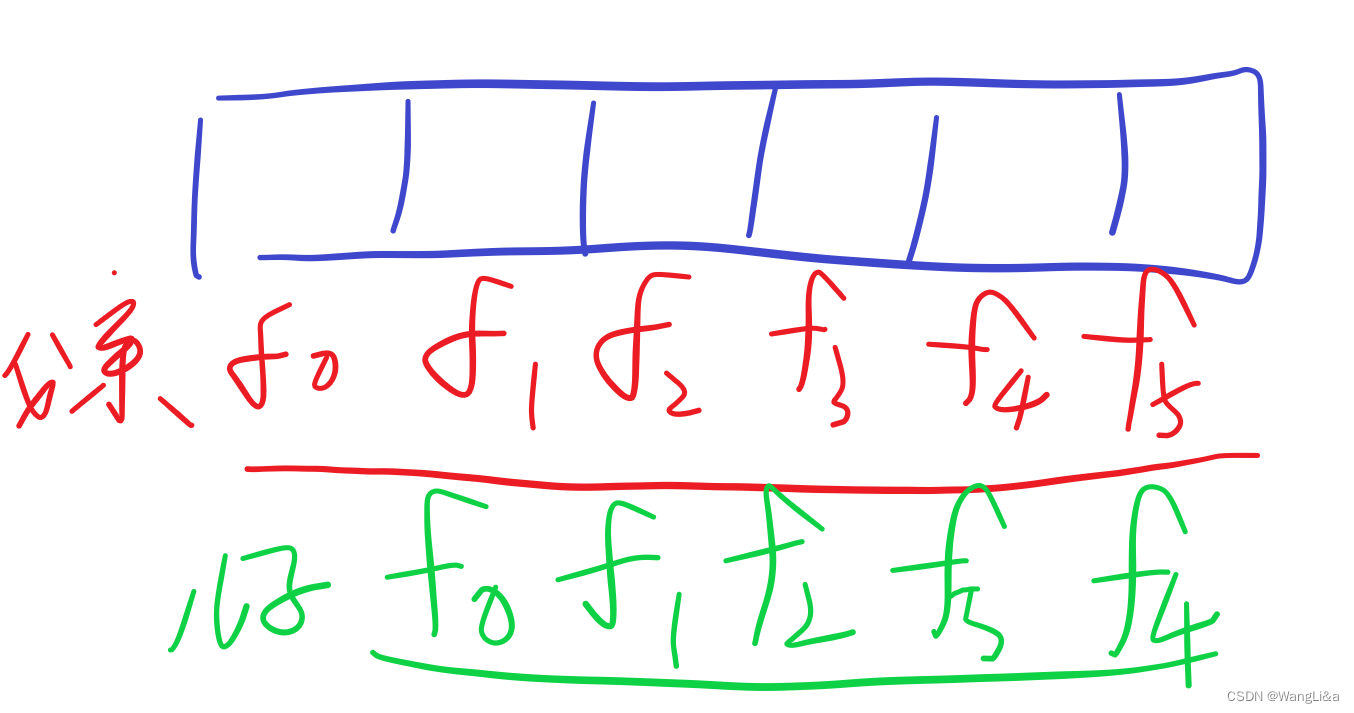
孙子的f数组在这里：

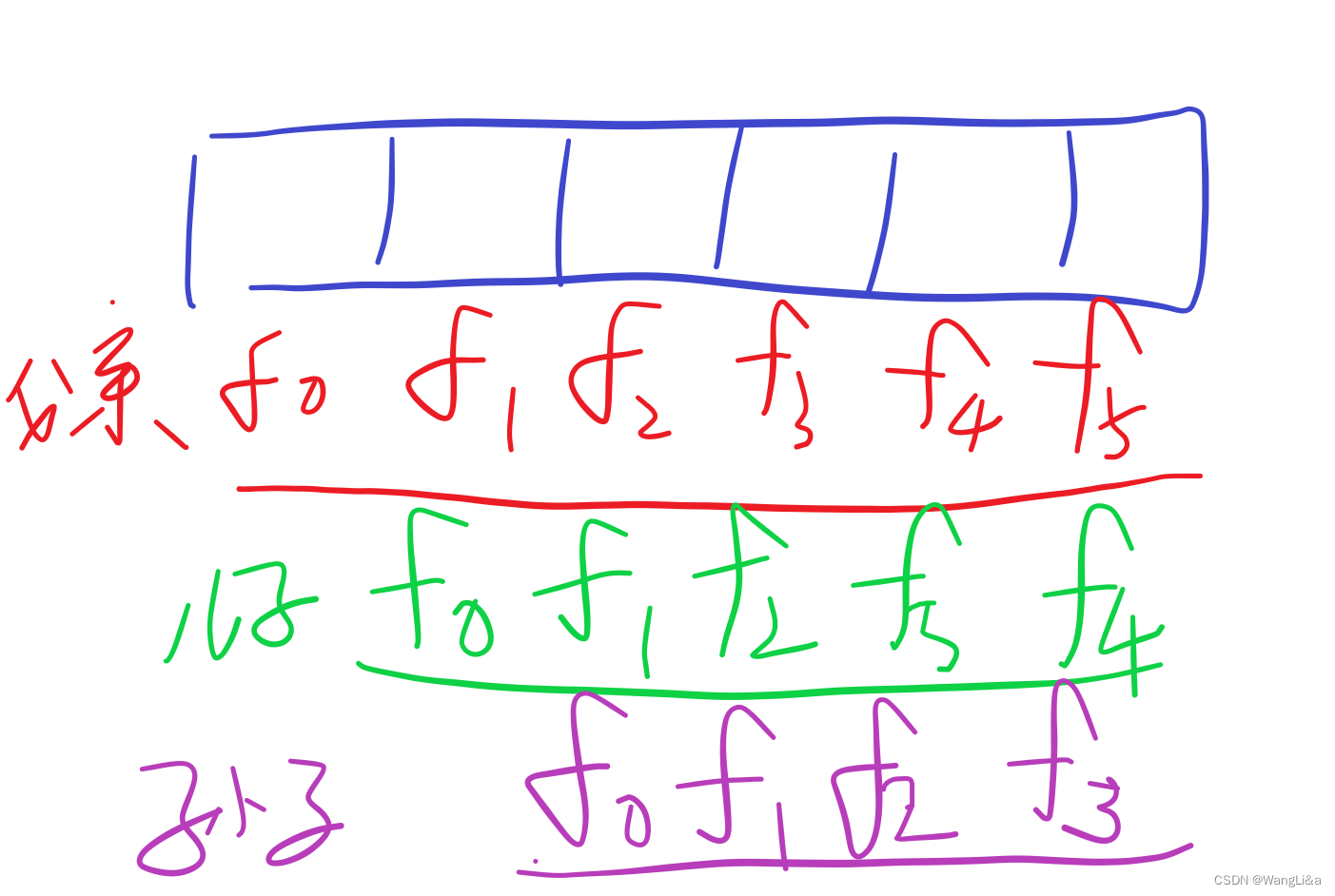
也就是要移动一位。
代码实现就是，我们用一个指针t[父亲]指向父亲的f[0]，然后用一个指针t[儿子]指向父亲的f[1]，用指针t[孙子]指向父亲的f[2]。
这里的父亲其实就是链顶。
怎么确定链顶u的位置呢，就设整棵树的内存起点是s，那么u的位置就是s[dfn[u]]所在的位置。
这样的话，每一条链上的所有点占用的空间就是本条链的链长。那么整棵树占用的空间就是所有链长的总和，也就是O(n)。这样空间复杂度就对了。
关于时间复杂度呢？
不难发现，每条链都仅被链顶的父亲暴力转移一次，单次转移复杂度是O(链长)，所以总复杂度是O(n)。

上代码：

#include<iostream>
#include<vector>
#include<cstdio>
using namespace std;
int deep[1000005],son[1000005],dest[1000005];
int n;
vector<vector<int>> a;
int dfs1(int u,int fa) {
	dest[u]=deep[u]=deep[fa]+1;
	for(auto&v:a[u]) 
		if(v^fa&&dest[u]<dfs1(v,u))
			dest[u]=dest[v],son[u]=v;
	return dest[u];
}
int dfn[1000005],cnt;
int top[1000005],len[1000005]; 
int dfs2(int u,int fa) {
	if(u==son[fa]) top[u]=top[fa];
	else top[u]=u;
	dfn[u]=++cnt;
	len[u]=1;
	if(son[u]) len[u]+=dfs2(son[u],u);
	for(auto&v:a[u])
		if(fa^v&&son[u]^v)
			dfs2(v,u);
	return len[u];
}
int s[1000005],*f[1000005];
void dfs3(int u,int fa) {
	f[u]=s+dfn[u];
	for(auto&v:a[u])
		if(v^fa)
			dfs3(v,u);
}
int ans[1000005];
int dfs4(int u,int fa) {
	f[u][0]=1;
	if(son[u]) {
		dfs4(son[u],u);
		if(f[son[u]][ans[son[u]]]>f[u][ans[u]])
			ans[u]=ans[son[u]]+1;
	}
	for(auto&v:a[u])
		if(v^fa&&v^son[u]) 
			for(int i=0,k=dfs4(v,u);i<k;i++) {
				f[u][i+1]+=f[v][i];
				if(f[u][i+1]>f[u][ans[u]]||(f[u][i+1]==f[u][ans[u]]&&i+1<ans[u]))
					ans[u]=i+1;
			}
	return len[u];
}
int main(){
	scanf("%d",&n);
	for(int i=0;i<=n;i++) a.push_back({});
	for(int i=1;i<n;i++) {
		int u,v;
		scanf("%d%d",&u,&v);
		a[u].push_back(v);
		a[v].push_back(u);
	}
	dfs1(1,0);
	dfs2(1,0);
	dfs3(1,0);
	dfs4(1,0);
//	for(int i=1;i<=n;i++)
//		cout<<len[i]<<endl;
	for(int i=1;i<=n;i++)
		printf("%d\n",ans[i]);
    return 0; 
} 

1. 这里的dest数组指的是"deepest"，也即当前子树下的最深节点深度。
2. 唯一的细节就是，在dfs4中，继承重儿子的ans时，仅有儿子的ans对应的f值大于1时才继承，这是因为题目说要求最小化答案，一开始的时候根节点答案默认为0，除非0不是一个答案，否则优先选0
3. 虽然这个题时间限制开到4.5s，但是用cin、cout仍然会超时。

长链剖分求树上k级祖先

长链剖分维护树上k级祖先可以获得O(nlogn)~O(1)的复杂度，但是在随机数据下慢于重链剖分 。
首先我们对树进行长链剖分。
然后我们倍增出每个节点的2^k级祖先。
然后我们初始化出每个链顶往上跳链长步，祖先分别是谁，再初始化出每个链顶，沿着链向下走链长步，经过的节点分别是谁。
对于询问x的k级祖先，我们倍增先跳到x的highbit(k)级祖先那里，这是O(1)的。
这样的话，由于性质，x的这个祖先所在的链长一定>highbit(k)>k-highbit(k)了，那么如果说剩下的步数跳完还在链上的话，就借助刚才初始化的数组从链顶往下跳，如果跳完已经超过链顶了，那么借助刚才初始化的另一个数组从链顶往上跳。这两种情况都是O(1)的。

倍增数组的复杂度，初始化O(nlogn)。

初始化数组的复杂度分析，每条链贡献O(链长)的复杂度，总复杂度就是O(n)。
空间上这两个数组可以使用嵌套vector，但是由于其实只记了O(n)的信息，也可以开数组存下。

highbit可以使用__builtin_clz(x)以O(1)求出，这个函数是(count leading zero)，即统计前导零个数。如果是long long类型的话，应当使用__builtin_ctzll(x)。
highbit也可以数组预处理。

代码：

#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
#define ui unsigned int
ui s;
inline ui get(ui x) {
	x ^= x << 13;
	x ^= x >> 17;
	x ^= x << 5;
	return s = x; 
}
int n,m;
vector<vector<int>> a;
int dest[500005],deep[500005],fa[500005],son[500005];
int dfs1(int u) {
	dest[u]=deep[u]=deep[fa[u]]+1;
	for(auto&v:a[u])
		if(v^fa[u]) 
			if(dest[fa[v]=u]<dfs1(v))
				dest[u]=dest[v],son[u]=v;
	return dest[u];
}
int dfn[500005],cnt,top[500005],len[500005];
int dfs2(int u) {
	dfn[u]=++cnt;
	len[u]=1;
	if(son[fa[u]]==u) top[u]=top[fa[u]];
	else top[u]=u;
	if(son[u]) len[u]+=dfs2(son[u]);
	for(auto&v:a[u])
		if(v^fa[u]&&v^son[u])
			dfs2(v);
	return len[u];
}
vector<vector<int>> g,h;//g向上，h向下 
void dfs3(int ux,int u,int k) {
	g[ux].push_back(u);
	if(k^len[ux]) dfs3(ux,fa[u],k+1);
}
void dfs4(int ux,int u,int k) {
	h[ux].push_back(u);
	if(k^len[ux]) dfs4(ux,son[u],k+1);
}
int f[20][500005];
int solve(int u,int k) {
	if(!k) return u;
	int x=31-__builtin_clz(k);
	u=f[x][u];
	k-=1<<x;
	if(deep[u]-deep[top[u]]>=k)
		return h[top[u]][deep[u]-deep[top[u]]-k];
	else
		return g[top[u]][k-(deep[u]-deep[top[u]])];
}
int main(){
	cin>>n>>m>>s;
	for(int i=0;i<=n;i++) a.push_back({}),g.push_back({}),h.push_back({});
	int root;
	for(int i=1;i<=n;i++) {
		int u=i;
		int v;
		cin>>v;
		if(!v) {
			root=u;
			continue;
		}
		a[u].push_back(v);
		a[v].push_back(u);
	}
	dfs1(root);
	dfs2(root);
	for(int i=1;i<=n;i++) f[0][i]=fa[i];
	for(int k=1;k<20;k++)
		for(int i=1;i<=n;i++)
			f[k][i]=f[k-1][f[k-1][i]];
	for(int i=1;i<=n;i++)
		if(i==top[i])
		dfs3(i,i,0),dfs4(i,i,1);
	long long sum=0,ans=0;
//	for(int i=1;i<=n;i++)
//		cout<<deep[i]<<' ';
//	cout<<endl;
	for(long long i=1;i<=m;i++) {
		int u=(get(s)^ans)%n+1;
		int k=(get(s)^ans)%deep[u];
		ans=solve(u,k);
//		cout<<ans<<endl;
		sum=sum^(i*ans);
	}
	cout<<sum;
    return 0;
} 

1. 唯一的细节就是注意在每一次求出新的询问的时候，要先算出u，再计算k，取模deep[u]时，不能再带入u的计算公式，因为get(s)会改变。

长链剖分与贪心

我们可以联想到，每一条长链的底端都是叶子结点。（事实上，所有的树链底端都是叶子结点。）

一个假装是对的贪心：
每次选择最大的路径，然后将路径上所有点的权值清零。
那么我们可以用长链剖分来实现这个贪心。
链长改为最大的路径权值和，这样子把每条长链的权值丢进一个堆里面取k次即可。
——yyb

后记

于是皆大欢喜。