注:本文为 “Dirac‘s Delta Function” 相关 csdn 文章重排。
如有内容异常,请看原文。
PDE——Delta 函数
itheta 原创于 2019-04-08 19:50:35 发布
Delta 函数的定义与性质
Delta 函数
δ
(
x
)
\delta(x)
δ(x) 并非传统意义上的函数,它不具有明确的自变量与函数值的对应关系。其“函数值”仅在积分运算中具有意义:
∫
−
∞
∞
f
(
x
)
δ
(
x
)
d
x
=
f
(
0
)
\int_{-\infty}^{\infty} f(x) \delta(x) \, \mathrm{d}x = f(0)
∫−∞∞f(x)δ(x)dx=f(0)
Delta 函数也可视为某些函数序列的极限。若函数序列
δ
l
(
x
)
\delta_l(x)
δl(x) 满足
lim
l
→
0
∫
−
∞
∞
f
(
x
)
δ
l
(
x
)
d
x
=
f
(
0
)
\lim_{l \to 0} \int_{-\infty}^{\infty} f(x) \delta_l(x) \, \mathrm{d}x = f(0)
l→0lim∫−∞∞f(x)δl(x)dx=f(0)
则称
δ
l
(
x
)
\delta_l(x)
δl(x) 收敛于
δ
(
x
)
\delta(x)
δ(x)。例如:
δ
(
x
)
=
lim
n
→
∞
n
π
e
−
n
2
x
2
δ
(
x
)
=
lim
n
→
∞
n
π
1
1
+
n
2
x
2
δ
(
x
)
=
sin
n
x
π
x
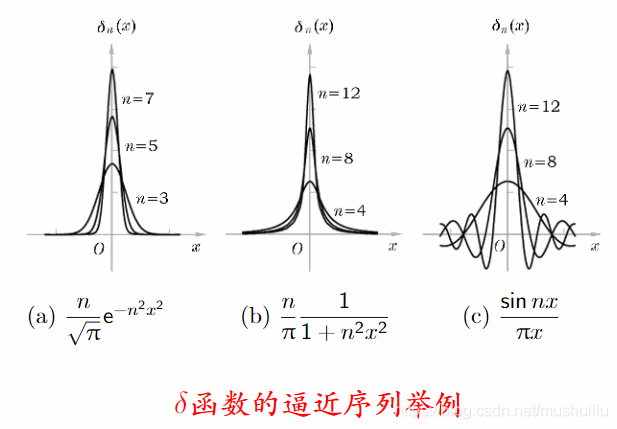
\begin{aligned} \delta(x) &= \lim_{n \to \infty} \frac{n}{\sqrt{\pi}} \mathrm{e}^{-n^2 x^2} \\ \delta(x) &= \lim_{n \to \infty} \frac{n}{\pi} \frac{1}{1 + n^2 x^2} \\ \delta(x) &= \frac{\sin n x}{\pi x}\end{aligned}
δ(x)δ(x)δ(x)=n→∞limπne−n2x2=n→∞limπn1+n2x21=πxsinnx
Delta 函数的基本运算规则
-
与常数的乘积
∫ − ∞ ∞ f ( x ) c δ ( x ) d x = c f ( 0 ) \int_{-\infty}^{\infty} f(x) c \delta(x) \, \mathrm{d}x = c f(0) ∫−∞∞f(x)cδ(x)dx=cf(0) -
平移变换 x → x − a x \to x - a x→x−a
∫ − ∞ ∞ f ( x ) δ ( x − a ) d x = f ( a ) \int_{-\infty}^{\infty} f(x) \delta(x - a) \, \mathrm{d}x = f(a) ∫−∞∞f(x)δ(x−a)dx=f(a) -
放大或缩小 x → α x x \to \alpha x x→αx
∫ − ∞ ∞ f ( x ) δ ( α x ) d x = 1 ∣ α ∣ f ( 0 ) \int_{-\infty}^{\infty} f(x) \delta(\alpha x) \, \mathrm{d}x = \frac{1}{|\alpha|} f(0) ∫−∞∞f(x)δ(αx)dx=∣α∣1f(0)
因此,
δ ( α x ) = 1 ∣ α ∣ δ ( x ) \delta(\alpha x) = \frac{1}{|\alpha|} \delta(x) δ(αx)=∣α∣1δ(x)
特别地,当 α = − 1 \alpha = -1 α=−1 时,
δ ( − x ) = δ ( x ) \delta(-x) = \delta(x) δ(−x)=δ(x) -
Delta 函数的导数
对于在 x = 0 x = 0 x=0 点连续且具有连续导数的函数 f ( x ) f(x) f(x),
∫ − ∞ ∞ f ( x ) δ ′ ( x ) d x = − f ′ ( 0 ) \int_{-\infty}^{\infty} f(x) \delta'(x) \, \mathrm{d}x = -f'(0) ∫−∞∞f(x)δ′(x)dx=−f′(0) -
Delta 函数的高阶导数
对于在 x = 0 x = 0 x=0 点连续且具有 n n n 阶连续导数的函数 f ( x ) f(x) f(x),
∫ − ∞ ∞ f ( x ) δ ( n ) ( x ) d x = ( − 1 ) n f ( n ) ( 0 ) \int_{-\infty}^{\infty} f(x) \delta^{(n)}(x) \, \mathrm{d}x = (-1)^n f^{(n)}(0) ∫−∞∞f(x)δ(n)(x)dx=(−1)nf(n)(0) -
Delta 函数与普通函数的乘积
∫ − ∞ ∞ f ( x ) g ( x ) δ ( x ) d x = f ( 0 ) g ( 0 ) \int_{-\infty}^{\infty} f(x) g(x) \delta(x) \, \mathrm{d}x = f(0) g(0) ∫−∞∞f(x)g(x)δ(x)dx=f(0)g(0)
因此,
f ( x ) δ ( x ) = f ( 0 ) δ ( x ) f(x) \delta(x) = f(0) \delta(x) f(x)δ(x)=f(0)δ(x)
例如,
x δ ( x ) = 0 x \delta(x) = 0 xδ(x)=0
Remarks
所有涉及 Delta 函数的等式均应在积分意义下理解。对于 Delta 函数的运算,通常将其转化为普通函数
f
(
x
)
f(x)
f(x) 的运算。例如,
x
δ
(
x
)
=
0
x \delta(x) = 0
xδ(x)=0 应理解为
∫
−
∞
∞
f
(
x
)
x
δ
(
x
)
d
x
=
0
\int_{-\infty}^{\infty} f(x) x \delta(x) \, \mathrm{d}x = 0
∫−∞∞f(x)xδ(x)dx=0
Exercises
- 计算积分
∫ − ∞ ∞ sin x x d x \int_{-\infty}^{\infty} \frac{\sin x}{x} \, \mathrm{d}x ∫−∞∞xsinxdx - 计算积分
∫ − ∞ ∞ sin 2 x x 2 + x + 1 d x \int_{-\infty}^{\infty} \frac{\sin 2x}{x^2 + x + 1} \, \mathrm{d}x ∫−∞∞x2+x+1sin2xdx
Delta 函数的 Fourier 展开
设有周期函数
f
(
x
)
f(x)
f(x),满足
f
(
x
)
=
f
(
x
+
2
π
)
f(x) = f(x + 2\pi)
f(x)=f(x+2π) 且符合 Dirichlet 条件,则可展开为
f
(
x
)
=
∑
n
=
−
∞
∞
c
n
e
i
n
x
f(x) = \sum_{n = -\infty}^{\infty} c_n \mathrm{e}^{\mathrm{i} n x}
f(x)=n=−∞∑∞cneinx
其中展开系数为
c
n
=
1
2
π
∫
−
π
π
f
(
x
)
e
−
i
n
x
d
x
c_n = \frac{1}{2\pi} \int_{-\pi}^{\pi} f(x) \mathrm{e}^{-\mathrm{i} n x} \, \mathrm{d}x
cn=2π1∫−ππf(x)e−inxdx
代入
c
n
c_n
cn 并交换积分与求和次序,得
f
(
x
)
=
∫
−
π
π
f
(
ξ
)
[
1
2
π
∑
n
=
−
∞
∞
e
i
n
(
x
−
ξ
)
]
d
ξ
f(x) = \int_{-\pi}^{\pi} f(\xi) \left[ \frac{1}{2\pi} \sum_{n = -\infty}^{\infty} \mathrm{e}^{\mathrm{i} n (x - \xi)} \right] \, \mathrm{d}\xi
f(x)=∫−ππf(ξ)[2π1n=−∞∑∞ein(x−ξ)]dξ
因此,
δ
(
ξ
−
x
)
=
1
2
π
∑
n
=
−
∞
∞
e
i
n
(
x
−
ξ
)
,
−
π
<
x
<
π
\delta(\xi - x) = \frac{1}{2\pi} \sum_{n = -\infty}^{\infty} \mathrm{e}^{\mathrm{i} n (x - \xi)}, \quad -\pi < x < \pi
δ(ξ−x)=2π1n=−∞∑∞ein(x−ξ),−π<x<π
常微分方程的 Green 函数
初值问题
Example 19.4 求解常微分方程初值问题
d
2
g
d
x
2
=
δ
(
x
−
t
)
,
x
,
t
>
0
\frac{\mathrm{d}^2 g}{\mathrm{d}x^2} = \delta(x - t), \quad x, t > 0
dx2d2g=δ(x−t),x,t>0
初始条件为
g
∣
x
=
0
=
0
,
d
g
d
x
∣
x
=
0
=
0
g|_{x = 0} = 0, \quad \left. \frac{\mathrm{d}g}{\mathrm{d}x} \right|_{x = 0} = 0
g∣x=0=0,dxdg
x=0=0
Solution: 直接积分得
d
g
d
x
=
η
(
x
−
t
)
+
α
(
t
)
\frac{\mathrm{d}g}{\mathrm{d}x} = \eta(x - t) + \alpha(t)
dxdg=η(x−t)+α(t)
再积分得
g
(
x
;
t
)
=
(
x
−
t
)
η
(
x
−
t
)
+
α
(
t
)
x
+
β
(
t
)
g(x; t) = (x - t) \eta(x - t) + \alpha(t) x + \beta(t)
g(x;t)=(x−t)η(x−t)+α(t)x+β(t)
由初始条件
g
∣
x
=
0
=
0
⇒
β
(
t
)
=
0
g|_{x = 0} = 0 \Rightarrow \beta(t) = 0
g∣x=0=0⇒β(t)=0
d
g
d
x
∣
x
=
0
=
0
⇒
α
(
t
)
=
0
\left. \frac{\mathrm{d}g}{\mathrm{d}x} \right|_{x = 0} = 0 \Rightarrow \alpha(t) = 0
dxdg
x=0=0⇒α(t)=0
因此,
g
(
x
;
t
)
=
(
x
−
t
)
η
(
x
−
t
)
g(x; t) = (x - t) \eta(x - t)
g(x;t)=(x−t)η(x−t)
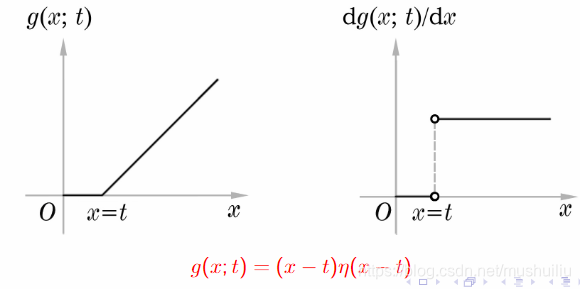
Analysis: 该问题的物理意义为 d 2 g d x 2 \frac{\mathrm{d}^2 g}{\mathrm{d}x^2} dx2d2g 表示加速度,质点在 x = t x = t x=t 时刻受到一个脉冲力,其总量为 1。初始位置为 0,受力后开始运动。
利用 Example 19.4 的结果,可以求解以下问题:
d
2
y
d
x
2
=
f
(
x
)
,
x
>
0
\frac{\mathrm{d}^2 y}{\mathrm{d}x^2} = f(x), \quad x > 0
dx2d2y=f(x),x>0
初始条件为
y
(
0
)
=
0
,
y
′
(
0
)
=
0
y(0) = 0, \quad y'(0) = 0
y(0)=0,y′(0)=0
Solution: 由于
f
(
x
)
=
∫
0
∞
f
(
t
)
δ
(
x
−
t
)
d
t
f(x) = \int_{0}^{\infty} f(t) \delta(x - t) \, \mathrm{d}t
f(x)=∫0∞f(t)δ(x−t)dt
根据常微分方程解的叠加性,形式解为
y
(
x
)
=
∫
0
∞
g
(
x
;
t
)
f
(
t
)
d
t
=
∫
0
x
(
x
−
t
)
f
(
t
)
d
t
y(x) = \int_{0}^{\infty} g(x; t) f(t) \, \mathrm{d}t = \int_{0}^{x} (x - t) f(t) \, \mathrm{d}t
y(x)=∫0∞g(x;t)f(t)dt=∫0x(x−t)f(t)dt
初值问题
Example 19.5 求解常微分方程初值问题
d
2
g
d
x
2
+
k
2
g
(
x
;
t
)
=
δ
(
x
−
t
)
,
x
,
t
>
0
\frac{\mathrm{d}^2 g}{\mathrm{d}x^2} + k^2 g(x; t) = \delta(x - t), \quad x, t > 0
dx2d2g+k2g(x;t)=δ(x−t),x,t>0
初始条件为
g
∣
x
=
0
=
0
,
d
g
d
x
∣
x
=
0
=
0
g|_{x = 0} = 0, \quad \left. \frac{\mathrm{d}g}{\mathrm{d}x} \right|_{x = 0} = 0
g∣x=0=0,dxdg
x=0=0
Solution:
- 当 x ≠ t x \neq t x=t 时,方程的非齐次项为 0。
- 在区间 ( 0 , t ) (0, t) (0,t) 内,齐次方程的解为零解。
- 在区间
(
t
,
∞
)
(t, \infty)
(t,∞) 内,齐次微分方程的通解为
g ( x ; t ) = [ C ( t ) sin k x + D ( t ) cos k x ] η ( x − t ) g(x; t) = [C(t) \sin kx + D(t) \cos kx] \eta(x - t) g(x;t)=[C(t)sinkx+D(t)coskx]η(x−t) - 由
x
=
t
x = t
x=t 点的连续性要求确定 Green 函数:
- 在
x
=
t
x = t
x=t 点,
g ( x ; t ) ∣ t − t + = 0 g(x; t)|_{t^-}^{t^+} = 0 g(x;t)∣t−t+=0
d g d x ∣ t − t + = 1 \left. \frac{\mathrm{d}g}{\mathrm{d}x} \right|_{t^-}^{t^+} = 1 dxdg t−t+=1 - 在区间
(
0
,
t
)
(0, t)
(0,t) 内,
d 2 g d x 2 + k 2 g = 0 \frac{\mathrm{d}^2 g}{\mathrm{d}x^2} + k^2 g = 0 dx2d2g+k2g=0
g ∣ x = 0 = 0 , d g d x ∣ x = 0 = 0 g|_{x = 0} = 0, \quad \left. \frac{\mathrm{d}g}{\mathrm{d}x} \right|_{x = 0} = 0 g∣x=0=0,dxdg x=0=0 - 在区间
(
t
,
∞
)
(t, \infty)
(t,∞) 内,
d 2 g d x 2 + k 2 g = 0 \frac{\mathrm{d}^2 g}{\mathrm{d}x^2} + k^2 g = 0 dx2d2g+k2g=0
解得
C ( t ) = 1 k cos k t , D ( t ) = − 1 k sin k t C(t) = \frac{1}{k} \cos kt, \quad D(t) = -\frac{1}{k} \sin kt C(t)=k1coskt,D(t)=−k1sinkt
因此,
g ( x ; t ) = 1 k sin k ( x − t ) η ( x − t ) g(x; t) = \frac{1}{k} \sin k(x - t) \eta(x - t) g(x;t)=k1sink(x−t)η(x−t)
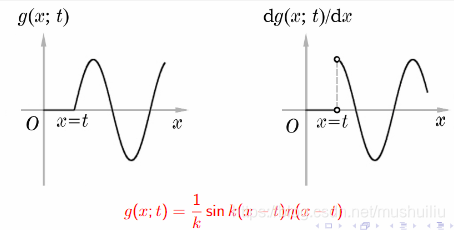
- 在
x
=
t
x = t
x=t 点,
Analysis: 现在可以写出如下非齐次方程的通解:
d
2
g
d
x
2
+
k
2
g
(
x
;
t
)
=
δ
(
x
−
t
)
,
x
,
t
>
0
\frac{\mathrm{d}^2 g}{\mathrm{d}x^2} + k^2 g(x; t) = \delta(x - t), \quad x, t > 0
dx2d2g+k2g(x;t)=δ(x−t),x,t>0
利用 Example 19.5 的结果,可以求解非齐次方程初值问题:
d
2
y
d
x
2
+
k
2
y
(
x
)
=
f
(
x
)
,
x
>
0
\frac{\mathrm{d}^2 y}{\mathrm{d}x^2} + k^2 y(x) = f(x), \quad x > 0
dx2d2y+k2y(x)=f(x),x>0
初始条件为
y
(
0
)
=
0
,
y
′
(
0
)
=
0
y(0) = 0, \quad y'(0) = 0
y(0)=0,y′(0)=0
Solution:
y
(
x
)
=
1
k
∫
0
x
f
(
t
)
sin
k
(
x
−
t
)
d
t
y(x) = \frac{1}{k} \int_{0}^{x} f(t) \sin k(x - t) \, \mathrm{d}t
y(x)=k1∫0xf(t)sink(x−t)dt
Remarks: 对于一般的常微分方程初值问题的 Green 函数
d
d
x
[
p
(
x
)
d
g
(
x
;
t
)
d
x
]
+
q
(
x
)
g
(
x
;
t
)
=
δ
(
x
−
t
)
,
x
,
t
>
0
\frac{\mathrm{d}}{\mathrm{d}x} \left[ p(x) \frac{\mathrm{d}g(x; t)}{\mathrm{d}x} \right] + q(x) g(x; t) = \delta(x - t), \quad x, t > 0
dxd[p(x)dxdg(x;t)]+q(x)g(x;t)=δ(x−t),x,t>0
初始条件为
g
(
0
;
t
)
=
0
,
d
g
(
x
;
t
)
d
x
∣
x
=
0
=
0
g(0; t) = 0, \quad \left. \frac{\mathrm{d}g(x; t)}{\mathrm{d}x} \right|_{x = 0} = 0
g(0;t)=0,dxdg(x;t)
x=0=0
且相应的齐次微分方程无奇点。则有:
- g ( x ; t ) g(x; t) g(x;t) 在 x < t x < t x<t 时一定为 0。
- g ( x ; t ) g(x; t) g(x;t) 在 x = t x = t x=t 时一定连续。
- d g ( x ; t ) d x ∣ t − t + = 1 p ( t ) \left. \frac{\mathrm{d}g(x; t)}{\mathrm{d}x} \right|_{t^-}^{t^+} = \frac{1}{p(t)} dxdg(x;t) t−t+=p(t)1
边值问题
Example 19.6 求解常微分方程边值问题
d
2
g
d
x
2
=
δ
(
x
−
t
)
,
a
<
x
,
t
<
b
\frac{\mathrm{d}^2 g}{\mathrm{d}x^2} = \delta(x - t), \quad a < x, t < b
dx2d2g=δ(x−t),a<x,t<b
边界条件为
g
(
a
;
t
)
=
0
,
g
(
b
;
t
)
=
0
g(a; t) = 0, \quad g(b; t) = 0
g(a;t)=0,g(b;t)=0
微分方程与 Example 19.4 相同,故有相同的通解:
g
(
x
;
t
)
=
(
x
−
t
)
η
(
x
−
t
)
+
α
(
t
)
x
+
β
(
t
)
g(x; t) = (x - t) \eta(x - t) + \alpha(t) x + \beta(t)
g(x;t)=(x−t)η(x−t)+α(t)x+β(t)
由边界条件:
a
α
(
t
)
+
β
(
t
)
=
0
a \alpha(t) + \beta(t) = 0
aα(t)+β(t)=0
b
−
t
+
b
α
(
t
)
+
β
(
t
)
=
0
b - t + b \alpha(t) + \beta(t) = 0
b−t+bα(t)+β(t)=0
解得:
α
(
t
)
=
−
b
−
t
b
−
a
,
β
(
t
)
=
a
(
b
−
t
)
b
−
a
\alpha(t) = -\frac{b - t}{b - a}, \quad \beta(t) = \frac{a(b - t)}{b - a}
α(t)=−b−ab−t,β(t)=b−aa(b−t)
因此,
g
(
x
;
t
)
=
(
x
−
t
)
η
(
x
−
t
)
−
b
−
t
b
−
a
(
x
−
a
)
g(x; t) = (x - t) \eta(x - t) - \frac{b - t}{b - a}(x - a)
g(x;t)=(x−t)η(x−t)−b−ab−t(x−a)
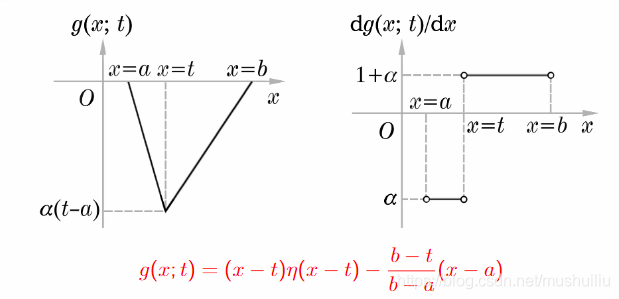
Question: 本例中的 Green 函数 g ( x ; t ) g(x; t) g(x;t) 是否仍然满足:
- g ( x ; t ) g(x; t) g(x;t) 在 x = t x = t x=t 点连续
- d g ( x ; t ) d x ∣ t − t + = 1 \left. \frac{\mathrm{d}g(x; t)}{\mathrm{d}x} \right|_{t^-}^{t^+} = 1 dxdg(x;t) t−t+=1
- Dirac delta function(狄拉克 δ 函数) | 定义、性质及物理意义…(篇 1)-优快云博客
https://blog.youkuaiyun.com/u013669912/article/details/151682410 - Dirac delta function(狄拉克 δ 函数) | 定义、性质及物理意义…(篇 2)-优快云博客
https://blog.youkuaiyun.com/u013669912/article/details/155164259
via:
- PDE——delta函数-优快云博客
https://blog.youkuaiyun.com/mushuiliu/article/details/89104377





















 2087
2087

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








