注:本文为 “梯度、散度、旋度、拉普拉斯算子” 相关合辑。
图片清晰度受引文原图所限。
略作重排,未整理去重。
如有内容异常,请看原文。
未完,待增订……
散度和旋度的物理意义
马同学
在数学书中接触散度和旋度时,若脱离物理背景仅审视数学公式,它们不过是曲线积分、曲面积分的具体应用形式。数学教材引入这些概念,本质上是为了深化对积分运算的理解。
有句名言恰如其分地揭示了数学与物理的关联:
数学没有物理是瞎子,物理没有数学是跛子
下文将结合物理场景解析散度和旋度。需说明的是,本人专业背景为数学而非物理,后续涉及的物理知识以直觉性描述为主,严谨性方面难免存在不足,敬请谅解。
1 通量与散度
理解散度的前提是掌握通量的概念。
1.1 通量
通量的定义为:单位时间内通过某一曲面的物理量多少。
1.1.1 太阳辐射与通量
为具象化这一概念,可结合太阳辐射现象分析:
人类生存依赖太阳能量,而太阳每秒向外辐射的总能量,可通过计算穿过太阳表面的能量总量来描述。

太阳的三维结构可简化为二维投影图(不影响分析):

太阳持续向外辐射能量,若沿其表面作一封闭曲面(三维空间中为球面):

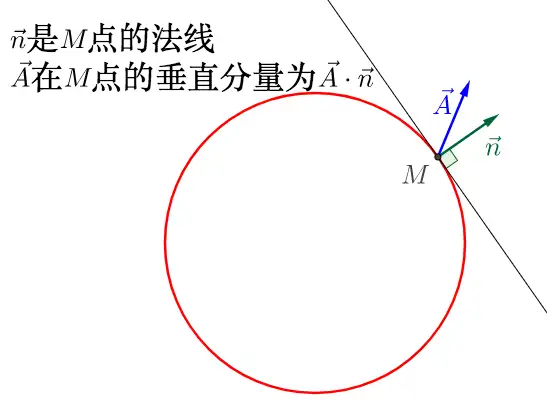
从直观上看,通量可理解为对封闭曲面上向量场 A ⃗ \vec{A} A 的累积效应,但向量 A ⃗ \vec{A} A 在曲面上不同点的方向存在差异,直接累加无法反映真实的传递效果,需明确有效分量的选取规则。
1.1.2 A ⃗ \vec{A} A 的方向影响
以太阳辐射模型说明方向效应不够直观,可换用雨水穿过窗户的场景分析:
假设存在一简化为多边形的房屋:
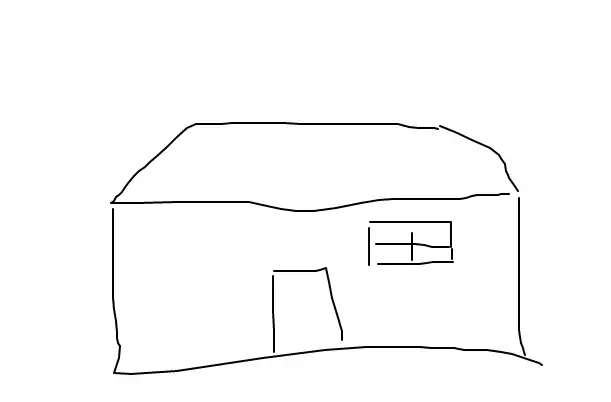
当屋外降下垂直于地面的雨滴时:
-
若屋顶天窗未关,地面形成的水渍面积最大;
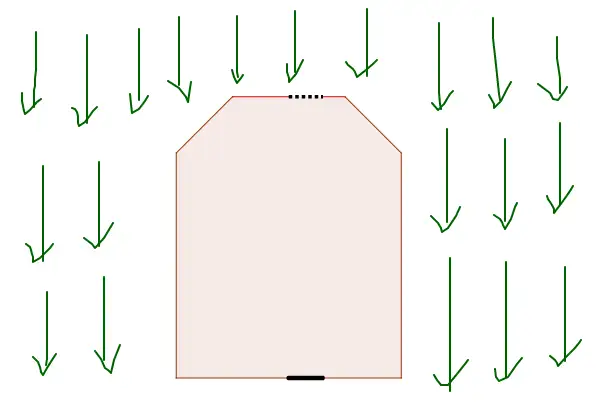
-
若侧面倾斜屋顶的同等大小窗户未关,水渍面积会减小;
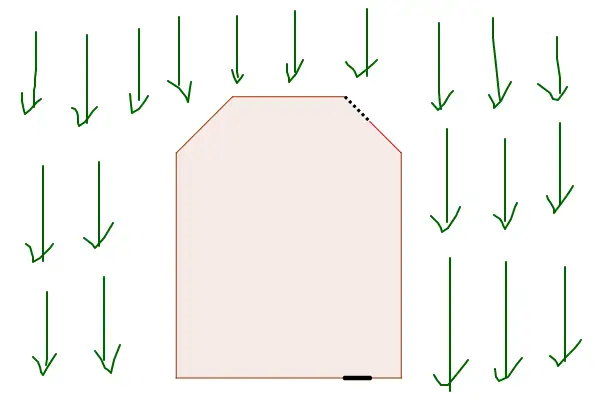
-
若垂直墙壁上的窗户未关,地面几乎无水渍。
这一现象表明:水渍面积与雨水方向和窗户平面的夹角相关——夹角为 0 ∘ 0^\circ 0∘(垂直)时面积最大,夹角为 9 0 ∘ 90^\circ 90∘(相切)时面积最小。本质上,有效传递的雨水量取决于向量场(雨水速度场)在曲面法向的投影分量。
因此,计算通量时只需关注
A
⃗
\vec{A}
A 垂直于曲面的分量:
1.1.3 小结
综上,通量的数学定义为向量场
A
⃗
\vec{A}
A 与曲面法向量
n
⃗
\vec{n}
n 的点积在曲面上的积分。对于曲面
Σ
\Sigma
Σ,其通量表达式为:
∬
Σ
A
⃗
⋅
n
⃗
d
S
\mathop{\iint}_{\Sigma} \vec{A} \cdot \vec{n} \, dS
∬ΣA⋅ndS
1.2 散度
计算太阳表面总辐射通量时,存在另一种思路:太阳辐射源于其内部持续发生的核聚变反应,每个核聚变点都是辐射的“发射源”,总辐射通量等于所有发射源贡献的叠加。但这一思路仅适用于封闭曲面——若仅计算太阳表面的一部分,内部发射源的辐射可能未完全穿过该部分曲面,叠加逻辑不再成立。
为通过这一思路精确计算通量,需量化单个点的辐射“发射强度”(即高斯公式的重要思想)。借助微积分的极限思想:将封闭曲面逐步缩小至极限为 0(近似与辐射点重合),此时通量与封闭曲面所围体积的比值,即为该点的辐射强度:
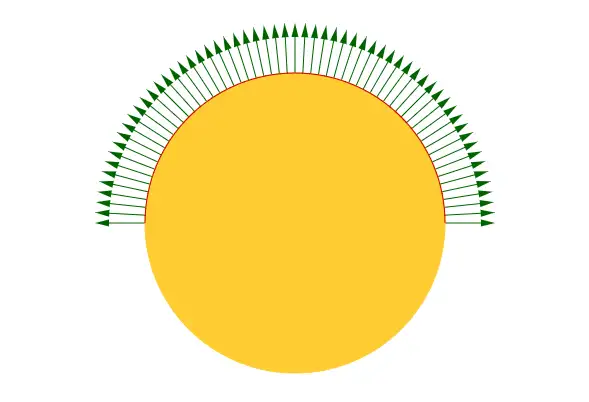
这一比值的极限即为散度。
对于向量场
A
⃗
\vec{A}
A 中任意一点
M
M
M,其散度的定义式为:
div
A
⃗
(
M
)
=
lim
Ω
→
M
1
V
∫
∫
◯
Σ
A
⃗
⋅
n
⃗
d
S
\text{div}\vec{A}(M) = \lim_{\Omega \to M} \frac{1}{V} \mathop{{\int\!\!\!\!\!\int}\mkern-21mu \bigcirc}\limits_{\Sigma} \vec{A} \cdot \vec{n} \, dS
divA(M)=Ω→MlimV1Σ∫∫◯A⋅ndS
其中,
Ω
\Omega
Ω 为封闭曲面
Σ
\Sigma
Σ 所围成的区域,
V
V
V 为
Ω
\Omega
Ω 的体积,积分符号上的圆圈表示积分域为封闭曲面。
1.3 散度与通量的符号意义
散度与通量的符号规律一致,以下以散度为例说明:
-
太阳内部发生核聚变的点:辐射向外发散,散度为正(“源”点);

-
黑洞等引力极强的天体:能量仅进入而不射出,表现为净汇聚,散度为负(“汇”点)。

2 环流量与旋度
环流量、旋度与通量、散度的定义逻辑具有对称性,可通过对比方式理解。
“水能载舟,亦能覆舟”描述了水的力学效应,而水流不仅能使船体上下颠簸,还能引发旋转运动。为量化这种旋转特性,引入环流量和旋度的概念。
2.1 环流量
环流量的定义为:单位时间内环绕某一闭合曲线的物理量累积效应。
以下分析限于二维向量场(三维情形逻辑一致,仅几何关系更复杂):
考虑一汪湖水形成的流速场,箭头方向表示水流方向,箭头长度表示流速大小:
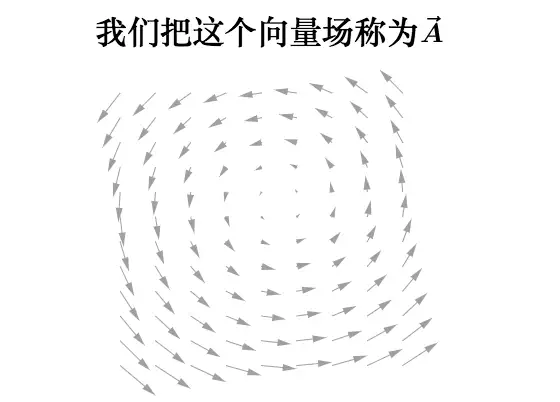
若将船体轮廓抽象为闭合曲线 Γ \Gamma Γ:

单位时间内,水流对船体产生的旋转驱动效应,即为环流量。对于圆形闭合曲线,旋转效应可直观观察:
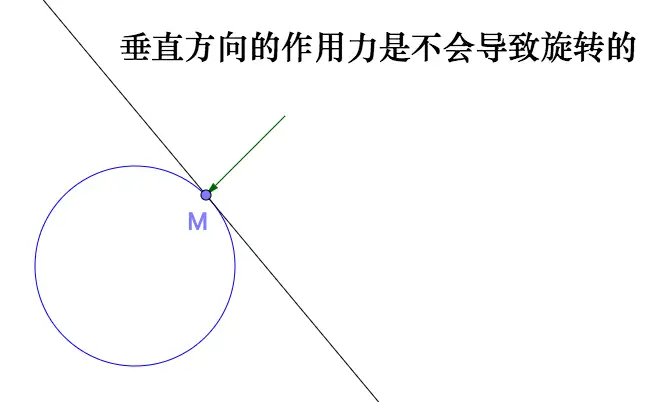
与通量关注法向分量不同,环流量的有效贡献来自向量场沿闭合曲线切线方向的分量:
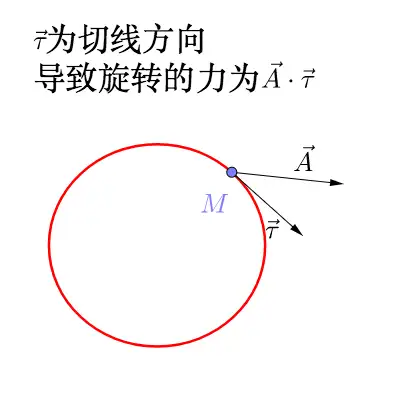
因此,环流量的数学表达式为:
∮
Γ
A
⃗
⋅
τ
⃗
d
l
\oint_{\Gamma} \vec{A} \cdot \vec{\tau} \, dl
∮ΓA⋅τdl
其中,
τ
⃗
\vec{\tau}
τ 为闭合曲线
Γ
\Gamma
Γ 的切向量,
d
l
dl
dl 为曲线弧长元素,积分符号为闭合曲线积分标记。
2.2 旋度
类比散度的定义逻辑:环流量是闭合曲线的宏观累积效应,而旋度是向量场中某点的微观旋转强度。通过将闭合曲线逐步缩小至极限为 0(近似与考察点重合),此时环流量与曲线所围面积的比值,即为该点的旋转强度:
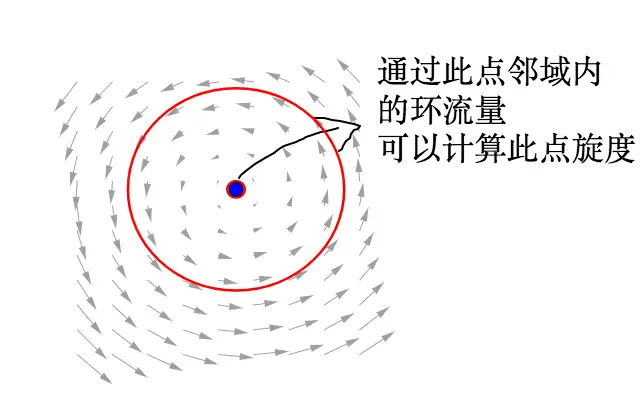
对于向量场中任意一点
M
M
M,其旋度的定义式为:
lim
Σ
→
M
1
S
∮
Γ
A
⃗
⋅
τ
⃗
d
l
\lim_{\Sigma \to M} \frac{1}{S} \oint_{\Gamma} \vec{A} \cdot \vec{\tau} \, dl
Σ→MlimS1∮ΓA⋅τdl
其中,
Σ
\Sigma
Σ 为闭合曲线
Γ
\Gamma
Γ 所围成的区域,
S
S
S 为
Σ
\Sigma
Σ 的面积。
旋度是向量,其方向需通过右手定则确定。
2.3 旋度的方向
旋转运动具有方向性,闭合曲线的环绕方向与旋度方向满足右手定则:

右手四指沿闭合曲线的环绕方向弯曲,大拇指所指方向即为旋度的方向。
维基百科中农业飞机翼尖气流的示意图直观展示了这一特性:烟雾的顺时针或逆时针旋转方向,对应旋度方向与飞机前行方向一致:

3 总结
通过物理场景的具象化分析,可清晰梳理以下重要概念:
- 通量:单位时间内通过某一曲面的物理量;
- 散度:向量场中某点的通量体密度(微观通量强度);
- 环流量:单位时间内环绕某一闭合曲线的物理量;
- 旋度:向量场中某点的环流量面密度(微观旋转强度)。
这些概念起源于物理学研究,物理学家提出物理模型后,数学家通过发展曲线积分、曲面积分及格林公式、高斯公式、斯托克斯公式等工具,完成了量化计算的理论构建。
推荐【马同学图解数学】系列教程
编辑于 2024-01-05 10:46
向量思想的萌芽与发展
向量思想的萌芽
向量思想的起源可追溯至古希腊学者亚里士多德,其在著作《力学》中提出:“当一个物体以一定比率移动时(即含有两个有常数比率的直线运动),物体一定沿一直线运动,这条直线是由这两条有给定比率的直线形成的平行四边形的对角线。” 这一表述本质上揭示了速度的合成满足平行四边形定则,成为向量思想的早期雏形。

平行四边形定则
历经两千余年,牛顿在《自然科学的数学原理》中将平行四边形定则作为运动定律的推论,指出:“直接的力 A D AD AD 由任意倾斜的力 A B AB AB 和 B D BD BD 合成,且反过来,任意直接的力 A D AD AD 分解为任意倾斜的力 A B AB AB 和 B D BD BD。这种合成与分解从力学已得到了充分的证实。” 尽管牛顿的论证已蕴含向量加法的重要逻辑,但并未明确提出“向量”这一数学概念。
向量思想在物理问题中长期酝酿,其正式确立却与复数的几何化密切相关。
复数是什么
数是人类为描述客观世界创造的概念。自然数可表示物体的数量与顺序,随着认知深化,数系逐步扩展为包含零、负数、分数、无理数的实数体系。
三次方程求解过程中,出现了平方后结果为负数的数——这与实数的乘法规则(“正×负=负”“负×负=正”)矛盾,但此类数是三次方程的有效解。为解决这一矛盾,定义虚数单位 i i i,满足 i 2 = − 1 i^2 = -1 i2=−1,此类数被称为虚数。
复数是实数与虚数的组合形式,记作 a + b i a + bi a+bi(其中 a a a、 b b b 为实数),例如 2 + 3 i 2 + 3i 2+3i、 0.5 − 2 i 0.5 - \sqrt{2}i 0.5−2i 等。其中, a a a 称为复数的实部, b b b 称为复数的虚部:
- 当 b = 0 b = 0 b=0 时,复数退化为实数;
- 当 a = 0 a = 0 a=0 时,复数为纯虚数。
复数诞生初期因“虚数”的抽象性未被广泛接受,其合法化的关键在于几何化表示的实现。
复数的几何化
复数提出约两个半世纪后,数学家韦赛尔通过三角测量工作的实践积累,建立了复数与有向线段的对应关系,完成了复数的几何化。
3.1 有向线段的加法
韦赛尔定义:两条有向线段相加时,第二条有向线段的始端与第一条的末端相连,由第一条的始端指向第二条的末端的有向线段,即为两者的和。这一规则与向量加法的三角形法则等价:
A
B
→
+
B
C
→
=
A
C
→
\overrightarrow{AB} + \overrightarrow{BC} = \overrightarrow{AC}
AB+BC=AC

向量加法的三角形法则
3.2 有向线段的乘法
韦赛尔的重要创新在于定义了有向线段乘法的几何意义:
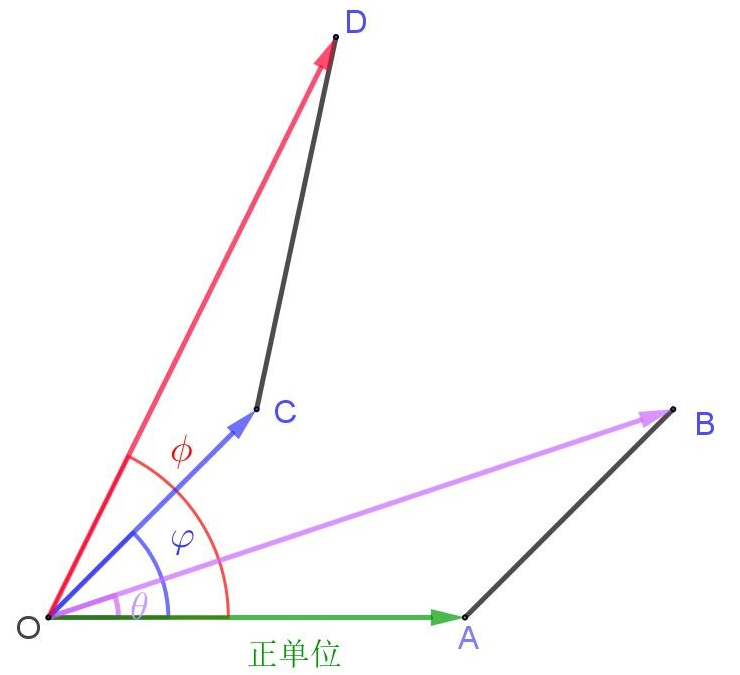
向量乘法的几何意义
- 取正单位有向线段 O A → \overrightarrow{OA} OA(长度为 1,方向沿正方向);
- 任取两条有向线段 O B → \overrightarrow{OB} OB 和 O C → \overrightarrow{OC} OC,构造相似三角形 Δ O A B ∼ Δ O C D \Delta OAB \sim \Delta OCD ΔOAB∼ΔOCD(顶点对应关系为 O → A → B O \to A \to B O→A→B 与 O → C → D O \to C \to D O→C→D),满足 ∠ A O B = ∠ C O D \angle AOB = \angle COD ∠AOB=∠COD;
- 由相似三角形的性质,乘积有向线段 O D → \overrightarrow{OD} OD 的长度为 O D = O B ⋅ O C OD = OB \cdot OC OD=OB⋅OC(因 O A = 1 OA = 1 OA=1);
- 乘积的方向角为两条有向线段方向角之和,即 ϕ = θ + φ \phi = \theta + \varphi ϕ=θ+φ( θ \theta θ 为 O B → \overrightarrow{OB} OB 的方向角, φ \varphi φ 为 O C → \overrightarrow{OC} OC 的方向角)。
在明确有向线段加法与数乘运算的几何解释后,基于已知两条有向线段,即可通过代数运算构造新的有向线段。这一过程仅需有限的代数操作即可完成,这正是韦赛尔(Wessel)原始构想的重要内容。
然而,这一理论框架的实际应用尚需进一步发展。实数域的运算结果仅具有正负符号属性:正值对应与正单位向量同向,负值对应反向。因此,向量方向始终受限于正单位向量所在的直线。为突破这一限制,韦赛尔引入了垂直于正单位向量且共原点的单位向量 ε \varepsilon ε,从而构建了二维向量空间的基础,使得复数的可视化得以实现。
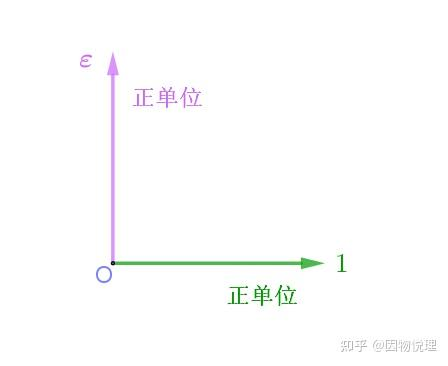
3.3 虚数单位的几何意义
为突破实数轴的限制,韦赛尔引入垂直于正单位的另一单位 ε \varepsilon ε:
- + 1 +1 +1 的方向角为 0 ∘ 0^\circ 0∘, − 1 -1 −1 的方向角为 18 0 ∘ 180^\circ 180∘;
- ε \; \; \varepsilon ε 的方向角为 9 0 ∘ 90^\circ 90∘, − ε -\varepsilon −ε 的方向角为 27 0 ∘ 270^\circ 270∘。
根据乘法的方向角叠加规则:
-
ε × ε \varepsilon \times \varepsilon ε×ε 的方向角为 9 0 ∘ + 9 0 ∘ = 18 0 ∘ 90^\circ + 90^\circ = 180^\circ 90∘+90∘=180∘,对应有向线段 − 1 -1 −1,即 ε 2 = − 1 \varepsilon^2 = -1 ε2=−1;
-
由此可知 ε \varepsilon ε 与虚数单位 i i i 等价,虚数 i i i 的几何意义为“将有向线段逆时针旋转 9 0 ∘ 90^\circ 90∘”。
-
+1,-1
( + 1 ) ( + 1 ) = + 1 (+1)(+1) = +1 (+1)(+1)=+1
( − 1 ) ( − 1 ) = + 1 (-1)(-1) = +1 (−1)(−1)=+1
( + 1 ) ( − 1 ) = − 1 (+1)(-1) = -1 (+1)(−1)=−1 -
+ ε +\varepsilon +ε, − ε -\varepsilon −ε
( + ε ) ( + ε ) = − 1 (+\varepsilon)(+\varepsilon) = -1 (+ε)(+ε)=−1
( + ε ) ( − ε ) = + 1 (+\varepsilon)(-\varepsilon) = +1 (+ε)(−ε)=+1
( − ε ) ( − ε ) = − 1 (-\varepsilon)(-\varepsilon) = -1 (−ε)(−ε)=−1 -
+1,-1; + ε +\varepsilon +ε, − ε -\varepsilon −ε
( + 1 ) ( + ε ) = + ε (+1)(+\varepsilon) = +\varepsilon (+1)(+ε)=+ε
( + 1 ) ( − ε ) = − ε (+1)(-\varepsilon) = -\varepsilon (+1)(−ε)=−ε
( − 1 ) ( + ε ) = − ε (-1)(+\varepsilon) = -\varepsilon (−1)(+ε)=−ε
( − 1 ) ( − ε ) = + ε (-1)(-\varepsilon) = +\varepsilon (−1)(−ε)=+ε把每个式子里的括号都看成是一个有向线段,乘积的结果也看成有向线段,那么上述式子很自然地就成立了。
3.4 复数与平面有向线段的对应
按照韦赛尔已经提出的有向线段的加法法则,任意平面有向线段
O
P
→
\overrightarrow{OP}
OP 可分解为沿
+
1
+1
+1 方向的分量
O
M
→
\overrightarrow{OM}
OM 和沿
ε
\varepsilon
ε 方向的分量
M
P
→
\overrightarrow{MP}
MP:
O
P
→
=
O
M
→
+
M
P
→
\overrightarrow{OP} = \overrightarrow{OM} + \overrightarrow{MP}
OP=OM+MP
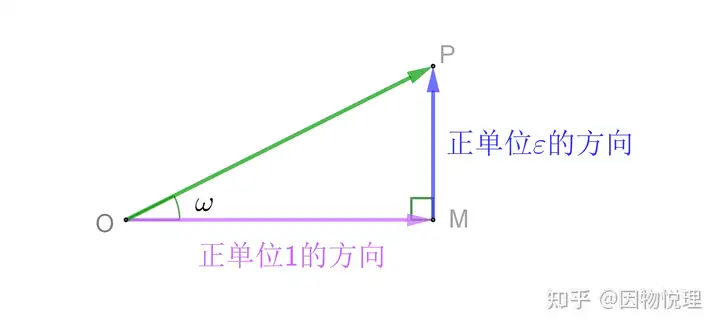
设
O
P
→
\overrightarrow{OP}
OP 的方向角为
ω
\omega
ω,则
O
M
=
cos
ω
OM = \cos\omega
OM=cosω,
M
P
=
sin
ω
MP = \sin\omega
MP=sinω,因此:
O
P
→
=
cos
ω
+
ε
sin
ω
\overrightarrow{OP} = \cos\omega + \varepsilon \sin\omega
OP=cosω+εsinω
将
ε
\varepsilon
ε 替换为
i
i
i,即得到复数的三角形式:
O
P
→
=
cos
ω
+
i
sin
ω
\overrightarrow{OP} = \cos\omega + i\sin\omega
OP=cosω+isinω
此表达式是欧拉公式的一个特例,它揭示了复数与三角函数之间的深刻联系。
若有向线段的长度为
r
r
r(
r
>
0
r > 0
r>0),则复数可表示为:
r
(
cos
ω
+
i
sin
ω
)
r(\cos\omega + i\sin\omega)
r(cosω+isinω)
这一结果表明,在复平面上,复数与有向线段一一对应,其运算可通过几何变换(平移、旋转、伸缩)解释,从而使复数的加法与乘法在几何上具有直观可视化的特性。
3.5 复数几何表示的局限性
复数的几何表示仅适用于平面有向线段(二维向量)。因为复数的实部和虚部分别对应平面直角坐标系的两个轴,有向线段无法脱离该平面,无法描述三维空间中的有向线段。这一局限性催生了将复数推广至三维空间的需求。
哈密顿的四元数
1. 数的空间维度与复数推广思路
实数可通过一维数轴实现几何表示(每个实数对应数轴上唯一一点),故称为“一维空间的数”;复数需借助二维平面坐标系表示,因此称为“二维空间的数”。
为将复数推广至三维空间,哈密顿提出假设:推广后的数形式为 a + b i + c j a + b i + c j a+bi+cj(其中 j 2 = − 1 j^2 = -1 j2=−1,与 i 2 = − 1 i^2 = -1 i2=−1 保持一致),此类数被定义为三元数,其设计目标是实现三维空间有向线段的数学表示。
2. 三元数的困境
复数的四则运算结果仍为复数,满足运算封闭性,但三元数的乘法存在根本性矛盾,具体表现如下:
2.1 三元数的乘法展开
对于两个三元数
z
1
=
a
0
+
a
1
i
+
a
2
j
z_1 = a_0 + a_1 i + a_2 j
z1=a0+a1i+a2j 与
z
2
=
b
0
+
b
1
i
+
b
2
j
z_2 = b_0 + b_1 i + b_2 j
z2=b0+b1i+b2j,按复数乘法法则展开并利用
i
2
=
j
2
=
−
1
i^2 = j^2 = -1
i2=j2=−1,结果为:
z
1
z
2
=
(
a
0
b
0
−
a
1
b
1
−
a
2
b
2
)
+
(
a
0
b
1
+
a
1
b
0
)
i
+
(
a
0
b
2
+
a
2
b
0
)
j
+
a
1
b
2
i
j
+
a
2
b
1
j
i
\begin{align*} z_1 z_2 &= (a_0b_0 - a_1b_1 - a_2b_2) + (a_0b_1 + a_1b_0)i + (a_0b_2 + a_2b_0)j + a_1b_2 ij + a_2b_1 ji \end{align*}
z1z2=(a0b0−a1b1−a2b2)+(a0b1+a1b0)i+(a0b2+a2b0)j+a1b2ij+a2b1ji
展开式中出现了
i
j
ij
ij 和
j
i
ji
ji 两项,无法通过三元数的现有形式消去或合并。
2.2 模运算性质的冲突
复数具有重要的模运算性质:乘积的模等于模的乘积。
对于任意复数
z
1
=
a
1
+
b
1
i
z_1 = a_1 + b_1 i
z1=a1+b1i、
z
2
=
a
2
+
b
2
i
z_2 = a_2 + b_2 i
z2=a2+b2i,即:
∣
z
1
z
2
∣
=
∣
z
1
∣
⋅
∣
z
2
∣
|z_1 z_2| = |z_1| \cdot |z_2|
∣z1z2∣=∣z1∣⋅∣z2∣
该性质展开后可表示为:
(
a
1
2
+
b
1
2
)
(
a
2
2
+
b
2
2
)
=
(
a
1
a
2
−
b
1
b
2
)
2
+
(
a
1
b
2
+
a
2
b
1
)
2
(a_1^2 + b_1^2)(a_2^2 + b_2^2) = (a_1 a_2 - b_1 b_2)^2 + (a_1 b_2 + a_2 b_1)^2
(a12+b12)(a22+b22)=(a1a2−b1b2)2+(a1b2+a2b1)2
(右侧为
∣
z
1
z
2
∣
2
|z_1 z_2|^2
∣z1z2∣2 的展开式,两侧通过代数运算可严格等价验证)。
若为使三元数乘积保持三元数形式,强制令
i
j
=
j
i
=
0
ij = ji = 0
ij=ji=0,则其模运算不再满足上述性质:
(
a
0
2
+
a
1
2
+
a
2
2
)
(
b
0
2
+
b
1
2
+
b
2
2
)
≠
(
a
0
b
0
−
a
1
b
1
−
a
2
b
2
)
2
+
(
a
0
b
1
+
a
1
b
0
)
2
+
(
a
0
b
2
+
a
2
b
0
)
2
(a_0^2 + a_1^2 + a_2^2)(b_0^2 + b_1^2 + b_2^2) \neq (a_0b_0 - a_1b_1 - a_2b_2)^2 + (a_0b_1 + a_1b_0)^2 + (a_0b_2 + a_2b_0)^2
(a02+a12+a22)(b02+b12+b22)=(a0b0−a1b1−a2b2)2+(a0b1+a1b0)2+(a0b2+a2b0)2
若令
i
j
=
−
j
i
ij = -ji
ij=−ji,虽能满足模运算性质,但乘积会引入新的非三元数项,破坏运算封闭性。
3. 四元数的创立
为解决三元数的乘法矛盾,哈密顿经过十余年探索,提出引入第四个分量
k
k
k,将数的形式扩展为:
a
+
b
i
+
c
j
+
d
k
a + b i + c j + d k
a+bi+cj+dk
此类数被称为四元数,其中
a
,
b
,
c
,
d
a, b, c, d
a,b,c,d 为实数,且满足以下运算规则:
- 平方规则: i 2 = j 2 = k 2 = − 1 i^2 = j^2 = k^2 = -1 i2=j2=k2=−1;
- 乘法反交换律: i j = − j i = k ij = -ji = k ij=−ji=k, j k = − k j = i jk = -kj = i jk=−kj=i, k i = − i k = j ki = -ik = j ki=−ik=j。
四元数的引入既解决了三维空间有向线段的数学表示问题,又保持了运算体系的自洽性。
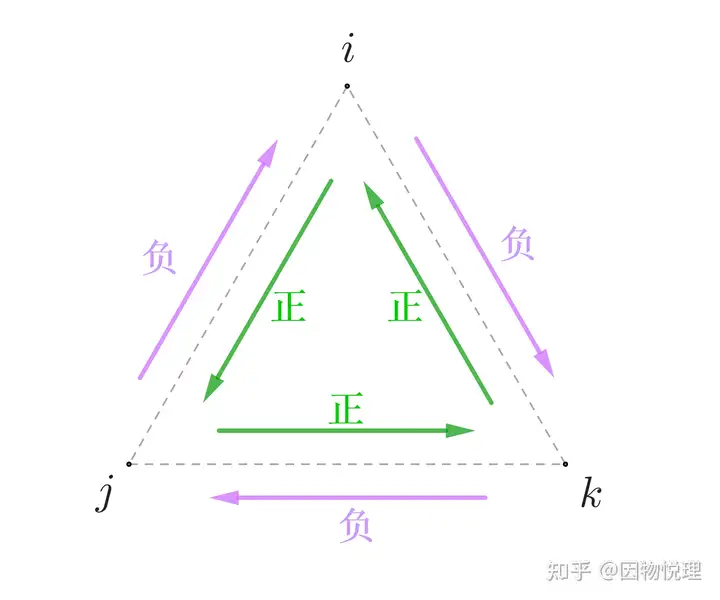
四元数乘法规则示意图(字母的字典顺序)
按图中绿色箭头的顺序任取两个分量求乘积,结果等于第三个分量:
绿色箭头:
i
j
=
k
ij = k
ij=k、
j
k
=
i
jk = i
jk=i、
k
i
=
j
ki = j
ki=j
按图中紫色箭头的顺序任取两个分量求乘积,结果等于第三个分量的相反数。
紫色箭头:
j
i
=
−
k
ji = -k
ji=−k、
k
j
=
−
i
kj = -i
kj=−i、
i
k
=
−
j
ik = -j
ik=−j)
四元数的乘法不满足交换律(如 i j ≠ j i ij \neq ji ij=ji),但保留了复数“乘积的模等于模的乘积”的性质,成功解决了三维空间有向线段的表示问题。
4.3 四元数的分解与向量的定义
哈密顿将四元数分为两部分:
- 纯量部分:仅含实数的 a a a(称为标量);
- 向量部分:虚数部分 b i + c j + d k bi + cj + dk bi+cj+dk(首次被命名为“向量”)。
向量部分可对应三维空间直角坐标系中的有向线段 ( b , c , d ) (b, c, d) (b,c,d),即此部分可以用一个有向线段来表示,其中 i , j , k i, j, k i,j,k 分别为三个坐标轴的单位向量。这一定义使空间有向线段与四元数的向量部分建立了对应关系,“向量”作为独立的数学概念正式诞生。
四元数的向量部分可表示为三维实数组 ( b , c , d ) (b, c, d) (b,c,d)(其中 b , c , d ∈ R b, c, d \in \mathbb{R} b,c,d∈R),该数组与三维空间直角坐标系中的有向线段存在一一对应关系。
在三维空间直角坐标系中,设
i
,
j
,
k
i, j, k
i,j,k 分别为
x
x
x 轴、
y
y
y 轴、
z
z
z 轴正方向的单位向量,则向量部分可通过有向线段的分量形式表示为:
b
i
+
c
j
+
d
k
bi + cj + dk
bi+cj+dk
这一对应关系的建立,直接关联空间有向线段的几何属性与四元数向量部分的代数运算,使‘向量’突破四元数的附属范畴,成为独立的数学概念。
4.4 向量的数学定义
后续数学家将向量抽象为更一般的数学概念:满足特定运算规则(加法、数乘、内积、外积等)的集合中的元素,称为向量。直观定义“有大小、有方向的量”是这一抽象定义的特例,二者本质一致。
向量的乘法
向量的乘法运算源于四元数的乘法分解,主要包括数乘、内积(数量积)和外积(叉积)三种形式。
5.1 四元数乘法的分解
设两个四元数为
A
=
a
0
+
a
A = a_0 + \mathbf{a}
A=a0+a 和
B
=
b
0
+
b
B = b_0 + \mathbf{b}
B=b0+b(其中
a
=
a
1
i
+
a
2
j
+
a
3
k
\mathbf{a} = a_1i + a_2j + a_3k
a=a1i+a2j+a3k,
b
=
b
1
i
+
b
2
j
+
b
3
k
\mathbf{b} = b_1i + b_2j + b_3k
b=b1i+b2j+b3k 为向量部分),其乘积展开后可分解为:
A
B
=
(
a
0
b
0
−
a
⋅
b
)
+
(
a
0
b
+
b
0
a
)
+
a
×
b
AB = (a_0b_0 - \mathbf{a} \cdot \mathbf{b}) + (a_0\mathbf{b} + b_0\mathbf{a}) + \mathbf{a} \times \mathbf{b}
AB=(a0b0−a⋅b)+(a0b+b0a)+a×b
其中:
- a 0 b a_0\mathbf{b} a0b 和 b 0 a b_0\mathbf{a} b0a 为向量数乘(实数与向量的乘积),结果仍为向量;
- a ⋅ b = a 1 b 1 + a 2 b 2 + a 3 b 3 \mathbf{a} \cdot \mathbf{b} = a_1b_1 + a_2b_2 + a_3b_3 a⋅b=a1b1+a2b2+a3b3 为向量内积(数量积),结果为标量;
- a × b = ( a 2 b 3 − a 3 b 2 ) i + ( a 3 b 1 − a 1 b 3 ) j + ( a 1 b 2 − a 2 b 1 ) k \mathbf{a} \times \mathbf{b} = (a_2b_3 - a_3b_2)i + (a_3b_1 - a_1b_3)j + (a_1b_2 - a_2b_1)k a×b=(a2b3−a3b2)i+(a3b1−a1b3)j+(a1b2−a2b1)k 为向量外积(叉积),结果仍为向量。
5.2 特殊情形:纯向量乘法
若四元数的标量部分为零(
a
0
=
b
0
=
0
a_0 = b_0 = 0
a0=b0=0),则乘法简化为:
A
B
=
a
b
=
−
a
⋅
b
+
a
×
b
AB=\mathbf{a}\mathbf{b} = -\mathbf{a} \cdot \mathbf{b} + \mathbf{a} \times \mathbf{b}
AB=ab=−a⋅b+a×b
这一等式清晰展示了内积与外积的关联,是向量运算的重要公式。
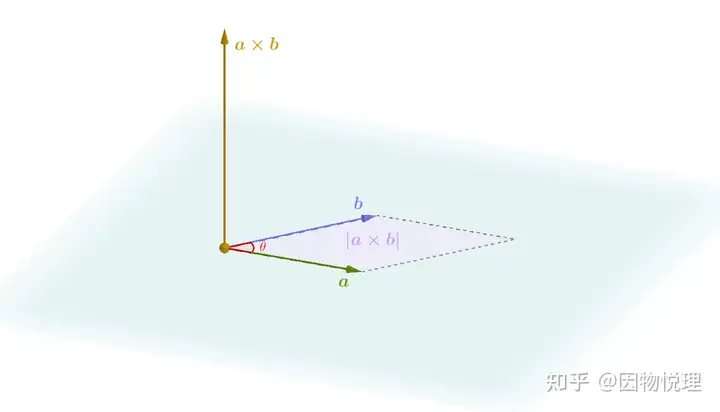
5.3 内积与外积的几何意义
作为哈密顿忠实粉丝的泰特在推广四元数的过程里发现了很多结论,其中就有
- 内积: a ⋅ b = a b cos θ \mathbf{a} \cdot \mathbf{b} = ab\cos\theta a⋅b=abcosθ( a , b a, b a,b 为向量的模, θ \theta θ 为两向量的夹角),反映向量在彼此方向上的投影累积;
- 外积:
a
×
b
=
a
b
sin
θ
n
^
\mathbf{a} \times \mathbf{b} = ab\sin\theta \hat{\mathbf{n}}
a×b=absinθn^(
n
^
\hat{\mathbf{n}}
n^ 为垂直于两向量所在平面的单位向量,方向由右手螺旋定则确定),反映向量的旋转效应和平面法向。
立体图:向量叉乘的几何意义
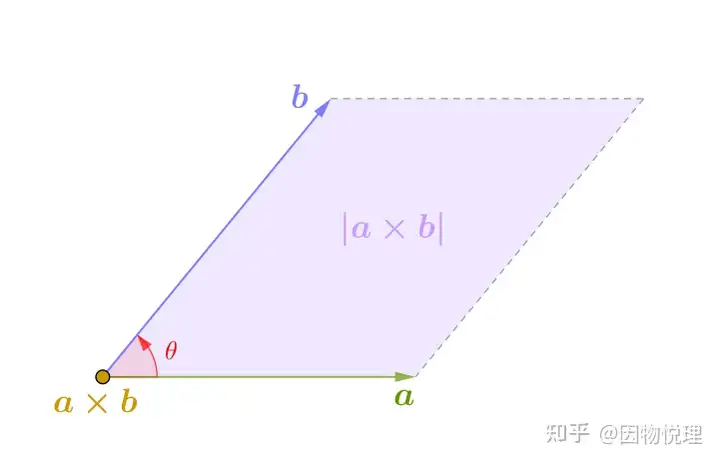
俯视图:向量叉乘与点乘的几何意义(右手螺旋定则:四指环绕方向与夹角一致,大拇指指向垂直纸面向外)
“∇”算子(Del 算子)
四元数的诞生恰逢电磁学快速发展阶段,描述电磁现象的物理量多为向量。为简化向量运算,无需依赖完整的四元数体系,向量分析在精简后的四元数基础上逐步建立。
为进一步简化向量场的运算,哈密顿引入“∇算子”(Del 算子)。该算子是形式化的向量微分算子,构成向量分析的重要运算工具。
6.1 算子定义
在三维直角坐标系中,∇ 算子定义为:
∇
=
i
∂
∂
x
+
j
∂
∂
y
+
k
∂
∂
z
\nabla = \mathbf{i}\frac{\partial}{\partial x} + \mathbf{j}\frac{\partial}{\partial y} + \mathbf{k}\frac{\partial}{\partial z}
∇=i∂x∂+j∂y∂+k∂z∂
∇ 算子本身无具体数值,需作用于标量场或向量场才能产生有意义的结果,其运算规则遵循向量的数乘、内积和外积法则。
6.2 ∇ 算子的基本运算
-
作用于标量场(梯度):
设标量场为 d ( x , y , z ) d(x, y, z) d(x,y,z),则 ∇ 与 d d d 的数乘为梯度:
∇ d = i ∂ d ∂ x + j ∂ d ∂ y + k ∂ d ∂ z \nabla d = \mathbf{i}\frac{\partial d}{\partial x} + \mathbf{j}\frac{\partial d}{\partial y} + \mathbf{k}\frac{\partial d}{\partial z} ∇d=i∂x∂d+j∂y∂d+k∂z∂d
结果为向量场。 -
作用于向量场(散度):
设向量场为 D = D x i + D y j + D z k \mathbf{D} = D_x\mathbf{i} + D_y\mathbf{j} + D_z\mathbf{k} D=Dxi+Dyj+Dzk,则 ∇ 与 D \mathbf{D} D 的内积为散度:
∇ ⋅ D = ∂ D x ∂ x + ∂ D y ∂ y + ∂ D z ∂ z \nabla \cdot \mathbf{D} = \frac{\partial D_x}{\partial x} + \frac{\partial D_y}{\partial y} + \frac{\partial D_z}{\partial z} ∇⋅D=∂x∂Dx+∂y∂Dy+∂z∂Dz
结果为标量场。 -
作用于向量场(旋度):
∇ 与 D \mathbf{D} D 的外积为旋度:
∇ × D = ∣ i j k ∂ ∂ x ∂ ∂ y ∂ ∂ z D x D y D z ∣ \nabla \times \mathbf{D} = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ D_x & D_y & D_z \end{vmatrix} ∇×D= i∂x∂Dxj∂y∂Dyk∂z∂Dz
结果为向量场。
6.3 高阶运算:拉普拉斯算子
两个 ∇ 算子的内积定义为拉普拉斯算子(Laplacian):
∇
2
=
∇
⋅
∇
=
∂
2
∂
x
2
+
∂
2
∂
y
2
+
∂
2
∂
z
2
\nabla^2 = \nabla \cdot \nabla = \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2} + \frac{\partial^2}{\partial z^2}
∇2=∇⋅∇=∂x2∂2+∂y2∂2+∂z2∂2
拉普拉斯算子是二阶偏微分算子,作用于标量场时结果为标量场,作用于向量场时结果为向量场(对各分量分别作用)。
6.4 重要恒等式
- 梯度的旋度为零: ∇ × ∇ f = 0 \nabla \times \nabla f = 0 ∇×∇f=0(“梯无旋”);
- 旋度的散度为零: ∇ ⋅ ( ∇ × V ) = 0 \nabla \cdot (\nabla \times \mathbf{V}) = 0 ∇⋅(∇×V)=0(“旋无散”);
- 向量旋度的旋度公式: ∇ × ( ∇ × V ) = ∇ ( ∇ ⋅ V ) − ∇ 2 V \nabla \times (\nabla \times \mathbf{V}) = \nabla (\nabla \cdot \mathbf{V}) - \nabla^2 \mathbf{V} ∇×(∇×V)=∇(∇⋅V)−∇2V。
这些恒等式是向量分析的基础,广泛应用于电磁学、流体力学等领域。
向量场的散度
麦克斯韦借鉴流体力学的描述框架,将散度概念引入电磁学,用于量化向量场的“源汇”特性。
7.1 向量场与标量场
- 向量场:某一区域内每一点都对应一个向量(如流速场、电场、磁场),该区域称为向量场;
- 标量场:某一区域内每一点都对应一个标量(如温度场、电势场),该区域称为标量场。
例如,管道中水流的速度分布构成向量场,而水温分布构成标量场。
7.2 通量的定义
7.2.1 流量的基础定义与推导
流量是指流体在单位时间内通过管道某一横截面的质量。

假设流体流速处处相同且恒定为 v v v,结合几何关系推导如下:
当截面与流速方向垂直时,取时间间隔
Δ
t
\Delta t
Δt,流体通过该截面的体积为
v
Δ
t
S
⊥
v \Delta t S_{\perp}
vΔtS⊥(
S
⊥
S_{\perp}
S⊥ 为垂直截面面积),对应质量为
ρ
v
Δ
t
S
⊥
\rho v \Delta t S_{\perp}
ρvΔtS⊥(
ρ
\rho
ρ 为流体密度)。单位时间内的质量即为流量:
Q
=
ρ
v
Δ
t
S
⊥
Δ
t
=
ρ
v
S
⊥
Q = \frac{\rho v \Delta t S_{\perp}}{\Delta t} = \rho v S_{\perp}
Q=ΔtρvΔtS⊥=ρvS⊥
由于同一管道内流量守恒,通过倾斜截面的流量与垂直截面流量相等,仍满足上式。
7.2.2 流量的一般表达式
计算流量时需引入截面法向(与截面垂直的方向)。设流速方向与截面法向夹角为
θ
\theta
θ,任意截面面积为
S
S
S,则垂直于流速方向的有效截面积为
S
cos
θ
S \cos \theta
Scosθ,流量的一般形式为:
Q
=
ρ
v
S
cos
θ
Q = \rho v S \cos \theta
Q=ρvScosθ
定义截面矢量
S
\mathbf{S}
S(大小为
S
S
S,方向沿截面法向),上式可表示为流速矢量
v
\mathbf{v}
v 与截面矢量
S
\mathbf{S}
S 的数量积:
Q
=
ρ
v
⋅
S
Q = \rho \mathbf{v} \cdot \mathbf{S}
Q=ρv⋅S
对于不可压缩流体,密度
ρ
\rho
ρ 为常数,若取
ρ
=
1
\rho = 1
ρ=1(归一化处理),流量简化为:
Q
=
v
⋅
S
Q = \mathbf{v} \cdot \mathbf{S}
Q=v⋅S
7.2.3 流速分布不均匀时的流量计算
当流体各处流速不同时,需通过积分求解流量:将截面划分为无数微小面积元
d
S
d\mathbf{S}
dS(方向沿面积元法向),每个面积元的流量为
d
Q
=
v
⋅
d
S
dQ = \mathbf{v} \cdot d\mathbf{S}
dQ=v⋅dS,对整个截面
S
S
S 积分得到总流量:
Φ
=
∬
S
v
⋅
d
S
\Phi = \iint_{S} \mathbf{v} \cdot d\mathbf{S}
Φ=∬Sv⋅dS
7.2.4 通量的定义与物理意义
麦克斯韦将流体流量的概念推广至矢量场理论:将流速矢量 v \mathbf{v} v 替换为任意矢量场(如电场、磁场等),对应的积分结果定义为矢量场的通量。
1. 通量的数学表达式
通量描述矢量场通过某一曲面的物理量累积,其数学定义为:
Φ
=
∬
S
A
⋅
d
S
\Phi = \iint_S \mathbf{A} \cdot d\mathbf{S}
Φ=∬SA⋅dS
其中,
A
\mathbf{A}
A 为任意矢量场,
d
S
=
n
d
S
d\mathbf{S} = \mathbf{n} dS
dS=ndS(
n
\mathbf{n}
n 为曲面法向量,
d
S
dS
dS 为面积元素)。
2. 通量的符号规则
根据数量积运算性质,通量的正负由矢量场方向与曲面法向量 n \mathbf{n} n 的夹角 θ \theta θ 决定:
- 当 0 ≤ θ < 9 0 ∘ 0 \leq \theta < 90^\circ 0≤θ<90∘ 时, cos θ > 0 \cos \theta > 0 cosθ>0,通量 Φ > 0 \Phi > 0 Φ>0;
- 当
9
0
∘
<
θ
≤
18
0
∘
90^\circ < \theta \leq 180^\circ
90∘<θ≤180∘ 时,
cos
θ
<
0
\cos \theta < 0
cosθ<0,通量
Φ
<
0
\Phi < 0
Φ<0。

从图中可以看到截面的法向是人为二选一的结果,所以通量结果的正负必须与截面的法向对应才行。
3. 闭合曲面的通量
对于闭合曲面,法向量统一规定为“由内向外”,此时通量的符号具有明确物理意义:
- Φ > 0 \Phi > 0 Φ>0:流出闭合曲面的物理量大于流入量,曲面内存在“源”;
- Φ < 0 \Phi < 0 Φ<0:流入量大于流出量,曲面内存在“汇”;
- Φ = 0 \Phi = 0 Φ=0:流入量与流出量相等,曲面内无净源汇。
闭合曲面的通量表达式为(积分符号中的圆圈表示闭合曲面):
Φ
=
∫
∫
◯
S
A
⋅
d
S
\Phi = \mathop{{\int\!\!\!\!\!\int}\mkern-21mu \bigcirc}\limits_S \mathbf{A} \cdot d\mathbf{S}
Φ=S∫∫◯A⋅dS
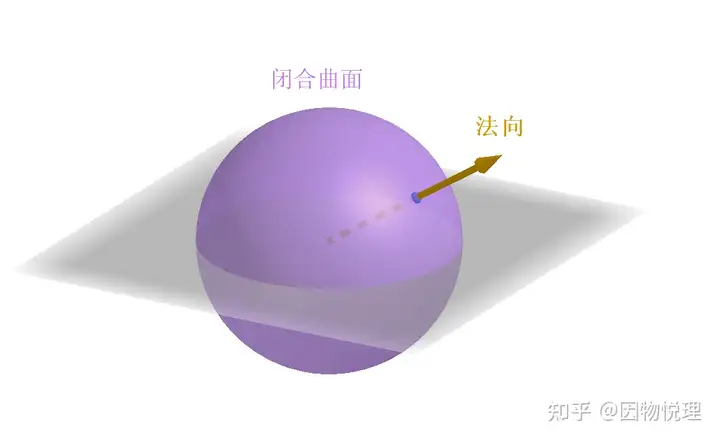
对于闭合曲面来说,选择其法向方式的共识:由截面里面指向外面为截面的法向。
7.3 散度的定义
散度是向量场中某点的“通量体密度”,描述该点的源汇强度。通过将闭合曲面缩小至极限为点,通量与体积的比值即为散度:
div
v
(
P
)
=
lim
S
→
P
1
V
S
∫
∫
◯
S
v
⋅
d
S
\text{div}\mathbf{v}(P) = \lim_{S \to P} \frac{1}{V_S} \mathop{{\int\!\!\!\!\!\int}\mkern-21mu \bigcirc}\limits_S \mathbf{v} \cdot d\mathbf{S}
divv(P)=S→PlimVS1S∫∫◯v⋅dS
其中,
V
S
V_S
VS 为闭合曲面
S
S
S 所围区域的体积,
P
P
P 为考察点。
从定义可知,散度为一个标量,其表示向量场中某一点处通量相对于体积的变化率,即该点处单位体积所穿过的通量,这便是该点处源的强度。
此外,散度的正负取决于通量的正负。因此,散度的结果不仅能够体现该点是源还是汇,还能体现源或汇的强度。
7.4 直角坐标系下的散度表达式
取直角坐标系中以
P
(
x
,
y
,
z
)
P(x, y, z)
P(x,y,z) 为中心的立方体,边长为
Δ
x
,
Δ
y
,
Δ
z
\Delta x, \Delta y, \Delta z
Δx,Δy,Δz,体积
V
S
=
Δ
x
Δ
y
Δ
z
V_S = \Delta x\Delta y\Delta z
VS=ΔxΔyΔz。计算向量场
v
=
v
x
i
+
v
y
j
+
v
z
k
\mathbf{v} = v_x\mathbf{i} + v_y\mathbf{j} + v_z\mathbf{k}
v=vxi+vyj+vzk 通过立方体表面的总通量,再除以体积并取极限(
Δ
x
,
Δ
y
,
Δ
z
→
0
\Delta x, \Delta y, \Delta z \to 0
Δx,Δy,Δz→0),可得:
div
v
=
∂
v
x
∂
x
+
∂
v
y
∂
y
+
∂
v
z
∂
z
\text{div}\mathbf{v} = \frac{\partial v_x}{\partial x} + \frac{\partial v_y}{\partial y} + \frac{\partial v_z}{\partial z}
divv=∂x∂vx+∂y∂vy+∂z∂vz
这一结果与 ∇ 算子的内积形式一致,即:
div
v
=
∇
⋅
v
\text{div}\mathbf{v} = \nabla \cdot \mathbf{v}
divv=∇⋅v
7.5 高斯公式(散度定理)
高斯公式建立了闭合曲面积分(通量)与体积分(散度累积)的联系:
Φ = ∭ V ( ∇ ⋅ v ) d V = ∬ S v ⋅ d S \Phi = \iiint\limits_V (\nabla \cdot \mathbf{v}) \, dV = \iint\limits_S \mathbf{v} \cdot d\mathbf{S} Φ=V∭(∇⋅v)dV=S∬v⋅dS
其物理意义为:向量场通过闭合曲面的总通量,等于该曲面所围区域内散度的体积分(所有源汇的总贡献)。
向量场的旋度
旋度用于量化向量场的局部旋转特性,与环流量构成微观与宏观的对应关系。
8.1 环流量的定义
环流量是向量场沿闭合曲线的累积效应,数学表达式为:
Γ
=
∮
L
v
⋅
d
l
\Gamma = \oint_L \mathbf{v} \cdot d\mathbf{l}
Γ=∮Lv⋅dl
其中,
d
l
=
τ
⃗
d
l
d\mathbf{l} = \vec{\tau}dl
dl=τdl(
τ
⃗
\vec{\tau}
τ 为曲线切向量,
d
l
dl
dl 为弧长元素)。
例如,水流沿闭合曲线的环流量,反映了水流对曲线所围区域的旋转驱动效应。
8.2 旋度的定义
旋度是向量场中某点的“环流量面密度”,且是具有方向的向量。通过将闭合曲线缩小至极限为点,环流量与面积的比值的最大值即为旋度的大小,对应的方向为旋度的方向(由右手定则确定):
rot
v
(
P
)
=
n
0
lim
L
→
P
1
S
L
∮
L
v
⋅
d
l
\text{rot}\mathbf{v}(P) = \mathbf{n}_0 \lim_{L \to P} \frac{1}{S_L} \oint_L \mathbf{v} \cdot d\mathbf{l}
rotv(P)=n0L→PlimSL1∮Lv⋅dl
其中,
S
L
S_L
SL 为闭合曲线
L
L
L 所围区域的面积,
n
0
\mathbf{n}_0
n0 为环流量面密度最大时的法向量。
旋度的方向是该点旋转效应最强的方向,大小为该方向上的环流量面密度。
8.3 直角坐标系下的旋度表达式
取直角坐标系中沿坐标轴法向的平面,构造矩形闭合曲线,计算环流量并取极限,可得旋度的分量形式:
rot
v
=
(
∂
v
z
∂
y
−
∂
v
y
∂
z
)
i
+
(
∂
v
x
∂
z
−
∂
v
z
∂
x
)
j
+
(
∂
v
y
∂
x
−
∂
v
x
∂
y
)
k
\text{rot}\mathbf{v} = \left( \frac{\partial v_z}{\partial y} - \frac{\partial v_y}{\partial z} \right)\mathbf{i} + \left( \frac{\partial v_x}{\partial z} - \frac{\partial v_z}{\partial x} \right)\mathbf{j} + \left( \frac{\partial v_y}{\partial x} - \frac{\partial v_x}{\partial y} \right)\mathbf{k}
rotv=(∂y∂vz−∂z∂vy)i+(∂z∂vx−∂x∂vz)j+(∂x∂vy−∂y∂vx)k
这一结果与 ∇ 算子的外积形式一致,即:
rot
v
=
∇
×
v
\text{rot}\mathbf{v} = \nabla \times \mathbf{v}
rotv=∇×v
8.4 斯托克斯公式
斯托克斯公式建立了闭合曲线积分(环流量)与曲面积分(旋度累积)的联系:
∬
S
(
∇
×
v
)
⋅
d
S
=
∮
L
v
⋅
d
l
\iint_S (\nabla \times \mathbf{v}) \cdot d\mathbf{S} = \oint_L \mathbf{v} \cdot d\mathbf{l}
∬S(∇×v)⋅dS=∮Lv⋅dl
其物理意义为:向量场沿闭合曲线的环流量,等于该曲线所张曲面的旋度通量(所有局部旋转效应的总贡献)。
斯托克斯公式的一个重要特性是:只要闭合曲线 L L L 固定,无论选取何种以 L L L 为边界的曲面 S S S,积分结果均不变。
标量场的梯度
梯度是标量场的方向导数最大值,用于描述标量场的局部变化率特性,其结果为向量场。
9.1 等值线与法向
- 等值线:标量场中数值相同的点构成的曲线(三维空间中为等值面),用于直观展示标量场的分布;
- 法向:等值线的垂直方向,规定为由高值区指向低值区。沿法向方向,标量场的变化率最大(单位距离上的数值变化最大)。
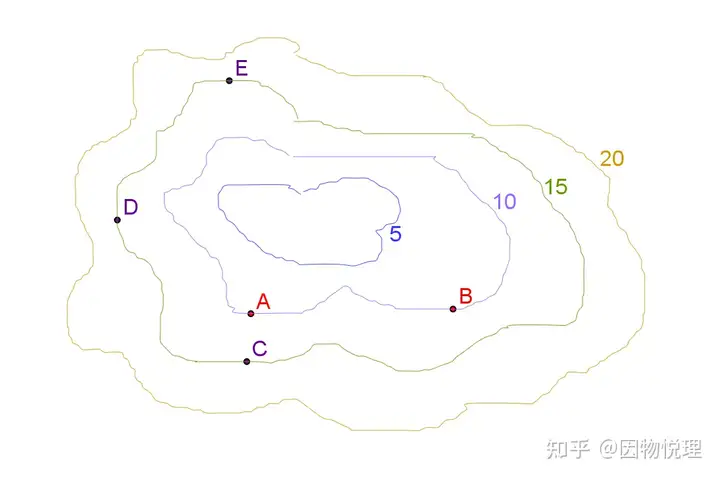
等值线的示意图
9.2 梯度的定义
标量场
f
(
x
,
y
,
z
)
f(x, y, z)
f(x,y,z) 在某点的梯度,是沿该点等值线法向、大小等于最大方向导数的向量:
grad
f
=
∂
f
∂
l
e
n
\text{grad}f = \frac{\partial f}{\partial l} \mathbf{e}_n
gradf=∂l∂fen
其中,
∂
f
∂
l
\frac{\partial f}{\partial l}
∂l∂f 为最大方向导数,
e
n
\mathbf{e}_n
en 为法向单位向量。
9.3 直角坐标系下的梯度表达式
通过多元函数的全增量展开,可得梯度在直角坐标系中的分量形式:
grad
f
=
∂
f
∂
x
i
+
∂
f
∂
y
j
+
∂
f
∂
z
k
\text{grad}f = \frac{\partial f}{\partial x}\mathbf{i} + \frac{\partial f}{\partial y}\mathbf{j} + \frac{\partial f}{\partial z}\mathbf{k}
gradf=∂x∂fi+∂y∂fj+∂z∂fk
这一结果与 ∇ 算子作用于标量场的形式一致,即:
grad
f
=
∇
f
\text{grad}f = \nabla f
gradf=∇f
9.4 梯度的性质
梯度的方向是标量场数值增长最快的方向,大小是该方向上的单位距离增长率。这一性质使其在优化算法(如梯度下降法)、物理场分析(如电势梯度与电场强度的关系)等领域具有广泛应用。
讨论补充
观点1:散度与旋度的直观理解(赖豪杰)
- 散度:通量密度。类比密度的定义 ρ = lim V → 0 ∫ V M V \rho = \lim_{V \to 0} \frac{\int_V M}{V} ρ=limV→0V∫VM,散度是通量对体积的极限比值,描述向量场中某点的源汇强度。在流体力学中,速度场的散度表示体积膨胀率,散度为零时流体不可压缩。
- 旋度:环量密度(向量特性,仅为类比)。旋度是环流量对面积的极限比值,描述向量场中某点的旋转强度。
重要公式关联:
- 散度与通量:高斯公式 ∭ V ( ∇ ⋅ A ) d V = ∫ ∫ ◯ S A ⋅ d S \iiint_V (\nabla \cdot \mathbf{A}) dV = \mathop{{\int\!\!\!\!\!\int}\mkern-21mu \bigcirc}\limits_S \mathbf{A} \cdot d\mathbf{S} ∭V(∇⋅A)dV=S∫∫◯A⋅dS;
- 旋度与环流量:斯托克斯公式 ∬ S ( ∇ × A ) ⋅ d S = ∮ L A ⋅ d l \iint_S (\nabla \times \mathbf{A}) \cdot d\mathbf{S} = \oint_L \mathbf{A} \cdot d\mathbf{l} ∬S(∇×A)⋅dS=∮LA⋅dl。
观点2:旋度与流体旋转的区别(andrew shen)
旋度描述的是流体微粒的自转(涡量),而非整体绕轴旋转。例如:
- 流体整体绕轴以角速度 Ω \Omega Ω 旋转时,速度场的旋度大小处处为 2 Ω 2\Omega 2Ω;
- 流体绕轴旋转且速度与半径成反比时,速度场的旋度处处为零(无自转,仅公转)。
这一区别表明,旋度是局部自转效应的度量,而非宏观旋转运动的描述。
观点3:旋度方向的补充(张小文)
旋度的方向是环流量面密度最大的方向,对应的闭合曲线所围平面的法向。这一方向由右手定则确定,确保旋度作为向量能唯一表征该点的旋转特性。
Del 算符与梯度、散度、旋度及拉普拉斯算子
gwave 编辑于 2021-12-09 13:46
Del 算子( ∇ \nabla ∇),又称哈密顿算子,在向量微积分和机器学习等领域应用广泛。其重要作用是通过数乘、点乘、叉乘等运算,将标量场或向量场转化为新的场,形成梯度、散度、旋度等关键概念。
1 梯度(Gradient)
- 定义:梯度是 Del 算子与标量场
f
f
f 的数乘,结果为向量场:
∇ f = ∂ f ∂ x i + ∂ f ∂ y j + ∂ f ∂ z k \nabla f = \frac{\partial f}{\partial x}\mathbf{i} + \frac{\partial f}{\partial y}\mathbf{j} + \frac{\partial f}{\partial z}\mathbf{k} ∇f=∂x∂fi+∂y∂fj+∂z∂fk - 物理意义:梯度的方向是标量场数值增长最快的方向,大小是该方向上的单位距离增长率。
- 重要性质:梯度无旋( ∇ × ∇ f = 0 \nabla \times \nabla f = 0 ∇×∇f=0),即沿梯度方向运动时,不会出现旋转效应。
- 应用:机器学习中的梯度下降算法,通过沿梯度反方向迭代,寻找函数最小值。
2 散度(Divergence)
- 定义:散度是 Del 算子与向量场
F
⃗
\vec{F}
F 的点乘,结果为标量场:
∇ ⋅ F ⃗ = ∂ F x ∂ x + ∂ F y ∂ y + ∂ F z ∂ z \nabla \cdot \vec{F} = \frac{\partial F_x}{\partial x} + \frac{\partial F_y}{\partial y} + \frac{\partial F_z}{\partial z} ∇⋅F=∂x∂Fx+∂y∂Fy+∂z∂Fz - 物理意义:描述向量场中某点的源汇强度,散度为正表示“源”(向外发散),为负表示“汇”(向内汇聚),为零表示无净源汇。
- 直观类比:装满水的塑料袋破洞后,水的喷射强度可通过散度量化。
- 重要性质:旋度无散( ∇ ⋅ ( ∇ × F ⃗ ) = 0 \nabla \cdot (\nabla \times \vec{F}) = 0 ∇⋅(∇×F)=0),即旋转运动不会产生净发散或汇聚。
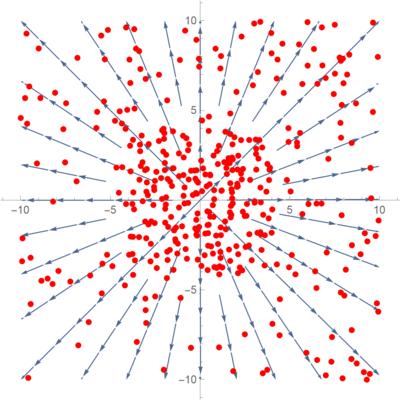
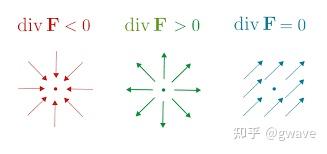
3 旋度(Curl)
- 定义:旋度是 Del 算子与向量场
F
⃗
\vec{F}
F 的叉乘,结果为向量场:
∇ × F ⃗ = ∣ i j k ∂ ∂ x ∂ ∂ y ∂ ∂ z F x F y F z ∣ \nabla \times \vec{F} = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ F_x & F_y & F_z \end{vmatrix} ∇×F= i∂x∂Fxj∂y∂Fyk∂z∂Fz - 物理意义:描述向量场中某点的局部旋转强度与方向,旋度的方向为旋转效应最强的方向,大小为该方向的环流量面密度。
- 直观类比:水流漩涡的旋转强度可通过旋度量化。
4 拉普拉斯算子(Laplacian)
- 定义:拉普拉斯算子是梯度的散度,即 Del 算子的二次内积,结果为标量场(作用于标量场)或向量场(作用于向量场):
∇ 2 = ∇ ⋅ ∇ = ∂ 2 ∂ x 2 + ∂ 2 ∂ y 2 + ∂ 2 ∂ z 2 \nabla^2 = \nabla \cdot \nabla = \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2} + \frac{\partial^2}{\partial z^2} ∇2=∇⋅∇=∂x2∂2+∂y2∂2+∂z2∂2 - 物理意义:描述标量场梯度的变化率,类比于单变量函数的二阶导数,反映场的“平滑程度”。
- ∇ 2 f > 0 \nabla^2 f > 0 ∇2f>0:场在该点的均值高于该点数值(如谷底);
- ∇ 2 f < 0 \nabla^2 f < 0 ∇2f<0:场在该点的均值低于该点数值(如山峰);
- ∇ 2 f = 0 \nabla^2 f = 0 ∇2f=0:场在该点的均值与该点数值相等(如平缓山坡)。
- 应用:
- 图像处理中作为边缘检测器,检测灰度值突变的区域;
- 物理中用于描述无源场的均衡状态(拉普拉斯方程 ∇ 2 ϕ = 0 \nabla^2 \phi = 0 ∇2ϕ=0),如无热源房间的温度分布。

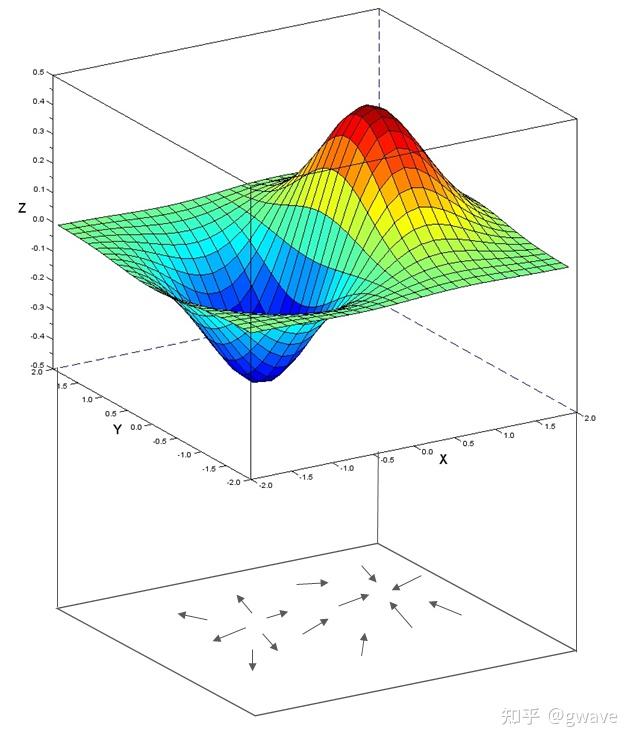
小结
| 算子组合 | 运算类型 | 输入场类型 | 输出场类型 | 物理意义 |
|---|---|---|---|---|
| ∇ f \nabla f ∇f | 数乘 | 标量场 | 向量场 | 标量场的最大变化率与方向 |
| ∇ ⋅ F ⃗ \nabla \cdot \vec{F} ∇⋅F | 点乘 | 向量场 | 标量场 | 向量场的源汇强度 |
| ∇ × F ⃗ \nabla \times \vec{F} ∇×F | 叉乘 | 向量场 | 向量场 | 向量场的局部旋转强度与方向 |
| ∇ 2 f \nabla^2 f ∇2f | 二阶内积 | 标量场 | 标量场 | 标量场梯度的变化率 |
Del 算子及其衍生的梯度、散度、旋度和拉普拉斯算子,构成了向量分析的框架,为描述物理场(如电场、磁场、流速场)提供了统一的数学工具。
via:
- 散度和旋度的物理意义是什么? - 知乎
https://www.zhihu.com/question/21912411 - Del 算符与梯度、散度、旋度与Laplacian - 知乎
https://zhuanlan.zhihu.com/p/349328782 - 中学生能理解最小作用量原理吗? - 知乎
https://zhuanlan.zhihu.com/p/451330274





















 597
597

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








