Dirac delta function(狄拉克 δ 函数) | 定义、性质及物理意义…（篇 1）

注：本文为 “Dirac‘s Delta Function” 相关合辑。
略作整理，未全校去重。
如有内容异常，请看原文。

---

狄拉克函数及其基本性质

1 狄拉克函数的定义

狄拉克函数（$\delta$ 函数）是数学物理领域中一类重要的广义函数，其概念由物理学家保罗・狄拉克（Paul Dirac）提出，用于描述具有“瞬时冲激”特性的物理现象（如瞬时作用力、点电荷的电荷密度等）。广义函数的严格数学理论由洛朗・施瓦兹（Laurent Schwartz）建立，其经典著作《广义函数论》（Théorie des Distributions）是该领域的关键参考资料。

作为广义函数，$\delta (t)$ 无法通过传统函数的“点取值”方式定义，而是通过其在积分运算中的作用来刻画，主要满足以下两个条件：

1. 积分归一性：$\delta (t)$ 在全数轴上的积分值为 1，即
   $${\int }_{-\infty }^{\infty }\delta (t)dt=1$$
   该条件保证了 $\delta (t)$ 的“冲激强度”为 1，是其作为“单位冲激”的重要特征。
2. 非零点零值性：当自变量 $t\ne 0$ 时，$\delta (t)$ 的取值为 0，即
   $$\delta (t)=0(t\ne 0)$$
   该条件表明 $\delta (t)$ 的“冲激”仅集中在 $t=0$ 这一点，体现了其“瞬时性”。

2 狄拉克函数（$\delta (t)$）的基本性质

$\delta (t)$ 的性质是其在信号处理、量子力学、微分方程等领域应用的基础，主要性质可归纳为以下 6 类：

2.1 筛选性（抽样性）

筛选性是 $\delta (t)$ 最重要的性质之一，其本质是通过积分运算“提取”函数在特定点的取值，实现对函数的“抽样”，具体表现为两种形式：

2.1.1 乘积形式

任意连续函数 $x(t)$ 与平移 $\delta$ 函数 $\delta (t-t_0)$ 的乘积，可简化为 $x(t)$ 在 $t=t_0$ 处的取值与 $\delta (t-t_0)$ 的乘积，即
$$x(t)\delta (t-t_0)=x(t_0)\delta (t-t_0)$$
当 $t_0=0$ 时（即 $\delta (t)$ 未平移），该式退化为
$$x(t)\delta (t)=x(0)\delta (t)$$
这一性质的物理意义是：$\delta (t-t_0)$ 仅在 $t=t_0$ 处有非零贡献，因此乘积 $x(t)\delta (t-t_0)$ 的“有效取值”仅由 $x(t)$ 在 $t=t_0$ 处的值决定。

2.1.2 积分形式

对乘积形式两边在全数轴上积分，可直接提取 $x(t)$ 在 $t=t_0$ 处的取值，即
$${\int }_{-\infty }^{\infty }x(t)\delta (t-t_0)dt=x(t_0)$$
当 $t_0=0$ 时，退化为
$${\int }_{-\infty }^{\infty }x(t)\delta (t)dt=x(0)$$
该式是筛选性的主要表达形式，例如在信号处理中，可通过该性质提取信号 $x(t)$ 在 $t=t_0$ 时刻的瞬时值。

2.2 偶函数性质

$\delta (t)$ 满足偶函数的定义，即其取值关于 $t=0$ 对称：
$$\delta (-t)=\delta (t)$$

证明思路：对 ${\int }_{-\infty }^{\infty }x(t)\delta (-t)dt$ 做变量替换（令 $\tau =-t$），结合筛选性可得
$${\int }_{-\infty }^{\infty }x(t)\delta (-t)dt={\int }_{-\infty }^{\infty }x(-\tau )\delta (\tau )d\tau =x(0)$$
而 ${\int }_{-\infty }^{\infty }x(t)\delta (t)dt=x(0)$，因此 $\delta (-t)=\delta (t)$。

2.3 尺度变换性质

对 $\delta (t)$ 的自变量进行线性尺度变换（$t\to at$，其中 $a\ne 0$）时，其形式满足
$$\delta (at)=\frac{1}{|a|}\delta (t)$$

系数意义：系数 $\frac{1}{|a|}$ 的引入是为了保证尺度变换后 $\delta$ 函数的积分归一性。例如，当 $a>0$ 时，通过变量替换 $\tau =at$ 可得
$${\int }_{-\infty }^{\infty }\delta (at)dt=\frac{1}{a}{\int }_{-\infty }^{\infty }\delta (\tau )d\tau =\frac{1}{a}$$
为使积分仍等于 1，需乘以 $\frac{1}{a}$（即 $\frac{1}{|a|}$），因此 $\delta (at)=\frac{1}{a}\delta (t)$；当 $a<0$ 时，同理可证系数为 $\frac{1}{|a|}$。

2.4 卷积特性

设任意函数 $x(t)$ 与 $\delta$ 函数的卷积定义为 $x(t)\ast \delta (t-t_0)={\int }_{-\infty }^{\infty }x(\tau )\delta (t-t_0-\tau )d\tau$，则该卷积等价于 $x(t)$ 沿时间轴平移 $t_0$，即
$$x(t)\ast \delta (t-t_0)=x(t-t_0)$$

特殊情况：当 $t_0=0$ 时，卷积结果为 $x(t)$ 本身：
$$x(t)\ast \delta (t)=x(t)$$
这表明 $\delta (t)$ 是卷积运算的单位元，类似于乘法运算中的“1”，是信号滤波、系统分析中的重要性质（如“理想延迟系统”的冲激响应为 $\delta (t-t_0)$，输入信号 $x(t)$ 通过该系统后输出为 $x(t-t_0)$）。

2.5 函数复合性质

若 $f(t)$ 是连续可微函数，且其所有零点 $t_i$（满足 $f(t_i)=0$）均为单零点（即 $f^{\prime }(t_i)\ne 0$），则复合函数 $\delta (f(t))$ 可分解为各零点处 $\delta$ 函数的线性叠加：
$$\delta (f(t))=\sum _i\frac{1}{|f^{\prime }(t_i)|}\delta (t-t_i)$$

应用场景：该性质可将复杂变量的 $\delta$ 函数（如 $\delta (t^2-1)$）转化为原变量的 $\delta$ 函数。例如，对 $f(t)=t^2-1$，其零点为 $t_1=1$、$t_2=-1$，且 $f^{\prime }(1)=2$、$f^{\prime }(-1)=-2$，因此
$$\delta (t^2-1)=\frac{1}{2}\delta (t-1)+\frac{1}{2}\delta (t+1)$$

2.6 与单位阶跃函数的关系

单位阶跃函数 $u(t)$ 的定义为
$$u(t)=\{\begin{array}{ll}1& (t>0)\\ 0& (t<0)\end{array}$$
（通常定义 $u(0)=\frac{1}{2}$，但这不影响积分运算）。$\delta (t)$ 与 $u(t)$ 满足严格的微积分关系：

2.6.1 积分关系

$\delta (t)$ 从 $-\infty$ 到 $t$ 的积分等于 $u(t)$，即
$${\int }_{-\infty }^t\delta (\tau )d\tau =u(t)$$
物理意义：对“瞬时冲激”$\delta (\tau )$ 从 $-\infty$ 到 $t$ 积分，本质是累积冲激的“效应”——当 $t<0$ 时，积分区间不包含 $\delta (\tau )$ 的非零区域，结果为 0；当 $t>0$ 时，积分区间包含 $\delta (\tau )$ 的非零区域，结果为 1，与 $u(t)$ 的定义完全一致。

2.6.2 微分关系

$u(t)$ 的导数等于 $\delta (t)$，即
$$\frac{d}{dt}u(t)=\delta (t)$$
理解：$u(t)$ 在 $t<0$ 和 $t>0$ 时均为常数（导数为 0），仅在 $t=0$ 处发生“跳变”（从 0 跳变到 1），而 $\delta (t)$ 恰好描述了这种“单位跳变”的导数特性，是广义函数中“导数”概念的延伸。

注意事项

同一时刻的 $\delta$ 函数及其各阶导数的乘积（如 ${\delta }^2(t)=\delta (t)\delta (t)$、$\delta (t){\delta }^{\prime }(t)$ 等）不满足广义函数的运算规则，在数学上无定义，需避免此类表达式的使用。

3 狄拉克函数的一阶导数（${\delta }^{\prime }(t)$）

${\delta }^{\prime }(t)$ 是 $\delta (t)$ 的一阶导数，属于高阶狄拉克函数，其定义同样基于广义函数的导数规则（即“导数的积分等于原函数的边界值”），性质是 $\delta (t)$ 性质的延伸。

3.1 积分特性

${\delta }^{\prime }(t)$ 在全数轴上的积分值为 0，即
$${\int }_{-\infty }^{\infty }{\delta }^{\prime }(t)dt=0$$

证明：根据广义函数导数的定义，对 ${\int }_{-\infty }^{\infty }{\delta }^{\prime }(t)dt$ 分部积分（令 $u=\delta (t)$，$dv=dt$），可得
$${\int }_{-\infty }^{\infty }{\delta }^{\prime }(t)dt=\delta (t){|}_{-\infty }^{\infty }=\delta (\infty )-\delta (-\infty )=0-0=0$$
（$\delta (t)$ 在 $\pm \infty$ 处取值为 0）。

3.2 筛选性（高阶抽样）

${\delta }^{\prime }(t)$ 的筛选性表现为对函数一阶导数的抽样，同样分为乘积形式和积分形式：

3.2.1 乘积形式

任意连续可微函数 $x(t)$ 与 ${\delta }^{\prime }(t)$ 的乘积，可展开为
$$x(t){\delta }^{\prime }(t)=x(0){\delta }^{\prime }(t)-x^{\prime }(0)\delta (t)$$
推导思路：对 ${\int }_{-\infty }^{\infty }x(t){\delta }^{\prime }(t)\varphi (t)dt$（$\varphi (t)$ 为测试函数）分部积分，结合 $\delta (t)$ 的筛选性可证得该式。

3.2.2 积分形式

对乘积形式两边积分，或直接对 ${\int }_{-\infty }^{\infty }x(t){\delta }^{\prime }(t)dt$ 分部积分，可得
$${\int }_{-\infty }^{\infty }x(t){\delta }^{\prime }(t)dt=-x^{\prime }(0)$$
当 ${\delta }^{\prime }(t)$ 平移 $t_0$ 时，退化为
$${\int }_{-\infty }^{\infty }x(t){\delta }^{\prime }(t-t_0)dt=-x^{\prime }(t_0)$$
式中负号源于分部积分的边界项，是 ${\delta }^{\prime }(t)$ 筛选性的重要特征。

3.3 奇函数性质

${\delta }^{\prime }(t)$ 满足奇函数的定义，即
$${\delta }^{\prime }(-t)=-{\delta }^{\prime }(t)$$

证明：对 $\delta (-t)=\delta (t)$（$\delta (t)$ 的偶函数性质）两边求导，左边由链式法则得 $-{\delta }^{\prime }(-t)$，右边为 ${\delta }^{\prime }(t)$，因此
$$-{\delta }^{\prime }(-t)={\delta }^{\prime }(t)⟹{\delta }^{\prime }(-t)=-{\delta }^{\prime }(t)$$

3.4 尺度变换性质

对 ${\delta }^{\prime }(t)$ 的自变量进行线性尺度变换（$t\to at$，$a\ne 0$）时，其形式满足
$${\delta }^{\prime }(at)=\frac{1}{a|a|}{\delta }^{\prime }(t)$$

推导思路：对 $\delta (at)=\frac{1}{|a|}\delta (t)$（$\delta (t)$ 的尺度变换性质）两边求导，左边由链式法则得 $a{\delta }^{\prime }(at)$，右边为 $\frac{1}{|a|}{\delta }^{\prime }(t)$，因此
$$a{\delta }^{\prime }(at)=\frac{1}{|a|}{\delta }^{\prime }(t)⟹{\delta }^{\prime }(at)=\frac{1}{a|a|}{\delta }^{\prime }(t)$$
例如，当 $a=2$ 时，${\delta }^{\prime }(2t)=\frac{1}{2\cdot 2}{\delta }^{\prime }(t)=\frac{1}{4}{\delta }^{\prime }(t)$；当 $a=-2$ 时，${\delta }^{\prime }(-2t)=\frac{1}{-2\cdot 2}{\delta }^{\prime }(t)=-\frac{1}{4}{\delta }^{\prime }(t)$。

4 狄拉克函数的 $k$ 阶导数（${\delta }^{(k)}(t)$）

${\delta }^{(k)}(t)$ 表示 $\delta (t)$ 的 $k$ 阶导数（$k$ 为非负整数，$k=0$ 时退化为 $\delta (t)$ 本身），其性质是 $\delta (t)$ 和 ${\delta }^{\prime }(t)$ 性质的高阶推广，主要性质如下：

4.1 筛选性（$k$ 阶抽样）

${\delta }^{(k)}(t)$ 的积分筛选性表现为对函数 $k$ 阶导数的抽样，即
$${\int }_{-\infty }^{\infty }{\delta }^{(k)}(t)x(t)dt=(-1{)}^k{x}^{(k)}(0)(k\ge 0)$$

说明：

• $(-1{)}^k$：是 $k$ 次分部积分后积累的符号（每次分部积分引入一个负号）；
• $x^{(k)}(0)$：表示 $x(t)$ 在 $t=0$ 处的 $k$ 阶导数（需 $x(t)$ 至少 $k$ 阶连续可微）；
• 平移扩展：当 ${\delta }^{(k)}(t)$ 平移 $t_0$ 时，该式退化为
  $${\int }_{-\infty }^{\infty }{\delta }^{(k)}(t-t_0)x(t)dt=(-1{)}^k{x}^{(k)}(t_0)$$

4.2 奇偶性

${\delta }^{(k)}(t)$ 的奇偶性由导数阶数 $k$ 决定，满足
$${\delta }^{(k)}(t)=(-1{)}^k{\delta }^{(k)}(-t)$$

分类讨论：

• 当 $k$ 为偶数时：$(-1{)}^k=1$，因此 ${\delta }^{(k)}(t)={\delta }^{(k)}(-t)$，即 $k$ 阶导数为偶函数（如 $\delta (t)$（$k=0$）、${\delta }^{\prime \prime }(t)$（$k=2$））；
• 当 $k$ 为奇数时：$(-1{)}^k=-1$，因此 ${\delta }^{(k)}(t)=-{\delta }^{(k)}(-t)$，即 $k$ 阶导数为奇函数（如 ${\delta }^{\prime }(t)$（$k=1$）、${\delta }^{\prime \prime \prime }(t)$（$k=3$））。

4.3 积分特性

当 $k\ge 1$ 时，${\delta }^{(k)}(t)$ 在全数轴上的积分值为 0，即
$${\int }_{-\infty }^{\infty }{\delta }^{(k)}(t)dt=0$$

证明：根据广义函数导数的积分规则，
$${\int }_{-\infty }^{\infty }{\delta }^{(k)}(t)dt={\delta }^{(k-1)}(t){|}_{-\infty }^{\infty }={\delta }^{(k-1)}(\infty )-{\delta }^{(k-1)}(-\infty )=0-0=0$$
（高阶 $\delta$ 函数在 $\pm \infty$ 处取值均为 0）。

4.4 函数乘积展开

若 $x(t)$ 的 $k$ 阶导数在 $t=0$ 处连续，则 $x(t)$ 与 ${\delta }^{(k)}(t)$ 的乘积可展开为各阶低阶 $\delta$ 函数的线性组合：
$$x(t){\delta }^{(k)}(t)=\sum _{m=0}^k(-1{)}^m(\genfrac{}{}{0ex}{}{k}{m})x^{(m)}(0){\delta }^{(k-m)}(t)(k\ge 0)$$

说明：

• $\left(\genfrac{}{}{0ex}{}{k}{m}\right)$：二项式系数（$\left(\genfrac{}{}{0ex}{}{k}{m}\right)=\frac{k!}{m!(k-m)!}$）；
• 低阶推广：当 $k=1$ 时，该式退化为 $x(t){\delta }^{\prime }(t)=x(0){\delta }^{\prime }(t)-x^{\prime }(0)\delta (t)$（与 ${\delta }^{\prime }(t)$ 的乘积形式一致）；当 $k=0$ 时，退化为 $x(t)\delta (t)=x(0)\delta (t)$（与 $\delta (t)$ 的乘积形式一致）。

4.5 卷积特性

任意函数 $x(t)$ 与 ${\delta }^{(k)}(t-t_0)$ 的卷积，等价于 $x(t)$ 在 $t=t_0$ 处的 $k$ 阶导数沿时间轴平移 $t_0$，即
$$x(t)\ast {\delta }^{(k)}(t-t_0)=x^{(k)}(t-t_0)$$

特殊情况：

• 当 $k=0$ 时：退化为 $x(t)\ast \delta (t-t_0)=x(t-t_0)$，与 $\delta (t)$ 的卷积特性一致；
• 当 $t_0=0$ 时：退化为 $x(t)\ast {\delta }^{(k)}(t)=x^{(k)}(t)$，即函数与 $\delta (t)$ 的 $k$ 阶导数卷积，结果为该函数的 $k$ 阶导数；
• 当 $k=-1$ 时（定义“-1 阶导数”为积分运算）：此时 ${\delta }^{(-1)}(t)$ 对应单位阶跃函数 $u(t)$，卷积结果为 $x(t)$ 的积分，即
  $$x(t)\ast u(t)={\int }_{-\infty }^{t}x(\tau )d\tau$$
  该式建立了卷积运算与积分运算的关联，是信号处理中“积分器”的数学表达。

5 总结

狄拉克函数（$\delta$ 函数）及其各阶导数是广义函数体系中的重要成员，其本质是通过积分运算定义的“功能性”数学工具，而非传统意义上的“点值函数”。主要结论可归纳为：

1. 定义重点：$\delta (t)$ 通过“积分归一性”和“非零点零值性”定义，刻画“单位瞬时冲激”特性；
2. 基础性质：$\delta (t)$ 的筛选性、偶函数性、尺度变换、卷积特性等，是其在物理和工程领域应用的关键（如信号抽样、系统分析）；
3. 高阶推广：${\delta }^{(k)}(t)$ 的性质随导数阶数 $k$ 变化（如奇偶性、筛选性的导数阶数），需通过广义函数的导数规则推导；
4. 运算边界：需避免同一时刻 $\delta$ 函数及其导数的乘积（如 ${\delta }^2(t)$、$\delta (t){\delta }^{\prime }(t)$），此类表达式无数学定义。

狄拉克函数的价值在于将“瞬时性”“点集中”的物理现象（如点电荷、瞬时力）转化为可计算的数学工具，是连接连续数学与离散物理现象的重要桥梁。

---

数学物理方法 - 狄拉克函数（$\delta$ 函数）

Marrine 发布于 2023-11-30 13:59・四川

$\delta$ 函数由英国物理学家保罗·狄拉克（Paul Dirac）于 20 世纪 20 年代首次引入，主要用于描述物理学中的“点源”物理量，如质点的质量密度、点电荷的电荷密度、瞬时脉冲信号的强度分布等。尽管 $\delta$ 函数不满足经典函数的定义（在 $x=0$ 处取值为无穷大，非零点取值为 0），但通过广义函数理论的严格化，其可按照特定规则参与微积分运算（如微分、积分）及微分方程求解，是数学物理领域中极具实用性的工具。下文将系统介绍 $\delta$ 函数的定义与物理含义、偶函数性质、卷积性质、傅里叶变换及导函数的相关理论。

一、$\delta$ 函数的定义和含义

$\delta$ 函数的主要功能是对“点源”的数学抽象，可用于描述一维单位点电荷的电荷密度分布，其定义、几何意义、筛选性质及物理含义如下：

1. 数学定义与几何意义

$\delta$ 函数（以 $x$ 为变量，平移量为 $x_0$）的数学定义满足以下两个条件：

• 取值特性：仅在 $x=x_0$ 处存在“冲激”，其余位置无贡献，表达式为：
  $$\delta (x-x_0)=\{\begin{array}{ll}\infty & (x=x_0)\\ 0& (x\ne x_0)\end{array}$$
• 积分归一性：“冲激总量”为 1，体现“单位点源”特性，表达式为：
  $${\int }_{-\infty }^{\infty }\delta (x-x_0)dx=1$$

$\delta$ 函数的几何意义为“无限高且无限窄，同时满足单位面积”，其图像示意如下：

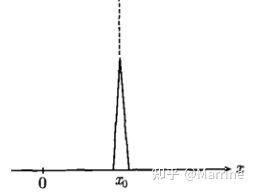
当 $x_0=0$ 时，$\delta$ 函数退化为原点处的单位冲激，定义简化为：

1. 取值特性：
   $$\delta (x)=\{\begin{array}{ll}\infty & (x=0)\\ 0& (x\ne 0)\end{array}$$
2. 积分归一性：
   $${\int }_{-\infty }^{\infty }\delta (x)dx=1$$

2. 筛选性质及证明

对于任意连续函数 $f(x)$，$\delta$ 函数满足“筛选性质”——通过积分可提取函数在 $x=x_0$ 处的函数值，本质是“点源对物理量的贡献抽样”（如点电荷电场计算中，直接提取目标位置的电荷贡献），表达式为：
$${\int }_{-\infty }^{\infty }f(x)\delta (x-x_0)dx=f(x_0)$$

证明过程

设 $\epsilon$ 为无穷小量（$\epsilon \to 0^{+}$），由于 $\delta (x-x_0)$ 仅在 $x\in [x_0-\epsilon ,x_0+\epsilon ]$ 内有贡献，积分区间可缩小为该无穷小区间：
$$\begin{array}{rl}{\int }_{-\infty }^{\infty }f(x)\delta (x-x_0)dx& ={\int }_{x_0-\epsilon }^{x_0+\epsilon }f(x)\delta (x-x_0)dx\\ & =f(x_0){\int }_{x_0-\epsilon }^{x_0+\epsilon }\delta (x-x_0)dx(\text{因 }f(x)\text{ 连续，区间内 }f(x)\approx f(x_0))\\ & =f(x_0)\cdot 1=f(x_0)(\text{由积分归一性})\end{array}$$
当 $x_0=0$ 时，筛选性质简化为：
$${\int }_{-\infty }^{\infty }f(x)\delta (x)dx=f(0)$$

3. 物理含义

$\delta$ 函数本质是“单位点源密度”的数学表达，常见物理场景举例如下：

• 位于 $x=x_0$ 处、质量为 $m$ 的质点，其线密度分布为 $\rho (x)=m\delta (x-x_0)$（积分 ${\int }_{-\infty }^{\infty }\rho (x)dx=m$，符合质量守恒）；
• 位于 $x=x_0$ 处、电荷量为 $q$ 的点电荷，其电荷密度分布为 $\rho (x)=q\delta (x-x_0)$（积分 ${\int }_{-\infty }^{\infty }\rho (x)dx=q$，符合电荷守恒）；
• 在 $t=t_0$ 时刻总强度为 1 的瞬时脉冲，其强度分布为 $p(t)=\delta (t-t_0)$（积分 ${\int }_{-\infty }^{\infty }p(t)dt=1$，符合总强度定义）。

二、$\delta$ 函数的偶函数性质

$\delta$ 函数满足偶函数定义，即 $\delta (-x)=\delta (x)$，严格证明需通过广义函数的“配对思想”（与任意检验函数的积分相等性）完成。

证明过程

设 $f(x)$ 为任意连续的检验函数（满足在无穷远处快速衰减），需证明 ${\int }_{-\infty }^{\infty }f(x)\delta (-x)dx={\int }_{-\infty }^{\infty }f(x)\delta (x)dx$：

1. 对左侧积分做变量替换：令 $t=-x$，则 $x=-t$，$dx=-dt$；当 $x\to \pm \infty$ 时，$t\to \mp \infty$，积分上下限交换后负号抵消：
   $${\int }_{-\infty }^{\infty }f(x)\delta (-x)dx={\int }_{\infty }^{-\infty }f(-t)\delta (t)(-dt)={\int }_{-\infty }^{\infty }f(-t)\delta (t)dt$$
2. 由 $\delta$ 函数的筛选性质，${\int }_{-\infty }^{\infty }f(-t)\delta (t)dt=f(-0)=f(0)$；
3. 右侧积分直接应用筛选性质：${\int }_{-\infty }^{\infty }f(x)\delta (x)dx=f(0)$。

综上，对任意检验函数 $f(x)$，均有 ${\int }_{-\infty }^{\infty }f(x)\delta (-x)dx={\int }_{-\infty }^{\infty }f(x)\delta (x)dx$，根据广义函数相等的定义，可得 $\delta (-x)=\delta (x)$。

三、$\delta$ 函数的卷积性质

卷积运算的定义为 $f(x)\ast g(x)={\int }_{-\infty }^{\infty }f(\tau )g(x-\tau )d\tau$，$\delta$ 函数的卷积性质本质是利用筛选性简化计算，具体包括三类情况：

1. $\delta (x)$ 与任意函数 $f(x)$ 的卷积

根据卷积定义，$\delta (x)$ 与 $f(x)$ 的卷积为：
$$\delta (x)\ast f(x)={\int }_{-\infty }^{\infty }f(\tau )\delta (x-\tau )d\tau$$
由 $\delta$ 函数的筛选性质（令 $x_0=x$、被积函数为 $f(\tau )$），积分结果为 $f(x)$，即：
$$\delta (x)\ast f(x)=f(x)$$
该性质表明，$\delta (x)$ 是卷积运算的单位元——任意函数与 $\delta (x)$ 卷积后，结果仍为该函数本身，不改变函数形态。

2. $\delta (x-a)$ 与任意函数 $f(x)$ 的卷积

根据卷积定义，$\delta (x-a)$ 与 $f(x)$ 的卷积为：
$$\delta (x-a)\ast f(x)={\int }_{-\infty }^{\infty }\delta (\tau -a)f(x-\tau )d\tau$$
对积分做变量替换：令 $t=\tau -a$，则 $\tau =t+a$，$d\tau =dt$，积分变为：
$${\int }_{-\infty }^{\infty }\delta (t)f(x-(t+a))dt={\int }_{-\infty }^{\infty }f((x-a)-t)\delta (t)dt$$
由筛选性质，积分结果为 $f(x-a)$，即：
$$\delta (x-a)\ast f(x)=f(x-a)$$
该性质的物理意义是：任意函数与平移后的 $\delta$ 函数卷积，等价于将原函数沿 $x$ 轴平移 $a$ 个单位（$a>0$ 向右平移，$a<0$ 向左平移）。

3. 两个 $\delta$ 函数的卷积

设两个平移 $\delta$ 函数分别为 $\delta (x-a)$ 和 $\delta (x-b)$，其卷积为：
$$\delta (x-a)\ast \delta (x-b)={\int }_{-\infty }^{\infty }\delta (\tau -a)\delta (x-\tau -b)d\tau$$
由筛选性质（令 $x_0=a$、被积函数为 $\delta (x-\tau -b)$），积分结果为 $\delta (x-a-b)$，即：
$$\delta (x-a)\ast \delta (x-b)=\delta \left[x-(a+b)\right]$$
该性质表明，两个平移 $\delta$ 函数的卷积结果仍为一个 $\delta$ 函数，其平移量为原两个平移量的和，体现“平移叠加”特性。

四、$\delta$ 函数的傅里叶变换

傅里叶变换的定义为 F { g ( x ) } = ∫ − ∞ ∞ g ( x ) e − i ω x d x \mathcal{F}\{g(x)\} = \int_{-\infty}^{\infty} g(x) e^{-i\omega x} dx F{g(x)}=∫−∞∞​g(x)e−iωxdx，逆傅里叶变换为 F − 1 { G ( ω ) } = 1 2 π ∫ − ∞ ∞ G ( ω ) e i ω x d ω \mathcal{F}^{-1}\{G(\omega)\} = \frac{1}{2\pi} \int_{-\infty}^{\infty} G(\omega) e^{i\omega x} d\omega F−1{G(ω)}=2π1​∫−∞∞​G(ω)eiωxdω。$\delta$ 函数的傅里叶变换在广义积分意义下成立，且形式简洁、物理意义明确。

1. $\delta (x-x_0)$ 的傅里叶变换

根据傅里叶变换定义，令 $g(x)=\delta (x-x_0)$，则：
F { δ ( x − x 0 ) } = ∫ − ∞ ∞ δ ( x − x 0 ) e − i ω x d x \mathcal{F}\left\{\delta(x - x_0)\right\} = \int_{-\infty}^{\infty} \delta(x - x_0) e^{-i\omega x} dx F{δ(x−x0​)}=∫−∞∞​δ(x−x0​)e−iωxdx
由 $\delta$ 函数的筛选性质（令 $f(x)=e^{-i\omega x}$、$x_0=x_0$），积分结果为 $e^{-i\omega x_0}$，即：
F { δ ( x − x 0 ) } = e − i ω x 0 \mathcal{F}\left\{\delta(x - x_0)\right\} = e^{-i\omega x_0} F{δ(x−x0​)}=e−iωx0​

当 $x_0=0$ 时，$\delta (x)$ 的傅里叶变换简化为：
F { δ ( x ) } = 1 \mathcal{F}\{\delta(x)\} = 1 F{δ(x)}=1
该结果表明，$\delta (x)$（时域的单位冲激）在频域中表现为“均匀谱”——所有频率分量的幅值均为 1，是信号处理中“冲激信号频谱”的重要结论。

2. $\delta (x)$ 的傅里叶逆变换

由 F { δ ( x ) } = 1 \mathcal{F}\{\delta(x)\} = 1 F{δ(x)}=1，对等式两边取逆傅里叶变换，令 $G(\omega )=1$，则：
δ ( x ) = F − 1 { 1 } = 1 2 π ∫ − ∞ ∞ e i ω x d ω \delta(x) = \mathcal{F}^{-1}\{1\} = \frac{1}{2\pi} \int_{-\infty}^{\infty} e^{i\omega x} d\omega δ(x)=F−1{1}=2π1​∫−∞∞​eiωxdω

利用欧拉公式 $e^{i\omega x}=\cos (\omega x)+i\sin (\omega x)$，其中 $\sin (\omega x)$ 是关于 $\omega$ 的奇函数，其在 $(-\infty ,\infty )$ 上的积分为 0，因此上式可简化为：
$$\delta (x)=\frac{1}{2\pi }{\int }_{-\infty }^{\infty }\cos (\omega x)d\omega$$

此外，对 $\delta (x)=\frac{1}{2\pi }{\int }_{-\infty }^{\infty }{e}^{i\omega x}d\omega$ 两边乘以 $2\pi$ 并交换变量（$x$ 替换为 $\omega$，$\omega$ 替换为 $x$），可得傅里叶变换中的重要“积分公式”：
$$2\pi \delta (\omega )={\int }_{-\infty }^{\infty }{e}^{-i\omega x}dx$$
该公式常用于简化其他函数的傅里叶变换计算。

五、$\delta$ 函数的导函数

在广义函数框架下，$\delta$ 函数可视为“任意阶可微函数”，以一阶导函数 ${\delta }^{\prime }(x)$ 为例，其定义需通过“分部积分”与检验函数配对实现，且具有明确的物理意义（如电偶极子的电荷密度分布）。

1. ${\delta }^{\prime }(x)$ 的积分定义及证明

对任意连续可微且在无穷远处快速衰减的检验函数 $f(x)$，${\delta }^{\prime }(x)$ 的定义通过以下积分关系确定：
$${\int }_{-\infty }^{\infty }f(x){\delta }^{\prime }(x)dx=-f^{\prime }(0)$$

证明过程

对积分 ${\int }_{-\infty }^{\infty }f(x){\delta }^{\prime }(x)dx$ 应用分部积分法：

• 设 $u=f(x)$，则 $du=f^{\prime }(x)dx$；
• 设 $dv={\delta }^{\prime }(x)dx$，则 $v=\delta (x)$；
• 根据分部积分公式 ${\int }_{-\infty }^{\infty }udv=uv{|}_{-\infty }^{\infty }-{\int }_{-\infty }^{\infty }vdu$，代入得：
  $${\int }_{-\infty }^{\infty }f(x){\delta }^{\prime }(x)dx={f(x)\delta (x)|}_{-\infty }^{\infty }-{\int }_{-\infty }^{\infty }{f}^{\prime }(x)\delta (x)dx$$

由于 $f(x)$ 在无穷远处快速衰减（$f(\pm \infty )=0$）且 $\delta (\pm \infty )=0$，故第一项 ${f(x)\delta (x)|}_{-\infty }^{\infty }=0$；第二项由 $\delta$ 函数的筛选性质，${\int }_{-\infty }^{\infty }{f}^{\prime }(x)\delta (x)dx=f^{\prime }(0)$，因此：
$${\int }_{-\infty }^{\infty }f(x){\delta }^{\prime }(x)dx=-f^{\prime }(0)$$

2. ${\delta }^{\prime }(x)$ 的物理意义（电偶极子的电荷密度）

${\delta }^{\prime }(x)$ 可用于描述单位电偶极子的电荷密度分布，具体物理模型如下：

考虑一对相距 $2\epsilon$（$\epsilon >0$，且 $\epsilon \to 0$）的点电荷：正电荷 $+q$ 位于 $x=\epsilon$ 处，负电荷 $-q$ 位于 $x=-\epsilon$ 处。该电荷系统的电荷密度分布为：
$${\rho }_{\epsilon }(x)=q\delta (x-\epsilon )-q\delta (x+\epsilon )$$

将上式变形为：
$${\rho }_{\epsilon }(x)=-2q\epsilon \cdot \frac{\delta (x+\epsilon )-\delta (x-\epsilon )}{2\epsilon }$$

定义电偶极矩 $p=2q\epsilon$（方向沿 $x$ 轴正方向，大小为电荷量与间距的乘积），则 $-2q\epsilon =-p$。当 $\epsilon \to 0$ 时，$\frac{\delta (x+\epsilon )-\delta (x-\epsilon )}{2\epsilon }$ 是 $\delta (x)$ 的导数定义（差商极限），即 ${\lim }_{\epsilon \to 0}\frac{\delta (x+\epsilon )-\delta (x-\epsilon )}{2\epsilon }={\delta }^{\prime }(x)$。

因此，当 $\epsilon \to 0$（电荷间距趋近于 0，电荷量趋近于无穷大，但偶极矩 $p$ 保持有限）时，电荷密度的极限为：
$$\rho (x)=\underset{\epsilon \to 0}{\lim }{\rho }_{\epsilon }(x)=-p{\delta }^{\prime }(x)$$

若取 $p=1$（单位电偶极矩），则 $\rho (x)=-{\delta }^{\prime }(x)$，即 ${\delta }^{\prime }(x)$ 对应“位于 $x=0$ 处、偶极矩为 $-1$ 的电偶极子”的电荷密度分布，这是 ${\delta }^{\prime }(x)$ 最典型的物理意义。

---

• Dirac delta function(狄拉克 δ 函数) | 定义、性质及物理意义…（篇 2）-优快云博客
  https://blog.youkuaiyun.com/u013669912/article/details/155164259
• Dirac delta function(狄拉克 δ 函数) | …（篇 3）-优快云博客
  https://blog.youkuaiyun.com/u013669912/article/details/155165765

---

via：

• 狄拉克函数解析-优快云博客 JadenNeal 于 2020-03-15 17:36:23 发布
  https://blog.youkuaiyun.com/HollyRan/article/details/104880077
• 数学物理方法-狄拉克函数(δ 函数) - 知乎 Marrine 发布于 2023-11-30 13:59・四川
  https://zhuanlan.zhihu.com/p/669614573