注:本文为 “Dirac‘s Delta Function” 相关 zhihu 文章重排。
如有内容异常,请看原文。
[数学物理] - δ 函数
张稀桧 编辑于 2022-06-11 09:34
定义 I
在经典表述中,δ 函数被定义为:
δ
(
x
−
x
0
)
=
{
∞
x
=
x
0
0
x
≠
x
0
\delta (x-x_0)= \begin {cases} \infty & x=x_0 \\ 0 & x\ne x_0 \end {cases}
δ(x−x0)={∞0x=x0x=x0
且满足归一化条件:
∫
−
∞
+
∞
δ
(
x
)
d
x
=
1
\int_{-\infty}^{+\infty}\delta (x)\text {d} x=1
∫−∞+∞δ(x)dx=1
该定义是 δ 函数最简洁且最契合物理直觉的表述形式,自然关联概率分布、点源与脉冲等物理模型。例如,三维欧几里得空间中的点电荷分布可描述为 q δ ( r − r 0 ) q\delta (\bold {r}-\bold {r}_0) qδ(r−r0);电信号中的理想脉冲信号可描述为 k δ ( t − t 0 ) k\delta (t-t_0) kδ(t−t0)。作为广义函数,δ 函数的极限特性使其具备独特的数学性质,以下基于定义 I 展开推导。
性质 I
1.0 正交性
x δ ( x ) = 0 x\delta (x)=0 xδ(x)=0
[证]:根据定义 I,
当
x
≠
0
x\ne0
x=0 时,
δ
(
x
)
=
0
\delta (x)=0
δ(x)=0,故
x
δ
(
x
)
=
0
x\delta (x)=0
xδ(x)=0;
当
x
=
0
x=0
x=0 时,结合广义函数的积分意义,对任意连续函数
f
(
x
)
f (x)
f(x),有
∫
−
∞
+
∞
x
δ
(
x
)
f
(
x
)
d
x
=
0
⋅
f
(
0
)
=
0
\int_{-\infty}^{+\infty} x\delta (x) f (x)\text {d} x=0\cdot f (0)=0
∫−∞+∞xδ(x)f(x)dx=0⋅f(0)=0
因此
x
δ
(
x
)
=
0
x\delta (x)=0
xδ(x)=0 在分布意义下成立。
该性质用于证明坐标本征函数(δ 函数)的正交归一性,且可推广为:
1.0* 若函数 f ( x ) f (x) f(x) 与 g ( x ) g (x) g(x) 满足 x f ( x ) = x g ( x ) xf (x)=xg (x) xf(x)=xg(x) 对所有 x x x 成立,则存在常数 c c c,使得 f ( x ) = g ( x ) + c δ ( x ) f (x)=g (x)+c\delta (x) f(x)=g(x)+cδ(x)。
1.1 筛选性
∫ − ∞ + ∞ f ( x ) δ ( x − x 0 ) d x = f ( x 0 ) \int_{-\infty}^{+\infty} f (x)\delta (x-x_0)\text {d} x=f (x_0) ∫−∞+∞f(x)δ(x−x0)dx=f(x0)
[证]:由 δ 函数的极限特性,积分仅在
x
0
x_0
x0 邻域非零,即
∫
−
∞
+
∞
f
(
x
)
δ
(
x
−
x
0
)
d
x
=
lim
ε
→
0
∫
x
0
−
ε
x
0
+
ε
f
(
x
)
δ
(
x
−
x
0
)
d
x
\int_{-\infty}^{+\infty} f (x)\delta (x-x_0)\text {d} x=\lim_{\varepsilon\rightarrow0}\int_{x_0-\varepsilon}^{x_0+\varepsilon} f (x)\delta (x-x_0)\text {d} x
∫−∞+∞f(x)δ(x−x0)dx=ε→0lim∫x0−εx0+εf(x)δ(x−x0)dx
若
f
(
x
)
f (x)
f(x) 在
x
0
x_0
x0 处连续,则在充分小的区间
(
x
0
−
ε
,
x
0
+
ε
)
(x_0-\varepsilon,x_0+\varepsilon)
(x0−ε,x0+ε) 内,
f
(
x
)
f (x)
f(x) 的值
f
(
x
)
‾
∣
x
∈
(
x
0
−
ε
,
x
0
+
ε
)
\overline{f(x)}|_{x\in(x_0-\varepsilon,x_0+\varepsilon)}
f(x)∣x∈(x0−ε,x0+ε) 可近似为
f
(
x
0
)
f (x_0)
f(x0),代入得
∫
−
∞
+
∞
f
(
x
)
δ
(
x
−
x
0
)
d
x
=
f
(
x
0
)
∫
x
0
−
ε
x
0
+
ε
δ
(
x
−
x
0
)
d
x
=
f
(
x
0
)
\int_{-\infty}^{+\infty} f (x)\delta (x-x_0)\text {d} x=f (x_0)\int_{x_0-\varepsilon}^{x_0+\varepsilon}\delta (x-x_0)\text {d} x=f (x_0)
∫−∞+∞f(x)δ(x−x0)dx=f(x0)∫x0−εx0+εδ(x−x0)dx=f(x0)
证毕。
该性质使 δ 函数具备对任意连续函数的筛选功能,是 δ 函数其他性质的重要基础。
1.2 奇偶性
δ ( x ) = δ ( − x ) \delta (x)=\delta (-x) δ(x)=δ(−x)
[证]:对任意连续函数
f
(
x
)
f (x)
f(x),考虑积分
I
=
∫
−
∞
+
∞
f
(
x
)
δ
(
−
x
)
d
x
I=\int_{-\infty}^{+\infty} f (x)\delta (-x)\text {d} x
I=∫−∞+∞f(x)δ(−x)dx
令
t
=
−
x
t=-x
t=−x,则
d
x
=
−
d
t
\text {d} x=-\text {d} t
dx=−dt,积分变为
I
=
∫
+
∞
−
∞
f
(
−
t
)
δ
(
t
)
(
−
d
t
)
=
∫
−
∞
+
∞
f
(
−
t
)
δ
(
t
)
d
t
=
f
(
0
)
I=\int_{+\infty}^{-\infty} f (-t)\delta (t)(-\text {d} t)=\int_{-\infty}^{+\infty} f (-t)\delta (t)\text {d} t=f (0)
I=∫+∞−∞f(−t)δ(t)(−dt)=∫−∞+∞f(−t)δ(t)dt=f(0)
另一方面,
∫
−
∞
+
∞
f
(
x
)
δ
(
x
)
d
x
=
f
(
0
)
\int_{-\infty}^{+\infty} f (x)\delta (x)\text {d} x=f (0)
∫−∞+∞f(x)δ(x)dx=f(0),故
δ
(
−
x
)
=
δ
(
x
)
\delta (-x)=\delta (x)
δ(−x)=δ(x)。
δ 函数为偶函数,该性质在积分运算中可简化变量替换过程。
1.3 伸缩性
δ ( a x ) = 1 ∣ a ∣ δ ( x ) \delta (ax)=\frac {1}{|a|}\delta (x) δ(ax)=∣a∣1δ(x)
[证]:对任意连续函数
f
(
x
)
f (x)
f(x),考虑积分
∫
−
∞
+
∞
f
(
x
)
δ
(
a
x
)
d
x
\int_{-\infty}^{+\infty} f (x)\delta (ax)\text {d} x
∫−∞+∞f(x)δ(ax)dx
当
a
>
0
a>0
a>0 时,令
t
=
a
x
t=ax
t=ax,则
d
x
=
1
a
d
t
\text {d} x=\frac {1}{a}\text {d} t
dx=a1dt,积分变为
∫
−
∞
+
∞
f
(
t
a
)
δ
(
t
)
⋅
1
a
d
t
=
1
a
f
(
0
)
\int_{-\infty}^{+\infty} f\left (\frac {t}{a}\right)\delta (t)\cdot\frac {1}{a}\text {d} t=\frac {1}{a} f (0)
∫−∞+∞f(at)δ(t)⋅a1dt=a1f(0)
当
a
<
0
a<0
a<0 时,令
t
=
a
x
t=ax
t=ax,则
d
x
=
1
a
d
t
\text {d} x=\frac {1}{a}\text {d} t
dx=a1dt,积分上下限交换,得
∫
+
∞
−
∞
f
(
t
a
)
δ
(
t
)
⋅
1
a
d
t
=
−
1
a
f
(
0
)
=
1
∣
a
∣
f
(
0
)
\int_{+\infty}^{-\infty} f\left (\frac {t}{a}\right)\delta (t)\cdot\frac {1}{a}\text {d} t=-\frac {1}{a} f (0)=\frac {1}{|a|} f (0)
∫+∞−∞f(at)δ(t)⋅a1dt=−a1f(0)=∣a∣1f(0)
又
∫
−
∞
+
∞
f
(
x
)
⋅
1
∣
a
∣
δ
(
x
)
d
x
=
1
∣
a
∣
f
(
0
)
\int_{-\infty}^{+\infty} f (x)\cdot\frac {1}{|a|}\delta (x)\text {d} x=\frac {1}{|a|} f (0)
∫−∞+∞f(x)⋅∣a∣1δ(x)dx=∣a∣1f(0),故
δ
(
a
x
)
=
1
∣
a
∣
δ
(
x
)
\delta (ax)=\frac {1}{|a|}\delta (x)
δ(ax)=∣a∣1δ(x)。
该性质可视为奇偶性的推广(当 a = − 1 a=-1 a=−1 时退化为奇偶性)。
1.4 自身筛选性
将筛选性应用于 δ 函数自身,可得:
∫
−
∞
+
∞
δ
(
x
−
a
)
δ
(
x
−
b
)
d
x
=
{
∞
a
=
b
0
a
≠
b
\int_{-\infty}^{+\infty}\delta (x-a)\delta (x-b)\text {d} x= \begin {cases} \infty & a=b \\ 0 & a\ne b \end {cases}
∫−∞+∞δ(x−a)δ(x−b)dx={∞0a=ba=b
由此进一步推广:
1.4* ∫ − ∞ + ∞ δ 2 ( x − a ) d x = ∞ \int_{-\infty}^{+\infty}\delta^2 (x-a)\text {d} x=\infty ∫−∞+∞δ2(x−a)dx=∞(其中 δ 2 ( x − a ) = ( δ ( x − a ) ) 2 \delta^2 (x-a)=(\delta (x-a))^2 δ2(x−a)=(δ(x−a))2)。
1.5 延时性
δ ( x − a ) ∗ f ( x ) = f ( x − a ) \delta (x-a)*f (x)=f (x-a) δ(x−a)∗f(x)=f(x−a)
[证]:根据卷积的定义
δ
(
x
−
a
)
∗
f
(
x
)
=
∫
−
∞
+
∞
f
(
ξ
)
δ
(
x
−
a
−
ξ
)
d
ξ
\delta (x-a)*f (x)=\int_{-\infty}^{+\infty} f (\xi)\delta (x-a-\xi)\text {d}\xi
δ(x−a)∗f(x)=∫−∞+∞f(ξ)δ(x−a−ξ)dξ
令
η
=
ξ
−
(
x
−
a
)
\eta=\xi-(x-a)
η=ξ−(x−a),则
d
ξ
=
d
η
\text {d}\xi=\text {d}\eta
dξ=dη,积分变为
∫
−
∞
+
∞
f
(
η
+
x
−
a
)
δ
(
−
η
)
d
η
=
f
(
x
−
a
)
∫
−
∞
+
∞
δ
(
η
)
d
η
=
f
(
x
−
a
)
\int_{-\infty}^{+\infty} f (\eta+x-a)\delta (-\eta)\text {d}\eta=f (x-a)\int_{-\infty}^{+\infty}\delta (\eta)\text {d}\eta=f (x-a)
∫−∞+∞f(η+x−a)δ(−η)dη=f(x−a)∫−∞+∞δ(η)dη=f(x−a)
证毕。
该结果直观体现了卷积的延时效应,即 δ 函数与任意函数的卷积等价于对该函数的平移操作。
进一步,两个 δ 函数的卷积满足:
1.5* δ ( x − a ) ∗ δ ( x − b ) = δ ( x − ( a + b ) ) \delta (x-a)*\delta (x-b)=\delta (x-(a+b)) δ(x−a)∗δ(x−b)=δ(x−(a+b))。
1.6 点源方程
δ 函数满足最简单的泊松方程:
−
∇
2
φ
=
4
π
q
δ
(
r
−
r
0
)
-\nabla^2\varphi=4\pi q\delta (\bold {r}-\bold {r}_0)
−∇2φ=4πqδ(r−r0)
由此可导出矢量分析恒等式:
∇
⋅
r
r
3
=
−
∇
2
1
r
=
4
π
δ
(
r
−
r
0
)
\nabla\cdot\frac {\bold {r}}{r^3}=-\nabla^2\frac {1}{r}=4\pi\delta (\bold {r}-\bold {r}_0)
∇⋅r3r=−∇2r1=4πδ(r−r0)
定义 II(傅里叶积分定义)
历史上,δ 函数最初作为傅里叶变换的辅助函数被提出。傅里叶在《热分析理论》(Théorie analytique de la chaleur)中考虑积分:
f
(
x
)
=
1
2
π
∫
−
∞
+
∞
d
α
f
(
α
)
∫
−
∞
+
∞
d
ω
cos
[
ω
(
x
−
α
)
]
f (x)=\frac {1}{2\pi}\int_{-\infty}^{+\infty}\text {d}\alpha f (\alpha)\int_{-\infty}^{+\infty}\text {d}\omega\cos [\omega (x-\alpha)]
f(x)=2π1∫−∞+∞dαf(α)∫−∞+∞dωcos[ω(x−α)]
采用现代傅里叶变换的指数形式,上式可改写为:
f
(
x
)
=
1
2
π
∫
−
∞
+
∞
F
(
ω
)
e
i
ω
x
d
ω
f (x)=\frac {1}{2\pi}\int_{-\infty}^{+\infty} F (\omega) e^{i\omega x}\text {d}\omega
f(x)=2π1∫−∞+∞F(ω)eiωxdω
其中
F
(
ω
)
=
∫
−
∞
+
∞
f
(
α
)
e
−
i
ω
α
d
α
F (\omega)=\int_{-\infty}^{+\infty} f (\alpha) e^{-i\omega\alpha}\text {d}\alpha
F(ω)=∫−∞+∞f(α)e−iωαdα 为
f
(
x
)
f (x)
f(x) 的傅里叶变换。
柯西指出,在分布意义下积分顺序可交换,即
f
(
x
)
=
1
2
π
∫
−
∞
+
∞
[
∫
−
∞
+
∞
e
i
ω
(
x
−
α
)
d
ω
]
f
(
α
)
d
α
f (x)=\frac {1}{2\pi}\int_{-\infty}^{+\infty}\left [\int_{-\infty}^{+\infty} e^{i\omega (x-\alpha)}\text {d}\omega\right] f (\alpha)\text {d}\alpha
f(x)=2π1∫−∞+∞[∫−∞+∞eiω(x−α)dω]f(α)dα
其中
∫
−
∞
+
∞
e
i
ω
(
x
−
α
)
d
ω
\int_{-\infty}^{+\infty} e^{i\omega (x-\alpha)}\text {d}\omega
∫−∞+∞eiω(x−α)dω 起到筛选作用,因此定义:
δ
(
x
−
α
)
=
1
2
π
∫
−
∞
+
∞
e
i
ω
(
x
−
α
)
d
ω
\delta (x-\alpha)=\frac {1}{2\pi}\int_{-\infty}^{+\infty} e^{i\omega (x-\alpha)}\text {d}\omega
δ(x−α)=2π1∫−∞+∞eiω(x−α)dω
δ 函数的傅里叶变换需在分布意义下理解(δ 函数不满足通常的绝对可积条件),其傅里叶变换为:
F
[
δ
(
x
−
x
0
)
]
=
∫
−
∞
+
∞
δ
(
x
−
x
0
)
e
−
i
ω
x
d
x
=
e
−
i
ω
x
0
\mathcal {F}[\delta (x-x_0)]=\int_{-\infty}^{+\infty}\delta (x-x_0) e^{-i\omega x}\text {d} x=e^{-i\omega x_0}
F[δ(x−x0)]=∫−∞+∞δ(x−x0)e−iωxdx=e−iωx0
当
x
0
=
0
x_0=0
x0=0 时,
F
[
δ
(
x
)
]
=
1
\mathcal {F}[\delta (x)]=1
F[δ(x)]=1,代入傅里叶逆变换公式,可得:
δ
(
x
)
=
1
2
π
∫
−
∞
+
∞
e
i
ω
x
d
ω
\delta (x)=\frac {1}{2\pi}\int_{-\infty}^{+\infty} e^{i\omega x}\text {d}\omega
δ(x)=2π1∫−∞+∞eiωxdω
该式与上述定义完全等价,称为 δ 函数的傅里叶积分定义。
性质 II
2.0 辅助函数(初生 δ 函数)
定义 I 的特征启发我们:存在一类经典函数,其极限形式可过渡为 δ 函数,这类函数称为 δ 函数的辅助函数(或初生 δ 函数)。
设定义在 R \mathbb {R} R 上的函数族 { f α ( x ) } \{f_\alpha (x)\} {fα(x)}( α \alpha α 为参数)满足以下条件:
- f α ( x ) f_\alpha (x) fα(x) 的最大值在 x = 0 x=0 x=0 处取得,即 f α ( x ) max = f α ( 0 ) f_\alpha (x)_{\text {max}}=f_\alpha (0) fα(x)max=fα(0);
- 归一化条件: ∫ − ∞ + ∞ f α ( x ) d x = 1 \int_{-\infty}^{+\infty} f_\alpha (x)\text {d} x=1 ∫−∞+∞fα(x)dx=1;
- 极限性质: lim α → α 0 f α ( 0 ) = ∞ \lim_{\alpha\rightarrow\alpha_0} f_\alpha (0)=\infty limα→α0fα(0)=∞。
则 lim α → α 0 f α ( x ) = δ ( x ) \lim_{\alpha\rightarrow\alpha_0} f_\alpha (x)=\delta (x) limα→α0fα(x)=δ(x)(在分布意义下收敛)。以下为常见的辅助函数(证明略):
- 抽样函数:
V
α
(
x
)
=
sin
α
x
π
x
V_\alpha (x)=\frac {\sin\alpha x}{\pi x}
Vα(x)=πxsinαx
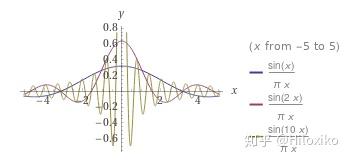
- 高斯核(热核):
G
α
(
x
)
=
1
π
α
e
−
x
2
α
G_\alpha (x)=\frac {1}{\sqrt {\pi\alpha}} e^{-\frac {x^2}{\alpha}}
Gα(x)=πα1e−αx2(由无限长细杆热传导问题导出)
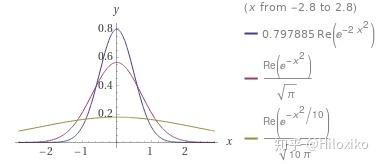
- 泊松核:
L
α
(
x
)
=
1
π
α
x
2
+
α
2
L_\alpha (x)=\frac {1}{\pi}\frac {\alpha}{x^2+\alpha^2}
Lα(x)=π1x2+α2α(由半平面拉普拉斯方程问题导出)
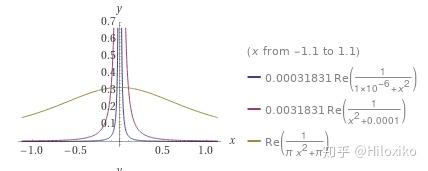
- 平方型抽样函数:
S
α
(
x
)
=
α
π
x
2
sin
2
(
x
α
)
S_\alpha (x)=\frac {\alpha}{\pi x^2}\sin^2\left (\frac {x}{\alpha}\right)
Sα(x)=πx2αsin2(αx)
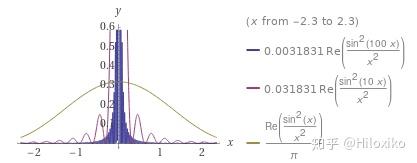
- 指数函数:
E
α
(
x
)
=
1
2
α
e
−
∣
x
∣
α
E_\alpha (x)=\frac {1}{2\alpha} e^{-\frac {|x|}{\alpha}}
Eα(x)=2α1e−α∣x∣
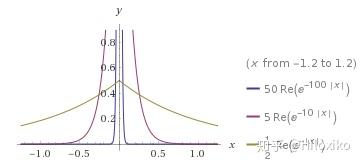
- 振荡函数:
I
α
(
x
)
=
α
π
e
i
π
4
e
−
i
α
x
2
I_\alpha (x)=\sqrt {\frac {\alpha}{\pi}} e^{i\frac {\pi}{4}} e^{-i\alpha x^2}
Iα(x)=παei4πe−iαx2(极限下逐点收敛于 δ 函数)
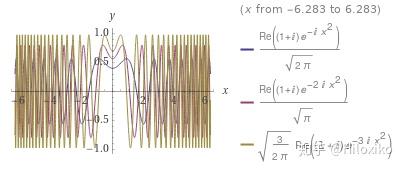
- 截断傅里叶积分: W α ( x ) = 1 2 π ∫ − α + α e i ω x d ω W_\alpha (x)=\frac {1}{2\pi}\int_{-\alpha}^{+\alpha} e^{i\omega x}\text {d}\omega Wα(x)=2π1∫−α+αeiωxdω(图略);
- 费耶核特例:
C
α
(
x
)
=
1
2
π
1
−
α
2
1
−
2
α
cos
x
+
α
2
C_\alpha (x)=\frac {1}{2\pi}\frac {1-\alpha^2}{1-2\alpha\cos x+\alpha^2}
Cα(x)=2π11−2αcosx+α21−α2(
α
∈
(
0
,
1
)
\alpha\in (0,1)
α∈(0,1),定义域为
[
−
π
,
π
]
[-\pi,\pi]
[−π,π],已归一化)
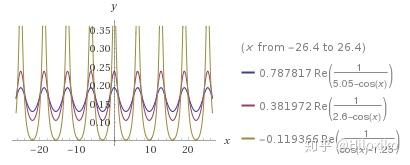
2.1 Dirichlet 核(δ 函数辅助函数的应用)
Dirichlet 核是 δ 函数的重要辅助函数,用于证明 Dirichlet 定理的充分性。
2.1.1 Dirichlet 核的定义
考虑求和 S m ( x ) = 1 + 2 ∑ n = 1 m cos n x S_m (x)=1+2\sum_{n=1}^m\cos nx Sm(x)=1+2∑n=1mcosnx,利用三角恒等式
sin x 2 cos n x = 1 2 [ sin ( n + 1 2 ) x − sin ( n − 1 2 ) x ] \sin\frac {x}{2}\cos nx=\frac {1}{2}\left [\sin\left (n+\frac {1}{2}\right) x-\sin\left (n-\frac {1}{2}\right) x\right] sin2xcosnx=21[sin(n+21)x−sin(n−21)x],
裂项求和得:
sin
x
2
S
m
(
x
)
=
1
2
[
sin
(
m
+
1
2
)
x
−
sin
x
2
]
\sin\frac {x}{2} S_m (x)=\frac {1}{2}\left [\sin\left (m+\frac {1}{2}\right) x-\sin\frac {x}{2}\right]
sin2xSm(x)=21[sin(m+21)x−sin2x]
因此
S
m
(
x
)
=
sin
(
m
+
1
2
)
x
sin
x
2
S_m (x)=\frac {\sin\left (m+\frac {1}{2}\right) x}{\sin\frac {x}{2}}
Sm(x)=sin2xsin(m+21)x
对
S
m
(
x
)
S_m (x)
Sm(x) 在
[
−
π
,
π
]
[-\pi,\pi]
[−π,π] 上积分,因余弦函数为偶函数,求和项积分均为 0,故
∫
−
π
π
sin
(
m
+
1
2
)
x
sin
x
2
d
x
=
2
π
\int_{-\pi}^{\pi}\frac {\sin\left (m+\frac {1}{2}\right) x}{\sin\frac {x}{2}}\text {d} x=2\pi
∫−ππsin2xsin(m+21)xdx=2π
定义归一化的 Dirichlet 核:
D
m
(
x
)
=
1
2
π
sin
(
m
+
1
2
)
x
sin
x
2
D_m (x)=\frac {1}{2\pi}\frac {\sin\left (m+\frac {1}{2}\right) x}{\sin\frac {x}{2}}
Dm(x)=2π1sin2xsin(m+21)x
其满足:
- 归一化条件: ∫ − π π D m ( x ) d x = 1 \int_{-\pi}^{\pi} D_m (x)\text {d} x=1 ∫−ππDm(x)dx=1;
- 极限性质: lim m → ∞ lim x → 0 D m ( x ) = lim m → ∞ 2 m + 1 2 π = ∞ \lim_{m\rightarrow\infty}\lim_{x\rightarrow0} D_m (x)=\lim_{m\rightarrow\infty}\frac {2m+1}{2\pi}=\infty limm→∞limx→0Dm(x)=limm→∞2π2m+1=∞。
因此 lim m → ∞ D m ( x ) = δ ( x ) \lim_{m\rightarrow\infty} D_m (x)=\delta (x) limm→∞Dm(x)=δ(x)( x ∈ [ − π , π ] x\in [-\pi,\pi] x∈[−π,π],分布意义下收敛)。
2.1.2 Dirichlet 倍核
定义 Dirichlet 倍核:
B
m
(
x
)
=
2
D
m
(
x
)
(
x
∈
[
0
,
π
]
)
B_m (x)=2D_m (x)\quad (x\in [0,\pi])
Bm(x)=2Dm(x)(x∈[0,π])
其在非对称区间
[
0
,
π
]
[0,\pi]
[0,π] 上满足归一化条件,极限形式同样为 δ 函数。
2.1.3 Dirichlet 定理的充分性证明
在傅里叶分析中,Dirichlet 定理表述为:
若函数 f ( x ) f (x) f(x) 满足:
- 在 ( − π , π ) (-\pi,\pi) (−π,π) 内除有限点外有定义且单值;
- 在 ( − π , π ) (-\pi,\pi) (−π,π) 外为周期 2 π 2\pi 2π 的周期函数;
- 在 ( − π , π ) (-\pi,\pi) (−π,π) 内分段光滑(即 f ( x ) f (x) f(x) 及其一阶导数 f ′ ( x ) f'(x) f′(x) 分段连续),
则 f ( x ) f (x) f(x) 的傅里叶级数 a 0 + ∑ n = 1 ∞ ( a n cos n x + b n sin n x ) a_0+\sum_{n=1}^{\infty}(a_n\cos nx+b_n\sin nx) a0+∑n=1∞(ancosnx+bnsinnx) 收敛于:
- f ( x ) f (x) f(x)(若 x x x 为连续点);
- f ( x − 0 ) + f ( x + 0 ) 2 \frac {f (x-0)+f (x+0)}{2} 2f(x−0)+f(x+0)(若 x x x 为第一类间断点, f ( x ± 0 ) f (x\pm0) f(x±0) 分别为左右极限)。
在傅里叶级数的研究中,必须分析其在连续点和第一类间断点的收敛性,因为这些点满足 Dirichlet 条件。一种有效的方法是将级数表示为部分和的形式进行计算,然后将求和上限的参数取极限趋近于无穷大。这一极限过程可以理解为积分内辅助函数向 Dirac δ 函数的过渡。
[证]:考虑傅里叶级数的部分和
F
m
(
x
)
=
a
0
+
∑
n
=
1
m
(
a
n
cos
n
x
+
b
n
sin
n
x
)
F_m (x)=a_0+\sum_{n=1}^m (a_n\cos nx+b_n\sin nx)
Fm(x)=a0+n=1∑m(ancosnx+bnsinnx)
其中傅里叶系数为:
a
0
=
1
2
π
∫
−
π
π
f
(
t
)
d
t
,
a
n
=
1
π
∫
−
π
π
f
(
t
)
cos
n
t
d
t
,
b
n
=
1
π
∫
−
π
π
f
(
t
)
sin
n
t
d
t
a_0=\frac {1}{2\pi}\int_{-\pi}^{\pi} f (t)\text {d} t,\quad a_n=\frac {1}{\pi}\int_{-\pi}^{\pi} f (t)\cos nt\text {d} t,\quad b_n=\frac {1}{\pi}\int_{-\pi}^{\pi} f (t)\sin nt\text {d} t
a0=2π1∫−ππf(t)dt,an=π1∫−ππf(t)cosntdt,bn=π1∫−ππf(t)sinntdt
将系数代入部分和,利用和角公式
cos
n
t
cos
n
x
+
sin
n
t
sin
n
x
=
cos
[
n
(
x
−
t
)
]
\cos nt\cos nx+\sin nt\sin nx=\cos [n (x-t)]
cosntcosnx+sinntsinnx=cos[n(x−t)],得
F m ( x ) = 1 2 π ∫ − π π f ( t ) d t + 1 π ∑ n = 1 m ∫ − π π f ( t ) ( cos n t cos n x + sin n t sin n x ) d t = 1 2 π ∫ − π π f ( t ) [ 1 + 2 ∑ n = 1 m cos n ( x − t ) ] d t = ∫ − π π f ( t ) D m ( x − t ) d t \begin{aligned} F_m(x) &= \frac{1}{2\pi}\int_{-\pi}^{\pi} f(t)\text{d}t + \frac{1}{\pi}\sum_{n=1}^m \int_{-\pi}^{\pi} f(t)\left(\cos nt \cos nx + \sin nt \sin nx\right)\text{d}t \\ &= \frac{1}{2\pi}\int_{-\pi}^{\pi} f(t)\left[1 + 2\sum_{n=1}^m \cos n(x-t)\right]\text{d}t \\ &= \int_{-\pi}^{\pi} f(t)D_m(x-t)\text{d}t \end{aligned} Fm(x)=2π1∫−ππf(t)dt+π1n=1∑m∫−ππf(t)(cosntcosnx+sinntsinnx)dt=2π1∫−ππf(t)[1+2n=1∑mcosn(x−t)]dt=∫−ππf(t)Dm(x−t)dt
- 连续点情形:
当 x x x 为连续点时, m → ∞ m\rightarrow\infty m→∞ 时 D m ( x − t ) D_m (x-t) Dm(x−t) 收敛于 δ ( x − t ) \delta (x-t) δ(x−t),故
lim m → ∞ F m ( x ) = lim m → ∞ ∫ − π π f ( t ) D m ( x − t ) d t = ∫ − π π f ( t ) δ ( x − t ) d t = f ( x ) \begin{aligned} \lim_{m \to \infty} F_m(x) &= \lim_{m \to \infty} \int_{-\pi}^{\pi} f(t) D_m(x - t) \, dt \\ &= \int_{-\pi}^{\pi} f(t) \delta(x - t) \, dt \\ &= f(x) \end{aligned} m→∞limFm(x)=m→∞lim∫−ππf(t)Dm(x−t)dt=∫−ππf(t)δ(x−t)dt=f(x)
-
第一类间断点情形:
利用 Dirichlet 核的偶性( D m ( t ) = D m ( − t ) D_m(t) = D_m(-t) Dm(t)=Dm(−t)),对积分区间拆分并做变量替换 t → x ± t t \to x \pm t t→x±t,结合 Dirichlet 倍核 B m ( t ) = 2 D m ( t ) B_m(t)=2D_m(t) Bm(t)=2Dm(t),可得:
F m ( x ) = ∫ − π π f ( t ) D m ( x − t ) d t = 1 2 [ ∫ − π π f ( x − t ) D m ( t ) d t + ∫ − π π f ( x + t ) D m ( t ) d t ] = 1 2 [ ∫ 0 π f ( x − t ) B m ( t ) d t + ∫ 0 π f ( x + t ) B m ( t ) d t ] \begin{aligned} F_m(x) &= \int_{-\pi}^{\pi} f(t)D_m(x-t)\text{d}t \\ &= \frac{1}{2}\left[ \int_{-\pi}^{\pi} f(x-t)D_m(t)\text{d}t + \int_{-\pi}^{\pi} f(x+t)D_m(t)\text{d}t \right] \\ &= \frac{1}{2}\left[ \int_{0}^{\pi} f(x-t)B_m(t)\text{d}t + \int_{0}^{\pi} f(x+t)B_m(t)\text{d}t \right] \end{aligned} Fm(x)=∫−ππf(t)Dm(x−t)dt=21[∫−ππf(x−t)Dm(t)dt+∫−ππf(x+t)Dm(t)dt]=21[∫0πf(x−t)Bm(t)dt+∫0πf(x+t)Bm(t)dt]令 m → ∞ m \to \infty m→∞,Dirichlet 倍核 B m ( t ) B_m(t) Bm(t) 收敛于 δ ( t ) \delta(t) δ(t),因此:
lim m → ∞ F m ( x ) = 1 2 [ ∫ 0 π f ( x − t ) δ ( t ) d t + ∫ 0 π f ( x + t ) δ ( t ) d t ] = 1 2 [ f ( x − 0 ) + f ( x + 0 ) ] \begin{aligned} \lim_{m \to \infty} F_m(x) &= \frac{1}{2}\left[ \int_{0}^{\pi} f(x-t)\delta(t)\text{d}t + \int_{0}^{\pi} f(x+t)\delta(t)\text{d}t \right] \\ &= \frac{1}{2}\left[f(x-0) + f(x+0)\right] \end{aligned} m→∞limFm(x)=21[∫0πf(x−t)δ(t)dt+∫0πf(x+t)δ(t)dt]=21[f(x−0)+f(x+0)]综上, 证毕(Dirichlet 定理的充分性得证)。
2.2 δ 函数与连续谱本征函数
2.2.1 坐标算符的连续谱本征函数
坐标算符
x
^
\hat {x}
x^ 的本征方程为:
x
^
∣
x
′
⟩
=
x
′
∣
x
′
⟩
\hat {x}|x'\rangle=x'|x'\rangle
x^∣x′⟩=x′∣x′⟩
由性质 1.0 可知,
x
δ
(
x
)
=
0
x\delta(x)=0
xδ(x)=0,
δ
(
x
−
x
′
)
\delta (x-x')
δ(x−x′) 满足
(
x
−
x
′
)
δ
(
x
−
x
′
)
=
0
(x-x')\delta (x-x')=0
(x−x′)δ(x−x′)=0,故
δ
(
x
−
x
′
)
\delta (x-x')
δ(x−x′) 是坐标算符在坐标表象中的本征函数,其满足:
- 正交归一性: ⟨ x ′ ∣ x ′ ′ ⟩ = ∫ − ∞ + ∞ δ ( x − x ′ ) δ ( x − x ′ ′ ) d x = δ ( x ′ − x ′ ′ ) \langle x'|x''\rangle=\int_{-\infty}^{+\infty}\delta (x-x')\delta (x-x'')\text {d} x=\delta (x'-x'') ⟨x′∣x′′⟩=∫−∞+∞δ(x−x′)δ(x−x′′)dx=δ(x′−x′′);
- 完备性:任意连续函数可按本征函数集展开
f ( x ) = ∫ − ∞ + ∞ f ( x ′ ) δ ( x − x ′ ) d x ′ f (x)=\int_{-\infty}^{+\infty} f (x')\delta (x-x')\text {d} x' f(x)=∫−∞+∞f(x′)δ(x−x′)dx′
坐标表象中力学量的矩阵表示
在坐标表象下,力学量对应的矩阵元( ⟨ x ′ ∣ O ^ ∣ x ′ ′ ⟩ \langle x'|\hat {O}|x''\rangle ⟨x′∣O^∣x′′⟩)形式如下:
矩阵元直接由坐标算符的本征性质(
x
^
∣
x
′
′
⟩
=
x
′
′
∣
x
′
′
⟩
\hat {x}|x''\rangle = x''|x''\rangle
x^∣x′′⟩=x′′∣x′′⟩)结合 δ 函数的筛选性得:
⟨
x
′
∣
x
^
∣
x
′
′
⟩
=
x
′
δ
(
x
′
−
x
′
′
)
\langle x'|\hat {x}|x''\rangle = x'\delta (x' - x'')
⟨x′∣x^∣x′′⟩=x′δ(x′−x′′)
势能算符是坐标的函数(
V
^
=
V
(
x
)
\hat {V}=V (x)
V^=V(x)),同理由本征性质得:
⟨
x
′
∣
V
^
∣
x
′
′
⟩
=
V
(
x
′
)
δ
(
x
′
−
x
′
′
)
\langle x'|\hat {V}|x''\rangle = V (x')\delta (x' - x'')
⟨x′∣V^∣x′′⟩=V(x′)δ(x′−x′′)
(其中
V
(
x
)
V (x)
V(x) 为势能函数)
推导过程:利用表象变换(插入动量本征态完备集
∬
d
p
′
d
p
′
′
∣
p
′
⟩
⟨
p
′
∣
⊗
∣
p
′
′
⟩
⟨
p
′
′
∣
\iint dp'dp'' |p'\rangle\langle p'| \otimes |p''\rangle\langle p''|
∬dp′dp′′∣p′⟩⟨p′∣⊗∣p′′⟩⟨p′′∣),结合坐标 - 动量表象变换关系
⟨
x
∣
p
⟩
=
1
2
π
ℏ
e
i
p
x
ℏ
\langle x|p\rangle = \frac {1}{\sqrt {2\pi\hbar}} e^{\frac {ipx}{\hbar}}
⟨x∣p⟩=2πℏ1eℏipx,及动量算符的本征方程
⟨
p
′
∣
p
^
∣
p
′
′
⟩
=
p
′
δ
(
p
′
−
p
′
′
)
\langle p'|\hat {p}|p''\rangle = p'\delta (p' - p'')
⟨p′∣p^∣p′′⟩=p′δ(p′−p′′),展开得:
⟨
x
′
∣
p
^
∣
x
′
′
⟩
=
∬
d
p
′
d
p
′
′
⟨
x
′
∣
p
′
⟩
⟨
p
′
∣
p
^
∣
p
′
′
⟩
⟨
p
′
′
∣
x
′
′
⟩
=
∬
d
p
′
d
p
′
′
⋅
1
2
π
ℏ
e
i
p
′
x
′
ℏ
⋅
p
′
δ
(
p
′
−
p
′
′
)
⋅
1
2
π
ℏ
e
−
i
p
′
′
x
′
′
ℏ
=
1
2
π
ℏ
∫
d
p
′
p
′
e
i
p
′
(
x
′
−
x
′
′
)
ℏ
\begin {aligned} \langle x'|\hat {p}|x''\rangle &= \iint dp'dp'' \langle x'|p'\rangle \langle p'|\hat {p}|p''\rangle \langle p''|x''\rangle \\ &= \iint dp'dp'' \cdot \frac {1}{\sqrt {2\pi\hbar}} e^{\frac {ip'x'}{\hbar}} \cdot p'\delta (p' - p'') \cdot \frac {1}{\sqrt {2\pi\hbar}} e^{\frac {-ip''x''}{\hbar}} \\ &= \frac {1}{2\pi\hbar} \int dp' \, p' e^{\frac {ip'(x' - x'')}{\hbar}} \end {aligned}
⟨x′∣p^∣x′′⟩=∬dp′dp′′⟨x′∣p′⟩⟨p′∣p^∣p′′⟩⟨p′′∣x′′⟩=∬dp′dp′′⋅2πℏ1eℏip′x′⋅p′δ(p′−p′′)⋅2πℏ1eℏ−ip′′x′′=2πℏ1∫dp′p′eℏip′(x′−x′′)
将动量
p
′
p'
p′ 替换为微分算符
p
′
=
−
i
ℏ
∂
∂
x
′
p' = -i\hbar\frac {\partial}{\partial x'}
p′=−iℏ∂x′∂(作用于指数项),再利用积分
∫
d
p
′
e
i
p
′
(
x
′
−
x
′
′
)
ℏ
=
2
π
ℏ
δ
(
x
′
−
x
′
′
)
\int dp' e^{\frac {ip'(x' - x'')}{\hbar}} = 2\pi\hbar\delta (x' - x'')
∫dp′eℏip′(x′−x′′)=2πℏδ(x′−x′′),最终得:
⟨
x
′
∣
p
^
∣
x
′
′
⟩
=
−
i
ℏ
∂
∂
x
′
δ
(
x
′
−
x
′
′
)
\langle x'|\hat {p}|x''\rangle = -i\hbar\frac {\partial}{\partial x'}\delta (x' - x'')
⟨x′∣p^∣x′′⟩=−iℏ∂x′∂δ(x′−x′′)
2.2.2 动量算符的连续谱本征函数
动量算符
p
^
\hat {p}
p^ 的本征方程为:
p
^
∣
p
′
⟩
=
p
′
∣
p
′
⟩
\hat {p}|p'\rangle=p'|p'\rangle
p^∣p′⟩=p′∣p′⟩
其本征函数在坐标表象中为
ψ
p
′
(
x
)
=
c
e
i
p
′
x
ℏ
\psi_{p'}(x)=ce^{\frac {ip'x}{\hbar}}
ψp′(x)=ceℏip′x,由正交归一性
⟨
p
′
∣
p
′
′
⟩
=
δ
(
p
′
−
p
′
′
)
\langle p'|p''\rangle=\delta (p'-p'')
⟨p′∣p′′⟩=δ(p′−p′′) 可确定归一化常数
c
=
1
2
π
ℏ
c=\frac {1}{\sqrt {2\pi\hbar}}
c=2πℏ1,即
ψ
p
′
(
x
)
=
1
2
π
ℏ
e
i
p
′
x
ℏ
\psi_{p'}(x)=\frac {1}{\sqrt {2\pi\hbar}} e^{\frac {ip'x}{\hbar}}
ψp′(x)=2πℏ1eℏip′x
动量本征函数满足完备性,任意连续函数的傅里叶变换可表示为:
f
(
x
)
=
∫
−
∞
+
∞
⟨
x
∣
p
′
⟩
⟨
p
′
∣
f
⟩
d
p
′
=
1
2
π
ℏ
∫
−
∞
+
∞
F
(
p
′
)
e
i
p
′
x
ℏ
d
p
′
f (x)=\int_{-\infty}^{+\infty}\langle x|p'\rangle\langle p'|f\rangle\text {d} p'=\frac {1}{\sqrt {2\pi\hbar}}\int_{-\infty}^{+\infty} F (p') e^{\frac {ip'x}{\hbar}}\text {d} p'
f(x)=∫−∞+∞⟨x∣p′⟩⟨p′∣f⟩dp′=2πℏ1∫−∞+∞F(p′)eℏip′xdp′
其中
F
(
p
′
)
=
⟨
p
′
∣
f
⟩
F (p')=\langle p'|f\rangle
F(p′)=⟨p′∣f⟩ 为
f
(
x
)
f (x)
f(x) 的傅里叶变换。δ 函数的展开式为:
δ
(
x
)
=
1
2
π
ℏ
∫
−
∞
+
∞
ψ
p
′
(
x
)
d
p
′
\delta (x)=\frac {1}{\sqrt {2\pi\hbar}}\int_{-\infty}^{+\infty}\psi_{p'}(x)\text {d} p'
δ(x)=2πℏ1∫−∞+∞ψp′(x)dp′
动量表象中力学量的矩阵表示可通过坐标表象变换得到,关键是将坐标替换为 i ℏ ∂ ∂ p ′ i\hbar\frac {\partial}{\partial p'} iℏ∂p′∂,δ 函数内的变量替换为动量。
定义 III(阶梯函数导数定义)
δ 函数可定义为阶梯函数的导数。阶梯函数(海维赛德函数)的定义为:
θ
(
x
)
=
{
1
x
>
0
0
x
<
0
\theta (x)= \begin {cases} 1 & x>0 \\ 0 & x<0 \end {cases}
θ(x)={10x>0x<0
其中
θ
(
0
)
\theta (0)
θ(0) 通常定义为
1
2
\frac {1}{2}
21(广义函数意义下不影响积分结果)。
[证]:对任意连续可微函数
f
(
x
)
f (x)
f(x),考虑积分
∫
−
∞
+
∞
f
(
x
)
θ
′
(
x
)
d
x
\int_{-\infty}^{+\infty} f (x)\theta'(x)\text {d} x
∫−∞+∞f(x)θ′(x)dx
分部积分得
∫
−
∞
+
∞
f
(
x
)
θ
′
(
x
)
d
x
=
f
(
x
)
θ
(
x
)
∣
−
∞
+
∞
−
∫
−
∞
+
∞
θ
(
x
)
f
′
(
x
)
d
x
\int_{-\infty}^{+\infty} f (x)\theta'(x)\text {d} x=f (x)\theta (x)\bigg|_{-\infty}^{+\infty}-\int_{-\infty}^{+\infty}\theta (x) f'(x)\text {d} x
∫−∞+∞f(x)θ′(x)dx=f(x)θ(x)
−∞+∞−∫−∞+∞θ(x)f′(x)dx
因
f
(
x
)
f (x)
f(x) 快速衰减(广义函数意义下),
f
(
∞
)
θ
(
∞
)
−
f
(
−
∞
)
θ
(
−
∞
)
=
0
f (\infty)\theta (\infty)-f (-\infty)\theta (-\infty)=0
f(∞)θ(∞)−f(−∞)θ(−∞)=0,且
θ
(
x
)
\theta (x)
θ(x) 在
x
<
0
x<0
x<0 时为 0,故
∫
−
∞
+
∞
f
(
x
)
θ
′
(
x
)
d
x
=
−
∫
0
+
∞
f
′
(
x
)
d
x
=
f
(
0
)
\int_{-\infty}^{+\infty} f (x)\theta'(x)\text {d} x=-\int_{0}^{+\infty} f'(x)\text {d} x=f (0)
∫−∞+∞f(x)θ′(x)dx=−∫0+∞f′(x)dx=f(0)
又
∫
−
∞
+
∞
f
(
x
)
δ
(
x
)
d
x
=
f
(
0
)
\int_{-\infty}^{+\infty} f (x)\delta (x)\text {d} x=f (0)
∫−∞+∞f(x)δ(x)dx=f(0),且
f
(
x
)
f (x)
f(x) 任意,故
θ
′
(
x
)
=
δ
(
x
)
\theta'(x)=\delta (x)
θ′(x)=δ(x)。
广义而言,任意非连续函数在间断点处的导数(分布意义下)均包含 δ 函数项。
性质 III
3.0 热统中的态密度应用
在统计物理中,δ 函数用于将离散的能级求和转化为连续的积分。宏观无穷小量
d
E
\text {d} E
dE 包含大量微观能级,引入态密度
D
(
ε
)
D (\varepsilon)
D(ε) 描述单位能量区间内的状态数,其定义为:
D
(
ε
)
d
ε
=
∫
ε
≤
H
<
ε
+
d
ε
d
p
d
r
h
3
D (\varepsilon)\text {d}\varepsilon=\int_{\varepsilon\leq H<\varepsilon+\text {d}\varepsilon}\frac {\text {d}\bold {p}\text {d}\bold {r}}{h^3}
D(ε)dε=∫ε≤H<ε+dεh3dpdr
其中
H
H
H 为哈密顿量,
d
p
d
r
h
3
\frac {\text {d}\bold {p}\text {d}\bold {r}}{h^3}
h3dpdr 为相空间的状态数密度。
利用阶梯函数的导数定义,态密度可改写为:
D
(
ε
)
d
ε
=
∫
[
θ
(
ε
+
d
ε
−
H
)
−
θ
(
ε
−
H
)
]
d
p
d
r
h
3
=
∫
δ
(
ε
−
H
)
d
ε
d
p
d
r
h
3
D (\varepsilon)\text {d}\varepsilon=\int\left [\theta (\varepsilon+\text {d}\varepsilon-H)-\theta (\varepsilon-H)\right]\frac {\text {d}\bold {p}\text {d}\bold {r}}{h^3}=\int\delta (\varepsilon-H)\text {d}\varepsilon\frac {\text {d}\bold {p}\text {d}\bold {r}}{h^3}
D(ε)dε=∫[θ(ε+dε−H)−θ(ε−H)]h3dpdr=∫δ(ε−H)dεh3dpdr
因此
D
(
ε
)
=
∫
δ
(
ε
−
H
)
d
p
d
r
h
3
D (\varepsilon)=\int\delta (\varepsilon-H)\frac {\text {d}\bold {p}\text {d}\bold {r}}{h^3}
D(ε)=∫δ(ε−H)h3dpdr
示例 1:经典非相对论粒子( H = p 2 2 m H=\frac {p^2}{2m} H=2mp2)
单粒子态密度为:
D
(
E
)
=
1
h
3
∫
δ
(
E
−
p
2
2
m
)
d
p
d
r
=
V
h
3
∫
δ
(
E
−
p
2
2
m
)
4
π
p
2
d
p
D (E)=\frac {1}{h^3}\int\delta\left (E-\frac {p^2}{2m}\right)\text {d}\bold {p}\text {d}\bold {r}=\frac {V}{h^3}\int\delta\left (E-\frac {p^2}{2m}\right) 4\pi p^2\text {d} p
D(E)=h31∫δ(E−2mp2)dpdr=h3V∫δ(E−2mp2)4πp2dp
令
t
=
p
2
2
m
t=\frac {p^2}{2m}
t=2mp2,则
p
=
2
m
t
p=\sqrt {2m t}
p=2mt,
d
p
=
2
m
2
t
d
t
\text {d} p=\frac {\sqrt {2m}}{2\sqrt {t}}\text {d} t
dp=2t2mdt,代入得
D
(
E
)
=
4
π
V
h
3
2
m
∫
δ
(
E
−
t
)
t
d
t
=
4
π
V
(
2
m
)
3
2
2
h
3
E
D (E)=\frac {4\pi V}{h^3}\sqrt {2m}\int\delta (E-t)\sqrt {t}\text {d} t=\frac {4\pi V (2m)^{\frac {3}{2}}}{2h^3}\sqrt {E}
D(E)=h34πV2m∫δ(E−t)tdt=2h34πV(2m)23E
多粒子系统(
N
N
N 个全同粒子)的态密度为:
D
(
E
)
=
V
N
(
2
m
)
3
N
2
k
3
N
2
N
!
h
3
N
E
3
N
2
−
1
D (E)=\frac {V^N (2m)^{\frac {3N}{2}} k_{3N}}{2N!h^{3N}} E^{\frac {3N}{2}-1}
D(E)=2N!h3NVN(2m)23Nk3NE23N−1
其中
k
n
=
2
π
n
2
Γ
(
n
2
)
k_n=\frac {2\pi^{\frac {n}{2}}}{\Gamma\left (\frac {n}{2}\right)}
kn=Γ(2n)2π2n 为
n
n
n 维球面积分系数。
3.1 复合 δ 函数
若函数
ψ
(
x
)
\psi (x)
ψ(x) 仅有单根
x
i
x_i
xi(即
ψ
(
x
i
)
=
0
\psi (x_i)=0
ψ(xi)=0 且
ψ
′
(
x
i
)
≠
0
\psi'(x_i)\ne0
ψ′(xi)=0),则
δ
[
ψ
(
x
)
]
=
∑
i
δ
(
x
−
x
i
)
∣
ψ
′
(
x
i
)
∣
\delta [\psi (x)]=\sum_i\frac {\delta (x-x_i)}{|\psi'(x_i)|}
δ[ψ(x)]=i∑∣ψ′(xi)∣δ(x−xi)
[证]:因
δ
[
ψ
(
x
)
]
\delta [\psi (x)]
δ[ψ(x)] 仅在
ψ
(
x
)
=
0
\psi (x)=0
ψ(x)=0 处非零,可设
δ
[
ψ
(
x
)
]
=
∑
i
a
i
δ
(
x
−
x
i
)
\delta [\psi (x)]=\sum_i a_i\delta (x-x_i)
δ[ψ(x)]=∑iaiδ(x−xi)。对任意连续函数
f
(
x
)
f (x)
f(x),考虑积分
∫
x
j
−
ε
x
j
+
ε
f
(
x
)
δ
[
ψ
(
x
)
]
d
x
=
a
j
f
(
x
j
)
\int_{x_j-\varepsilon}^{x_j+\varepsilon} f (x)\delta [\psi (x)]\text {d} x=a_jf (x_j)
∫xj−εxj+εf(x)δ[ψ(x)]dx=ajf(xj)
令
t
=
ψ
(
x
)
t=\psi (x)
t=ψ(x),则
d
x
=
d
t
ψ
′
(
x
)
\text {d} x=\frac {\text {d} t}{\psi'(x)}
dx=ψ′(x)dt,当
ε
→
0
\varepsilon\rightarrow0
ε→0 时,
ψ
(
x
)
\psi (x)
ψ(x) 在
x
j
x_j
xj 附近单调,积分变为
∫
ψ
(
x
j
−
ε
)
ψ
(
x
j
+
ε
)
f
(
ψ
−
1
(
t
)
)
δ
(
t
)
⋅
d
t
∣
ψ
′
(
ψ
−
1
(
t
)
)
∣
=
f
(
x
j
)
⋅
1
∣
ψ
′
(
x
j
)
∣
\int_{\psi (x_j-\varepsilon)}^{\psi (x_j+\varepsilon)} f\left (\psi^{-1}(t)\right)\delta (t)\cdot\frac {\text {d} t}{|\psi'(\psi^{-1}(t))|}=f (x_j)\cdot\frac {1}{|\psi'(x_j)|}
∫ψ(xj−ε)ψ(xj+ε)f(ψ−1(t))δ(t)⋅∣ψ′(ψ−1(t))∣dt=f(xj)⋅∣ψ′(xj)∣1
故
a
j
=
1
∣
ψ
′
(
x
j
)
∣
a_j=\frac {1}{|\psi'(x_j)|}
aj=∣ψ′(xj)∣1,因此
δ
[
ψ
(
x
)
]
=
∑
i
δ
(
x
−
x
i
)
∣
ψ
′
(
x
i
)
∣
\delta [\psi (x)]=\sum_i\frac {\delta (x-x_i)}{|\psi'(x_i)|}
δ[ψ(x)]=∑i∣ψ′(xi)∣δ(x−xi)。
常见推论:
δ
(
x
2
−
a
2
)
=
1
2
∣
x
∣
[
δ
(
x
−
a
)
+
δ
(
x
+
a
)
]
(
a
≠
0
)
\delta (x^2-a^2)=\frac {1}{2|x|}\left [\delta (x-a)+\delta (x+a)\right]\quad (a\ne0)
δ(x2−a2)=2∣x∣1[δ(x−a)+δ(x+a)](a=0)
δ
(
sin
x
)
=
∑
k
∈
Z
δ
(
x
−
k
π
)
∣
cos
(
k
π
)
∣
=
∑
k
∈
Z
δ
(
x
−
k
π
)
\delta (\sin x)=\sum_{k\in\mathbb {Z}}\frac {\delta (x-k\pi)}{|\cos (k\pi)|}=\sum_{k\in\mathbb {Z}}\delta (x-k\pi)
δ(sinx)=k∈Z∑∣cos(kπ)∣δ(x−kπ)=k∈Z∑δ(x−kπ)
δ
(
cos
x
)
=
∑
k
∈
Z
δ
(
x
−
(
k
+
1
2
)
π
)
∣
sin
(
(
k
+
1
2
)
π
)
∣
=
∑
k
∈
Z
δ
(
x
−
(
k
+
1
2
)
π
)
\delta (\cos x)=\sum_{k\in\mathbb {Z}}\frac {\delta\left (x-\left (k+\frac {1}{2}\right)\pi\right)}{|\sin\left (\left (k+\frac {1}{2}\right)\pi\right)|}=\sum_{k\in\mathbb {Z}}\delta\left (x-\left (k+\frac {1}{2}\right)\pi\right)
δ(cosx)=k∈Z∑∣sin((k+21)π)∣δ(x−(k+21)π)=k∈Z∑δ(x−(k+21)π)
示例 2:非极端相对论粒子( H = p 2 c 2 + m 2 c 4 H=\sqrt {p^2c^2+m^2c^4} H=p2c2+m2c4)
单粒子态密度为:
D
(
E
)
=
1
h
3
∫
δ
(
E
−
p
2
c
2
+
m
2
c
4
)
d
p
d
r
=
V
h
3
∫
δ
(
E
−
p
2
c
2
+
m
2
c
4
)
4
π
p
2
d
p
D (E)=\frac {1}{h^3}\int\delta\left (E-\sqrt {p^2c^2+m^2c^4}\right)\text {d}\bold {p}\text {d}\bold {r}=\frac {V}{h^3}\int\delta\left (E-\sqrt {p^2c^2+m^2c^4}\right) 4\pi p^2\text {d} p
D(E)=h31∫δ(E−p2c2+m2c4)dpdr=h3V∫δ(E−p2c2+m2c4)4πp2dp
令
t
=
p
2
c
2
+
m
2
c
4
t=\sqrt {p^2c^2+m^2c^4}
t=p2c2+m2c4,则
t
2
=
p
2
c
2
+
m
2
c
4
t^2=p^2c^2+m^2c^4
t2=p2c2+m2c4,
2
t
d
t
=
2
p
c
2
d
p
2t\text {d} t=2pc^2\text {d} p
2tdt=2pc2dp,即
d
p
=
t
d
t
p
c
2
\text {d} p=\frac {t\text {d} t}{pc^2}
dp=pc2tdt,代入复合 δ 函数性质:
δ
(
E
−
t
)
=
1
∣
d
t
d
p
∣
δ
(
p
−
p
0
)
=
p
c
2
t
δ
(
p
−
p
0
)
\delta (E-t)=\frac {1}{|\frac {\text {d} t}{\text {d} p}|}\delta (p-p_0)=\frac {pc^2}{t}\delta (p-p_0)
δ(E−t)=∣dpdt∣1δ(p−p0)=tpc2δ(p−p0)
其中
p
0
=
E
2
−
m
2
c
4
c
p_0=\frac {\sqrt {E^2-m^2c^4}}{c}
p0=cE2−m2c4,
t
=
E
t=E
t=E,故
D
(
E
)
=
4
π
V
h
3
∫
p
2
⋅
p
c
2
E
δ
(
p
−
p
0
)
d
p
=
4
π
V
c
2
E
h
3
p
0
3
=
4
π
V
E
E
2
−
m
2
c
4
c
3
h
3
D (E)=\frac {4\pi V}{h^3}\int p^2\cdot\frac {pc^2}{E}\delta (p-p_0)\text {d} p=\frac {4\pi V c^2}{E h^3} p_0^3=\frac {4\pi V E\sqrt {E^2-m^2c^4}}{c^3h^3}
D(E)=h34πV∫p2⋅Epc2δ(p−p0)dp=Eh34πVc2p03=c3h34πVEE2−m2c4
定义 IV(分布 / 测度定义)
从广义函数(分布)理论出发,δ 函数的严格定义为:
4.1 分布意义下的定义
δ 函数是施瓦茨空间 S ( R n ) S (\mathbb {R}^n) S(Rn) 上的线性连续泛函,即 δ : S ( R n ) → C \delta:S (\mathbb {R}^n)\rightarrow\mathbb {C} δ:S(Rn)→C,满足:
- 线性性:对任意
ϕ
1
,
ϕ
2
∈
S
(
R
n
)
\phi_1,\phi_2\in S (\mathbb {R}^n)
ϕ1,ϕ2∈S(Rn) 及复数
λ
1
,
λ
2
\lambda_1,\lambda_2
λ1,λ2,有
δ ( λ 1 ϕ 1 + λ 2 ϕ 2 ) = λ 1 δ ( ϕ 1 ) + λ 2 δ ( ϕ 2 ) \delta (\lambda_1\phi_1+\lambda_2\phi_2)=\lambda_1\delta (\phi_1)+\lambda_2\delta (\phi_2) δ(λ1ϕ1+λ2ϕ2)=λ1δ(ϕ1)+λ2δ(ϕ2) - 连续性:若序列
{
ϕ
k
}
⊂
S
(
R
n
)
\{\phi_k\}\subset S (\mathbb {R}^n)
{ϕk}⊂S(Rn) 满足 “快速衰减” 和 “各阶导数快速衰减”(即对任意非负整数多重指标
α
,
β
\alpha,\beta
α,β,
sup
x
∈
R
n
∣
x
α
∂
β
ϕ
k
(
x
)
∣
→
0
\sup_{x\in\mathbb {R}^n}|x^\alpha\partial^\beta\phi_k (x)|\rightarrow0
supx∈Rn∣xα∂βϕk(x)∣→0),则
lim k → ∞ δ ( ϕ k ) = 0 \lim_{k\rightarrow\infty}\delta (\phi_k)=0 k→∞limδ(ϕk)=0
且该泛函的作用形式为:
⟨ δ x 0 , ϕ ⟩ = ϕ ( x 0 ) ∀ ϕ ∈ S ( R n ) \langle\delta_{x_0},\phi\rangle=\phi (x_0)\quad\forall\phi\in S (\mathbb {R}^n) ⟨δx0,ϕ⟩=ϕ(x0)∀ϕ∈S(Rn)
其中 δ x 0 \delta_{x_0} δx0 表示集中在点 x 0 x_0 x0 的 δ 函数,当 x 0 = 0 x_0=0 x0=0 时简记为 δ \delta δ,即 ⟨ δ , ϕ ⟩ = ϕ ( 0 ) \langle\delta,\phi\rangle=\phi (0) ⟨δ,ϕ⟩=ϕ(0)。
4.2 测度意义下的定义
从测度论角度,δ 函数是集中在点 x 0 x_0 x0 的狄拉克测度 μ x 0 \mu_{x_0} μx0,满足:
- 对任意波莱尔集
A
⊂
R
n
A\subset\mathbb {R}^n
A⊂Rn,有
μ x 0 ( A ) = { 1 x 0 ∈ A 0 x 0 ∉ A \mu_{x_0}(A)= \begin {cases} 1 & x_0\in A \\ 0 & x_0\notin A \end {cases} μx0(A)={10x0∈Ax0∈/A - 对任意非负可测函数
f
f
f 或积分绝对收敛的可测函数
f
f
f,有
∫ R n f ( x ) d μ x 0 ( x ) = f ( x 0 ) \int_{\mathbb {R}^n} f (x)\text {d}\mu_{x_0}(x)=f (x_0) ∫Rnf(x)dμx0(x)=f(x0)
分布定义与测度定义等价,均为 δ 函数的严格数学基础,避免了经典定义中 “无穷大” 的直观表述。
- Dirac delta function(狄拉克 δ 函数) | 定义、性质及物理意义…(篇 1)-优快云博客
https://blog.youkuaiyun.com/u013669912/article/details/151682410 - Dirac delta function(狄拉克 δ 函数) | …(篇 3)-优快云博客
https://blog.youkuaiyun.com/u013669912/article/details/155165765
via:
- [数学物理]- δ 函数 - 知乎 张稀桧 发布于 2020-08-04 10:54
https://zhuanlan.zhihu.com/p/166150375





















 2087
2087

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








