注:本文为 “数分 · 实分 | 求和与积分” 相关讨论合辑。
英文引文,机翻未校。
如有内容异常,请看原文。
When can a sum and integral be interchanged?
何时可以交换求和与积分的顺序?
When can we interchange the integral and summation in
我们何时可以交换下式中积分与求和的顺序:
∫ 0 ∞ ∑ n = 0 ∞ f n ( x ) d x \int_{0}^{\infty}\sum_{n=0}^{\infty}f_{n}(x)dx ∫0∞∑n=0∞fn(x)dx
with
f
n
(
x
)
f_{n}(x)
fn(x) being continuous functions.
其中
f
n
(
x
)
f_{n}(x)
fn(x) 为连续函数。
Is
f
n
(
x
)
≥
0
f_{n}(x)\geq0
fn(x)≥0 for all
x
x
x and for all
n
n
n sufficient? How about when
∑
f
n
(
x
)
\sum f_{n}(x)
∑fn(x) converges absolutely? If so why?
对所有
x
x
x 和所有
n
n
n 而言,
f
n
(
x
)
≥
0
f_{n}(x)\geq0
fn(x)≥0 是否为充分条件?当
∑
f
n
(
x
)
\sum f_{n}(x)
∑fn(x) 绝对收敛时又是否可行?若可行,原因是什么?
edited Aug 3 at 8:38
Starlight
asked Nov 19, 2011 at 19:08
user192837
I’m used to proving it capable with monotone convergence or the Lebesgue dominated convergence methods. But those are hardly sharp, I think. There are many versions of MC and LDC, so I don’t know which you know.
我习惯用单调收敛定理或勒贝格控制收敛定理来证明这种交换的可行性,但我认为这些定理的条件并非最优。单调收敛定理(MC)和勒贝格控制收敛定理(LDC)有多个版本,所以我不知道你了解的是哪一个版本。
– davidlowryduda♦
Commented Nov 19, 2011 at 19:21
Commented Oct 4, 2020 at 1:31
Answers
I like to remember this as a special case of the Fubini/Tonelli theorems, where the measures are counting measure on
N
\mathbb{N}
N and Lebesgue measure on
R
\mathbb{R}
R (or
[
0
,
∞
)
[0,\infty)
[0,∞) as you’ve written it here). In particular, Tonelli’s theorem says if
f
n
(
x
)
≥
0
f_{n}(x)\geq0
fn(x)≥0 for all
n
,
x
n,x
n,x, then
我倾向于将其视为 富比尼/托内利定理 的一个特例,其中测度分别为
N
\mathbb{N}
N(自然数集)上的计数测度和
R
\mathbb{R}
R(实数集)上的勒贝格测度(或你此处所写的
[
0
,
∞
)
[0,\infty)
[0,∞) 区间上的勒贝格测度)。具体而言,托内利定理指出,若对所有
n
,
x
n,x
n,x 都有
f
n
(
x
)
≥
0
f_{n}(x)\geq0
fn(x)≥0,则有:
∑ ∫ f n ( x ) d x = ∫ ∑ f n ( x ) d x \sum\int f_{n}(x)dx=\int\sum f_{n}(x)dx ∑∫fn(x)dx=∫∑fn(x)dx
without any further conditions needed. (You can also prove this with the monotone convergence theorem.)
且无需其他额外条件。(也可通过单调收敛定理证明该结论。)
Then Fubini’s theorem says that for general
f
n
f_{n}
fn, if
∫
∑
∣
f
n
∣
<
∞
\int\sum|f_{n}|<\infty
∫∑∣fn∣<∞ or
∑
∫
∣
f
n
∣
<
∞
\sum\int|f_{n}|<\infty
∑∫∣fn∣<∞ (by Tonelli the two conditions are equivalent), then
∫
∑
f
n
=
∑
∫
f
n
\int\sum f_{n}=\sum\int f_{n}
∫∑fn=∑∫fn. (You can also prove this with the dominated convergence theorem.)
而富比尼定理则表明,对于一般的
f
n
f_{n}
fn,若
∫
∑
∣
f
n
∣
<
∞
\int\sum|f_{n}|<\infty
∫∑∣fn∣<∞ 或
∑
∫
∣
f
n
∣
<
∞
\sum\int|f_{n}|<\infty
∑∫∣fn∣<∞(由托内利定理可知这两个条件等价),则有
∫
∑
f
n
=
∑
∫
f
n
\int\sum f_{n}=\sum\int f_{n}
∫∑fn=∑∫fn。(也可通过勒贝格控制收敛定理证明该结论。)
There may be weaker conditions that would also suffice, but these tend to work in 99% of cases.
或许存在更弱的充分条件,但上述两个定理的条件在 99% 的场景下均适用。
Elaborating on request: the usual statement of Fubini’s theorem goes something like this:
应要求补充说明:富比尼定理的常见表述如下:
Let ( X , F , μ ) , ( Y , G , ν ) (X,\mathcal{F},\mu),(Y,\mathcal{G},\nu) (X,F,μ),(Y,G,ν) be σ \sigma σ-finite measure spaces, and let g : X × Y → R g:X\times Y\rightarrow\mathbb{R} g:X×Y→R be measurable with respect to the product σ \sigma σ-algebra F ⊗ G \mathcal{F}\otimes\mathcal{G} F⊗G. Suppose that ∫ X ∫ Y ∣ g ( x , y ) ∣ ν ( d y ) μ ( d x ) \int_{X}\int_{Y}|g(x,y)|\nu(dy)\mu(dx) ∫X∫Y∣g(x,y)∣ν(dy)μ(dx) is finite. (Note: By Tonelli’s theorem, this happens if and only if ∫ Y ∫ X ∣ g ( x , y ) ∣ μ ( d x ) ν ( d y ) \int_{Y}\int_{X}|g(x,y)|\mu(dx)\nu(dy) ∫Y∫X∣g(x,y)∣μ(dx)ν(dy) is finite, since both iterated integrals are equal.) Then
设 ( X , F , μ ) (X,\mathcal{F},\mu) (X,F,μ)、 ( Y , G , ν ) (Y,\mathcal{G},\nu) (Y,G,ν) 为 σ \sigma σ-有限测度空间, g : X × Y → R g:X\times Y\rightarrow\mathbb{R} g:X×Y→R 关于乘积 σ \sigma σ-代数 F ⊗ G \mathcal{F}\otimes\mathcal{G} F⊗G 可测。若 ∫ X ∫ Y ∣ g ( x , y ) ∣ ν ( d y ) μ ( d x ) \int_{X}\int_{Y}|g(x,y)|\nu(dy)\mu(dx) ∫X∫Y∣g(x,y)∣ν(dy)μ(dx) 有限(注:由托内利定理可知,此条件等价于 ∫ Y ∫ X ∣ g ( x , y ) ∣ μ ( d x ) ν ( d y ) \int_{Y}\int_{X}|g(x,y)|\mu(dx)\nu(dy) ∫Y∫X∣g(x,y)∣μ(dx)ν(dy) 有限,因为这两个累次积分相等),则有:
∫ X ∫ Y g ( x , y ) ν ( d y ) μ ( d x ) = ∫ Y ∫ X g ( x , y ) μ ( d x ) ν ( d y ) \int_{X}\int_{Y}g(x,y)\nu(dy)\mu(dx)=\int_{Y}\int_{X}g(x,y)\mu(dx)\nu(dy) ∫X∫Yg(x,y)ν(dy)μ(dx)=∫Y∫Xg(x,y)μ(dx)ν(dy).
Let
X
=
R
X=\mathbb{R}
X=R,
F
\mathcal{F}
F the Borel
σ
\sigma
σ-algebra, and
μ
\mu
μ Lebesgue measure. Let
Y
=
N
Y=\mathbb{N}
Y=N,
G
=
2
N
\mathcal{G}=2^{\mathbb{N}}
G=2N the discrete
σ
\sigma
σ-algebra, and
ν
\nu
ν counting measure. Define
g
(
x
,
n
)
=
f
n
(
x
)
g(x,n)=f_{n}(x)
g(x,n)=fn(x). Exercise: since each
f
n
f_{n}
fn is measurable, verify that
g
g
g is measurable with respect to
F
⊗
G
\mathcal{F}\otimes\mathcal{G}
F⊗G. Exercise: verify that integration with respect to counting measure is the same as summation, where the integral exists and is finite iff the sum converges absolutely. (That is, given a sequence of real numbers
a
n
a_{n}
an, define a function
b
:
N
→
R
b:\mathbb{N}\rightarrow\mathbb{R}
b:N→R by
b
(
n
)
=
a
n
b(n)=a_{n}
b(n)=an. Then
∫
N
b
d
ν
=
∑
n
=
1
∞
a
n
\int_{\mathbb{N}}b d\nu=\sum_{n=1}^{\infty}a_{n}
∫Nbdν=∑n=1∞an.)
设
X
=
R
X=\mathbb{R}
X=R,
F
\mathcal{F}
F 为博雷尔
σ
\sigma
σ-代数,
μ
\mu
μ 为勒贝格测度;设
Y
=
N
Y=\mathbb{N}
Y=N,
G
=
2
N
\mathcal{G}=2^{\mathbb{N}}
G=2N(
N
\mathbb{N}
N 的幂集)为离散
σ
\sigma
σ-代数,
ν
\nu
ν 为计数测度。定义
g
(
x
,
n
)
=
f
n
(
x
)
g(x,n)=f_{n}(x)
g(x,n)=fn(x)。练习:因每个
f
n
f_{n}
fn 均可测,验证
g
g
g 关于
F
⊗
G
\mathcal{F}\otimes\mathcal{G}
F⊗G 可测。练习:验证关于计数测度的积分与求和运算等价,且该积分存在且有限的充要条件是相应的级数绝对收敛。(即:给定实数列
a
n
a_{n}
an,定义函数
b
:
N
→
R
b:\mathbb{N}\rightarrow\mathbb{R}
b:N→R 满足
b
(
n
)
=
a
n
b(n)=a_{n}
b(n)=an,则有
∫
N
b
d
ν
=
∑
n
=
1
∞
a
n
\int_{\mathbb{N}}b d\nu=\sum_{n=1}^{\infty}a_{n}
∫Nbdν=∑n=1∞an。)
As such, the conclusion of Fubini’s theorem reduces to the statement that was to be proved.
由此,富比尼定理的结论即可简化为待证明的命题。
edited Dec 11, 2020 at 20:31
Michael Hardy
answered Nov 19, 2011 at 21:32
Nate Eldredge
I am a bit confused because first you say that
∑
∫
f
n
(
x
)
d
x
=
∫
∑
f
n
(
x
)
d
x
\sum\int f_{n}(x)dx=\int\sum f_{n}(x)dx
∑∫fn(x)dx=∫∑fn(x)dx holds if
f
n
(
x
)
≥
0
f_{n}(x)\geq0
fn(x)≥0 which implies that even if the double integral is not finite the equality does hold and then you quote the Fubini theorem which says that the two integrals are equal if the double integral is finite. I would be grateful if you could explain this to me? Its probably as very stupid question but it makes me very uncomfortable
我有点困惑:你先提到若
f
n
(
x
)
≥
0
f_{n}(x)\geq0
fn(x)≥0,则
∑
∫
f
n
(
x
)
d
x
=
∫
∑
f
n
(
x
)
d
x
\sum\int f_{n}(x)dx=\int\sum f_{n}(x)dx
∑∫fn(x)dx=∫∑fn(x)dx 成立,这意味着即便二重积分无限,该等式仍成立;但之后你又引用富比尼定理,称当二重积分有限时两个积分才相等。若你能为我解释这一点,我将十分感激。这可能是个很基础的问题,但确实让我感到困惑。
– user3503589
Commented Nov 5, 2014 at 9:24
Yes, that’s what I said - I’m not sure what part is confusing you? Notice that I did not say “if and only if”! The two theorems give two different hypotheses, each of which leads to the same conclusion. (And note carefully the appearance of the absolute value bars in the hypothesis of Fubini’s theorem.)
是的,我确实是这么说的——我不确定哪部分让你困惑?请注意我并未使用“当且仅当”!这两个定理给出了不同的前提条件,但每个条件都能推导出相同的结论。(同时请仔细留意富比尼定理前提条件中的绝对值符号。)
– Nate Eldredge
Commented Nov 5, 2014 at 14:48
@User31443: Are you looking for a reference for the usual general statement of Fubini’s theorem (Folland’s Real Analysis, for instance) or for how the general statement implies this special case? It is literally just the general case applied with Lebesgue measure and counting measure.
@User31443:你是在寻找富比尼定理常见一般表述的参考资料(例如福兰的《实分析》),还是想了解该一般表述如何推导出这个特例?实际上,只需将一般表述应用于勒贝格测度和计数测度,就能得到这个特例。
– Nate Eldredge
Commented Aug 15, 2017 at 20:38
@NateEldredge: I am looking for a reference for how the general statement implies the special case mentioned.
@NateEldredge:我正在寻找能说明一般表述如何推导出上述特例的参考资料。
– user389066
Commented Aug 15, 2017 at 20:42
@NateEldredge: I am unable to grasp how the general statement reduces to this special case if the measures are counting measure on
N
\mathbb{N}
N and Lebesgue measure in
R
\mathbb{R}
R. Can you please elaborate that?
@NateEldredge:我无法理解,当测度分别为
N
\mathbb{N}
N 上的计数测度和
R
\mathbb{R}
R 上的勒贝格测度时,一般表述如何简化为这个特例。你能详细说明一下吗?
– user389066
Commented Aug 15, 2017 at 20:47
This is a theorem that will work:
以下定理可解决该问题:
Theorem. If { f n } n \{f_{n}\}_{n} {fn}n is a positive sequence of integrable functions and f = ∑ n f n f=\sum_{n}f_{n} f=∑nfn then
定理:若 { f n } n \{f_{n}\}_{n} {fn}n 为正可积函数列,且 f = ∑ n f n f=\sum_{n}f_{n} f=∑nfn,则有:
∫ f = ∑ n ∫ f n \int f=\sum_{n}\int f_{n} ∫f=∑n∫fn.
Proof. Consider first two functions,
f
1
f_{1}
f1 and
f
2
f_{2}
f2. We can now find sequences
{
ϕ
j
}
j
\{\phi_{j}\}_{j}
{ϕj}j and
{
ψ
j
}
j
\{\psi_{j}\}_{j}
{ψj}j of (non-negative) simple functions by a basic theorem from measure theory that increase to
f
1
f_{1}
f1 and
f
2
f_{2}
f2 respectively. Obviously
ϕ
j
+
ψ
j
↑
f
1
+
f
2
\phi_{j}+\psi_{j}\uparrow f_{1}+f_{2}
ϕj+ψj↑f1+f2. We can do the same for any finite sum.
证明:首先考虑两个函数
f
1
f_{1}
f1 和
f
2
f_{2}
f2。根据测度论的一个基本定理,可找到(非负)简单函数列
{
ϕ
j
}
j
\{\phi_{j}\}_{j}
{ϕj}j 和
{
ψ
j
}
j
\{\psi_{j}\}_{j}
{ψj}j,它们分别单调递增至
f
1
f_{1}
f1 和
f
2
f_{2}
f2。显然有
ϕ
j
+
ψ
j
↑
f
1
+
f
2
\phi_{j}+\psi_{j}\uparrow f_{1}+f_{2}
ϕj+ψj↑f1+f2(
ϕ
j
+
ψ
j
\phi_{j}+\psi_{j}
ϕj+ψj 单调递增至
f
1
+
f
2
f_{1}+f_{2}
f1+f2)。对于任意有限项和,均可采用类似方法。
Note that
∫
∑
1
N
f
n
=
∑
1
N
∫
f
n
\int\sum_{1}^{N}f_{n}=\sum_{1}^{N}\int f_{n}
∫∑1Nfn=∑1N∫fn for any finite
N
N
N. Now using the monotone convergence theorem we get
注意,对任意有限的
N
N
N,有
∫
∑
1
N
f
n
=
∑
1
N
∫
f
n
\int\sum_{1}^{N}f_{n}=\sum_{1}^{N}\int f_{n}
∫∑1Nfn=∑1N∫fn。结合单调收敛定理,可得:
∑ ∫ f n = ∫ f \sum\int f_{n}=\int f ∑∫fn=∫f.
Note 1: If you’re talking about positive functions, absolute convergence is the same as normal convergence, as
∣
f
n
∣
=
f
n
|f_{n}|=f_{n}
∣fn∣=fn.
注 1:对于正函数,因
∣
f
n
∣
=
f
n
|f_{n}|=f_{n}
∣fn∣=fn,故绝对收敛与通常意义下的收敛一致。
Note 2: Continuous functions will be certainly integrable if they have compact support or tend to
0
0
0 fast enough as
x
→
±
∞
x\rightarrow\pm\infty
x→±∞.
注 2:连续函数若具有紧支集,或当
x
→
±
∞
x\rightarrow\pm\infty
x→±∞ 时趋于
0
0
0 的速度足够快,则该函数必定可积。
edited Jun 28, 2019 at 5:48
J. W. Tanner
answered Nov 19, 2011 at 19:24
user1120
@JonasTeuwen What does
ϕ
j
↑
f
1
\phi_{j}\uparrow f_{1}
ϕj↑f1 mean? I am not familiar with this notation.
@JonasTeuwen:
ϕ
j
↑
f
1
\phi_{j}\uparrow f_{1}
ϕj↑f1 是什么意思?我不熟悉这个符号。
– Noir
Commented Jun 17, 2018 at 17:30
It means that
{
ϕ
j
}
\{\phi_{j}\}
{ϕj} is a monotonically non-decreasing sequence of functions which converges to
f
1
f_{1}
f1 pointwise.
它表示
{
ϕ
j
}
\{\phi_{j}\}
{ϕj} 是一个单调非减函数列,且该函数列逐点收敛至
f
1
f_{1}
f1。
– Sean Haight
Commented Oct 31, 2018 at 15:40
Is this theorem called Beppo-Levi?
这个定理是不是叫做贝波-列维定理?
– AgentSmith
Commented Nov 5, 2018 at 12:21
you’re the man. that was the explanation i was looking for.
太感谢了,这正是我想要的解释。
– user2550228
Commented Jan 9, 2022 at 17:18
While most of the time I would use the Fubini/Tonelli conditions, the dominated convergence theorem is actually strictly stronger in this mixed sum/integral case, because it can take into account the order structure of the integers. An example (that I first worked up back in 2009_):
虽然大多数情况下我会使用富比尼/托内利定理的条件,但在这种求和与积分混合的情形中,控制收敛定理实际上更强,因为它能利用整数的序结构。以下是一个例子(我最早在 2009 年推导得出):
Consider the calculation
考虑如下计算:
ln 2 = ? ∫ 0 1 1 1 + x d x = ∫ 0 1 ∑ n = 0 ∞ ( − 1 ) n x n d x = ∑ n = 0 ∞ ∫ 0 1 ( − 1 ) n x n d x = 1 − 1 2 + 1 3 − 1 4 + ⋯ \ln 2 \stackrel{?}{=} \int_{0}^{1}\frac{1}{1+x}dx = \int_{0}^{1}\sum_{n=0}^{\infty}(-1)^n x^n dx = \sum_{n=0}^{\infty}\int_{0}^{1}(-1)^n x^n dx = 1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \cdots ln2=?∫011+x1dx=∫01∑n=0∞(−1)nxndx=∑n=0∞∫01(−1)nxndx=1−21+31−41+⋯
Fubini’s theorem isn’t strong enough to justify the interchange. If we put absolute values on the terms, it blows up to
∫
0
1
1
1
−
x
d
x
=
1
+
1
2
+
1
3
+
1
4
+
⋯
=
∞
\int_{0}^{1}\frac{1}{1 - x}dx = 1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \cdots = \infty
∫011−x1dx=1+21+31+41+⋯=∞.
富比尼定理的强度不足以证明此处交换顺序的合理性。若对各项取绝对值,积分会发散至无穷大,即
∫
0
1
1
1
−
x
d
x
=
1
+
1
2
+
1
3
+
1
4
+
⋯
=
∞
\int_{0}^{1}\frac{1}{1 - x}dx = 1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \cdots = \infty
∫011−x1dx=1+21+31+41+⋯=∞。
On the other hand, the dominated convergence theorem cares about the partial sums
∑
n
=
0
N
(
−
1
)
n
x
n
\sum_{n=0}^{N}(-1)^n x^n
∑n=0N(−1)nxn. By the alternating series estimate,
另一方面,控制收敛定理关注的是部分和
∑
n
=
0
N
(
−
1
)
n
x
n
\sum_{n=0}^{N}(-1)^n x^n
∑n=0N(−1)nxn。根据交错级数估计:
0 ≤ ∑ n = 0 N ( − 1 ) n x n ≤ 1 0 \leq \sum_{n=0}^{N}(-1)^n x^n \leq 1 0≤∑n=0N(−1)nxn≤1
for all
x
∈
[
0
,
1
]
x \in [0,1]
x∈[0,1].
1
1
1 is integrable on this interval, and the interchange
对所有
x
∈
[
0
,
1
]
x \in [0,1]
x∈[0,1] 均成立。
1
1
1 在该区间上可积,因此交换顺序:
∫ 0 1 ( lim N → ∞ ∑ n = 0 N ( − 1 ) n x n ) d x = lim N → ∞ ∫ 0 1 ∑ n = 0 N ( − 1 ) n x n d x \int_{0}^{1}\left(\lim_{N \to \infty}\sum_{n=0}^{N}(-1)^n x^n\right)dx = \lim_{N \to \infty}\int_{0}^{1}\sum_{n=0}^{N}(-1)^n x^n dx ∫01(limN→∞∑n=0N(−1)nxn)dx=limN→∞∫01∑n=0N(−1)nxndx
is justified, proving the result
1
−
1
2
+
1
3
−
1
4
+
⋯
=
ln
2
1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \cdots = \ln 2
1−21+31−41+⋯=ln2.
具有合理性,进而证明
1
−
1
2
+
1
3
−
1
4
+
⋯
=
ln
2
1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \cdots = \ln 2
1−21+31−41+⋯=ln2 这一结果。
This situation with the dominated convergence theorem being stronger than Fubini’s theorem can come up when we’ve got a reasonable bound on partial sums but not absolute convergence as a whole.
The monotone convergence theorem, on the other hand, is exactly the same as Tonelli’s theorem - when everything’s positive, either both sides are the same and finite or both sides are infinite.
当部分和存在合理上界,但整体不满足绝对收敛时,就会出现控制收敛定理强于富比尼定理的情况。
另一方面,单调收敛定理与托内利定理完全等价——当所有项均为正时,要么等式两边相等且有限,要么两边均为无穷大。
edited Jun 28, 2019 at 5:50
J. W. Tanner
answered Dec 30, 2018 at 11:19
jmerry
- How do you apply DCT when x = 1 x=1 x=1? The integrand on the left hand side ( lim N → ∞ ∑ n = 0 N ( − 1 ) n x n ) \left(\lim_{N \to \infty}\sum_{n=0}^{N}(-1)^n x^n\right) (limN→∞∑n=0N(−1)nxn) isn’t defined at x = 1 x=1 x=1
当 x = 1 x=1 x=1 时,如何应用控制收敛定理(DCT)?左侧被积函数 ( lim N → ∞ ∑ n = 0 N ( − 1 ) n x n ) \left(\lim_{N \to \infty}\sum_{n=0}^{N}(-1)^n x^n\right) (limN→∞∑n=0N(−1)nxn) 在 x = 1 x=1 x=1 处无定义。
– alphacapture
Commented May 31, 2022 at 11:20
@alphacapture That is just a single point, which can be ignored with Lebesgue integral.
@alphacapture:这只是一个单点,在勒贝格积分中可忽略不计。
– Kangyeon Moon
Commented Nov 26, 2022 at 5:09
Why do people interchange between ∫ \int ∫ and ∑ \sum ∑ so easily?
为何能轻松交换 ∫ \int ∫ 与 ∑ \sum ∑ 的顺序?
One of the things I found curious in many texts is how in certain cases interchange the
∑
\sum
∑ operator with
∫
\int
∫. What are the “terms” for such a swap? I understand that integration in the early days was seen as an approximation of the area under the curve by using the very definition of multiplication and area to lend a hand with very small increments where the number of samples goes to infinity.
在许多文献中,我发现一个有趣的现象:在某些情况下,人们会直接交换
∑
\sum
∑ 与
∫
\int
∫ 的运算顺序。这种交换的“条件”是什么?我知道,在早期微积分中,积分被视为曲线下面积的近似——通过乘法和面积的定义,对无穷多个微小增量求和,以此近似面积。
Beyond the original question, is this also the reason why we keep the right hand
d
x
dx
dx (or any other infinitesimal variable), just to remind us of the origin because it “multiplies against the function”, hence giving area. Or is there more to it?
除了原问题之外,我还想知道:我们在积分中保留右侧的
d
x
dx
dx(或其他无穷小变量),是否也是出于这个原因——为了提醒我们积分的起源,因为
d
x
dx
dx 与函数“相乘”后可表示面积?还是说背后有更深层的原因?
Hints, answers, references to books… I’d appreciate anything you can give me.
无论是提示、答案还是书籍参考,任何信息我都将感激不尽。
edited Apr 25, 2012 at 17:45
Michael Hardy
asked Apr 25, 2012 at 15:42
Fractal Resurgence
Do you mean
∑
∫
f
i
d
x
=
∫
∑
f
i
d
x
\sum\int f_{i}dx = \int\sum f_{i}dx
∑∫fidx=∫∑fidx as in here or
∫
f
i
d
x
=
∑
f
i
Δ
x
\int f_{i}dx = \sum f_{i}\Delta x
∫fidx=∑fiΔx as in here?
你指的是 此处 提到的
∑
∫
f
i
d
x
=
∫
∑
f
i
d
x
\sum\int f_{i}dx = \int\sum f_{i}dx
∑∫fidx=∫∑fidx,还是 此处 提到的
∫
f
i
d
x
=
∑
f
i
Δ
x
\int f_{i}dx = \sum f_{i}\Delta x
∫fidx=∑fiΔx?
– user2468
Commented Apr 25, 2012 at 15:53
@J.D. Not the first one (sum rule, right?)… That just an addition for loop, that’s justified. It’s the second one. I would like to understand that more.
@J.D.:不是第一个(求和法则,对吗?)……它只是循环加法,合理性已得到证明。我想问的是第二个,我想更深入地理解它。
– Fractal Resurgence
Commented Apr 25, 2012 at 16:02
- have a look at Euler–Maclaurin_formula which essentially says
∑
=
∫
+
e
r
r
o
r
t
e
r
m
\sum = \int + error \ term
∑=∫+error term,where the error term is hopefully controllable for nice functions. A derivation is sketched here
可以参考 欧拉-麦克劳林公式,该公式本质上表明 ∑ = ∫ + 误差项 \sum = \int + 误差项 ∑=∫+误差项,对于性质良好的函数,误差项通常是可控的。此处有该公式的推导概述: - big list - Pseudo Proofs that are intuitively reasonable
https://math.stackexchange.com/questions/123633/pseudo-proofs-that-are-intuitively-reasonable/123895#123895
– Matthew Towers
Commented Apr 25, 2012 at 17:18
- Summation of positive terms is a special case of integral for counting measure.
正项求和是计数测度下积分的一个特例。
– sdcvvc
Commented Jun 23, 2012 at 13:11
Answers
In elementary analysis, a Riemann/Darboux integral is defined (among other equivalent definitions) as a suitable limit of a (finite) sum. Whence the folklore according to which “an integral is essentially a series”. This is rather false, but you know, in elementary analysis/calculus you can almost say whatever you wish.
在初等分析中,黎曼/达布积分(除其他等价定义外)被定义为(有限)和的适当极限。由此产生了“积分本质上是级数”的通俗说法。这种说法并不完全准确,但在初等分析/微积分中,这种简化表述很常见。
The
d
x
dx
dx is clearly a deformation of
Δ
x
\Delta x
Δx in Riemann sums. Nowadays, it denotes the measure for which the integral is defined. If the integral is just a Riemann integral, some authors suggest to write
∫
a
b
f
\int_{a}^{b}f
∫abf instead of
∫
a
b
f
(
x
)
d
x
\int_{a}^{b}f(x)dx
∫abf(x)dx. They are right, since the Riemann integral depend on
a
a
a,
b
b
b, and the function
f
f
f. The variable of integration is a dummy one.
d
x
dx
dx 显然是黎曼和中
Δ
x
\Delta x
Δx 的变形。如今,
d
x
dx
dx 表示积分所定义的测度。若积分仅指黎曼积分,部分作者建议将
∫
a
b
f
(
x
)
d
x
\int_{a}^{b}f(x)dx
∫abf(x)dx 简写为
∫
a
b
f
\int_{a}^{b}f
∫abf。这种简化是合理的,因为黎曼积分仅依赖于积分上下限
a
a
a、
b
b
b 和函数
f
f
f,积分变量是哑变量(无实际意义)。
Finally, remember that
∫
\int
∫ is a calligraphic deformation of an “S”, while
∑
\sum
∑ is the greek “S”. Hence many pioneers used to kind of confuse
∑
\sum
∑ and
∫
\int
∫ in their manuscripts. But, honestly, contemporary textbooks should not swap the two signs, since we live in 2012 and Cauchy died many years ago ;
最后需注意,
∫
\int
∫ 是字母“S”的书法变形(代表“和”,sum),而
∑
\sum
∑ 是希腊字母“S”(同样代表“和”)。因此,许多早期数学家在手稿中常将两者混用。但说实话,现代教科书不应再混淆这两个符号——毕竟我们处于 2012 年,柯西已逝世多年;
edited Jun 23, 2012 at 12:04
answered Apr 25, 2012 at 16:07
Siminore
Very nice, thank you. On another note, your text could benefit from some formatting (a paragraph or two).
非常好,谢谢。另外,你的回答若能调整一下格式(比如分一两个段落),阅读体验会更好。
– Fractal Resurgence
Commented Apr 25, 2012 at 16:30
Since a picture says more than words …
一张图胜过千言万语……
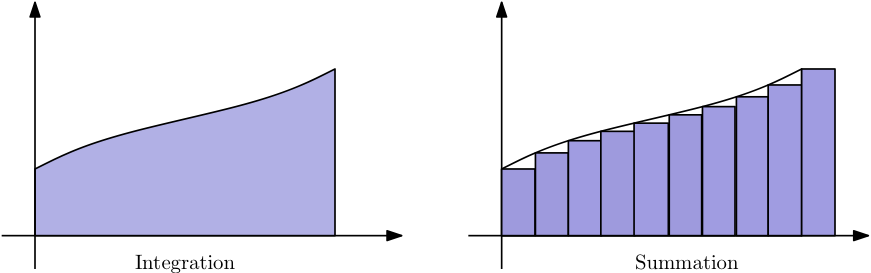
answered Nov 29, 2012 at 13:47
A.Schulz
In your summation picture, the center of each rectangle should be on the line. This would demonstrate how the summation end up being a higher value than the integration.
在你求和的示意图中,每个矩形的中心应落在函数线上。这样能更清楚地展示求和结果为何会大于积分结果。
– woz
Commented Nov 29, 2012 at 13:53
Reversing the Order of Integration and Summation
积分与求和的顺序交换
I am trying to understand when we can interchange the order of Integration and Summation. I am increasingly encountering Integrals; some of which are being solved by interchanging the order of Summation and Integration, and some which cannot (for no given reason) be solved using this. Despite looking at a variety of sites, I was unable to understand when we can do so.
我正在尝试理解何时可以交换积分与求和的顺序。我遇到的积分问题越来越多,其中有些通过交换求和与积分顺序就能解决,而有些却无法用这种方法解决(且未给出原因)。尽管我查阅了多个网站,仍未能搞清楚可交换顺序的条件。
I came up with the following two requirements here on MSE:
我在数学栈交换(MSE)上整理出了以下两个条件:
If
f
n
(
x
)
≥
0
f_{n}(x)\geq0
fn(x)≥0 for all
x
,
n
x,n
x,n
若对所有
x
x
x 和
n
n
n,均有
f
n
(
x
)
≥
0
f_{n}(x)\geq0
fn(x)≥0,则:
∑ ∫ f n ( x ) d x = ∫ ∑ f n ( x ) d x \sum\int f_{n}(x)dx=\int\sum f_{n}(x)dx ∑∫fn(x)dx=∫∑fn(x)dx
Also if
∑
∫
∣
f
n
∣
<
∞
\sum\int|f_{n}|<\infty
∑∫∣fn∣<∞ or
∫
∑
∣
f
n
∣
<
∞
\int\sum|f_{n}|<\infty
∫∑∣fn∣<∞, then
此外,若
∑
∫
∣
f
n
∣
<
∞
\sum\int|f_{n}|<\infty
∑∫∣fn∣<∞ 或
∫
∑
∣
f
n
∣
<
∞
\int\sum|f_{n}|<\infty
∫∑∣fn∣<∞,则:
∫ ∑ f n = ∑ ∫ f n \int\sum f_{n}=\sum\int f_{n} ∫∑fn=∑∫fn
I would be grateful if somebody could please explain this to me. Thanks very much in advance.
若有人能为我解释这些条件,我将十分感激。提前感谢大家!
edited Apr 20, 2020 at 12:50
asked Jun 22, 2015 at 13:18
User1234
- If I recall correctly, then if the sum of the integral converges, then the integral of the sum converges to the same value and vice versa. This is an application of Fubini’s theorem.
若我没记错,当积分的和收敛时,和的积分也会收敛到相同的值,反之亦然。这是富比尼定理的一种应用。
– kbau
Commented Jun 22, 2015 at 13:21
评论于 2015 年 6 月 22 日 13 点 21 分
- You are presumably integrating over
x
x
x and summing over
n
n
n
想必你是对 x x x 进行积分,对 n n n 进行求和。
– Henry
Commented Jun 22, 2015 at 13:28
Regarding the notation
f
n
(
x
)
f_{n}(x)
fn(x), I imagine
n
n
n is a summation index. Not sure about swapping the sum and integral in
∫
g
(
x
)
∑
f
(
x
)
d
x
\int g(x)\sum f(x)dx
∫g(x)∑f(x)dx. Better wait for someone more knowledgeable to answer. Although, if you use the
f
n
(
x
)
f_{n}(x)
fn(x) notation properly, then swapping the sum and the integral shouldn’t be a problem assuming it can be done without
g
(
x
)
g(x)
g(x) in the expression.
关于符号
f
n
(
x
)
f_{n}(x)
fn(x),我认为
n
n
n 是求和指标。对于
∫
g
(
x
)
∑
f
(
x
)
d
x
\int g(x)\sum f(x)dx
∫g(x)∑f(x)dx 中求和与积分的交换,我不太确定。最好等更专业的人来回答。不过,若正确使用
f
n
(
x
)
f_{n}(x)
fn(x) 符号,且表达式中不含
g
(
x
)
g(x)
g(x),那么在满足可交换条件的情况下,交换求和与积分的顺序应该没问题。
– kbau
Commented Jun 22, 2015 at 13:30
- If you don’t like
f
n
(
x
)
f_{n}(x)
fn(x), you can write
f
(
n
,
x
)
f(n,x)
f(n,x). It means the same thing. We tend to separate
n
n
n and
x
x
x for various reasons (mainly so that we can conveniently isolate the function
g
(
x
)
=
f
(
n
,
x
)
g(x)=f(n,x)
g(x)=f(n,x) for a fixed
n
n
n, by simply writing
f
n
f_{n}
fn).
若你不喜欢 f n ( x ) f_{n}(x) fn(x) 这种写法,也可以写成 f ( n , x ) f(n,x) f(n,x),二者含义相同。我们倾向于将 n n n 和 x x x 分开表示,原因有很多(主要是为了在固定 n n n 时,能简单地用 f n f_{n} fn 表示,方便分离出函数 g ( x ) = f ( n , x ) g(x)=f(n,x) g(x)=f(n,x))。
– Ian
Commented Jun 22, 2015 at 13:33
- If you don’t understand what
f
n
(
x
)
f_{n}(x)
fn(x) means, then could you give us an example of an expression involving
∑
∫
\sum\int
∑∫ or
∫
∑
\int\sum
∫∑ about which you have questions? I’m having trouble understanding what you could be asking about if you don’t understand what
f
n
(
x
)
f_{n}(x)
fn(x) means. If you have
∫
∫
\int\int
∫∫ there’s a “
d
x
dx
dx” in there somewhere – a variable with respect to which you’re integrating. And if you have
∑
∑
\sum\sum
∑∑ the you must have
∑
n
=
1
∞
\sum_{n=1}^{\infty}
∑n=1∞ or the like, with the index called
n
n
n. There’s an
x
x
x and there’s an
n
n
n; otherwise you haven’t got an integral and a sum.
若你不理解 f n ( x ) f_{n}(x) fn(x) 的含义,能否给出一个包含 ∑ ∫ \sum\int ∑∫ 或 ∫ ∑ \int\sum ∫∑ 的表达式示例,说明你有疑问的地方?如果你不理解 f n ( x ) f_{n}(x) fn(x),我很难搞清楚你想问的是什么。若表达式中有 ∫ ∫ \int\int ∫∫,就必然存在某个“ d x dx dx”——即积分变量;若有 ∑ ∑ \sum\sum ∑∑,就必然有 ∑ n = 1 ∞ \sum_{n=1}^{\infty} ∑n=1∞ 这类带求和指标 n n n 的符号。表达式中必须同时存在 x x x 和 n n n,否则就谈不上积分与求和的顺序交换。
– Michael Hardy
Commented Jun 22, 2015 at 13:34
Answer
The more general question is about interchanging limits and integration. With infinite sums, this is a special case, because by definition
∑
n
=
1
∞
f
n
(
x
)
=
lim
N
→
∞
∑
n
=
1
N
f
n
(
x
)
\sum_{n=1}^{\infty}f_{n}(x)=\lim_{N\rightarrow\infty}\sum_{n=1}^{N}f_{n}(x)
∑n=1∞fn(x)=limN→∞∑n=1Nfn(x). So because one can always interchange finite sums and integration, the only question is about interchanging the limit and the integration.
更一般的问题是关于“极限”与“积分”的顺序交换。无穷求和是其中的特例,因为根据定义,
∑
n
=
1
∞
f
n
(
x
)
=
lim
N
→
∞
∑
n
=
1
N
f
n
(
x
)
\sum_{n=1}^{\infty}f_{n}(x)=\lim_{N\rightarrow\infty}\sum_{n=1}^{N}f_{n}(x)
∑n=1∞fn(x)=limN→∞∑n=1Nfn(x)。由于有限求和与积分的顺序总能交换,因此唯一需要关注的问题是“极限”与“积分”的顺序交换。
Writing what I just said in symbols, we want conditions such that
用符号表示上述内容,我们需要找到满足以下等式的条件:
∑ n = 1 ∞ ∫ X f n ( x ) d x = ∫ X ∑ n = 1 ∞ f n ( x ) d x \sum_{n=1}^{\infty}\int_{X}f_{n}(x)dx=\int_{X}\sum_{n=1}^{\infty}f_{n}(x)dx ∑n=1∞∫Xfn(x)dx=∫X∑n=1∞fn(x)dx.
Expanding the definition:
将定义展开可得:
lim N → ∞ ∑ n = 1 N ∫ X f n ( x ) d x = ∫ X lim N → ∞ ∑ n = 1 N f n ( x ) d x \lim_{N\rightarrow\infty}\sum_{n=1}^{N}\int_{X}f_{n}(x)dx=\int_{X}\lim_{N\rightarrow\infty}\sum_{n=1}^{N}f_{n}(x)dx limN→∞∑n=1N∫Xfn(x)dx=∫XlimN→∞∑n=1Nfn(x)dx.
Now one interchange is free:
其中有一步交换是无条件成立的:
lim N → ∞ ∑ n = 1 N ∫ X f n ( x ) d x = lim N → ∞ ∫ X ∑ n = 1 N f n ( x ) d x \lim_{N\rightarrow\infty}\sum_{n=1}^{N}\int_{X}f_{n}(x)dx=\lim_{N\rightarrow\infty}\int_{X}\sum_{n=1}^{N}f_{n}(x)dx limN→∞∑n=1N∫Xfn(x)dx=limN→∞∫X∑n=1Nfn(x)dx.
The issue is with the last interchange, which is what most of the rest of this answer is about.
关键问题在于最后一步交换(极限与积分的交换),这也是本回答后续要讨论的大部分内容。
The most general result of this type is the Vitali convergence theorem. It says that if
f
n
f_{n}
fn is a sequence of measurable functions,
f
n
→
f
f_{n}\rightarrow f
fn→f pointwise,
f
n
f_{n}
fn is uniformly integrable, and
f
n
f_{n}
fn is tight, then
∫
X
f
n
(
x
)
d
x
→
∫
X
f
(
x
)
d
x
\int_{X}f_{n}(x)dx\rightarrow\int_{X}f(x)dx
∫Xfn(x)dx→∫Xf(x)dx. (Here
X
X
X is the set over which we integrate.) You can look up the formal definitions of “uniformly integrable” and “tight” yourself. Roughly speaking they mean that you cannot “compress mass into a point” and that you can’t “move mass to infinity”. These intuitions are illustrated by the failure of the conclusion of the theorem for the sequences
f
n
(
x
)
=
{
n
x
∈
[
0
,
1
/
n
]
0
o
t
h
e
r
w
i
s
e
f_{n}(x)=\begin{cases}n & x\in[0,1/n]\\0 & otherwise\end{cases}
fn(x)={n0x∈[0,1/n]otherwise on
[
0
,
1
]
[0,1]
[0,1] and
g
n
(
x
)
=
{
1
x
∈
[
n
,
n
+
1
]
0
o
t
h
e
r
w
i
s
e
g_{n}(x)=\begin{cases}1 & x\in[n,n+1]\\0 & otherwise\end{cases}
gn(x)={10x∈[n,n+1]otherwise on the whole line.
此类问题中最具一般性的结论是维他利收敛定理。该定理指出:若
f
n
f_{n}
fn 是可测函数列,满足
f
n
f_{n}
fn 逐点收敛至
f
f
f、
f
n
f_{n}
fn 一致可积且
f
n
f_{n}
fn 是紧的,则有
∫
X
f
n
(
x
)
d
x
→
∫
X
f
(
x
)
d
x
\int_{X}f_{n}(x)dx\rightarrow\int_{X}f(x)dx
∫Xfn(x)dx→∫Xf(x)dx(其中
X
X
X 是积分区域)。你可以自行查阅“一致可积”和“紧的”的正式定义,大致来说,它们分别表示“不能将质量压缩到单点”和“不能将质量移至无穷远处”。以下两个函数列可直观说明定理结论不成立的情况:一是在
[
0
,
1
]
[0,1]
[0,1] 区间上的
f
n
(
x
)
=
{
n
x
∈
[
0
,
1
/
n
]
0
o
t
h
e
r
w
i
s
e
f_{n}(x)=\begin{cases}n & x\in[0,1/n]\\0 & otherwise\end{cases}
fn(x)={n0x∈[0,1/n]otherwise,二是在整个实轴上的
g
n
(
x
)
=
{
1
x
∈
[
n
,
n
+
1
]
0
o
t
h
e
r
w
i
s
e
g_{n}(x)=\begin{cases}1 & x\in[n,n+1]\\0 & otherwise\end{cases}
gn(x)={10x∈[n,n+1]otherwise。
The Vitali convergence theorem is general but it is not convenient. The result with perhaps the best balance between generality and convenience to check is the dominated convergence theorem. This says that if
f
n
→
f
f_{n}\rightarrow f
fn→f pointwise and there is a fixed integrable function
g
g
g such that
∣
f
n
(
x
)
∣
≤
g
(
x
)
|f_{n}(x)|\leq g(x)
∣fn(x)∣≤g(x) for all
n
n
n and
x
x
x, then
∫
X
f
n
(
x
)
d
x
→
∫
X
f
(
x
)
d
x
\int_{X}f_{n}(x)dx\rightarrow\int_{X}f(x)dx
∫Xfn(x)dx→∫Xf(x)dx.
维他利收敛定理虽具一般性,但使用不便。在“一般性”与“验证便利性”之间平衡得最好的结论,或许是控制收敛定理。该定理指出:若
f
n
f_{n}
fn 逐点收敛至
f
f
f,且存在一个固定的可积函数
g
g
g,使得对所有
n
n
n 和
x
x
x 均有
∣
f
n
(
x
)
∣
≤
g
(
x
)
|f_{n}(x)|\leq g(x)
∣fn(x)∣≤g(x),则
∫
X
f
n
(
x
)
d
x
→
∫
X
f
(
x
)
d
x
\int_{X}f_{n}(x)dx\rightarrow\int_{X}f(x)dx
∫Xfn(x)dx→∫Xf(x)dx。
One relatively basic result is the monotone convergence theorem, which says that if
f
n
f_{n}
fn is an increasing sequence of nonnegative functions and
f
n
→
f
f_{n}\rightarrow f
fn→f pointwise, then
∫
X
f
n
(
x
)
d
x
→
∫
X
f
(
x
)
d
x
\int_{X}f_{n}(x)dx\rightarrow\int_{X}f(x)dx
∫Xfn(x)dx→∫Xf(x)dx. In particular this holds whether or not
f
f
f is actually integrable (if it isn’t, then the limit of the integrals is
+
∞
+\infty
+∞). This is also applicable to the case when
f
n
f_{n}
fn are nonpositive and decrease to
f
f
f (this is easy to prove, since
∫
X
−
g
(
x
)
d
x
=
−
∫
X
g
(
x
)
d
x
\int_{X}-g(x)dx=-\int_{X}g(x)dx
∫X−g(x)dx=−∫Xg(x)dx). This is useful for summation, because if
f
n
(
x
)
≥
0
f_{n}(x)\geq0
fn(x)≥0 then
g
N
(
x
)
=
∑
n
=
1
N
f
n
(
x
)
g_{N}(x)=\sum_{n=1}^{N}f_{n}(x)
gN(x)=∑n=1Nfn(x) is an increasing sequence of nonnegative functions.
一个相对基础的结论是单调收敛定理,它指出:若
f
n
f_{n}
fn 是单调递增的非负函数列,且
f
n
f_{n}
fn 逐点收敛至
f
f
f,则
∫
X
f
n
(
x
)
d
x
→
∫
X
f
(
x
)
d
x
\int_{X}f_{n}(x)dx\rightarrow\int_{X}f(x)dx
∫Xfn(x)dx→∫Xf(x)dx。特别地,无论
f
f
f 是否可积,该结论均成立(若
f
f
f 不可积,则积分的极限为
+
∞
+\infty
+∞)。该定理也适用于
f
n
f_{n}
fn 为非正函数且单调递减至
f
f
f 的情况(证明简单,因
∫
X
−
g
(
x
)
d
x
=
−
∫
X
g
(
x
)
d
x
\int_{X}-g(x)dx=-\int_{X}g(x)dx
∫X−g(x)dx=−∫Xg(x)dx)。这一定理对求和问题很有用,因为若
f
n
(
x
)
≥
0
f_{n}(x)\geq0
fn(x)≥0,则
g
N
(
x
)
=
∑
n
=
1
N
f
n
(
x
)
g_{N}(x)=\sum_{n=1}^{N}f_{n}(x)
gN(x)=∑n=1Nfn(x) 是单调递增的非负函数列。
Finally in the special case of interchanging summation and integration, one can apply the abstract version of the Fubini-Tonelli theorem. This is because summation can be identified as integration with respect to the counting measure. As a result, if either
最后,在积分与求和顺序交换的特例中,可应用富比尼-托内利定理的抽象形式。这是因为求和可视为关于“计数测度”的积分。因此,若满足以下两个条件之一:
∑ n = 1 ∞ ∫ X ∣ f n ( x ) ∣ d x < ∞ \sum_{n=1}^{\infty}\int_{X}|f_{n}(x)|dx<\infty ∑n=1∞∫X∣fn(x)∣dx<∞
or
或
∫ X ∑ n = 1 ∞ ∣ f n ( x ) ∣ d x < ∞ \int_{X}\sum_{n=1}^{\infty}|f_{n}(x)|dx<\infty ∫X∑n=1∞∣fn(x)∣dx<∞
then one may interchange summation and integration. (This requires a hypothesis about
X
X
X; because this holds for the case of
R
n
\mathbb{R}^{n}
Rn, I won’t state it, since this is already a more advanced writeup than you wanted.)
则可交换求和与积分的顺序。(该结论对
X
X
X 有一个前提假设,但由于
R
n
\mathbb{R}^{n}
Rn 满足该假设,且本文已比你预期的更深入,因此不再赘述该假设。)
edited Oct 26, 2020 at 16:07
answered Jun 22, 2015 at 21:45
Ian
- @BetterWorld
X
X
X can be
R
\mathbb{R}
R; usually we write
∫
−
∞
∞
\int_{-\infty}^{\infty}
∫−∞∞ instead of
∫
R
\int_{\mathbb{R}}
∫R.
@BetterWorld: X X X 可以是 R \mathbb{R} R(实数集);通常我们会写成 ∫ − ∞ ∞ \int_{-\infty}^{\infty} ∫−∞∞,而非 ∫ R \int_{\mathbb{R}} ∫R。
– Ian
Commented Jun 23, 2015 at 10:14
- @BetterWorld The limits being infinite doesn’t matter. (Again, there is a condition in the last result, which is that the space
X
X
X has to be “
σ
\sigma
σ-finite”, but
R
\mathbb{R}
R and
R
n
\mathbb{R}^{n}
Rn are
σ
\sigma
σ-finite, so that’s not an obstacle for your purposes). As for your second question, everything works out if you use different indices. You can even sum over the whole set of integers
Z
\mathbb{Z}
Z and it works out the same.
@BetterWorld:积分限为无穷大并不影响结论。(再次说明,最后一个结论有一个前提条件:空间 X X X 需是“ σ \sigma σ-有限”的,但 R \mathbb{R} R 和 R n \mathbb{R}^{n} Rn 均为 σ \sigma σ-有限空间,因此对你的需求而言,这并非障碍。)关于你的第二个问题,若使用不同的指标,所有结论均成立。你甚至可以对整个整数集 Z \mathbb{Z} Z 求和,结论依然不变。
– Ian
Commented Jun 23, 2015 at 10:39
-
I am afraid that you have wasted a lot of your time writeing down this nice answers: as you can see, the OP wasn’t asking about the subtle problem of switching limits with integrals, he was asking about what f n ( x ) f_{n}(x) fn(x) means…
恐怕你白费功夫写了这么好的回答:显然,提问者(OP)并非在询问极限与积分交换的复杂问题,而是在问 f n ( x ) f_{n}(x) fn(x) 是什么意思……
– Alex M.
Commented Jun 23, 2015 年 6 月 23 日 10 点 39 分
- @BetterWorld Sure, that’s just a special case.
@BetterWorld:当然,那只是一个特例。
– Ian
Commented Jun 23, 2015 at 11:30
- @Ian, Could you address the cases the integral is
∫
−
∞
∞
\int_{-\infty}^{\infty}
∫−∞∞ and the case of indefinite integral? Namely not only in the context of measures. Thank You.
@Ian,你能讲讲积分是 ∫ − ∞ ∞ \int_{-\infty}^{\infty} ∫−∞∞(无穷区间积分)以及不定积分的情况吗?也就是不局限于测度论的语境。谢谢。
– Royi
Commented Sep 26, 2017 at 13:53
What is the difference between sum and integral?
求和与积分的区别是什么?
I am a beginner in calculus and I want to know what is the difference between sum and integral. More specifically I came across this example:
我是微积分初学者,想知道求和与积分的区别。具体来说,我遇到了这样一个例子:
Compare
∑ 1 ∞ 1 x \sum_{1}^{\infty}\frac{1}{x} ∑1∞x1 and ∫ 1 ∞ 1 x d x \int_{1}^{\infty}\frac{1}{x}dx ∫1∞x1dx
It would be really helpful if someone explains this to me. I want to know the difference between the two.
若有人能为我解释,我将非常感激。我想了解这两者之间的区别。
Thanks for any help!
感谢所有帮助!
edited Feb 7, 2016 at 3:59
JKnecht
asked Feb 7, 2016 at 1:56
Soham
What do you exactly mean by
∑
1
/
x
\sum 1/x
∑1/x?
你说的
∑
1
/
x
\sum 1/x
∑1/x 具体指什么?
– Vim
Commented Feb 7, 2016 at 2:04
Your question is analogous to “what is the difference between difference quotient and derivative?”
你的问题类似于“差商与导数的区别是什么?”
– zhw.
Commented Feb 7, 2016 at 3:13
Answers
Basically, an integral adds up infinitely small pieces, whereas a sum adds up distinct pieces.
本质上,积分是对无穷多个无穷小的“片段”求和,而求和是对有限或无限个离散的“片段”求和。
∫ 1 ∞ 1 x d x \int_{1}^{\infty}\frac{1}{x}dx ∫1∞x1dx
Will add up all of the area under
f
(
x
)
=
1
x
f(x)=\frac{1}{x}
f(x)=x1, whereas
该积分表示累加函数
f
(
x
)
=
1
x
f(x)=\frac{1}{x}
f(x)=x1 曲线下方的所有面积;而
∑ x = 1 ∞ 1 x \sum_{x=1}^{\infty}\frac{1}{x} ∑x=1∞x1
Will add up each value for
x
x
x from whatever you start, until you stop.
该求和表示从起始的
x
x
x 值开始,累加每一个离散
x
x
x 对应的函数值,直到
x
x
x 趋于无穷。
For
f
(
x
)
=
1
x
f(x)=\frac{1}{x}
f(x)=x1 this is the difference between the area under
1
x
\frac{1}{x}
x1, and the series
1
+
1
2
+
1
3
+
1
4
+
⋯
+
1
n
1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \cdots + \frac{1}{n}
1+21+31+41+⋯+n1 (the harmonic series).
对于
f
(
x
)
=
1
x
f(x)=\frac{1}{x}
f(x)=x1 而言,二者的区别在于:一个是
1
x
\frac{1}{x}
x1 曲线下的面积,另一个是级数
1
+
1
2
+
1
3
+
1
4
+
⋯
+
1
n
1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \cdots + \frac{1}{n}
1+21+31+41+⋯+n1(即调和级数)的和。
Both of these values diverge.
这两个表达式的结果均为发散(即趋于无穷大)。
edited Feb 7, 2016 at 2:15
answered Feb 7, 2016 at 2:09
Noah Harris
For sum, Does “add up each y value on the function” refer to only integers? If not, how does the sum account for the infinitely many irrational numbers that the y value takes?
对于求和来说,“累加函数上的每个 y 值”是否仅指 x 取整数时的 y 值?如果不是,求和如何处理 y 值对应的无穷多个无理数 x 的情况?
– user1112591
Commented Feb 7, 2023 at 18:36
I think Noah Harris’s answer is on the right track, but let’s make it more precise for a beginner.
我认为诺亚·哈里斯的回答方向正确,但针对初学者,我们可以表述得更精确一些。
First, the notation:
∑
x
=
1
∞
1
x
\sum_{x=1}^{\infty}\frac{1}{x}
∑x=1∞x1 is a bit informal. Usually, we write
∑
n
=
1
∞
1
n
\sum_{n=1}^{\infty}\frac{1}{n}
∑n=1∞n1 where
n
n
n is a positive integer (1, 2, 3, …). This is the harmonic series, and it adds up the function values only at integer points.
首先看符号:
∑
x
=
1
∞
1
x
\sum_{x=1}^{\infty}\frac{1}{x}
∑x=1∞x1 的写法稍显不规范。通常我们会写成
∑
n
=
1
∞
1
n
\sum_{n=1}^{\infty}\frac{1}{n}
∑n=1∞n1,其中
n
n
n 为正整数(1、2、3……)。这就是调和级数,它仅累加函数在整数点处的函数值。
In contrast,
∫
1
∞
1
x
d
x
\int_{1}^{\infty}\frac{1}{x}dx
∫1∞x1dx is a definite integral (improper, since the upper limit is infinity). It calculates the area under the curve
y
=
1
x
y=\frac{1}{x}
y=x1 from
x
=
1
x=1
x=1 to
x
=
∞
x=\infty
x=∞, and it includes all real numbers
x
x
x in this interval (not just integers).
与之相对,
∫
1
∞
1
x
d
x
\int_{1}^{\infty}\frac{1}{x}dx
∫1∞x1dx 是一个反常定积分(因积分上限为无穷大)。它计算的是曲线
y
=
1
x
y=\frac{1}{x}
y=x1 在
x
=
1
x=1
x=1 到
x
=
∞
x=\infty
x=∞ 区间下方的面积,且涵盖该区间内所有实数
x
x
x(而非仅整数)。
Another key difference is how they “add”:
二者的另一区别在于“累加方式”:
-
For the sum ∑ n = 1 ∞ 1 n \sum_{n=1}^{\infty}\frac{1}{n} ∑n=1∞n1, each term is a fixed, finite value ( 1 1 \frac{1}{1} 11, 1 2 \frac{1}{2} 21, 1 3 \frac{1}{3} 31, …), and we add them one by one. Even though there are infinitely many terms, each term is discrete.
对于求和 ∑ n = 1 ∞ 1 n \sum_{n=1}^{\infty}\frac{1}{n} ∑n=1∞n1,每一项都是固定的有限值( 1 1 \frac{1}{1} 11、 1 2 \frac{1}{2} 21、 1 3 \frac{1}{3} 31……),我们逐项累加。尽管项数无穷多,但每一项都是离散的。
-
For the integral ∫ 1 ∞ 1 x d x \int_{1}^{\infty}\frac{1}{x}dx ∫1∞x1dx, we think of dividing the interval [ 1 , ∞ ) [1, \infty) [1,∞) into infinitely many tiny subintervals (each with width d x dx dx, an infinitesimally small number). For each subinterval, the “height” is f ( x ) = 1 x f(x)=\frac{1}{x} f(x)=x1, so the area of each tiny rectangle is f ( x ) d x f(x)dx f(x)dx (infinitely small). The integral adds up all these infinitely small areas.
对于积分 ∫ 1 ∞ 1 x d x \int_{1}^{\infty}\frac{1}{x}dx ∫1∞x1dx,我们将区间 [ 1 , ∞ ) [1, \infty) [1,∞) 分割成无穷多个微小的子区间(每个子区间的宽度为 d x dx dx,即无穷小量)。每个子区间对应的“高度”为 f ( x ) = 1 x f(x)=\frac{1}{x} f(x)=x1,因此每个小矩形的面积为 f ( x ) d x f(x)dx f(x)dx(无穷小量)。积分就是对所有这些无穷小面积进行累加。
To tie it back to your example: Both the harmonic series and the improper integral of
1
x
\frac{1}{x}
x1 diverge, but they diverge for the same reason—their terms/areas get small very slowly, so the total keeps growing without bound. But they describe different things: one is a sum of discrete values, the other is an area under a curve.
回到你的例子:调和级数与
1
x
\frac{1}{x}
x1 的反常积分均发散,但发散原因相同——它们的项/面积减小得非常缓慢,导致总和/总面积无界增长。但二者描述的对象不同:一个是离散值的和,另一个是曲线下的面积。
answered Feb 7, 2016 at 3:02
user296602
Let me use a simpler example to explain. Suppose we want to calculate the “total” of
f
(
x
)
=
2
x
f(x)=2x
f(x)=2x from
x
=
1
x=1
x=1 to
x
=
2
x=2
x=2.
我用一个更简单的例子来解释。假设我们要计算
f
(
x
)
=
2
x
f(x)=2x
f(x)=2x 在
x
=
1
x=1
x=1 到
x
=
2
x=2
x=2 范围内的“总量”。
-
If we use a sum: Let’s take integer x x x values only: x = 1 x=1 x=1 and x = 2 x=2 x=2. The sum is f ( 1 ) + f ( 2 ) = 2 ( 1 ) + 2 ( 2 ) = 2 + 4 = 6 f(1) + f(2) = 2(1) + 2(2) = 2 + 4 = 6 f(1)+f(2)=2(1)+2(2)=2+4=6. This only includes two discrete points.
若用求和:仅取 x x x 的整数值,即 x = 1 x=1 x=1 和 x = 2 x=2 x=2。求和结果为 f ( 1 ) + f ( 2 ) = 2 ( 1 ) + 2 ( 2 ) = 2 + 4 = 6 f(1) + f(2) = 2(1) + 2(2) = 2 + 4 = 6 f(1)+f(2)=2(1)+2(2)=2+4=6。该结果仅包含两个离散点的函数值。
-
If we use an integral: ∫ 1 2 2 x d x = [ x 2 ] 1 2 = 2 2 − 1 2 = 4 − 1 = 3 \int_{1}^{2}2x dx = [x^2]_{1}^{2} = 2^2 - 1^2 = 4 - 1 = 3 ∫122xdx=[x2]12=22−12=4−1=3. This is the area under f ( x ) = 2 x f(x)=2x f(x)=2x from 1 1 1 to 2 2 2, which includes every x x x in between (1.1, 1.01, 1.001, …) and adds up the tiny areas.
若用积分: ∫ 1 2 2 x d x = [ x 2 ] 1 2 = 2 2 − 1 2 = 4 − 1 = 3 \int_{1}^{2}2x dx = [x^2]_{1}^{2} = 2^2 - 1^2 = 4 - 1 = 3 ∫122xdx=[x2]12=22−12=4−1=3。这是 f ( x ) = 2 x f(x)=2x f(x)=2x 在 1 1 1 到 2 2 2 区间下方的面积,涵盖了区间内所有 x x x 值(1.1、1.01、1.001……),并累加了所有微小面积。
The key takeaway: A sum is for discrete “chunks” (like integer x-values), while an integral is for continuous “chunks” (all real x-values in an interval). Even if both are infinite (like your original example with
1
x
\frac{1}{x}
x1), this core difference stays the same.
要点:求和用于离散的“片段”(如
x
x
x 的整数值),而积分用于连续的“片段”(区间内所有实数
x
x
x 值)。即便二者均为无穷(如你最初提到的
1
x
\frac{1}{x}
x1 例子),这一核心区别依然存在。
answered Feb 7, 2016 at 3:51
Kyle Miller
To add one more point: The relationship between sum and integral is not just “different ways to add”—they can also approximate each other.
再补充一点:求和与积分的关系不仅是“不同的累加方式”,它们还能相互近似。
For example, the Riemann sum (the basis of the Riemann integral) uses a sum of rectangle areas to approximate the integral. If you take more and more rectangles (make their widths smaller), the Riemann sum gets closer and closer to the integral value.
例如,黎曼和(黎曼积分的基础)就是用矩形面积的和来近似积分。当你取越来越多的矩形(减小矩形宽度)时,黎曼和会越来越接近积分值。
In your original example, the harmonic series
∑
n
=
1
∞
1
n
\sum_{n=1}^{\infty}\frac{1}{n}
∑n=1∞n1 can be compared to the integral
∫
1
∞
1
x
d
x
\int_{1}^{\infty}\frac{1}{x}dx
∫1∞x1dx using the integral test for convergence. This test says that for positive, decreasing functions like
1
x
\frac{1}{x}
x1, the series and the integral either both converge or both diverge. This works because the series is like a “stepwise” approximation of the integral (each term
1
n
\frac{1}{n}
n1 is the height of a rectangle with width 1 under the curve).
在你最初的例子中,调和级数
∑
n
=
1
∞
1
n
\sum_{n=1}^{\infty}\frac{1}{n}
∑n=1∞n1 可通过积分判别法与积分
∫
1
∞
1
x
d
x
\int_{1}^{\infty}\frac{1}{x}dx
∫1∞x1dx 进行收敛性比较。该判别法指出,对于
1
x
\frac{1}{x}
x1 这类正的递减函数,级数与积分要么同时收敛,要么同时发散。这一方法可行的原因是,级数可看作积分的“阶梯式”近似(每一项
1
n
\frac{1}{n}
n1 都是曲线下宽度为 1 的矩形的高度)。
answered Feb 7, 2016 at 4:15
David K
积分与求和的顺序交换:条件、性质与总结
一、积分与求和的顺序可以交换的条件
交换积分与求和顺序需满足特定条件,依据是测度论中的收敛定理与富比尼 - 托内利定理,具体可分为以下 3 类场景 :
1. 非负函数列场景(托内利定理 / 单调收敛定理)
若对所有积分变量 x x x 和求和指标 n n n,均满足 f n ( x ) ≥ 0 f_{n}(x) \geq 0 fn(x)≥0,则无需额外条件,可直接交换顺序,即:
∑ n ∫ X f n ( x ) d x = ∫ X ∑ n f n ( x ) d x \sum_{n} \int_{X} f_{n}(x) dx = \int_{X} \sum_{n} f_{n}(x) dx n∑∫Xfn(x)dx=∫Xn∑fn(x)dx
该结论同时适用于“两边均有限”和“两边均发散至 + ∞ +\infty +∞”的情况,可通过单调收敛定理证明(因部分和序列 g N ( x ) = ∑ n = 1 N f n ( x ) g_{N}(x) = \sum_{n=1}^{N} f_{n}(x) gN(x)=∑n=1Nfn(x) 是单调递增的非负函数列)。
2. 绝对收敛场景(富比尼定理)
若积分与求和的“绝对形式”满足有限性(两个条件等价,满足其一即可),则可交换顺序:
- 条件 1: ∑ n ∫ X ∣ f n ( x ) ∣ d x < ∞ \sum_{n} \int_{X} |f_{n}(x)| dx < \infty ∑n∫X∣fn(x)∣dx<∞
- 条件 2: ∫ X ∑ n ∣ f n ( x ) ∣ d x < ∞ \int_{X} \sum_{n} |f_{n}(x)| dx < \infty ∫X∑n∣fn(x)∣dx<∞
此时等式 ∑ n ∫ X f n ( x ) d x = ∫ X ∑ n f n ( x ) d x \sum_{n} \int_{X} f_{n}(x) dx = \int_{X} \sum_{n} f_{n}(x) dx ∑n∫Xfn(x)dx=∫X∑nfn(x)dx 成立,本质是将求和视为“计数测度下的积分”,通过富比尼定理实现累次积分顺序交换。
3. 一般函数列场景(控制收敛定理)
若函数列 f n ( x ) f_{n}(x) fn(x) 满足以下两个条件,可通过“极限与积分交换”间接实现求和与积分交换(因无穷和是部分和的极限 ∑ n f n ( x ) = lim N → ∞ ∑ n = 1 N f n ( x ) \sum_{n} f_{n}(x) = \lim_{N \to \infty} \sum_{n=1}^{N} f_{n}(x) ∑nfn(x)=limN→∞∑n=1Nfn(x)):
- 逐点收敛:对所有 x ∈ X x \in X x∈X, lim N → ∞ ∑ n = 1 N f n ( x ) = ∑ n f n ( x ) \lim_{N \to \infty} \sum_{n=1}^{N} f_{n}(x) = \sum_{n} f_{n}(x) limN→∞∑n=1Nfn(x)=∑nfn(x);
- 控制条件:存在一个固定的可积函数 g ( x ) g(x) g(x)(即 ∫ X g ( x ) d x < ∞ \int_{X} g(x) dx < \infty ∫Xg(x)dx<∞),使得对所有 N N N 和 x x x,均有 ∣ ∑ n = 1 N f n ( x ) ∣ ≤ g ( x ) |\sum_{n=1}^{N} f_{n}(x)| \leq g(x) ∣∑n=1Nfn(x)∣≤g(x)。
此时等式 lim N → ∞ ∫ X ∑ n = 1 N f n ( x ) d x = ∫ X lim N → ∞ ∑ n = 1 N f n ( x ) d x \lim_{N \to \infty} \int_{X} \sum_{n=1}^{N} f_{n}(x) dx = \int_{X} \lim_{N \to \infty} \sum_{n=1}^{N} f_{n}(x) dx limN→∞∫X∑n=1Nfn(x)dx=∫XlimN→∞∑n=1Nfn(x)dx 成立,即求和与积分可交换。
二、不定积分的定义和性质
1. 不定积分的定义
设函数 f ( x ) f(x) f(x) 在区间 I I I 上有定义,若存在可导函数 F ( x ) F(x) F(x),使得对所有 x ∈ I x \in I x∈I,均满足 F ′ ( x ) = f ( x ) F'(x) = f(x) F′(x)=f(x),则称 F ( x ) F(x) F(x) 是 f ( x ) f(x) f(x) 在区间 I I I 上的一个原函数。
f ( x ) f(x) f(x) 的所有原函数构成的集合,称为 f ( x ) f(x) f(x) 在区间 I I I 上的不定积分,记为:
∫ f ( x ) d x = F ( x ) + C \int f(x) dx = F(x) + C ∫f(x)dx=F(x)+C
其中 C C C 为任意常数(称为积分常数), f ( x ) f(x) f(x) 称为被积函数, x x x 称为积分变量, d x dx dx 称为积分微元。
2. 不定积分的性质
(1)线性性质
对任意常数 k 1 , k 2 k_{1}, k_{2} k1,k2 和可积函数 f ( x ) , g ( x ) f(x), g(x) f(x),g(x),有:
∫ [ k 1 f ( x ) + k 2 g ( x ) ] d x = k 1 ∫ f ( x ) d x + k 2 ∫ g ( x ) d x \int [k_{1} f(x) + k_{2} g(x)] dx = k_{1} \int f(x) dx + k_{2} \int g(x) dx ∫[k1f(x)+k2g(x)]dx=k1∫f(x)dx+k2∫g(x)dx
该性质表明不定积分对“函数线性组合”具有分配性,可拆分计算。
(2)导数与不定积分的互逆性
- 不定积分的导数等于被积函数:
d d x ( ∫ f ( x ) d x ) = f ( x ) \frac{d}{dx} \left( \int f(x) dx \right) = f(x) dxd(∫f(x)dx)=f(x)
- 函数导数的不定积分等于该函数加积分常数:
∫ F ′ ( x ) d x = F ( x ) + C \int F'(x) dx = F(x) + C ∫F′(x)dx=F(x)+C
这两个性质直接体现了“不定积分是导数逆运算”的本质。
(3)区间关联性
不定积分的结果与积分区间 I I I 相关:同一函数在不同区间上的原函数可能存在差异,需结合区间定义域讨论。例如, ∫ 1 x d x = ln ∣ x ∣ + C \int \frac{1}{x} dx = \ln|x| + C ∫x1dx=ln∣x∣+C,在 x > 0 x > 0 x>0 时为 ln x + C \ln x + C lnx+C,在 x < 0 x < 0 x<0 时为 ln ( − x ) + C \ln(-x) + C ln(−x)+C。
(4)无唯一性
不定积分的结果不唯一,任意两个原函数之间相差一个常数。若 F ( x ) F(x) F(x) 和 G ( x ) G(x) G(x) 均为 f ( x ) f(x) f(x) 的原函数,则 F ( x ) − G ( x ) = C F(x) - G(x) = C F(x)−G(x)=C( C C C 为常数)。
三、求和与积分区别及交换条件
| 对比维度 | 求和(以无穷和 ∑ n = 1 ∞ a n \sum_{n=1}^{\infty} a_{n} ∑n=1∞an 为例) | 积分(以定积分 ∫ X f ( x ) d x \int_{X} f(x) dx ∫Xf(x)dx 为例) |
|---|---|---|
| 定义本质 | 离散项的累加,无穷和是部分和的极限 lim N → ∞ ∑ n = 1 N a n \lim_{N \to \infty} \sum_{n=1}^{N} a_{n} limN→∞∑n=1Nan | 连续区间上“无穷小量的累加”,定积分是黎曼和的极限(或测度论下的抽象积分) |
| 作用对象 | 离散指标 n n n(通常为整数),项 a n a_{n} an 与离散点对应 | 连续变量 x x x(通常为实数),函数 f ( x ) f(x) f(x) 定义在连续集合 X X X 上 |
| 计算结果 | 可能收敛(有限值)或发散(至 ± ∞ \pm\infty ±∞ 或无极限) | 可能收敛(有限值)或发散(至 ± ∞ \pm\infty ±∞ 或无意义) |
| 关联 | 可视为“计数测度下的积分”(求和指标对应计数测度的原子) | 定积分是“勒贝格测度 / 黎曼测度下的积分”,是求和的连续推广 |
| 交换顺序的条件 | 1. 非负项:所有
a
n
≥
0
a_{n} \geq 0
an≥0(或
f
n
(
x
)
≥
0
f_{n}(x) \geq 0
fn(x)≥0); 2. 绝对收敛: ∑ n ∣ a n ∣ < ∞ \sum_{n} \lvert a_{n} \rvert < \infty ∑n∣an∣<∞(或 ∑ n ∫ ∣ f n ∣ < ∞ \sum_{n} \int \lvert f_{n} \rvert < \infty ∑n∫∣fn∣<∞); 3. 控制条件:部分和被可积函数控制 | 1. 非负函数:
f
n
(
x
)
≥
0
f_{n}(x) \geq 0
fn(x)≥0(托内利定理); 2. 绝对可积: ∫ X ∑ ∣ f n ∣ < ∞ \int_{X} \sum \lvert f_{n} \rvert < \infty ∫X∑∣fn∣<∞(富比尼定理); 3. 控制收敛:部分和被可积函数控制(控制收敛定理) |
| 常见应用场景 | 数列求和、级数分析、离散概率等 | 面积 / 体积计算、连续概率、物理量累积(如位移、功)等 |
\lvert 和 \rvert
可以避免公式中的竖杠与表格竖杠冲突,确保表格显示正常。
可以确保绝对值符号的大小与内部内容匹配。
via:
- real analysis - When can a sum and integral be interchanged? - Mathematics Stack Exchange
https://math.stackexchange.com/questions/83721/when-can-a-sum-and-integral-be-interchanged - real analysis - Why do people interchange between
∫
\int
∫ and
∑
\sum
∑ so easily? - Mathematics Stack Exchange
https://math.stackexchange.com/questions/136833/why-do-people-interchange-between-int-and-sum-so-easily - integration - Difference between
∑
\sum
∑ and
∫
\int
∫ - Mathematics Stack Exchange
https://math.stackexchange.com/questions/247212/difference-between-sum-and-int - calculus - Reversing the Order of Integration and Summation - Mathematics Stack Exchange
https://math.stackexchange.com/questions/1334907/reversing-the-order-of-integration-and-summation - calculus - What is the difference between sum and integral? - Mathematics Stack Exchange
https://math.stackexchange.com/questions/1643968/what-is-the-difference-between-sum-and-integral





















 17万+
17万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








