数学史 | 负数的历史

负数的历史与发展

最新推荐文章于 2025-10-31 16:12:16 发布

原创最新推荐文章于 2025-10-31 16:12:16 发布 · 848 阅读

17 ·

CC 4.0 BY-SA版权

文章标签：

#负数的历史

mathematics 专栏收录该内容

186 篇文章

订阅专栏

注：本文为英文引文，机翻未校。
如有内容异常，请看原文。

The history of negative numbers

负数的历史

Although the first set of rules for dealing with negative numbers was stated in the 7th century by the Indian mathematician Brahmagupta, it is surprising that in 1758 the British mathematician Francis Maseres was claiming that negative numbers “… darken the very whole doctrines of the equations and make dark of the things which are in their nature excessively obvious and simple” .
尽管印度数学家婆罗摩笈多（Brahmagupta）在 7 世纪首次提出了处理负数的规则，但令人惊讶的是，英国数学家弗朗西斯·马塞雷斯（Francis Maseres）在 1758 年却声称，负数“……会使整个方程理论变得晦涩难懂，还会把本质上极其清晰简单的事物弄得模糊不清”。

Maseres and his contemporary, William Friend took the view that negative numbers did not exist. However, other mathematicians around the same time had decided that negative numbers could be used as long as they had been eliminated during the calculations where they appeared.
马塞雷斯和他的同时代人威廉·弗伦德（William Friend）认为负数并不存在。然而，当时其他一些数学家却认为，只要在出现负数的计算过程中能将其消去，负数就可以使用。

在这里插入图片描述

It was not until the 19th century when British mathematicians like De Morgan, Peacock, and others, began to investigate the ‘laws of arithmetic’ in terms of logical definitions that the problem of negative numbers was finally sorted out.
直到 19 世纪，英国数学家如德摩根（De Morgan）、皮科克（Peacock）等人开始从逻辑定义的角度研究“算术法则”，负数问题才最终得到解决。

However, there were references to negative numbers far earlier…
然而，关于负数的记载其实要早得多……

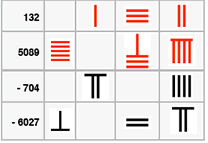
在这里插入图片描述

In 200 BCE the Chinese number rod system (see note 1 below) represented positive numbers in Red and Negative numbers in black. An article describing this system can be found here . These were used for commercial and tax calculations where the black cancelled out the red. The amount sold was positive (because of receiving money) and the amount spent in purchasing something was negative (because of paying out); so a money balance was positive, and a deficit negative.
公元前 200 年，中国的算筹系统（见下文注释 1）用红色表示正数，用黑色表示负数。关于该系统的介绍文章可在此处查看（链接不变）。这套系统用于商业和税务计算，其中黑色（表示的负数）可与红色（表示的正数）抵消。卖出的数量为正数（因为会收到钱），购买物品花费的数量为负数（因为要付钱）；因此，资金余额为正数，亏空则为负数。

The concept also appeared in Astronomy where the ideas of ‘strong’ and ‘weak’ were used for approximating a number from above or below. For example approaching 5 from above means for example, starting with 5.2 you can find better approximations 5.1, 5.05, 5.025. Thus 5.025 was called a ‘strong’ approximation and a number like 4.9 ‘weak’. So ‘strong’ numbers were called positive and ‘weak’ numbers negative
这一概念也出现在天文学中，当时人们用“强”和“弱”来表示从上方或下方逼近某个数。例如，从上方逼近 5，就是指从 5.2 开始，逐步得到更精确的近似值 5.1、5.05、5.025。因此，5.025 被称为“强”近似值，而像 4.9 这样的数则被称为“弱”近似值。所以，“强”数被称为正数，“弱”数被称为负数。

In India , negative numbers did not appear until about 620 CE in the work of Brahmagupta (598 - 670) who used the ideas of ‘fortunes’ and ‘debts’ for positive and negative. By this time a system based on place-value was established in India, with zero being used in the Indian number sytem. Brahmagupta used a special sign for negatives and stated the rules for dealing with positive and negative quantities as follows:
在印度，直到公元 620 年左右，负数才出现在婆罗摩笈多（Brahmagupta，598-670）的著作中。他用“财富”和“债务”来分别表示正数和负数。此时，印度已建立起基于位值的数字系统，并且在印度数字系统中开始使用零。婆罗摩笈多为负数设计了特殊符号，并将处理正量和负量的规则阐述如下：

A debt minus zero is a debt.
债务减去零仍为债务。

A fortune minus zero is a fortune.
财富减去零仍为财富。

Zero minus zero is a zero.
零减去零等于零。

A debt subtracted from zero is a fortune.
从零中减去债务得到财富。

A fortune subtracted from zero is a debt.
从零中减去财富得到债务。

The product of zero multiplied by a debt or fortune is zero.
零与债务或财富的乘积为零。

The product of zero multiplied by zero is zero.
零与零的乘积为零。

The product or quotient of two fortunes is one fortune.
两个财富的乘积或商为一个财富。

The product or quotient of two debts is one fortune.
两个债务的乘积或商为一个财富。

The product or quotient of a debt and a fortune is a debt.
债务与财富的乘积或商为债务。

The product or quotient of a fortune and a debt is a debt.
财富与债务的乘积或商为债务。

在这里插入图片描述

The conflict between geometry and algebra

几何学与代数学的冲突

The ancient Greeks did not really address the problem of negative numbers, because their mathematics was founded on geometrical ideas. Lengths, areas, and volumes resulting from geometrical constructions necessarily all had to be positive. Their proofs consisted of logical arguments based on the idea of magnitude. Magnitudes were represented by a line or an area, and not by a number (like 4.3 metres or 26.5 cubic centimetres). In this way they could deal with ‘awkward’ numbers like square roots by representing them as a line. For example, you can draw the diagonal of a square without having to measure it (see note 2 below).
古希腊人并未真正探讨过负数问题，因为他们的数学建立在几何思想之上。通过几何作图得到的长度、面积和体积在本质上都必然是正数。他们的证明是基于“量”的概念展开的逻辑论证。“量”用线段或面积表示，而非用数字（如 4.3 米或 26.5 立方厘米）表示。这样一来，他们就能将平方根这类“棘手”的数用线段表示，从而进行处理。例如，无需测量就能画出正方形的对角线（见下文注释 2）。

About 300 CE, the Alexandrian mathematician Diophantus (200 - c.284 CE) wrote his Arithmetica , a collection of problems where he developed a series of symbols to represent the ‘unknown’ in a problem, and powers of numbers. He dealt with what we now call linear and quadratic equations. In one problem Diophantus wrote the equivalent of $4 = 4 x + 20$ which would give a negative result, and he called this result ‘absurd’.
公元 300 年左右，亚历山大城的数学家丢番图（Diophantus，200-约 284）撰写了《算术》（Arithmetica）。这部著作收录了一系列数学问题，丢番图在书中创造了一套符号来表示问题中的“未知数”以及数的幂。他研究了我们现在所说的一次方程和二次方程。在其中一个问题中，丢番图写出了相当于 $4 = 4 x + 20$ 的等式，这个等式的解是负数，而他称这个结果“荒谬”。

In the 9th century in Baghdad Al - Khwarizmi (c.780 - c.850 CE) presented six standard forms for linear or quadratic equations and produced solutions using algebraic methods and geometrical diagrams. In his algebraic methods he acknowledged that he derived ideas from the work of Brahmagupta and therefore was happy with the notion of negative numbers. However, his geometrical models (based on the work of Greek mathematicians) persuaded him that negative results were meaningless (how can you have a negative square?). In a separate treatise on the laws of inheritance, Al-Khwarizmi represents negative quantities as debts.
9 世纪时，在巴格达，花拉子米（Al-Khwarizmi，约 780-约 850）提出了一次方程或二次方程的六种标准形式，并运用代数方法和几何图形给出了求解过程。在代数方法层面，他承认自己的思想源自婆罗摩笈多的著作，因此认可负数的概念。然而，他基于古希腊数学家成果建立的几何模型却让他认为，负的结果是没有意义的（毕竟怎么会有负的正方形面积呢？）。在另一部关于继承法的专著中，花拉子米将负量表示为债务。

In the 10th century Abul - Wafa (940-998 CE) used negative numbers to represent a debt in his work on ‘what is necessary from the science of arithmetic for scribes and businessmen’?. This seems to be the only place where negative numbers have been found in medieval Arabic mathematics. Abul-Wafa gives a general rule and gives a special case where subtraction of 5 from 3 gives a “debt” of 2. He then multiples this by 10 to obtain a “debt” of 20, which when added to a ‘fortune’ of 35 gives 15.
10 世纪时，阿布·瓦法（Abul-Wafa，940-998）在其著作《文书与商人必备算术知识》（“what is necessary from the science of arithmetic for scribes and businessmen”）中，用负数表示债务。这似乎是在中世纪阿拉伯数学中唯一发现负数的地方。阿布·瓦法提出了一条通用法则，并给出了一个特例：用 3 减去 5，得到的“债务”为 2；随后将这个“债务”乘以 10，得到“债务”20；再将其与“财富”35 相加，结果为 15。

In the 12th century Al - Samawal (1130 - 1180) had produced an algebra where he stated that:
12 世纪时，萨马瓦尔（Al-Samawal，1130-1180）撰写了一部代数学著作，其中他指出：

if we subtract a positive number from an ‘empty power’, the same negative number remains,
若从“空幂”中减去一个正数，结果仍为同一个负数；

if we subtract the negative number from an ‘empty power’, the same positive number remains,
若从“空幂”中减去一个负数，结果仍为同一个正数；

the product of a negative number by a positive number is negative, and by a negative number is positive.
负数与正数的乘积为负数，负数与负数的乘积为正数。

Negative numbers did not begin to appear in Europe until the 15th century when scholars began to study and translate the ancient texts that had been recovered from Islamic and Byzantine sources. This began a process of building on ideas that had gone before, and the major spur to the development in mathematics was the problem of solving quadratic and cubic equations.
直到 15 世纪，当学者们开始研究和翻译从伊斯兰世界及拜占庭帝国流传下来的古代文献时，负数才开始在欧洲出现。这开启了在已有数学思想基础上继续发展的进程，而求解二次方程和三次方程的问题则成为了推动数学发展的主要动力。

As we have seen, practical applications of mathematics often motivate new ideas and the negative number concept was kept alive as a useful device by the Franciscan friar Luca Pacioli (1445 - 1517) in his Summa published in 1494, where he is credited with inventing double entry book-keeping.
正如我们所见，数学的实际应用往往会催生新思想。方济各会修士卢卡·帕乔利（Luca Pacioli，1445-1517）在其 1494 年出版的《算术、几何、比及比例概要》（Summa）中，将负数概念作为一种实用工具保留了下来。他也因在该书中发明复式记账法而闻名。

Solving equations

方程求解

The story of the solution of equations begins in Italy in the 16th century (see note 3 below). This story is full of intrigue and deception because methods of solution were kept secret. The issue which caused most consternation at the time was the meaning of $\sqrt{-1}$ . In fact, Cardano (1501 - 1576) in his Ars Magna of 1545 had to solve a problem where $\sqrt{-15}$ appeared.
方程求解的历程始于 16 世纪的意大利（见下文注释 3）。这段历程充满了阴谋与欺骗，因为当时的求解方法都被秘而不宣。彼时最令人困惑的问题是 $\sqrt{-1}$ 的含义。事实上，卡尔达诺（Cardano，1501-1576）在其 1545 年出版的《大术》（Ars Magna）中，就曾遇到一个需要求解包含 $\sqrt{-15}$ 的问题。

Cardano found a sensible answer (see note 4 below) by working through the algorithm, but he called these numbers ‘ficticious’ because not only did they disappear during the calculation, but they did not seem to have any real meaning. However, by 1572, the Italian engineer, Bombelli (1526 - 1572) had provided the correct rules for working with these ‘imaginary’ numbers(see note 5 below).
卡尔达诺按照算法逐步计算，得到了一个合理的答案（见下文注释 4），但他将这类数称为“虚构的”（ficticious），因为它们不仅会在计算过程中消去，而且似乎没有任何实际意义。然而，到了 1572 年，意大利工程师邦贝利（Bombelli，1526-1572）已经给出了处理这些“虚数”（imaginary numbers）的正确法则（见下文注释 5）。

In the 17th and 18th century, while they might not have been comfortable with their ‘meaning’ many mathematicians were routinely working with negative and imaginary numbers in the theory of equations and in the development of the calculus.
在 17、18 世纪，尽管许多数学家可能对负数和虚数的“含义”仍感不适，但他们已在方程理论和微积分的发展中常规性地使用这两类数了。

The English mathematician, John Wallis (1616 - 1703) is credited with giving some meaning to negative numbers by inventing the number line, and in the early 18th century a controversy ensued between Leibniz, Johan Bernoulli, Euler and d’Alembert about whether $\log(-x)$ was the same as $\log(x)$ .
英国数学家约翰·沃利斯（John Wallis，1616-1703）因发明数轴而为负数赋予了一定含义，这一贡献广受认可。18 世纪早期，莱布尼茨（Leibniz）、约翰·伯努利（Johan Bernoulli）、欧拉（Euler）和达朗贝尔（d’Alembert）之间还引发了一场争论，争论的焦点是 $\log(-x)$ 与 $\log(x)$ 是否相等。

在这里插入图片描述

By the beginning of the 19th century Caspar Wessel (1745 - 1818) and Jean Argand (1768 - 1822) had produced different mathematical representations of ‘imaginary’ numbers, and around the same time Augustus De Morgan (1806 - 1871), George Peacock (1791 - 1858), William Hamilton (1805 - 1865) and others began to work on the ‘logic’ of arithmetic and algebra and a clearer definition of negative numbers, imaginary quantities, and the nature of the operations on them began to emerge.
到了 19 世纪初，卡斯帕·韦塞尔（Caspar Wessel，1745-1818）和让·阿尔冈（Jean Argand，1768-1822）分别提出了“虚数”的不同数学表示方法。与此同时，奥古斯都·德摩根（Augustus De Morgan，1806-1871）、乔治·皮科克（George Peacock，1791-1858）、威廉·哈密顿（William Hamilton，1805-1865）等人开始研究算术和代数的“逻辑基础”，关于负数、虚数的更清晰定义，以及对这两类数进行运算的本质，也逐渐开始形成。

Negative numbers and imaginaries are now built into the mathematical models of the physical world of science, engineering and the commercial world.
如今，负数和虚数已融入科学、工程等领域描述物理世界的数学模型，以及商业领域的数学模型中。

There are many applications of negative numbers today in banking, commodity markets, electrical engineering, and anywhere we use a frame of reference as in coordinate geometry, or relativity theory.
如今，负数在多个领域都有广泛应用，如银行业、商品市场、电气工程，以及任何需要使用参考系的领域（如解析几何或相对论）。

Pedagogical Note:

教学说明：

It seems that the problems that people had (and now have - see the Lottery incident ) in understanding the use of negative numbers concerns:
人们过去（乃至现在）在理解负数用法时遇到的问题（见“彩票事件”），似乎主要涉及以下几点：

the difference between the operation of subtraction and the object (a negative number), since the same sign is used for both
一是减法运算与（作为运算对象的）负数之间的区别——因为两者使用相同的符号；

the language involved like ‘minus minus 3’ as opposed to ‘subtract negative 3’
二是相关表述的混淆，如“minus minus 3”（负负 3）与“subtract negative 3”（减去负 3）；

separating the physical model or analogy (be it profit/loss or rise/fall in temperature or rotation/direction in the plane) from the rules of operating on the entities.
三是难以将物理模型或类比（无论是盈利/亏损、温度上升/下降，还是平面内的旋转/方向）与对负数本身的运算规则区分开来。

References

参考文献

English Mathematicians

英国数学家

Francis Maseres (1731 - 1824)
A dissertation on the use of the negative sign in algebra. (1758)
Fellow of Clare College Cambridge and Fellow of the Royal Society
弗朗西斯·马塞雷斯（Francis Maseres，1731-1824）
《代数中负号用法的专题论述》（A dissertation on the use of the negative sign in algebra），1758 年；
剑桥大学克莱尔学院研究员、英国皇家学会会员。
William Frend
Principles of Algebra (1796)
Printed by J. Davis, for G. G. and J. Robinson, Paternoster Row
威廉·弗伦德（William Frend）
《代数原理》（Principles of Algebra），1796 年；
由 J. 戴维斯（J. Davis）印刷，为 G. G. 与 J. 罗宾逊（J. Robinson）出版，出版地：帕特诺斯特街（Paternoster Row）。

Other Sources

其他文献来源

Berggen, J.L. (1986) Episodes in the Mathematics of Mediaeval Islam . Springer-Verlag N.Y. and Berlin.
伯格根（Berggen, J.L.），1986 年，《中世纪伊斯兰数学史话》（Episodes in the Mathematics of Mediaeval Islam），施普林格出版社（Springer-Verlag），纽约与柏林。
Menninger, K. (1969) Number Words and Number Symbols . M.I.T. Press Cambridge, Mass. and London.
门宁格（Menninger, K.），1969 年，《数字词汇与数字符号》（Number Words and Number Symbols），麻省理工学院出版社（M.I.T. Press），马萨诸塞州剑桥市与伦敦。
Schubring, G. (2005) Conflicts Between Generalization, Rigor, and Intuition: Number Concepts Underlying the Development of Analysis in 17 - 19th Century France and Germany . Springer-Verlag N.Y.
舒布林（Schubring, G.），2005 年，《推广、严谨与直觉的冲突：17-19 世纪法德两国分析学发展背后的数概念》（Conflicts Between Generalization, Rigor, and Intuition: Number Concepts Underlying the Development of Analysis in 17-19th Century France and Germany），施普林格出版社（Springer-Verlag），纽约。
Ifrah, G. (1998) The Universal History of Numbers . Harvill Press, London.
伊夫拉（Ifrah, G.），1998 年，《数的通用史》（The Universal History of Numbers），哈维尔出版社（Harvill Press），伦敦。
Li Yan and Du Shiran (Tr. Crossley, J.N and Lun A. W. ) (1987) Chinese Mathematics: a Concise History . O.U.P. Oxford.
李俨、杜石然，1987 年，《中国数学简史》（Chinese Mathematics: a Concise History），由克罗斯利（Crossley, J.N）与伦（Lun, A.W.）翻译，牛津大学出版社（O.U.P.），牛津。

Notes

注释

The counting rod system was certainly in operation in the period (475 - 221 BCE) - called the period of the ‘Warring States’ [Yan and Shiran 1987, 7/8])
算筹系统在公元前 475-公元前 221 年的“战国时期”就已在使用[李俨、杜石然，1987 年，第 7-8 页]。
In our notation, $\sqrt{2}$ and $\sqrt{5}$ occurred when finding the diagonal of a square or constructing the Golden Section.
在我们现在的表示法中，求正方形的对角线或构造黄金分割时，会用到 $\sqrt{2}$ 和 $\sqrt{5}$ 。
The period from Pacioli (1494) to Descartes (1637), a period of about 150 years brings the solution of equations to a stage where they could be understood by school pupils today.
从帕乔利（1494 年）到笛卡尔（1637 年）的这段时期，时长约 150 年，它将方程求解发展到了如今的学生也能理解的程度。
In modern notation, Cardano’s multiplication was $\sqrt{-15})(5 + \sqrt{-15})$ , and applying the rule for brackets this becomes $(\sqrt{-15})^2 = 25 - (-15) = 40$ .
用现代表示法来看，卡尔达诺的乘法运算为 $\sqrt{-15})(5 + \sqrt{-15})$ ，运用去括号法则展开后，该式变为 $(\sqrt{-15})^2 = 25 - (-15) = 40$ 。
Even though mathematicians did not find a suitable representation for negative numbers, it did not prevent them from following the ordinary rules of arithmetic and developing rules for the imaginary numbers as well. This is where the beauty of mathematical invention is not limited by the ‘real’ world.
尽管数学家们当时尚未找到负数的合适表示方法，但这并未阻碍他们遵循常规的算术法则，也未阻碍他们进一步制定虚数的运算规则。这正是数学创造之美——它不受“现实”世界的限制。

Negative numbers

负数

Nowadays we use negative numbers in many contexts and, as a result, they seem perfectly natural to us. That’s because we’ve been taught to see numbers as a continuous number line, stretching out from zero in both the positive and negative directions. To us, $- 3$ is just as real as $+ 3$ is, but this was not always the case. Negative numbers have only fairly recently become accepted as part of the system of numbers that mathematicians are allowed to use. While a great deal of very advanced maths was developed by ancient civilisations, mathematicians in most cultures had no understanding of what a negative number could mean. In this article we’re going to explore some of the earliest appearances of negative numbers and how attitudes towards them have changed over the centuries.
如今，我们在许多场景中都会使用负数，因此负数对我们而言似乎是理所当然的存在。这是因为我们在学习中被引导将数视为一条连续的数轴，从零出发，向正、负两个方向延伸。对我们来说， $- 3$ 和 $+ 3$ 一样真实，但情况并非一直如此。负数是近些年才被接纳为数学家可使用的数系的一部分。尽管古代文明已发展出大量高深的数学知识，但大多数文化中的数学家都无法理解负数的含义。在本文中，我们将探寻负数最早的一些出现场景，以及几个世纪以来人们对负数的态度如何变迁。

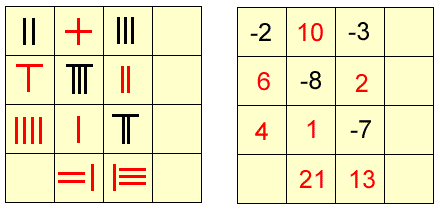
Among the earliest people to use negative numbers in calculations were the ancient Chinese. They used counting rods to perform calculations, with red rods for positive numbers and black rods for negative numbers. The example below shows some Chinese numerals represented by rods, and the diagram on the right shows which numbers these symbols represent.
古代中国人是最早在计算中使用负数的人群之一。他们用算筹进行计算，其中红色算筹表示正数，黑色算筹表示负数。下方示例展示了一些用算筹表示的中国数字，右侧图表则标注了这些符号所代表的具体数值。

在这里插入图片描述

Indian mathematicians also used negative numbers long before Western civilisations. An ancient manuscript from 200 BC shows that they used to use the $+$ sign that we now associate with addition and positive numbers, to denote a negative number. Although negative numbers were used in calculations, negative answers to mathematical problems were usually considered meaningless and were discarded.
印度数学家也比西方文明早很久就使用了负数。一份公元前 200 年的古老手稿显示，他们曾使用如今我们用来表示加法和正数的 $+$ 符号来表示负数。尽管负数被用于计算，但数学问题的负答案通常被认为毫无意义，会被舍弃。

The ancient Greeks also dismissed any solutions to equations that came out negative. They called them “absurd” and “impossible” and completely ignored them. They couldn’t see how a negative answer could be meaningful, because it was not possible to have a quantity that was less than nothing. This opinion was passed down to later mathematicians in Europe for more than a thousand years, so very little progress in negative number arithmetic was made for a long time.
古希腊人同样摒弃方程所有得出负数的解。他们称这些解“荒谬”（absurd）且“不可能”（impossible），并完全无视它们。古希腊人无法理解负答案如何能具有意义，因为他们认为不存在“小于零”的量。这种观点在随后的一千多年里传给了欧洲后世的数学家，因此在很长一段时间里，负数算术的发展几乎停滞不前。

Can you think of something in the real world where you can have a negative quantity that actually means something? Today we are quite familiar with the idea of somebody being in debt and therefore having a negative amount of money. It means that they have no money in their possession, and actually owe someone else money as well. It’s not a very nice position to be in, but debt is a form of negative quantity that has been around for thousands of years. In fact calculations involving money were the only ones that were allowed to have negative answers, but most mathematicians weren’t interested in that kind of problem.
你能想到现实世界中存在具有实际意义的“负量”吗？如今，我们对“某人负债，因此拥有负金额的钱”这一概念相当熟悉。这意味着此人手中没有钱，甚至还欠着别人的钱。负债并非理想状态，但“债务”作为一种负量，已经存在了数千年。事实上，只有涉及金钱的计算才被允许出现负答案，而大多数数学家对这类问题并不感兴趣。

So, even though everyone was quite happy to allow subtraction, and could understand the notion of debt, it took centuries before mathematicians understood or accepted that negative numbers could exist as genuine numbers in their own right. In 1759 Francis Meseres wrote that negative numbers:
因此，尽管所有人都完全接受减法运算，也能理解债务的概念，但数学家们花了几个世纪才理解并接纳“负数本身可作为真正的数存在”这一事实。1759 年，弗朗西斯·马塞雷斯（Francis Meseres）曾这样评价负数：

“darken the very whole doctrines of the equations and to make dark of the things which are in their nature excessively obvious and simple. It would have been desirable in consequence that the negative roots were never allowed in algebra or that they were discarded” .

“（负数）会使整个方程理论变得晦涩难懂，还会把本质上极其清晰简单的事物弄得模糊不清。因此，理想的情况是，代数中永远不允许出现负根，或将其舍弃。”

Even as late as 1803 the famous French mathematician Carnot was worried about the reality of negative numbers:
即便到了 1803 年，法国著名数学家卡诺（Carnot）仍对负数的真实性表示担忧：

“to really obtain an isolated negative quantity, it would be necessary to cut off an effective quantity from zero, to remove something of nothing: impossible operation. How thus to conceive an isolated negative quantity?”
“若要真正得到一个孤立的负量，就必须从零中切去一个有效量，从无中移除某物——这是不可能的操作。那么，该如何理解一个孤立的负量呢？”

Some mathematicians in the 17th century discovered that negative numbers did have their uses. Provided they didn’t worry about what negative numbers meant, and more particularly what the square roots of negative numbers meant, they found that they could solve some very tricky equations, like cubic and quartic equations. What’s more, although the intermediate steps of a calculation may have involved negative numbers, the solution often came out as a real, positive number which was exactly what they wanted.
17 世纪的一些数学家发现，负数确实有其用途。只要他们不去纠结负数的含义——尤其是负平方根的含义，就能用负数解决一些非常复杂的方程，比如三次方程（cubic equations）和四次方程（quartic equations）。此外，尽管计算的中间步骤可能涉及负数，但最终解往往是一个真实的正数，而这正是他们所需要的。

Since then mathematicians and scientists have found all sorts of uses for negative numbers. We now recognise that in many cases a negative answer can be a real, meaningful solution and can be thought of in terms of direction. For instance, if I wanted to calculate how many steps forward Robert has taken, and the answer is $- 5$ , then it means he has taken 5 steps backwards. The first person to recognise the link between negative numbers and direction was John Wallis, a mathematician in the 17th century. He was the first to come up with the idea of a number line as a geometrical representation of the number system. Confusingly however, he also thought that negative numbers were larger than infinity!
从那以后，数学家和科学家们为负数找到了各种各样的用途。如今我们认识到，在许多情况下，负答案可以是真实、有意义的解，并且可以从“方向”的角度去理解。例如，若我想计算罗伯特向前走了多少步，而结果是 $- 5$ ，这就意味着他向后走了 5 步。17 世纪的数学家约翰·沃利斯（John Wallis）是首位发现负数与方向关联的人，他也是首个提出“数轴”概念的人——将数轴作为数系的几何表示。但令人困惑的是，他还认为负数比无穷大更大！

在这里插入图片描述

Nowadays we use negative numbers just like any other numbers without even a second thought. Their troubled history shows how the simple mathematical principles we take for granted have taken thousands of years to develop. Physical meaning has given way to algebraic utility, but negative numbers and their derivatives have turned out to have all kinds of practical applications. Take the square root of $- 1$ for example - it seems meaningless in itself, but many calculations in science and engineering wouldn’t be possible without it.
如今，我们使用负数时就像使用其他任何数一样，不假思索。负数坎坷的历史表明，那些我们视为理所当然的简单数学原理，其实经历了数千年才发展成熟。尽管其物理意义已让位于代数实用性，但负数及其衍生概念（如虚数）已被证明具有各种各样的实际应用。以 $- 1$ 的平方根（即虚数单位 $i$ ）为例——它本身看似毫无意义，但如果没有它，科学和工程领域的许多计算都无法进行。