对数 | 历史发展、理论及应用

原创已于 2025-11-01 16:50:26 修改 · 350 阅读

4 ·

CC 4.0 BY-SA版权

文章标签：

#对数 | 历史

于 2025-10-31 16:12:16 首次发布

mathematics 专栏收录该内容

189 篇文章

订阅专栏

注：本文为 “对数 | 历史发展与应用” 相关合辑。
英文引文，机翻未校。
图片清晰度受引文原图所限。
略作重排，如有内容异常，请看原文。

Logarithms: A History of Mathematics and Technology

对数：数学与技术的历史

Logarithms are a fundamental mathematical concept that has greatly advanced mathematics, science, and technology. By transforming complex multiplication into simple addition, logarithms have completely changed the way calculations are performed and have laid the foundation for advancements in astronomy, engineering, and physics.
对数是一种基本的数学概念，极大地推动了数学、科学和技术的发展。通过对复杂乘法运算转化为简单的加法运算，对数彻底改变了计算方式，并为天文学、工程学和物理学的进步奠定了基础。

The Origin of Logarithms: Napier’s Insight

对数的起源：纳皮尔的洞察

The concept of logarithms was first introduced by the Scottish mathematician John Napier (1550–1617) in the early 17th century. In 1614, Napier published his groundbreaking work “Mirifici Logarithmorum Canonis Descriptio,” which provided logarithm tables and explained their applications. Napier’s motivation stemmed from the cumbersome calculations required for astronomical observations and navigation. Logarithms offered a way to simplify these calculations, reducing the time and effort needed.
对数的概念最早由苏格兰数学家约翰·纳皮尔（John Napier，1550–1617）在 17 世纪初提出。1614 年，纳皮尔出版了他的开创性著作《奇妙对数表的描述》（Mirifici Logarithmorum Canonis Descriptio），提供了对数表并解释了其应用。纳皮尔的动机源于天文观测和航海所需的繁琐计算。对数提供了一种简化这些计算的方法，减少了所需的时间和精力。

Napier defined logarithms as a relationship between geometric and arithmetic sequences. Although his definition differs from the modern common logarithms (base $10$ ) or natural logarithms, it established the fundamental idea of linking multiplication to addition through a logarithmic scale.
纳皮尔将对数定义为几何序列和算术序列之间的关系。尽管他的定义与现代的常用对数（以 $10$ 为底）或自然对数不同，但它建立了通过对数尺度将乘法与加法联系起来的基本思想。

Henry Briggs and Common Logarithms

亨利·布里格斯与常用对数

Shortly after Napier’s work was published, the English mathematician Henry Briggs (1561–1630) improved and popularized the concept of logarithms. Briggs collaborated with Napier to propose logarithms with base $10$ , also known as common logarithms. In 1617, Briggs published “Logarithmorum Chilias Prima,” which contained the first logarithm tables with base $10$ .
在纳皮尔的著作出版后不久，英国数学家亨利·布里格斯（Henry Briggs，1561–1630）改进并普及了对数的概念。布里格斯与纳皮尔合作，提出了以 $10$ 为底的对数，也称为常用对数。1617 年，布里格斯出版了《对数初千》（Logarithmorum Chilias Prima），其中包含了第一张以 $10$ 为底的对数表。

Briggs’ base- $10$ system was more intuitive and practical, as it aligned with the widely used decimal system in Europe at the time. This improvement made logarithms more accessible to a broader audience, including scientists, engineers, and navigators.
布里格斯的以 $10$ 为底的系统更直观、实用，因为它与当时欧洲广泛使用的十进制系统一致。这一改进使对数为更广泛的受众所接受，包括科学家、工程师和航海家。

Logarithmic Scales: Slide Rules and Early Calculators

对数尺度：计算尺和早期计算器

One of the earliest applications of logarithms was the development of the slide rule. In 1622, the English mathematician William Oughtred invented the circular slide rule, which utilized logarithmic scales for rapid calculations. By the mid-17th century, linear slide rules became a common tool for scientists, engineers, and students.
对数最早的应用之一是计算尺的发展。1622 年，英国数学家威廉·奥特雷德（William Oughtred）发明了圆形计算尺，利用对数尺度进行快速计算。到 17 世纪中期，线性计算尺成为科学家、工程师和学生的常用工具。

The slide rule, as an important computing device, was used for over 300 years until the advent of electronic calculators in the mid-20th century. It relied on the principles of logarithms, proving the enduring value of logarithms in simplifying calculations.
计算尺作为一种重要的计算设备使用了 300 多年，直到 20 世纪中期电子计算器的出现。它依赖对数原理，证明了对数在简化计算中的持久价值。

Applications in Astronomy and Navigation

对数在天文学和航海中的应用

During the 17th and 18th centuries, logarithms played a crucial role in advancing astronomy and navigation. Astronomers such as Johannes Kepler and Isaac Newton relied on logarithm tables for complex calculations related to planetary motion and celestial mechanics. By reducing the computational burden, logarithms enabled astronomers to make precise predictions and refine their models of the universe.
在 17 和 18 世纪，对数在推动天文学和航海方面发挥了关键作用。像约翰内斯·开普勒（Johannes Kepler）和艾萨克·牛顿（Isaac Newton）这样的天文学家依赖对数表来进行与行星运动和天体力学相关的复杂计算。通过对计算负担的减少，对数使天文学家能够进行精确的预测，并完善他们对宇宙的模型。

Navigators also benefited from logarithms, particularly in determining longitude and calculating maritime distances. The efficiency of logarithm tables enabled sailors to increase the accuracy of their chart plotting and voyages.
航海家也从对数中受益，特别是在确定经度和计算海上距离方面。对数表的效率使航海者能够提高他们在绘制航线和进行探险中的准确性。

Natural Logarithms and Euler’s Contributions

自然对数与欧拉的贡献

Although Napier and Briggs focused on base- $10$ logarithms, the natural logarithms (logarithms with base $e$ ) emerged as an important concept in mathematics and science. The irrational number $e$ (approximately $2.718$ ) is a fundamental constant that naturally appears in many areas, including calculus, exponential growth, and complex analysis.
尽管纳皮尔和布里格斯专注于以 $10$ 为底的对数，但自然对数（以 $e$ 为底的对数）作为数学和科学中的一个重要概念出现了。无理数 $e$ （约等于 $2.718$ ）是一个基本常数，它自然地出现在许多领域，包括微积分、指数增长和复分析。

The Swiss mathematician Leonhard Euler (1707–1783) played a key role in popularizing natural logarithms. Euler formally established the connection between logarithms and exponential functions, introduced the notation $e^x$ , and cemented the logarithm as the inverse function of the exponential. His work laid the foundation for modern calculus and analysis, influencing generations of mathematicians to come.
瑞士数学家莱昂哈德·欧拉（Leonhard Euler，1707–1783）在推广自然对数方面发挥了关键作用。欧拉正式确立了对数与指数函数之间的联系，引入了 $e^x$ 的符号，并将对数确立为指数函数的反函数。他的工作为现代微积分和分析奠定了基础，影响了后续几代数学家。

Logarithms in the Age of Scientific Revolution

科学革命时代的对数

The 17th and 18th centuries marked significant scientific advancements, many of which relied on logarithms. For example:
17 和 18 世纪标志着重大的科学进步，其中许多都依赖于对数。例如：

Isaac Newton used logarithms in developing calculus and the theory of gravitation, enabling him to make precise calculations of forces and motion.
艾萨克·牛顿（Isaac Newton）在发展微积分和引力理论中使用了对数，使他能够精确计算力和运动。
Robert Hooke and Edmond Halley applied logarithmic principles to understand the inverse-square law of gravitation, a fundamental concept in physics and astronomy.
罗伯特·胡克（Robert Hooke）和埃德蒙·哈雷（Edmond Halley）应用对数原理来理解引力的平方反比定律，这是物理学和天文学的基础。
Gottfried Wilhelm Leibniz, a co-founder of calculus, integrated the concept of logarithms into his work on infinitesimal calculus and mathematical notation.
戈特弗里德·威廉·莱布尼茨（Gottfried Wilhelm Leibniz，微积分的共同创始人）将对数概念整合到他的无穷小微积分和数学符号工作中。

These applications demonstrate how logarithms became a cornerstone of the Scientific Revolution, driving progress in multiple disciplines.
这些应用表明了对数如何成为科学革命的基石，推动了多个学科的进步。

The Modern Evolution of Logarithms

对数的现代转变

As mathematics continued to evolve in the 18th and 19th centuries, logarithms continued to adapt. The introduction of digital and mechanical calculators made traditional logarithm tables obsolete, but the fundamental principles of logarithms remained a core part of mathematics and science.
随着 18 和 19 世纪数学的发展，对数继续演变。数字和机械计算器的引入使传统的对数表过时了，但对数的基本原理仍然是数学和科学的核心部分。

In the 19th century, mathematicians such as Carl Friedrich Gauss and Augustin-Louis Cauchy further refined the theoretical understanding of logarithms within the context of complex analysis and number theory. Their work helped solidify logarithms as a fundamental tool in advanced mathematics.
在 19 世纪，像卡尔·弗里德里希·高斯（Carl Friedrich Gauss）和奥古斯丁-路易·柯西（Augustin-Louis Cauchy）这样的数学家进一步完善了对数在复分析和数论中的理论理解。他们的工作帮助巩固了对数作为高级数学中的一个基本工具的地位。

Today, logarithms remain essential in various fields, including computer science, information theory, and financial mathematics. They continue to be a fundamental concept taught in mathematics education worldwide.
如今，对数仍然在计算机科学、信息论和金融数学等多个领域中发挥着重要作用。它们仍然是全球数学教育中的一个基本概念。

The Impact of Logarithms on Mathematics and Science

对数对数学和科学的影响

Logarithms have profoundly influenced the development of mathematics and science. By simplifying calculations, they accelerated the progress of disciplines like astronomy, physics, and engineering.
对数深刻地影响了数学和科学的发展。通过对复杂计算的简化，它们加速了天文学、物理学和工程学等学科的进步。

Logarithms also enriched the mathematical framework, contributing to fields such as calculus, number theory, and complex analysis.
对数还丰富了数学框架，为微积分、数论和复分析等领域做出了贡献。

Beyond their practical applications, logarithms embody the power of abstraction in mathematics. They demonstrate how a simple idea—relating multiplication to addition—can unlock profound insights into the natural world.
除了实际应用之外，对数体现了数学中抽象的力量。它们展示了如何通过一个简单的想法——将乘法与加法联系起来——来揭示自然世界的深刻见解。

—

The Digital Age and Logarithms

数字时代与对数

With the advent of digital technology, the role of logarithms has evolved. While electronic calculators and computers have largely replaced manual logarithm tables, the underlying principles of logarithms are still deeply embedded in digital algorithms and data processing.
随着数字技术的到来，对数的作用已经发生了演变。尽管电子计算器和计算机在很大程度上取代了手动对数表，但对数的基本原理仍然深深嵌入在数字算法和数据处理中。

For example, logarithms are used in the design of efficient algorithms for sorting and searching data. The time complexity of many algorithms is expressed using logarithmic functions, such as $O(\log n)$ , which indicates that the time required to process data grows logarithmically with the size of the input.
例如，对数被用于设计高效的排序和搜索数据的算法。许多算法的时间复杂度用对数函数表示，如 $O(\log n)$ ，这表明处理数据所需的时间随输入大小呈对数增长。

In computer science, logarithms are also crucial for understanding the efficiency of data structures and the performance of computational processes. They help in analyzing how algorithms scale with increasing data sizes and are fundamental in the study of computational complexity.
在计算机科学中，对数对于理解数据结构的效率和计算过程的性能至关重要。它们有助于分析算法如何随着数据量的增加而扩展，并且是计算复杂性研究中的一个基本工具。

Logarithms in Information Theory

信息论中的对数

In information theory, logarithms play a central role in measuring information and entropy. The concept of information entropy, introduced by Claude Shannon in the 1940s, uses logarithms to quantify the amount of uncertainty or information in a message.
在信息论中，对数在测量信息和熵方面发挥着核心作用。信息熵的概念由克劳德·香农在 20 世纪 40 年代引入，使用对数来量化消息中的不确定量或信息量。

The entropy $H$ of a message is calculated using the formula $-\sum p_i \log p_i$ , where $p_i$ is the probability of the $i$ -th possible message. This formula shows that logarithms provide a natural way to measure information content.
消息的熵 $H$ 使用公式 $-\sum p_i \log p_i$ 计算，其中 $p_i$ 是第 $i$ 条可能消息的概率。这个公式表明，对数提供了一种自然的方式来衡量信息内容。

Logarithms are also used in the calculation of channel capacity, which determines the maximum rate at which information can be transmitted over a communication channel without error. This application highlights the importance of logarithms in ensuring reliable and efficient communication systems.
对数还用于计算信道容量，信道容量决定了信息可以在通信信道中无错误传输的最大速率。这一应用突出了对数在确保可靠和高效的通信系统中的重要性。

Financial Mathematics and Logarithms

金融数学中的对数

In financial mathematics, logarithms are used to model exponential growth and decay, which are fundamental concepts in finance. For example, the calculation of compound interest often involves logarithms to determine the time required for an investment to grow to a certain amount.
在金融数学中，对数被用于模拟指数增长和衰减，这是金融学中的基本概念。例如，计算复利通常涉及对数，以确定投资增长到一定金额所需的时间。

The formula for continuous compounding interest is $A = Pe^{rt}$ , where $A$ is the amount of money accumulated after time $t$ , $P$ is the principal amount, $r$ is the interest rate, and $e$ is the base of the natural logarithm. Logarithms are used to solve for $t$ when the other variables are known.
连续复利的公式是 $A = Pe^{rt}$ ，其中 $A$ 是时间 $t$ 后积累的金额， $P$ 是本金， $r$ 是利率， $e$ 是自然对数的底数。当其他变量已知时，对数用于求解 $t$ 。

Logarithms are also used in the Black-Scholes model for pricing options, which is a cornerstone of modern financial theory. This model uses logarithms to handle the exponential nature of asset price movements and to calculate the fair price of options.
对数还用于定价期权的布莱克-舒尔斯模型，这是现代金融理论的基石。该模型使用对数来处理资产价格变动的指数特性，并计算期权的公平价格。

Conclusion

结论

From their origins in the early 17th century to their continued use in modern technology and science, logarithms have proven to be a versatile and essential mathematical tool. They have simplified complex calculations, enabled scientific discoveries, and remain a fundamental part of mathematical education and various scientific disciplines.
从 17 世纪初的起源到在现代技术和科学中的持续使用，对数已被证明是一种多功能且必不可少的数学工具。它们简化了复杂的计算，促成了科学发现，并且仍然是数学教育和各种科学学科的一个基本部分。

Whether in the design of efficient algorithms, the analysis of information systems, or the modeling of financial markets, logarithms continue to play a vital role. Their enduring importance is a testament to the power and elegance of mathematical principles.
无论是在高效算法的设计、信息系统的分析，还是金融市场的建模中，对数继续发挥着至关重要的作用。它们持久的重要性证明了数学原理的力量和优雅。

The history of logarithms is a testament to human ingenuity and the quest for mathematical understanding. From Napier’s original tables to Euler’s contributions to calculus and modern applications in technology, logarithms have shaped the trajectory of mathematics and science.
对数的历史证明了人类的聪明才智和对数学理解的追求。从纳皮尔最初的对数表到欧拉对微积分的贡献以及在现代技术中的应用，对数塑造了数学和科学的发展轨迹。

Their ability to simplify complex problems and provide new perspectives has made them indispensable tools for centuries.
它们简化复杂问题并提供新视角的能力，使它们几个世纪以来一直是不可或缺的工具。

As we continue to explore the frontiers of science and mathematics, the legacy of logarithms reminds us of the enduring value of innovation and collaboration. By building on the work of pioneers like Napier, Briggs, and Euler, we can continue to advance our understanding of the universe and solve the challenges of tomorrow.
当我们继续探索科学和数学的前沿时，对数的遗产提醒我们创新和合作的持久价值。通过在纳皮尔、布里格斯和欧拉等先驱的工作基础上进行建设，我们可以继续推进对宇宙的理解并解决未来的挑战。

What is the natural log, and why do we need it

什么是“自然”对数？我们为何需要它？

History & The Natural Log

历史与自然对数

A logarithm can have any positive value (other than 1) as its base, but logs with two particular bases are generally regarded as being more useful than the others: the “common” log with a base of 10, and the “natural” log with a base of the number $e$ .
对数的底数可以是任意正数值（1 除外），但以两个特定数值为底的对数通常被认为比其他对数更实用：以 10 为底的“常用”对数，以及以数字 $e$ 为底的“自然”对数。

(There is also the base-2 log, favored by computer-science types, because computers are built on the base-two binary system.)
（此外还有以 2 为底的对数，深受计算机科学领域人员青睐，因为计算机是基于二进制（以 2 为底）系统构建的。）

What is the common log?

常用对数

The common log is the base-10 log. It was also the first form of logarithm, back when logs were invented. The common log is popular for historical reasons, and is usually written as $\text{log}(x)$ ; that is, without the base being included. For instance, pH (being the measure of a substance’s acidity or alkalinity), decibels (being the measure of sound intensity), and the Richter scale (being the measure of earthquake intensity) all involve base-10 logs.
常用对数是以 10 为底的对数。在对数刚被发明时，它也是第一种对数形式。由于历史原因，常用对数应用广泛，其通常表示为 $\text{log}(x)$ ，即不标注底数。例如，pH 值（衡量物质酸碱度的指标）、分贝（衡量声音强度的单位）以及里氏震级（衡量地震强度的等级），均涉及以 10 为底的对数。

So if a log has no base written, you should generally (at least in your algebra classes) assume that the base is 10. (This is similar to the assumption we make when a radical has no index included; that is, we assume [correctly] that the radical is a square root.)
因此，若一个对数未标注底数，通常（至少在代数课程中）可默认其底数为 10。（这与根式未标注根指数时的默认规则类似：我们会（正确地）默认该根式为平方根。）

What is the natural log?

自然对数

The natural log is the base- $e$ log, where $e$ is the natural exponential (expofcns4.htm), being a number that is approximately equal to 2.71828. The natural log has its own notation, being denoted as $\ln(x)$ and usually pronounced as “ell-enn-of-x”. (Note: That’s “ell-enn”, not “one-enn” or “eye-enn”.) Just as the number $\pi$ arises naturally in geometry, so also $e$ arises naturally (http://www.amazon.com/Story-Number-Princeton-ScienceLibrary/dp/0691141347/) in math and the sciences. As a result, the natural log is common in science and finance, which is why you need to be familiar with it.
自然对数是以 $e$ 为底的对数，其中 $e$ 代表自然指数，其近似值约为 2.71828。自然对数有专属符号，记为 $\ln(x)$ ，通常读作“ell-enn-of-x”（注：是“ell-enn”，而非“one-enn”或“eye-enn”）。正如数字 $\pi$ 在几何学中自然出现一样，数字 $e$ 也在数学和科学领域自然涌现。因此，自然对数在科学和金融领域应用广泛，这也是你需要熟悉它的原因。

Because the common and natural logs are pretty much the only logs that are used “in real life”, these are the only two for which you have calculator keys. Make sure you know where these keys are, and how to use them.
由于常用对数和自然对数几乎是“实际应用”中仅有的两种对数，因此计算器上也只为这两种对数设置了专属按键。请务必确认你知道这些按键的位置及其使用方法。

What is the difference between “log” and “ln”?

“log”与“ln”的区别

The difference between “log” and “ln” is their bases. The “log” has a base of 10 and the “ln” has a base of $e \approx 2.71828$ .
“log”与“ln”的区别在于它们的底数。“log”的底数为 10，而“ln”的底数为 $e \approx 2.71828$ 。

Why the natural log’s notation is ln rather than nl

为何自然对数的符号是“ln”而非“nl”

Why would the natural log be denoted by ln, rather than by “nl”? One popular idea relates to Euler (his name is pronounced as “OY-lur”), who was one of the guys connected to the natural exponential (expofcns5.htm). Euler was Swiss and spoke French, so he might have called the function “le Logarithme Naturel”, rather than “the natural log”, in which case, ln makes sense. However, history shows that Euler actually used the notation “l(x)” for the logarithm using “his” number $e$ as its base.
为何自然对数的符号是“ln”而非“nl”？一种广为流传的说法与欧拉（Euler，发音为“OY-lur”）有关，他是与自然指数相关的学者之一。欧拉是瑞士人，且会说法语，因此他可能将该函数称为“le Logarithme Naturel”（法语，意为“自然对数”），而非“the natural log”（英语，意为“自然对数”），在这种情况下，“ln”的符号就合理了。然而，历史记载显示，欧拉实际上用“l(x)”表示以“他所关联的”数字 $e$ 为底的对数。

Some think the notation came from the use of Latin (which had been in common use among European scholars) for “natural log”, the Latin being “logarithmus nātūrālis”. I’m not aware of any evidence for this, though.
也有人认为，该符号源于“自然对数”的拉丁语表达——“logarithmus nātūrālis”（拉丁语，意为“自然对数”），而拉丁语在当时的欧洲学者中普遍使用。不过，我并未发现支持这一说法的相关证据。

The first published use of the ln notation for the base- $e$ logarithm is generally regarded as being Stringham’s, in his 1893 text “Uniplanar Algebra”. Prof. Stringham was an American, so I have no idea why he would have used the notation ln, other than perhaps to reflect a common, though mistaken, idea that Napier’s log was a base- $e$ log. That is, “ln” might have meant to stand for “Log of Napier”.
普遍认为，首次在出版物中使用“ln”表示以 $e$ 为底的对数的人是斯特林厄姆（Stringham），他在 1893 年的著作《单平面代数》（Uniplanar Algebra）中采用了这一符号。斯特林厄姆教授是美国人，我无法确定他为何使用“ln”这一符号，除非是为了体现一种普遍但错误的观点——即纳皮尔对数（Napier’s log）是以 $e$ 为底的对数。也就是说，“ln”可能是“Log of Napier”（纳皮尔的对数）的缩写。

On the other hand, the German mathematician Anton Steinhauser (https://babel.hathitrust.org/cgi/pt?id=uc1.%24b531832&view=1up&seq=293) appears to have proposed using ln.a to mean “the natural log of a” (“logarithmus naturalis a”) in 1875.
另一方面，德国数学家安东·施泰因豪泽（Anton Steinhauser）似乎在 1875 年就提出用“ln.a”表示“a 的自然对数”（拉丁语：logarithmus naturalis a）。

Mercator (not the map guy) used a Latin form of the term, log naturalis, in his 1668 book on logarithms, and, as of the late 1800s, various Englishspeakers were using the notation log.nat. for the natural logarithm. In short, the origin of this notation seems somewhat obscure, perhaps even unknown - which is unusual for such a recent invention.
麦卡托（Mercator，非地图学家麦卡托）在其 1668 年关于对数的著作中，使用了该术语的拉丁语形式“log naturalis”（意为“自然对数”）；而到了 19 世纪末，各类以英语为母语的人群开始用“log.nat.”表示自然对数。简而言之，“ln”这一符号的起源似乎有些模糊，甚至可能无从考证——对于这样一项较晚出现的发明而言，这种情况并不常见。

Logarithms_ The Early History of a Familiar Function - John Napier Introduces Logarithms

对数：一种熟悉函数的早期历史——约翰·纳皮尔引入对数

Author(s)

Kathleen M. Clark (The Florida State University) and Clemency Montelle (University of Canterbury)
凯瑟琳·M·克拉克（Kathleen M. Clark，美国佛罗里达州立大学）、克莱门西·蒙特尔（Clemency Montelle，新西兰坎特伯雷大学）

Main Content

主要内容

In such conditions, it is hardly surprising that many mathematicians were acutely aware of the issues of computation and were dedicated to relieving practitioners of the calculation burden. In particular, the Scottish mathematician John Napier was famous for his devices to assist with computation. He invented a well-known mathematical artifact, the ingenious numbering rods more quaintly known as “Napier’s bones,” that offered mechanical means for facilitating computation. (For additional information on “Napier’s bones,” see the article, “John Napier: His Life, His Logs, and His Bones” (2006).) In addition, Napier recognized the potential of the recent developments in mathematics, particularly those of prosthaphaeresis, decimal fractions, and symbolic index arithmetic, to tackle the issue of reducing computation. He appreciated that, for the most part, practitioners who had laborious computations generally did them in the context of trigonometry. Therefore, as well as developing the logarithmic relation, Napier set it in a trigonometric context so it would be even more relevant.
在这样的背景下，许多数学家敏锐地意识到计算领域存在的问题，并致力于为从业者减轻计算负担，这一现象不足为奇。其中，苏格兰数学家约翰·纳皮尔（John Napier）以其发明的计算辅助工具而闻名。他创造了一种著名的数学工具——设计精巧的计数杆，其更古朴的名称是“纳皮尔骨”（Napier’s bones），该工具为简化计算提供了机械方法。（关于“纳皮尔骨”的更多信息，可参见文章《约翰·纳皮尔：他的生平、他的对数与他的“骨”》（2006 年）。）此外，纳皮尔认识到当时数学领域最新进展的潜力——尤其是积化和差公式（prosthaphaeresis）、十进制分数以及符号指数算术——这些进展可用于解决计算简化问题。他意识到，大多数情况下，需要进行繁重计算的从业者通常是在三角学背景下开展计算的。因此，纳皮尔在提出对数关系的同时，还将其置于三角学背景下，使其适用性更强。

John Napier: His Life, His Logs, and His Bones

约翰·纳皮尔：他的生平、他的对数与他的“骨”

Author(s):
作者：
Michael J. Caulfield (Gannon University)
迈克尔·J·考尔菲尔德（Michael J. Caulfield，甘农大学）

Editor’s note: This article was published in April 2006.
编者按：本文发表于 2006 年 4 月。

An introduction to the life and work of John Napier while introducing students to logarithms will bring the “dry” material to life.
在向学生介绍对数的同时，若能引入约翰·纳皮尔的生平与工作，可让这些“枯燥”的知识变得生动有趣。

John Napier
约翰·纳皮尔

Napier was a Scottish mathematician who lived from 1550 to 1617. He worked for more than twenty years to develop his theory and tables of what he called logarithms, a word he derived from two Greek roots: logos, meaning word, or study, or reasoning, or in Napier’s use, “reckoning”, and arithmos, meaning “number”.
纳皮尔是一位苏格兰数学家，生于1550年，卒于1617年。他耗时二十余年，创立了自己称之为“对数”（logarithms）的理论并编制了对数表。“对数”一词源于两个希腊语词根：“logos”，意为“言辞”“研究”“推理”，而在纳皮尔的用法中，该词根指“计算”；“arithmos”，意为“数”。

Much of our mathematical terminology, and indeed our English vocabulary, derives from Greek and Latin roots. It is a useful exercise to take a few moments when new terms are introduced to explore the etymology of the word and to have the class try to name other words also deriving from these roots.
我们的许多数学术语，乃至英语词汇，都源于希腊语和拉丁语词根。在学习新术语时，花点时间探究其词源，并让学生尝试列举其他源于这些词根的词汇，是一项很有意义的练习。

For example, you might ask “Where else have you seen a word derived from arithmos?
例如，你可以提问：“你还在哪些词汇中见过源于‘arithmos’（数）的词根？”

If etymology is not your strong suit, you will find The Words of Mathematics by Steven Schwartzman an excellent resource. It is published by the MAA.
若词源学非你所长，你会发现史蒂文·施瓦茨曼（Steven Schwartzman）所著的《数学词汇》（The Words of Mathematics）是优质参考资料。该书由美国数学协会（MAA）出版。

Napier chose the name “logarithms” because he thought of them as “reckoning numbers”. Their use could save computational time, especially the time of beleaguered astronomers. These men had to carry out computations involving very large numbers. Any simplifying devices were welcomed with joy.
纳皮尔将这种工具命名为“对数”，是因为他认为对数本质是“计算数”（reckoning numbers）。使用对数可节省计算时间，尤其能为饱受计算之苦的天文学家节省时间——这些天文学家必须处理涉及极大数字的运算，因此任何能简化计算的工具都会备受欢迎。

In fact, the French mathematician Pierre Laplace (1749-1833) said that Napier’s new tool “doubled the life of the astronomer.” Come back to this idea after students have seen that logarithms are exponents and after they have learned the rules for working with logarithms.
事实上，法国数学家皮埃尔·拉普拉斯（Pierre Laplace，1749-1833）曾评价，纳皮尔的这一新工具“使天文学家的有效工作寿命延长了一倍”。待学生理解“对数即指数”这一本质，并掌握对数的运算规则后，再回顾这一评价会更有意义。

Then the students will be able to appreciate the computational improvements – especially when the lack of computers and calculators is borne in mind!
届时，学生便能切实体会到计算效率的提升——尤其是考虑到当时尚无计算机和计算器这一背景时，这种提升的价值更显突出！

Michael J. Caulfield (Gannon University), “John Napier: His Life, His Logs, and His Bones,” Convergence (July 2010)

Napier first published his work on logarithms in 1614 under the title Mirifici logarithmorum canonis descriptio, which translates literally as A Description of the Wonderful Table of Logarithms. Indeed, the very title Napier selected reveals his high ambitions for this technique—the provision of tables based on a relation that would be nothing short of “wonder-working” for practitioners. As well as providing a short overview of the mathematical details, Napier gave technical expression to his concept. He coined a term from the two ancient Greek terms logos, meaning proportion, and arithmos, meaning number; compounding them to produce the word “logarithm.” Napier used this word as well as the designations “natural” and “artificial” for numbers and their logarithms, respectively, in his text.
1614 年，纳皮尔首次发表了关于对数的著作，书名是《奇妙的对数表之描述》（Mirifici logarithmorum canonis descriptio，字面意思为“奇妙的对数表之描述”）。事实上，纳皮尔所选择的书名本身就体现了他对这一技术的远大期望——基于某种关系构建的表格，对从业者而言，其效用不亚于“神奇工具”。除了简要概述数学细节外，纳皮尔还对自己的概念进行了技术性表述。他从两个古希腊词汇中创造了一个术语：“logos”（意为“比例”）和“arithmos”（意为“数”），将二者组合形成了“logarithm”（对数）一词。在著作中，纳皮尔不仅使用“logarithm”这一术语，还分别用“natural”（自然的）和“artificial”（人为的）来称谓数字及其对数。

在这里插入图片描述

Figure 1. John Napier (1550-1617) (from MacTutor History of Mathematics Archive)

Napier’s Kinematic Framework for Logarithms

纳皮尔对数的运动学框架

Despite the obvious connection with the existing techniques of prosthaphaeresis and sequences, Napier grounded his conception of the logarithm in a kinematic framework. The motivation behind this approach is still not well understood by historians of mathematics. Napier imagined two particles traveling along two parallel lines. The first line was of infinite length and the second of a fixed length (see Figures 2 and 3). Napier imagined the two particles to start from the same (horizontal) position at the same time with the same velocity. The first particle he set in uniform motion on the line of infinite length so that it covered equal distances in equal times. The second particle he set in motion on the finite line segment so that its velocity was proportional to the distance remaining from the particle to the fixed terminal point of the line segment.
尽管对数与已有的积化和差公式及数列技术存在明显关联，但纳皮尔将其对数概念建立在了运动学框架之上。数学史学家至今仍未完全理解这种方法背后的动机。纳皮尔设想两个质点沿两条平行线运动：第一条线为无限长，第二条线为固定长度（见图 2 和图 3）。他假设这两个质点从同一（水平）位置同时出发，且初始速度相同。其中，第一个质点在无限长的直线上做匀速运动，即单位时间内移动的距离相等；第二个质点在有限线段上运动，其速度与该质点到线段固定端点的剩余距离成正比。

(Traversed distance on the first (infinite) line was the logarithm of the sine.) This had the result that as the sines decreased, Napier’s logarithms increased. Furthermore, the sines decreased in geometric proportion, and the logarithms increased in arithmetic proportion. We can summarize Napier’s explanation as follows (Descriptio I, 1 (p. 4); see Figure 3):
（在纳皮尔的模型中）第一个（无限长）直线上质点的已移动距离即为正弦（值）的对数。这就导致了一个结果：当正弦值减小时，纳皮尔对数的值会增大。此外，正弦值按等比数列减小，而对数按等差数列增大。我们可以将纳皮尔的解释总结如下：

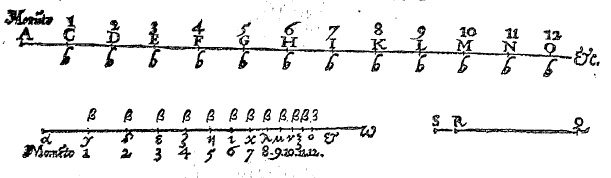
在这里插入图片描述

Figure 2. Napier’s two parallel lines with moving particles (Image used courtesy of Landmarks of Science Series, NewsBank-Readex)
图 2 纳皮尔的两条平行线与运动质点（图片来源：科学里程碑系列（Landmarks of Science Series），NewsBank-Readex 授权使用）

More specifically, at any moment the distance not yet covered on the second (finite) line was the sine and the (traversed distance on the first infinite line was the logarithm of that sine), (note: Napier’s logarithm concept differs from the modern one, distinguished by a specific symbol here):
更具体地说，在任意时刻，第二个（有限）线段上质点尚未移动的距离为正弦（值），而第一个无限长直线上质点的已移动距离为该正弦值的对数，依此类推。（注：纳皮尔的对数概念与现代对数概念不同，此处用特定符号区分）：

$C=\log _{nap }(\gamma \omega) \ where \ \gamma \omega=\sin \theta_{1}$

$D=\log _{n a p}(\delta \omega) \ where \ \delta \omega=\sin \theta_{2}$

$E=\log _{nap }(\epsilon \omega) \ where \ \epsilon \omega=\sin \theta_{3}$

and so on, so that, more generally:
因此，更一般的表达式为

$x=\sin(\theta)$

$y=\log _{nap }(x)$

where $log _{nap }$ has been used to distinguish Napier’s particular understanding of the logarithm concept from the modern one.
其中， $log _{nap }$ 用于区分纳皮尔对对数概念的特定理解与现代对数概念。

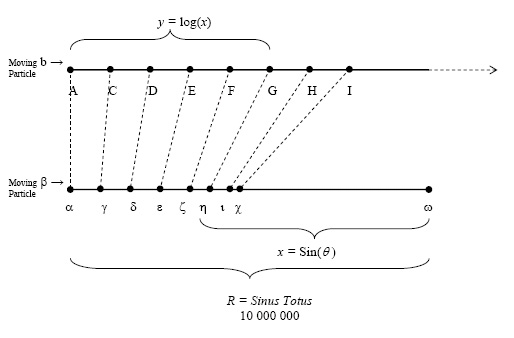
在这里插入图片描述

Figure 3. The relation between the two lines and the logs and sines
图 3 两条直线与对数、正弦值之间的关系

Figure 3 Related Symbols & Caption
$y=\log(x)$ Moving b Particle; C D E F G H I (Points on the line); Moving B Particle; CL Y 6 8 5 ntx (Symbolic marks); $x=\sin(\theta)$ ; $R=\text{Sinus Totus}$ (Latin for “total sine”, i.e., sine of $90^\circ$ ) = 10000000
$y=\log(x)$ （运动的 b 质点）；C、D、E、F、G、H、I（线段上的点）；运动的 B 质点；CL、Y、6、8、5、ntx（符号标记）； $x=\sin(\theta)$ ； $R=\text{Sinus Totus}$ （拉丁语，意为“全正弦”，即 $90^\circ$ 角的正弦值）= 10000000

Napier’s Logarithm Table Construction

纳皮尔对数表的构建

Napier generated numerical entries for a table embodying this relationship. From the table’s presentation, it seemed he took increments of arc $\theta$ in minutes (1° = 60′), first listed the sine of each minute of arc, then its corresponding logarithm. However, in terms of how he actually computed these entries, he worked in the opposite manner: first generated logarithms, then selected those corresponding to the sine of a minute of arc (the sine being the argument of the logarithm). For example, he computed the values in the first column of Table 1 via the relation:
纳皮尔生成了体现这种关系的表格数值条目。从表格呈现形式来看，他似乎是按弧 $\theta$ 的分（角度单位，1°=60′）为增量，先列出每一分弧的正弦值，再列出其对应的对数。然而，从实际计算条目方式来看，他采用的却是相反的流程：先计算出对数，再选择那些与某一分弧的正弦值相对应的对数（该正弦值即为对数的自变量）。例如，他通过以下关系式计算出表 1 第一列中的数值：

$p_{n+1}=p_{n}\left(1-\frac{1}{10^{7}}\right) where \ p_{0}=10^{7}$

Table 1: Napier’s Logarithms

表 1：纳皮尔对数表

$p_n$	$n = \log_{nap} p_n$	$\theta$ Corresponding Angle
10000000.0000000	0	$90^\circ 00'$
9999999.0000000	1	$89^\circ 59'$
9999998.0000001	2	$89^\circ 58'$
9999997.0000003	3
9999996.0000006	4	$89^\circ 57'$
9999995.0000010	5
9999994.0000015	6
9999993.0000021	7	$89^\circ 56'$
9999992.0000028	8
9999991.0000036	9
9999990.0000045	10
9999989.0000055	11	$89^\circ 55'$

(Empty values in parentheses)
The values in the first column (in bold) corresponding to the sines of minutes of arcs (third column) were extracted, along with their accompanying logarithms (second column), and arranged in the table. The appropriate values from Table 1 can be seen in rows 1 to 6 of the last three columns in Figure 4. Napier tabulated his logarithms from $0^\circ$ to $45^\circ$ in minutes of arc, and provided values for the entire first quadrant by symmetry. The excerpt in Figure 4 shows the first half of the first degree (in minutes of arc) and, by symmetry, the last half of the eighty-ninth degree (in minutes of arc) on the right.
第一列中（加粗的）与分弧正弦值（第三列）对应的数值，会连同其对应的对数（第二列）一起被提取出来，并整理到表格中。表 1 中的相应数值可在图 4 最后三列的第一至第六行中看到。纳皮尔以弧的分为增量，将对数从 $0^\circ$ 制表到 $45^\circ$ ；并利用对称性，给出了整个第一象限的对数数值。图 4 中的摘录部分展示了第一度的前半部分（分弧）对应的对数，同时利用对称性，在右侧展示了第八十九度的后半部分（分弧）对应的对数。

Effort for Table Completion

表格完成的工作量

To complete the tables, Napier computed almost ten million entries from which he selected the appropriate values. Napier himself reckoned that computing this many entries had taken him twenty years, which would put the beginning of his endeavors as far back as 1594.
为完成这些表格，纳皮尔计算了近 1000 万个数值条目，再从中筛选出合适的数值。纳皮尔本人估计，计算如此多的条目花费了他 20 年时间，这意味着他早在 1594 年就开始着手这项工作了。

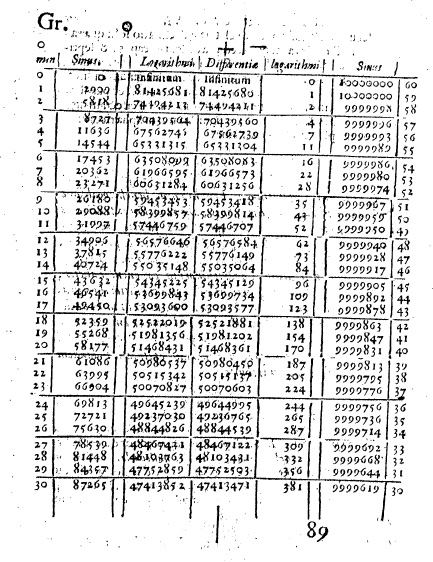
在这里插入图片描述
(Image used courtesy of Landmarks of Science Series, NewsBank-Readex)

Example of Napier’s Logarithm Application

纳皮尔对数的应用示例

Napier frequently demonstrated the benefits of his method. For example, he worked through a problem involving the computation of mean proportionals, sometimes known as the geometric mean. He reviewed the usual way in which this would have been computed, and pointed out that his technique using logarithms not only finds the answer “earlier” (that is, faster!), but also uses only one addition and one division by two! He stated:
纳皮尔经常展示其方法的优势。例如，他曾解决一个涉及“中项比例”（有时也称为“几何平均数”）计算的问题。他回顾了常规的计算方法，并指出，他的对数方法不仅能“更快”（即更迅速地）得出答案，而且只需一次加法和一次除以 2 的运算！他表示：

“Let the extremes 1000000 and 500000 bee given, and let the meane proportionall be sought: that commonly is found by multiplying the extreames given, one by another, and extracting the square root of the product. But we finde it earlier thus; We adde the Logarithme of the extreames 0 and 693147, the summe whereof is 693147 which we divide by 2 and the quotient 346573 shall be the Logar. of the middle proportionall desired. By which the middle proportionall 707107, and his arch 45 degrees are found as before… found by addition onely, and division by two.” (Book I, 5 (p. 25), as translated by Edward Wright)
“已知两个极值 1000000 和 500000，求其中项比例：常规方法是将两个已知极值相乘，再对乘积开平方根。但我们的方法能更快得出结果：将两个极值的对数 0 和 693147 相加，和为 693147；将该和除以 2，商 346573 即为所求中项比例的对数。通过这个对数，可求出中项比例为 707107，其对应的弧为 45 度，与之前的结果一致……只需通过加法和除以 2 的运算即可得出结果。”

In order to find the mean proportional by traditional methods, Napier observed that one has to compute the product and then take the square root; that is:
纳皮尔指出，用传统方法求中项比例时，需先计算乘积，再开平方根，即：

${\sqrt {1000000 \times 500000}} = {\sqrt {500000000000}} \approx 707106.78$

This method involves the multiplication of two large numbers and a lengthy square-root extraction. As an alternative, Napier proposed (with computations to 6 significant figures): which he rightly deemed was much simpler to compute.
这种方法需要计算两个大数的乘积，还要进行繁琐的开平方运算。作为替代方案，纳皮尔提出了以下方法（计算结果保留 6 位有效数字）：他认为这种方法的计算过程要简单得多。

$log _{nap}(1000000) + \log _{nap}(500000) = 0 + 693147 = 693147$

$\ to \ 6 \ significant \ figures（保留 6 位有效数字）$

$\Rightarrow \ mean \ proportional =707107, as \ required,$
$\Rightarrow 中项比例 = 707107 \quad （符合要求）$

Kathleen M. Clark (The Florida State University) and Clemency Montelle (University of Canterbury), “Logarithms: The Early History of a Familiar Function - John Napier Introduces Logarithms,” Convergence (January 2011), DOI:10.4169/loci003495
凯瑟琳·M·克拉克（美国佛罗里达州立大学）、克莱门西·蒙特尔（新西兰坎特伯雷大学），《对数：一种熟悉函数的早期历史——约翰·纳皮尔引入对数》，《Convergence》（2011 年 1 月），数字对象标识符：10.4169/loci003495

Logarithm and Natural Logarithm Theory and Applications

对数与自然对数理论及应用

1. Definition and Basic Concepts of Natural Logarithm

1. 自然对数的定义与基本概念

1.1 Definition of Natural Logarithm

1.1 自然对数的定义

The natural logarithm is a logarithm with the mathematical constant $e$ as its base, denoted by $\ln$ , i.e., $ln(x) = \log_e(x)$ . Here, $e$ is a transcendental number with an approximate value of $2.718281828459$ . Similar to the圆周率 $\pi$ , $e$ is an important constant with a fixed value in mathematics.
自然对数是以数学常数 $e$ 为底的对数，记为 $\ln$ ，即 $ln(x) = \log_e(x)$ 。其中， $e$ 是超越数，近似值为 $2.718281828459$ ，与圆周率 $\pi$ 类似，是数学中具有固定值的重要常数。

The geometric meaning of the natural logarithm can be stated as: $\ln(x)$ represents the time required for a variable to grow from $1$ to $x$ (for the natural growth model), while $e^x$ represents the total growth of the variable after time $x$ . This definition is widely used in mathematics, physics, and economics. Scenarios such as decay equations, growth equations, and compound interest calculations all require the use of natural logarithms for analysis.
自然对数的几何意义可表述为： $\ln(x)$ 表示变量从 $1$ 增长到 $x$ 所需的时间（针对自然增长模型），而 $e^x$ 则表示经过时间 $x$ 后变量的增长总量。该定义在数学、物理及经济学领域应用广泛，如衰减方程、增长方程及复利计算等场景均需借助自然对数进行分析。

1.2 Relationship Between $\ln$ and $e$

1.2 $\ln$ 与 $e$ 的关系

The natural logarithm $\ln$ and the exponential function with base $e$ (i.e., $e^x$ ) are inverse functions of each other. This inverse relationship is reflected in two key properties:
自然对数 $\ln$ 与以 $e$ 为底的指数函数（即 $e^x$ ）互为反函数，这种反函数关系体现在两个关键性质中：

$ln(e^x) = x$ :

Taking the natural logarithm of $e^x$ (the exponential function with base $e$ ) results in the exponent $x$ itself.
对以 $e$ 为底的指数函数 $e^x$ 取自然对数，结果等于指数 $x$ 本身。
$e^{\ln(x)} = x$ :

Raising $e$ to the power of $\ln(x)$ (the natural logarithm of $x$ ) results in the argument $x$ itself.
以 $e$ 为底、 $\ln(x)$ （ $x$ 的自然对数）为指数的幂运算，结果等于真数 $x$ 本身。

This inverse relationship is the fundamental basis for solving equations involving natural logarithms and exponential functions, and it is also a key point in distinguishing natural logarithms from other types of logarithms.
这种反函数关系是求解含自然对数与指数函数方程的根本依据，也是区分自然对数与其他类型对数的关键点。

2. Key Rules of Natural Logarithms

2. 自然对数的关键法则

The key rules of natural logarithms are derived from the properties of exponents and are the basis for simplifying natural logarithm operations. The specific rules and application examples are as follows:
自然对数的关键法则由指数性质推导而来，是简化自然对数运算的基础，具体法则及应用示例如下：

2.1 Product Rule

2.1 乘积法则

Rule Expression: 法则表达式：
$\ln(x \cdot y) = \ln(x) + \ln(y)$
Description: The natural logarithm of the product of two numbers $x$ and $y$ is equal to the sum of the natural logarithms of $x$ and $y$ respectively.
描述：两个数 $x$ 与 $y$ 乘积的自然对数，等于 $x$ 的自然对数与 $y$ 的自然对数之和。
Example: 示例：
$\ln(7 \times 5) = \ln(7) + \ln(5)$

2.2 Quotient Rule

2.2 商数法则

Rule Expression: 法则表达式：

$\ln\left(\frac{y}{x}\right) = \ln(y) - \ln(x)$
Description: The natural logarithm of the quotient of two numbers $y$ and $x$ is equal to the difference between the natural logarithm of $y$ and the natural logarithm of $x$ .
描述：两个数 $y$ 与 $x$ 商的自然对数，等于 $y$ 的自然对数与 $x$ 的自然对数之差。
Example: 示例：
$\ln\left(\frac{8}{4}\right) = \ln(8) - \ln(4)$

2.3 Reciprocal Rule

2.3 倒数法则

Rule Expression: 法则表达式：

$\ln\left(\frac{1}{x}\right) = -\ln(x)$
Description: The natural logarithm of the reciprocal of a number $x$ is equal to the negative of the natural logarithm of $x$ . This rule is a special case of the quotient rule (when $y = 1$ , since $\ln(1) = 0$ ).
描述：一个数 $x$ 倒数的自然对数，等于 $x$ 的自然对数的相反数。该法则是商数法则的特殊情况（当 $y = 1$ 时，因 $\ln(1) = 0$ ）。
Example: 示例：
$\ln\left(\frac{1}{3}\right) = -\ln(3)$

2.4 Power Rule

2.4 幂法则

Rule Expression: 法则表达式：

$\ln(x^y) = y \cdot \ln(x)$
Description: The natural logarithm of a number $x$ raised to the power of $y$ is equal to the product of the exponent $y$ and the natural logarithm of $x$ .
描述：一个数 $x$ 的 $y$ 次幂的自然对数，等于指数 $y$ 与 $x$ 的自然对数的乘积。
Example: 示例：
$\ln(5^2) = 2 \cdot \ln(5)$

Along with these rules, we have several other rules of logarithms. All logarithm rules are mentioned below:
除上述关键法则外，还有其他若干对数规则，完整规则如下：

Rule of Logarithms

对数法则表

Rule Name 法则名称	Property 法则表达式与说明
Log of 1 1 的对数	$log_b 1 = 0$ 任意底数 $b$ 下，1 的对数等于 0
Log of the same number as base 底数与真数相同的对数	$log_b b = 1$ 底数 $b$ 与真数 $b$ 相同时，对数等于 1
Product Rule 乘积法则	$log_b (mn) = \log_b m + \log_b n$ 两数乘积的对数，等于两数各自对数的和
Quotient Rule 商数法则	$\log_b \left(\frac{m}{n}\right) = \log_b m - \log_b n$ 两数商的对数，等于两数各自对数的差
Power Rule 幂法则	$log_b m^n = n \log_b m$ 真数带指数时，指数可提到对数前相乘
Change of Base Rule 换底法则	$\log_b a = \frac{\log_c b}{\log_c a}$ (OR) $\log_a b \cdot \log_c a = \log_c b$ 将底数 $b$ 的对数转换为底数 $c$ 的对数，两种等价形式
Equality Rule 等式法则	$\log_b a = \log_b c \Rightarrow a = c$ 同底数的两个对数相等，则它们的真数相等
Number Raised to Log 指数对数转换法则	$b^{\log_b x} = x$ 以 $b$ 为底、 $log_b x$ 为指数的幂，结果等于真数 $x$
Other Rules 其他法则	$\log_{b^n} {a^m} = \frac{m}{n} \log_b a$ 真数为幂的形式时，指数可拆分 $-\log_b a = \log_b \frac{1}{a}= \log_b a^{-1}$ 对数的相反数，等于真数倒数的对数（或）等于真数为负指数形式的对数

3. Key Properties of Natural Logarithms

3. 自然对数的关键性质

The properties of natural logarithms are constraints and fixed relationships that apply when the argument or base of the natural logarithm takes specific values. Mastering these properties can help quickly judge the validity of expressions and simplify calculations.
自然对数的性质是指当自然对数的真数或底数取特定值时，所遵循的约束条件与固定关系。掌握这些性质可帮助快速判断表达式的有效性并简化计算。

Scenario (具体场景)	Property of $\ln$ ( $\ln$ 的性质)
$\ln$ of a Negative Number 负数的 $\ln$	The natural logarithm of a negative number is undefined. 任何负数的自然对数均无定义
$\ln$ of $0$ $0$ 的 $\ln$	$\ln(0)$ is undefined. 0 的自然对数无定义
$\ln$ of $1$ $1$ 的 $\ln$	$\ln(1) = 0$ 即1的自然对数等于0
$\ln$ of Infinity 无穷大的 $\ln$	$\ln(\infty) = \infty$ 即无穷大的自然对数仍为无穷大
$\ln$ of $e$ $e$ 的 $\ln$	$\ln(e) = 1$ 即自然底数 $e$ 的自然对数等于1
$\ln$ of $e^x$ $e$ 的 $x$ 次幂的 $\ln$	$ln(e^x) = x$ 即 $e$ 的 $x$ 次幂的自然对数等于指数 $x$
$e$ raised to $\ln(x)$ 以 $\ln(x)$ 为指数的 $e$	$e^{\ln(x)} = x$ 即 $e$ 的 $\ln(x)$ 次幂等于真数 $x$

4. Difference Between Natural Logarithms and Common Logarithms

4. 自然对数与常用对数的区别

Common logarithms (denoted by $\log$ , with base $10$ by default) and natural logarithms (denoted by $\ln$ , with base $e$ by default) are two common types of logarithms. Their main difference lies in the base, while their operation rules are similar.
常用对数（记为 $\log$ ，默认以 $10$ 为底）与自然对数（记为 $\ln$ ，默认以 $e$ 为底）是两种常见的对数类型，主要区别在于底数，运算规则则具有相似性。

4.1 Main Difference: Base

4.1 主要区别：底数

Common Logarithm: Default base is $10$ , i.e.,
常用对数：默认底数为 $10$ ，即
$log(x) = \log_{10}(x)$ .
Natural Logarithm: Default base is $e$ , i.e.,
自然对数：默认底数为 $e$ ，即
$ln(x) = \log_e(x)$ .

4.2 Conversion Formula Between the Two

4.2 两者间的转换公式

To convert between common logarithms and natural logarithms, the following two formulas are used:
若需在常用对数与自然对数之间转换，可使用以下两个公式：

$\log_{10}(x) = \frac{\ln(x)}{\ln(10)}$
$\ln(x) = \frac{\log_{10}(x)}{\log_{10}(e)}$

4.3 Comparison of Operation Rules

4.3 运算规则对比

Rule Type 法则类型	Common Logarithm Rules ( $log = \log_{10}$ ) 常用对数法则	Natural Logarithm Rules ( $ln = \log_e$ ) 自然对数法则
Product Rule 乘积法则	$\log(x \cdot y) = \log(x) + \log(y)$ 即两数乘积的常用对数等于两数常用对数之和	$\ln(x \cdot y) = \ln(x) + \ln(y)$ 即两数乘积的自然对数等于两数自然对数之和
Quotient Rule 商数法则	$\log\left(\frac{x}{y}\right) = \log(x) - \log(y)$ 即两数商的常用对数等于两数常用对数之差	$\ln\left(\frac{x}{y}\right) = \ln(x) - \ln(y)$ 即两数商的自然对数等于两数自然对数之差
Power Rule 幂法则	$\log(x^y) = y \cdot \log(x)$ 即数的幂次的常用对数等于幂次乘该数的常用对数	$\ln(x^y) = y \cdot \ln(x)$ 即数的幂次的自然对数等于幂次乘该数的自然对数
Inverse with Exponent 与指数的反函数关系	$10^{\log(x)} = x$ 即 10 的常用对数次幂等于真数本身 $log(10^x) = x$ 即 10 的 x 次幂的常用对数等于指数 x	$e^{\ln(x)} = x$ 即 e 的自然对数次幂等于真数本身 $ln(e^x) = x$ 即 e 的 x 次幂的自然对数等于指数 x

5. Problem-Solving Examples of Natural Logarithms

5. 自然对数的解题示例

5.1 Simplification of Natural Logarithm Expressions

5.1 自然对数表达式的化简

Problem: Evaluate $\ln\left(\frac{7^2}{5}\right)$ .
问题：计算 $\ln\left(\frac{7^2}{5}\right)$ 的值。

Solution:

Apply the Quotient Rule first: 首先应用商数法则：
$\ln\left(\frac{7^2}{5}\right) = \ln(7^2) - \ln(5)$ .
Apply the Power Rule to $ln(7^2)$ : 对 $ln(7^2)$ 应用幂法则：
$\ln(7^2) = 2 \cdot \ln(7)$ .
Substitute the approximate values of natural logarithms (using a calculator): 代入自然对数的近似值（使用计算器）：
$\ln(7) \approx 1.946$ , $\ln(5) \approx 1.609$ .
Calculate the result: 计算结果：
$\times 1.946 - 1.609 = 3.892 - 1.609 = 2.283$ .

5.2 Solving Equations Involving Natural Logarithms

5.2 求解含自然对数的方程

Problem: Solve the equation
问题：求解方程
$\ln(5x - 6) = 2$ .

Solution:

Use the inverse relationship between $\ln$ and $e$ : Raise both sides of the equation to the power of $e$ , i.e.,
利用 $\ln$ 与 $e$ 的反函数关系：对等式两边以 $e$ 为底取幂，即

$e^{\ln(5x - 6)} = e^2$ .
Simplify using the property $e^{\ln(x)} = x$ :
利用 $e^{\ln(x)} = x$ 的性质化简：
$5x - 6 = e^2$ .
Substitute the approximate value of $e$ (about $2.718$ ):
代入 $e$ 的近似值（约 $2.718$ ）：

$e^2 \approx 7.389$ .

Solve for $x$ : 求解 $x$ ：
$5 x = 7.389 + 6 = 13.389$ ,

so
因此
$\frac{13.389}{5} = 2.678$ .

6. Change of Base Formula for Logarithms

6. 对数的换底公式

6.1 Definition and Expression of the Change of Base Formula

6.1 换底公式的定义与表达式

The change of base formula is used to convert a logarithm with a given base into a ratio of two logarithms with the same new base. This solves the problem of calculating logarithms with non-standard bases (bases other than $10$ or $e$ ) using a calculator.
换底公式用于将一个给定底数的对数，转化为两个具有相同新底数的对数的比值。该公式解决了利用计算器计算非标准底数（非 $10$ 或 $e$ 为底）对数的问题。

Formula Expression: 公式表达式：

$\log_b a = \frac{\log_c a}{\log_c b}$
- $a$ : The argument of the original logarithm.
  $a$ ：原对数的真数。
- $b$ : The base of the original logarithm ( $b > 0$ , $\neq 1$ ).
  $b$ ：原对数的底数（ $b > 0$ ， $\neq 1$ ）。
- $c$ : The new base (can be any positive real number except $1$ , usually $10$ or $e$ for calculation convenience).
  $c$ ：新底数（可为除 $1$ 外的任意正实数，计算时通常取 $10$ 或 $e$ 以方便操作）。
Alternative Form: $\log_b a \cdot \log_c b = \log_c a$ (derived by cross-multiplying the original formula)
等价形式： $\log_b a \cdot \log_c b = \log_c a$ （由原公式交叉相乘推导得出）

6.2 Derivation of the Change of Base Formula

6.2 换底公式的推导

Assume $log_b a = p$ , $log_c a = q$ , $log_c b = r$ . Convert these logarithms to exponential form:
设 $log_b a = p$ ， $log_c a = q$ ， $log_c b = r$ ，将这些对数转化为指数形式：
- $\log_b a = p \Rightarrow a = b^p$
- $\log_c a = q \Rightarrow a = c^q$
- $\log_c b = r \Rightarrow b = c^r$
From $a = b^p$ and $a = c^q$ , we get $b^p = c^q$ .
由 $a = b^p$ 与 $a = c^q$ ，可得 $b^p = c^q$ 。
Substitute $b = c^r$ into $b^p = c^q$ :
将 $b = c^r$ 代入 $b^p = c^q$ ：
$c^r)^p = c^q$ .
Simplify using the power rule of exponents ( $a^m)^n = a^{mn}$ ): $c^{rp} = c^q$ .
利用指数幂法则（ $a^m)^n = a^{mn}$ ）化简： $c^{rp} = c^q$ 。
Since the bases are equal, their exponents must be equal:
因底数相等，指数必相等：
$\Rightarrow p = \frac{q}{r}$ .
Substitute back
代回
$p = \log_b a$ , $q = \log_c a$ , $r = \log_c b$ : $\log_b a = \frac{\log_c a}{\log_c b}$ .

6.3 Application Examples of the Change of Base Formula

6.3 换底公式的应用示例

Example 1: Evaluate $log_{64} 8$ using the change of base formula.
示例 1：利用换底公式计算 $log_{64} 8$ 的值。

Solution:
Choose $c = 10$ (common logarithm base) as the new base:
选择 $c = 10$ （常用对数底数）作为新底数：

$\log_{64} 8 = \frac{\log_{10} 8}{\log_{10} 64}$

Since $64 = 8^2$ , substitute into the formula:
因 $64 = 8^2$ ，代入公式：

$\frac{\log_{10} 8}{\log_{10} 8^2} = \frac{\log_{10} 8}{2 \cdot \log_{10} 8} = \frac{1}{2}$

Example 2: Calculate $log_9 8$ using a calculator (round to 4 decimal places).
示例 2：用计算器计算 $log_9 8$ 的值（保留4位小数）。

Solution:
Use the change of base formula with $c = 10$ :
利用换底公式，取 $c = 10$ ：

$\log_9 8 = \frac{\log_{10} 8}{\log_{10} 9}$

Using a calculator,
通过计算器得

$\log_{10} 8 \approx 0.9031$ , $\log_{10} 9 \approx 0.9542$ .

Thus, 因此，

$\log_9 8 \approx \frac{0.9031}{0.9542} \approx 0.9464$ .

7. Conversion Between Exponential Form and Logarithmic Form

7. 指数形式与对数形式的转换

7.1 Definition of Conversion

7.1 转换的定义

Exponential form and logarithmic form are two equivalent representations of the same mathematical relationship. Converting between them helps simplify complex calculations (e.g., converting multiplication/division of large numbers into addition/subtraction via logarithms).
指数形式与对数形式是同一数学关系的两种等价表示形式。二者间的转换有助于简化复杂计算（如通过对数将大数的乘法/除法转化为加法/减法）。

7.2 Main Conversion Formula

7.2 主要转换公式

For any positive real numbers $a$ ( $\neq 1$ ) and $N$ , and real number $b$ :
The exponential form $a^b = N$ is equivalent to the logarithmic form $log_a N = b$ .
对于任意正实数 $a$ （ $\neq 1$ ）、 $N$ 及实数 $b$ ：
指数形式 $a^b = N$ 与对数形式 $log_a N = b$ 等价。

Example 1: Exponential form $2^3 = 8$ $\Leftrightarrow$ Logarithmic form $log_2 8 = 3$ .
示例 1：指数形式 $2^3 = 8$ $\Leftrightarrow$ 对数形式 $log_2 8 = 3$ 。
Example 2: Exponential form $e^2 \approx 7.389$ $\Leftrightarrow$ Logarithmic form $\ln(7.389) = 2$ .
示例 2：指数形式 $e^2 \approx 7.389$ $\Leftrightarrow$ 对数形式 $\ln(7.389) = 2$ 。

7.3 Key Formulas for Exponents and Logarithms

7.3 指数与对数的关键公式

7.3.1 Exponential Formulas

7.3.1 指数公式

$a^p = a \times a \times \ldots \times a$ (with $p$ factors of $a$ )
$a^p = a \times a \times \ldots \times a$ （共 $p$ 个 $a$ 相乘）
$a^p \cdot a^q = a^{p+q}$ (When multiplying powers with the same base, keep the base unchanged and add the exponents)
$a^p \cdot a^q = a^{p+q}$ （同底数幂相乘，底数不变，指数相加）
$\frac{a^p}{a^q} = a^{p-q}$ (When dividing powers with the same base, keep the base unchanged and subtract the exponents)
$\frac{a^p}{a^q} = a^{p-q}$ （同底数幂相除，底数不变，指数相减）
$a^p)^q = a^{pq}$ (When raising a power to a power, keep the base unchanged and multiply the exponents)
$a^p)^q = a^{pq}$ （幂的乘方，底数不变，指数相乘）
$a^0 = 1$ (Any non-zero number raised to the power of $0$ is $1$ )
$a^0 = 1$ （任何非零数的 $0$ 次幂均为 $1$ ）
$a^{-1} = \frac{1}{a}$ (A number raised to the power of $- 1$ is its reciprocal)
$a^{-1} = \frac{1}{a}$ （一个数的 $- 1$ 次幂等于其倒数）

7.3.2 Logarithmic Formulas

7.3.2 对数公式

Product Rule：乘积法则
$log_a(xy) = \log_a x + \log_a y$
Quotient Rule：商数法则
$\log_a\left(\frac{x}{y}\right) = \log_a x - \log_a y$
Power Rule:幂法则
$\log_a(x^k) = k \cdot \log_a x$
Logarithm of the base to itself is $1$ :底数的自对数为 $1$
$log_a a = 1$
Logarithm of $1$ is $0$ for any valid base:任何有效底数下， $1$ 的对数为 $0$
$log_a 1 = 0$
Change of Base Rule:换底法则
$\log_a b = \frac{\log_c b}{\log_c a}$

8. Differentiation of $e^x$ (Supplementary Knowledge)

8. $e^x$ 的导数（补充知识）

8.1 Derivative Formula of $e^x$

8.1 $e^x$ 的导数公式

The derivative of the exponential function $e^x$ with respect to $x$ is equal to itself, i.e., $\frac{d(e^x)}{dx} = e^x$ . This is a unique property of the exponential function with base $e$ .
指数函数 $e^x$ 关于自变量 $x$ 的导数等于其本身，即 $\frac{d(e^x)}{dx} = e^x$ 。这是以 $e$ 为底的指数函数的独特性质。

8.2 Proof Using the First Principle of Derivatives

8.2 利用导数第一性原理证明

The first principle of derivatives defines the derivative of a function $f (x)$ as:
导数的第一性原理将函数 $f (x)$ 的导数定义为：

$\lim_{h \to 0} \frac{f(x+h) - f(x)}{h}$

For $f(x) = e^x$ , $e^{x+h} = e^x \cdot e^h$ (by the product rule of exponents). Substitute into the first principle:
对于 $f(x) = e^x$ ，由指数乘积法则得 $e^{x+h} = e^x \cdot e^h$ 。将其代入第一性原理：

$\frac{d(e^x)}{dx} = \lim_{h \to 0} \frac{e^{x+h} - e^x}{h} = \lim_{h \to 0} \frac{e^x \cdot e^h - e^x}{h}$

Factor out $e^x$ (which is independent of $h$ ):
将与 $h$ 无关的 $e^x$ 提出极限外：

$e^x \cdot \lim_{h \to 0} \frac{e^h - 1}{h}$

Using the important limit $\lim_{h \to 0} \frac{e^h - 1}{h} = 1$ , we get:
利用重要极限 $\lim_{h \to 0} \frac{e^h - 1}{h} = 1$ ，可得：

$\frac{d(e^x)}{dx} = e^x \times 1 = e^x$

8.3 Important Notes

8.3 重要说明

The $n$ -th derivative of $e^x$ is still $e^x$ , i.e., $\frac{d^n(e^x)}{dx^n} = e^x$ .
$e^x$ 的 $n$ 阶导数仍等于其本身，即 $\frac{d^n(e^x)}{dx^n} = e^x$ 。
For the function $e^{ax}$ (where $a$ is a constant), its derivative is $\cdot e^{ax}$ . When $a = 1$ , it reduces to the derivative of $e^x$ ( $\frac{d(e^x)}{dx} = e^x$ ).
对于函数 $e^{ax}$ （ $a$ 为常数），其导数为 $\cdot e^{ax}$ 。当 $a = 1$ 时，即退化为 $e^x$ 的导数（ $\frac{d(e^x)}{dx} = e^x$ ）。