代数的发展历程 | 从几何直观到符号代数的演变

注：本文为 “代数的发展历程” 相关合辑。
英文引文，机翻未校。
如有内容异常，请看原文。

---

The development of algebra - 1

代数学的发展（一）

Article by
Leo Rogers
Published Tue, 01/02/2011 - 00:00

1. In the beginning …

最初的发展……

Knowledge about the possible beginnings of human mental development comes from research on the co-evolution of language and the human brain. The central idea that comes out of this research is that mankind, uniquely, is what is called a ‘symbolic species’. That is, we have the ability to make ideas ‘visible in the mind’. This means we can create, manage, manipulate and blend images in ways that help us to form new relationships and produce new concepts.
关于人类心智发展可能的起源，其知识来源于对语言与人类大脑共同进化的研究。这项研究得出的核心观点是：人类是独一无二的“符号物种”。也就是说，我们具备让思想“在脑海中可视化”的能力。这意味着我们能够通过创造、处理、操控和融合图像的方式，帮助自己建立新的关联并产生新的概念。

We can only speculate on the earliest stages in the development of mathematics but we do have evidence which shows that we have the power to visualise and represent physical objects in our mind. This power is seen in the representations of counting, bartering and building activities of early civilisations. In particular, our perceptions of symmetry seem to have produced many kinds of geometrical representations in different cultures.
我们只能推测数学发展的最初阶段，但确实有证据表明，人类具备在脑海中可视化并呈现实物的能力。这种能力体现在早期文明中计数、物物交换和建筑活动的表达形式上。尤其是在不同文化中，人类对对称性的认知似乎催生了多种几何表达形式。

---

2. The Pythagoreans (c. 550 - c. 450 BCE)

毕达哥拉斯学派（约公元前 550 年—约公元前 450 年）

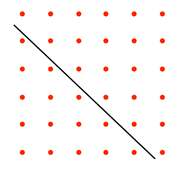
Imagine, for example, what might be done with arrangements of stones in the sand:
例如，试想一下用沙子中的石头排列可以实现什么：

In these images, a square pattern has been divided into different areas, making rectangles or triangles.
在这些图像中，正方形图案被分割成不同的区域，形成了长方形或三角形。

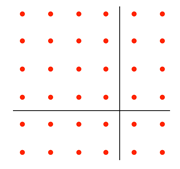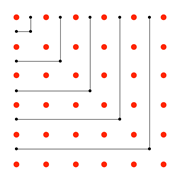In the above two images, other shapes have been produced, leading to speculations about relationships between numbers and areas, and it is thought that the elementary number theories of the Pythagoreans might have been generated by images like these [see Note 1 below].
在上述两幅图像中，还形成了其他形状，这引发了人们对数字与面积之间关系的推测。人们认为，毕达哥拉斯学派的初等数论可能就是由这类图像衍生而来的[参见下文注释 1]。

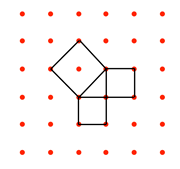
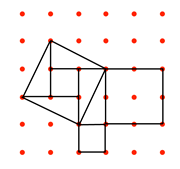
Further manipulation, dissection of squares and rearrangement, leads to images of right-angled triangles and the familiar relationship between numbers and areas. For example:
通过进一步的操控、正方形分割与重新排列，可以得到直角三角形的图像，以及我们熟知的数字与面积之间的关系。例如：

---

3. Egypt: The Rhind Papyrus.

3. 埃及：林德纸草书

Early methods for solving problems come from the Rhind Mathematical Papyrus, written in Egypt about 1,550 years BCE. It is a ‘problem text’ of exercises for training scribes, who were the administrators. It has examples of methods for weighing, measuring and surveying, for finding areas and volumes, and for working out rates of pay for workers of various kinds.
早期的解题方法来源于《林德数学纸草书》，这份纸草书约于公元前 1550 年在埃及写成。它是一本用于培训文书（当时的行政人员）的“习题集”，包含了称重、测量、测绘、求面积与体积，以及计算各类工人薪资标准的方法示例。

In particular, the Papyrus has a series of problems showing how to solve what we could call ‘linear equations’ by a method that became commonly used by merchants throughout the Mediterranean countries for some three thousand years, called the ‘Method of False Position’. It is used for all kinds of calculations involving comparison of values and quantities. This method still appeared in school text books in the early 20th century.
尤为重要的是，这份纸草书中包含一系列题目，展示了如何用“假设法”求解我们如今所说的“线性方程”。这种方法在约三千年的时间里，被地中海各国的商人广泛使用，适用于所有涉及数值与数量比较的计算。20 世纪初期，这种方法仍出现在学校课本中。

Here is Problem 26:
题目 26 如下：

This belongs to the group of ‘$h$’ problems, sometimes written as ‘heap’ meaning ‘quantity’ or ‘number’. $\bar{4}$ is an example of the usual way we represent Egyptian ‘unit’ fractions.
这道题属于“$h$类”题目，“$h$”有时写作“heap”，意为“数量”或“数字”。$\bar{4}$是我们表示埃及“单位分数”的常用形式之一。

In a quantity and its $\bar{4}$ is added to it so that 15 results
一个数量加上它的$\bar{4}$，结果为 15
A quantity is added to a quarter of itself and the answer is 15
一个数量加上它的四分之一，结果为 15

Calculate with 4. You shall calculate its $\bar{4}$ as 1. Total 5.
以 4 为基础计算。将它的$\bar{4}$算作 1，总和为 5。

You begin by assuming h = 4, so, as the left hand side is h + h/4 this gives 4 + 1=5: h = 4 does not work as it gives an answer of 5 not 15.
先假设数量$h=4$，由于左边式子为$h+\frac{h}{4}$，可得$4+1=5$；但$h=4$不成立，因为它得出的结果是 5 而非 15。

Work with 5 to find 15. 5 2 10 3 shall result.
用 5 推导 15（计算过程：5×2=10），最终结果为 3。

Now take the 5 and divide it into 15 to get 3.
现在用 15 除以 5，得到 3。

Multiply 3 times 4 . 3 2 6 4 12 12 shall result
用 3 乘以 4（计算过程：3×2=6，4×3=12），最终结果为 12。

Multiply the 4 by 3 to find the result you want, 12.
用 4 乘以 3，得到所需结果 12。

12 $\bar{4}$ 3 total 15 The quantity 12 its $\bar{4}$ 3. Total 15
12、$\bar{4}$、3，总和 15；该数量为 12，其$\bar{4}$为 3，总和 15。

So, 12 add a quarter of 12 is 15.
因此，12 加上 12 的四分之一，结果为 15。

In modern notation, the problem looks very easy: $$h+\frac{h}{4}=15$$
用现代符号表示，这道题非常简单：$$h+\frac{h}{4}=15$$

We begin by using $h=4$ which immediately makes the fraction $\frac{h}{4}=1$
我们先假设 $h=4$，这样分数 $\frac{h}{4}$ 就等于 $1$。

So the left hand side is $5$, but we need $15$.
因此，方程左边的结果是 $5$，但我们需要的结果是 $15$。

If by using $4$ we obtain $5$, what do we need to use to get $15$?
如果用 $4$ 得到的结果是 $5$，那么需要用什么数才能得到 $15$ 呢？

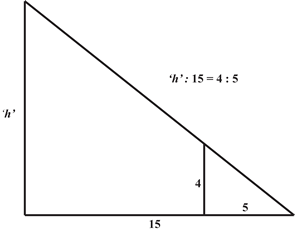
The sundial was one of the first instruments used for measuring time, and the properties of the right-angled triangle were well known to ancient people (Problem 56 deals with similar triangles). The slopes of pyramids and other sloping surfaces were measured by the ‘seked’ - the horizontal distance measured for every cubit of height.
日晷是最早用于计时的工具之一，古人早已熟知直角三角形的性质（题目 56 涉及相似三角形）。金字塔及其他倾斜面的坡度用“赛克德”（seked) 来衡量，即每立方腕尺高度对应的水平距离。

Visualising a triangle like this would make the problem much simpler and the ratios could then easily be compared. KaTeX parse error: Undefined control sequence: \mbox at position 7: \frac{\̲m̲b̲o̲x̲{'}h\mbox{'}}{1…
将这样的三角形可视化会让问题变得更简单，比例也更容易比较：$$\frac{h}{15}=\frac{4}{5}$$

So, for the denominator of the right hand ratio to be $15$, we need to multiply the numerator and denominator of the ratio $\frac{4}{5}$ by $3$.
因此，要使右边比例的分母变为 $15$，我们需要将比例 $\frac{4}{5}$ 的分子和分母同时乘以 $3$。

---

4. Early Indian Mathematics (c. 1500 - 500 BCE)

早期印度数学（约公元前 1500 年—公元前 500 年）

Similar traces of the above kind of visualisation appeared in the Indus valley in roughly the same period, although there are claims that the procedures were much older [see Note 2 below].
大约同一时期，在印度河流域也出现了类似上述可视化方法的痕迹，不过有观点认为这些方法的起源要早得多[参见下文注释 2]。

The Vedic people entered India about 1500 BCE. The name comes from their sacred rituals called the Vedas. These date from about the 15th to the 5th century BCE and were used for sacrificial rites which took place at an altar.
吠陀人约于公元前 1500 年进入印度，其名称来源于他们名为“吠陀”（Vedas）的神圣仪式。这些仪式可追溯至公元前 15 世纪至公元前 5 世纪，用于在祭坛举行的祭祀活动。

The name Sulbasutras (meaning ‘cord-rules’) applies to the part of the Vedas which gives the rules for building the brick altars used in ritual sacrifice. Instructions were given:
“苏尔巴经”（Sulbasutras，意为“绳规”）是吠陀文献的一部分，记载了建造祭祀用砖质祭坛的规则，其中有如下说明：

“He who desires heaven is to construct a fire-altar in the form of a falcon” and “a fire-altar in the form of a tortoise is to be constructed by one desiring to win the world of Brahmin” [see Note 3 below]. Many of these instructions contain transformations for preserving areas, such as changing a rectangle into a square of the same size. See examples below:
“欲登天堂者，当建隼形火坛”，“欲入婆罗门之界者，当建龟形火坛”[参见下文注释 3]。这些说明中包含许多等积变换的方法，例如将长方形变换为等面积的正方形。示例如下：

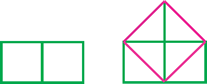
For two squares of the same size, it is easy to see how to combine the areas to make one square, but not obvious for squares of different sizes.
对于两个等大的正方形，很容易看出如何将它们的面积合并成一个正方形，但对于大小不同的正方形，合并方法则不那么明显。

“If it is desired to combine two squares of different measures, a [rectangular] part is cut off from the larger [square] with the side of the smaller; the diagonal of the cut-off [rectangular] part is the side of the combined square.”
“若需合并两个不同大小的正方形，可从较大正方形中截取一个以较小正方形边长为边长的长方形部分；该截取长方形的对角线即为合并后正方形的边长。”

“Alternatively if it is desired to combine two squares of different measures, a rectangle is formed with the side of the smaller [square] [as breadth] and that of the larger [as length]; the diagonal of the rectangle [thus formed] is the side of the combined square.”
“另一种方法：若需合并两个不同大小的正方形，可将较小正方形的边长作为宽、较大正方形的边长作为长，构成一个长方形；该长方形的对角线即为合并后正方形的边长。”

These instructions clearly show a knowledge of the ‘Pythagorean relation’.
这些说明清楚地表明（当时的人们）已掌握“毕达哥拉斯关系”（即勾股定理）。

The base line for the altar was always East - West and careful and precise interpretation of the instructions enabled the priests to build the falcon ‘fire-altar’.
祭坛的基准线始终为东西走向，通过对规则细致精准的解读，祭司们能够建造出隼形的“火坛”。

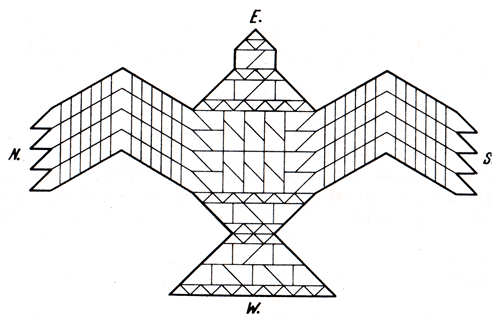
The Sulbasutras were written in Sanscrit and the texts often used ‘code words’ or abbreviations for lengths, areas and other quantities. For example, the word ‘eyes’ represented number two and ‘teeth’ represented ‘thirty-two’, so a sentence might read something like: ‘we have the eyes, so do this to find the teeth’, and the geometry was hidden under a cloak of instructions coded in number language.
《苏尔巴经》以梵文写成，文中常使用“密码词”或缩写来表示长度、面积及其他数量。例如，“眼睛”代表数字 2，“牙齿”代表数字 32，因此文中可能会出现类似“我们已有‘眼睛’（即 2），按此方法可求‘牙齿’（即 32）”的表述，而几何知识则隐藏在这种数字语言编码的规则之下。

---

5. Old Babylonian Mathematics (c. 1850 - 1600 BCE)

古巴比伦数学（约公元前 1850 年—公元前 1600 年）

The earliest mathematics appeared in Mesopotamia some 3,500 or more years BCE with a variety of specific number systems for trading with different things like grain and cereals, milk and dairy produce, or things made out of clay or wood. The ‘sexagesimal system’ as it is popularly known, appeared before 2000 BCE and was well-established by the time of Hammurabi, (1795-1750 BCE) the first king of Babylon. Most of the well-known evidence we have on clay tablets comes from the Babylonian Kingdom period that ended about 1600 BCE.
最早的数学出现于约公元前 3500 年或更早的美索不达米亚地区，当时有多种特定的计数系统，分别用于谷物、奶制品、黏土制品或木制品等不同物品的贸易。我们熟知的“六十进制”出现于公元前 2000 年之前，到巴比伦第一任国王汉谟拉比（公元前 1795 年—公元前 1750 年）时期已十分成熟。我们目前掌握的、刻在泥板上的著名证据，大多来自于约公元前 1600 年结束的巴比伦王国时期。

Accounts for cereals, beer or oil - about 3,000 BCE

谷物、啤酒或油脂账目——约公元前 3000 年

The ‘Old Babylonian’ Empire had a well-organised society with an efficient administration which enabled scribes to administer social justice through a system of fair management and distribution of goods. Central to this system were the schools where scribes were trained. The school culture was basically oral, depending on the memorisation of texts and routines for calculation; tables for multiplication, division, reciprocals and other useful units were available. Emphasis on administration, labour management and quantity surveying led to the use of ‘word problems’ that could be solved using standard algorithms such as:
古巴比伦帝国拥有组织完善的社会和高效的行政体系，文书们能够通过公平的物品管理与分配制度维护社会公平。该体系的核心是培训文书的学校，学校文化以口头传授为主，依赖对文献和计算流程的记忆；当时已有乘法表、除法表、倒数表及其他实用单位表。由于对行政管理、劳动力管理和工程量测量的重视，“文字题”开始出现，这类题目可通过标准算法求解，例如：

‘Cut and Paste’ Geometry: Removing a Square from a larger Square.

“剪拼”几何：从大正方形中移除小正方形

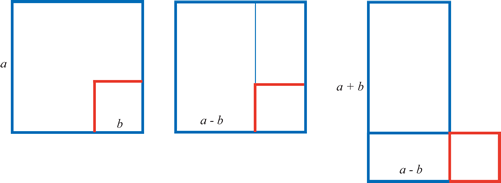
The claim that the Babylonians were doing ‘arithmetical algebra’ (or even quadratic equations) is now seen as an error. Recent research into the language has tried to recover the original thought processes, and shows that the underlying concepts were essentially geometrical. We don’t really need the algebraic labels here, because the geometrical procedure is quite general. The size of the smaller red square does not matter, and the numerical instructions hid the underlying geometrical visualisation [see Note 5 below].
如今看来，认为巴比伦人在研究“算术代数”（甚至二次方程）的观点是错误的。近期对（当时）语言的研究试图还原其原始思维过程，结果表明，其核心概念本质上是几何性的。我们在此无需使用代数术语，因为这种几何方法具有普适性。红色小正方形的大小无关紧要，数值运算的步骤掩盖了背后的几何可视化思维[参见下文注释 5]。

Word Problems

文字题

This example of a ‘sum and product’ problem is from a Babylonian ‘school tablet’. The problem has been rewritten to convey the geometrical nature of the original procedure [see Note 6 below].
以下是一道来自巴比伦“学校泥板”的“和积问题”示例。题目经过重述，以体现原始解题过程的几何本质[参见下文注释 6]。

Length, Width. I have raised, length and width. Surface: 252 I have put together length and width: 32 32 put together, 252 surface: 18 length, 14 width
长与宽问题。已知长和宽的乘积（面积）为 252，长与宽的和为 32。当长加宽为 32、面积为 252 时，长为 18，宽为 14

The problem and answers are stated, and the method is described.
问题、答案已说明，方法已描述。

This is the way of doing it:
解题方法如下：

Here is the arithmetic:
具体运算如下：

break off half of 32: this gives 16
取 32 的一半：得 16
$\frac{32}{2}=16$

raise 16 by itself: 256
16 自乘：256
$16^2=256$

leave out the surface: 256 - 252 = 4
减去面积：256 - 252 = 4
$256-252=4$

find the side of this square 4: it is 2
求正方形 4 的边长：得 2
$\sqrt{4}=2$

put together 16 and 2: 18 length
16 加 2：长为 18
$16+2=18$

tear out 2 from 16: 14 width
16 减 2：宽为 14
$16-2=14$

I have raised length and width. 252
长和宽的乘积验证：252
$(16+2)(16-2)=252$

The visual thinking behind the calculation appears to have gone like this:
该计算过程背后的可视化思维大致如下：

We have the area of a rectangle, $252$;
已知长方形面积为 $252$；

We have the sum of its length and width, $ 32$ (the semi-perimeter);
已知长与宽的和为 $32$（即半周长的 2 倍）；

We know from practical experience (see diagram above); that by removing a small (red) square from a larger (blue) square, we can make a rectangle.
根据实践经验（见上图），从大（蓝色）正方形中移除一个小（红色）正方形，可得到一个长方形。

So, if we make the side of the large square half of $32$; then the area of the large square will be $256$.
因此，若设大正方形的边长为 $32$ 的一半（即 $16$），则大正方形的面积为 $16^2=256$。

Now take away the rectangle, (area $252$), and we are left with the small (red) square.
移除面积为 $252$ 的长方形后，剩余部分即为小（红色）正方形。

Geometrically, this will always work whatever the lengths of the sides concerned. Arithmetically , the problems were arranged so that the numbers used in the calculation always resulted in a perfect (red) square.
从几何角度看，无论相关边长为多少，这种方法始终成立；从算术角度看，题目中的数字经过设计，确保计算结果始终为一个完全平方数（即红色小正方形的面积为完全平方数）。

Many more examples like this have been discovered, and as well as the underlying geometrical visualisation, there is also the clear emergence of an algorithmic process . The Babylonians had established one of the important essential aspects of problem-solving. They had established a method for solving particular types of area problems , and it was this method that was taken over by later generations of scholars and eventually developed into the algorithm we use in classrooms today.
类似的例子还有很多。除了背后的几何可视化思维，一种“算法化”流程也已明确出现。巴比伦人确立了解题的一个重要核心要素：他们发明了“求解特定类型面积问题的方法”。这种方法被后世学者沿用，并最终发展为我们如今在课堂上使用的算法。

---

6. Greek Geometry

希腊几何

By about 350 BCE the numerical and intuitive geometry of these cultures was changed into the deductive science we know as Euclidean Geometry. Book II of the Elements, (still often labelled ‘geometric algebra’) contains much of the knowledge discussed above in terms of geometric theorems. The transformation of rectangles and parallelograms into other shapes of equal area is demonstrated in general terms from a deductive point of view. The myth that the Greeks could not deal with irrational magnitudes has no basis in fact. The first diagram below shows how, from rational measurements of the sides of the rectangle, it is possible to create a square with non-rational sides [see Note 7 below].
约公元前 350 年，这些文明中的数值几何与直观几何，转变为我们熟知的、具有演绎性质的欧几里得几何。《几何原本》第二卷（至今仍常被称为“几何代数”）以几何定理的形式，包含了大量上述提及的知识。书中从演绎的角度，一般性地证明了长方形、平行四边形如何变换为其他等面积图形。“希腊人无法处理无理量”的说法是毫无根据的。下图第一幅展示了：即使长方形的边长为有理长度，也能构造出边长为无理数的正方形[参见下文注释 7]。

Constructing a square equivalent in area to a rectangle

构造与长方形等面积的正方形

Image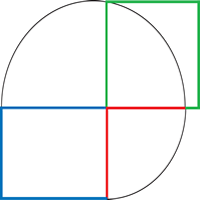		将长方形的红色边长沿上方蓝色边延长，以红色边长为半径画弧；将（红色+蓝色）的总长度二等分，找到圆心并画半圆；所需正方形的边长即为绿色垂线段的长度。
Image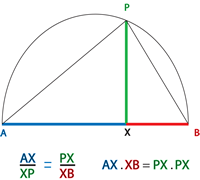		图中包含三个相似的直角三角形：半圆内的 $△APB$、$△AXP$ 和 $△PXB$。三角形的彩色边长与上图中的边长一一对应，图中体现的关系是对应边的比例相等。

Thomas Heath, in his translation of Euclid [see Note 8 below], states:
托马斯·希思（Thomas Heath）在其翻译的《欧几里得几何原本》[参见下文注释 8] 中指出：

“For want of the necessary notation the Greeks had no algebra in our sense. They were obliged to use geometry as a substitute for algebraical operations; and the result is that a large part of their geometry may appropriately be called ‘geometrical algebra’.”
“由于缺乏必要的符号体系，希腊人没有我们所说的代数学。他们不得不以几何替代代数运算，因此，他们的大部分几何学可恰当地称为‘几何代数’。”

So for Heath, referring to the diagram above, and in modern notation,KaTeX parse error: Undefined control sequence: \mbox at position 2: \̲m̲b̲o̲x̲{ if } AX = a, …
因此，对于希思而言，结合上图，用现代符号表示即为：若 $AX=a$、$XB=b$ 且 $PX=x$，则 $ab=x^2$。

This attitude influenced the way we interpreted much of Greek mathematics as algebra until quite recently.
直到最近，这种观点仍影响着我们将大部分希腊数学解读为代数的方式。

---

7. The Arab Civilisation

阿拉伯文明

The Abbasid Caliph al-Mansur (754-755) moved his capital to Baghdad in 762 CE. Euclid was translated into Arabic by al-Hajjaj later in this century, and Indian scholars brought Brahmagupta’s astronomical works where they were translated into Arabic. The work of Diophantus was also translated and Baghdad became a centre for learning, attracting many scholars from the known world. Later, the Caliph al-Ma’mun (813-833) established the ‘House of Wisdom’, which through the 9th and 10th centuries acted as a centre for the great translation programme of knowledge that scholars had accumulated and had built on through their own discoveries.
阿拔斯王朝哈里发曼苏尔（al-Mansur，754 年—755 年在位）于公元 762 年将首都迁至巴格达。公元 8 世纪后期，哈贾吉（al-Hajjaj）将《欧几里得几何原本》译为阿拉伯文；印度学者带来了婆罗摩笈多（Brahmagupta）的天文学著作，这些著作也被译为阿拉伯文。丢番图（Diophantus）的著作同样被翻译，巴格达由此成为学术中心，吸引了当时已知世界的众多学者。后来，哈里发马蒙（al-Ma’mun，813 年—833 年在位）建立了“智慧宫”（House of Wisdom）。在 9 至 10 世纪期间，智慧宫成为大型知识翻译项目的核心，学者们在此翻译积累的知识，并基于自身发现进行拓展。

Out of this accumulation of knowledge came solutions to problems asking for the discovery of numerical and geometrical unknowns, and Islamic civilisation created and named a new science - Algebra.
从这些知识积累中，人们找到了求解数值与几何未知量问题的方法，伊斯兰文明由此创造并命名了一门新学科——代数学（Algebra）。

Conceptual Blending

概念融合

The scholar al-Khowarizmi (c770-c840 CE) took advantage of the works that had been translated and wrote Al-Kitab al-mukhtasar fi Hisab al-gabr wa’l-muqabala , (The Compendious Book on Calculation by Completion and Balancing) and from this title we take the word
‘Algebra’ from ‘al-jabr’, meaning ‘setting back in its place’, or ‘restoring’. Al–Khowarizmi’s name also gives us the words ‘algorithm’ or ‘algorism’.
学者花拉子米（al-Khowarizmi，约公元 770 年—840 年）利用已翻译的著作，撰写了《代数学》（Al-Kitab al-mukhtasar fi Hisab al-gabr wa’l-muqabala，直译为《还原与对消计算概要》）。我们从书名中的“al-jabr”（意为“还原”或“移项”）一词衍生出“Algebra”（代数学），从“Al-Khowarizmi”的名字衍生出“algorithm”（算法）或“algorism”（算术）。

Portrait of Al-Khowarizmi        ~~~~~~        A page from the Algebra
花拉子米肖像        ~~~~~~        《代数学》书页

Al-Khowarizmi was probably first among a number of scholars who showed how the geometrical constructions of Euclid Book II and the arithmetical heritage from Diophantus’ Arithmetica , and the ideas from the Middle East and Indian scholars could be shown to be equivalent. What is special about Al-Khowarismi’s conceptual blending is that for the first time we find the objects of study (the unknowns) and the equations that define clearly the classes of problems to be solved.
在众多学者中，花拉子米或许是首位证明以下内容等价的人：《欧几里得几何原本》第二卷中的几何构造、丢番图《算术》中的算术传统，以及中东与印度学者的思想。花拉子米概念融合的特别之处在于：首次明确界定了“研究对象”（未知量），以及清晰定义“待解问题类别”的方程。

The six cases of equations were 方程的六种情况	In our notation 现代符号表示
1. Roots equal numbers 一次项等于常数项	1. $px=q$
2. Mal [see Note 9 below] equal roots 二次项等于一次项（见下方注 9）	2. $x^2=px$
3. Mal equal numbers 二次项等于常数项	3. $x^2=q$
4. Mal and numbers equal roots 二次项加常数项等于一次项	4. $x^2+q=px$
5. Mal and roots equal numbers 二次项加一次项等于常数项	5. $x^2+px=q$
6. Mal equals numbers and roots 二次项等于常数项加一次项	6. $x^2=q+px$

“Mal”是中世纪对二次项的称呼

Case 5. Square and Roots are Equal to Numbers

形式 5：平方加根等于数

One square and ten roots of the same, amount to thirty-nine dirhams [see Note 10 below].
“一个平方与其十个根相加，结果为三十九迪拉姆（dirham，参见下文注释 10）。”

"This means, what must be the square which, when increased by ten of its own roots, amounts to thirty-nine?
“这意味着，求一个平方数，当它加上自身的十个根时，结果为三十九。”

The solution is this:
解法如下：

You halve the number of roots, which in this case gives five.
将根的系数（即 10）取半，得 5。

This you multiply by itself, the product is twenty-five.
将 5 自乘，得 25。

Add this to thirty-nine, the sum is sixty-four.
将 25 与 39 相加，得 64。

Now take the root of this, which is eight, and subtract from it half the number of roots, which is five, the remainder is three.
求 64 的平方根，得 8；用 8 减去根系数的一半（即 5），余数为 3。

This is the root of the square you sought for, and the square itself is nine.
这个余数 3 就是所求平方数的根，所求平方数即为 9。

The solution is the same when two squares or three, or more or less are specified. You reduce them to one single square, and in the same proportion you reduce the roots and simple numbers which are contained therewith."
若方程中出现两个、三个或更多/更少的平方数，解法相同：先将平方数化为一个平方数，根的系数与常数项也按相同比例缩减。”

Notice that the words of the procedure indicate almost exactly the same actions as in the Babylonian Algorithm.
需注意的是，该解法的步骤描述与巴比伦算法几乎完全一致。

Although the Arabs were probably aware of negative numbers at this time, because they had translated Brahmagupta’s work, (Reference: History of Negative Numbers ) the equations were arranged so that the numbers were all positive. Clearly, if the visualisation of the geometric model involves squares and rectangles, these areas must be represented by positive quantities.
尽管阿拉伯人此时可能已了解负数，因他们翻译了婆罗摩笈多的著作，但方程中的数字均被整理为正数。显然，若几何模型的可视化涉及正方形与长方形，这些图形的面积必须用正数表示。

Case 4. Squares and Numbers are Equal to Roots.

形式 4：平方加数等于根

Example :
示例：

A square and twenty-one in numbers are equal to ten roots of the same square.
“一个平方加二十一，等于该平方的十个根。”

"That is to say, what must be the amount of a square, which when twenty-one dihrams are added to it, becomes equal to the equivalent of ten roots of that square?
“这意味着，求一个平方数，当它加上二十一迪拉姆时，结果等于该平方数的十个根。”

Solution:
解法：

Halve the number of the roots, the half is five.
将根的系数（即 10）取半，得 5。

Multiply this by itself, the product is twenty-five.
将 5 自乘，得 25。

Subtract from this [my italics] the twenty-one which are connected with the square;
从 25 中减去（笔者加斜体）与平方数相加的 21；

the remainder is four.
余数为 4。

Extract its root, it is two.
求 4 的平方根，得 2。

Subtract this from the half of the roots, which is five, the remainder is three. This is the root of the square which you required, and the square is nine.
用根系数的一半（即 5）减去 2，余数为 3，这是所求平方数的一个根，对应的平方数为 9。

Or, you may add the root to the half of the roots, the sum is seven.
或者，将 2 与根系数的一半（即 5）相加，和为 7。

This is the root of the square which you sought for, and the square is forty-nine."
这是所求平方数的另一个根，对应的平方数为 49。”

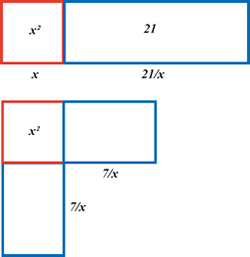
Compared with the Babylonian word problem in section 5 above, this is another case where the semi-perimeter of the sides of the rectangle are given, so that the area of the square made with half the root is larger than the area of the rectangle. In this case the algebra of his first solution is:$$\frac{10}{2}-\sqrt{\frac{10^2}{4}-21}$$
与上文第 5 部分中的巴比伦文字题类似，本题给出的是长方形边长的半周长相关条件，因此以根系数一半为边长的正方形面积，大于长方形的面积。本题第一种解法的代数表达式为：$$\frac{10}{2}-\sqrt{\frac{10^2}{4}-21}$$

and his second procedure is
第二种解法的表达式为：$$5+\sqrt{5^2-21}=7$$

which gives the diagram opposite, where the $7\times 7=49$ fills the empty space.
其中 $7\times 7=49$ 填补了空白区域。

"When you meet with an instance which refers you to this case, try its solution by addition, and if that does not serve, then subtraction certainly will.
“当遇到属于此类的题目时，可先尝试用加法求解；若加法不适用，则用减法必定可行。”

For in this case, both addition and subtraction may be employed, which will not answer in any of the other three cases in which the number of roots must be halved. And know that when in a question belonging to this case you have halved the number of roots and multiplied the half by itself, if the product be less than the number of dihrams connected with the square, then the instance is impossible, but if the product be equal to the dihrams by themselves, than the root of the square is equal to the half of the roots alone, without either addition or subtraction."
“因为在这类题目中，加法和减法均可使用，而在其他三种需将根系数取半的题目中，并非两种方法都适用。需注意：对于此类题目，当你将根系数取半并自乘后，若乘积小于与平方数相加的迪拉姆数（即常数项），则题目无解；若乘积等于该常数项，则平方数的根就等于根系数的一半，无需加或减。”

So, in terms of our algebra, and referring to our usual quadratic formula, he recognised that when ‘$b^2+4ac$’ is positive there are two possible solutions, and when he says ", if the product be less than the number of dihrams connected with the square, then the instance is impossible" he has recognised that’$b^2+4ac$’ is negative, and when ‘$b^2=4ac$’ he says there is only one root.
因此，用现代代数语言（结合二次方程求根公式）表述：花拉子米已认识到，当“$b^2-4ac$”（原文中符号表述略有差异，核心一致）为正时，方程有两个解；当他提到“若乘积小于与平方数相加的迪拉姆数，则题目无解”时，实则认识到“$b^2-4ac$”为负；当“$b^2=4ac$”时，方程只有一个根。

After the breakthrough by al-Khowarizmi, other Islamic scholars tried to show that that geometrical demonstrations of the solutions of these problems were possible. The most successful of these was Thabit ibn Qurra (836 - 901 CE) who finally provided general Euclidean proofs for all the six cases by comparing them to the theorems in Euclid Book II.
花拉子米取得突破后，其他伊斯兰学者试图为这些方程解法提供几何证明。其中最成功的是萨比特·伊本·库拉（Thabit ibn Qurra，公元 836 年—901 年），他通过将六种方程形式与《欧几里得几何原本》第二卷中的定理对比，最终为所有六种形式提供了通用的欧几里得式证明。

It was some time before all this knowledge was passed on to European scholars, but the formulas and routines for solving these problems persisted in the texts used by the merchants, but the geometrical background began to disappear from view. When the Greek and Arabic knowledge began to be translated into Latin, European scholars at last discovered the secrets of what came to be called ‘The Cossic Art’.
这些知识过了一段时间才传入欧洲学者手中，但求解这些问题的公式与流程仍保留在商人使用的文献中，其几何背景却逐渐被遗忘。当希腊与阿拉伯的知识开始被译为拉丁文时，欧洲学者终于发现了后来被称为“代数术”（The Cossic Art）的奥秘。

N.B. Pedagogical notes related to the history of algebra discussed here can be found by clicking on the " Notes’ tab at the top of this article .
注： 点击本文顶部的“注释”（Notes）标签，可查看与本文所讨论代数学历史相关的教学注释 。

---

Notes

注释

1. Evidence for this kind of activity is deduced from fragments of writings by the early Pythagoreans. Also, the elementary number theory in Euclid Book VII. Katz (1998) has a section on the Pythagoreans (pp. 48-51)
   此类活动的证据来源于早期毕达哥拉斯学派的文献残片，也可从《欧几里得几何原本》第七卷的初等数论中推导得出。卡茨（Katz）在其 1998 年的著作中设有关于毕达哥拉斯学派的章节（第 48-51 页）。

2. The dating of early Indian mathematics has always been controversial. As with other civilisations it was basically an oral culture, and what was written down appeared long after it was first conceived. Added to this the Indian scholars wrote on palm leaves that rotted away quite quickly in the humid climate. Documents were copied and copied many times, so we never have the original text and it is virtually impossible to reconstruct the early history of Indian mathematics with any certainty.
   早期印度数学的年代测定一直存在争议。与其他文明类似，早期印度数学以口头传承为主，文字记录的出现远晚于思想的诞生。此外，印度学者在棕榈叶上书写，而棕榈叶在潮湿气候下极易腐烂。文献经过多次抄写，我们无法获得原始文本，因此几乎无法确切还原印度数学的早期历史。

3. Quoted from Kim Plofker’s chapter on Indian Mathematics in Katz (2007 p.387).
   引自金·普洛夫克（Kim Plofker）在卡茨（2007 年）著作中关于印度数学的章节（第 387 页）。

4. Both quotations are from the Baudhayana - Sulbasutra (c. 1,000 - 500 BCE) in Kim Plofker’s chapter 4 in Katz 2007.
   上述两段引文均来自《包德哈亚那苏尔巴经》（Baudhayana - Sulbasutra，约公元前 1000 年—公元前 500 年），参见金·普洛夫克在卡茨 2007 年著作中的第 4 章。

5. Evidence for this geometrical basis comes from recent research into the language and culture of the period by a group including Jens Hoyrup from Roskilde University in Denmark and Eleanor Robson from Cambridge.
   这种几何基础的证据，来源于近期丹麦罗斯基勒大学的延斯·霍伊鲁普（Jens Hoyrup）与英国剑桥大学的埃莉诺·罗布森（Eleanor Robson）等人对该时期语言与文化的研究。

6. This is my version of the problem using Hoyrup’s (1984) Babylonian ‘word list’. See also Pedagogical Notes item 5.
   本题是笔者基于霍伊鲁普（1984 年）整理的巴比伦“词汇表”改编而成，另参见教学注释第 5 条。

7. The ‘Pythagorean’ diagram on the right hand grid in section 1 above has a rational area of 5 units, and non-rational sides.
   上文第 1 部分右侧网格中的“毕达哥拉斯式”图形，面积为有理值 5（单位），边长却为无理数。

8. Heath, T. L. (1963) A Manual of Greek Mathematics. Dover (original Oxford University Press, 1931)
   希思，T. L.（1963）.《希腊数学手册》. 多佛出版社（原版由牛津大学出版社于 1931 年出版）。

9. ‘Mal’ was Euclid’s word for ‘wealth’ (the unknown).
   “Mal”是欧几里得用于表示“未知量”的术语，原意为“财富”。

10. A Dihram is a unit of currency, still used in the Arab Emirates.
    迪拉姆（Dihram）是一种货币单位，至今仍在阿联酋等国使用。

11. All translations in this section are quoted from Berggren, Chapter 5 in Katz (2007).
    本节所有译文均引自伯格伦（Berggren）在卡茨（2007 年）著作中的第 5 章。

---

References

参考文献

This list indicates the main sources I have used in this story. For the school or college library, I suggest Katz (2007) and Robson & Stedall (2009) as the best available sources for the new research and attitudes to mathematics of the ancient world.
以下是本文主要参考的文献｡对于中小学或大学图书馆,笔者推荐卡茨(2007 年)与罗布森､斯特德尔(2009 年)的著作,它们是关于古代数学新研究与新观点的最佳文献｡

Berggren, J.L. (1986) Episodes in the Mathematics of Medieval Islam. New York. Springer.
伯格伦,J.L.(1986).《中世纪伊斯兰数学史话》. 纽约:斯普林格出版社｡

This book shows how the Islamic scholars developed the arithmetic, geometry, and trigonometry they translated from different sources, and how this knowledge helped them develop the new science of Algebra.
该书展示了伊斯兰学者如何发展从不同来源翻译而来的算术､几何与三角学,以及这些知识如何帮助他们发展出代数学这门新学科｡

Hoyrup, J. (1985) Babylonian Algebra from the Viewpoint of Geometrical Heuristics. Roskilde University Centre, Roskilde, Denmark.
霍伊鲁普,J.(1985).《从几何启发法视角看巴比伦代数》. 丹麦罗斯基勒:罗斯基勒大学中心｡

This is the seminal work that helped to develop new ways of looking at the mathematics of the past. It examines the language and culture of ancient Iraq and provides new translations of much of the available material.
该书是开创性著作,为研究古代数学提供了新视角｡它探讨了古代伊拉克的语言与文化,并对大量现有文献材料进行了新的翻译｡

Katz, Victor, J. (1999) (Second Edition, Corrected) A History of Mathematics: An Introduction. Harlow, England. Addison-Wesley.
卡茨,维克多,J.(1999).《数学史导论》(修订第二版). 英国哈洛:艾迪生-韦斯利出版社｡

The best, most comprehensive and up-to-date general history of mathematics available.
当前最优秀､最全面且最新的数学通史著作｡

Katz, V. (2007) The Mathematics of Egypt, Mesopotamia, China, India and Islam. New Jersey. Princeton University Press.
卡茨,V.(2007).《埃及､美索不达米亚､中国､印度与伊斯兰的数学》. 新泽西州:普林斯顿大学出版社｡

Four internationally renowned authors write on their own subjects of expertise. This is the real background for the ‘elementary’ mathematics taught in school: Arithmetic, practical geometry, proto-algebra and trigonometry.
四位国际知名学者分别就各自专长领域撰写内容,展现了学校教授的“初等"数学(算术､实用几何､原始代数与三角学)的真实历史背景｡

Plofker, Kim (2009) Mathematics in India. New Jersey. Princeton University Press.
普洛夫克,金(2009).《印度数学》. 新泽西州:普林斯顿大学出版社｡

This is a comprehensive and expert treatment of the history of Indian mathematics.
对印度数学史全面且专业的论述｡

Robson, Eleanor. (2008) Mathematics in Ancient Iraq: A Social History. New Jersey. Princeton University Press.
罗布森,埃莉诺(2008).《古代伊拉克数学:一部社会史》. 新泽西州:普林斯顿大学出版社｡

This book sets mathematics in the social, cultural and economic context of ancient Iraq; it shows how an oral, visual culture developed the practices of sophisticated mathematics in response to economic and political influences.
该书将数学置于古代伊拉克的社会､文化与经济背景中,展现了一种口头化､可视化的文化如何在经济与政治影响下,发展出复杂的数学实践｡

Robson, Eleanor & Stedall, Jackie (2009) The Oxford Handbook of the History of Mathematics. Oxford. Oxford University Press
罗布森,埃莉诺 & 斯特德尔,杰姬(2009).《牛津数学史手册》. 牛津:牛津大学出版社｡

This history of mathematics is quite unlike any other. It draws on a wide variety of experts who show how mathematics was developed and used in different cultural contexts and the diversity of what we call mathematical practice.
这部数学史与其他著作截然不同,它汇集了众多领域专家的观点,展现了数学在不同文化背景下的发展与应用,以及“数学实践"的多样性｡

If you can reach a library that carries journals in mathematics education, then you might find the following article of interest:
若能获取收藏数学教育期刊的图书馆资源,以下文章或许值得一读:

Arcavi, A. (2003) The role of visualisation in the learning and teaching of mathematics. Educational Studies in Mathematics 52 (3) 2003 (215-224)
阿卡维,A.(2003). 可视化在数学教与学中的作用.《数学教育研究》,52(3),215-224｡

---

The development of algebra - 2

代数学的发展（二）

Article by
Leo Rogers
Published Tue, 01/02/2011 - 00:00

The first part of this brief history of algebra focussed on the important practical origins of the problems that led to the procedures we have for solving equations, and the ways in which the problems were visualised as manipulation of geometrical shapes.
本代数学简史的第一部分，聚焦于方程求解方法所源自的重要实际问题，以及这些问题如何通过几何图形操控实现可视化。

This second part shows how the visual images slowly give way to literal representations, abbreviations, and finally, in the 17th century, to a more developed algebraic symbolism close to what we use in schools today [see: Note 1].
第二部分将展示：这些可视化图像如何逐渐让位于文字表述、缩写形式，并最终在 17 世纪发展为与当今学校所用符号体系相近的、更完善的代数符号[参见：注释 1]。

1. Mediaeval Algebra

1. 中世纪代数学

The expansion of the Arab Empire into Asia Minor (Modern Turkey) at the end of the 11th century led to a series of Crusades to recapture the Holy Land. The major period of these military and political disturbances lasted until the end of the 14th century. In 1340 the ‘Black Death’ spread into Western Europe killing some 40% of the population by about 1370. In spite of these upheavals, exchange of ideas and translations of Arab scholarship were brought to Europe. After 1450 the printing press enabled many people to read the Latin translations of Arab and Greek science.
11 世纪末，阿拉伯帝国向小亚细亚（今土耳其）扩张，引发了一系列旨在夺回圣地的十字军东征。这一军事与政治动荡的主要时期持续至 14 世纪末。1340 年，“黑死病”传入西欧，到 1370 年左右导致约 40%的人口死亡。尽管面临这些动荡，思想交流及阿拉伯学术著作的翻译仍传入欧洲。1450 年后，印刷术的出现让更多人得以阅读阿拉伯与希腊科学著作的拉丁文译本。

Mediaeval Algebra in Western Europe was first learnt from the works of al-Khowarizmi, Abu Kamil and Fibonacci. The algebra consisted of simple linear and quadratic equations and a few cubic equations, together with the methods for solving them; rules for operating with positive and negative numbers, finding squares, cubes and their roots; the rule of False Position (see History of Algebra Part 1 ) and the Rule of Three (simple proportion). These methods were applied to business and legal problems. There was some justification of the solution using diagrams, but mostly it was a matter of ‘memorising the rules’ and applying them to standard problems.
西欧中世纪的代数学最初源自花拉子米、阿布·卡米勒（Abu Kamil）与斐波那契（Fibonacci）的著作。当时的代数学包含简单的线性方程、二次方程及少量三次方程，以及相应的求解方法；还包括正负数运算法则、平方、立方及其开方运算；假设法（参见《代数学的发展（一）》）与三率法（简单比例）。这些方法被应用于商业与法律问题的求解。虽有用图形对解法进行佐证的情况，但主要还是“记忆规则”并将其应用于标准问题。

Leonardo Fibonacci (1170 - 1250)
莱昂纳多·斐波那契（1170 年—1250 年）

Well known for his collection of mathematical techniques [see: Note 2] and the promotion of the Hindu numeral system in the Liber Abaci of 1202, he also wrote Flos , a book where he shows that the root of the cubic equation $10x+2x^2+x^3=20$ can neither be a rational number, nor the square root of a rational number [see: Note 3].
斐波那契因在 1202 年的著作《算盘书》（Liber Abaci）中汇集数学方法[参见：注释 2]、推广印度数字体系而闻名。他还撰写了《花》（Flos）一书，在书中他证明了三次方程 $10x+2x^2+x^3=20$ 的根既不是有理数，也不是有理数的平方根[参见：注释 3]。

In his Book of Squares 1225 he turned much of Euclid’s geometrical work into arithmetic, developing new ideas from Arab science, and other techniques used by the ‘Abacus Masters’ who taught commercial arithmetic [see: Note 4]. He organised the rules as a series of logical propositions and supported his arguments using proportional triangles, squares and rectangles, which as we have seen, are perfectly general.
在 1225 年的《平方数书》（Book of Squares）中，他将欧几里得的大部分几何内容转化为算术形式，既借鉴阿拉伯科学发展新思想，也融入了教授商业算术的“算盘大师”（Abacus Masters）所用的其他方法[参见：注释 4]。他将这些规则整理为一系列逻辑命题，并借助比例三角形、正方形和长方形佐证观点——正如我们所见，这些图形的应用具有完全的普遍性。

Proposition 1 shows how the sum of the odd numbers always makes a perfect square. In our notation, the substance of Leonardo’s argument is:$$(1+3+5+7)+9=(1+3+5+7+9)$$
命题 1 证明了奇数之和始终为完全平方数。用现代符号表示，莱昂纳多的核心论证为：$$(1+3+5+7)+9=(1+3+5+7+9)$$

Proposition 2 states “Any square number exceeds the square before it by the sum of the roots.” Leonardo’s first example is simple:
命题 2 指出“任意平方数与其前一个平方数的差值，等于这两个平方数的根之和”。莱昂纳多给出的第一个示例十分简洁：
KaTeX parse error: Undefined control sequence: \mbox at position 21: … 4^2 = 25 - 16 \̲m̲b̲o̲x̲{, which is } 9…
$$5^2-4^2=25-16=9$$，而 9 正是 25 的根（5）与 16 的根（4）之和。

Proposition 10 finds the sum of a sequence of square numbers: $$6(1^2+2^2+3^2+....+n^2)=n(n+1)(2n+1)$$
命题 10 推导出平方数序列的和：$$6(1^2+2^2+3^2+....+n^2)=n(n+1)(2n+1)$$

Proposition 19 shows how to find numbers $A$, $B$, and $C$ such that: KaTeX parse error: Undefined control sequence: \mbox at position 15: B^2 - B = A^2 \̲m̲b̲o̲x̲ ̲{ and } B^2 + B…
命题 19 演示了如何找到满足以下条件的数 $A$、$B$ 和 $C$：KaTeX parse error: Undefined control sequence: \且 at position 15: B^2 - B = A^2 \̲且̲ B^2 + B = C^2

These and many other numerical relationships helped mathematicians of the 15th and 16th centuries to develop techniques for solving quadratic and cubic equations.
这些及其他众多数值关系，为 15 至 16 世纪的数学家开发二次方程与三次方程的求解方法提供了帮助。

Jordanus de Nemore (1225 - 1260)
若尔当努斯·德·内莫尔（1225 年—1260 年）

The mediaeval student’s attitude towards solving equations was quite different to ours. Today we arrange the algebra to isolate the unknown and we make $x$ the ‘subject’ of the equation. In Mediaeval times, the student worked with the known numbers in order to find the ‘root’. Jordanus’ book, De Numeris Datis (Concerning given numbers) was written about 1250 and is considered to be the first advanced algebra written in Western Europe since Diophantos . It offers a generalised treatment of quadratic, simultaneous and proportional equations. For solving quadratics, the procedure earlier described by Abu Kamil (c850 - c930) as ‘completing the square’ was simplified, Part 1 (Section 7 Case 5) , and for a problem like ‘A square and 10 of its roots equal 39’ you make a square, and attach to two of its sides rectangles whose length is half the number of roots, and proceed to fill in the empty space with another square.
中世纪学生的解方程思路与我们如今截然不同。现在我们会通过代数变形分离未知量，将 $x$ 作为方程的“主语”；而在中世纪，学生通过已知数去寻找“根”（root）。若尔当努斯的著作《论给定的数》（De Numeris Datis）约于 1250 年写成，被认为是自丢番图（Diophantos）之后西欧首部高阶代数学著作。书中对二次方程、联立方程及比例方程进行了一般性论述。在二次方程求解方面，他简化了阿布·卡米勒（约 850 年—约 930 年）此前提出的“配方法”[参见《代数学的发展（一）第 7 部分第 5 种形式》]：对于“一个平方数与其 10 个根之和等于 39”这类问题，先构造一个正方形，在其两条边上各附加一个“长为根系数一半”的长方形，再用另一个正方形填补空白区域。

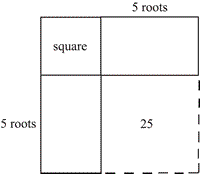
In the diagram, since the rectangles are $5$ roots long the dotted square must be $25$ roots. But the total of square and roots are given as $39$, so the side of the unknown square must be $3$, and the whole square $64$.
图中，由于长方形的长为 5 个根（根系数 10 的一半），虚线正方形的面积必为 25（5 的平方）。已知平方数与根的总和为 39，因此未知正方形的边长为 3，整个大正方形的面积为 64。

The 'Datis ’ shows how, by analysis of basic geometrical properties and using letters of the alphabet to represent numerical relationships, it is possible to establish generalised knowledge. Jordanus then illustrates each case with numerical examples.
《论给定的数》表明：通过分析基本几何性质，并使用字母表示数值关系，可建立具有普遍性的知识。随后，若尔当努斯为每种情况都搭配了数值示例进行说明。

For example, in Book IV Proposition 6, he shows that “If the ratio of two numbers and the sum of their squares is known, then each of the numbers is known.” [see: Note 6].
例如，在《论给定的数》第四卷命题 6 中，他证明了“若已知两个数的比值及其平方和，则可求出这两个数”[参见：注释 6]。

In modern symbols, he proceeds like this:KaTeX parse error: Undefined control sequence: \mbox at position 1: \̲m̲b̲o̲x̲{Given, }x : y …
用现代符号表示，他的推导过程如下：已知 $x:y=a$ 且 $x^2+y^2=b$

Let $d$ be the square of $x$, and $c$ the square of $y$, and let $d+c$ be known , so we have:
设 $d=x^2$、$c=y^2$，且已知 $d+c=b$，由此可得：
KaTeX parse error: Undefined control sequence: \mbox at position 46: …~~~~y^2 = c, ~~\̲m̲b̲o̲x̲ ̲{and so } ~~d +…

Now the ratio of $d$ to $c$ is the square of the ratio of $x$ to $y$, so KaTeX parse error: Undefined control sequence: \mbox at position 111: …)y^2=b~~~~~~~~ \̲m̲b̲o̲x̲ ̲{and so }y=\sqr…
由于 $d$ 与 $c$ 的比值等于 $x$ 与 $y$ 比值的平方，因此 $\frac{d}{c}=\frac{x^2}{y^2}=a^2$，代入得 $\frac{d}{c}{y}^2=b-y^2$，整理后 $\left(\frac{d}{c}+1\right)y^2=b$，最终解得 $y=\sqrt{\frac{b}{\left(a^2+1\right)}}$

KaTeX parse error: Undefined control sequence: \mbox at position 39: …}\frac{x}{y}=2 \̲m̲b̲o̲x̲ ̲{ and } x^2+y^2…
例如，若 $\frac{x}{y}=2$ 且 $x^2+y^2=500$，则 $y=\sqrt{\frac{500}{\left(4+1\right)}}=10$，进而 $x=20$。

The work of Jordanus was a significant change in the way equations were tackled. Much more emphasis was given to the number relationships that were based on proportional reasoning. It was the understanding of these relationships that was so important to Francois Viete later in the sixteenth century.
若尔当努斯的研究使方程求解方法发生了重大转变：他更加强调基于比例推理的数值关系——对这些关系的理解，对 16 世纪后期的弗朗索瓦·韦达（Francois Viete）而言至关重要。

---

2. Early Renaissance Algebra

文艺复兴早期的代数学

Nicolas Chuquet (1445 - 1488)
尼古拉·许凯（1445 年—1488 年）

Nicolas Chuquet was described as an ‘algoriste’ and his manuscript on Le Triparty en la Science des Nombres (1484) was known only to a few of his contemporaries. ‘Triparty’ means three parts, and the first section was on Numbers and their operations; the second on Surds $\left(3+\sqrt{5}\right)$ and Roots of Surds $\sqrt{\left(3+\sqrt{5}\right)}$; and the third on Algebra, where he invented special symbols for the unknown, squares and cubes up to the fourth power, and a system of indices which included $x^0=1$. He also used the first letters of operations like p for plus and m for minus. His algebra was developed as a series of general methods and in this work negative numbers appear as coefficients, exponents and solutions to problems. His rules for solving arithmetic problems also used zero and negative numbers. Unfortunately his work was little known, and not published until 1880, but his ideas reappear in the early 17th century.
尼古拉·许凯被称为“算术家”（algoriste），其手稿《数论三部分》（Le Triparty en la Science des Nombres，1484 年）在其同时代人中仅有少数人知晓。“Triparty”意为“三部分”：第一部分论述数字及其运算；第二部分研究无理数（如 $\left(3+\sqrt{5}\right)$）与复合无理数（如 $\sqrt{\left(3+\sqrt{5}\right)}$）；第三部分为代数学内容——他为未知量、平方、立方直至四次方发明了特殊符号，并提出一套指数体系（其中包含 $x^0=1$）。他还使用运算词的首字母表示符号，如 p 代表加（plus）、m 代表减（minus）。他的代数学以一系列通用方法构建，书中负数可作为系数、指数，也可作为问题的解；其算术解题规则还用到了零和负数。遗憾的是，他的研究鲜为人知，直至 1880 年才得以出版，但他的思想在 17 世纪早期重新受到关注。

Luca Pacioli (1445 - 1517)
卢卡·帕乔利（1445 年—1517 年）

Pacioli was a contemporary of Chuquet, and famous for the Summa de Arithmetica, geometria, proportioni et proportionibus (1494) and the Divina Proportione (1509) Pacioli’s works were important popular collections of current practical mathematics and were more useful for passing on known techniques and problems than for any original contributions. Pacioli is also famous for publishing the first description of double entry book-keeping where negative numbers had an obvious practical significance as debts or losses, and numerous works on accounting soon appeared in other languages, obviously copied from Pacioli [see: Note 7].
帕乔利与许凯是同时代人，因《算术、几何、比例与比例论概要》（Summa de Arithmetica, geometria, proportioni et proportionibus，1494 年）和《神圣比例》（Divina Proportione，1509 年）闻名。他的著作是当时实用数学的重要普及合集，虽在原创贡献方面有限，但对传播已知方法与问题起到了重要作用。帕乔利还因首次系统阐述复式记账法而闻名——在复式记账中，负数具有“债务”或“亏损”的明确实际意义。此后，大量会计著作以其他语言出版，内容明显借鉴了帕乔利的成果[参见：注释 7]。

---

3. Late Renaissance and Early Modern Algebra

文艺复兴后期与近代早期的代数学

Girolamo Cardano (1501 - 1576)
吉罗拉莫·卡尔达诺（1501 年—1576 年）

Cardano earned his living as a doctor and by casting horoscopes; he wrote on probability and published other books but his importance for us rests on his Artis Magnae sive de Regulis Algebraicis Liber Unus (1545) “Of the Great Art, or the First Book on the Rules of Algebra” the ‘Ars Magna’ as it is often called [see: Note 8].
卡尔达诺以行医和占星为生，曾撰写概率论著作及其他书籍，但他对代数学的重要性主要体现在其 1545 年的著作《大术，或代数法则第一书》（Artis Magnae sive de Regulis Algebraicis Liber Unus）——该书常被简称为《大术》（Ars Magna）[参见：注释 8]。

While the methods for solving quadratic problems were well known as a collection of geometrically based proportional relations and arithmetical algorithms, a unified and general approach was still not commonly available.
尽管二次方程的求解方法已发展为一套基于几何的比例关系与算术算法，但当时仍缺乏通用、统一的求解思路。

The big unsolved problem of the time was finding solutions to cubic equations. By this time mathematicians had identified about 13 different cases of cubic equations which included various combinations of cubes, squares and numbers [see: Note 9]. The Ars Magna contains the proportional methods and rules that had been developed by mathematicians before him, his own work was also a significant contribution, and he acknowledged the discoveries of his contemporaries.
当时未解决的重大问题是三次方程的求解。截至那时，数学家已识别出约 13 种不同形式的三次方程，涵盖立方项、平方项与常数项的各种组合[参见：注释 9]。《大术》既收录了前辈数学家提出的比例方法与规则，也包含他本人的重要贡献，同时他还认可了同时代学者的发现。

Existing methods for solving cubic equations relied on finding substitutions to reduce them to quadratics; many of these tricks could only be applied to special cases. For example this is the first problem in Chapter XXV:
当时的三次方程求解方法依赖“代换法”将其转化为二次方程，但许多方法仅适用于特殊情况。例如，该书第二十五章的第一道题：

When the cube is equal to the first power and a constant, divide the coefficient of x into two parts that the sum of each multiplied by the square root of the other is half the constant of the equation. The roots of these two parts added together make the value of $x$.
“若立方项等于一次项与常数项之和，将 $x$ 的系数拆分为两部分，使得‘每一部分乘以另一部分的平方根’的和等于方程常数项的一半。这两部分的平方根之和即为 $x$ 的值。”

Example: $x^3=10x+24$
示例：$x^3=10x+24$

Solution: “Ten divides into two parts, $9$ and $1$, either of which multiplied by the square root of the other makes $9$ and $3$, the sum of which is $12$, one half of $24$. Therefore R $9$ plus R $1$ which are $3$ and $1$ added together, produce $4$, the value of x.”[see: Note 10]
解法：“将 10 拆分为 9 和 1 两部分：9 乘以 1 的平方根得 9，1 乘以 9 的平方根得 3，两者之和为 12（即 24 的一半）。因此，R9（9 的平方根）加R1（1 的平方根），即 3 加 1，结果为 4，也就是 $x$ 的值。”[参见：注释 10]

Throughout the book, every rule was written in Latin; the only notations used were p for plus and m for minus and an elaborate capital R for radix, to indicate square roots.
全书所有法则均以拉丁文表述，仅使用少量符号：p 代表加，m 代表减，复杂的大写字母 R（源自“根”的拉丁文“radix”）代表平方根。

This symbol was invented by Regiomontanus (1436 - 1476)

该符号由雷格蒙塔努斯（Regiomontanus，1436 年—1476 年) 发明

This symbol was not commonly used until about 1630

该符号（ \sqrt{} ​) 直至 1630 年左右才被广泛使用

Discovering Imaginary Numbers

虚数的发现

In Chapter XXXVII Cardano discusses the use of negative numbers in calculations, and in Rule II appears his first use of negative square roots.
在《大术》第三十七章中，卡尔达诺探讨了负数在计算中的应用，并在第二条法则中首次使用了“负平方根”。

The problem is to ‘divide $10$ into two parts whose product is $40$’
问题为“将 10 拆分为两部分，使其乘积为 40”

His method is exactly the same as the ‘Babylonian Algorithm’ shown in Part 1 (Teachers’ notes 5) and if we think of the problem as: $ x(10 - x) = 40$, we have a quadratic equation $x^2+40=10x$ (squares and numbers equal roots) with $10$ as the coefficient of $x$ which we divide in half, and proceed with the algorithm .
他的解法与《代数学的发展（一）（教学注释 5）》中的“巴比伦算法”完全一致：将问题转化为 $ x(10 - x) = 40$，得到二次方程 $x^2+40=10x$（平方项加常数项等于一次项），将 $x$ 的系数 10 取半后，按算法步骤求解。

Cardano gives two solutions
卡尔达诺给出的两个解为：
$5$p : R : m $15$ and $5$m : R : m $15$. [see: Note 11]
$5$p : R : m $15$ 与 $5$m : R : m $15$[参见：注释 11]（即现代符号中的 $5+\sqrt{-15}$ 与 $5-\sqrt{-15}$）。

The product of these two results is, in fact $40$, and he demonstrates how to solve four other problems that give negative square roots. He was clearly mystified by these ‘imaginary’ square roots of negative numbers, and this is still a problem for many who meet them for the first time.
这两个解的乘积确实为 40，他还演示了另外四道会出现负平方根的问题的解法。显然，他对这些“虚构的”负平方根感到困惑——这一点，至今仍让许多初次接触虚数的人感到棘手。

---

4. Introducing the 17th Century

17 世纪的代数学

Image
图片

Francois Viete (1540-1603)
弗朗索瓦·韦达（1540 年—1603 年）

In his two major works, In Artem Analyticem Isagoge (Introduction to the Analytic Art, 1591) and De Potestatum Resolutione (On the Numerical Resolution of Powers 1600) Viete made probably the most important contributions to the development of algebra at this time.
在其两部重要著作《分析术引论》（In Artem Analyticem Isagoge，1591 年）与《幂的数值解法》（De Potestatum Resolutione，1600 年）中，韦达为这一时期代数学的发展做出了或许是最重要的贡献。

Viete used a consistent symbolic notation with vowels A, E, I, O, U and Y for unknown quantities, and given terms by the letters B, G, D and other consonants.
韦达采用了一套统一的符号体系：用元音字母 A、E、I、O、U、Y 表示未知量，用辅音字母 B、G、D 等表示已知量。

Addition and Subtraction used the symbols + and -. For Multiplication he used the word ‘in’ and for Division used the fraction bar. So KaTeX parse error: Undefined control sequence: \mbox at position 7: \frac{\̲m̲b̲o̲x̲ ̲{B in C}}{\mbox…
加法与减法使用符号 + 和 -；乘法用单词“in”表示；除法用分数线表示。例如，KaTeX parse error: Undefined control sequence: \mbox at position 7: \frac{\̲m̲b̲o̲x̲ ̲{B in C}}{\mbox… 表示 KaTeX parse error: Undefined control sequence: \mbox at position 7: \frac{\̲m̲b̲o̲x̲ ̲{BC}}{A^2}。

Powers were N (for numerus - a pure number), Q (quadratus - a square) C (cubus - a cube) further powers were expressed by combinations of these symbols, so QQ was a fourth power, CQ, a fifth power and so on.
幂的表示：N（源自“数”的拉丁文“numerus”）代表纯数字，Q（源自“平方”的拉丁文“quadratus”）代表平方，C（源自“立方”的拉丁文“cubus”）代表立方；更高次幂用这些符号组合表示，如 QQ 代表四次方，CQ 代表五次方（立方加平方），以此类推。

For Roots he used the symbol $L$ (for Latus - a side) and sometimes the $R$ symbol . So $L9$ meant the square root of $9$, and $LC27$ meant the cube root of $27$.
根的表示：用符号 $L$（源自“边”的拉丁文“latus”），有时也用 $R$；例如，$L9$ 表示 9 的平方根，$LC27$ 表示 27 的立方根。

All his equations were homogeneous - that means the dimensions of all the terms in the equation had to be the same.
他的所有方程均为“齐次方程”——即方程中所有项的“维度”必须一致。

In the equation $AQ+AB=ZQ,AQ$ and $ZQ$ represent squares, and AB a rectangle.
例如方程 $AQ+AB=ZQ$ 中，$AQ$（A 的平方）与 $ZQ$（Z 的平方）代表平方项，$AB$（A 乘以 B）代表矩形面积项（维度与平方项一致）。

Some of these notational ideas were already being used; for example, Johannes Scheubel (1494 - 1570) writing in 1551 used special combinations of symbols for powers of the unknown:
其中一些符号思想已被前人采用，例如约翰内斯·朔贝尔（Johannes Scheubel，1494 年—1570 年）在 1551 年的著作中，用特殊符号组合表示未知量的幂：

The English mathematician, Robert Recorde used the same notation in his book [see: Note 12] on algebra in 1557 but describes the powers of numbers in this way:
英国数学家罗伯特·雷科德（Robert Recorde）在 1557 年的代数学著作[参见：注释 12] 中使用了相同符号，但对幂的描述如下：

Using his literal notation, Viete exposed the structural aspects of polynomial equations and gave solution methods for whole classes of equations.
通过这套文字符号体系，韦达揭示了多项式方程的结构特征，并给出了整类方程的求解方法。

Viete’s solution of quadratic equations used the three proportional triangles in a semi-circle shown in Part 1 (Section 6. Greek Geometry)
韦达的二次方程解法，借鉴了《代数学的发展（一）第 6 部分“希腊几何”》中提到的“半圆内三个比例三角形”模型：

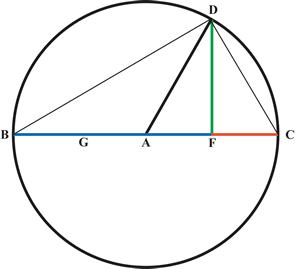
The equation: $ A$ quadratus $+ AB = Z $ quadratus or $ (A^2 + AB = Z^2) $, in Viete’s symbols is $AQ+AB=ZQ$, which can be written as $A(A+B)=ZZ$ and rearranged as equal proportions becomes: $$\frac{A}{Z}=\frac{Z}{(A+B)}$$
方程“$A$的平方加$A$乘$B$等于$Z$的平方”（即 $A^2+AB=Z^2$），用韦达的符号表示为 $AQ+AB=ZQ$，可变形为 $A(A+B)=Z^2$，进一步整理为比例形式：$$\frac{A}{Z}=\frac{Z}{(A+B)}$$

In the diagram there are three lines of increasing magnitude, $FC,FD$ and $FB$.
图中有三条长度递增的线段：$FC$、$FD$ 和 $FB$。
$FC$ is $A$, $FD$ is $Z$ and $FB$ is $A+B$
其中 $FC=A$，$FD=Z$，$FB=A+B$。

For three magnitudes in proportion, the well-known rule is:
对于成比例的三个量，有著名的“比例中项定理”：
‘the product of the extremes is equal to the square of the mean’.
“两外项之积等于中项的平方”。

The lines $A$ and $(A+B)$ are the extremes and $Z$ is the mean .
线段 $A$ 与 $A+B$ 是“外项”，线段 $Z$ 是“中项”。

For the equation $A^2+10A=144,Z=12$ and $A:12=12:(A+10)$ so we have to find a number $A$, so that the ratios are equal. The three numbers are $8,12$ and $18$.
对于方程 $A^2+10A=144$，可得 $Z=12$，比例关系为 $A:12=12:(A+10)$。我们需要找到满足该比例的数 $A$，最终得三个数为 $8$、$12$ 和 $18$（即 $A=8$，$A+B=18$）。

---

The Fundamental Theorem of Algebra

代数基本定理

Thomas Harriot (c1560 - 1621) and Albert Girard (1595-1632)
托马斯·哈里奥特（约 1560 年—1621 年）与阿尔贝·吉拉尔（1595 年—1632 年）

By this time, many mathematicians were working on similar problems and developing their own notations. The most important of these were Thomas Harriot, an English mathematician and explorer, and Albert Girard, a Dutch Army Engineer. Harriot’s work remains mainly in manuscript form, even today. His Artis Analyticae Praxis (The Practice of the Analytical Art) only appeared in 1661 well after his death, but his papers show that he had developed a sophisticated notation, almost like we use today, using $aa$ for $a^2,aaa$ for $a^3$ etc. and through this realised that multiplying brackets like $(b-a)(c-a)(d-a)$ led to a clear relationship between the roots and coefficients of an equation.
此时，许多数学家都在研究类似问题并发展各自的符号体系，其中最重要的两位是英国数学家兼探险家托马斯·哈里奥特，以及荷兰陆军工程师阿尔贝·吉拉尔。哈里奥特的研究成果至今仍多以手稿形式留存，其著作《分析术实践》（Artis Analyticae Praxis）直至他去世多年后的 1661 年才出版。但从他的手稿可见，他已开发出一套接近现代的精密符号：用 $aa$ 表示 $a^2$，用 $aaa$ 表示 $a^3$ 等；并通过这种符号发现，将 $(b-a)(c-a)(d-a)$ 等括号相乘，可清晰呈现方程的根与系数之间的关系。

The first explicit statement of the idea that every polynomial equation of degree $n$ has $n$ roots appeared in 1629 in Girard’s L’Invention Nouvelle en L’Algebre (A New Discovery in Algebra). Here, Girard states his basic theorem,
“$n$ 次多项式方程有 $n$ 个根”这一思想的首次明确表述，出现在吉拉尔 1629 年的著作《代数新发现》（L’Invention Nouvelle en L’Algebre）中。他在书中提出了基本定理：
“Every algebraic equation … admits of as many solutions as the denomination of the highest quantity indicates …”
“每个代数方程……的解的个数，与其最高次项的次数相等……”

Girard gave examples, but did not show how he derived his theorem, and did not clearly account for ‘imaginary’ roots. The search for a general proof occupied mathematicians for many years to come.
吉拉尔给出了示例，但未说明定理的推导过程，也未明确解释“虚根”的情况。此后多年，数学家们一直致力于寻找该定理的一般性证明。

Rene Descartes (1596 - 1650)
勒内·笛卡尔（1596 年—1650 年）

Even though many improvements in notation had begun to expose the structure of algebraic equations, and begun to transform the representation of the problems from geometric images to written expressions, mathematicians still used geometry as a way of demonstrating the ‘truth’ and generality of the algebra.
尽管符号体系的诸多改进已开始揭示代数方程的结构，并推动问题的表述从几何图像转向文字表达式，但数学家仍将几何作为证明代数“真实性”与普遍性的手段。

In 1637 he published his Discours de la Methode’… a work on ‘how to undertake investigation to make ideas clear, and to seek for truth in the sciences’. As an example of this method he included La Geometrie which states on the first page that,
1637 年，笛卡尔出版了《方法论》（Discours de la Methode）——该书探讨“如何通过研究理清思路、在科学中寻求真理”。作为该方法的示例，他在书中收录了《几何学》（La Geometrie），其开篇即指出：
“Any problem in geometry can easily be reduced to such terms that a knowledge of the length of certain straight lines is sufficient for its construction.”
“任何几何问题都可轻松转化为这样的形式：只需知道某些线段的长度，即可完成作图。”

Descartes demonstrates how this may be done:
笛卡尔演示了具体的转化方法：

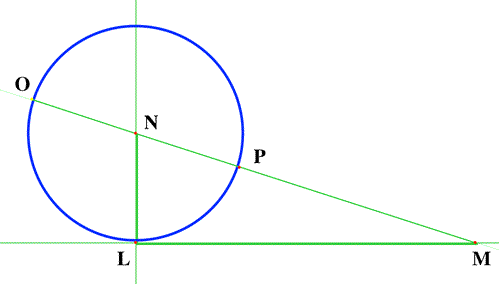
The equation is $z^2\propto az-bb$. Construct $LM$ and $LN$ so that $LM=b$ and $LN=\frac{a}{2}$
方程为 $z^2=az-bb$（原文符号 $\propto$ 此处表示相等关系）。构造线段 $LM$ 与 $LN$，使得 $LM=b$，$LN=\frac{a}{2}$。

The unknown $z$, is $OM$. In triangle$NLM$, KaTeX parse error: Undefined control sequence: \mbox at position 43: …ight)^2 + bb ~~\̲m̲b̲o̲x̲ ̲{ and }~~NM = \…
未知量 $z$ 即为线段 $OM$ 的长度。在 $△NLM$ 中，$ NM^2 =\left(\frac{a}{2} \right)^2 + bb$，因此 $NM=\sqrt{{\left(\frac{a}{2}\right)}^2+bb}$，进而可得 $ z=\frac{a}{2}+\sqrt{\left(\frac{a}{2} \right)^2 + bb}$。

However, Descartes still appealed to a theorem from Euclid Book II Proposition 6 to justify his solution to the reader.
不过，笛卡尔仍引用《欧几里得几何原本》第二卷命题 6 的定理，向读者证明该解法的合理性。

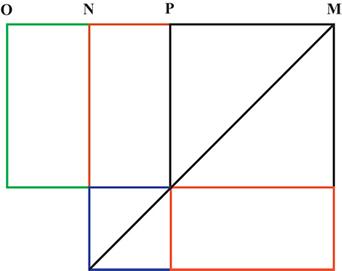
The rectangle contained by $OM$ and $PM$, plus the square on $NP$, is equal in area to the square on $NM$. ($N$ bisects $OP$.) The area of the green rectangle is the same as the areas of the red rectangles.
“线段 $OM$ 与 $PM$ 构成的矩形面积，加上线段 $NP$ 上的正方形面积，等于线段 $NM$ 上的正方形面积”（$N$ 是 $OP$ 的中点）。绿色矩形的面积与两个红色矩形的面积之和相等。
$$OM.PM+N{P}^2=N{M}^2$$

Here is Descartes’ original description of the problem:
以下是笛卡尔对该问题的原始描述：

---

5. Notation and Representation [see: Note 13]

符号与表述[参见：注释 13]

By the middle of the 17th Century the representation of elementary algebraic problems and relations looked much as it is today. The major factors influencing change were the printing press that provided wider communication of ideas, and the slow appreciation of the similarity in the structure of the algorithms brought about by the changes in notation. Most of this happened in the period from 1500 to 1650; by then the standard notation had become generally accepted.
到 17 世纪中期，初等代数问题与关系的表述已与当今形式十分接近。推动这一变化的主要因素有二：一是印刷术促进了思想的广泛传播；二是符号体系的变革，使人们逐渐认识到不同算法在结构上的相似性。这些变化主要发生在 1500 年至 1650 年间，到 1650 年左右，标准符号体系已被广泛接受。

There were no clear stages in this process. Some historians proposed a ‘literal’ stage where all the problems are written, sometimes in very complicated language; a ‘syncopated’ stage with a mixture of words and symbols; and a final ‘symbolic’ stage where the mathematics consists only of symbols. But this is not the case, even today when you look at a text, words are still there. Another aspect was the technical language . Translating from Greek and Arabic into Latin, and then into the common language of a country, new words were invented to describe new ideas, and were then taken over by others. For example, the German for ‘thing’ or the unknown, was ‘Die Coss’, the title of a book by Michael Stifel (1487 - 1567). So, in England, algebra became known as the Cossic Art . Borrowing from the French, the pentagon was known as a cinqangle and so on. There are many more examples among the writings of English mathematicians of the 16th and 17th centuries.
这一过程并无明确的阶段划分。部分历史学家提出“文字阶段”（所有问题均用文字表述，有时语言十分复杂）、“简记阶段”（文字与符号混用）、“符号阶段”（仅用符号表述数学内容）的划分，但实际并非如此——即便在今天的文献中，文字仍不可或缺。另一重要方面是“专业术语”的演变：从希腊文、阿拉伯文译为拉丁文，再译为各国通用语言的过程中，人们为描述新思想发明了新术语，并被广泛采用。例如，德语中用“Die Coss”（意为“事物”）表示未知量，迈克尔·施蒂费尔（Michael Stifel，1487 年—1567 年）曾以此为书名；因此在英国，代数学曾被称为“Cossic Art”（事物术）。又如“五边形”一词，曾借鉴法语“cinqangle”（cinq 为“五”，angle 为“角”）。在 16 至 17 世纪英国数学家的著作中，类似例子还有很多。

Representation of the objects, relationships, operations, and the structure of processes together with the evolution of the printing press, were the most important aspects which aided the development of mathematics during this period.
对“研究对象、关系、运算、流程结构”的表述，再加上印刷术的发展，是这一时期推动数学发展的最重要因素。

The signs for Addition and Subtraction first appear in print in 1526, and the Equals sign appears in 1557. The cross X for Multiplication is later, about 1628; the Colon (: ) for Division in 1633 and the Obelus ($÷$) in 1659. The signs for inequality , > and < are first used in 1631.
加号（+）与减号（-） 于 1526 年首次在印刷品中出现；等号（=） 出现于 1557 年；乘号（×） 较晚，约在 1628 年；除号（:） 出现于 1633 年，另一种除号（$÷$）出现于 1659 年；不等号（>、<） 于 1631 年首次使用。

Square and other roots start as the capital R (as in the picture above) in about 1465 and eventually our usual sign \sqrt{} ​ by 1630; Powers were first expressed by whole number indices in 1484 and had become widely accepted by 1637, and negative indices also appear in 1484, but fractional indices not until 1676.
平方根及其他根 的符号：约 1465 年开始使用大写字母 R（如前文图示），直至 1630 年左右演变为如今的 \sqrt{} ​；幂 的表示：1484 年首次用整数指数表示幂，1637 年已被广泛接受；1484 年还出现了负指数，但分数指数直至 1676 年才出现。

The symbols for the unknown and for constants are greatly varied. All kinds of signs and combinations of signs were initially used. Jordanus used letters to replace numbers as a sign of generality, Vieta was the first to use vowels (A, E, I, O, U) for the unknown and consonants (A, B, C, …) for known quantities, and Descartes introduced the convention of letters at the end of the alphabet (x, y, z) for unknown and at the beginning (a, b, c) for known quantities which is what we use today.
未知量与常量 的符号差异极大：最初使用过各种符号及符号组合。若尔当努斯用字母代替数字以体现普遍性；韦达首次用元音字母（A、E、I、O、U）表示未知量，用辅音字母（A、B、C 等）表示已知量；笛卡尔则确立了“用字母表末尾的字母（x、y、z）表示未知量，用开头的字母（a、b、c）表示已知量”的惯例——这一惯例沿用至今。

N.B. Teachers’ notes related to the history of algebra discussed here can be found by clicking on the ‘Notes’ tab at the top of this article .
注：点击本文顶部的“注释”（Notes）标签，可查看与本文所讨论代数学历史相关的教学注释 。

---

Notes

注释

1. It is important to note that there were many people throughout this period from the 11th to the 17th century who made significant contributions to the story of the development of algebra, and have not been mentioned here. Further information can be found by consulting the references.
   需注意的是，在 11 至 17 世纪这一时期，还有许多人为代数学的发展做出了重要贡献，本文未一一提及。更多信息可参考文末参考文献。

2. We are very lucky that copies of Fibonacci’s books have survived. The Liber Abaci (1202 ), Practica Geometriae (1220), Flos and the Book of Squares both produced in 1225 tell us a great deal about mathematics in the early Mediaeval period.
   斐波那契的著作得以留存，实属幸运。其《算盘书》（1202 年）、《实用几何》（1220 年）、《花》（1225 年）与《平方数书》（1225 年），为我们了解中世纪早期的数学提供了大量信息。

3. Fibonnaci’s approximate result is correct to nine decimal places. This equation was solved by Omar Khayyam (1048 - 1122) using the intersection of a circle with a hyperbola.
   斐波那契给出的近似解精确到小数点后 9 位。该方程此前由奥马尔·海亚姆（Omar Khayyam，1048 年—1122 年）通过“圆与双曲线的交点”求解。

4. The Abacus Schools were training courses for merchants in commercially useful arithmetic, but they also included ‘puzzle problems’. Fibonacci has been mistakenly seen as the father of the Abacus Schools, but they existed well before his time.
   “算盘学校”是为商人开设的商业算术培训课程，课程中也包含“趣味谜题”。斐波那契曾被误称为“算盘学校之父”，但实际上这类学校在他之前早已存在。

5. The Arithmetica of Diophantos (c200 - c284) had been translated and developed by the Arabs and was available in Latin at this time.
   丢番图（约 200 年—约 284 年）的《算术》已被阿拉伯人翻译并发展，此时已有拉丁文版本。

6. I have taken this example from the translation by Barnabas Hughes, pages 167-168.
   本示例引自巴纳巴斯·休斯（Barnabas Hughes）的译本，第 167-168 页。

7. It is interesting to contrast the social circumstances and the quality of the work of Chuquet and Pacioli. Chuquet had access to many mathematical works, and made the most of his opportunities in developing original ideas. However he was relatively isolated, hardly went outside his home city of Lyon, and his manuscript work was not printed at the time. Pacioli on the other hand was born into a commercial milleu in Italy, was known to two famous artists, Piero della Francesca and Leone Battista Alberti, was a tutor to the sons of powerful people in Venice and Rome, and had his books printed. This is not to denigrate Pacioli, but only to point out that different circumstances and the printing press played a large part in their fortunes.
   对比许凯与帕乔利的社会背景及研究成果特点，颇具启发意义：许凯能接触到大量数学著作，并充分利用机会发展原创思想，但他相对孤立，几乎未离开过家乡里昂，其手稿在当时也未出版；而帕乔利出生于意大利的商业环境，与皮耶罗·德拉·弗朗切斯卡（Piero della Francesca）、莱昂·巴蒂斯塔·阿尔伯蒂（Leone Battista Alberti）两位著名艺术家相识，曾担任威尼斯与罗马权贵之子的导师，其著作得以印刷出版。这并非贬低帕乔利，而是想指出：不同的环境与印刷术的出现，对两人的学术影响力起到了重要作用。

8. Most recent histories of mathematics give versions of the story of the solution of equations in 15th and 16th century Italy. Chapter 4 of John Derbyshire’s Unknown Quantity gives a good account of the convolutions surrounding Cardan’s work.
   近期多数数学史著作，都讲述了 15 至 16 世纪意大利数学家求解方程的故事。约翰·德比希尔（John Derbyshire）的《未知量》（Unknown Quantity）第四章，详细叙述了卡尔达诺著作背后的复杂历程。

9. We know that a cubic equation has three roots that are real or imaginary according to whether the graph cuts the x-axis in three places, touches the axis at a minimum, or cuts it only once. Clearly, these concepts were not available to Cardano.
   我们如今知道，三次方程有三个根（实根或虚根），根的类型取决于函数图像与 x 轴的交点情况：与 x 轴交于三点（三个不同实根）、在最低点与 x 轴相切（重根），或仅交于一点（一个实根与两个共轭虚根）。显然，卡尔达诺当时并不了解这些概念。

10. The substitution ‘trick’ comes from the works of Fibonacci and Jordanus: in our notation, if $x^3=ax+N$, let $a=f+g $ and let $ f \sqrt{g}+g\sqrt{f}=\frac{N}{2}$ then $x=\sqrt{f}+\sqrt{g}$
    此处的“代换技巧”源自斐波那契与若尔当努斯的研究：用现代符号表示，若 $x^3=ax+N$，设 $a=f+g$，且满足 $ f \sqrt{g}+g\sqrt{f}=\frac{N}{2}$，则 $x=\sqrt{f}+\sqrt{g}$。

11. $5+\sqrt{-15}$ and $5-\sqrt{-15}$
    即现代符号中的 $5+\sqrt{-15}$ 与 $5-\sqrt{-15}$。

12. Robert Recorde The Whetstone of Witte 1557. Another interesting aspect of the evolution of mathematical understanding is the development of a universal technical language. In England, many words were taken over from French (moitie meaning half) and German (zenzike meaning square). This is where the strange z symbol comes from.
    指罗伯特·雷科德 1557 年的著作《智力磨石》（The Whetstone of Witte）。数学认知演变的另一有趣方面，是通用专业语言的发展：在英国，许多术语借鉴了法语（如“moitie”意为“一半”）与德语（如“zenzike”意为“平方”，文中特殊符号“z”正源于此）。

References

参考文献

a) General sources covering the mathematics of the Middle Ages and Renaissance:
a) 涵盖中世纪与文艺复兴时期数学的通用文献:

Boyer, C. B. (1968) A History of Mathematics . London. John Wiley. A popular book with many reprints. Chapters XV and XVI cover the Middle Ages and the Renaissance.
博耶,C. B.(1968).《数学史》. 伦敦:约翰·威利出版社｡该书广受欢迎,多次再版,第十五､十六章涵盖中世纪与文艺复兴时期的数学｡

Cajori, F. A. (2007) A History of Mathematical Notations 2 Vols. . This is the principal source book for information in this area. Originally published in 1928/9 by Open Court, there is a new paperback edition available from Amazon at £ 17 for each volume. A bargain for your college library.
卡约里,F. A.(2007).《数学符号史》(两卷本). 该书是该领域的核心资料,原版由开放法院出版社于 1928/1929 年出版,亚马逊现有平装新版,每卷售价 17 英镑,是高校图书馆的性价比之选｡

Derbyshire, J. (2008) The Unknown Quantity . London. Atlantic Books Now in paperback at £9.99 this is a popular story of the problem of finding the ‘thing’ of ancient algebra up to the 20th Century. The Introduction and Part 1 up to page 94 1591cover the ideas in both parts of this NRICH account. There are useful sections giving reasonable straightforward explanations of the mathematics involved.
德比希尔,J.(2008).《未知量》. 伦敦:大西洋图书公司｡该书现为平装本,售价 9.99 英镑,通俗讲述了从古代代数中“未知事物"的求解,到 20 世纪代数学发展的历程｡引言及第 1 部分(至第 94 页)涵盖了本 NRICH 文章两部分的核心思想,并设有实用章节,对相关数学知识进行了清晰易懂的解释｡

Katz, Victor, J. (1999) (Second Edition, Corrected) A History of Mathematics : An Introduction Harlow, England. Addison-Wesley The best and most comprehensive and up-to-date general history of mathematics available. Chapter 9 ‘Algebra in the Renaissance’ (pages 342 - 384) covers most of the material in this article.
卡茨,维克多,J.(1999).《数学史导论》(修订第二版). 英国哈洛:艾迪生-韦斯利出版社｡当前最优秀､最全面且最新的数学通史著作,第九章“文艺复兴时期的代数学"(第 342-384 页)涵盖了本文的大部分内容｡

Kline, M. (1972) Mathematical Thought from Ancient to Modern Times. Oxford. O.U.P. Before Katz, this was the best available and has been reprinted a number of times. Chapters 11 to 13 on the Renaissance and its mathematics are still very useful.
克莱因,M.(1972).《古今数学思想》. 牛津:牛津大学出版社｡在卡茨的著作出版前,该书是最权威的数学史著作,多次再版,第十一至十三章关于文艺复兴及其数学的内容仍极具参考价值｡

b) More specialised sources available in translation:
b) 可获取译本的专项文献:

Girolamo Cardano (1545) The Great Art, or the Rules of Algebra. (Translated by R. Witmer) 1968. M.I.T. Press.
吉罗拉莫·卡尔达诺(1545).《大术,或代数法则》(R. 维特默译). 1968 年:麻省理工学院出版社｡

Nicolas Chuquet, Renaissance Mathematician (1985) Translated by Graham Flegg, Cynthia Hay and Barbara Moss of Le Triparty en la Science des Nombres . Lancaster Reidel Publishing Company.
《尼古拉·许凯:文艺复兴时期的数学家》(1985). 格雷厄姆·弗莱格､辛西娅·海伊､芭芭拉·莫斯译,译自许凯《数论三部分》. 兰卡斯特:莱德尔出版公司｡

Rene Descartes (1637) La Geometrie (Translated by D.E. Smith and Marcia Latham) 1954. This Dover edition of the Geometry is still available. The English translation is on one page, and a facsimile of the original French on the facing page. The French is not too difficult, and the notation for a quadratic equation virtually the same as today.
勒内·笛卡尔(1637).《几何学》(D.E. 史密斯､玛西娅·莱瑟姆译). 1954 年:多佛出版社｡该版本至今仍可获取,书页左侧为英文译文,右侧为法文原版影印件｡法文原文难度不高,其中二次方程的符号表述与当今几乎一致｡

Leonardo Fibonacci The Book of Squares (Translated by L.E. Sigler ) 1987) London. Academic Press.
莱昂纳多·斐波那契.《平方数书》(L.E. 西格勒译). 1987 年:伦敦学术出版社｡

Jordanus de Nemore De Numeris Datis (Translated by Barnabas Hughes) 1981 University of California Press.
若尔当努斯·德·内莫尔.《论给定的数》(巴纳巴斯·休斯译). 1981 年:加利福尼亚大学出版社｡

Recorde, Robert (1557) The Whetstone of Witte From the original English Text.
罗伯特·雷科德(1557).《智力磨石》(英文原版).

Johannes Scheubel (1551) Algebrae Compendiosa From the Original Latin Text Francois
约翰内斯·朔贝尔(1551).《简明代数学》(拉丁文原版).

Viete (1591) The Analytic Art (Translated by R. Witmer) 1983 Kent State University Press
弗朗索瓦·韦达(1591).《分析术》(R. 维特默译). 1983 年:肯特州立大学出版社｡

---

via:

• The Development of Algebra - 1 | NRICH
  http://nrich.maths.org/articles/development-algebra-1
• The Development of Algebra - 2 | NRICH
  http://nrich.maths.org/articles/development-algebra-2