注:本文为 “微分方程” 相关合辑。
英文引文,机翻未校。
中文引文,略作重排。
如有内容异常,请看原文。
Methods of Solving Differential Equations: Definition, Types, Solutions, Examples
微分方程的求解方法:定义、类型、解与示例
Written By P_C
Last Modified 02-01-2025
Methods of Solving Differential Equation: A differential equation is an equation that contains one or more functions with its derivatives. It is primarily used in physics, engineering, biology, etc. The differential equation’s primary purpose is to study solutions that satisfy the equations. The solution of the differential equation is the relationship between the variables included, which satisfies the given differential equation.
微分方程的求解方法:微分方程是包含一个或多个函数及其导数的方程。它主要应用于物理学、工程学、生物学等领域。微分方程的主要用途是研究满足该方程的解。微分方程的解是所含变量之间的一种关系,这种关系能够满足给定的微分方程。
There are two types of solutions of differential equations, namely, the general solution and the particular solution. The general and the particular solutions of differential equations make use of some steps of integration to solve the equations. In this article, let us learn more about methods to solve the differential equation such as variable separable method, homogenous differential equation, and linear differential equation with the help of indefinite integration formula.
微分方程的解分为两类,即通解和特解。微分方程的通解和特解均需通过若干积分步骤求解。本文将借助不定积分公式,详细介绍微分方程的求解方法,如分离变量法、齐次微分方程解法和线性微分方程解法等。
Solution of Differential Equations
微分方程的解
The solution of a differential equation is an expression for the dependent variable in terms of the independent variable which satisfies the given differential equation, so the solution can be classified into two types;
微分方程的解是将因变量用自变量表示的表达式,且该表达式满足给定的微分方程。因此,微分方程的解可分为两类:
1. General Solution
通解
A solution that consists of as many arbitrary constants as the order of the differential equation is called a general solution.
含有与微分方程阶数相同个数的任意常数的解,称为通解。
2. Particular Solution
特解
The solution is obtained by assigning particular values to the arbitrary constants in the general solution of the differential equation, and then the resulting solution is a particular solution. The result of eliminating one arbitrary constant yields a first-order differential equation, and eliminating two arbitrary constants yields a second-order differential equation.
通过给微分方程通解中的任意常数赋予特定值而得到的解,称为特解。消去一个任意常数可得到一阶微分方程,消去两个任意常数可得到二阶微分方程。
Methods to Solve First Order, First Degree Differential Equations
一阶一阶微分方程的求解方法
There are several methods to solve the first order, first-degree differential equation;
一阶一阶微分方程的求解方法有多种:
-
Solution by inspection method
观察法求解 -
Variable separable method
分离变量法 -
Homogenous equations
齐次方程解法 -
First-order, linear equations
一阶线性方程解法
Inspection Method
观察法
If the differential equation is of the form
若微分方程具有如下形式:
f
(
f
1
(
x
,
y
)
)
d
(
f
1
(
x
,
y
)
)
+
φ
(
f
2
(
x
,
y
)
)
d
(
f
2
(
x
,
y
)
)
+
⋯
=
0
,
f(f_1(x,y))d(f_1(x,y)) + \varphi(f_2(x,y))d(f_2(x,y)) + \cdots = 0,
f(f1(x,y))d(f1(x,y))+φ(f2(x,y))d(f2(x,y))+⋯=0,
then each term can be integrated separately. So, the solution of the differential equation can be obtained by using the inspection method. There are a few results that will help us to find the solution of differential equation
则其中每一项均可单独积分,因此可通过观察法求得该微分方程的解。以下是一些有助于求解微分方程的常用结果:
| Type 类型 | Solution 对应微分形式 |
|---|---|
| d ( x + y ) d(x+y) d(x+y) | d x + d y dx + dy dx+dy |
| d ( x y ) d(xy) d(xy) | x d y + y d x xdy + ydx xdy+ydx |
| d ( x y ) d\left(\frac{x}{y}\right) d(yx) | y d x − x d y y 2 \frac{ydx - xdy}{y^2} y2ydx−xdy |
| d ( y x ) d\left(\frac{y}{x}\right) d(xy) | x d y − y d x x 2 \frac{xdy - ydx}{x^2} x2xdy−ydx |
| d ( x 2 y ) d\left(\frac{x^2}{y}\right) d(yx2) | 2 x y d x − x 2 d y y 2 \frac{2xydx - x^2dy}{y^2} y22xydx−x2dy |
Variable Separable Method
分离变量法
The first order, first-degree differential equation is of the form
一阶一阶微分方程的一般形式为:
d
y
d
x
=
f
(
x
,
y
)
(i)
\frac{dy}{dx} = f(x,y) \tag{i}
dxdy=f(x,y)(i)
If
f
(
x
,
y
)
f(x,y)
f(x,y) is expressed as the product of
f
(
x
)
f(x)
f(x) and
g
(
y
)
g(y)
g(y), where
f
(
x
)
f(x)
f(x) is a function of
x
x
x and
g
(
y
)
g(y)
g(y) is a function of
y
y
y; then the differential equation is said to be variable separable type. Then, we can write (i) as
若
f
(
x
,
y
)
f(x,y)
f(x,y) 可表示为
f
(
x
)
f(x)
f(x) 与
g
(
y
)
g(y)
g(y) 的乘积(其中
f
(
x
)
f(x)
f(x) 仅为
x
x
x 的函数,
g
(
y
)
g(y)
g(y) 仅为
y
y
y 的函数),则该微分方程称为可分离变量的微分方程。此时,式 (i) 可改写为:
d
y
d
x
=
f
(
x
)
g
(
y
)
\frac{dy}{dx} = f(x)g(y)
dxdy=f(x)g(y)
We can follow three simple steps to find the solution using the variable separable method.
使用分离变量法求解时,可遵循以下三个步骤:
Step 1: Move all
y
y
y terms including
d
y
dy
dy to one side of the equation and all the
x
x
x terms including
d
x
dx
dx to the other side.
步骤 1:将所有含
y
y
y 的项(包括
d
y
dy
dy)移至方程一侧,所有含
x
x
x 的项(包括
d
x
dx
dx)移至方程另一侧。
Step 2: Integrate one side with respect to
y
y
y and the other side with respect to
x
x
x, and add the constant of integration.
步骤 2:对含
y
y
y 的一侧关于
y
y
y 积分,对含
x
x
x 的一侧关于
x
x
x 积分,并添加积分常数。
Step 3: Simplify the final result to the simplest form.
步骤 3:将最终结果化简至最简形式。
Homogenous Differential Equations
齐次微分方程
A homogeneous differential equation is an equation that contains a derivative and a function with a set of variables. The function
f
(
x
,
y
)
f(x,y)
f(x,y) in a homogeneous differential equation is a homogeneous function such that
f
(
t
x
,
t
y
)
=
t
n
f
(
x
,
y
)
f(tx,ty) = t^n f(x,y)
f(tx,ty)=tnf(x,y), for non-zero constant
t
t
t. So, the general form of the homogenous differential equation is of the form
f
(
x
,
y
)
d
y
+
g
(
x
,
y
)
d
x
=
0
f(x,y)dy + g(x,y)dx = 0
f(x,y)dy+g(x,y)dx=0.
齐次微分方程是含有导数和一组变量构成的函数的方程。齐次微分方程中的函数
f
(
x
,
y
)
f(x,y)
f(x,y) 为齐次函数,即对于非零常数
t
t
t,满足
f
(
t
x
,
t
y
)
=
t
n
f
(
x
,
y
)
f(tx,ty) = t^n f(x,y)
f(tx,ty)=tnf(x,y)。因此,齐次微分方程的一般形式为
f
(
x
,
y
)
d
y
+
g
(
x
,
y
)
d
x
=
0
f(x,y)dy + g(x,y)dx = 0
f(x,y)dy+g(x,y)dx=0。
Note: The homogenous differential equation does not contain any constant term within the equation.
注:齐次微分方程的表达式中不包含常数项。
Some of the examples of a homogenous differential equation are:
以下是一些齐次微分方程的示例:
- d y d x = x + y x − y \frac{dy}{dx} = \frac{x+y}{x-y} dxdy=x−yx+y
- d y d x = x ( x − y ) y 2 \frac{dy}{dx} = \frac{x(x-y)}{y^2} dxdy=y2x(x−y)
Steps to Solve Homogenous Differential Equations
齐次微分方程的求解步骤
To solve the homogenous differential equation, we follow these steps.
齐次微分方程的求解可遵循以下步骤:
Case 1:
情形 1:
If the differential equation is of the type
d
y
d
x
=
F
(
x
,
y
)
=
g
(
y
x
)
\frac{dy}{dx} = F(x,y) = g\left(\frac{y}{x}\right)
dxdy=F(x,y)=g(xy).
若微分方程具有形式
d
y
d
x
=
F
(
x
,
y
)
=
g
(
y
x
)
\frac{dy}{dx} = F(x,y) = g\left(\frac{y}{x}\right)
dxdy=F(x,y)=g(xy)。
Step 1: Substitute
y
=
v
x
y = vx
y=vx in the given differential equation.
步骤 1:令
y
=
v
x
y = vx
y=vx,代入给定的微分方程。
Step 2: Differentiate with respect to
x
x
x, then
d
y
d
x
=
v
+
x
d
v
d
x
\frac{dy}{dx} = v + x\frac{dv}{dx}
dxdy=v+xdxdv. Now substitute the values of
y
y
y and
d
y
d
x
\frac{dy}{dx}
dxdy in the given differential equation, then we have
步骤 2:对
y
=
v
x
y = vx
y=vx 关于
x
x
x 求导,得
d
y
d
x
=
v
+
x
d
v
d
x
\frac{dy}{dx} = v + x\frac{dv}{dx}
dxdy=v+xdxdv。将
y
y
y 和
d
y
d
x
\frac{dy}{dx}
dxdy 的表达式代入原微分方程,得到:
v
+
x
d
v
d
x
=
g
(
v
)
v + x\frac{dv}{dx} = g(v)
v+xdxdv=g(v)
⇒
x
d
v
d
x
=
g
(
v
)
−
v
\Rightarrow x\frac{dv}{dx} = g(v) - v
⇒xdxdv=g(v)−v
Step 3: Separating the variables, then
d
v
g
(
v
)
−
v
=
d
x
x
\frac{dv}{g(v) - v} = \frac{dx}{x}
g(v)−vdv=xdx.
步骤 3:分离变量,得
d
v
g
(
v
)
−
v
=
d
x
x
\frac{dv}{g(v) - v} = \frac{dx}{x}
g(v)−vdv=xdx。
Step 4: Apply integration on both sides, then
∫
d
v
g
(
v
)
−
v
d
v
=
∫
d
x
x
+
C
\int \frac{dv}{g(v) - v} dv = \int \frac{dx}{x} + C
∫g(v)−vdvdv=∫xdx+C.
步骤 4:对等式两端积分,得
∫
d
v
g
(
v
)
−
v
d
v
=
∫
d
x
x
+
C
\int \frac{dv}{g(v) - v} dv = \int \frac{dx}{x} + C
∫g(v)−vdvdv=∫xdx+C。
Step 5: After the integration, substitute the value of
v
v
v from Step 1.
步骤 5:积分完成后,将步骤 1 中
v
=
y
x
v = \frac{y}{x}
v=xy 代回,得到原方程的解。
Case 2:
情形 2:
If the differential equation is of the type
d
x
d
y
=
F
(
x
,
y
)
=
g
(
x
y
)
\frac{dx}{dy} = F(x,y) = g\left(\frac{x}{y}\right)
dydx=F(x,y)=g(yx). These kinds of homogenous differential equations can be solved by putting
x
=
v
y
x = vy
x=vy, after that, follow the same five steps which we applied for case 1.
若微分方程具有形式
d
x
d
y
=
F
(
x
,
y
)
=
g
(
x
y
)
\frac{dx}{dy} = F(x,y) = g\left(\frac{x}{y}\right)
dydx=F(x,y)=g(yx),此类齐次微分方程可通过令
x
=
v
y
x = vy
x=vy 求解,后续步骤与情形 1 中的五个步骤一致。
Linear Differential Equation
线性微分方程
The linear differential equation involves a variable, a derivative of this variable, and a few other functions. The standard equation of a linear differential equation is
线性微分方程包含一个变量、该变量的导数以及若干其他函数。线性微分方程的标准形式为:
d
y
d
x
+
P
y
=
Q
,
\frac{dy}{dx} + Py = Q,
dxdy+Py=Q,
where
P
P
P and
Q
Q
Q are functions of
x
x
x.
其中
P
P
P 和
Q
Q
Q 均为
x
x
x 的函数。
Similarly,
类似地,
d
x
d
y
+
P
1
x
=
Q
1
\frac{dx}{dy} + P_1x = Q_1
dydx+P1x=Q1
is also the standard equation of a linear differential equation. Here
P
1
P_1
P1 and
Q
1
Q_1
Q1 are functions of
y
y
y.
也是线性微分方程的标准形式,其中
P
1
P_1
P1 和
Q
1
Q_1
Q1 均为
y
y
y 的函数。
General Solution of Linear Differential Equation
线性微分方程的通解
Type 1: The general solution of differential equation of the type
d
y
d
x
+
P
y
=
Q
\frac{dy}{dx} + Py = Q
dxdy+Py=Q, where
P
P
P and
Q
Q
Q are functions of
x
x
x is
y
(
I
.
F
)
=
∫
(
Q
(
I
.
F
)
d
x
)
+
C
y(I.F) = \int (Q(I.F)dx) + C
y(I.F)=∫(Q(I.F)dx)+C, where Integrating Factor (I.F)
=
e
∫
P
d
x
= e^{\int Pdx}
=e∫Pdx.
类型 1:对于形如
d
y
d
x
+
P
y
=
Q
\frac{dy}{dx} + Py = Q
dxdy+Py=Q(其中
P
P
P 和
Q
Q
Q 为
x
x
x 的函数)的线性微分方程,其通解为
y
(
I
.
F
)
=
∫
(
Q
⋅
I
.
F
)
d
x
+
C
y(I.F) = \int (Q \cdot I.F)dx + C
y(I.F)=∫(Q⋅I.F)dx+C,其中积分因子(I.F)
=
e
∫
P
d
x
= e^{\int Pdx}
=e∫Pdx。
Type 2: The general solution of differential equation of the type
d
x
d
y
+
P
x
=
Q
\frac{dx}{dy} + Px = Q
dydx+Px=Q, where
P
P
P and
Q
Q
Q are functions of
y
y
y is
x
(
I
.
F
)
=
∫
(
Q
(
I
.
F
)
d
y
)
+
C
x(I.F) = \int (Q(I.F)dy) + C
x(I.F)=∫(Q(I.F)dy)+C, where Integrating Factor (I.F)
=
e
∫
P
d
y
= e^{\int Pdy}
=e∫Pdy.
类型 2:对于形如
d
x
d
y
+
P
x
=
Q
\frac{dx}{dy} + Px = Q
dydx+Px=Q(其中
P
P
P 和
Q
Q
Q 为
y
y
y 的函数)的线性微分方程,其通解为
x
(
I
.
F
)
=
∫
(
Q
⋅
I
.
F
)
d
y
+
C
x(I.F) = \int (Q \cdot I.F)dy + C
x(I.F)=∫(Q⋅I.F)dy+C,其中积分因子(I.F)
=
e
∫
P
d
y
= e^{\int Pdy}
=e∫Pdy。
Steps to Solve Linear Differential Equation
线性微分方程的求解步骤
The general solution of the linear differential equation can be solved by using the following three simple steps;
线性微分方程的通解可通过以下三个步骤求解:
Step 1: Simplify the given differential equation in the form of
d
y
d
x
+
P
y
=
Q
\frac{dy}{dx} + Py = Q
dxdy+Py=Q or
d
x
d
y
+
P
x
=
Q
\frac{dx}{dy} + Px = Q
dydx+Px=Q, where
P
P
P and
Q
Q
Q are functions of
x
x
x or
P
P
P and
Q
Q
Q are functions of
y
y
y.
步骤 1:将给定的微分方程化为标准形式
d
y
d
x
+
P
y
=
Q
\frac{dy}{dx} + Py = Q
dxdy+Py=Q 或
d
x
d
y
+
P
x
=
Q
\frac{dx}{dy} + Px = Q
dydx+Px=Q,其中
P
P
P 和
Q
Q
Q 要么均为
x
x
x 的函数,要么均为
y
y
y 的函数。
Step 2: Find the integrating factor by using
(
I
.
F
)
=
e
∫
P
d
x
(I.F) = e^{\int Pdx}
(I.F)=e∫Pdx or
(
I
.
F
)
=
e
∫
P
d
y
(I.F) = e^{\int Pdy}
(I.F)=e∫Pdy.
步骤 2:根据标准形式,利用
I
.
F
=
e
∫
P
d
x
I.F = e^{\int Pdx}
I.F=e∫Pdx 或
I
.
F
=
e
∫
P
d
y
I.F = e^{\int Pdy}
I.F=e∫Pdy 计算积分因子。
Step 3: Finally obtain the general solution by using the formula:
步骤 3:利用以下公式得到通解:
y ( I . F ) = ∫ ( Q ⋅ I . F ) d x + C or x ( I . F ) = ∫ ( Q ⋅ I . F ) d y + C \begin{align*} &\quad y(I.F) = \int (Q \cdot I.F)dx + C \\ \text{or} \quad & \\ &\quad x(I.F) = \int (Q \cdot I.F)dy + C \end{align*} ory(I.F)=∫(Q⋅I.F)dx+Cx(I.F)=∫(Q⋅I.F)dy+C
Solved Examples on Methods of Solving Differential Equations
微分方程求解方法的例题解析
Q.1. Find the general solution of the following differential equation
例 1:求下列微分方程的通解
x
d
y
−
(
y
+
2
x
2
)
d
x
=
0
xdy - (y + 2x^2)dx = 0
xdy−(y+2x2)dx=0
Ans: Given:
x
d
y
−
(
y
+
2
x
2
)
d
x
=
0
xdy - (y + 2x^2)dx = 0
xdy−(y+2x2)dx=0
解: 已知:
x
d
y
−
(
y
+
2
x
2
)
d
x
=
0
xdy - (y + 2x^2)dx = 0
xdy−(y+2x2)dx=0
⇒
d
y
d
x
−
y
x
=
2
x
\Rightarrow \frac{dy}{dx} - \frac{y}{x} = 2x
⇒dxdy−xy=2x
On comparing with the linear differential equation
d
y
d
x
+
P
y
=
Q
\frac{dy}{dx} + Py = Q
dxdy+Py=Q, we have
将其与线性微分方程标准形式
d
y
d
x
+
P
y
=
Q
\frac{dy}{dx} + Py = Q
dxdy+Py=Q 对比,可得:
P
=
−
1
x
,
Q
=
2
x
P = -\frac{1}{x}, \quad Q = 2x
P=−x1,Q=2x
Now, the integrating factor is
计算积分因子:
I
.
F
=
e
∫
−
1
x
d
x
=
e
−
log
x
∴
I
.
F
=
1
x
\begin{aligned}I.F &= e^{\int -\frac{1}{x}dx}\\&= e^{-\log x}\\\therefore I.F &= \frac{1}{x}\end{aligned}
I.F∴I.F=e∫−x1dx=e−logx=x1
Therefore, the general solution is
因此,通解为:
y
×
1
x
=
∫
(
2
x
×
1
x
)
d
x
+
C
⇒
y
x
=
∫
2
d
x
+
C
⇒
y
x
=
2
x
+
C
∴
y
=
2
x
2
+
C
x
\begin{aligned} y \times \frac{1}{x} &= \int \left(2x \times \frac{1}{x}\right)dx + C\\ \Rightarrow \frac{y}{x} &= \int 2dx + C\\ \Rightarrow \frac{y}{x} &= 2x + C\\ \therefore y &= 2x^2 + Cx\end{aligned}
y×x1⇒xy⇒xy∴y=∫(2x×x1)dx+C=∫2dx+C=2x+C=2x2+Cx
is the required general solution of the given differential equation.
即为给定微分方程的通解。
Q.2. Find the integrating factor of the following differential equation
例 2:求下列微分方程的积分因子
d
y
d
x
+
sec
x
⋅
y
=
tan
x
\frac{dy}{dx} + \sec x \cdot y = \tan x
dxdy+secx⋅y=tanx
Ans: Given:
d
y
d
x
+
sec
x
⋅
y
=
tan
x
\frac{dy}{dx} + \sec x \cdot y = \tan x
dxdy+secx⋅y=tanx
解: 已知:
d
y
d
x
+
sec
x
⋅
y
=
tan
x
\frac{dy}{dx} + \sec x \cdot y = \tan x
dxdy+secx⋅y=tanx
On comparing with the linear differential equation
d
y
d
x
+
P
y
=
Q
\frac{dy}{dx} + Py = Q
dxdy+Py=Q, we have
将其与线性微分方程标准形式
d
y
d
x
+
P
y
=
Q
\frac{dy}{dx} + Py = Q
dxdy+Py=Q 对比,可得:
P
=
sec
x
,
Q
=
tan
x
P = \sec x, \quad Q = \tan x
P=secx,Q=tanx
Now, the integrating factor is
计算积分因子:
I
.
F
=
e
∫
sec
x
d
x
=
e
ln
∣
sec
x
+
tan
x
∣
∴
I
.
F
=
∣
sec
x
+
tan
x
∣
\begin{aligned}I.F &= e^{\int \sec x dx}\\&= e^{\ln |\sec x + \tan x|}\\\therefore I.F &= |\sec x + \tan x|\end{aligned}
I.F∴I.F=e∫secxdx=eln∣secx+tanx∣=∣secx+tanx∣
Q.3. Show that the following differential equation
(
x
+
y
)
d
y
d
x
=
(
x
+
2
y
)
(x+y)\frac{dy}{dx} = (x+2y)
(x+y)dxdy=(x+2y) is a homogeneous differential equation.
例 3:证明微分方程
(
x
+
y
)
d
y
d
x
=
(
x
+
2
y
)
(x+y)\frac{dy}{dx} = (x+2y)
(x+y)dxdy=(x+2y) 是齐次微分方程。
Ans: Given:
(
x
+
y
)
d
y
d
x
=
(
x
+
2
y
)
(x+y)\frac{dy}{dx} = (x+2y)
(x+y)dxdy=(x+2y)
解: 已知:
(
x
+
y
)
d
y
d
x
=
(
x
+
2
y
)
(x+y)\frac{dy}{dx} = (x+2y)
(x+y)dxdy=(x+2y)
To prove that the above differential equation is a homogeneous differential equation, we first rewrite it as
F
(
x
,
y
)
=
x
+
2
y
x
+
y
F(x,y) = \frac{x+2y}{x+y}
F(x,y)=x+yx+2y.
要证明该方程为齐次微分方程,首先将其改写为
F
(
x
,
y
)
=
x
+
2
y
x
+
y
F(x,y) = \frac{x+2y}{x+y}
F(x,y)=x+yx+2y。
Substitute
x
=
t
x
x = tx
x=tx and
y
=
t
y
y = ty
y=ty (where
t
t
t is a non-zero constant), then
令
x
=
t
x
x = tx
x=tx,
y
=
t
y
y = ty
y=ty(其中
t
t
t 为非零常数),则:
F
(
t
x
,
t
y
)
=
t
x
+
2
t
y
t
x
+
t
y
=
t
(
x
+
2
y
)
t
(
x
+
y
)
=
t
0
F
(
x
,
y
)
∴
F
(
t
x
,
t
y
)
=
t
0
F
(
x
,
y
)
\begin{aligned}F(tx, ty) &= \frac{tx + 2ty}{tx + ty}\\&= \frac{t(x + 2y)}{t(x + y)}\\[1em]&= t^0 F(x,y)\\ \therefore F(tx, ty) &= t^0 F(x,y)\end{aligned}
F(tx,ty)∴F(tx,ty)=tx+tytx+2ty=t(x+y)t(x+2y)=t0F(x,y)=t0F(x,y)
Hence, the given differential equation is homogeneous.
因此,给定的微分方程为齐次微分方程。
Q.4. Find the general solution of the following differential equation
d
y
d
x
=
6
y
2
x
\frac{dy}{dx} = \frac{6y^2}{x}
dxdy=x6y2.
例 4:求下列微分方程的通解
d
y
d
x
=
6
y
2
x
\frac{dy}{dx} = \frac{6y^2}{x}
dxdy=x6y2。
Ans: Given:
d
y
d
x
=
6
y
2
x
\frac{dy}{dx} = \frac{6y^2}{x}
dxdy=x6y2.
解: 已知:
d
y
d
x
=
6
y
2
x
\frac{dy}{dx} = \frac{6y^2}{x}
dxdy=x6y2。
It is clear that the given differential equation is variable separable as we can separate the variables.
该方程为可分离变量的微分方程,可按以下步骤分离变量求解。
Now, separating the variables, we get
分离变量,得:
1
y
2
d
y
=
6
x
d
x
⇒
y
−
2
d
y
=
6
x
−
1
d
x
\frac{1}{y^2}dy = \frac{6}{x}dx\\[1em] \Rightarrow y^{-2}dy = 6x^{-1}dx
y21dy=x6dx⇒y−2dy=6x−1dx
Apply integration on both sides, then we get:
对等式两端积分:
∫
y
−
2
d
y
=
∫
6
x
−
1
d
x
⇒
−
1
y
=
6
ln
∣
x
∣
+
C
∴
−
1
y
=
3
x
2
+
C
\begin{aligned}\int y^{-2}dy &= \int 6x^{-1}dx\\ \Rightarrow -\frac{1}{y} &= 6\ln |x| + C\\ \therefore -\frac{1}{y} &= 3x^2 + C\end{aligned}
∫y−2dy⇒−y1∴−y1=∫6x−1dx=6ln∣x∣+C=3x2+C
is the required general solution.
即为所求通解。
Q.5. Find the general solution of the following differential equation
d
y
d
x
=
x
2
+
y
2
x
y
\frac{dy}{dx} = \frac{x^2 + y^2}{xy}
dxdy=xyx2+y2.
例 5:求下列微分方程的通解
d
y
d
x
=
x
2
+
y
2
x
y
\frac{dy}{dx} = \frac{x^2 + y^2}{xy}
dxdy=xyx2+y2。
Ans: Given:
d
y
d
x
=
x
2
+
y
2
x
y
\frac{dy}{dx} = \frac{x^2 + y^2}{xy}
dxdy=xyx2+y2.
解: 已知:
d
y
d
x
=
x
2
+
y
2
x
y
\frac{dy}{dx} = \frac{x^2 + y^2}{xy}
dxdy=xyx2+y2。
It is clear that the given differential equation is a homogeneous differential equation as it can be rewritten as
F
(
y
x
)
F\left(\frac{y}{x}\right)
F(xy):
将方程右边化简为
x
2
+
y
2
x
y
=
x
y
+
y
x
\frac{x^2 + y^2}{xy} = \frac{x}{y} + \frac{y}{x}
xyx2+y2=yx+xy,可知其为齐次微分方程(形式为
F
(
y
x
)
F\left(\frac{y}{x}\right)
F(xy))。
Now, substitute
y
=
v
x
y = vx
y=vx
令
y
=
v
x
y = vx
y=vx,则:
Differentiate with respect to
x
x
x, then we get
对
y
=
v
x
y = vx
y=vx 关于
x
x
x 求导,得:
d
y
d
x
=
v
+
x
d
v
d
x
\frac{dy}{dx} = v + x\frac{dv}{dx}
dxdy=v+xdxdv
Therefore,
将其代入原方程:
v
+
x
d
v
d
x
=
1
v
+
v
⇒
x
d
v
d
x
=
1
v
v + x\frac{dv}{dx} = \frac{1}{v} + v\\[1em] \Rightarrow x\frac{dv}{dx} = \frac{1}{v}
v+xdxdv=v1+v⇒xdxdv=v1
Now, separate the variables, then
分离变量,得:
v
d
v
=
1
x
d
x
vdv = \frac{1}{x}dx
vdv=x1dx
Apply integration on both sides; then we get
对等式两端积分:
∫
v
d
v
=
∫
1
x
d
x
⇒
v
2
2
=
ln
∣
x
∣
+
C
\int vdv = \int \frac{1}{x}dx\\\Rightarrow \frac{v^2}{2} = \ln |x| + C
∫vdv=∫x1dx⇒2v2=ln∣x∣+C
Let
C
=
ln
k
C = \ln k
C=lnk (where
k
k
k is a positive constant), then
令
C
=
ln
k
C = \ln k
C=lnk(其中
k
k
k 为正常数),则:
v
2
2
=
ln
∣
x
∣
+
ln
k
⇒
v
2
2
=
ln
(
k
x
)
⇒
v
=
±
2
ln
(
k
x
)
\frac{v^2}{2} = \ln |x| + \ln k\\ \Rightarrow \frac{v^2}{2} = \ln (kx)\\ \Rightarrow v = \pm \sqrt{2\ln (kx)}
2v2=ln∣x∣+lnk⇒2v2=ln(kx)⇒v=±2ln(kx)
Resubstitute
v
=
y
x
v = \frac{y}{x}
v=xy, we get
将
v
=
y
x
v = \frac{y}{x}
v=xy 代回,得:
y
x
=
±
2
ln
(
k
x
)
∴
y
=
±
x
2
ln
(
k
x
)
\frac{y}{x} = \pm \sqrt{2\ln (kx)}\\ \therefore y = \pm x\sqrt{2\ln (kx)}
xy=±2ln(kx)∴y=±x2ln(kx)
which is the required general solution.
即为所求通解。
Summary of Methods of Solving Differential Equations
微分方程求解方法总结
The solution of the differential equation is the relationship between the variables included, which satisfies the given differential equation. There are two types of solutions for differential equations such as the general solution and the particular solution. These solutions of differential equations make use of some steps of integration to solve the equations. Later, explained the types of differential equations followed by methods of the differential equation such as variable separable method, homogenous method, and linear differential equation along with some solved examples are explained.
微分方程的解是所含变量之间满足该方程的关系,分为通解和特解两类,两者均需通过积分步骤求解。本文先后介绍了微分方程的类型,以及分离变量法、齐次方程解法和线性微分方程解法等求解方法,并结合例题进行了详细说明。
Frequently Asked Questions (FAQs)
常见问题解答(FAQ)
Q.1. Which method is used to solve differential equations?
问题 1:求解微分方程的方法有哪些?
Ans: We can use the following methods to solve the given differential equations:
答: 求解微分方程的常用方法包括:
-
Inspection method
观察法 -
Variable separable method
分离变量法 -
Homogenous differential equation method
齐次微分方程解法 -
Linear differential equation method
线性微分方程解法
Q.2. How many types of differential equations are there?
问题 2:微分方程有多少种类型?
Ans: There are several types of differential equations such as ordinary differential equations, partial differential equations, linear differential equations, non-linear differential equations, homogenous differential equations, and non-homogenous differential equations.
答: 微分方程的类型较多,常见的有常微分方程、偏微分方程、线性微分方程、非线性微分方程、齐次微分方程和非齐次微分方程等。
Q.3. What are homogenous differential equations?
问题 3:什么是齐次微分方程?
Ans: A homogeneous differential equation is an equation that contains a derivative and a function with a set of variables. The function
f
(
x
,
y
)
f(x,y)
f(x,y) in a homogeneous differential equation is a homogeneous function such that
f
(
μ
x
,
μ
y
)
=
μ
n
f
(
x
,
y
)
f(\mu x, \mu y) = \mu^n f(x,y)
f(μx,μy)=μnf(x,y), for non-zero constant
μ
\mu
μ. So the general form of the homogenous differential equation is of the form
f
(
x
,
y
)
d
y
+
g
(
x
,
y
)
d
x
=
0
f(x,y)dy + g(x,y)dx = 0
f(x,y)dy+g(x,y)dx=0.
答: 齐次微分方程是含有导数和一组变量构成的函数的方程。其中的函数
f
(
x
,
y
)
f(x,y)
f(x,y) 为齐次函数,即对于非零常数
μ
\mu
μ,满足
f
(
μ
x
,
μ
y
)
=
μ
n
f
(
x
,
y
)
f(\mu x, \mu y) = \mu^n f(x,y)
f(μx,μy)=μnf(x,y)。齐次微分方程的一般形式为
f
(
x
,
y
)
d
y
+
g
(
x
,
y
)
d
x
=
0
f(x,y)dy + g(x,y)dx = 0
f(x,y)dy+g(x,y)dx=0。
Q.4. What is the variable separable method of differential equations?
问题 4:微分方程的分离变量法是什么?
Ans: If the differential equation is of the form
f
(
x
)
d
x
=
g
(
y
)
d
y
f(x)dx = g(y)dy
f(x)dx=g(y)dy, where
f
(
x
)
f(x)
f(x) and
g
(
y
)
g(y)
g(y) are functions of
x
x
x and
y
y
y only. Then we say that the variables are separable in the differential equation. Thus, integrating both sides of the equation, we get its general solution.
答: 若微分方程可化为
f
(
x
)
d
x
=
g
(
y
)
d
y
f(x)dx = g(y)dy
f(x)dx=g(y)dy 的形式(其中
f
(
x
)
f(x)
f(x) 仅为
x
x
x 的函数,
g
(
y
)
g(y)
g(y) 仅为
y
y
y 的函数),则称该方程为可分离变量的微分方程。对等式两端分别积分,即可得到其通解,这种求解方法称为分离变量法。
Q.5. What is an ordinary differential equation? Give an example.
问题 5:什么是常微分方程?请举例说明。
Ans: The ordinary differential equation is an equation that contains only one independent variable and one or more of its derivatives with respect to the variable. Hence, the ordinary differential equation is represented as a relation involving one independent variable
x
x
x, the dependent variable
y
y
y, and some of its derivatives
y
′
,
y
′
′
⋯
y', y''\cdots
y′,y′′⋯ with respect to
x
x
x.
答: 常微分方程是只含有一个自变量,以及该自变量的一个或多个导数的方程。它表示自变量
x
x
x、因变量
y
y
y 及其关于
x
x
x 的若干导数
y
′
,
y
′
′
⋯
y', y''\cdots
y′,y′′⋯ 之间的关系。
Example:
d
y
d
x
=
cos
x
\frac{dy}{dx} = \cos x
dxdy=cosx
示例:
d
y
d
x
=
cos
x
\frac{dy}{dx} = \cos x
dxdy=cosx
微分方程解法总结
JasonKQLin 原创于 2019-06-19 17:59:45
1 微分方程的概念
微分方程是描述函数与其各阶导数之间关系的数学方程,其解通常为函数;而初等代数方程的解通常为数值。
2 分类
2.1 常微分方程与偏微分方程
常微分方程的未知量是单一变量的函数,其通式可表示为:
f
(
x
,
y
,
y
′
,
y
′
′
,
…
,
y
(
n
)
)
=
0
f(x, y, y', y'', \dots, y^{(n)}) = 0
f(x,y,y′,y′′,…,y(n))=0
方程中出现的未知函数的最高阶导数的阶数,称为该微分方程的阶。
偏微分方程的未知量是多个自变量的函数,且方程中包含未知函数对自变量的偏导数。偏微分方程的阶数定义与常微分方程类似,常见类型包括椭圆型、双曲线型和抛物线型。
2.2 线性与非线性
线性微分方程是指关于未知函数及其各阶导数均为一次幂的微分方程;若方程中未知函数或其导数出现非一次幂形式,则称为非线性微分方程。
线性微分方程的一般形式为:
a
n
(
x
)
D
n
y
(
x
)
+
a
n
−
1
(
x
)
D
n
−
1
y
(
x
)
+
⋯
+
a
1
(
x
)
D
y
(
x
)
+
a
0
(
x
)
y
(
x
)
=
f
(
x
)
(1)
a_n(x)D^n y(x) + a_{n-1}(x)D^{n-1} y(x) + \dots + a_1(x)D y(x) + a_0(x)y(x) = f(x) \tag{1}
an(x)Dny(x)+an−1(x)Dn−1y(x)+⋯+a1(x)Dy(x)+a0(x)y(x)=f(x)(1)
其中
D
D
D 表示微分算子(即
D
k
y
=
d
k
y
d
x
k
D^k y = \frac{d^k y}{dx^k}
Dky=dxkdky)。
在式 (1) 中,若 f ( x ) = 0 f(x) = 0 f(x)=0,则该方程称为齐次线性微分方程。齐次线性微分方程的解满足线性叠加性:若 y 1 ( x ) , y 2 ( x ) , … , y k ( x ) y_1(x), y_2(x), \dots, y_k(x) y1(x),y2(x),…,yk(x) 是方程的解,则它们的任意线性组合 ∑ i = 1 k C i y i ( x ) \sum_{i=1}^k C_i y_i(x) ∑i=1kCiyi(x)( C i C_i Ci 为常数)也是该方程的解。所有解构成的集合是一个向量空间,称为解空间。
若 f ( x ) f(x) f(x) 为非零函数,则该方程称为非齐次线性微分方程。非齐次线性微分方程的所有解构成一个仿射空间,其结构为:对应的齐次线性微分方程的解空间加上该非齐次方程的一个特解。
3 可分离变量的微分方程
若一阶微分方程可化为如下形式:
g
(
y
)
d
y
=
h
(
x
)
d
x
g(y)dy = h(x)dx
g(y)dy=h(x)dx
则称该方程为可分离变量的微分方程。求解方法为对等式两端分别积分,即:
∫
g
(
y
)
d
y
=
∫
h
(
x
)
d
x
+
C
\int g(y)dy = \int h(x)dx + C
∫g(y)dy=∫h(x)dx+C
其中
C
C
C 为积分常数,积分后可解得函数
y
(
x
)
y(x)
y(x)。
4 可化为齐次的微分方程
4.1 齐次方程
若一阶微分方程可表示为:
d
y
d
x
=
φ
(
y
x
)
\frac{dy}{dx} = \varphi\left(\frac{y}{x}\right)
dxdy=φ(xy)
则称该方程为齐次方程。求解的关键是引入中间变量
μ
=
y
x
\mu = \frac{y}{x}
μ=xy,即
y
=
μ
x
y = \mu x
y=μx,对其求导得:
d
y
d
x
=
μ
+
x
d
μ
d
x
\frac{dy}{dx} = \mu + x\frac{d\mu}{dx}
dxdy=μ+xdxdμ
将其代入原方程,可转化为可分离变量的微分方程:
μ
+
x
d
μ
d
x
=
φ
(
μ
)
\mu + x\frac{d\mu}{dx} = \varphi(\mu)
μ+xdxdμ=φ(μ)
分离变量并积分后,再将
μ
=
y
x
\mu = \frac{y}{x}
μ=xy 代回,即可得到原方程的解。

4.2 可化为齐次的方程
考虑形如以下的一阶线性微分方程:
d
y
d
x
=
a
1
x
+
b
1
y
+
c
1
a
2
x
+
b
2
y
+
c
2
\frac{dy}{dx} = \frac{a_1 x + b_1 y + c_1}{a_2 x + b_2 y + c_2}
dxdy=a2x+b2y+c2a1x+b1y+c1
其中
a
1
,
b
1
,
c
1
,
a
2
,
b
2
,
c
2
a_1, b_1, c_1, a_2, b_2, c_2
a1,b1,c1,a2,b2,c2 为常数。
- 当 c 1 = c 2 = 0 c_1 = c_2 = 0 c1=c2=0 时,方程即为齐次方程;
- 当 c 1 , c 2 c_1, c_2 c1,c2 不全为 0 时,若系数行列式 ∣ a 1 b 1 a 2 b 2 ∣ ≠ 0 \begin{vmatrix}a_1 & b_1 \\ a_2 & b_2\end{vmatrix} \neq 0 a1a2b1b2 =0,可通过变量替换 { x = X + h y = Y + k \begin{cases}x = X + h \\ y = Y + k\end{cases} {x=X+hy=Y+k(其中 h , k h, k h,k 为常数),将方程化为齐次方程;若行列式为 0,则方程可通过其他变量替换转化为可分离变量的形式。


5 一阶线性微分方程
5.1 方程形式
一阶线性微分方程的标准形式为:
d
y
d
x
+
P
(
x
)
y
=
Q
(
x
)
(2)
\frac{dy}{dx} + P(x)y = Q(x) \tag{2}
dxdy+P(x)y=Q(x)(2)
其中
P
(
x
)
P(x)
P(x) 和
Q
(
x
)
Q(x)
Q(x) 是关于
x
x
x 的已知函数。

5.2 对应的齐次线性微分方程的解
式 (2) 对应的齐次线性微分方程为:
d
y
d
x
+
P
(
x
)
y
=
0
\frac{dy}{dx} + P(x)y = 0
dxdy+P(x)y=0
这是可分离变量的方程,分离变量得:
d
y
y
=
−
P
(
x
)
d
x
\frac{dy}{y} = -P(x)dx
ydy=−P(x)dx
积分后可得通解:
y
=
C
e
−
∫
P
(
x
)
d
x
(3)
y = C e^{-\int P(x)dx} \tag{3}
y=Ce−∫P(x)dx(3)
其中
C
C
C 为积分常数。

5.3 常数变易法求非齐次方程的解
为求解非齐次方程 (2),采用常数变易法:将齐次方程通解 (3) 中的常数
C
C
C 替换为关于
x
x
x 的函数
C
(
x
)
C(x)
C(x),即设:
y
=
C
(
x
)
e
−
∫
P
(
x
)
d
x
y = C(x) e^{-\int P(x)dx}
y=C(x)e−∫P(x)dx
将其代入方程 (2),化简后可得:
C
′
(
x
)
e
−
∫
P
(
x
)
d
x
=
Q
(
x
)
C'(x) e^{-\int P(x)dx} = Q(x)
C′(x)e−∫P(x)dx=Q(x)
解得:
C
(
x
)
=
∫
Q
(
x
)
e
∫
P
(
x
)
d
x
d
x
+
C
C(x) = \int Q(x) e^{\int P(x)dx} dx + C
C(x)=∫Q(x)e∫P(x)dxdx+C
将
C
(
x
)
C(x)
C(x) 代回,得到非齐次方程的通解:
y
=
e
−
∫
P
(
x
)
d
x
(
∫
Q
(
x
)
e
∫
P
(
x
)
d
x
d
x
+
C
)
y = e^{-\int P(x)dx} \left( \int Q(x) e^{\int P(x)dx} dx + C \right)
y=e−∫P(x)dx(∫Q(x)e∫P(x)dxdx+C)
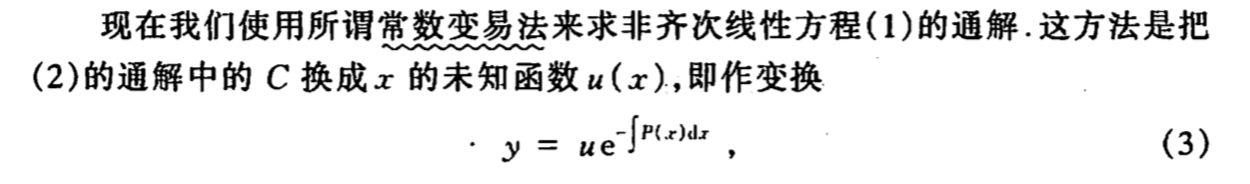

5.4 伯努利方程
形如以下的方程称为伯努利方程:
d
y
d
x
+
P
(
x
)
y
=
Q
(
x
)
y
n
(
n
≠
0
,
1
)
\frac{dy}{dx} + P(x)y = Q(x)y^n \quad (n \neq 0, 1)
dxdy+P(x)y=Q(x)yn(n=0,1)
其中
n
n
n 为常数。通过变量替换
z
=
y
1
−
n
z = y^{1-n}
z=y1−n,可将伯努利方程转化为一阶线性微分方程:
d
z
d
x
+
(
1
−
n
)
P
(
x
)
z
=
(
1
−
n
)
Q
(
x
)
\frac{dz}{dx} + (1 - n)P(x)z = (1 - n)Q(x)
dxdz+(1−n)P(x)z=(1−n)Q(x)
求解该线性方程后,将
z
=
y
1
−
n
z = y^{1-n}
z=y1−n 代回,即可得到原伯努利方程的解。

6 可降阶的高阶微分方程
对于高阶微分方程(阶数 ≥ 2),常通过降阶法转化为低阶微分方程求解。以下是三类常见的可降阶高阶微分方程及其求解方法。
6.1 y ( n ) = f ( x ) y^{(n)} = f(x) y(n)=f(x) 型
该类方程的特点是右端仅含自变量 x x x。求解方法为连续积分 n n n 次:
- 第一次积分: y ( n − 1 ) = ∫ f ( x ) d x + C 1 y^{(n-1)} = \int f(x)dx + C_1 y(n−1)=∫f(x)dx+C1
- 第二次积分: y ( n − 2 ) = ∫ ( ∫ f ( x ) d x + C 1 ) d x + C 2 y^{(n-2)} = \int \left( \int f(x)dx + C_1 \right) dx + C_2 y(n−2)=∫(∫f(x)dx+C1)dx+C2
- … \dots …
- 第 n n n 次积分:得到含 n n n 个独立积分常数的通解。

6.2 y ′ ′ = f ( x , y ′ ) y'' = f(x, y') y′′=f(x,y′) 型
该类方程的特点是不含未知函数
y
y
y。令
p
=
y
′
p = y'
p=y′,则
y
′
′
=
d
p
d
x
y'' = \frac{dp}{dx}
y′′=dxdp,方程转化为关于
x
x
x 和
p
p
p 的一阶微分方程:
d
p
d
x
=
f
(
x
,
p
)
\frac{dp}{dx} = f(x, p)
dxdp=f(x,p)
求解该方程得
p
=
φ
(
x
,
C
1
)
p = \varphi(x, C_1)
p=φ(x,C1),再通过
y
′
=
φ
(
x
,
C
1
)
y' = \varphi(x, C_1)
y′=φ(x,C1) 积分一次,得到原方程的通解:
y
=
∫
φ
(
x
,
C
1
)
d
x
+
C
2
y = \int \varphi(x, C_1)dx + C_2
y=∫φ(x,C1)dx+C2

6.3 y ′ ′ = f ( y , y ′ ) y'' = f(y, y') y′′=f(y,y′) 型
该类方程的特点是不含自变量
x
x
x。令
p
=
y
′
p = y'
p=y′,则
y
′
′
=
d
p
d
y
⋅
d
y
d
x
=
p
d
p
d
y
y'' = \frac{dp}{dy} \cdot \frac{dy}{dx} = p \frac{dp}{dy}
y′′=dydp⋅dxdy=pdydp,方程转化为关于
y
y
y 和
p
p
p 的一阶微分方程:
p
d
p
d
y
=
f
(
y
,
p
)
p \frac{dp}{dy} = f(y, p)
pdydp=f(y,p)
求解该方程得
p
=
ψ
(
y
,
C
1
)
p = \psi(y, C_1)
p=ψ(y,C1),再通过
y
′
=
ψ
(
y
,
C
1
)
y' = \psi(y, C_1)
y′=ψ(y,C1) 分离变量并积分,得到原方程的通解:
∫
d
y
ψ
(
y
,
C
1
)
=
x
+
C
2
\int \frac{dy}{\psi(y, C_1)} = x + C_2
∫ψ(y,C1)dy=x+C2

7 高阶线性微分方程
7.1 常见形式
n
n
n 阶线性微分方程的一般形式为:
y
(
n
)
+
a
1
(
x
)
y
(
n
−
1
)
+
⋯
+
a
n
−
1
(
x
)
y
′
+
a
n
(
x
)
y
=
f
(
x
)
y^{(n)} + a_1(x)y^{(n-1)} + \dots + a_{n-1}(x)y' + a_n(x)y = f(x)
y(n)+a1(x)y(n−1)+⋯+an−1(x)y′+an(x)y=f(x)
其中
a
1
(
x
)
,
a
2
(
x
)
,
…
,
a
n
(
x
)
a_1(x), a_2(x), \dots, a_n(x)
a1(x),a2(x),…,an(x) 和
f
(
x
)
f(x)
f(x) 是关于
x
x
x 的已知函数。当
f
(
x
)
=
0
f(x) = 0
f(x)=0 时,方程为齐次线性微分方程;当
f
(
x
)
≠
0
f(x) \neq 0
f(x)=0 时,方程为非齐次线性微分方程。

7.2 解的基本定理
定理 7.1(解的存在唯一性定理)
若 a 1 ( x ) , a 2 ( x ) , … , a n ( x ) a_1(x), a_2(x), \dots, a_n(x) a1(x),a2(x),…,an(x) 和 f ( x ) f(x) f(x) 在区间 I I I 上连续, x 0 ∈ I x_0 \in I x0∈I,则对于初始条件 y ( x 0 ) = y 0 , y ′ ( x 0 ) = y 0 ′ , … , y ( n − 1 ) ( x 0 ) = y 0 ( n − 1 ) y(x_0) = y_0, y'(x_0) = y_0', \dots, y^{(n-1)}(x_0) = y_0^{(n-1)} y(x0)=y0,y′(x0)=y0′,…,y(n−1)(x0)=y0(n−1),方程在区间 I I I 上存在唯一解。

定理 7.2(齐次方程解的线性叠加性)
若 y 1 ( x ) , y 2 ( x ) , … , y k ( x ) y_1(x), y_2(x), \dots, y_k(x) y1(x),y2(x),…,yk(x) 是 n n n 阶齐次线性微分方程的解,则它们的任意线性组合 ∑ i = 1 k C i y i ( x ) \sum_{i=1}^k C_i y_i(x) ∑i=1kCiyi(x)( C i C_i Ci 为常数)也是该方程的解。

定理 7.3(线性无关解的判定)
设 y 1 ( x ) , y 2 ( x ) , … , y n ( x ) y_1(x), y_2(x), \dots, y_n(x) y1(x),y2(x),…,yn(x) 是 n n n 阶齐次线性微分方程在区间 I I I 上的 n n n 个解,若它们的朗斯基行列式
W ( x ) = ∣ y 1 y 2 … y n y 1 ′ y 2 ′ … y n ′ ⋮ ⋮ ⋱ ⋮ y 1 ( n − 1 ) y 2 ( n − 1 ) … y n ( n − 1 ) ∣ W(x) = \begin{vmatrix} y_1 & y_2 & \dots & y_n \\ y_1' & y_2' & \dots & y_n' \\ \vdots & \vdots & \ddots & \vdots \\ y_1^{(n-1)} & y_2^{(n-1)} & \dots & y_n^{(n-1)} \end{vmatrix} W(x)= y1y1′⋮y1(n−1)y2y2′⋮y2(n−1)……⋱…ynyn′⋮yn(n−1)
在 I I I 上某点 x 0 x_0 x0 处不等于零,则这 n n n 个解在 I I I 上线性无关,且构成方程的一个基本解组。

定理 7.4(齐次方程通解结构)
n
n
n 阶齐次线性微分方程的通解可表示为其基本解组
y
1
(
x
)
,
y
2
(
x
)
,
…
,
y
n
(
x
)
y_1(x), y_2(x), \dots, y_n(x)
y1(x),y2(x),…,yn(x) 的线性组合,即:
y
=
C
1
y
1
(
x
)
+
C
2
y
2
(
x
)
+
⋯
+
C
n
y
n
(
x
)
y = C_1 y_1(x) + C_2 y_2(x) + \dots + C_n y_n(x)
y=C1y1(x)+C2y2(x)+⋯+Cnyn(x)
其中
C
1
,
C
2
,
…
,
C
n
C_1, C_2, \dots, C_n
C1,C2,…,Cn 为独立的积分常数。

定理 7.5(非齐次方程通解结构)
n
n
n 阶非齐次线性微分方程的通解等于其对应的齐次方程的通解加上该非齐次方程的一个特解,即:
y
=
C
1
y
1
(
x
)
+
C
2
y
2
(
x
)
+
⋯
+
C
n
y
n
(
x
)
+
y
∗
(
x
)
y = C_1 y_1(x) + C_2 y_2(x) + \dots + C_n y_n(x) + y^*(x)
y=C1y1(x)+C2y2(x)+⋯+Cnyn(x)+y∗(x)
其中
y
∗
(
x
)
y^*(x)
y∗(x) 是非齐次方程的一个特解,
C
1
y
1
(
x
)
+
⋯
+
C
n
y
n
(
x
)
C_1 y_1(x) + \dots + C_n y_n(x)
C1y1(x)+⋯+Cnyn(x) 是对应齐次方程的通解。

7.3 常数变易法求非齐次方程的解
若已知
n
n
n 阶齐次线性微分方程的基本解组
y
1
(
x
)
,
y
2
(
x
)
,
…
,
y
n
(
x
)
y_1(x), y_2(x), \dots, y_n(x)
y1(x),y2(x),…,yn(x),则其通解为
y
=
∑
i
=
1
n
C
i
y
i
(
x
)
y = \sum_{i=1}^n C_i y_i(x)
y=∑i=1nCiyi(x)。采用常数变易法,设非齐次方程的特解为:
y
∗
(
x
)
=
∑
i
=
1
n
C
i
(
x
)
y
i
(
x
)
y^*(x) = \sum_{i=1}^n C_i(x) y_i(x)
y∗(x)=i=1∑nCi(x)yi(x)
其中
C
i
(
x
)
C_i(x)
Ci(x) 是关于
x
x
x 的待定函数。将
y
∗
(
x
)
y^*(x)
y∗(x) 代入非齐次方程,结合齐次方程的性质,可得到关于
C
i
′
(
x
)
C_i'(x)
Ci′(x) 的线性方程组,求解该方程组并积分,即可确定
C
i
(
x
)
C_i(x)
Ci(x),进而得到特解
y
∗
(
x
)
y^*(x)
y∗(x)。
8 常系数齐次线性微分方程
8.1 常见形式
n
n
n 阶常系数齐次线性微分方程的形式为:
y
(
n
)
+
a
1
y
(
n
−
1
)
+
⋯
+
a
n
−
1
y
′
+
a
n
y
=
0
y^{(n)} + a_1 y^{(n-1)} + \dots + a_{n-1} y' + a_n y = 0
y(n)+a1y(n−1)+⋯+an−1y′+any=0
其中
a
1
,
a
2
,
…
,
a
n
a_1, a_2, \dots, a_n
a1,a2,…,an 为常数。

8.2 特征方程法求解
对于常系数齐次线性微分方程,可通过假设解的形式
y
=
e
r
x
y = e^{rx}
y=erx(
r
r
r 为常数)求解。将
y
=
e
r
x
y = e^{rx}
y=erx 代入方程,由于
e
r
x
≠
0
e^{rx} \neq 0
erx=0,可得到关于
r
r
r 的
n
n
n 次代数方程:
r
n
+
a
1
r
n
−
1
+
⋯
+
a
n
−
1
r
+
a
n
=
0
r^n + a_1 r^{n-1} + \dots + a_{n-1} r + a_n = 0
rn+a1rn−1+⋯+an−1r+an=0
该方程称为原微分方程的特征方程,其根称为特征根。根据特征根的不同情况,可得到微分方程的通解:
(1)二阶常系数齐次线性微分方程
二阶方程的特征方程为 r 2 + p r + q = 0 r^2 + p r + q = 0 r2+pr+q=0( p , q p, q p,q 为常数),其通解形式如下:
- 若特征方程有两个不相等的实根 r 1 ≠ r 2 r_1 \neq r_2 r1=r2,则通解为 y = C 1 e r 1 x + C 2 e r 2 x y = C_1 e^{r_1 x} + C_2 e^{r_2 x} y=C1er1x+C2er2x;
- 若特征方程有两个相等的实根 r 1 = r 2 = r r_1 = r_2 = r r1=r2=r,则通解为 y = ( C 1 + C 2 x ) e r x y = (C_1 + C_2 x) e^{r x} y=(C1+C2x)erx;
- 若特征方程有一对共轭复根 r 1 , 2 = α ± i β r_{1,2} = \alpha \pm i \beta r1,2=α±iβ( β ≠ 0 \beta \neq 0 β=0),则通解为 y = e α x ( C 1 cos β x + C 2 sin β x ) y = e^{\alpha x} (C_1 \cos \beta x + C_2 \sin \beta x) y=eαx(C1cosβx+C2sinβx)。

(2) n n n 阶常系数齐次线性微分方程
对于 n n n 阶方程,根据特征根的类型,对应解的形式如下:
- 单实根 r r r:对应一项 C e r x C e^{r x} Cerx;
- k k k 重实根 r r r:对应 k k k 项 ( C 1 + C 2 x + ⋯ + C k x k − 1 ) e r x (C_1 + C_2 x + \dots + C_k x^{k-1}) e^{r x} (C1+C2x+⋯+Ckxk−1)erx;
- 一对单共轭复根 r 1 , 2 = α ± i β r_{1,2} = \alpha \pm i \beta r1,2=α±iβ:对应两项 e α x ( C 1 cos β x + C 2 sin β x ) e^{\alpha x} (C_1 \cos \beta x + C_2 \sin \beta x) eαx(C1cosβx+C2sinβx);
- 一对 k k k 重共轭复根 r 1 , 2 = α ± i β r_{1,2} = \alpha \pm i \beta r1,2=α±iβ:对应 2 k 2k 2k 项 e α x ( ( C 1 + C 2 x + ⋯ + C k x k − 1 ) cos β x + ( D 1 + D 2 x + ⋯ + D k x k − 1 ) sin β x ) e^{\alpha x} \left( (C_1 + C_2 x + \dots + C_k x^{k-1}) \cos \beta x + (D_1 + D_2 x + \dots + D_k x^{k-1}) \sin \beta x \right) eαx((C1+C2x+⋯+Ckxk−1)cosβx+(D1+D2x+⋯+Dkxk−1)sinβx)。
所有特征根对应的解组合起来,即为 n n n 阶常系数齐次线性微分方程的通解。

9 常系数非齐次线性微分方程
二阶常系数非齐次线性微分方程的基本形式为:
y
′
′
+
p
y
′
+
q
y
=
f
(
x
)
y'' + p y' + q y = f(x)
y′′+py′+qy=f(x)
其中
p
,
q
p, q
p,q 为常数,
f
(
x
)
≠
0
f(x) \neq 0
f(x)=0。根据非齐次方程通解结构,其通解为对应齐次方程的通解加上非齐次方程的一个特解
y
∗
(
x
)
y^*(x)
y∗(x)。以下针对两类常见的
f
(
x
)
f(x)
f(x) 形式,给出特解
y
∗
(
x
)
y^*(x)
y∗(x) 的构造方法。
9.1 f ( x ) = e λ x P m ( x ) f(x) = e^{\lambda x} P_m(x) f(x)=eλxPm(x) 型
其中 λ \lambda λ 为常数, P m ( x ) P_m(x) Pm(x) 是 m m m 次多项式( P m ( x ) = a 0 x m + a 1 x m − 1 + ⋯ + a m P_m(x) = a_0 x^m + a_1 x^{m-1} + \dots + a_m Pm(x)=a0xm+a1xm−1+⋯+am)。特解 y ∗ ( x ) y^*(x) y∗(x) 的形式根据 λ \lambda λ 是否为特征方程的根确定:
- 若 λ \lambda λ 不是特征方程的根,设 y ∗ ( x ) = e λ x Q m ( x ) y^*(x) = e^{\lambda x} Q_m(x) y∗(x)=eλxQm(x),其中 Q m ( x ) = b 0 x m + b 1 x m − 1 + ⋯ + b m Q_m(x) = b_0 x^m + b_1 x^{m-1} + \dots + b_m Qm(x)=b0xm+b1xm−1+⋯+bm( b i b_i bi 为待定系数);
- 若 λ \lambda λ 是特征方程的 k k k 重根( k = 1 k = 1 k=1 或 k = 2 k = 2 k=2),设 y ∗ ( x ) = x k e λ x Q m ( x ) y^*(x) = x^k e^{\lambda x} Q_m(x) y∗(x)=xkeλxQm(x)。
将所设特解代入原方程,通过比较等式两端多项式的系数,可求解出待定系数 b i b_i bi,进而得到特解 y ∗ ( x ) y^*(x) y∗(x)。

9.2 f ( x ) = e λ x [ P l ( x ) cos ω x + P n ( x ) sin ω x ] f(x) = e^{\lambda x} [P_l(x) \cos \omega x + P_n(x) \sin \omega x] f(x)=eλx[Pl(x)cosωx+Pn(x)sinωx] 型
其中 λ , ω \lambda, \omega λ,ω 为常数( ω > 0 \omega > 0 ω>0), P l ( x ) P_l(x) Pl(x) 和 P n ( x ) P_n(x) Pn(x) 分别是 l l l 次和 n n n 次多项式,令 m = max { l , n } m = \max\{l, n\} m=max{l,n}。特解 y ∗ ( x ) y^*(x) y∗(x) 的形式根据 λ ± i ω \lambda \pm i \omega λ±iω 是否为特征方程的根确定:
- 若 λ ± i ω \lambda \pm i \omega λ±iω 不是特征方程的根,设 y ∗ ( x ) = e λ x [ R m ( x ) cos ω x + S m ( x ) sin ω x ] y^*(x) = e^{\lambda x} [R_m(x) \cos \omega x + S_m(x) \sin \omega x] y∗(x)=eλx[Rm(x)cosωx+Sm(x)sinωx],其中 R m ( x ) , S m ( x ) R_m(x), S_m(x) Rm(x),Sm(x) 是 m m m 次多项式(系数待定);
- 若 λ ± i ω \lambda \pm i \omega λ±iω 是特征方程的根,设 y ∗ ( x ) = x e λ x [ R m ( x ) cos ω x + S m ( x ) sin ω x ] y^*(x) = x e^{\lambda x} [R_m(x) \cos \omega x + S_m(x) \sin \omega x] y∗(x)=xeλx[Rm(x)cosωx+Sm(x)sinωx]。
将所设特解代入原方程,比较等式两端同类项的系数,求解出待定系数,即可得到特解 y ∗ ( x ) y^*(x) y∗(x)。
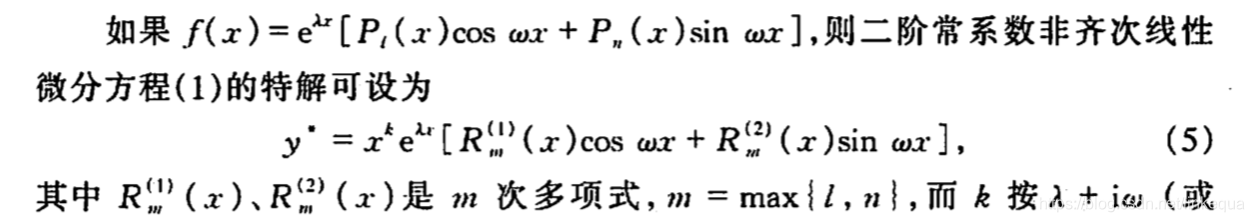

10 欧拉方程
10.1 欧拉方程形式
形如以下的方程称为欧拉方程:
x
n
y
(
n
)
+
a
1
x
n
−
1
y
(
n
−
1
)
+
⋯
+
a
n
−
1
x
y
′
+
a
n
y
=
f
(
x
)
x^n y^{(n)} + a_1 x^{n-1} y^{(n-1)} + \dots + a_{n-1} x y' + a_n y = f(x)
xny(n)+a1xn−1y(n−1)+⋯+an−1xy′+any=f(x)
其中
a
1
,
a
2
,
…
,
a
n
a_1, a_2, \dots, a_n
a1,a2,…,an 为常数,
x
>
0
x > 0
x>0(若
x
<
0
x < 0
x<0,可令
x
=
−
t
x = -t
x=−t 转化为
t
>
0
t > 0
t>0 的情况)。

10.2 求解方法
欧拉方程的求解关键是通过变量替换将其转化为常系数线性微分方程。令
x
=
e
t
x = e^t
x=et(即
t
=
ln
x
t = \ln x
t=lnx),引入微分算子
D
=
d
d
t
D = \frac{d}{dt}
D=dtd,则有以下导数变换公式:
x
y
′
=
D
y
,
x
2
y
′
′
=
D
(
D
−
1
)
y
,
x
3
y
′
′
′
=
D
(
D
−
1
)
(
D
−
2
)
y
,
…
,
x
k
y
(
k
)
=
D
(
D
−
1
)
…
(
D
−
k
+
1
)
y
x y' = D y, \quad x^2 y'' = D(D - 1)y, \quad x^3 y''' = D(D - 1)(D - 2)y, \dots, x^k y^{(k)} = D(D - 1)\dots(D - k + 1)y
xy′=Dy,x2y′′=D(D−1)y,x3y′′′=D(D−1)(D−2)y,…,xky(k)=D(D−1)…(D−k+1)y
将上述变换代入原欧拉方程,可将其转化为以
t
t
t 为自变量的常系数线性微分方程。求解该方程后,将
t
=
ln
x
t = \ln x
t=lnx 代回,即可得到原欧拉方程的解。
11 经典例题
例题
求微分方程 ( x − 1 ) y ′ ′ − x y ′ + y = 1 (x - 1)y'' - x y' + y = 1 (x−1)y′′−xy′+y=1 的通解。

解答:
根据二阶非齐次线性微分方程的解的性质:
非齐次方程的两个解之差,是其对应齐次方程的解。
-
求对应齐次方程的解
首先考虑齐次方程 ( x − 1 ) y ′ ′ − x y ′ + y = 0 (x-1)y'' - xy' + y = 0 (x−1)y′′−xy′+y=0。已知 y = 1 , y = x , y = x 2 y=1, y=x, y=x^2 y=1,y=x,y=x2 是非齐次方程的解,因此可以得到齐次方程的两个解:
y 1 = x − 1 y_1 = x - 1 y1=x−1(由 y = x y=x y=x 与 y = 1 y=1 y=1 之差得到)
y 2 = x 2 − 1 y_2 = x^2 - 1 y2=x2−1(由 y = x 2 y=x^2 y=x2 与 y = 1 y=1 y=1 之差得到) -
验证 y 1 , y 2 y_1, y_2 y1,y2 线性无关
计算朗斯基行列式:
W ( x ) = ∣ y 1 y 2 y 1 ′ y 2 ′ ∣ = ∣ x − 1 x 2 − 1 1 2 x ∣ = ( x − 1 ) ⋅ 2 x − ( x 2 − 1 ) ⋅ 1 = 2 x ( x − 1 ) − ( x 2 − 1 ) = ( x − 1 ) ( 2 x − x − 1 ) = ( x − 1 ) 2 \begin{aligned} W(x) & =\left| \begin{matrix} {{y}_{1}} & {{y}_{2}} \\ {{y}_{{{1}'}}} & {{y}_{{{2}'}}} \\ \end{matrix} \right| \\ & =\left| \begin{matrix} x-1 & {{x}^{2}}-1 \\ 1 & 2x \\ \end{matrix} \right| \\ & =(x-1)\cdot 2x-({{x}^{2}}-1)\cdot 1 \\ & =2x(x-1)-({{x}^{2}}-1) \\ & =(x-1)(2x-x-1) \\ & ={{(x-1)}^{2}} \end{aligned} W(x)= y1y1′y2y2′ = x−11x2−12x =(x−1)⋅2x−(x2−1)⋅1=2x(x−1)−(x2−1)=(x−1)(2x−x−1)=(x−1)2
当 x ≠ 1 x \neq 1 x=1 时, W ( x ) ≠ 0 W(x) \neq 0 W(x)=0,因此 y 1 y_1 y1 和 y 2 y_2 y2 是线性无关的。
-
齐次方程的通解
齐次方程的通解为:
Y = C 1 ( x − 1 ) + C 2 ( x 2 − 1 ) Y = C_1(x-1) + C_2(x^2-1) Y=C1(x−1)+C2(x2−1)
(其中 C 1 , C 2 C_1, C_2 C1,C2 为任意常数) -
非齐次方程的通解
已知 y = 1 y=1 y=1 是非齐次方程的一个特解,因此非齐次方程的通解为:
y = Y + y ∗ = C 1 ( x − 1 ) + C 2 ( x 2 − 1 ) + 1 y = Y + y^* = C_1(x-1) + C_2(x^2-1) + 1 y=Y+y∗=C1(x−1)+C2(x2−1)+1最终通解
y = C 1 ( x − 1 ) + C 2 ( x 2 − 1 ) + 1 y = C_1(x-1) + C_2(x^2-1) + 1 y=C1(x−1)+C2(x2−1)+1
其中 C 1 , C 2 C_1, C_2 C1,C2 为任意常数。
- 微分方程 | 定义、类型、解与示例(篇 2)-优快云博客
https://blog.youkuaiyun.com/u013669912/article/details/155314485
via:
-
Methods of Solving Differential Equations: Definition, Solutions - Embibe
https://www.embibe.com/exams/methods-of-solving-differential-equations/ -
微分方程的求解方法-优快云博客
https://blog.youkuaiyun.com/acceptedday/article/details/111088294





















 1926
1926

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








