三角学发展史 | 从起源到现代

注：本文为 “三角学发展史” 相关合辑。
英文引文，机翻未校。
如有内容异常，请看原文。

---

The history of trigonometry- part 1

三角学发展史（第一部分）

Article by
Leo Rogers
利奥·罗杰斯

Published Tue, 01/02/2011 - 00:00

Early Astronomy and the Beginnings of a Mathematical Science

早期天文学与数学科学的起源

1. Ancient Instruments and Measuring the Stars

古代仪器与星体测量

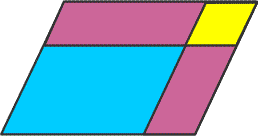
The most ancient device found in all early civilisations, is a “shadow stick”. The shadow cast from a shadow stick was used to observe the motion of the Sun and thus to tell time. Today we call this instrument a Gnomon. The name gnomon comes from the Greek and refers to any L-shaped instrument, originally used to draw a right angle.
在所有早期文明中，最古老的工具是“影杆”。人们通过影杆投射的影子观察太阳运动，进而判断时间。如今，我们将这种仪器称为“指时针（Gnomon）”。“Gnomon”一词源自希腊语，指任何 L 形工具，最初用于绘制直角。

In Euclid Book II, where Euclid deals with the transformation of areas, the gnomon takes the form of an “L-shaped” area touching two adjacent sides of a parallelogram. Today, a gnomon is the vertical rod or similar device that makes the shadow on a sundial.
在欧几里得《几何原本》第二卷中，欧几里得探讨面积变换时，将“指时针”定义为与平行四边形两条邻边相接的“L 形”区域。如今，指时针指日晷上用于投射影子的垂直杆或类似装置。

For more about sundials go to Leo’s article - Brief History of Time Measurement.
如需了解更多关于日晷的内容，可参阅利奥的文章——《时间测量简史》。

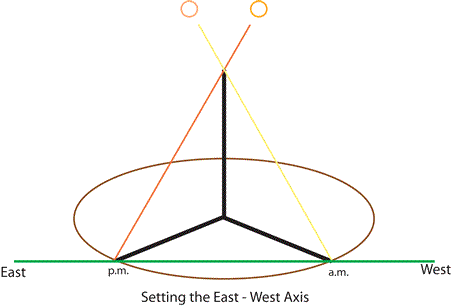
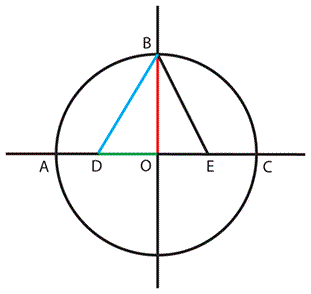
At midday the shadow of a stick is shortest, and the civilisations of Mesopotamia, Egypt, and China took the North - South direction from this alignment. In contrast, the Hindus used the East - West direction, the rising and setting of the sun, to orient their “fire-altars” for religious practices. To do this they constructed the “gnomon circle” whose radius was the square root of the sum of the square of the height of the gnomon and its shadow [See Note 2 below].
正午时分，杆影最短。美索不达米亚、埃及和中国的文明均通过这一现象确定南北方向。与之不同，印度人则利用太阳的东升西落（即东西方向）来确定用于宗教仪式的“火坛”朝向。为实现这一目的，他们构建了“指时针圆”，其半径等于指时针高度的平方与影长的平方之和的平方根（详见下文注释 2）。

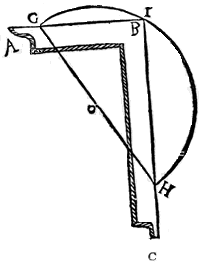
The Merkhet is one of the oldest known astronomical instruments. It was developed around 600 BCE and uses a plumb line to obtain a true vertical, as in the picture. The other object is the rib of a palm leaf, split at one end to make a thin slit for a sight. Babylonian and Egyptian astronomers were able to measure the altitude and lateral displacement of heavenly objects from a particular direction by using a Merkhet, thus giving the earliest ideas of turning, or angle.
默克 het（Merkhet）是已知最古老的天文仪器之一。它约在公元前 600 年被发明，如图所示，通过铅垂线确定真正的竖直方向。另一部件是棕榈叶的叶脉，一端劈开形成细缝，用于观测。巴比伦和埃及的天文学家借助默克 het，能够测量天体相对于特定方向的高度和横向位移，由此产生了关于“转动”或“角”的最早概念。

A pair of merkhets were used to establish a North-South direction by lining them up, one behind the other, with the Pole Star. Viewing the plumb lines through the sight made sure the two merkhets and the sight were in the same straight line with the Pole Star. Using a water clock to determine timings, this arrangement of merkhets allowed people to take measurements of night-time events, for example times when certain stars crossed the vertical plumb line (a “transit line”).
人们将两个默克 het 前后排列并对准北极星，以此确定南北方向。通过观测缝观察铅垂线，可确保两个默克 het、观测缝与北极星处于同一直线上。借助水钟计时，这种默克 het 装置能够测量夜间天体现象，例如特定星体穿过竖直铅垂线（“凌日线”）的时间。

The Egyptians divided the 360 degrees of the ecliptic into 36 sections of 10 degrees each. [see Note 1 below]. This division was known before 2300 BCE. Each ten degree section (called a decan from the Greek for ten) contained a constellation of stars lined up along the ecliptic. Since the Earth makes a full rotation in 24 hours, the stars in a new decan will rise above the horizon about every 40 minutes. The system of decans was used for determining the night hours and the seasons.
埃及人将黄道的 $360^{\circ }$ 划分为 36 个部分，每部分为 $10^{\circ }$（详见下文注释 1）。这种划分方式在公元前 2300 年之前就已存在。每个 $10^{\circ }$ 的部分被称为“旬星（decan）”，该词源自希腊语“十”，每个旬星区域内包含一组沿黄道排列的星座。由于地球自转一周需 24 小时，因此每隔约 40 分钟，就会有新的旬星区域的星体升起至地平线以上。旬星系统被用于确定夜间时辰和季节。

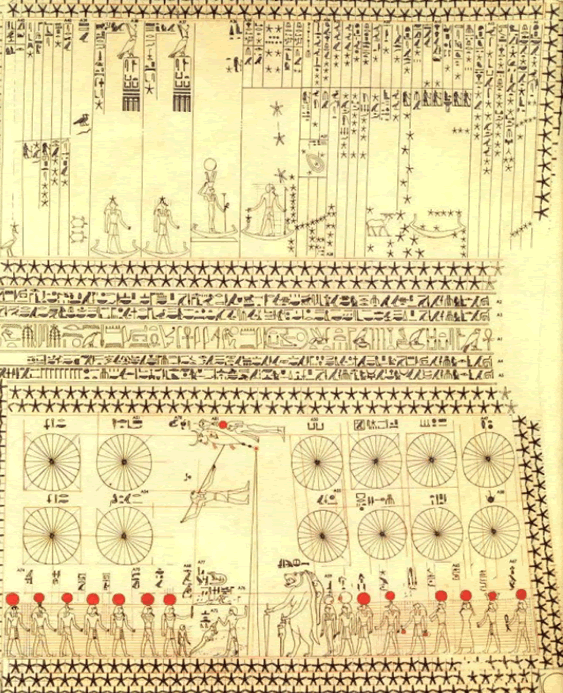
The divisions in the top part of the chart represent decans. The chart was read from right to left and the pictures represent Mars (the boat and the bull), Orion with the three stars including the Sun and Moon, Sirius, Jupiter, Saturn, Mercury and Venus. The lower section contains pictures of star gods or demons. They represent some of the most important days of the year. The chart is largely symbolic and functional but does contain pictures of some significant groups of stars.
图表顶部的分区代表旬星。该图表需从右至左阅读，其中图案分别代表火星（船与公牛）、包含太阳和月亮的猎户座三星、天狼星、木星、土星、水星和金星。图表下方是星神或星魔的图案，代表一年中一些重要的日子。该图表兼具象征意义与实用功能，同时也包含了一些重要星群的图案。

2. Babylonian Astronomers

巴比伦天文学家

Observations of celestial bodies by the Babylonians from about 1,800 BCE gave rise to the eventual division of the circle into 360 degrees, and by about 500 BCE, the division of the heavens into twelve regions of 30 degrees each, often referred to as the 12 houses of the zodiac. The Babylonians recorded the events of the lunar month, the daily movement of the sun across the sky over the year, and the rising and setting of the major planets. So, by 750 BCE astronomers had a reasonably accurate means of measuring the elevation (latitude) and lateral direction (longitude) of all objects in the heavens. They built up an extensive collection of data, and made tables of the positions of objects in the sky at any given time through a year (these tables are called ephemerides).
约公元前 1800 年起，巴比伦人对天体的观测最终促成了“将圆划分为 $360^{\circ }$”这一制度；到约公元前 500 年，他们又将天空划分为 12 个区域，每个区域为 $30^{\circ }$，这通常被称为“黄道十二宫”。巴比伦人记录了太阴月的各种现象、太阳一年内的每日天际运动，以及主要行星的升降规律。因此，到公元前 750 年，天文学家已能较为精确地测量天空中所有天体的高度（纬度）和横向方位（经度）。他们积累了大量数据，并编制出一年内任意时刻天体位置的表格（这类表格被称为“星历表”）。

Using observational techniques like heliacal rising, which occurs when a planet, star or other body first becomes visible above the eastern horizon at dawn , it was discovered that:
通过“偕日升”等观测技术（即行星、恒星或其他天体在黎明时分首次出现在东方地平线以上的现象），人们发现：

• the constellations of the zodiac completed a full circle through the sky once a year

  黄道十二宫的星座每年在天空中完成一次完整的圆周运动

• the Sun’s apparent movement daily across the sky formed $\frac{1}{360}$ of a circle

  太阳每日在天空中的视运动轨迹约为一个圆的 $\frac{1}{360}$

• the moon moved through about $\frac{13}{360}$ of a circle each day

  月球每日的运动轨迹约为一个圆的 $\frac{13}{360}$

• the Ecliptic was inclined to the horizon (about $23\frac{1}{2}$ degrees)

  黄道与地平线存在倾角（约 $23{\frac{1}{2}}^{\circ }$）

• planets were travelling through the starry background in regular paths that were sometimes moving back on themselves in a loop (retrograde)

  行星在恒星背景中沿规律轨道运行，有时会出现反向循环运动（逆行）

• eclipses of the moon and the sun could be predicted

  月食和日食可被预测

• transits of planets (e.g. Venus) moving across the face of the sun, and occultations (where the moon covered the stars) could be observed.

  可观测到行星（如金星）从太阳表面穿过的“凌日”现象，以及月球遮挡恒星的“掩星”现象。

These observations continued over many centuries, slowly becoming more accurate, so that ancient people were able to make star maps, and detect the regular events in the heavens.
这些观测持续了多个世纪，精度逐渐提高，古人由此得以绘制星图，并发现天空中的规律性现象。

Many seasonal phenomena like the flooding of the Nile, or special events like religious ceremonies were linked to astronomical phenomena. The ability to predict some of these major astronomical events gave rise to astrology, where people believed that there was a link between heavenly and earthly events, and that the stars had some control over their lives. See this BBC news item about a prehistoric star map.
许多季节性现象（如尼罗河泛滥）或特殊活动（如宗教仪式）都与天文现象相关。预测重大天文现象的能力催生了占星术——人们认为天体事件与地球事件之间存在关联，且星体对人类生活具有一定支配力。关于史前星图，可参阅 BBC 新闻报道。

The Babylonians and Chinese both believed that the earth and the moon were spherical, that the earth and the moon rotated on an axis, and that the sun and the planets moved in circles round the earth. This enabled them to be able to explain the phases of the moon, and predict eclipses of the moon and the sun by believing that the earth cast a shadow on the moon, and the moon cast a shadow over the sun. They were able to predict paths of other objects across the sun, for example the transit of Venus, a description and explanation of which can be found here on Wikipedia.
巴比伦人和中国人都认为地球与月球是球形的，二者均绕轴自转，而太阳和行星则绕地球做圆周运动。这一认知使他们能够解释月相变化，并通过“地球在月球上投下阴影”“月球遮挡太阳”的理论预测月食和日食。他们还能预测其他天体穿过太阳的轨迹，例如金星凌日，其相关描述与解释可在维基百科上查阅。

The Babylonian astronomers recorded astronomical data systematically and by the Seleucid period (330-125BCE) there were a great many astronomical tablets showing ephemerides for the moon and the major planets. Many of the tablets contain “procedures” or instructions for how to calculate intervals between astronomical events using the properties of simple arithmetic progressions. These procedural processes were the earliest steps of a mathematical astronomy, and both the procedures and the data were used by those who came later. The Babylonians wrote down lists of numbers, in what we would call an arithmetic progression and recognised that numbers repeated themselves over periods of time.
巴比伦天文学家系统地记录天文数据，到塞琉古时期（公元前 330-125 年），已出现大量刻有月球及主要行星星历表的天文泥板。许多泥板包含“计算步骤”或说明，指导人们利用简单等差数列的性质计算天文事件之间的间隔。这些计算步骤是数学天文学的雏形，其方法与数据均为后世所用。巴比伦人会记录一系列数字（即我们所说的“等差数列”），并发现这些数字会随时间周期性重复。

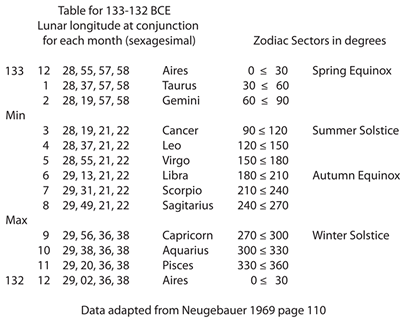
As you can see, Neugebauer published the sexagesimal values for twelve measurements of the position of the Moon taken from a clay tablet dated 133/132 BCE.
如图所示，诺伊格鲍尔（Neugebauer）公布了源自公元前 133-132 年泥板的 12 组月球位置测量数据的六十进制数值。

In the table above, the top line shows the end of the year 133 BCE with the last month Aires, so the start of the Babylonian year was at the vernal equinox, and the bottom line represents the end of year 132 BCE. The height of the lines on the zig-zag graph below approximately represent the sequence of the numerical values in the table. There are two groups of numbers, one starting with 28, followed by another starting 29. The results for Gemini and Cancer differ only in the third place of sexagesimals and the minimum on the graph is interpolated from the results in the table. Similarly the results for Sagitarius and Capricorn indicate the maximum value for the longitude.
在上方表格中，首行代表公元前 133 年末，最后一个月为“白羊座月”，由此可知巴比伦历法的新年始于春分；末行代表公元前 132 年末。下方锯齿图中线条的高度大致对应表格中数值的序列。表格中的数字分为两组，一组以 28 开头，另一组以 29 开头。双子座与巨蟹座对应的数值仅在六十进制的第三位存在差异，图表中的最小值是通过表格数据插值得到的。同样，射手座与摩羯座对应的数值代表经度的最大值。

Looking at the first three sets of sexagesimal numbers: 28, 55, 57, 58; 28, 37, 57, 58 and 28, 19, 57, 58 we can notice that the significant differences in the second place between 55, 37 and 19 are all giving a constant 18, which is the difference in height of the vertical lines on the zig-zag graph (except at the minimum and maximum). The graph was drawn to illustrate the periodicity of the data. It is important to realise that the Babylonians recognised the events repeated themselves after some time, but they did not see these results as a ‘graph’ as we can [see Note 3 below].
观察前三组六十进制数字：28, 55, 57, 58；28, 37, 57, 58；28, 19, 57, 58，可发现第二位数 55、37、19 之间的差值恒为 18，这与锯齿图中竖线的高度差（最小值和最大值处除外）一致。绘制该图表是为了体现数据的周期性。需注意的是，巴比伦人虽已发现事件会随时间重复，但并未像我们这样将这些结果视为“图表”（详见下文注释 3）。

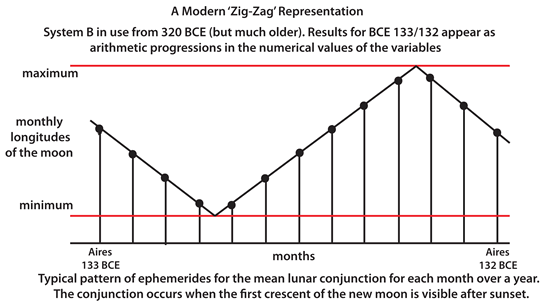
The use of graphs as a way of recording the data comes from Neugebauer’s book The Exact Sciences in Antiquity.
将图表用作数据记录方式的做法，源自诺伊格鲍尔的著作《古代精密科学》（The Exact Sciences in Antiquity）。

The Babylonian astronomers recognised the events were periodic but they did not have a theory of planetary motion.
巴比伦天文学家虽已发现事件的周期性，但并未形成行星运动理论。

3. The Hindu Sulbasutras

印度《绳法经》（Sulbasutras）

The Sulbasutras are the only early sources of Hindu mathematical knowledge and originally come from the Vedic period (during the second millennium BCE). The earliest written texts we have from this oral tradition date from about 800 BCE. The Sulbasutras are the instructions for constructing various geometrical shapes to make ‘fire-altars’ using the “Peg and Cord” technique. Each ‘fire-altar’ was a different shape and associated with unique gifts from the Gods.
《绳法经》（Sulbasutras）是印度早期数学知识的唯一来源，其起源可追溯至吠陀时期（公元前 2000 年左右）。这一知识最初以口头形式传承，现存最早的书面文本约成书于公元前 800 年。《绳法经》记载了利用“钉线法”（Peg and Cord technique）构建各种几何图形以制作“火坛”的方法。每个火坛的形状各不相同，且对应着神明赐予的独特福祉。

For more information on Peg and Cord geometry see: The Development of Algebra Part 1: Section 4 “Early Indian Mathematics” an article by Leo already published on NRICH.
如需了解更多关于“钉线几何”的内容，可参阅利奥已发表在 NRICH 上的文章《代数学发展史（第一部分）》，其中第 4 节“印度早期数学”有相关介绍。

The Vedic people knew how to find the cardinal directions (NSEW). The Sulbasutras gave procedures for the construction of the altars by starting with a line marking the E-W direction (sun rises in east and sinks in west), thus the E-W direction had special religious significance.
吠陀时期的人们已掌握确定基本方位（东南西北）的方法。《绳法经》中记载的火坛建造步骤，以标记东西方向的直线为起点（太阳东升西落），因此东西方向具有特殊的宗教意义。

At the end of the fourth century BCE the Indian part of Alexander the Great’s empire broke up into small kingdoms run by Indian Greeks. Around this time there was a collection of mathematical knowledge called jyotsia, a mixture of astronomy, calendar calculations and astrology. The rulers still maintained trading links between western India and the Hellenistic culture of the Roman Empire. At this time, Indian horoscope astrology became popular needing precise calendar and astronomical calculations.
公元前 4 世纪末，亚历山大大帝帝国在印度的领土分裂为多个由印度希腊人统治的小王国。大约在此时期，出现了名为“Jyotsia”的数学知识集合，涵盖天文学、历法计算与占星术。当时的统治者仍维持着西印度与罗马帝国希腊文化圈之间的贸易往来。与此同时，印度占星术开始流行，这需要精确的历法与天文计算作为支撑。

The Panca-siddhantica is a collection of five astronomical works composed in the sixth century CE by Vrahamihira. These works contain earlier mathematical knowledge and here we find an approximation for $\pi$ as $\sqrt{10}$, because they used the relationship between the circumference of a circle, $C$ and its diameter $D$ as $D=\sqrt{\frac{C^2}{10}}$. Sines were calculated at intervals of $\frac{30^{\circ }}{8}$ or $3^{\circ }45^{\prime }$, giving a series of values for Sines of angles in the first quadrant and, using the same terms in Sanskrit as the Babylonians for the radius of a circle. Also, the use of similar calculation methods as the Babylonians suggest that this is the earliest surviving Indian sine table. [See Note 4 below]
《五大历算书》（Panca-siddhantica）是公元 6 世纪由瓦拉哈米希拉（Vrahamihira）编撰的五部天文著作的合集。这些著作包含了早期数学知识，其中将 $\pi$ 的近似值取为 $\sqrt{10}$，因为书中采用的圆周长 $C$ 与直径 $D$ 的关系为 $D=\sqrt{\frac{C^2}{10}}$。书中以 $\frac{30^{\circ }}{8}$（即 $3^{\circ }45^{\prime }$）为间隔计算正弦值，得到了第一象限内一系列角度的正弦值；在描述圆半径时，所用的梵语术语与巴比伦人一致。此外，其计算方法与巴比伦人相似，这表明这是现存最早的印度正弦表（详见下文注释 4）。

The method of calculation and the values used by Vrahamihira is very similar to a Greek Chord table for arcs up to $120^{\circ }$ and intervals of the quadrant into sixths, namely arcs of $15^{\circ }$. This suggests that the Indian invention of the trigonometry of Sines was inspired by replacing the Greek Chord geometry of right triangles in a semicircle by the simpler Sine geometry of right triangles in a quadrant [See Note 5 below].
瓦拉哈米希拉采用的计算方法与数值，与希腊人用于计算 up to $120^{\circ }$ 弧长的弦表高度相似，且均将象限分为六等份（即每段弧为 $15^{\circ }$）。这表明印度人发明正弦三角学的灵感，可能源自将希腊人“半圆内直角三角形的弦几何”替换为“象限内直角三角形的简单正弦几何”（详见下文注释 5）。

This discovery is much earlier than the account usually given of the sine table derived from chords by Aryabhata the Elder (476-550 CE) who used the word jiya for sine. Brahmagupta reproduced the same table in 628 CE and Bhaskara gave a detailed method for constructing a table of sines for any angle in 1150 CE.
这一发现的时间远早于通常记载的“老阿耶波多（Aryabhata the Elder，公元 476-550 年）从弦长推导正弦表”的时间——老阿耶波多将正弦称为“jiya”。公元 628 年，婆罗摩笈多（Brahmagupta）复刻了同一正弦表；公元 1150 年，巴斯卡拉（Bhaskara）提出了构建任意角度正弦表的详细方法。

4. Chinese Astronomy

中国天文学

The Chinese were the most accurate observers of celestial phenomena before the Arabs. “Oracle Bones” with star names engraved on them dating back to the Chinese Bronze Age (about 2,000 BCE) have been found, and very old star maps have been found on pottery, engraved on stones, and painted on the walls of caves.
在阿拉伯人之前，中国人是天体现象最精确的观测者。目前已发现可追溯至中国青铜时代（约公元前 2000 年）、刻有星名的“甲骨文”，同时还在陶器、石刻与洞穴壁画上发现了非常古老的星图。

Surviving records of astronomical observations made by two astronomers Shi Shen and Gan De date from the 4th century BCE.
现存的、由石申与甘德两位天文学家完成的天文观测记录，可追溯至公元前 4 世纪。

Shi Shen wrote a book on astronomy, and made a star map and a star catalogue. In 364 BCE Gan De made the first recorded observation of sunspots, and the moons of Jupiter and they both made accurate observations of the five major planets. Their observations were based on the principle of the stars rotating about the pole (equivalent to the earth rotating on its axis).
石申撰写了天文学著作，并绘制了星图、编制了星表。公元前 364 年，甘德首次有记录地观测到太阳黑子与木星卫星；二人还对五大行星进行了精确观测。他们的观测基于“星体绕极旋转”的原理（相当于地球绕轴自转）。

A famous map due to Su Song (1020-1101) and drawn on paper in 1092 represents the whole sky with the positions of some 1,350 stars.
北宋苏颂（1020-1101 年）于 1092 年绘制的纸质星图十分著名，该图呈现了整个天空的样貌，并标注了约 1350 颗星体的位置。

The equator is represented by the horizontal straight line running through the star chart, while the ecliptic curves above it.
星图中，水平线代表赤道，黄道则以曲线形式呈现于赤道上方。

The oldest star map found so far is from Dunhuang. Earlier thought to date from about 940 CE, it was made with precise mathematical methods by the astronomer and mathematician Li Chunfeng (602-670) and shows 1339 stars in 257 Chinese star groups with a precision between 1.5 and 4 degrees of arc. In all there are 12 charts each in 30 degree sections displaying the full sky visible from the Northern hemisphere. Up to now it is the oldest complete preserved star atlas discovered from any civilisation. It has been on display this year in the British Library to celebrate 2009 as the International Year of Astronomy. [see Note 6 below]
目前发现的最古老星图出自敦煌。该星图最初被认为成书于公元 940 年左右，实则由天文学家、数学家李淳风（602-670 年）采用精确数学方法绘制而成。图中呈现了 257 个中国星官中的 1339 颗星体，精度在 $1.5^{\circ }$ 至 $4^{\circ }$ 之间。整套星图共 12 幅，每幅对应 $30^{\circ }$ 天区，完整呈现了北半球可见的天空。它是目前所有文明中发现的、保存完整的最古老星图。为庆祝 2009 年“国际天文年”，该星图于今年在大英图书馆展出（详见下文注释 6）。

Some elements of Indian astronomy reached China with the expansion of Buddhism (25-220 CE). Later, during the period (618-907 CE) a number of Indian astronomers came to live in China and Islamic astronomers collaborated closely with their Chinese counterparts particularly during (1271-1368).
随着佛教的传播（公元 25-220 年），印度天文学的部分内容传入中国。此后，在唐朝（公元 618-907 年），有多位印度天文学家来华定居；而在元朝（公元 1271-1368 年），伊斯兰天文学家与中国天文学家展开了密切合作。

Very little of the knowledge of the Indians and the Chinese was known in Europe before the Portuguese navigators and the Jesuit scientist Matteo Ricci in the fifteenth century.
在 15 世纪葡萄牙航海家与耶稣会科学家利玛窦（Matteo Ricci）来华之前，欧洲人对印度和中国的这些知识知之甚少。

Babylonian astronomy contributed direct empirical data as a foundation for Greek theory and exactly the same data which provided the information for the “zig-zag” data results in Babylonian theory were used to calculate the mean motions of the sun and moon by Hipparchus.
巴比伦天文学为希腊理论提供了直接的经验数据基础。希帕恰斯（Hipparchus）在计算太阳与月球的平均运动时，所用的数据与巴比伦理论中用于生成“锯齿形”数据结果的数据完全一致。

Pedagogical notes to support this article can be found in the Teachers’ Notes accompanying this resource.
本文的教学辅助注释可参阅本资源附带的《教师注释》。

Explanations for some of the astronomical terms used in this article can be found here.
本文中部分天文术语的解释可在此处 查阅。

References

参考文献

Katz, V. (1998) A History of Mathematics. New York. Addison Wesley. Recommended as the best general history of mathematics currently available. There is good coverage of aspects of astronomy in antiquity, and the discussion on ‘functions’ (p. 156) is worth reading. Trigonometry is dealt with in sections on Ancient Civilisations, Mediaeval Europe, Renaissance Europe
卡茨，V.（1998）.《数学史》（A History of Mathematics）. 纽约：艾迪生·韦斯利出版社. 本书被推荐为目前最优秀的数学通史著作，对古代天文学相关内容有充分论述，其中关于“函数”的讨论（第 156 页）值得一读。三角学内容分布在“古代文明”“中世纪欧洲”“文艺复兴时期欧洲”等章节中。

Katz, V. (Ed.) (2007) The Mathematics of Egypt, Mesopotamia, China, India, and Islam. Princeton. Princeton University Press. This book contains a wealth of up-to-date information on mathematics and some aspects of astronomy in these ancient civilisations.
卡茨，V.（编）（2007）.《埃及、美索不达米亚、中国、印度与伊斯兰世界的数学》（The Mathematics of Egypt, Mesopotamia, China, India, and Islam）. 普林斯顿：普林斯顿大学出版社. 本书包含大量关于这些古代文明中数学及部分天文学内容的最新研究成果。

Linton, C. M. (2004) From Eudoxus to Einstein: A History of Mathematical Astronomy. Cambridge University Press The first chapter deals with ancient people and early Greek astronomy.
林顿，C. M.（2004）.《从欧多克索斯到爱因斯坦：数学天文学史》（From Eudoxus to Einstein: A History of Mathematical Astronomy）. 剑桥：剑桥大学出版社. 本书第一章探讨了古代人类与早期希腊天文学。

Needham, J. (1959) Science and Civilisation in China. Vol. 3. Mathematics and the Sciences of the Heavens and the Earth. Cambridge University Press.
李约瑟，J.（1959）.《中国科学技术史》（Science and Civilisation in China）. 第 3 卷《数学与天学》. 剑桥：剑桥大学出版社.

Neugebauer, O. (1983)(1955) Astronomical Cuneiform Texts. Vol. 1 The Moon. Heidelberg. Springer-Verlag These two books are the big classics on China and Mesopotamia, but much work has been done in these areas since the 1950s.
诺伊格鲍尔，O.（1983）（1955 年首版）.《天文楔形文字文本》（Astronomical Cuneiform Texts）. 第 1 卷《月球》. 海德堡：施普林格出版社. 上述两部著作（指李约瑟与诺伊格鲍尔的著作）是关于中国与美索不达米亚的经典文献，但自 20 世纪 50 年代以来，这些领域已涌现出大量新研究。

Neugebauer, O. (1969) (original 1952) The Exact Sciences in Antiquity. New York. Dover Books. Still available, this is a more popular book and contains much information on Egypt, Babylon and Greek Science.
诺伊格鲍尔，O.（1969）（1952 年首版）.《古代精密科学》（The Exact Sciences in Antiquity）. 纽约：多佛出版社. 本书仍在版，属于普及性著作，包含大量关于埃及、巴比伦与希腊科学的内容。

Plofker, K. (2009) Mathematics in India. Princeton. Princeton University Press. This is the most recent book on the history of Mathematics in India by a renowned expert.
普洛夫克，K.（2009）.《印度数学》（Mathematics in India）. 普林斯顿：普林斯顿大学出版社. 本书由知名专家撰写，是关于印度数学史的最新著作。

Web Links

网络链接

Wikipedia is quite good for first-level information on early astronomy, and should lead you to more reliable sources. However, more recent work - as found in Katz (2007) is the best generally available today.
维基百科（Wikipedia）可提供关于早期天文学的基础信息，并引导读者查阅更可靠的资料来源。但目前最优质的资料仍是最新研究成果，如卡茨（2007）的著作。

The MacTutor site has a topic list and there you can find material on Trigonometry and Greek astronomy, but look also at Geography. In the biography list, you can find Ptolemy, Eudoxus, Menelaos, Brahmagupta and others.
MacTutor 网站（数学史网站）设有主题列表，可在其中查阅三角学与希腊天文学相关资料，也可关注“地理学”板块。在人物传记列表中，可找到托勒密、欧多克索斯、梅涅劳斯（Menelaos）、婆罗摩笈多等人的传记。

Note 6 below, has a link to the oldest Chinese Star Map
下文注释 6 中提供了最古老中国星图的链接。

Here is Gary Thompson’s huge collection of data on Egyptian, Babylonian, Chinese and other Ancient Astronomy:
以下是加里·汤普森（Gary Thompson）收集的关于埃及、巴比伦、中国及其他古代文明天文学的大量数据：
https://members.westnet.com.au/gary-david-thompson/index1.html

This site shows some of the oldest star diagrams from prehistoric times: <
该网站展示了部分史前时期最古老的星图：
https://www.spacetoday.org/SolSys/Earth/OldStarCharts.html

This is a site on Egyptian Astronomy
以下是关于埃及天文学的网站：
https://www.egyptologyonline.com/astronomy.htm

Here you can find the ‘Decan’ chart
可在以下链接查阅“旬星图”：
https://www.moses-egypt.net/star-map/senmut1-mapdate_en.asp

Notes

注释

1. The radius of the circle depends on the time of year. The truest E - W direction will be achieved by marking the end of the shadow at sunrise and sunset (possibly at the equinoxes). As long as the times of marking the shadow after sunrise and before sunset are the same, the true E - W direction could still be found. In the surviving documents, there are no diagrams, and the instructions are somewhat ambiguous. These ancient people knew that the diagonal of any rectangle was the square root of the square on the hypotenuse of a right triangle by at least 2,000 BCE. At that time, the square root of the square on the hypotenuse was conceived of as the length of a rope i.e. the side of the square, not a numerical result, as we think of it today.

   圆的半径随季节变化。通过标记日出与日落时的影端（可能在分点时刻），可得到最精确的东西方向。只要在日出后与日落前标记影端的时间对称，仍能确定真实的东西方向。现存文献中未包含图示，相关说明也存在一定模糊性。至少在公元前 2000 年，这些古人就已知道：矩形的对角线长度等于其内含直角三角形斜边的平方的平方根。当时，人们将“斜边平方的平方根”理解为绳子的长度（即正方形的边长），而非如今我们所理解的数值结果。

2. The ecliptic is the apparent path of the Sun in the sky throughout the year on the celestial sphere. The angle between the plane of the equator and the plane of the ecliptic is about 23${}^{\circ }$ 26’ and is called the obliquity of the ecliptic. Babylonian astronomers recognised the rotation of constellations of stars along the zodiac circle (the ecliptic). The intersections of the celestial equator and the ecliptic are the equinox points where the lengths of the day and night are equal.

   黄道（ecliptic）* 是指太阳在天球上一年内的视运动轨迹。赤道面与黄道面之间的夹角约为 $23^{\circ }26^{\prime }$，该角被称为“黄赤交角（obliquity of the ecliptic）”。巴比伦天文学家已发现星座沿黄道圈（即黄道）的旋转现象。天赤道与黄道的交点为分点，分点时刻昼夜时长相等。

3. The common unit of measure for these calculations was usually the nidan or cubit (about 50 cm.) but other units were used at different times, so there is little consistency from one period to another. 1 degree of arc was about 4 minutes of time and 1 finger was 1/12 of a degree. 30 fingers (but sometimes 24) made 1 cubit. It is thus quite difficult to decide which unit of measure was being used to construct the tables. Angular distances were usually given by naming the constellation and an angle such as: Taurus 23${}^{\circ }$ (= 30${}^{\circ }$ + 23${}^{\circ }$ = 53${}^{\circ }$ ) and Leo 14${}^{\circ }$ (= 120${}^{\circ }$ + 14${}^{\circ }$ = 134${}^{\circ }$ ). In adding and subtracting sexagesimals, we are working in base 60, so if we think of the numbers representing degrees, minutes, seconds, or hours, minutes and seconds they are the same units we use today.

   这些计算中常用的单位通常是“尼丹（nidan）”或“腕尺（cubit）”（约 50 厘米），但不同时期也会使用其他单位，因此各时期的单位缺乏一致性。$1^{\circ }$ 弧长约对应 4 分钟时间，1“指（finger）”等于 ${\frac{1}{12}}^{\circ }$。30 指（有时为 24 指）等于 1 腕尺。因此，很难确定这些表格编制时所使用的单位。角距离通常通过“星座名称 + 角度”的方式表示，例如“金牛座 23${}^{\circ }$”（即 $30^{\circ }+23^{\circ }=53^{\circ }$）、“狮子座 14${}^{\circ }$”（即 $120^{\circ }+14^{\circ }=134^{\circ }$）。六十进制的加减运算基于 60 进制，若将其中的数字理解为度、分、秒或时、分、秒，则与我们如今使用的单位一致。

4. The use of the capital S in Sine is to show that the radius of the circle used is not unity, or the same as sin $\theta$ in our system, but could be an arbitrary length R. This means that Sin $\theta$ is equal to R sin $\theta$.

   “Sine”一词首字母大写（Sin），是为了表明所用圆的半径并非单位半径（即与我们体系中的 $\sin \theta$ 不同），而是任意长度 $R$。这意味着 $\text{Sin}\theta =R\sin \theta$。

5. The exact dating of this ‘table of Sines’ is uncertain. These texts were regularly being revised and added to by different scholars. The similarity in the calculation to the Greek table of chords from Hipparchus (190-120 BCE) (we know his data came from the Babylonians) suggests that this Indian work appeared some time in the first century CE. Did the data in the Indian table come directly from the Babylonians, or via the Greeks? Nobody knows for sure. The important point is that the Indians made the technical and conceptual change from ‘Chord’ to ‘Sine’.

   这份“正弦表”的具体成书时间尚无定论。这些文献曾被不同学者反复修订和增补。其计算方式与希帕恰斯（公元前 190-120 年）的希腊弦表（已知希帕恰斯的数据源自巴比伦）相似，这表明这份印度文献可能成书于公元 1 世纪前后。印度正弦表中的数据是直接源自巴比伦，还是经由希腊传入？目前尚无定论。重要的是，印度人实现了从“弦（Chord）”到“正弦（Sine）”的技术与概念转变。

6. The Dunhuang star chart, now in the British Library, is recognised to have been made about 649-84 BCE by Li Chunfen (602-670) and was constructed with quite remarkable accuracy. The Dunhuang project is an international archaeology project and much more information about the project and its discoveries can be found at http://idp.bl.uk/ and the star chart http://apod.nasa.gov/apod/ap090619.html.

   现藏于大英图书馆的敦煌星图，公认由李淳风（602-670 年）绘制于约公元 649-684 年（原文“649-84 BCE”应为笔误，此处按史实修正），其绘制精度极高。敦煌项目（Dunhuang project）是一项国际考古项目，可在 http://idp.bl.uk/ 查阅该项目及相关发现的更多信息，敦煌星图的链接为 http://apod.nasa.gov/apod/ap090619.html。

---

History of trigonometry - part 2

三角学发展史（第二部分）

Article by Leo Rogers
利奥·罗杰斯

Published Tue, 01/02/2011 - 00:00

5. The Beginnings of Mathematical Astronomy

数学天文学的起源

As we have seen, the Babylonians were interested in predicting the time at which a particular celestial event would occur whereas Greek astronomy became much more interested in predicting where a celestial body would be at any particular time. This contrast is clearly illustrated by the development of a geometrical model of the motions of the heavens by the Greek mathematician Eudoxus.
正如前文所述，巴比伦人关注“预测特定天文事件发生的时间”，而希腊天文学则更关注“预测天体在任意时刻的位置”。希腊数学家欧多克索斯（Eudoxus）提出的“天体运动几何模型”，清晰地体现了这种差异。

Eudoxus (408-355 BCE)

欧多克索斯（公元前 408-355 年）

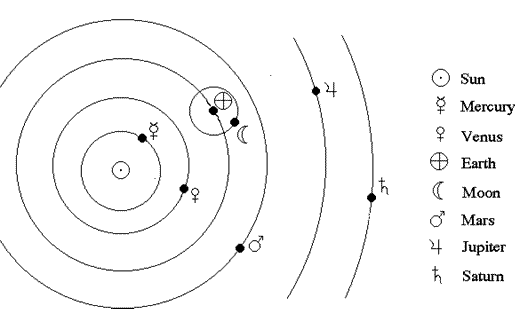
The original belief of an Earth-centred system in perfect circles came from the Pythagoreans (6th/5th centuries BCE) and was discussed and elaborated over the years. Eudoxus was taught by Archytas, one of the leading Pythagorean philosophers of his time, who maintained that the most perfect shape was a circle, so Eudoxus proposed a system of concentric spheres to describe the movement of the planets. This idea, where the planets moved about the Earth in circles on the surfaces of different spheres, remained the widely held theory of the universe until it was challenged by Nicolaus Copernicus in 1543. The simple idea is shown in the diagram below. However, there were enough data from the Babylonians and others to show that the system was much more complicated, and Eudoxus finally produced a system with 27 spheres altogether.
“以地球为中心、天体沿正圆轨道运行”的最初观点源自毕达哥拉斯学派（公元前 6-5 世纪），该观点多年来不断被讨论和完善。欧多克索斯的老师是当时毕达哥拉斯学派的核心哲学家阿尔库塔斯（Archytas），阿尔库塔斯认为“圆是最完美的形状”，因此欧多克索斯提出了“同心球体系”来描述行星运动。这一“行星在不同球面沿圆轨道绕地球运行”的观点，一直是被广泛认可的宇宙理论，直到 1543 年被尼古拉·哥白尼（Nicolaus Copernicus）质疑。下图展示了该理论的简化模型。然而，巴比伦人及其他文明积累的数据表明，宇宙体系远比这复杂，最终欧多克索斯提出了一个包含 27 个球的体系。

Using data derived from the Babylonian astronomers, Eudoxus was able to calculate that the variation in latitude of the Moon was about $+/-5^{\circ }$ (in our terms), and the angle between the equator and the ecliptic [See Note 1 below] was measured as $\frac{1}{15}$ of a circle or $24^{\circ }$ which is the angle subtended at the centre of a 15 sided polygon. This construction was included in Euclid’s Elements Book IV proposition 16, because it was so useful for astronomy.
利用源自巴比伦天文学家的数据，欧多克索斯计算出月球纬度的变化范围约为 $+/-5^{\circ }$（按现代单位），并测量出赤道与黄道之间的夹角（详见下文注释 1）为一个圆的 $\frac{1}{15}$（即 $24^{\circ }$）——这一角度恰好是正 15 边形中心角的大小。由于该几何构造对天文学极具价值，欧几里得将其收录于《几何原本》第四卷第 16 命题中。

Eudoxus also developed the theory of proportion, now contained in Book V of Euclid’s Elements, which became the major logical tool for empirical investigaton until the seventeenth century, and his method of exhaustion became the foundation of the technique developed by Archimedes (287-212 BCE) for finding areas of circles and other shapes.
欧多克索斯还提出了“比例理论”（现收录于《几何原本》第五卷），该理论在 17 世纪前一直是经验研究的核心逻辑工具。他提出的“穷竭法”，成为阿基米德（Archimedes，公元前 287-212 年）开发的“圆及其他图形面积计算方法”的基础。

The theory of the solar system that the Greeks developed was principally an “explanatory device” more descriptive than predictive, and as observations became more accurate, it needed constant revision and modification.
希腊人提出的太阳系理论，本质上是一种“解释工具”，其描述性强于预测性。随着观测精度的提高，该理论需要不断修订和完善。

Aristarchus (310-230 BCE)

阿利斯塔克（公元前 310-230 年）

Using Eudoxus’ theory of proportion, Aristarchus measured the relative sizes and distances to the Moon and Sun and found the Sun to be bigger than Earth! So, he reasoned that the Sun rather than Earth is the centre of the Universe and the Earth is one of the planets.
阿利斯塔克运用欧多克索斯的比例理论，测量了月球与太阳的相对大小及距离，发现太阳比地球大！因此，他推断“太阳而非地球是宇宙的中心，地球是一颗行星”。

In his book On the Sizes and Distances of the Sun and the Moon he assumed that the Earth is at the centre of a sphere on which the Moon moves, and at half Moon the edge of the shadow is in a direct line with the eye. At this time he claimed that its angular distance from the Sun is $87^{\circ }$ (actually it is about $89^{\circ }$). Using the time taken for a complete eclipse he estimated that the width of the Earth’s shadow is two Moon diameters (actually it is nearer three), and the Moon had an angular diameter of $2^{\circ }$ (this is about four times too large).
在其著作《论太阳与月球的大小和距离》（On the Sizes and Distances of the Sun and the Moon）中，他假设“地球位于月球运行的球面中心”，且在弦月时刻，阴影边缘与观测者视线在同一直线上。他认为此时月球与太阳的角距离为 $87^{\circ }$（实际约为 $89^{\circ }$）。通过全食持续时间，他估算出地球阴影的宽度为月球直径的 2 倍（实际接近 3 倍），并认为月球的角直径为 $2^{\circ }$（约为实际值的 4 倍）。

Using these hypotheses he obtained the ratio of the distance from the earth to the sun as:
基于这些假设，他得出地日距离与地月距离的比值为：
$$18\le \frac{d_1}{d_m}\le 20$$
（其中 $d_1$ 为地日距离，$d_m$ 为地月距离）

Today, this would simply involve finding $cos87^{\circ }(=sin{3}^{\circ })$ but the concepts of $cos$ and $sin$ were not thought of until much later.
如今，计算这一比值只需计算 $cos87^{\circ }(=sin{3}^{\circ })$，但“余弦（cos）”和“正弦（sin）”的概念在当时尚未出现，直到很久以后才被提出。

Applying his logical reasoning to the theory of proportion, he arrived at an estimate for the distance to the Sun of about 19 times the distance to the Moon. This estimate was generally accepted for the next 2,000 years.
通过将逻辑推理应用于比例理论，他估算出地日距离约为地月距离的 19 倍。这一估算结果在之后的 2000 年里被广泛认可。

Aristarchus’ observations showed that Eudoxus’ model was not able to account for some of the simplest motions of the planets, and so Greek mathematicians like Apollonius (262-190 BCE) managed to find more complicated geometrical constructions in order to keep the Earth at the centre of the universe.
阿利斯塔克的观测表明，欧多克索斯的模型无法解释部分行星的简单运动。因此，阿波罗尼奥斯（Apollonius，公元前 262-190 年）等希腊数学家不得不设计更复杂的几何结构，以维持“地球为宇宙中心”的观点。

Although it might seem like a missed opportunity to us for Greek scholars to abandon Aristarchus’ model of the solar system, even though he had shown that the Sun was larger than the Earth, there was no real evidence to show that the Sun was the centre of our system. The fact that the Sun might be larger than the Earth was no reason to suppose that the Sun was at the centre when the obvious apparent rotation of the Sun, Moon and Planets around the Earth was so strong.
尽管在我们看来，希腊学者放弃阿利斯塔克的太阳系模型（即便他已证明太阳比地球大）是“错失良机”，但当时并无确凿证据表明太阳是太阳系的中心。当“太阳、月球和行星绕地球旋转”的视运动现象如此明显时，“太阳比地球大”这一事实，并不能成为“太阳是中心”的充分理由。

Hipparchus (190-120 BCE)

希帕恰斯（公元前 190-120 年）

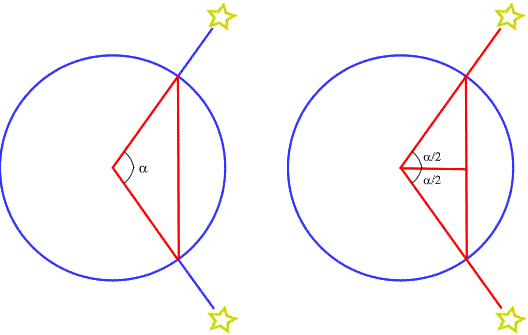
The first known table of chords was produced by the Greek mathematician Hipparchus in about 140 BC. Although nothing has survived, it is claimed that he wrote twelve books of tables of chords, but Neugebauer shows this to be impossible. Hipparchus developed great observational skills, improved the design of instruments and compiled a catalogue of about 850 stars. He also tried to improve the geometrical model of the universe. His most important discovery was the “Precession of the Equinoxes”. Since the Earth’s axis is tilted with respect to the stars it slowly describes a circle. This results in the intersection points of the celestial equator and the ecliptic (the equinoxes) changing slowly. Precession also explains why the “Polar Star” changes its position in the heavens over the centuries. [See details on precession here]
希腊数学家希帕恰斯约在公元前 140 年编制了已知最早的弦表。尽管该弦表已无存世版本，但有记载称他曾撰写 12 卷弦表著作，不过诺伊格鲍尔（Neugebauer）证明这一说法并不成立。希帕恰斯具备高超的观测技巧，改进了天文仪器设计，并编制了包含约 850 颗星体的星表。他还试图完善宇宙几何模型，其最重要的发现是“岁差（Precession of the Equinoxes）”。由于地轴相对于恒星存在倾斜，地轴会缓慢地绕一个圆周旋转，这导致天赤道与黄道的交点（分点）缓慢移动。岁差也解释了为何“北极星”的天际位置会随世纪变迁而改变。

Hipparchus is credited with constructing the first known table of chords. The importance of Hipparchus’ achievement in doing this was to change the mathematical tools involved from the arithmetical ‘procedures’ of the Babylonian scholars to a geometrical device’ , namely the use of arcs of a circle imagined to be on the surface of the ‘heavenly sphere’. Even so, he was still using the new technique to investigate the location of heavenly bodies, and the process was still clearly embedded in astronomy. Trigonometry, as a separately identifiable science in its own right, does not appear before the Arab scholars developed it much further in the eleventh and twelfth centuries CE.[See Note 2 below]
希帕恰斯被认为编制了已知最早的弦表。他这一成就的重要性在于，将数学工具从巴比伦学者的“算术步骤”转变为“几何工具”——即利用“天球表面上的圆弧”进行计算。尽管如此，他仍将这一新技术用于天体位置研究，其过程仍深深植根于天文学领域。三角学作为一门独立的、可明确界定的学科，直到公元 11-12 世纪阿拉伯学者对其进一步发展后才正式形成（详见下文注释 2）。

Menelaos (70-130 BCE)

梅涅劳斯（公元前 70-130 年）

In about 100 BCE Menelaos compiled a Book of Spherical Proportions Sphaerica, in which he set up the basis for treating spherical triangles by using arcs of great circles instead of arcs of parallel circles on the sphere. [To learn more about spherical triangles go here].
约公元前 100 年，梅涅劳斯编撰了《球面比例论》（Sphaerica）。在该书中，他以球面上的“大圆孤”而非“平行圆孤”为基础，建立了“球面三角形”的处理方法。

The plane triangle version of the theorem states:
该定理的平面三角形版本表述如下：
If a straight line crosses the three sides of a triangle (one of the sides has to be produced) then the product of three of the non-adjacent segments thus formed is equal to the product of the other three segments of the triangle.
若一条直线与三角形的三边（其中一边需延长）相交，则由此形成的三组不相邻线段的乘积相等。

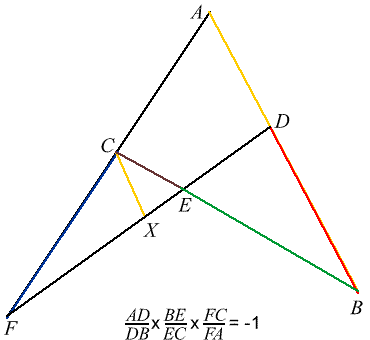
This proof uses similar triangles
该证明利用了相似三角形的性质：

$ABC$ is a triangle with a transversal $DE$ that cuts $AC$ produced in$F$
设 $ABC$ 为三角形，截线 $DE$ 与延长后的 $AC$ 交于点 $F$

First, insert a construction line $CX$ parallel to $AD$
首先，作辅助线 $CX$ 平行于 $AD$

($CX$ will be eliminated later). Now triangles $△ADF$ and $△CXF$ are similar, so $\frac{AD}{CX}=\frac{FA}{FC}\text{, and in the cyclic quadrilateral }BFCD,\frac{BE}{EC}=\frac{DB}{CX}$

（后续将消去 $CX$）。由于 $△ADF\sim △CXF$，因此 $\frac{AD}{CX}=\frac{FA}{FC}$；在圆内接四边形 $BFCD$ 中，$\frac{BE}{EC}=\frac{DB}{CX}$

$\text{Multiply }\frac{AD}{CX}=\frac{FA}{FC}\text{ by equal quantities,}$
将 $\frac{AD}{CX}=\frac{FA}{FC}$ 与等比相乘，

and 可得 $\frac{AD}{CX}\times \frac{BE}{EC}=\frac{FA}{FC}\times \frac{DB}{CX}$

$\text{Insert the ratio }\frac{CX}{CX}(=1)\text{ into the Left Hand Side product before cancellation, and}$
在消元前，向左端乘积中插入比值 $\frac{CX}{CX}(=1)$，可得

$\frac{AD}{DB}\times \frac{BE}{EC}\times \frac{FC}{FA}=1$

Note: The orientation of $FC$ is important.
注：$FC$ 的方向至关重要。

Menelaus produced a spherical triangle version of this theorem and a modification of it appears in Ptolemy’s Almagest. [This is explored in the NRICH problem Pythagoras on a Sphere]
梅涅劳斯还提出了该定理的球面三角形版本，其修正形式被收录于托勒密的《天文学大成》（Almagest）中。

Claudius Ptolemy (c85-c165 CE)

克劳狄乌斯·托勒密（约公元 85-165 年）

Ptolemy was the most influential Greek astronomer of this time. He supported the geocentric theory of the universe, and his book The Mathematical Compilation dominated astronomical thought until Copernicus (1473-1543) published his heliocentric theory in 1543.
直到 1543 年哥白尼（1473-1543）发表日心说理论，这一局面才被打破。

The aim of the Almagest was to provide numerical data for astronomical phenomena and observation and to explain the empirical foundations and theoretical reasons for the data.
《天文学大成》的目的是为天文现象与观测提供数值数据，并解释这些数据的经验基础与理论依据。

The Almagest contains a collection of all the then known astronomical knowledge: geometrical and numerical procedures, the longitude and latitude of heavenly bodies, information about parallax, the distance and relative sizes of the Sun and the Moon, lunar theory, solar motion, and the occurrence of eclipses, transits and occultations. This was the reason the Arab scholars called it “Al Megiste” (the great one) and the name has remained.
《天文学大成》汇集了当时所有已知的天文知识，包括几何与数值计算方法、天体的经纬度、视差信息、太阳与月球的距离及相对大小、月球理论、太阳运动，以及日食、凌日和掩星的发生规律。正因如此，阿拉伯学者将其称为“Al Megiste”（意为“伟大之作”），这一名称沿用至今。

Ptolemy was the author of a new table of chords, based on exactly the same principles inherited from the Babylonians, and using more sophisticated observational techniques, more accurate data, and the new mathematics of Euclid, Apollonius Archimedes and Menelaos.
托勒密编撰了新的弦表，其核心原理完全继承自巴比伦人，但融入了更精密的观测技术、更准确的数据，以及欧几里得、阿波罗尼奥斯、阿基米德和梅涅劳斯的新数学成果。

He divided the circle into 360 parts and used a diameter of 120 units, and calculated in the traditional sexagesimal numbers that astronomers had been using for two thousand years. Ptolemy calculated chords by constructing a series of regular polygons in a circle as shown by Euclid.
他将圆分为 360 等份，取直径为 120 单位，采用天文学家已使用两千年的传统六十进制进行计算。托勒密借鉴欧几里得的方法，通过在圆内构造一系列正多边形来计算弦长。

The Chords of regular polygons of 3, 4, 5, 6 and 10 sides respectively subtend angles of $120^{\circ },90^{\circ },72^{\circ },60^{\circ }$, and $10^{\circ }$ at the centre of a circle. By continued bisection and interpolaton he could find chords for many other angles which he expressed as ratios of chord to diameter finally arriving at chords of angles of ${\frac{1}{2}}^{\circ }$ where in our terms, chord KaTeX parse error: Undefined control sequence: \mbox at position 22: …f{\alpha = 120 \̲m̲b̲o̲x̲{ }Sin \alpha}
正 3 边形、4 边形、5 边形、6 边形和 10 边形的弦长，在圆心处对应的圆心角分别为 $120^{\circ }$、$90^{\circ }$、$72^{\circ }$、$60^{\circ }$ 和 $10^{\circ }$。通过不断二分弧长与插值计算，托勒密得以求出更多角度的弦长，并将其表示为“弦长与直径的比值”，最终计算出 ${\frac{1}{2}}^{\circ }$ 角度的弦长。用现代术语表述，其关系为 弦长 $\alpha =120\times \sin \alpha$。

In sexagesimal notation, the chords for the regular polygons are:
在六十进制表示法中，正多边形的弦长如下：

chord $36^{\circ }$ = 37; 4, 55,
$36^{\circ }$ 弦长 = 37；4，55（六十进制，即 37 + 4/60 + 55/3600）

chord $60^{\circ }$ = 1, 0; 0
$60^{\circ }$ 弦长 = 1，0；0（六十进制，即 60 + 0/60 + 0/3600）

chord $72^{\circ }$ = 1, 10; 32. 3
$72^{\circ }$ 弦长 = 1，10；32，3（六十进制，即 70 + 32/60 + 3/3600）

chord $90^{\circ }$ = 1, 24; 51, 10
$90^{\circ }$ 弦长 = 1，24；51，10（六十进制，即 84 + 51/60 + 10/3600）

from Pythagoras’ theorem:
根据勾股定理：
chord ${}^2\alpha$ + chord${}^2(180-\alpha )=120^2$
弦长 ${}^2\alpha$ + 弦长 ${}^2(180-\alpha )=120^2$

he obtained chord $120^{\circ }$ = 1, 43; 55, 23. and chord $144^{\circ }$ = 1, 54; 7, 37.
由此他算出 $120^{\circ }$ 弦长 = 1，43；55，23（六十进制），$144^{\circ }$ 弦长 = 1，54；7，37（六十进制）。

Converting Ptolemy’s chord calculations with base ten:
将托勒密的弦长计算结果转换为十进制：

for chord $60^{\circ }$ the sexagesimal 1, 0; 0. is 60 in base ten and 120 sin $30^{\circ }$ = 120 $\times \frac{1}{2}$ or 60 units, which is the radius of the circle.
对于 $60^{\circ }$ 弦长，六十进制的“1，0；0”对应十进制的 60，而 $120\times \sin 30^{\circ }=120\times \frac{1}{2}=60$（单位），这恰好等于圆的半径。

similarly, chord $90^{\circ }$ = 1, 24; 51, 10. or in base ten,
同理，$90^{\circ }$ 弦长的六十进制“1，24；51，10”转换为十进制为：

chord $90^{\circ }$ = 60 + 24 + $\frac{51}{60}+\frac{10}{3600}$ which is 84.8527 units
$90^{\circ }$ 弦长 = 60 + 24 + $\frac{51}{60}+\frac{10}{3600}\approx 84.8527$（单位）

and chord $90^{\circ }$ = 120 x sin $45^{\circ }$ or 120 x $\frac{\sqrt{2}}{2}\approx 84.8536$ units
而根据现代公式，$90^{\circ }$ 弦长 = $120\times \sin 45^{\circ }=120\times \frac{\sqrt{2}}{2}\approx 84.8536$（单位），二者高度吻合。

Using what is now called “Ptolemy’s theorem” (this property of cyclic quadrilaterals was known much earlier) he set up a system where one of the sides of the quadrilateral was a diameter, that enabled him to calculate sums and products of chords.
托勒密利用如今被称为“托勒密定理”的原理（圆内接四边形的这一性质在更早之前就已被发现），构建了一套计算体系——令四边形的一边为圆的直径，从而能够计算弦长的和与积。

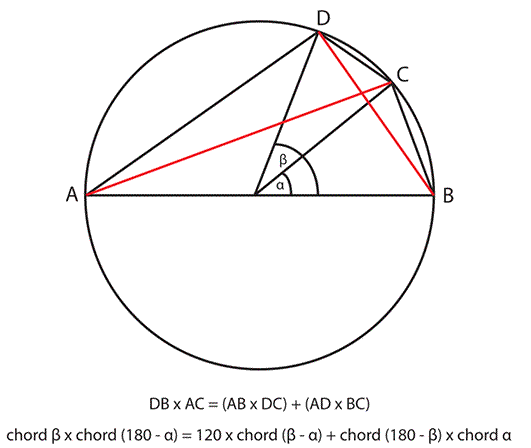
Converting the chords expression to modern notation, and putting $x=\frac{\beta }{2}$ and $y=\frac{\alpha }{2}$ this is equivalent to:
将弦长表达式转换为现代三角函数符号，令 $x=\frac{\beta }{2}$、$y=\frac{\alpha }{2}$，其关系等价于：
$$sin(x-y)=sinxcosy-cosxsiny$$

Similarly he obtained
同理，他推导出：
$$sin(x+y)=sinxcosy+cosxsiny$$

and also derived
还进一步推导出：
$$2si{n}^{2}x=1-cos2x$$

Using the table of chords with the geometry and formulae above, Ptolemy was able to solve all the triangles he needed to create his table of chords in steps of half degrees from ${\frac{1}{2}}^{\circ }$ to $180^{\circ }$ which is equivalent to a table of sines from ${\frac{1}{4}}^{\circ }$ to $90^{\circ }$.
借助上述几何方法、公式及已有的弦长数据，托勒密能够求解所有所需的三角形，并编制出从 ${\frac{1}{2}}^{\circ }$ 到 $180^{\circ }$、以 ${\frac{1}{2}}^{\circ }$ 为间隔的弦表——这相当于一份从 ${\frac{1}{4}}^{\circ }$ 到 $90^{\circ }$ 的正弦表。

6. Ptolemy’s use of Spherical Triangles

托勒密对球面三角形的应用

Menelaus’ Sphaerica was the major work that established the science of spherical geometry, and this was, in a sense, a non-Euclidean geometry where the sides of a triangle were formed by the intersections of three great circles on a sphere, and the angle sum of a triangle could be more than $180^{\circ }$. At the time, it was not seen as a radically new geometry, but more as an extension of Euclid, and most of the time the triangles used were constructed with only one right angle. At this time, spherical geometry was included in the quadrivum (arithmetic, geometry, music, astronomy), and taught as part of astronomy. The new relationships developed were possible by the use of proportional reasoning, a direct result of Eudoxus’ theory. Ptolemy was well aware of the new possibilities, because finding the distance between two stars was equivalent to measuring an arc of a circle, and he adapted the spherical geometry for use with tables of chords.
梅涅劳斯的《球面比例论》（Sphaerica）是建立球面几何学的核心著作。从某种意义上说，球面几何属于非欧几里得几何——其三角形的边由球面上三个大圆的交点构成，三角形的内角和可大于 $180^{\circ }$。但在当时，它并未被视为一种全新的几何学，更多被看作欧几里得几何的延伸，且当时所用的球面三角形大多为直角三角形（仅一个直角）。彼时，球面几何被纳入“四艺”（算术、几何、音乐、天文）体系，作为天文学的一部分进行教学。球面几何中新关系的建立，得益于比例推理的应用，而这正是欧多克索斯比例理论的直接成果。托勒密深知这一理论的应用潜力：由于两颗星体间的距离等价于球面上一段圆弧的长度，他将球面几何与弦表结合起来使用。

7. Passing on the Knowledge

知识的传承

By this time, mathematicians and astronomers had developed a complex mathematically based science, had a wide range of geometrical techniques whereby they measured the Earth, estimated the distances of the Moon and the Sun, developed a theory of the movement of the planets, and precisely catalogued hundreds of stars. A substantial body of geometrically based mathematics had been developed and scholars made commentaries on the works of Euclid, Apollonius, Archimedes, and others. In the next centuries, Diophantos wrote his Arithmetica, which was to inspire Fermat centuries later, Pappus recorded much of the earlier learning for later generations, and contacts along the trade routes began to be made with people in India and China. In September 622 Mohammed made his famous escape from persecution in Mecca to safety in Medina, and within two hundred years, the Arab culture had established an empire from India through the Middle East and North Africa and into Spain.
至此，数学家与天文学家已建立起一门以数学为基础的复杂学科，掌握了丰富的几何方法——可用于测量地球大小、估算地月与地日距离、构建行星运动理论，以及精确编制包含数百颗星体的星表。以几何为基础的数学体系已初具规模，学者们还为欧几里得、阿波罗尼奥斯、阿基米德等人的著作撰写评注。在随后的几个世纪里，丢番图（Diophantos）撰写了《算术》（Arithmetica），该书在数百年后启发了费马（Fermat）；帕普斯（Pappus）记录了大量早期知识，为后世留存宝贵资料；同时，通过贸易路线，（西方）开始与印度和中国建立联系。公元 622 年 9 月，穆罕默德从麦加逃离迫害、前往麦地那避难（史称“希吉拉”）；此后两百年间，阿拉伯文明建立起一个庞大帝国，疆域从印度延伸至中东、北非，直至西班牙。

Pedagogical notes to support this article can be found in the Teachers’ Notes accompanying this resource.
本文的教学辅助注释可参阅本资源附带的《教师注释》。

References

参考文献

Katz, V. (1998) A History of Mathematics. New York. Addison Wesley. Recommended as the best general history of mathematics currently available. There is good coverage of aspects of astronomy in antiquity, and the discussion on ‘functions’ (p. 156) is worth reading. Trigonometry is dealt with in sections on Ancient Civilisations, Mediaeval Europe, Renaissance Europe
卡茨，V.（1998）.《数学史》（A History of Mathematics）. 纽约：艾迪生·韦斯利出版社. 本书被推荐为目前最优秀的数学通史著作，对古代天文学相关内容有充分论述，其中关于“函数”的讨论（第 156 页）值得一读。三角学内容分布在“古代文明”“中世纪欧洲”“文艺复兴时期欧洲”等章节中。

Katz, V. (Ed.) (2007) The Mathematics of Egypt, Mesopotamia, China, India, and Islam. Princeton. Princeton University Press. This book contains a wealth of up-to-date information on mathematics and some aspects of astronomy in these ancient civilisations.
卡茨，V.（编）（2007）.《埃及、美索不达米亚、中国、印度与伊斯兰世界的数学》（The Mathematics of Egypt, Mesopotamia, China, India, and Islam）. 普林斯顿：普林斯顿大学出版社. 本书包含大量关于这些古代文明中数学及部分天文学内容的最新研究成果。

Linton, C. M. (2004) From Eudoxus to Einstein: A History of Mathematical Astronomy. Cambridge University Press The first chapter deals with ancient people and early Greek astronomy.
林顿，C. M.（2004）.《从欧多克索斯到爱因斯坦：数学天文学史》（From Eudoxus to Einstein: A History of Mathematical Astronomy）. 剑桥：剑桥大学出版社. 本书第一章探讨了古代人类与早期希腊天文学。

Needham, J. (1959) Science and Civilisation in China. Vol. 3. Mathematics and the Sciences of the Heavens and the Earth. Cambridge University Press.
李约瑟，J.（1959）.《中国科学技术史》（Science and Civilisation in China）. 第 3 卷《数学与天学》. 剑桥：剑桥大学出版社.

Neugebauer, O. (1983)(1955) Astronomical Cuneiform Texts. Vol. 1 The Moon. Heidelberg. Springer-Verlag These two books are the big classics on China and Mesopotamia, but much work has been done in these areas since the 1950s.
诺伊格鲍尔，O.（1983）（1955 年首版）.《天文楔形文字文本》（Astronomical Cuneiform Texts）. 第 1 卷《月球》. 海德堡：施普林格出版社. 上述两部著作（指李约瑟与诺伊格鲍尔的著作）是关于中国与美索不达米亚的经典文献，但自 20 世纪 50 年代以来，这些领域已涌现出大量新研究。

Neugebauer, O. (1969) (original 1952) The Exact Sciences in Antiquity. New York. Dover Books. Still available, this is a more popular book and contains much information on Egypt, Babylon and Greek Science.
诺伊格鲍尔，O.（1969）（1952 年首版）.《古代精密科学》（The Exact Sciences in Antiquity）. 纽约：多佛出版社. 本书仍在版，属于普及性著作，包含大量关于埃及、巴比伦与希腊科学的内容。

Plofker, K. (2009) Mathematics in India. Princeton. Princeton University Press. This is the most recent book on the history of Mathematics in India by a renowned expert.
普洛夫克，K.（2009）.《印度数学》（Mathematics in India）. 普林斯顿：普林斯顿大学出版社. 本书由知名专家撰写，是关于印度数学史的最新著作。

Web Links

This Wikipedia site on the Celestial Spheres provides much information on the change from the Ptolemaic to the Copernican system:
以下维基百科链接提供了关于“从托勒密体系到哥白尼体系”转变的详细信息：
https://en.wikipedia.org/wiki/Celestial_spheres

Menelaos’ Theorem: a neat proof step by step is here:
梅涅劳斯定理的详细分步证明可参见：
https://agutie.homestead.com/FiLes/menelaus1.htm

and a related property is Intersecting Chords Theorem:
相关性质“相交弦定理”可参见：
https://www.mathopenref.com/secantsintersecting.html

For animated models of planetary motion see Craig McConnell’s website: https://web.archive.org/web/20180811035103/faculty.fullerton.edu/cmcconnell/Planets.html
行星运动的动画模型可参见克雷格·麦康奈尔（Craig McConnell）的网站：https://web.archive.org/web/20180811035103/faculty.fullerton.edu/cmcconnell/Planets.html

Notes

注释

1. By the time of Eudoxus, (4th century BCE) enough data had been accumulated by the Babylonians and others over a long enough time to show the retrograde movement of the planets by studying their movement across the sky, and so to explain all this, Eudoxus’ system required 27 spheres. (1 outer one the fixed stars, 3 each for the Sun and the Moon, and 4 each for the 5 planets Mercury, Venus Mars Jupiter and Saturn.) Here is a splendid site: where you can download a simulation of the ‘Spheres of Eudoxus’ and accompanying information and worksheets together with other free java simulations of all the planetary systems from the Ancient Greeks to Newton.
   到欧多克索斯所处的公元前 4 世纪时，巴比伦人及其他文明已积累了足够长时间的数据，通过观测行星在天空中的运动，发现了行星的逆行现象。为解释这一切，欧多克索斯的同心球体系共需 27 个球：1 个外层球对应固定恒星，太阳与月球各需 3 个球，水星、金星、火星、木星、土星这 5 颗行星各需 4 个球。

2. Hipparchus did not ‘invent’ ‘trigonometry’. (See Part 1 Pedagogical Notes 1.) The claim is made by many writers that Hipparchus invented trigonometry, and the article on Hipparchus on the MacTutor website has various references about this ‘event’, for example: “He made an early contribution to trigonometry producing a table of chords” and "Even if he did not invent it, Hipparchus is the first person whose systematic use of trigonometry we have documentary evidence." And in the article on Trigonometric Functions, in referring to Hipparchus’ table of chords we have, “This makes Hipparchus the founder of trigonometry.” In this section, I explain why I think this is not so, and in Part 3 I will show how the work of the Arabs turned trigonometry into an independent area of mathematics, not only for application to Astronomy, but to many other sciences as well.
   希帕恰斯并未“发明”三角学（详见《三角学发展史（第一部分）》教学注释 1）。许多学者声称希帕恰斯是三角学的发明者，MacTutor 网站的希帕恰斯传记中也有相关表述，例如：“他编制弦表，为三角学做出了早期贡献”“即便未发明三角学，希帕恰斯仍是首位有文献证据表明系统使用三角学的人”；在“三角函数”相关文章中，提及希帕恰斯弦表时也提到“这使希帕恰斯成为三角学的奠基人”。本节中，笔者已解释为何不认同这一观点；在第三部分将进一步说明，阿拉伯学者的工作如何将三角学转变为一门独立的数学领域——不仅应用于天文学，还广泛应用于其他学科。

---

History of trigonometry - part 3

三角学发展史（第三部分）

Article by
Leo Rogers
Published Tue, 01/02/2011 - 00:00

8. The Arabs collect knowledge from the known world

阿拉伯人汇聚已知世界的知识

The Arab civilisation traditionally marks its beginning from the year 622 CE the date when Muhammad, threatened with assassination, fled from Mecca to Medina where Muhammad and his followers found safety and respect. Over a century later, the Arabs had established themselves as a powerful unified force across large parts of the Middle East and The Caliph Abu Ja’far Al-Mansour moved from Damascus to establish the city of Baghdad during the years 762 to 766. Al-Mansour sent his emissaries to search for and collect knowledge. From China, they learnt how to produce paper, and using this new skill they started a programme of translation of texts on mathematics, astronomy, science and philosophy into Arabic. This work was continued by his successors, Caliphs Mohammad Al-Mahdi and Haroun Al-Rasheed. The quest for knowledge became a lasting and significant part of Arab culture.
阿拉伯文明传统上以公元 622 年为开端。这一年，穆罕默德因遭遇暗杀威胁，从麦加逃往麦地那，并在那里与追随者获得安全与尊重。一个多世纪后，阿拉伯人已在中东大部分地区建立起强大的统一力量。公元 762 至 766 年间，哈里发阿布·贾法尔·曼苏尔（Abu Ja’far Al-Mansour）从大马士革迁都，建立了巴格达城。曼苏尔派遣使者四处探寻并收集知识：他们从中国学会了造纸术，借助这一新技术，启动了将数学、天文、科学与哲学文献译为阿拉伯语的项目。其继任者穆罕默德·马赫迪（Mohammad Al-Mahdi）与哈伦·拉希德（Haroun Al-Rasheed）两位哈里发继续推进这项工作。对知识的追求由此成为阿拉伯文化中持久且重要的组成部分。

Al-Mansour had founded a scientific academy that became called ‘The House of Wisdom’. This academy attracted scholars from many different countries and religions to Baghdad to work together and establish the traditions of Arabic science that were to continue well into the Middle Ages. Some of this work was later translated into Latin by Mediaeval scholars and passed on into Europe. The dominance of Baghdad and the influence of the Arab World was to last for the next 500 years.
曼苏尔创立了一所科学院，后被称为“智慧宫（The House of Wisdom）”。这所学院吸引了来自不同国家、不同宗教的学者汇聚巴格达，共同合作并确立了阿拉伯科学传统，该传统一直延续至中世纪。其中部分成果后来由中世纪学者译为拉丁语，传入欧洲。巴格达的主导地位与阿拉伯世界的影响力在此后 500 年间持续存在。

The scholars in the House of Wisdom came from many cultures and translated the works of Egyptian, Babylonian, Greek, Indian and Chinese astronomers and mathematicians. The Mathematical Treatise of Ptolemy was one of the first to be translated from the Greek into Arabic by Ishaq ben Hunayn (830-910). It was admired for its extensive content and became known in Arabic as Al-Megiste (the Great Book). The name ‘Almagest’ has continued to this day and it is recognized as both the great synthesis and the culmination of mathematical astronomy of the ancient Greek world. It was translated into Arabic at least five times and constituted the basis of the mathematical astronomy carried out in the Islamic world.
智慧宫的学者来自多元文化背景，他们翻译了埃及、巴比伦、希腊、印度和中国天文学家及数学家的著作。托勒密的《数学汇编》（即《天文学大成》）是最早被译为阿拉伯语的希腊文献之一，译者为伊沙克·本·胡奈因（Ishaq ben Hunayn，830-910）。该书因内容广博而备受推崇，阿拉伯语中称之为“Al-Megiste”（意为“伟大之书”），“Almagest”这一名称沿用至今。它被视为古希腊数学天文学的集大成之作与巅峰成就，至少被译为阿拉伯语五次，成为伊斯兰世界开展数学天文学研究的基础。

9. India: The Sine, Cosine and Versine

印度：正弦、余弦与正矢

Greek astronomy began to be known in India during the period 300-400 CE. However, Indian astronomers had long been using planetary data and calculation methods from the Babylonians, and even though it was well after Ptolemy had written the Almagest, 4th century Indian astronomers did not entirely take over Greek planetary theory. Ancient works like the Panca-siddhantica (now lost) that had been transmitted through the version by Vrahamihira [See Part 1 section 3] and Aryabhata’s Aryabhatiya (499 CE) demonstrated that Indian scholars had their own ways of dealing with astronomical problems and that they had great skill in calculation.[See Note 1 below]
公元 300-400 年间，希腊天文学开始传入印度。但印度天文学家早已在使用源自巴比伦的行星数据与计算方法；即便在托勒密撰写《天文学大成》之后，4 世纪的印度天文学家也未完全采纳希腊的行星理论。通过瓦拉哈米希拉（Vrahamihira）版本流传下来的《五大历算书》（Panca-siddhantica，现已失传，详见《三角学发展史（第一部分）》第 3 节），以及阿耶波多（Aryabhata）的《阿耶波多论》（Aryabhatiya，公元 499 年）等古籍表明，印度学者有自己解决天文问题的方法，且计算技艺精湛（详见下文注释 1）。

Even in the oldest Indian texts, the Chord [to remind yourself about Chords see the section on Claudius Ptolemy in the previous article] is not used, and instead there appear some very early versions of trigonometric tables using Sines. However, the Indian astronomers divided the $90^{\circ }$ arc into $24$ sections, thus obtaining values of Sines for every $3^{\circ }45^{\prime }$ of arc.
即便在最古老的印度文献中，也未使用“弦（Chord）”（关于弦的内容，可参阅《三角学发展史（第二部分）》中克劳狄乌斯·托勒密相关章节），而是出现了最早使用“正弦（Sine）”的三角表雏形。印度天文学家将 $90^{\circ }$ 弧段分为 24 等份，从而得到每 $3^{\circ }45^{\prime }$ 弧对应的正弦值。

In this diagram, $SB$ is the arc for the angle $\theta$ and $AS$ is the jiya. So the relation between the jiya and our sine is:
在该图中，$SB$ 为角度 $\theta$ 对应的弧段，$AS$ 被称为“jiya”（梵语中“弦”的意思，后演变为正弦）。因此，“jiya”与现代正弦函数的关系为：

$$jiya(\theta )=R\sin \theta$$

where $R$ is the radius of the circle.
其中 $R$ 为圆的半径。

Many Indian Sine tables use $R=3438$ which is the result if the circumference of the circle is $360\times 60$ or $21,600$ minutes. [See Note 2 below]
许多印度正弦表采用 $R=3438$ 这一数值，该值由“圆周长为 $360\times 60=21600$ 分”推导而来（详见下文注释 2）。

By the 5th century, two other functions had been defined and used. The length $EA$ was called the kotijya (our cosine), and AB was called the utkrama-jya (our versine). This was sometimes called the sama meaning an ‘arrow’, or sagitta in Latin
到 5 世纪时，印度学者又定义并使用了另外两种三角函数：长度 $EA$ 被称为“kotijya”（对应现代的“余弦”），长度 $AB$ 被称为“utkrama-jya”（对应现代的“正矢”）。正矢有时也被称为“sama”（意为“箭”），拉丁语中称为“sagitta”。

The versine function for a circle radius $R$ is: $\text{vers }\theta =R-\cos \theta$ [See Note 3 below]
对于半径为 $R$ 的圆，正矢函数的定义为：$\text{vers }\theta =R-\cos \theta$（详见下文注释 3）。

In Aryabhata’s work, he uses $R=3438$ and took this value to calculate his table of Sines. This became the standard for later works. Comparison with Varhamihira’s Sines (in sexagesimal numbers) and Hipparchs’ table (in lengths of chords) suggests a possible transmission of at least some of the Greek works to the Hindus. However, we have no way of knowing this for certain, and it is quite possible that the Hindus calculated their values independently.
阿耶波多在其著作中采用 $R=3438$ 计算正弦表，这一数值后来成为后续著作的标准。将瓦拉哈米希拉的正弦值（六十进制）与希帕恰斯的弦长表对比后发现，部分希腊著作可能传入了印度。但目前尚无确凿证据证明这一点，印度学者也有可能独立计算出这些数值。

The ‘Great Work’ (the Mahabhaskariya) of Bhaskara I was written in about 600 CE. He produced a remarkable method for approximating values for the Sines, by using the ratio of two quadratic functions. This was based entirely on comparing the results of his calculations with earlier values. [See Note 4 below ]
巴斯卡拉一世（Bhaskara I）的“伟大著作”《马哈巴斯卡拉论》（Mahabhaskariya）约成书于公元 600 年。他提出了一种精妙的正弦值近似计算方法——利用两个二次函数的比值进行求解，该方法完全基于其计算结果与早期数值的对比（详见下文注释 4）。

However, since these tables only gave values for every $3^{\circ }45^{\prime }$, there was considerable room for improvement. It is curious that since Ptolemy’s table of chords enabled him to find values equivalent to Sines from ${\frac{1}{4}}^{\circ }$ to $90^{\circ }$ that the Indian scholars did not go further at this stage. Later, Brahmagupta (598-670) produced an ingenious method based on second order differences to obtain the Sine of any angle from an initial set of only six values from $0^{\circ }$ in $15^{\circ }$ intervals to $90^{\circ }$.
但由于这些正弦表仅给出每 $3^{\circ }45^{\prime }$ 的数值，仍有很大改进空间。耐人寻味的是，既然托勒密的弦表已能求出从 ${\frac{1}{4}}^{\circ }$ 到 $90^{\circ }$ 的正弦等效值，印度学者在这一阶段却未进一步细化。后来，婆罗摩笈多（Brahmagupta，598-670）提出了一种巧妙的方法：基于二阶差分，仅通过 $0^{\circ }$ 到 $90^{\circ }$ 间每 $15^{\circ }$ 一个的 6 个初始值，即可求出任意角度的正弦值。

10. Trigonometry in the Arab Civilisation

阿拉伯文明中的三角学

The introduction and development of trigonometry into an independent science in the Arab civilisation took, in all, some 400 years. In the early 770s Indian astronomical works reached the Caliph Al-Mansur in Baghdad, and were translated as the Zij al-Sindhind, and this introduced Indian calculation methods into Islam.
在阿拉伯文明中，三角学从传入到发展为独立学科，共耗时约 400 年。公元 770 年代初，印度天文著作传入巴格达，被译为《信德欣德天文表》（Zij al-Sindhind），印度的计算方法由此进入伊斯兰世界。

Famous for his algebra book, Abu Ja’far Muhammad ibn Musa al-Khwarizmi (see History of Trigonometry Part 1.) had also written a book on Indian methods of calculation (al-hisab al-hindi) and he produced an improved version of the Zij al-Sindhind. Al-Khwarizmi’s version of Zij used Sines and Versines, and developed procedures for tangents and cotangents to solve astronomical problems. Al-Khwarizmi’s Zij was copied many times and versions of it were used for a long time.
以代数学著作闻名的阿布·贾法尔·穆罕默德·伊本·穆萨·花拉子米（Abu Ja’far Muhammad ibn Musa al-Khwarizmi），还撰写了一本关于印度计算方法的著作《印度算术》（al-hisab al-hindi），并修订完善了《信德欣德天文表》。花拉子米版的天文表使用正弦与正矢，并提出了利用正切和余切解决天文问题的方法。该版本被多次抄写，长期沿用。

Many works in Greek, Sanskrit, and Syriac were brought by scholars to Al-Mansur’s House of Wisdom and translated. Among these were the works of Euclid, Archimedes Apollonius and of course, Ptolemy. The Arabs now had two competing versions of astronomy, and soon the Almagest prevailed.
学者们将大量希腊语、梵语和叙利亚语著作带入曼苏尔的智慧宫并进行翻译，其中包括欧几里得、阿基米德、阿波罗尼奥斯以及托勒密的著作。此时阿拉伯世界有两种相互竞争的天文学体系，不久后《天文学大成》的体系占据了主导地位。

The Indian use of the sine and its related functions were much easier to apply in calculations, and the sexagesimal system from the Babylonians continued to be used, so apart from these two changes, the early Arabic versions of the Almagest remained faithful to Ptolemy. [See Note 5 below]
印度的正弦及相关函数在计算中更易应用，而源自巴比伦的六十进制也继续被使用。因此，除这两点改进外，早期阿拉伯语版的《天文学大成》基本忠实于托勒密的原著（详见下文注释 5）。

Abu al-Wafa al-Buzjani (Abul Wafa 940-998) made important contributions to both geometry and arithmetic and was the first to study trigonometric identities systematically. The study of identities was important because by establishing relationships between sums and differences, and fractions and multiples of angles, more efficient astronomical calculations could be conducted and more accurate tables could be established.
阿布·瓦法·布扎尼（Abu al-Wafa al-Buzjani，940-998）在几何学与算术学领域均有重要贡献，且是首位系统研究三角恒等式的学者。三角恒等式的研究至关重要：通过建立角度的和差、分数倍与整数倍之间的关系，可实现更高效的天文计算，并编制更精确的数表。

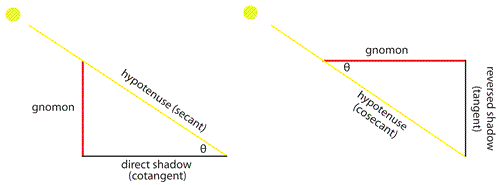
The sine, versine and cosine had been developed in the context of astronomical problems, whereas the tangent and cotangent were developed from the study of shadows of the gnomon. In his Almagest, Abul Wafa brought them together and established the relations between the six fundamental trigonometric functions for the first time. He also used $R=1$ for the radius of the basic circle.
正弦、正矢和余弦是在解决天文问题的背景下发展而来的，而正切和余切则源自对指时针（gnomon）影子的研究。阿布·瓦法在其《天文学大成》评注中，首次将这六种三角函数整合，并建立了它们之间的关系。他还将基础圆的半径设为 $R=1$。

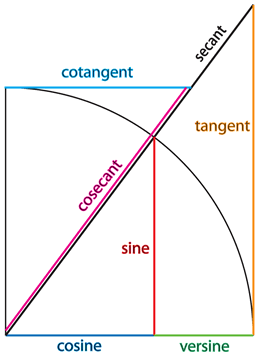
From these relations Abul Wafa was able to demonstrate a number of new identities using these new functions:
基于这些关系，阿布·瓦法推导出多个新的三角恒等式：

$$se{c}^2\theta =1+ta{n}^2\theta cose{c}^2\theta =1+co{t}^2\theta$$

Abul Wafa also devised methods for calculating trigonometric tables by an improved differencing technique to obtain values that were accurate to $5$ sexagesimal ($8$ decimal) places.
阿布·瓦法还通过改进的差分技术编制三角表，使数值精度达到 5 位六十进制（即 8 位十进制）。

Greek astronomers had long since introduced a model of the universe with the stars on the inside of a vast sphere. They had also worked with spherical triangles, but Abul Wafa was the first Arab astronomer to develop ways of measuring the distance between stars using his new system of trigonometric functions including the versine.
希腊天文学家早已提出“恒星位于巨大球面内侧”的宇宙模型，也研究过球面三角形。但阿布·瓦法是首位阿拉伯天文学家，他利用包含正矢在内的新三角函数体系，提出了测量恒星间距离的方法。

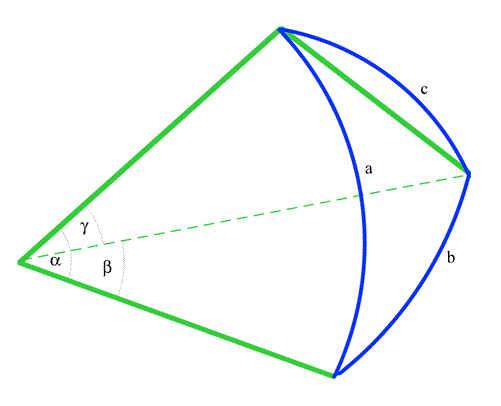
In the diagram above, the blue triangle with sides $a$, $b$, and $c$ represents the distances between stars on the inside of a sphere. The apex where the three angles $\alpha$, $\beta$, and $\gamma$ are marked, is the position of the observer. The blue curves are Great Circles on the sphere, and by measuring the angles, finding more accurate values for their functions, and assuming a value for $R$ the radius of the sphere, it became possible to find the great-circle distances between the stars.
在上图中，边长为 $a$、$b$、$c$ 的蓝色三角形代表球内恒星间的距离。标注有三个角 $\alpha$、$\beta$、$\gamma$ 的顶点为观测者位置，蓝色曲线为球面上的大圆。通过测量角度、获取更精确的三角函数值，并设定球的半径 $R$，即可求出恒星间的大圆弧距离。

By an ingenious application of Menelaos’ Theorem [See History of Trigonometry Part 2] using special cases of great circles with two right angles, Abul Wafa showed how the theorem could be applied in spherical triangles. This was a considerable advance in Spherical Trigonometry that enabled the calculation of the correct direction for prayer (the quibla) and was to have important applications in Navigation and Cartography.
阿布·瓦法巧妙地应用梅涅劳斯定理（详见《三角学发展史（第二部分）》），结合“含两个直角的大圆”这一特殊情况，证明了该定理在球面三角形中的适用性。这是球面三角学的重大突破，不仅能用于计算正确的礼拜方向（朝向麦加的方向，quibla），还在航海与制图领域有重要应用。

The Abul Wafa crater of the Moon is named in recognition of his work in astronomy.
月球上的“阿布·瓦法环形山”便是为纪念他在天文学领域的贡献而命名的。

Abu al-Rayhan Muhammad ibn Ahmad Al-Biruni (973-1050) was an outstanding scholar reputed to have written over 100 treatises on astronomy, science, mathematics, geography, history, geodesy and philosophy. Only about twenty of these works now survive, and only about a dozen of these have been published. Al-Biruni’s treatise entitled Maqalid 'ilm al-hay’a (Keys to the Science of Astronomy) ran to over one thousand pages and contained extensive developments in on trigonometry. Among many theorems, he produced a demonstration of the tangent formula, shown below.
阿布·拉伊汗·穆罕默德·伊本·艾哈迈德·比鲁尼（Abu al-Rayhan Muhammad ibn Ahmad Al-Biruni，973-1050）是一位杰出学者，据称撰写了超过 100 篇关于天文、科学、数学、地理、历史、大地测量学与哲学的论文。目前仅存约 20 篇，已出版的仅 12 篇左右。他的著作《天文学的钥匙》（Maqalid 'ilm al-hay’a) 长达 1000 多页，包含大量三角学方面的拓展内容。在众多定理中，他证明了正切公式，如下所示。

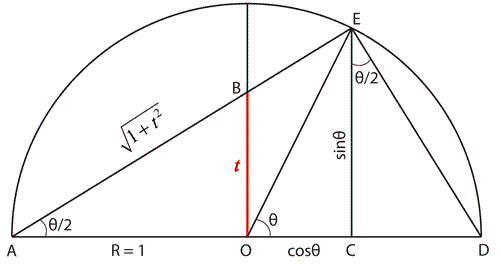
From the diagram, $O$ is the centre of the semicircle, and $AED$ a right-angled triangle with a perpendicular from $E$ to $C$.
如图所示，$O$ 为半圆的圆心，$AED$ 为直角三角形，且 $E$ 到 $C$ 有一条垂线。

Consequently, triangles $AEC$ and $EDC$ are similar.
由此可知，$△AEC\sim △EDC$（相似）。

Angle $EOD$ is twice angle $EAD$, and angles $EAC$ and $DEC$ are equal.
$\angle EOD=2\angle EAD$，且 $\angle EAC=\angle DEC$。

If the radius of the circle $R=1$, then $EC=\sin \theta$ and $OC=\cos \theta$
若圆的半径 $R=1$，则 $EC=\sin \theta$，$OC=\cos \theta$。

$\text{So }\tan \left(\frac{\theta }{2}\right)=\frac{EC}{AC}=\frac{\sin \theta }{1+\cos \theta }\tan \left(\frac{\theta }{2}\right)=\frac{DC}{EC}=\frac{1-\cos \theta }{\sin \theta }$

From which he derived the half angle and multiple angle formulae. [See Note 6 below]
基于此，他推导出了半角公式与倍角公式（详见下文注释 6）。

While many new aspects of trigonometry were being discovered, the chord, sine, versine and cosine were developed in the investigation of astronomical problems, and conceived of as properties of angles at the centre of the heavenly sphere. In contrast, tangent and cotangent properties were derived from the measurement of shadows of a gnomon and the problems of telling the time.
尽管三角学的诸多新领域不断被探索，但弦、正弦、正矢和余弦始终与天文问题研究相关，被视为天球球心角的属性；与之相反，正切和余切的性质则源自对指时针影子的测量与计时问题的研究。

In his Demarcation of the Coordinates of Cities he used spherical triangles for finding the coordinates of cities and other places to establish local meridian (the quibla) and thereby finding the correct direction of Mecca, and in his Exhaustive Treatise on Shadows he showed how to use gnomons for finding the time of day.
在《城市坐标划定》一书中，比鲁尼利用球面三角形求解城市及其他地点的坐标，确定当地子午线（即礼拜方向），进而找到朝向麦加的正确方向；在《影子详尽论述》中，他展示了如何使用指时针判断一天中的时间。

Abu Muhammad Jabir ibn Aflah (Jabir ibn Aflah c1100 - c1160) probably worked in Seville during the first part of the 12th century. His work is seen as significant in passing on knowledge to Europe. Jabir ibn Aflah was considered a vigorous critic of Ptolemy’s astronomy. His treatise helped to spread trigonometry in Europe in the 13th century, and his theorems were used by the astronomers who compiled the influential Libro del Cuadrante Sennero (Book of the Sine Quadrant) under the patronage of King Alfonso X the Wise of Castille (1221-1284).
阿布·穆罕默德·贾比尔·伊本·阿夫拉（Abu Muhammad Jabir ibn Aflah，约 1100-1160）可能在 12 世纪上半叶于塞维利亚开展研究。他的工作对知识传入欧洲起到了重要作用，且他被认为是托勒密天文学的激烈批判者。其著作在 13 世纪推动了三角学在欧洲的传播，卡斯蒂利亚国王阿方索十世（Alfonso X the Wise，1221-1284）资助编撰的颇具影响力的《正弦象限全书》（Libro del Cuadrante Sennero）便采用了他的定理。

A result of this project was the creation of much more accurate astronomical tables for calculating the position of the Sun, Moon and Planets, relative to the fixed stars, called the Alfonsine Tables made in Toledo somewhere between 1252 and 1270. These were the tables Columbus used to sail to the New World, and they remained the most accurate tables until the 16th century.
该项目的成果之一是编制了更精确的天文表——《阿方索星表》（Alfonsine Tables）。该星表于 1252-1270 年间在托莱多编制而成，可用于计算太阳、月球及行星相对于固定恒星的位置。哥伦布正是使用这份星表航行至新大陆，且它在 16 世纪前一直是最精确的天文表。

By the end of the 10th century trigonometry occupied an important place in astronomy texts with chapters on sines and chords, shadows (tangents and cotangents) and the formulae for spherical calculations. There was also considerable interest in the resolution of plane triangles. But a completely new type of work by Nasir al-Din al-Tusi (Al-Tusi 1201-1274) entitled Kashf al-qina 'an asrar shakl al-qatta (Treatise on the Secrets of the Sector Figure), was the first treatment of trigonometry in its own right, as a complete subject apart from Astronomy. The work contained a systematic discussion on the application of proportional reasoning to solving plane and spherical triangles, and a thorough treatment of the formulae for solving triangles and trigonometric identities. Al-Tusi originally wrote in Persian, but later wrote an Arabic version. The only surviving Persian version of his work is in the Bodleian Library in Oxford.
到 10 世纪末，三角学在天文文献中已占据重要地位，相关章节涵盖正弦与弦、影子（正切与余切）及球面计算公式，平面三角形求解也备受关注。但纳西尔丁·图西（Nasir al-Din al-Tusi，1201-1274）的著作《扇形图形奥秘揭秘》（Kashf al-qina 'an asrar shakl al-qatta）开创了全新范式——它首次将三角学作为独立于天文学的完整学科进行论述。该书系统探讨了比例推理在平面与球面三角形求解中的应用，全面阐述了三角形求解公式与三角恒等式。图西最初以波斯语撰写，后又推出阿拉伯语版本，目前仅存的波斯语版本藏于牛津大学博德利图书馆。

This was a collection and major improvement on earlier knowledge. Books I, II and IV contain parts of the Elements, the Almagest and a number of other Greek sources. Book III deals with the basic geometry for spherical triangles and the resolution of plane triangles using the sine theorem:
该书是对早期知识的整合与重大改进：第一、二、四卷包含《几何原本》《天文学大成》及其他希腊文献的部分内容；第三卷探讨球面三角形的基础几何，以及利用正弦定理求解平面三角形：

$$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}$$

Book V contains the principal chapters on trigonometry dealing with right-angled triangles and the six fundamental relations equivalent to those we use today; sine, cosine, tangent, cotangent, secant and cosecant. He provided many new proofs and showed how they could be used to solve many problems more easily.
第五卷是三角学的核心章节，涉及直角三角形及六种基本三角函数关系（与现代所用一致：正弦、余弦、正切、余切、正割、余割）。图西提供了许多新的证明方法，并展示了如何利用这些方法更简便地解决问题。

Al-Tusi invented a new geometrical technique now called the ‘Al-Tusi couple’ that generated linear motion from the sum of two circular motions. He used this technique to replace the equant used by Ptolemy, and this device was later used by Copernicus in his heliocentric model of the universe.
图西发明了一种新的几何方法，现称为“图西偶合（Al-Tusi couple）”——通过两个圆周运动的叠加产生直线运动。他用这一方法替代了托勒密体系中的“偏心匀速点（equant)”，而哥白尼在其日心说模型中也采用了这一装置。

Al-Tusi was one of the greatest scientists of Mediaeval Islam and responsible for some 150 works ranging from astronomy, mathematics and science to philosophy and poetry.
图西是中世纪伊斯兰世界最伟大的科学家之一，撰写了约 150 篇著作，涵盖天文、数学、科学、哲学与诗歌等多个领域。

11. Arab Science and Technology Reaches Europe

阿拉伯科技传入欧洲

The Arab astronomers had learnt much from India, and there was contact with the Chinese along the Silk Road and through the sea routes, so that Arab trading posts were established in India and in China. Through these contacts Indian Buddhism spread into China and was well established by the 3rd century BCE, probably later carrying with it some of the calculation techniques of Indian astronomy. However few, if any, technological innovations seemed to have passed from China to India or Arabia.
阿拉伯天文学家从印度学到了许多知识，且通过丝绸之路与海上航线与中国保持联系，在印度和中国建立了贸易据点。通过这些交流，印度佛教在公元前 3 世纪传入中国并站稳脚跟，或许也带入了部分印度天文计算技术。但几乎没有中国的技术革新传入印度或阿拉伯世界（若有，也极为罕见）。

By 790 CE, the Arab empire had reached its furthest expansion in Europe, conquering most of the Iberian peninsula, an area called Al-Andalus by the Arabs. [See Note 7 below]
到公元 790 年，阿拉伯帝国在欧洲的扩张达到顶峰，征服了伊比利亚半岛的大部分地区，阿拉伯人将该地区称为“安达卢斯（Al-Andalus）”（详见下文注释 7）。

At this time many religions and races coexisted in Iberia, each contributing to the culture. The Muslim religion was generally very tolerant towards others, and literacy in Islamic Iberia was more widespread than any other country in Western Europe. By the 10th century Cordoba was said to have equally good libraries and educational establishments as Baghdad, and the cities of Cordoba and Toledo became centres of a flourishing translation business.
当时伊比利亚半岛上多种宗教与种族共存，共同推动文化发展。伊斯兰教对其他信仰通常较为包容，伊斯兰统治下的伊比利亚半岛识字率高于西欧任何国家。到 10 世纪，科尔多瓦的图书馆与教育机构据称已与巴格达相当，科尔多瓦和托莱多成为繁荣的翻译中心。

Between 1095 and 1291 a series of religiously inspired military Crusades were waged by the Christians of Europe against the Arab Empire. The principal reason was the restoration of Christian control over the Holy Land, but there were also many other political and economic reasons. [See Note 8 below]
1095-1291 年间，欧洲基督徒在宗教信仰的驱动下，对阿拉伯帝国发动了一系列军事远征（即“十字军东征”）。其主要目的是夺回圣地的基督教统治权，但也存在诸多政治与经济因素（详见下文注释 8）。

In all this turmoil and conflict there were periods of calm and centres of stability, where scholars of all cultures were able to meet and knowledge was developed, translated and transmitted into Western Europe. The three principal routes through which Greek and Arab science became known were Constantinople (now Istanbul) Sicily and Spain. Greek texts became known to European monks and scholars who travelled with the armies through Constantinople on their way South to the Holy Land. These people learnt Greek and were able to translate the classical works into Latin. From Sicily, Arabs traded with Italy, and translation took place there, but probably the major route by which Arabic science reached Europe was from the translation houses of Toledo and Cordoba, across the Pyrenees into south-western France.
在这场动荡与冲突中，也存在短暂的和平时期与稳定区域，不同文化背景的学者得以在此交流，知识得以发展、翻译并传入西欧。希腊与阿拉伯科学传入欧洲的三条主要路径为：君士坦丁堡（现伊斯坦布尔）、西西里岛与西班牙。跟随军队南下前往圣地的欧洲僧侣与学者，途经君士坦丁堡时接触到希腊文献，他们学习希腊语后将经典著作译为拉丁语；在西西里岛，阿拉伯人与意大利开展贸易，翻译工作也在此进行。但阿拉伯科学传入欧洲的主要路径，或许是从托莱多和科尔多瓦的翻译机构出发，跨越比利牛斯山脉进入法国西南部。

During the twelfth and thirteenth century hundreds of works from Arabic, Greek and Hebrew sources were translated into Latin and the new knowledge was gradually disseminated across Christian Europe.
12-13 世纪期间，数百部阿拉伯语、希腊语和希伯来语著作被译为拉丁语，这些新知识逐渐在基督教欧洲传播开来。

Geometrical knowledge in early Mediaeval Europe was a very practical subject. It dealt with areas, heights, volumes and calculations with fractions for measuring fields and the building of large manors, churches, castles and cathedrals.
中世纪早期欧洲的几何知识以实用为导向，主要涉及面积、高度、体积的计算及分数运算，用于土地测量与大型宅邸、教堂、城堡和大教堂的建造。

Hugh of St. Victor (1078-1141) in his Practica Geometriae divides the material into Theorica (what is known and practised by a teacher) and Practica (what is done by a builder or mason). Theoretical geometry in the Euclidean sense was virtually unknown until the first translations of Euclid appeared in the West.
圣维克多的休（Hugh of St. Victor，1078-1141）在其著作《实用几何》（Practica Geometriae）中，将几何内容分为“理论部分（Theorica）”（教师掌握与传授的知识）与“实践部分（Practica）”（工匠或石匠的应用技术）。在欧几里得著作首次被译为西方语言之前，欧洲人几乎不了解欧氏几何体系下的理论几何。

The astrolabe was commonly used to measure heights by using its ‘medicline’ (a sighting instrument fixed at the centre of the circle) and the shadow square engraved in the centre of the instrument, and then comparing the similar triangles. The horizontal distance from the centre of the astrolabe to the edge of the square was marked with twelve equal divisions.
星盘（astrolabe）是当时常用的测高工具：通过其“准星（medicline，固定在圆盘中心的瞄准装置）”与盘面中心的“影子方格”，结合相似三角形原理进行测量。从星盘中心到方格边缘的水平距离被划分为 12 等份。

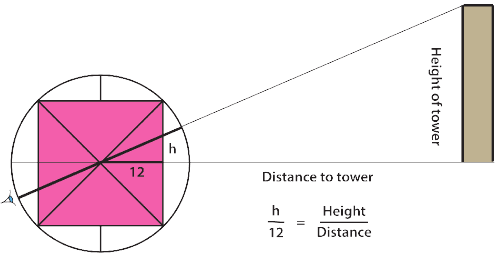
This system was in use well into the 16th century as seen in the illustration below:
如下所示，该方法一直沿用至 16 世纪：

This is from Thomas Digges’ Pantometria of 1571. The same system is still used, but the square in the quadrant is marked with six divisions.
该图源自托马斯·迪格斯（Thomas Digges）1571 年的著作《全测法》（Pantometria）。图中所用方法与此前一致，但象限内的方格被划分为 6 等份。

A popular twelfth century text, the Artis Cuiuslibet Consummatio shows the gradual insertion of more technical knowledge, where the measuring of heights (altimetry) was much more related to astronomy, showing how to construct gnomons and shadow squares. Gradually the translations made on the continent of Europe came to England.
12 世纪广为流传的《各类技艺大全》（Artis Cuiuslibet Consummatio）一书，体现了技术知识的逐步融入：书中的高度测量（测高法）与天文学联系更为紧密，还介绍了指时针与影子方格的制作方法。此后，欧洲大陆的翻译著作逐渐传入英国。

Richard of Wallingford (1292-1336)

理查德·沃林福德（1292-1336）

Richard’s early work was a series of instructions (canons) for the use of astronomical tables that had been drawn up by John Maudith, the Merton College Astronomer. Later he wrote an important work, the Quadripartitum, on the fundamentals of trigonometry needed for the solution of problems of spherical astronomy. The first part of this work is a theory of trigonometrical identities, and was regarded as a basis for the calculation of sines, cosines, chords and versed sines. The next two parts of the Quadripartitum dealt with a systematic and rigorous exposition of Menelaos’ theorem. The work ends with an application of these principles to astronomy. The main sources of the work appear to be Ptolemy’s Almagest, and Thabit ibn Qurra (826-901 CE).
理查德早期的工作是为默顿学院天文学家约翰·莫迪思（John Maudith）编制的天文表撰写使用说明（准则）。后来，他撰写了重要著作《四卷论》（Quadripartitum），阐述球面天文学问题求解所需的三角学基础。该书第一部分探讨三角恒等式理论，被视为正弦、余弦、弦与正矢计算的基础；第二、三部分系统且严谨地阐述了梅涅劳斯定理；最后一部分则将这些原理应用于天文学。其主要参考资料包括托勒密的《天文学大成》与萨比特·伊本·库拉（Thabit ibn Qurra，826-901) 的著作。

The Quadripartitum was probably the first comprehensive mediaeval treatise on trigonometry to have been written in Europe, at least outside Spain and Islam. When Richard was abbot of St. Albans, he revised the work, taking into account the Flores of Jabir ibn Afla.
《四卷论》或许是欧洲（至少是西班牙与伊斯兰世界之外的欧洲）首部完整的中世纪三角学专著。理查德担任圣奥尔本斯修道院院长期间，结合贾比尔·伊本·阿夫拉的《精华》（Flores）对该书进行了修订。

In 1326 to 1327 Richard also designed a calculation device, called an equatorium, a complex geared astrolabe with four faces. He described how this could be used to calculate lunar, solar and planetary longitudes and thereby predict eclipses in his Tractatus Albionis. It is possible that this led to his design for an astronomical clock described in his Tractatus Horologii Asronomici, (Treatise on the Astronomical Clock) of 1327, which was the most complex clock mechanism known at the time. The mechanism comprised a rotating star map that modeled the lunar eclipse and planets by gearing, presented as a geocentric model. It appeared at a transitional period in clock design, just before the advent of the escapement. This makes it one of the first true clocks, and certainly one of first self powered models of the heavens. Unfortunately it was destroyed during Henry VIII’s reformation at the dissolution of St Albans Monastery in 1539.
1326-1327 年间，理查德还设计了一种名为“等分仪（equatorium）”的计算装置——这是一种四面装有齿轮的复杂星盘。他在《阿尔比恩论》（Tractatus Albionis）中描述了如何使用该装置计算月球、太阳与行星的经度，进而预测日食和月食。这一设计可能启发他在 1327 年的《天文钟论》（Tractatus Horologii Astronomici）中提出天文钟设计方案，该钟是当时已知最复杂的时钟装置。其机械结构包含一个旋转星图，通过齿轮模拟月食与行星运动（基于地心说模型），诞生于时钟设计的过渡时期（擒纵机构出现之前）。因此，它被视为最早的真正意义上的时钟之一，也是最早的自动天体模型之一。遗憾的是，1539 年亨利八世宗教改革期间，圣奥尔本斯修道院被解散，该天文钟也随之被毁。

Georg von Peuerbach (1423-1461)

格奥尔格·冯·皮尔巴赫（1423-1461）

Peuerbach’s work helped to pave the way for the Copernican conception of the world system; he created a new theory of the planets, made better calculations for eclipses and movements of the planets and introduced the use of the sine into his trigonometry.
皮尔巴赫的工作为哥白尼宇宙体系的提出奠定了基础：他创立了新的行星理论，改进了日食与行星运动的计算方法，并将正弦函数引入自身的三角学研究。

His early work, Tabulae Eclipsium circulated in manuscript was not published until 1514, contained tables of his eclipse calculations that were based on the Alfonsine Tables. He calculated sines for every minute of arc for a radius of 600,000 units and he introduced the Hindu-Arabic numerals in his tables. [See Note 9 below]

他的早期著作《日食表》（Tabulae Eclipsium）最初以手稿形式流传，直至 1514 年才出版。该书基于《阿方索星表》编制日食计算表，以 600000 为半径，计算出每分弧对应的正弦值，并在表中引入了印度-阿拉伯数字（详见下文注释 9)。

Peuerbach’s Theoricae Novae Planetarum, (New Theories of the Planets) was composed about 1454 was published in 1473 by Regiomontanus’ printing press in Nuremburg. While the book was involved in attempting a technical resolution of the theories of Eudoxus and Ptolemy, Peuerbach claimed that the movement of the planets was determined by the Sun, and this has been seen as a step towards the Copernican theory. This book was read by Copernicus, Galileo and Kepler and became the standard astronomical text well into the seventeenth century.
皮尔巴赫的《新行星理论》（Theoricae Novae Planetarum）约成书于 1454 年，1473 年由雷格蒙塔努斯（Regiomontanus）在纽伦堡的印刷厂出版。尽管该书试图从技术层面调和欧多克索斯与托勒密的理论，但皮尔巴赫提出“行星运动由太阳决定”，这被视为向哥白尼理论迈出的一步。哥白尼、伽利略与开普勒均研读过该书，它在 17 世纪前一直是标准的天文教材。

In 1460 he began working on a new translation of Ptolemy’s Almagest, but he had only completed six of the projected thirteen books before died in 1461.
1460 年，他开始重新翻译托勒密的《天文学大成》，计划翻译 13 卷，但在 1461 年去世前仅完成 6 卷。

Johannes Muller von Konigsberg or Regiomontanus (1436-1476)

约翰内斯·米勒·冯·柯尼斯堡（又名雷格蒙塔努斯，1436-1476）

Regiomontanus had become a pupil of Peuerbach at the University of Vienna in 1450. Later, he undertook with Peuerbach to correct the errors found in the Alfonsine Tables. He had a printing press where he produced tables of sines and tangents and continued Puerbach’s innovation of using Hindu-Arabic numerals.

1450 年，雷格蒙塔努斯在维也纳大学成为皮尔巴赫的学生。后来，他与皮尔巴赫合作修正《阿方索星表》中的错误。他拥有自己的印刷厂，出版正弦表与正切表，并延续了皮尔巴赫引入印度-阿拉伯数字的创新做法。

As promised, he finished Peuerbach’s Epitome of the Almagest, which he completed in 1462 and was printed in Venice. The Epitome was not just a translation, it added new observations, revised calculations and made critical comments about Ptolemy’s work.

他信守承诺，完成了皮尔巴赫未竟的《天文学大成纲要》（Epitome of the Almagest），于 1462 年定稿，后在威尼斯出版。该纲要并非单纯的翻译，还加入了新的观测数据、修正了计算结果，并对托勒密的工作提出了批判性见解。

Realising that there was a need for a systematic account of trigonometry, Regiomontanus began his major work, the De Triangulis Omnimodis (Concerning Triangles of Every Kind) 1464. In his preface to the Reader he says,
雷格蒙塔努斯意识到需要一部系统的三角学著作，于是在 1464 年开始撰写其代表作《论各种三角形》（De Triangulis Omnimodis）。他在给读者的序言中写道：

“For no one can bypass the science of triangles and reach a satisfying knowledge of the stars … You, who wish to study great and wonderful things, who wonder about the movement of the stars, must read these theorems about triangles. Knowing these ideas will open the door to all of astronomy and to certain geometric problems. For although certain figures must be transformed into triangles to be solved, the remaining questions of astronomy require these books.” [See Note 10 below]
“任何人若想充分了解星体，都无法绕过三角形科学……若你渴望研究宏伟奇妙之物、对星体运动充满好奇，就必须研读这些三角形定理。掌握这些知识，将为你打开通往整个天文学与特定几何问题的大门。因为尽管某些图形需转化为三角形才能求解，但天文学的其他问题也离不开这些知识。”（详见下文注释 10）

The first book gives the basic definitions of quantity, ratio, equality, circles, arcs, chords and the sine function. Next come a list of axioms he will assume, and then $33$ theorems for right, isosceles and scalene triangles. The formula for the area of a triangle is given followed by the sine rule giving examples of its application. Books III to V cover the all-important theory of spherical trigonometry. The whole book is organised in the style of Euclid with propositions and theorems set out in a logical hierarchical manner. This work, published in 1533 was of great value to Copernicus.
该书第一卷给出了量、比、相等、圆、弧、弦与正弦函数的基本定义，随后列出了预设的公理，以及 33 个关于直角三角形、等腰三角形与不等边三角形的定理，还给出了三角形面积公式及正弦定理的应用示例。第三至五卷涵盖至关重要的球面三角学理论。全书以欧几里得式的逻辑层级结构组织命题与定理，1533 年出版后对哥白尼极具参考价值。

Regiomontanus also built the first astronomical observatory in Germany at Nuremburg with a workshop where he built astronomical instruments. He also took observations on a comet in 1472 that were accurate enough to allow it to be identified as Halley’s Comet that reappeared 210 years later.
雷格蒙塔努斯还在纽伦堡建造了德国第一座天文台，并设立工坊制造天文仪器。1472 年，他对一颗彗星进行了观测，其精度足以确认该彗星即为 210 年后再次出现的哈雷彗星。

Regiomontanus died during an outbreak of plague in Rome in 1476.
1476 年，雷格蒙塔努斯在罗马的一场瘟疫中去世。

12. The Final Chapter: Trigonometry Changes the World System

终章：三角学改变宇宙体系

Nicolaus Copernicus (1473 - 1543)

尼古拉·哥白尼（1473-1543）

Copernicus wrote a brief outline of his proposed system called the Commentariolus that he circulated to friends somewhere between 1510 and 1514. By this time he had used observations of the planet Mercury and the Alfonsine Tables to convince himself that he could explain the motion of the Earth as one of the planets. The manuscript of Copernicus’ work has survived and it is thought that by the 1530s most of his work had been completed, but he delayed publishing the book.
1510-1514 年间，哥白尼撰写了其宇宙体系的简要纲要《短论》（Commentariolus），并分发给友人。此时，他已通过对水星的观测与《阿方索星表》的研究，确信自己能将地球视为一颗行星来解释其运动。哥白尼的著作手稿得以留存，研究认为到 16 世纪 30 年代，他的大部分工作已完成，但他迟迟未出版该书。

His student, Rheticus read the manuscript and made a summary of Copernicus’ theory and published it as the Narratio Prima (the First Account) in 1540. Since it seemed that the Narratio had been well accepted by colleagues, Copernicus was persuaded to publish more of his main work, and in 1542 he published a section on his spherical trigonometry as De lateribus et angulis traingulorum (On the sides and angles of triangles). Further persuaded by Rheticus and others, he finally agreed to publish the whole work, De Revolutionibus Orbium Coelestium (The Revolutions of the Heavenly Spheres) and dedicated it to Pope Paul III. It appeared just before Copernicus’ death in 1543. [See Note 11 below]
他的学生雷蒂库斯（Rheticus）阅读手稿后，撰写了哥白尼理论的摘要，于 1540 年以《初述》（Narratio Prima）为名出版。由于《初述》似乎得到同行的广泛认可，哥白尼被说服出版更多核心内容：1542 年，他将球面三角学部分单独出版，名为《论三角形的边与角》（De lateribus et angulis traingulorum）。在雷蒂库斯等人的进一步劝说下，他最终同意出版完整著作《天体运行论》（De Revolutionibus Orbium Coelestium），并将其献给教皇保罗三世。该书在 1543 年哥白尼去世前夕问世（详见下文注释 11）。

Georg Joachim von Lauchen called Rheticus (1514-1574)

格奥尔格·约阿希姆·冯·劳岑（又名雷蒂库斯，1514-1574）

Rheticus had facilitated the publication of Copernicus’ work, and had clearly understood the basic principles of the new planetary theory. In 1551, with the help of six assistants, Rheticus recalculated and produced the Opus Palatinum de Triangulis (Canon of the Science of Triangles) which became the first publication of tables of all six trigonometric functions. This was intended to be an introduction to his greatest work, The Science of Triangles. When he died his work was still unfinished, but like Copernicus, Rheticus acquired a student, Valentinus Otho who supervised the calculation (by hand) of some one hundred thousand ratios to at least ten decimal places filling some 1,500 pages. This was finally completed in 1596. These tables were accurate enough to be used as the basis for astronomical calculations up to the early 20th century.
雷蒂库斯推动了哥白尼著作的出版，并深刻理解新行星理论的基本原理。1551 年，在六位助手的协助下，他重新计算并出版了《巴拉丁三角学著作》（Opus Palatinum de Triangulis，又称《三角学准则》），该书是首部包含全部六种三角函数表的出版物，原本计划作为其巨著《三角学》的导论。雷蒂库斯去世时，《三角学》仍未完成，但与哥白尼类似，他的学生瓦伦丁·奥托（Valentinus Otho) 接手了后续工作：监督手工计算约 10 万个比值，精度至少达 10 位十进制，内容长达 1500 页，最终于 1596 年完成。这些表格精度极高，直至 20 世纪初仍被用作天文计算的基础。

Bartholomaeus Pitiscus (1561 - 1613)

巴托洛梅乌斯·皮蒂斯库斯（1561-1613）

The term trigonometry is due to Pitiscus and as first appeared in his Trigonometria: sive de solutione triangulorum tractatus brevis et perspicuus, published in 1595. A revised version in1600 was the Canon triangularum sive tabulae sinuum, tangentium et secantium ad partes radii 100000 (A Canon of triangles, or tables of sines tangents and secants with a radius of 100,000 parts.) The book shows how to construct sine and other tables, and presents a number of theorems on plane and spherical trigonometry with their proofs. [See Note 11 below]
“三角学（trigonometry）”这一术语由皮蒂斯库斯提出，首次出现于他 1595 年出版的著作《三角学：简明清晰的三角形求解论述》（Trigonometria: sive de solutione triangulorum tractatus brevis et perspicuus）中。1600 年的修订版名为《三角学准则：半径为 100000 单位的正弦、正切与正割表》（Canon triangularum sive tabulae sinuum, tangentium et secantium ad partes radii 100000）。该书介绍了正弦表及其他三角函数表的编制方法，并呈现了平面与球面三角学的多个定理及其证明（详见下文注释 11)。

However, soon after Rheticus’ Opus Palatinum was published, serious inaccuracies were found in the tangent and secant tables at the ends near $1^{\circ }$ and $90^{\circ }$. Pitiscus was commissioned to correct these errors and obtained a manuscript copy of Rheticus’ work. Many of the results were recalculated and new pages were printed incorporating the corrections. Eventually, Pitiscus published a new work in 1613 incorporating that of Rheticus with a table of sines calculated to fifteen decimal places entitled the Thesaurus Mathematicus.
但在雷蒂库斯的《巴拉丁三角学著作》出版后不久，人们发现其正切表与正割表在接近 $1^{\circ }$ 和 $90^{\circ }$ 处存在严重误差。皮蒂斯库斯受委托修正这些错误，并获得了雷蒂库斯著作的手稿副本。他重新计算了大量结果，印刷新页面纳入修正内容。最终，皮蒂斯库斯在 1613 年出版了一部新著作，整合了雷蒂库斯的成果，并加入了精度达 15 位十进制的正弦表，书名定为《数学宝库》（Thesaurus Mathematicus）。

By the beginning of the seventeenth century, the science of trigonometry had become a sophisticated technique used in calculating more and more accurate tables for use in astronomy and navigation, and had been instrumental in fundamentally changing man’s concept of his world.
到 17 世纪初，三角学已发展成为一门精密技术，用于编制日益精确的数表，应用于天文学与航海领域，并在从根本上改变人类宇宙观的过程中发挥了关键作用。

References

参考文献

Aveni, A, (1997) Stairways to the Stars. N.Y and Chichester Wiley
阿韦尼，A.（1997）.《通往星辰的阶梯》（Stairways to the Stars）. 纽约、奇切斯特：威利出版社.
Skywatching in three ancient cultures: Megalithic Astronomy, the Maya and the Inca. The first chapter (almost a third of the book) gives a delightful and straightforward explanation of how much we can discover with the naked eye.
该书探讨了三种古代文明的观星活动：巨石阵天文学、玛雅天文学与印加天文学。第一章（约占全书三分之一）以生动易懂的方式，解释了通过肉眼可观测到的天文现象。
With clear diagrams and explanations this give a fascinating insight into the less well-known aspects of these ancient cultures.
书中配有清晰图表与解析，让读者深入了解这些古代文明中鲜为人知的方面。

Van Brummelen, G. (2009) The Mathematics of the Heavens and the Earth: The Early History of Trigonometry. Princeton, Princeton University Press.
范·布鲁梅伦，G.（2009）.《天地间的数学：三角学早期史》（The Mathematics of the Heavens and the Earth: The Early History of Trigonometry）. 普林斯顿：普林斯顿大学出版社.
This is the first major history in English of the early development of trigonometry . Glen van Brummelen’s extensive research shows how the earliest activities in Egypt and Babylon led to the mathematical work of the Hindus and the Greeks that was developed by the Arabs over some 400 years into a sophisticated science separate from astronomy before it was passed on to Western European astronomers and mathematicians.
该书是首部以英语撰写的三角学早期发展史专著。格伦·范·布鲁梅伦通过深入研究，梳理了三角学的发展脉络：从埃及与巴比伦的早期探索，到印度与希腊的数学成果，再到阿拉伯人用约 400 年时间将其发展为独立于天文学的精密学科，最终传入西欧天文学家与数学家手中。

Evans, J. (1998) The History and Practice of Ancient Astronomy. Oxford. O.U.P.
埃文斯，J.（1998）.《古代天文学的历史与实践》（The History and Practice of Ancient Astronomy）. 牛津：牛津大学出版社.
Beginning from about 700 BCE this book examines in detail both the practical and theoretical astronomy developed by the Egyptians, Babylonians and Greeks, up to the 16th century with the final resolution of the planetary system with Copernicus and Kepler.
该书以公元前 700 年为起点，详细探讨了埃及、巴比伦与希腊发展的实用天文学与理论天文学，时间跨度直至 16 世纪——哥白尼与开普勒最终确立了行星体系。

Hughes, B. (1967) Regiomontanus on Triangles. London, University of Wisconsin Press
休斯，B.（1967）.《雷格蒙塔努斯的三角学》（Regiomontanus on Triangles）. 伦敦：威斯康星大学出版社.
This is a translation with an introduction and notes, of the work completed in 1464, but published posthumously in 1533 of De triangulis omnimodis (On triangles of every kind) by Johan Muller, known as Regiomontanus. In this first edition, reproductions of the original Latin pages face the English translations. The book was written principally as a contribution to the science of astronomy, but we now recognise Regiomontanus as the first European scholar who treated trigonometry as a theoretical science, setting out a series of logical propositions and proofs in the style of Euclid.
该书是约翰·米勒（即雷格蒙塔努斯）《论各种三角形》（De triangulis omnimodis）的英译本，附带导论与注释。这部著作完成于 1464 年，雷格蒙塔努斯死后于 1533 年出版。首个英译本中，原版拉丁文页面的复刻本与英文译文相对照。该书最初旨在为天文学发展提供助力，但如今我们认为，雷格蒙塔努斯是首位将三角学视为理论科学的欧洲学者——他以欧几里得的风格，提出了一系列逻辑命题与证明。

Maor E. (1998) Trigonometric Delights. Princeton, Princeton University Press.
毛尔，E.（1998）.《三角之趣》（Trigonometric Delights）. 普林斯顿：普林斯顿大学出版社.
Eli Maor presents a selection of the main elements of trigonometry and an account of its vital contribution to astronomy, science and social development. Interesting mathematical episodes to suit pupils at all levels, with notes and references for further exploration.
伊莱·毛尔在书中精选了三角学的核心内容，阐述了其对天文学、科学与社会发展的重要贡献。书中包含适合各阶段学习者的有趣数学片段，并附有注释与参考文献，方便进一步探索。

Rashed, R. (1996) (Ed.) Encyclopaedia of the History of Arabic Science. Vol 2.
拉希德，R.（编）（1996）.《阿拉伯科学史百科全书》（Encyclopaedia of the History of Arabic Science）. 第 2 卷.
This volume includes numeration and arithmetic, algebra, geometry and trigonometry. London. Routledge.
该卷涵盖记数法与算术、代数、几何及三角学等内容。伦敦：罗德里奇出版社.

Victor, S.K. (1979) Practical Geometry in the High Middle Ages: Artis Cuiuslibet Consummatio and the Practike de Geometrie.
维克托，S.K.（1979）.《中世纪盛期的实用几何》（Practical Geometry in the High Middle Ages）：《各类技艺大全》（Artis Cuiuslibet Consummatio）与《几何实践》（Practike de Geometrie）.
This is a translation and critical edition of these two major Mediaeval works. Philadelphia. American Philosophical Society
该书是这两部中世纪重要著作的英译本与校注版。费城：美国哲学学会.

Bender, D. (1998) “A proposal for the striking mechanism on the Wallingford Clock.” Antiquarian Horology 24, 2 1998a (134-140).
本德，D.（1998a）.《关于沃林福德时钟报时机制的推测》. 《古钟表学》（Antiquarian Horology），第 24 卷第 2 期，134-140 页.
“A proposal for the eclipse mechanism for the Wallingford Clock.” Antiquarian Horology 24, 3 1998b (217-224)
《关于沃林福德时钟食相机制的推测》. 《古钟表学》（Antiquarian Horology），第 24 卷第 3 期，217-224 页.
A fascinating description of one person’s ‘detective quest’ to understand Richard of Wallingford’s description of the workings of his amazing device.
文章生动描述了作者如何通过“探索过程”，解读理查德·沃林福德对其精妙时钟装置运作原理的记载。

Web Links

The Mactutor website for biographies of mathematicians and a special section on Trigonometry.
MacTutor：包含数学家传记及三角学专题板块.

The Muslim Heritage Site is very interesting. It is a valuable source of information on “1,000 years of missing history from 600 to 1600.” You can find a large number of biographies of Muslim Scholars of the Past, a time Line of Events, and much more.
The Muslim Heritage Site 内容丰富，是研究“600-1600 年这段被忽略的千年历史”的重要信息来源。网站包含大量古代穆斯林学者传记、历史事件时间线等内容。

The Wallingford Clock Here is the general description and explanation of the various mechanisms of the reconstruction of the clock. Some parts of this site may not work.
The Wallingford Clock：该网站对时钟复制品的各类机制进行了总体介绍与解析，部分板块可能无法访问。

There are many specialised websites where you can obtain information. If you ‘Google’ your enquiry and use the Wikipedia option you can usually obtain reasonably reliable results and ideas for more searches if you need to look any further.
此外还有许多专业网站可提供相关信息。若你通过谷歌搜索并选择维基百科结果，通常能获取较为可靠的信息，若需进一步研究，也能获得更多搜索方向。

Notes

注释

1. See Part 1 section 3 on the Sulbasutras.

   详见《三角学发展史（第一部分）》第 3 节关于《绳法经》的内容。

2. See Note 4 in Part 1. The use of the capital S in Sine is to show that the radius of the circle used is not unity, or the same as $\sin \theta$ in our system, but could be an arbitrary length R. This means that Sin$\theta$ is equal to R sin$\theta$. In the Indian texts, different astronomers took different values for R, and in most cases the value had to be deduced from the context.
   详见《三角学发展史（第一部分）》注释 4。“Sine”首字母大写（Sin），是为了表明所用圆的半径并非单位半径（即与现代体系中的 $\sin \theta$ 不同），而是任意长度 $R$，即 $\text{Sin}\theta =R\sin \theta$。在印度文献中，不同天文学家采用的 $R$ 值不同，多数情况下需结合上下文推断具体数值。

3. The advantage of the ‘versine’ (or reversed sine) is that it’s value is always positive and so its logarithm is defined everywhere (except at $0^{\circ }$ and $180^{\circ }$). A positive logarithm was necessary when calculations had to be done using tables. The most important use was in navigation, for calculating the distance between two points on a sphere. The perpendicular distance from the mid point of a chord to a curve is still used as a measure of ‘deviation from straightness’, for example, by railway engineers. It is used also in optics for measuring the curvature of lenses and mirrors, where the versine is sometimes called the sagitta from the Latin for arrow.
   正矢（versine，又称“反弦”）的优势在于其值恒为正，因此除 $0^{\circ }$ 和 $180^{\circ }$ 外，其对数在所有角度下均有定义。在需用数表计算的时代，正的对数值至关重要。正矢最重要的应用是在航海领域，用于计算球面上两点间的距离。弦中点到曲线的垂直距离至今仍被用作“直线偏差”的度量标准（如铁路工程师的应用），在光学中也用于测量透镜与镜面的曲率，此时正矢有时被称为“sagitta”（源自拉丁语“箭”）。

4. Compare the sine curve from $0^{\circ }$ to $180^{\circ }$ with $y=-a(x-\pi /2{)}^2+c$. By adjusting the values of $a$ and $c$, it is possible to produce a curve of ‘best fit’ inside the sine curve. You can obtain a remarkably good fit for $0<x<\pi$.
   将 $0^{\circ }$ 至 $180^{\circ }$ 的正弦曲线与二次函数 $y=-a(x-\pi /2{)}^2+c$ 对比，通过调整 $a$ 和 $c$ 的值，可在正弦曲线内得到一条“最佳拟合”曲线。在 $0<x<\pi$ 区间内，该拟合曲线的精度极高。

5. The Hindu word jiya for the sine was adopted by the Arabs who called the sine jiba. Eventually jiba became jaib and this word actually meant a ‘fold’. When Europeans translated the Arabic works into Latin they translated jaib into the word sinus meaning a fold in Latin. In his Practica Geometriae (1220) Fibonacci uses the term sinus rectus arcus which soon encouraged the universal use of the word sine.
   印度语中表示正弦的“jiya”一词被阿拉伯人采纳，称为“jiba”，后逐渐演变为“jaib”（意为“褶皱”）。欧洲人将阿拉伯文献译为拉丁语时，将“jaib”译为“sinus”（拉丁语中“褶皱”之意）。斐波那契（Fibonacci）在其 1220 年的著作《实用几何》（Practica Geometriae）中使用“sinus rectus arcus”（弧的正弦）这一术语，该术语随后推动“sine（正弦）”一词的广泛使用。

6. In the diagram, if $OB=t$ and $R=1$, then in triangle $ABO,A{O}^2+O{B}^2=1+t^2$. From which we get the familiar parametric formulae: $\cos \theta =\frac{1-t^2}{1+t^2}$ etc.
   图中若设 $OB=t$ 且 $R=1$，则在 $△ABO$ 中，$A{O}^2+O{B}^2=1+t^2$，由此可推导出常见的参数方程：$\cos \theta =\frac{1-t^2}{1+t^2}$ 等。

7. The maximum area occupied by the Arabs was most of Spain and Portugal with the exception of the kingdom of Asturias in the North, and a part of France now called the Languedoc.
   阿拉伯帝国在欧洲的最大疆域涵盖西班牙与葡萄牙的大部分地区（北部的阿斯图里亚斯王国除外），以及如今法国的朗格多克地区。

8. The Holy Land with its capital Jerusalem, consisted roughly of what is now Israel and Palestine. There were many other reasons for the Crusades; the loss of power and territory of the older Christian Empires, the growing problem of the slave trade run by Arabs, and by taking part in these campaigns, some Christian kingdoms thought they could gain political advantage over their rivals.
   以耶路撒冷为首都的“圣地”，大致对应如今的以色列与巴勒斯坦地区。十字军东征的原因还有很多：老牌基督教帝国的权力与领土丧失、阿拉伯人主导的奴隶贸易问题日益严重，以及部分基督教王国认为参与东征可在与对手的竞争中获得政治优势。

9. The reason for using such large numbers for the radius is much the same as in the past, the arithmetic was much easier using a large unit like 100,000 where the small parts (in this case minutes of arc) could be managed in integral parts rather than fractions. Similar considerations were applied by Napier, Briggs and Burgi in their invention of logarithms.
   采用如此大的半径数值（如 600000），原因与过去一致：使用 100000 这类大单位时，小数部分（此处为分弧）可通过整数处理，无需分数运算，算术计算更简便。纳皮尔（Napier）、布里格斯（Briggs）与比尔吉（Burgi）发明对数时，也基于类似考量。

10. This quotation comes from the preface to the reader in De Triangulis, translated by Barnabas Hughes.
    该引文源自巴纳巴斯·休斯（Barnabas Hughes）翻译的《论各种三角形》序言。

11. You can see Copernicus’ book on Wikipedia at: http://en.wikipedia.org/wiki/De_revolutionibus_orbium_coelestium
    可在维基百科查看哥白尼著作相关内容：http://en.wikipedia.org/wiki/De_revolutionibus_orbium_coelestium

---

三角学发展阶段

一、古代奠基阶段（公元前 2000 年 - 公元 5 世纪）

确立角度度量标准，构建几何化基础工具，为三角学提供早期实践与理论框架。

时间	文明/人物	关键事件与突破
公元前 2300 年之前	埃及	将黄道划分为 36 个 $10^{\circ }$ 旬星区域，用于确定夜间时辰与季节，开创角度分段实践
公元前 1800 年左右	巴比伦	确立圆周 $360^{\circ }$ 与 60 进制计算体系，为角度度量和三角数值计算提供统一标准；积累行星、日月食观测数据，编制星历表
公元前 140 年左右	希腊（希帕恰斯）	编制首个弦表，以 60 进制计算不同角度弦长，首次用圆弧几何实现天文数值计算
公元前 100 年左右	希腊（梅涅劳斯）	著《球面比例论》，提出球面三角形定理，用大圆弧替代平行圆弧，奠定球面三角学基础
公元 2 世纪	希腊（托勒密）	著《天文学大成》，完善弦表（间隔 ${\frac{1}{2}}^{\circ }$），推导托勒密定理并转化为两角和差正弦公式；建立弦长 = $120\sin \alpha$ 关系，为正弦函数铺垫

二、印阿过渡阶段（公元 5 世纪 - 13 世纪）

革新函数定义，整合多元成果，推动三角学从天文学附属向独立学科雏形发展。

时间	文明/人物	关键事件与突破
公元 499 年	印度（阿耶波多）	著《阿耶波多论》，取圆半径 $R=3438$（由 21600 分弧长推导），统一正弦表计算基准；定义正弦（jiya）、余弦（kotijya），替代希腊弦概念
公元 7 世纪	印度（婆罗摩笈多）	提出二阶差分法，仅通过 $0^{\circ }$-$90^{\circ }$ 间 6 个 $15^{\circ }$ 间隔的初始正弦值，可推导任意角度正弦值，提升计算效率
公元 8 世纪（762-766 年）	阿拉伯（曼苏尔）	建立智慧宫，组织翻译希腊《天文学大成》、印度《信德欣德天文表》等文献，整合多元三角学成果
公元 9 世纪	阿拉伯（花拉子米）	改进《信德欣德天文表》，引入正弦、正矢计算；开发正切、余切的天文应用方法，解决天体方位问题
公元 10 世纪	阿拉伯（阿布·瓦法）	首次整合正弦、余弦、正切、余切、正割、余割六种三角函数，建立恒等关系（如 ${\sec }^2\theta =1+{\tan }^2\theta$）；采用 $R=1$ 的基准圆，简化计算逻辑
公元 11 世纪	阿拉伯（比鲁尼）	推导半角公式 $\left(\tan \left(\frac{\theta }{2}\right)=\frac{\sin \theta }{1+\cos \theta }\right)$ 与倍角公式；用三角函数测量恒星距离，通过指时针影子完善正切、余切的实际应用
公元 13 世纪	阿拉伯（纳西尔丁·图西）	著《扇形图形奥秘揭秘》，首次将三角学从天文学分离，作为独立学科系统阐述；规范平面与球面三角形求解公式，统一恒等式推导逻辑

三、欧洲完善与应用阶段（12 世纪 - 17 世纪）

完成理论系统化与术语规范化，拓展跨领域应用，使三角学成为成熟学科。

时间	人物/事件	关键事件与突破
12 世纪	欧洲（托莱多/科尔多瓦翻译中心）	将阿拉伯三角学文献（如贾比尔·伊本·阿夫拉的著作）译为拉丁语，推动三角学传入西欧
14 世纪（1326-1336 年）	欧洲（理查德·沃林福德）	著《四卷论》，系统阐述三角恒等式与梅涅劳斯定理，是欧洲首部非伊斯兰文化圈的三角学专著
15 世纪（1454 年）	欧洲（皮尔巴赫）	著《新行星理论》，提出行星运动由太阳决定；编制每分弧正弦表（半径 600000），引入印度 - 阿拉伯数字提升精度
1464 年	欧洲（雷格蒙塔努斯）	著《论各种三角形》，以欧几里得式逻辑组织平面与球面三角学，包含 33 个三角形定理、面积公式及正弦定理应用，成为欧洲标准教材
1543 年	欧洲（哥白尼）	出版《天体运行论》，用球面三角学计算行星位置，验证日心说模型，将三角学升级为宇宙观论证工具
1551 年	欧洲（雷蒂库斯）	出版《巴拉丁三角学著作》，编制首部包含全部六种三角函数的数表（精度 10 位十进制），后续由学生奥托完善（1596 年）
1595 年	欧洲（皮蒂斯库斯）	著《三角学：简明清晰的三角形求解论述》，首次提出 “trigonometry”（三角学）术语；1600 年修订版规范三角函数表编制方法与定理证明

四、分析化转型阶段（17 世纪 - 19 世纪）

用代数与微积分重新定义三角函数，打破几何依赖；建立严密理论体系，拓展至分析学、物理学领域。

时间	人物/事件	关键事件与突破
1637 年	法国（笛卡尔）	创立直角坐标系，将三角函数与坐标点（x,y,r）绑定，首次实现三角学的代数化表达
1667 年	英国（格雷戈里）	推导反正切函数的幂级数展开式，为三角函数的解析表达提供首个严格公式
1714 年	英国（泰勒）	提出泰勒级数，推导出正弦、余弦函数的幂级数形式 $\left(\sin x=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\dots \right)$，彻底脱离几何定义
1748 年	瑞士（欧拉）	出版《无穷分析引论》，首次引入弧度制，确立 $\pi$ 与圆周长的关系；提出欧拉公式 $\left(e^{i\theta }=\cos \theta +i\sin \theta \right)$，打通三角函数与复数的关联
1807 年	法国（傅里叶）	提出傅里叶级数，证明“任意周期函数可分解为正弦/余弦函数叠加”，将三角学应用拓展到热传导、波动等物理领域
1829 年	德国（高斯）	在非欧几何研究中，推导球面三角学的非欧版本，突破传统欧氏几何对三角学的限制

五、现代应用与深化阶段（20 世纪-至今）

依托计算机技术实现高精度计算，渗透至工程、信息、航天等多元领域；理论层面与抽象代数、拓扑学结合。

时间	领域/事件	关键事件与突破
1946 年	计算机领域	第一台电子计算机 ENIAC 实现三角函数数值快速计算，替代传统数表，精度达小数点后 10 位以上
1950 年代	信号处理领域	基于傅里叶变换开发“快速傅里叶算法（FFT）”，使三角学成为音频、图像、雷达信号处理的核心工具
1970 年代	航天领域	美国阿波罗计划用球面三角学计算航天器轨道与地球、月球的相对位置，确保登月精准定位
2000 年代	数学理论领域	三角学与李群、微分几何结合，用于描述量子力学中的粒子运动轨迹，成为前沿物理的数学基础

总结

从公元前 2000 年埃及旬星划分到 21 世纪现代应用，三角学经历了工具实践（古代）→ 整合创新（印阿）→ 系统成熟（欧洲近代）→ 分析化转型（17-19 世纪）→ 现代应用（20 世纪至今）的发展路径。

每阶段的突破均围绕简化计算、拓展应用、独立学科三大目标，最终成为连接几何、天文、航海、物理、工程的重要数学分支。

---

vai:

• The History of Trigonometry- Part 1 | NRICH
  https://nrich.maths.org/articles/history-trigonometry-part-1
• History of Trigonometry - Part 2 | NRICH
  http://nrich.maths.org/articles/history-trigonometry-part-2
• History of Trigonometry - Part 3 | NRICH
  http://nrich.maths.org/articles/history-trigonometry-part-3