微积分 · 原函数 | antiderivative

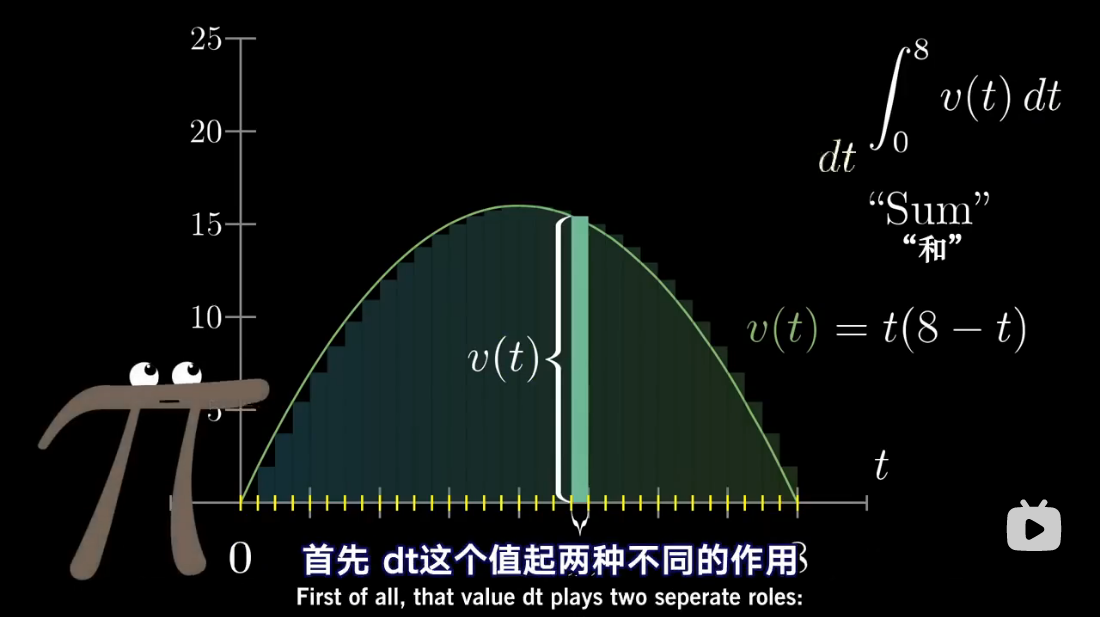
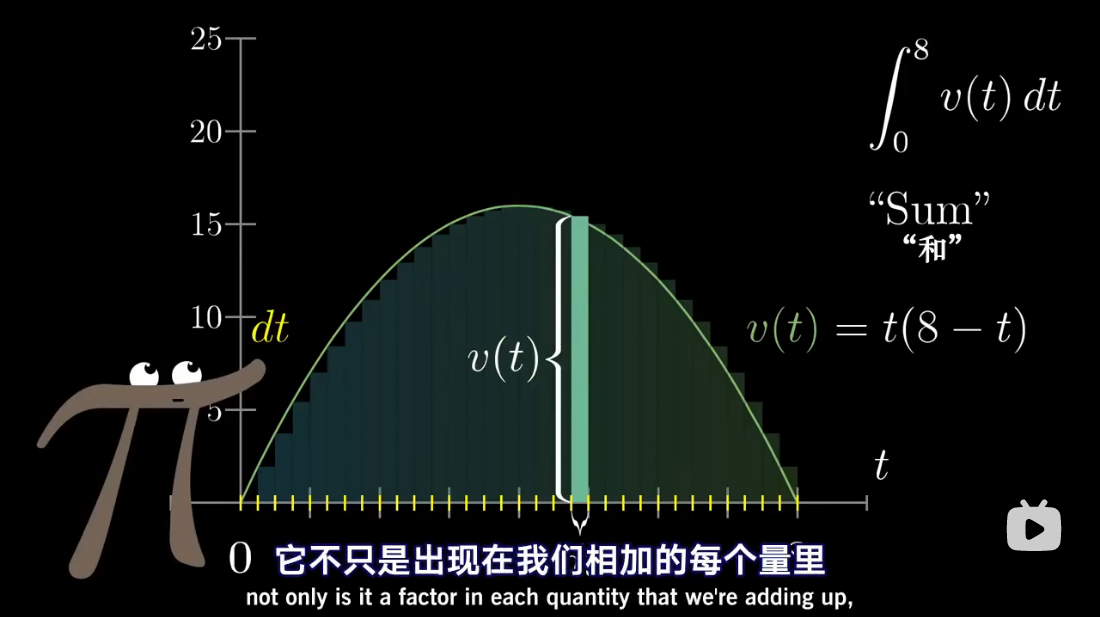
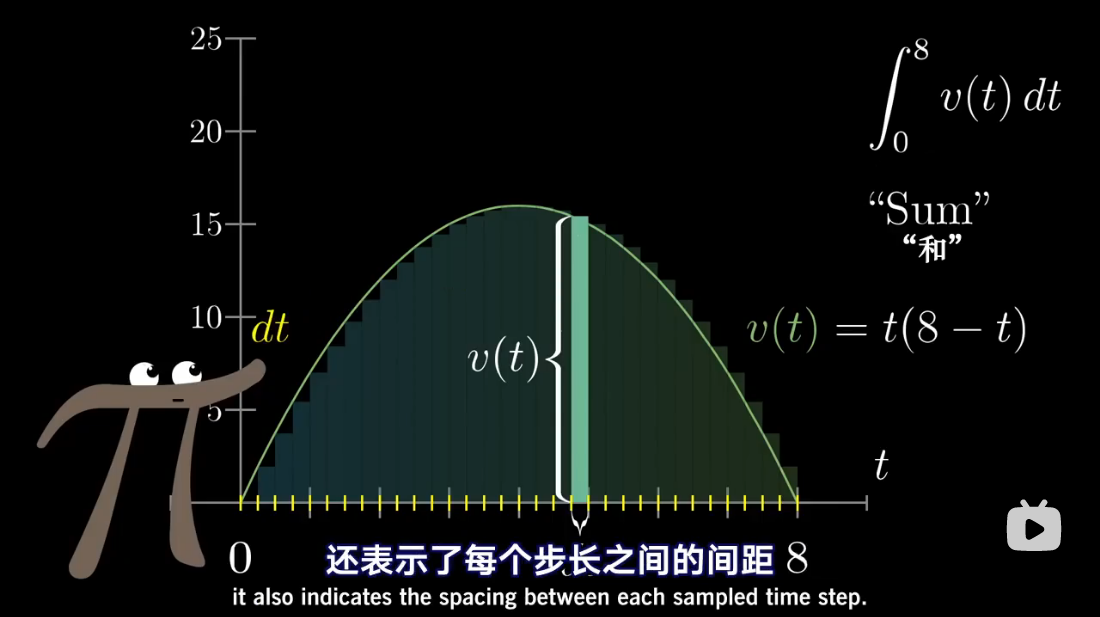
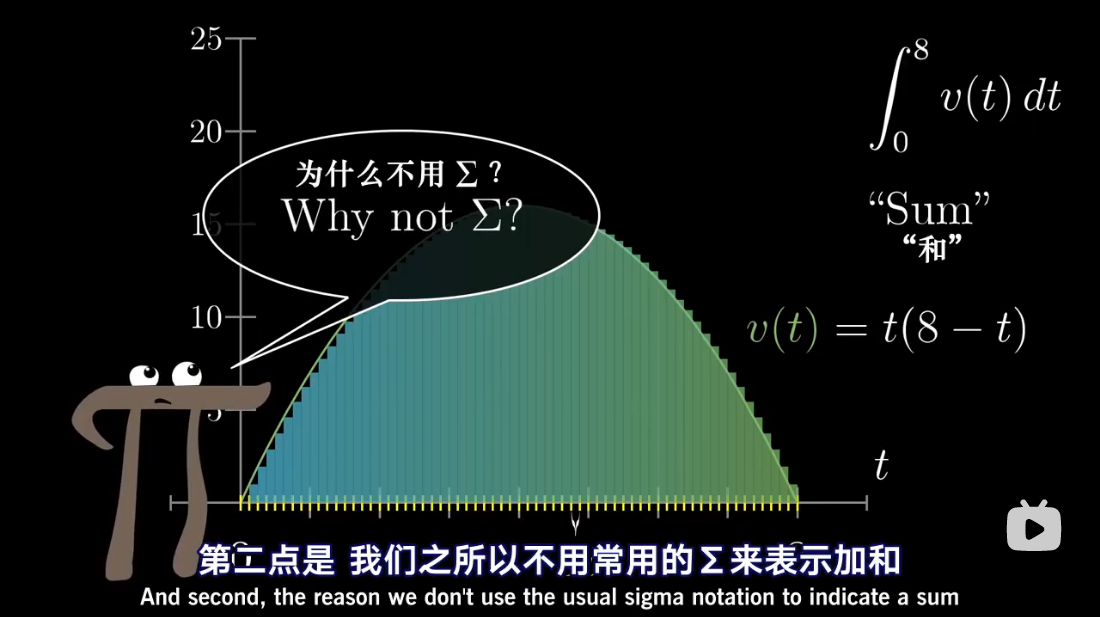
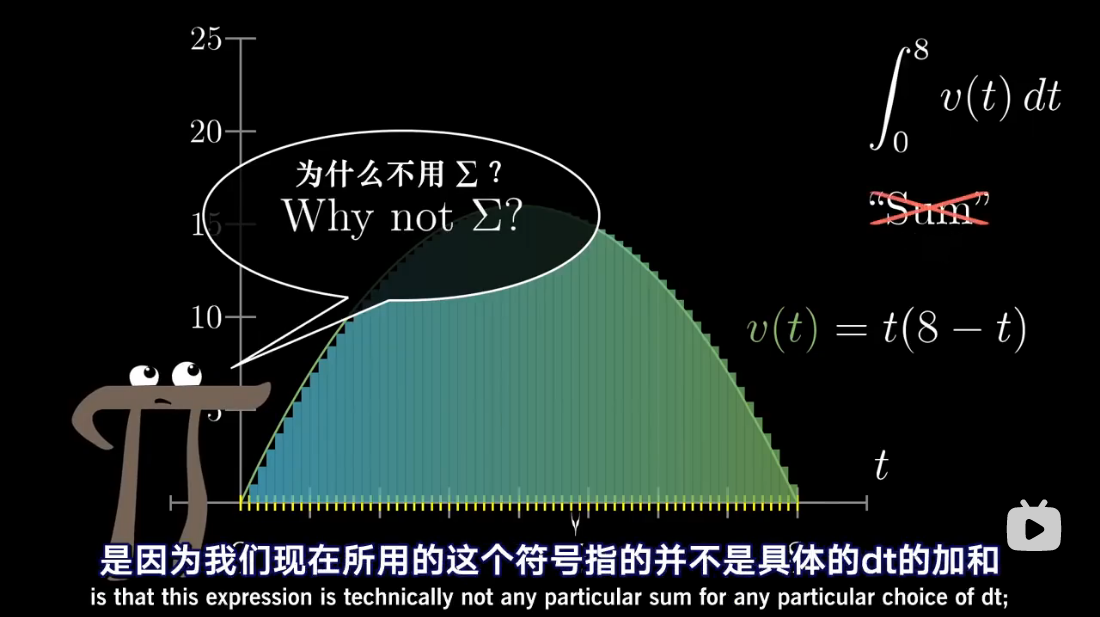
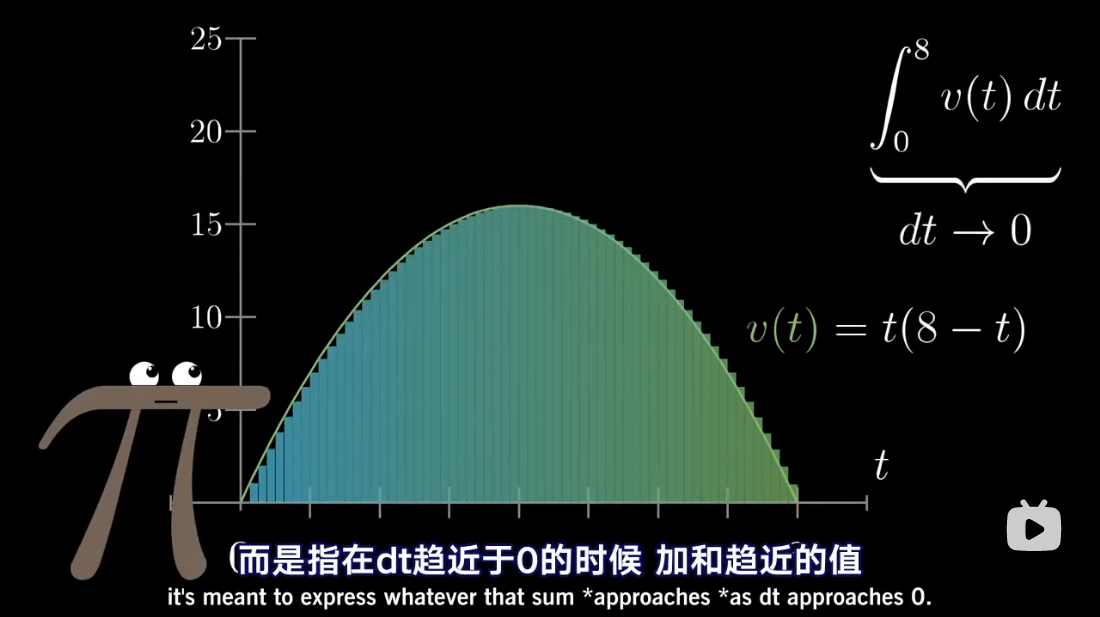
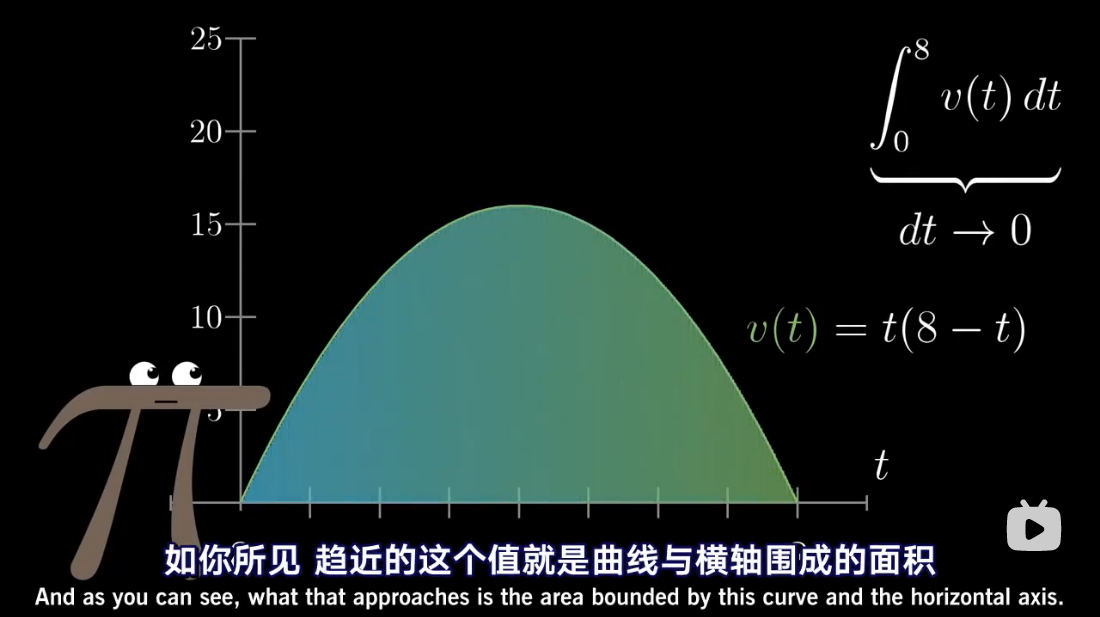
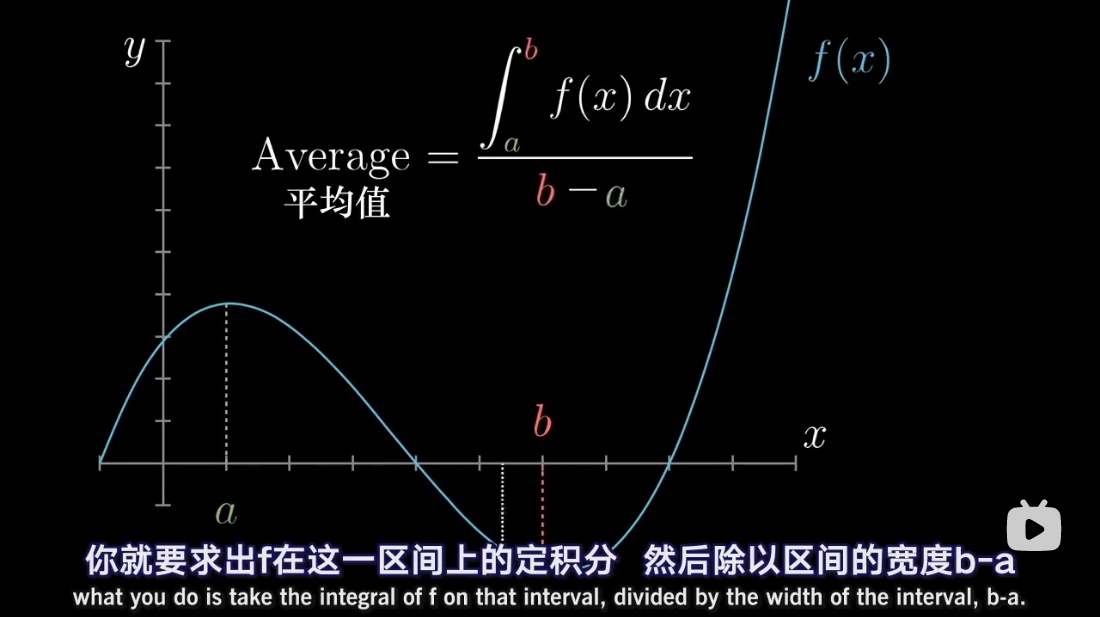
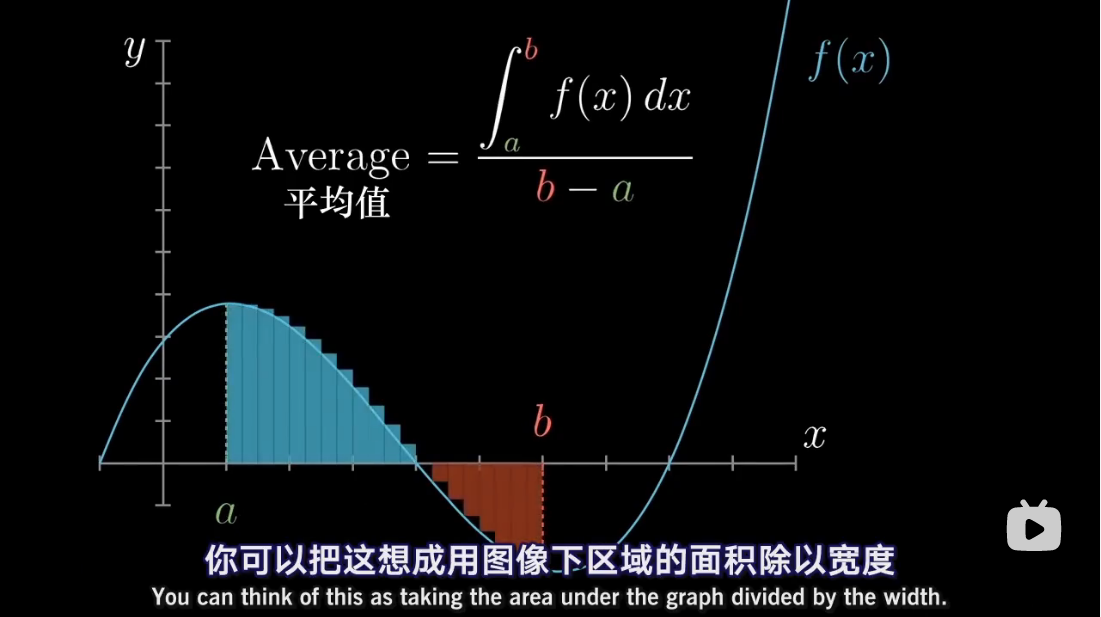
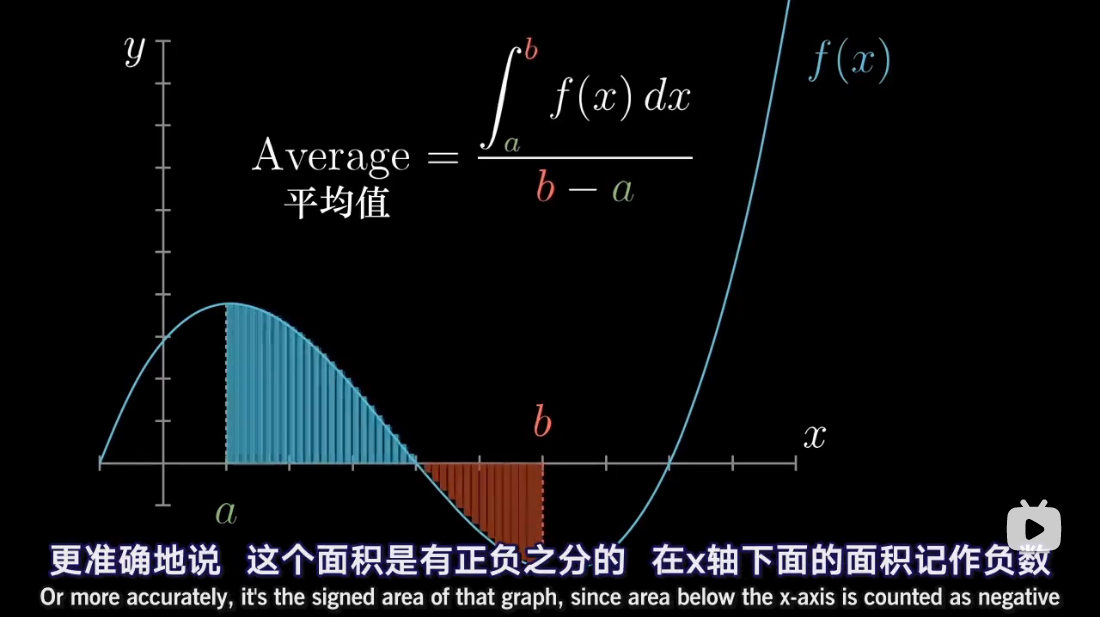
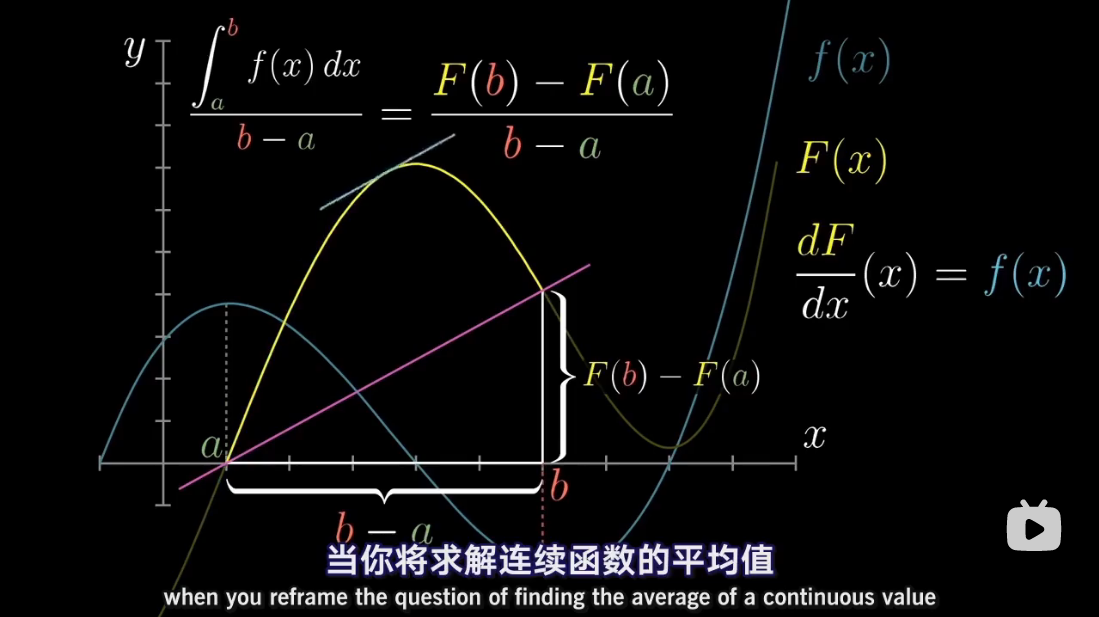
注：本文为 “微积分 | antiderivative” 相关合辑。
英文引文，机翻未校。
如有内容异常，请看原文。

---

Antiderivative – Definition, Techniques, and Examples

原函数——定义、方法及示例

Knowing how to find antiderivatives is one of the most important techniques that we’ll be learning in our integral calculus classes. In Physics, for example, we can find the function of the velocity given the function for the object’s acceleration. Given the rate of increase or decrease from a specimen, a researcher can find the original quantity or population. We can list more applications, but yes, these are all thanks to antiderivatives.
掌握如何求 原函数 是我们在积分微积分课程中要学习的最重要技巧之一。例如，在物理学中，已知物体的加速度函数，我们可以求出速度函数。研究人员根据样本的增减速率，可以求出原来的数量或种群数量。我们还能列举出更多应用，但这些都得益于原函数。

What if we’re given the function’s derivative, $\mathbf{f}(\mathbf{x})$, and this time, we need to find the function’s expression? We can work backwards and find an expression for the function, $\mathbf{F}(\mathbf{x})$.This is the foundation of antiderivatives: $\mathbf{F}(\mathbf{x})$ is the antiderivative of $\mathbf{f}(\mathbf{x})$.
如果已知一个函数的导数 $\mathbf{f}(\mathbf{x})$，而这次我们需要求出该函数的表达式，该怎么办呢？我们可以逆向推导，求出函数 $\mathbf{F}(\mathbf{x})$ 的表达式。这就是原函数的基础：$\mathbf{F}(\mathbf{x})$ 是 $\mathbf{f}(\mathbf{x})$ 的原函数。

In this article, we’ll show you how derivatives and antiderivatives are related to each other. We’ll also learn about the different antiderivatives that will come in handy when finding the antiderivative of a given function. You’ll also be able to test out your understanding of the exercises that follow!
在本文中，我们将为你展示导数和原函数之间的关系。我们还将学习各种不同的原函数，这些原函数在求给定函数的原函数时会很有用。你也可以通过后面的练习来检验自己的理解程度！

What is an antiderivative?

什么是原函数？

The antiderivative of a function simply the result of reversing the derivative of a given function. When we have $F(x)$, it is considered the antiderivative of $f(x)$ when ${\mathbf{F}}^{\prime }(\mathbf{x})=\mathbf{f}(\mathbf{x})$, for all values of $x$ within the allowed domain. To better understand the definition of antiderivatives, try listing down at least three functions, { F 1 ( x ) , F 2 ( x ) , F 3 ( x ) } \{F_1 (x), F_2 (x), F_3 (x)\} {F1​(x),F2​(x),F3​(x)}, where all three functions have $x^3$ as its derivative.
函数的原函数就是对给定函数的导数进行逆向运算的结果。当我们有函数 $F(x)$ 时，如果对于定义域内的所有 $x$ 值，都有 ${\mathbf{F}}^{\prime }(\mathbf{x})=\mathbf{f}(\mathbf{x})$，那么 $F(x)$ 就被认为是 $f(x)$ 的原函数。为了更好地理解原函数的定义，试着列出至少三个函数 { F 1 ( x ) , F 2 ( x ) , F 3 ( x ) } \{F_1 (x), F_2 (x), F_3 (x)\} {F1​(x),F2​(x),F3​(x)}，使得这三个函数的导数都是 $x^3$。

A great guess would be $F(x)=x^4$, but if we try to differentiate this using the power rul e, we’ll end up with $F^{\prime }(x)=4x^3$. To account for the coefficient, $F(x)$ must have $\frac{1}{4}$ as its constant factor. Hence, $F(x)=\frac{1}{4}{x}^4$. Now, how do we list down three unique functions? Recall that the derivative of constant will always be zero, so we simply add a unique constant to $F(x)$:
一个不错的猜测是 $F(x)=x^4$，但如果我们用幂法则对其求导，会得到 $F^{\prime }(x)=4x^3$。为了得到正确的系数，$F(x)$ 必须有 $\frac{1}{4}$ 作为常数因子。因此，$F(x)=\frac{1}{4}{x}^4$。现在，我们如何列出三个不同的函数呢？回想一下，常数的导数始终为零，所以我们只需给 $F(x)$ 加上一个独特的常数即可：

Antiderivative 原函数	Derivative 导数 (${\mathbf{F}}^{\prime }(\mathbf{x})=\mathbf{f}(\mathbf{x})$)
$$\begin{array}{rl}{F}_1(x)& =\frac{1}{4}{x}^4+1\\ F_2(x)& =\frac{1}{4}{x}^4-1\\ F_3(x)& =\frac{1}{4}{x}^4+\pi \end{array}$$	$$\begin{array}{rl}f(x)& =x^3\end{array}$$

This shows that a function may have multiple antiderivatives since we can add any constant after the antiderivative, $F(x)$, and the derivative function, $f(x)$, will still be the same.
这表明 一个函数可以有多个原函数，因为我们可以在原函数 $F(x)$ 后面加上任意常数，而导数函数 $f(x)$ 仍然保持不变。

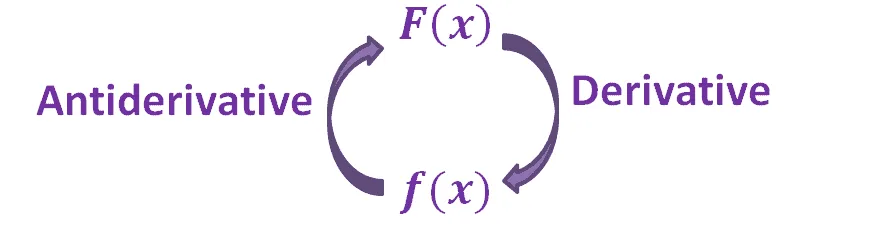
Here’s a helpful guide to remember how derivatives and antiderivatives are related to each other:
下面是一个有助于记住导数和原函数之间关系的指南：

$$\begin{array}{rl}{F}^{\prime }(x)& =f(x)\end{array}$$

This means that finding the antiderivative is simply reversing the process of finding the function’s derivative.
这意味着求原函数就是对求函数导数的过程进行逆向操作。

The general form of the antiderivative

原函数的一般形式

In the previous table, we’ve shown you that there can be multiple possible antiderivatives for one given function. That’s because expressions with identical terms except for their constants will have identical derivatives.
在前面的表格中，我们已经向你展示了一个给定的函数可以有多个可能的原函数。这是因为除了常数项不同外，其他项都相同的表达式，其导数是相同的。

$$\begin{array}{r}{F}^{\prime }(x)=f(x)=G^{\prime }(x)\end{array}$$

Let’s say we have $F(x)$ and $G(x)$, where the two functions only vary by a constant $C$. This means that they’ll be sharing a common derivative, $f(x)$. Since $F(x)$ and $G(x)$ differ by $C$, we can rewrite $G(x)$ as $F(x)+C$.
假设我们有函数 $F(x)$ 和 $G(x)$，这两个函数仅相差一个常数 $C$。这意味着它们有相同的导数 $f(x)$。由于 $F(x)$ 和 $G(x)$ 相差 $C$，我们可以将 $G(x)$ 改写为 $F(x)+C$。

This generalizes the antiderivatives of $f(x)$ as $F(x)+C$, where $C$ is an arbitrary constant.
由此可推广，$f(x)$ 的原函数为 $F(x)+C$，其中 $C$ 是任意常数。

$$\begin{array}{rl}{F}^{\prime }(x)& =f(x)\\ \text{Indefinite Integral of }f(x)& =F(x)+C\end{array}$$

This is the general form of a function’s antiderivative. Keep in mind that $C$ is an arbitrary constant and $\mathbf{F}(\mathbf{x})+\mathbf{C}$ is the antiderivative of $\mathbf{f}(\mathbf{x})$. The process of antidifferentiation is simply finding the function’s antiderivative.
这就是函数原函数的一般形式。要记住，$C$ 是任意常数，且 $\mathbf{F}(\mathbf{x})+\mathbf{C}$ 是 $\mathbf{f}(\mathbf{x})$ 的原函数。求原函数的过程其实就是求函数的原函数。

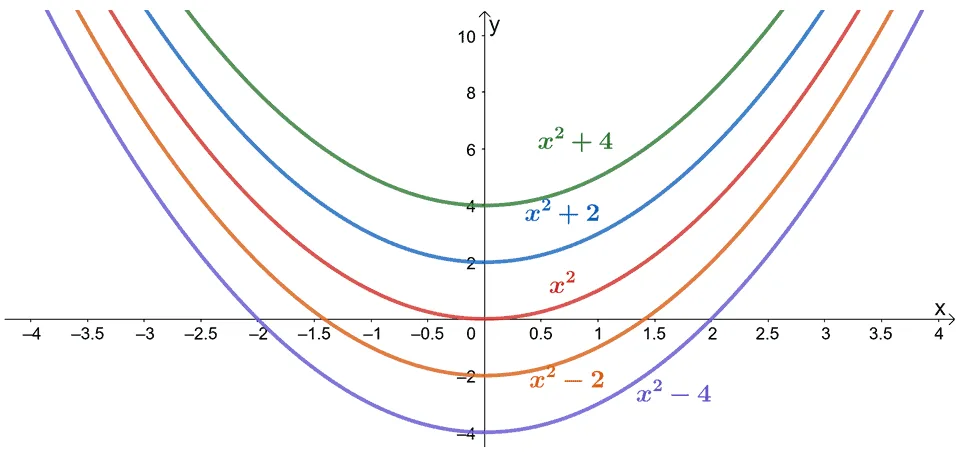
Here’s an example of a family of antiderivatives that shared the same derivative of $2x$. From this, we can see that that the functions of the form $x^2+C$ will always have a derivative of $2x$.
下面是一个原函数族的例子，它们都有相同的导数 $2x$。从中我们可以看出，形如 $x^2+C$ 的函数，其导数始终是 $2x$。

Integration and indefinite integral

积分与不定积分

Integration and antidifferentitation are interchangeable processes since we’re performing the same process for both. We can also represent antiderivatives using the integration symbol, $\int$. When $f(x)$ is a function with an antiderivative of $F(x)$, we have the relationship shown below:
积分和求原函数是可以互换的过程，因为两者执行的是相同的操作。我们也可以用积分符号 $\int$ 来表示原函数。当 $f(x)$ 是一个以 $F(x)$ 为原函数的函数时，我们有如下关系：

$$\begin{array}{rl}\int f(x)dx& =F(x)+C\end{array}$$

This means that $\int f(x)$ and $F(x)+C$ both represent the antiderivative or indefinite integral of $f(x)$.
这意味着 $\int f(x)$ 和 $F(x)+C$ 都表示 $f(x)$ 的原函数或不定积分。

Using our earlier example, since
用我们前面的例子来说，由于

$\frac{d}{dx}\frac{1}{4}{x}^4=x^3$,

we have
我们有

$\int x^{3}dx=\frac{1}{4}{x}^4+C$.

This is a more common format for antiderivatives, so make sure to familiarize yourself with rewriting antiderivatives using the symbol, $\int$. We call this the integral symbol. The function that’s being integrated is called the integrand.
这是原函数的一种更常见形式，所以一定要熟悉用符号$\int$来表示原函数。我们称这个符号为积分符号。被积分的函数称为被积函数。

How to find the antiderivative?

如何求原函数？

One way for us to find the antiderivative of a function is by working backward and recalling a derivative rule that may have been applied. Given $f(x)$, we’ll need to think of a function, $F(x)$, that satisfies the condition, $F^{\prime }(x)=f(x)$.
求函数原函数的一种方法是逆向推导，并回忆可能用到的求导法则。已知 $f(x)$，我们需要找到一个函数 $F(x)$，使其满足 $F^{\prime }(x)=f(x)$。

For example, if we want to find the antiderivative of $y=6$, we’re simply looking for a function that when differentiated, returns $6$. Recall that when we have $kx$, $\frac{d}{dx}kx=k$, where $k$ is a constant. This means that the antiderivative of $y=6$ is $6x+C$.
例如，如果我们想求 $y=6$ 的原函数，我们只是在寻找一个函数，对其求导后结果为 $6$。回想一下，当我们有 $kx$ 时，$\frac{d}{dx}kx=k$，其中 $k$ 是常数。这意味着 $y=6$ 的原函数是 $6x+C$。

$$\begin{array}{rl}\frac{d}{dx}6x& =6\\ \int 6dx& =6x+C\end{array}$$

We can apply a similar process to derive the different integral rules and antiderivative formulas. Below are a few examples of integral rules derived from known derivative rules.
我们可以用类似的方法推导出不同的积分法则和原函数公式。下面是一些由已知求导法则推导出的积分法则的例子。

$$\begin{array}{ccc}\frac{d}{dx}\sin x=\cos x& \Rightarrow & \int \cos xdx=\sin x+C\\ \frac{d}{dx}\cos x=-\sin x& \Rightarrow & \int -\sin xdx=\cos x+C\\ \frac{d}{dx}{e}^x=e^x& \Rightarrow & \int e^{x}dx=e^x+C\\ \frac{d}{dx}\frac{1}{n+1}\cdot x^{n+1}=x^n& \Rightarrow & \int x^{n}dx=\frac{x^{n+1}}{n+1}+C\end{array}$$

When finding the integral of more complex functions, combine indefinite integral properties and antiderivative rules. For now, take a look at this comprehensive list of helpful antiderivative rules.
在求更复杂函数的积分时，要结合不定积分性质和原函数法则。现在，来看一下这个实用的原函数法则综合列表。

List of antiderivative formulas

原函数公式列表

Here’s a list of integral or antiderivative formulas that will be handy when finding the antiderivative of a function. We’re showing the derivative rule used to come up with each integration rule shown to highlight how closely related these two concepts are.
下面是一系列积分或原函数公式，在求函数的原函数时会很有用。我们列出了推导出每个积分法则所用到的求导法则，以强调这两个概念之间的密切关系。

Differentiation Rule求导法则	Integration Rule 积分法则
$$\begin{array}{r}\frac{d}{dx}(k)=0\end{array}$$	$$\begin{array}{r}\int kdx=kx+C\end{array}$$
$$\begin{array}{r}\frac{d}{dx}(x^n)=n{x}^{n-1}\end{array}$$	$$\begin{array}{r}\int x^{n}dx=\frac{x^{n+1}}{n+1}+C\end{array}$$
$$\begin{array}{r}\frac{d}{dx}(\ln |x|)=\frac{1}{x}\end{array}$$	$$\begin{array}{r}\int \frac{1}{x}dx=\ln |x|+C\end{array}$$
$$\begin{array}{r}\frac{d}{dx}(e^x)=e^x\end{array}$$	$$\begin{array}{r}\int e^{x}dx=e^x+C\end{array}$$
$$\begin{array}{r}\frac{d}{dx}(\sin x)=\cos x\end{array}$$	$$\begin{array}{r}\int \cos xdx=\sin x+C\end{array}$$
$$\begin{array}{r}\frac{d}{dx}(\cos x)=-\sin x\end{array}$$	$$\begin{array}{r}\int \sin xdx=-\cos x+C\end{array}$$
$$\begin{array}{r}\frac{d}{dx}(\tan x)={\sec }^{2}x\end{array}$$	$$\begin{array}{r}\int {\sec }^{2}xdx=\tan x+C\end{array}$$
$$\begin{array}{r}\frac{d}{dx}(\csc x)=-\csc x\cot x\end{array}$$	$$\begin{array}{r}\int \csc x\cot xdx=-\csc x+C\end{array}$$
$$\begin{array}{r}\frac{d}{dx}(\sec x)=\sec x\tan x\end{array}$$	$$\begin{array}{r}\int \sec x\tan xdx=\sec x+C\end{array}$$
$$\begin{array}{r}\frac{d}{dx}(\cot x)=-{\csc }^{2}x\end{array}$$	$$\begin{array}{r}\int {\csc }^{2}xdx=-\cot x+C\end{array}$$
$$\begin{array}{r}\frac{d}{dx}({\sin }^{-1}x)=\frac{1}{\sqrt{1–x^2}}\end{array}$$	$$\begin{array}{r}\int \frac{1}{\sqrt{1–x^2}}dx={\sin }^{-1}x+C\end{array}$$
$$\begin{array}{r}\frac{d}{dx}({\tan }^{-1}x)=\frac{1}{1+x^2}\end{array}$$	$$\begin{array}{r}\int \frac{1}{1+x^2}dx={\tan }^{-1}x+C\end{array}$$
$$\begin{array}{r}\frac{d}{dx}({\sec }^{-1}|x|)=\frac{1}{x\sqrt{x^2-1}}\end{array}$$	$$\begin{array}{r}\int \frac{1}{x\sqrt{x^2–1}}dx={\sec }^{-1}|x|+C\end{array}$$

Here’s a list of integral or antiderivative formulas that will be handy when finding the antiderivative of a function. We’re showing the derivative rule used to come up with each integration rule shown to highlight how closely related these two concepts are.
下面是一系列积分或原函数公式，在求函数的原函数时会很有用。我们列出了推导出每个积分法则所用到的求导法则，以强调这两个概念之间的密切关系。

Applying the antiderivative formulas to integrate a function

应用原函数公式积分函数

Keep the formulas handy especially when integrating complex functions. By complex functions, we mean functions that may require two or more antiderivative rules before we can integrate the complex function.
要把这些公式放在手边，尤其是在对复杂函数积分时。所谓复杂函数，是指在对其积分之前可能需要用到两个或多个原函数法则的函数。

Aside from these antiderivative rules, these three integral properties will come in handy when integrating complex functions.
除了这些原函数法则外，在对复杂函数积分时，以下三个积分性质也会很有用。

$$\begin{array}{rl}\int k\cdot f(x)dx& =k\int f(x)dx\\ \int [f(x)+g(x)]dx& =\int f(x)dx+\int g(x)dx\\ \int [f(x)–g(x)]dx& =\int f(x)dx–\int g(x)dx\end{array}$$

These three properties are similar to the constant multiple, sum, and different properties of differentiation.
这三个性质与求导的常数倍数、和、差性质相似。

Follow the guide shown below whenever you need to integrate functions that contain multiple terms.
当你需要对包含多个项的函数积分时，请遵循下面的指南。

• Factor out the constants of the integrals whenever possible.
  尽可能地把积分中的常数因子提出来。

• Distribute the $\int$ symbol using the sum and difference properties of integration.
  利用积分的和差性质分配$\int$符号。

• Apply appropriate antiderivative formulas to each group of terms.
  对每一组项应用适当的原函数公式。

Let’s try finding the antiderivative of $f(x)=x^4–3x^3+4x^2–8$. Meaning, we need to evaluate $\int x^4–3x^3+4x^2–8dx$. Begin by distributing the integral operation then factoring out the constants from $3x^3$ and $4x^2$.
让我们试着求 $f(x)=x^4–3x^3+4x^2–8$ 的原函数。也就是说，我们需要计算 $\int x^4–3x^3+4x^2–8dx$。首先分配积分运算，然后从 $3x^3$ 和 $4x^2$ 中提取常数因子。

$$\begin{array}{rl}\int x^4–3x^3+4x^2-8dx& =\int x^{4}dx–\int 3x^{3}dx+\int 4x^{2}dx-\int 8dx\\ & =\int x^{4}dx–3\int x^{3}dx+4\int x^{2}dx-\int 8dx\end{array}$$

At this point, we’ll have to rely on the antiderivative formulas to simplify each term.
在这一步，我们必须依靠原函数公式来简化每一项。

• Apply the antiderivative formula, $\int x^{n}dx=\frac{x^{n+1}}{n+1}+C$, to simplify the first three terms.
  应用原函数公式 $\int x^{n}dx=\frac{x^{n+1}}{n+1}+C$ 来简化前三项。

$$\begin{array}{rl}\int x^{4}dx& =\frac{1}{5}{x}^5+C\end{array}$$	$$\begin{array}{rl}\int x^{3}dx& =\frac{1}{3}{x}^3+C\end{array}$$	$$\begin{array}{rl}\int x^{2}dx& =\frac{1}{2}{x}^2+C\end{array}$$

• Use the antiderivative formula, $\int kdx=kx+C$, to simplify the fourth term.
  用原函数公式$\int kdx=kx+C$来简化第四项。

$$\begin{array}{rl}\int 8dx& =8x+C\end{array}$$

• Since $C$ represents an arbitrary constant, we can simply use one $C$ at the end.
  由于 $C$ 表示任意常数，我们在最后只需用一个 $C$ 即可。

$$\begin{array}{rl}\int x^4–3x^3+4x^2-8dx& =\frac{1}{5}{x}^5–3\cdot \frac{x^{3+1}}{3+1}+4\cdot \frac{x^{2+1}}{2+1}–8x+C\\ & =\frac{1}{5}{x}^5–\frac{3}{4}{x}^4+\frac{4}{3}{x}^3–8x+C\end{array}$$

Hence, we’ve shown you how to integrate $f(x)=x^4–3x^3+4x^2–8$ using the different integral properties and formulas. We have shown that $\int x^4–3x^3+4x^2-8dx=\frac{1}{5}{x}^5–\frac{3}{4}{x}^4+\frac{4}{3}{x}^3–8x+C$.
因此，我们向你展示了如何利用不同的积分性质和公式对 $f(x)=x^4–3x^3+4x^2–8$ 进行积分。我们已经得出 $\int x^4–3x^3+4x^2-8dx=\frac{1}{5}{x}^5–\frac{3}{4}{x}^4+\frac{4}{3}{x}^3–8x+C$。

Apply similar processes when integrating the functions shown in the exercises below. But before that, make sure to take note of the antiderivative formulas we’ve provided as we’ll needing most of them in the examples shown.
在对下面练习中的函数积分时，应用类似的方法。但在此之前，一定要注意我们提供的原函数公式，因为在所示的例子中我们会用到其中的大部分。

Example 1

示例 1

Find the antiderivatives of the following functions:

求下列函数的原函数：

a. $\int x^{4}dx$

b. $\int \frac{1}{x^3}dx$

c. $\int \sqrt{x}dx$

d. $\int \frac{1}{x^e}dx$

Solution

解

All four functions contain only one term. Each term contains a base of $x$ and an exponent, so we’ll use the power rule for integration: $\int x^{n}dx=\frac{x^{n+1}}{n+1}+C$.
这四个函数都只包含一个项。每个项都以 $x$ 为底且带有指数，所以我们将使用积分的幂法则：$\int x^{n}dx=\frac{x^{n+1}}{n+1}+C$。

• Find the antiderivative by increasing the exponent by $1$.
  通过将指数加 1 来求原函数。

• Divide the resulting expression by new exponent of $x$.
  将得到的表达式除以$x$的新指数。

• Include a “$+C$” after the antiderivative to cover all functions belonging in the same family.
  在原函数后加上“$+C$”，以涵盖同一家族中的所有函数。

Let’s go ahead and evaluate $\int x^{4}dx$ using this approach.
让我们用这种方法来计算$\int x^{4}dx$。

$$\begin{array}{rl}\int x^{4}dx& =\frac{x^{4+1}}{4+1}+C\\ & =\frac{x^5}{5}+C\end{array}$$

Rewrite $\frac{1}{x^3}$ as a power of $x$: $\frac{1}{x^3}=x^{-3}$. With this form, we can find the antiderivative of the second function using the power rule.
将 $\frac{1}{x^3}$ 改写为 $x$ 的幂形式：$\frac{1}{x^3}=x^{-3}$。通过这种形式，我们可以用幂法则求出第二个函数的原函数。

$$\begin{array}{rl}\int \frac{1}{x^3}dx& =\int x^{-3}dx\\ & =\frac{x^{-3+1}}{-3+1}+C\\ & =\frac{x^{-2}}{-2}+C\\ & =-\frac{1}{2x^2}+C\end{array}$$

We’ll apply a similar process for the third item. Use the fact that $\sqrt{x}=x^{\frac{1}{2}}$.
对于第三个函数，我们将应用类似的方法。利用$\sqrt{x}=x^{\frac{1}{2}}$这一事实。

$$\begin{array}{rl}\int \sqrt{x}dx& =\int x^{\frac{1}{2}}dx\\ & =\frac{x^{\frac{1}{2}+1}}{\frac{1}{2}+1}+C\\ & =\frac{x^{\frac{3}{2}}}{\frac{3}{2}}+C\\ & =\frac{2}{3}{x}^{\frac{3}{2}}+C\end{array}$$

For the fourth function, we’ll still be using the power rule and treat $e$ as a constant found at the exponent. Begin by rewriting $\frac{1}{x^e}$ as $x^{-e}$.
对于第四个函数，我们仍将使用幂法则，并将 $e$ 视为指数中的常数。首先将 $\frac{1}{x^e}$ 改写为 $x^{-e}$。

$$\begin{array}{r}\int \frac{1}{x^e}dx=\int x^{-e}dx\\ =\frac{x^{-e+1}}{-e+1}+C\\ =\frac{x^{1-e}}{1-e}+C\end{array}$$

Hence, we have the following antiderivatives:
因此，我们得到以下原函数：

a. $\int x^{4}dx=\frac{x^5}{5}+C$

b. $\int \frac{1}{x^3}dx=-\frac{1}{2x^2}+C$

c. $\int \sqrt{x}dx=\frac{2}{3}{x}^{\frac{3}{2}}+C$

d. $\int \frac{1}{x^e}dx=\frac{x^{1-e}}{1-e}+C$

Example 2

示例 2

Find the antiderivatives of the following functions:
求下列函数的原函数：

a. $\int 4x^{3}dx$

b. $\int \frac{1}{3x^2}dx$

c. $\int (4x^2–2x+5)dx$

d. $\int (\sin x–\cos x)dx$

Solution

解

Each of the four functions requires two or more rules of integration. We’ll break down the process for each item and include the antiderivative formulas used.
这四个函数中的每一个都需要用到两个或更多的积分法则。我们将分解每个函数的求解过程，并列出所使用的原函数公式。

Let’s begin working on the first function – $\int 4x^{3}dx$.

让我们开始处理第一个函数——$\int 4x^{3}dx$。

• Factor out $4$ from the integral expression using the integral property, $\int kf(x)dx=k\int f(x)dx$.
  利用积分性质 $\int kf(x)dx=k\int f(x)dx$，从积分表达式中提取 $4$。

• Integrate the expression, $\int x^{3}dx$, using the power rule: $\int x^{n}dx=\frac{x^{n+1}}{n+1}+C$.
  用幂法则对表达式 $\int x^{3}dx$ 积分：$\int x^{n}dx=\frac{x^{n+1}}{n+1}+C$。

$$\begin{array}{rl}4x^{3}dx& =4\int x^{3}dx\\ & =4\cdot \frac{x^{3+1}}{3+1}+C\\ & =4\cdot \frac{x^4}{4}+C\\ & =x^4+C\end{array}$$

For the second function, rewrite $\frac{1}{3x^2}x$ as $\frac{1}{3}{x}^{-2}$ first. Use the same rules to find its antiderivative.
对于第二个函数，首先将 $\frac{1}{3x^2}x$ 改写为 $\frac{1}{3}{x}^{-2}$。用同样的法则求其原函数。

$$\begin{array}{rl}\int \frac{1}{3x^2}dx& =\int \frac{1}{3}{x}^{-2}dx\\ & =\frac{1}{3}\int x^{-2}dx\\ & =\frac{1}{3}\cdot \frac{x^{-2+1}}{-2+1}+C\\ & =\frac{1}{3}\cdot \frac{x^{-1}}{-1}+C\\ & =-\frac{1}{3x}+C\end{array}$$

For the third function, apply the sum and difference properties first. Integrate each of the term using the constant multiple and power rules.
对于第三个函数，首先应用和差性质。利用常数倍数法则和幂法则对每一项积分。

• Distribute the integral operation to each term.
  将积分运算分配到每一项。

• Factor out $4$ and $2$ out of the integrands and apply the antiderivative formula, $\int x^{n}dx=\frac{x^{n+1}}{n+1}+C$.
  从被积函数中提取 $4$ 和 $2$，并应用原函数公式$\int x^{n}dx=\frac{x^{n+1}}{n+1}+C$。

• Integrate the third expression using the integration rule, $\int kdx=kx+C$.
  用积分法则 $\int kdx=kx+C$ 对第三个表达式积分。

$$\begin{array}{rl}\int (4x^2-2x+5)dx& =\int 4x^{2}dx–\int 2xdx+\int 5dx\\ & =4\int x^{2}dx–2\int xdx+\int 5dx\\ & =4\cdot \frac{x^{2+1}}{2+1}–2\cdot \frac{x^{1+1}}{1+1}+\int 5dx\\ & =\frac{4}{3}{x}^3–x^2+5x+C\end{array}$$

Before working on the fourth function, recall that $\int \sin xdx=–\cos x$ and $\int \cos xdx=\sin x$. Use these two antiderivative formulas when finding the antiderivative of the function.
在处理第四个函数之前，回想一下 $\int \sin xdx=–\cos x$ 和 $\int \cos xdx=\sin x$。在求该函数的原函数时，使用这两个原函数公式。

$$\begin{array}{rl}\int (\cos x–\sin x)dx& =\int \cos xdx–\int \sin xdx\\ & =(-\sin x)–(\cos x)+C\\ & =-\sin x–\cos x+C\end{array}$$

Hence, we have the following antiderivatives:
因此，我们得到以下原函数：

a. $\int 4x^{3}dx=x^4+C$

b. $\int \frac{1}{3x^2}dx=-\frac{1}{3x}+C$

c. $\int (4x^2-2x+5)dx=\frac{4}{3}{x}^3-x^2+5x+C$

d. $\int (\sin x–\cos x)dx=-\sin x–\cos x+C$

Example 3

示例 3

Find the antiderivative of the function $f(x)=\frac{x^6–3x^4+1}{x^3}$.
求函数$f(x)=\frac{x^6–3x^4+1}{x^3}$的原函数。

Solution

解

We want to find $\int \frac{x^6–3x^4+1}{x^3}dx$. We don’t have an equivalent quotient rule for integration, so what we can do is rewrite the integrand by dividing each term of the numerator by the denominator.
我们要求 $\int \frac{x^6–3x^4+1}{x^3}dx$。我们没有对应的积分商法则，所以我们可以通过将分子的每一项除以分母来重写被积函数。

$$\begin{array}{rl}\int \frac{x^6-3x^4+1}{x^3}dx& =\int \left(\frac{x^6}{x^3}-\frac{3x^4}{x^3}+\frac{1}{x^3}\right)dx\\ & =\int \left(x^3–3x+\frac{1}{x^3}\right)dx\end{array}$$

Focus on each of the integral expressions and use the different antiderivative rules we’ve just learned to evaluate each expression.
关注每个积分表达式，并使用我们刚刚学到的不同原函数法则来计算每个表达式。

$$\begin{array}{r}\int {\mathbf{x}}^3\mathbf{dx}\end{array}$$	$$\begin{array}{rl}\int x^{3}dx& =\frac{x^{3+1}}{3+1}+C\\ & =\frac{x^4}{4}+C\end{array}$$
$$\begin{array}{r}\int 3\mathbf{x}\mathbf{dx}\end{array}$$	$$\begin{array}{rl}\int 3xdx& =3\int xdx\\ & =3\cdot \frac{x^{1+1}}{1+1}+C\\ & =\frac{3x^2}{2}+C\end{array}$$
$$\begin{array}{r}\int \frac{1}{{\mathbf{x}}^3}\mathbf{dx}\end{array}$$	$$\begin{array}{rl}\int \frac{1}{x^3}dx& =\int x^{-3}dx\\ & =\frac{x^{-3+1}}{-3+1}+C\\ & =\frac{x^{-2}}{-2}+C\\ & =-\frac{1}{2x^2}\end{array}$$

Going back to our previous expression, distribute the integral operation and use the antiderivatives shown above:

回到我们之前的表达式，分配积分运算并使用上面所示的原函数：

$$\begin{array}{rl}\int x^{3}dx–\int 3xdx+\int \frac{1}{x^3}dx& =\left(\frac{x^4}{4}\right)–\left(\frac{3x^2}{2}\right)+\left(-\frac{1}{2x^2}\right)+C\\ & =\frac{x^4}{4}–\frac{3x^2}{2}-\frac{1}{2x^2}+C\end{array}$$

Hence, the antiderivative of $f(x)$ is equal to
因此，$f(x)$ 的原函数等于

$\frac{x^4}{4}–\frac{3x^2}{2}-\frac{1}{2x^2}+C$.

Practice Questions

练习题

1. Find the antiderivatives of the following functions:
   求下列函数的原函数：

   a. $\int x^{5}dx$

   b. $\int \frac{1}{x^4}dx$

   c. $\int \sqrt[3]{x^2}dx$

   d. $\int \frac{1}{x^{\pi }}dx$

2. Find the antiderivatives of the following functions:
   求下列函数的原函数：

   a. $\int -6x^{5}dx$

   b. $\int \frac{1}{3x^4}dx$

   c. $\int (3x^4–6x^2+12)dx$

   d. $\int (\frac{1}{x}–{\sec }^{2}x)dx$

3. Find the antiderivatives of the following functions:
   求下列函数的原函数：

   a. $\int 6\sqrt{x}–\sqrt[5]{x}dx$

   b. $\int \frac{4x^3–5}{x^2}dx$

   c. $\int (3e^x–8{\sec }^{2}x)dx$

   d. $\int \frac{6–5x^6–2x^3}{x^3}dx$

Answer Key

答案

1. –

   a. $\int x^{5}dx=\frac{x^6}{6}+C$

   b. $\int \frac{1}{x^4}dx=-\frac{1}{3x^3}+C$

   c. $\int \sqrt[3]{x^2}dx=\frac{3}{5}{x}^{\frac{5}{3}}+C$

   d. $\int \frac{1}{x^{\pi }}dx=\frac{x^{1–\pi }}{1–\pi }+C$

2. –

   a. $\int -6x^{5}dx=–x^6+C$

   b. $\int \frac{1}{3x^4}dx=-\frac{1}{9x^3}+C$

   c. $\int (3x^4–6x^2+12)dx=\frac{3x^5}{5}–2x^3+12x+C$

   d. $\int (\frac{1}{x}–{\sec }^{2}x)dx=\ln |x|–\tan x+C$

3. –

   a. $\int 6\sqrt{x}–\sqrt[5]{x}dx=\frac{x^4}{4}–\frac{3x^2}{2}-\frac{1}{2x^2}+C$

   b. $\int \frac{4x^3–5}{x^2}dx=2x^2+\frac{5}{x}+C$

   c. $\int (3e^x–8{\sec }^{2}x)dx=3e^x-8\tan \left(x\right)+C$

   d. $\int \frac{6–5x^6–2x^3}{x^3}dx=-\frac{3}{x^2}-\frac{5x^4}{4}-2x+C$

---

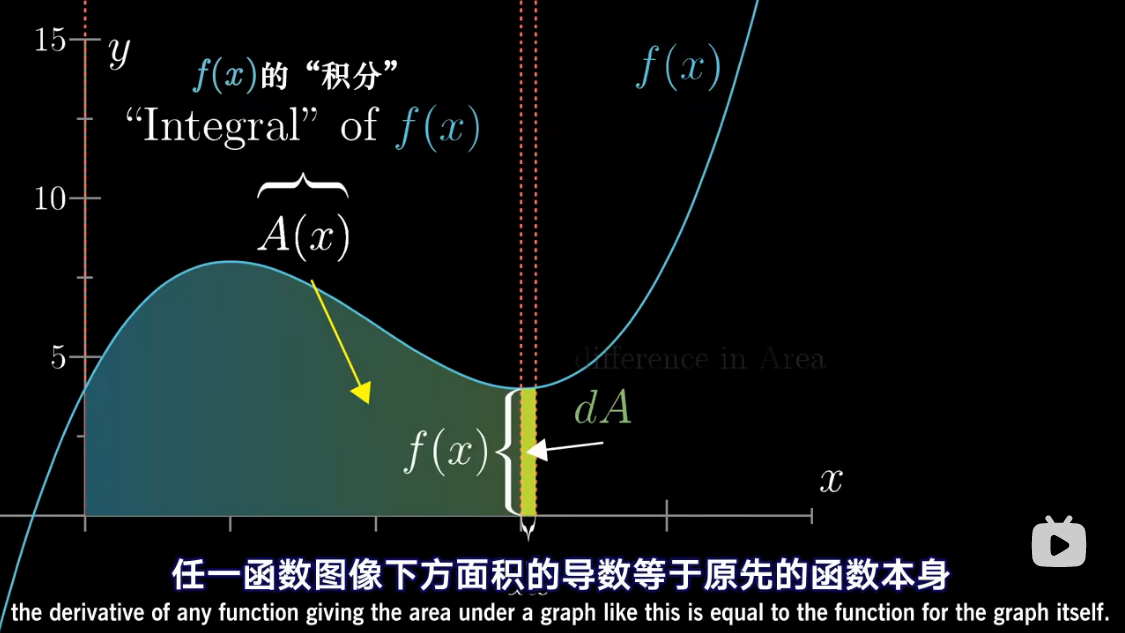
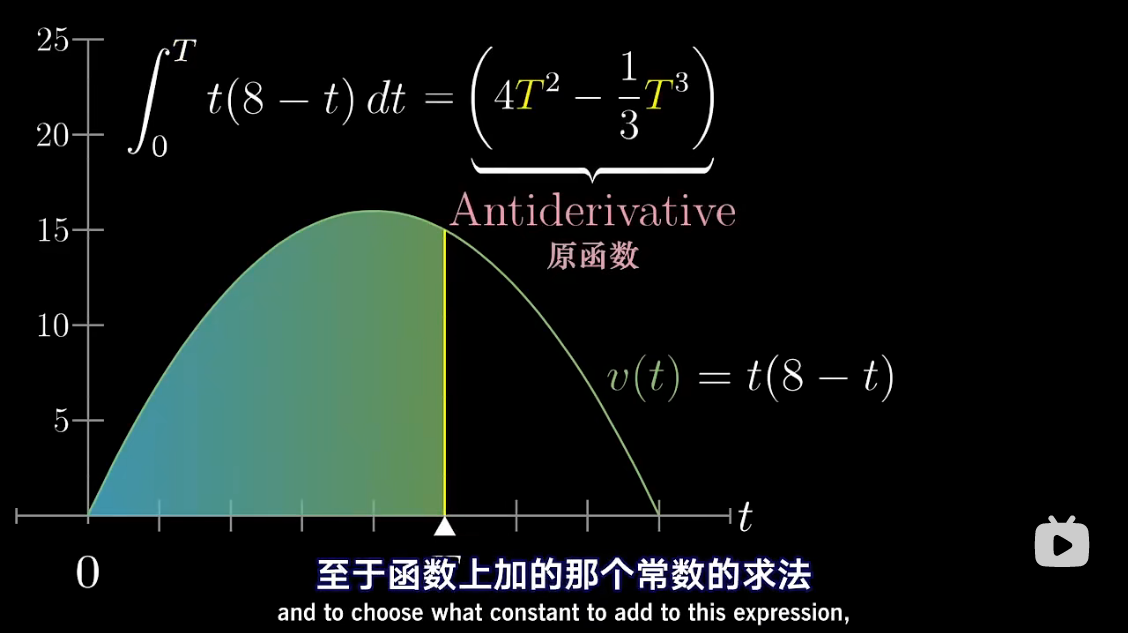
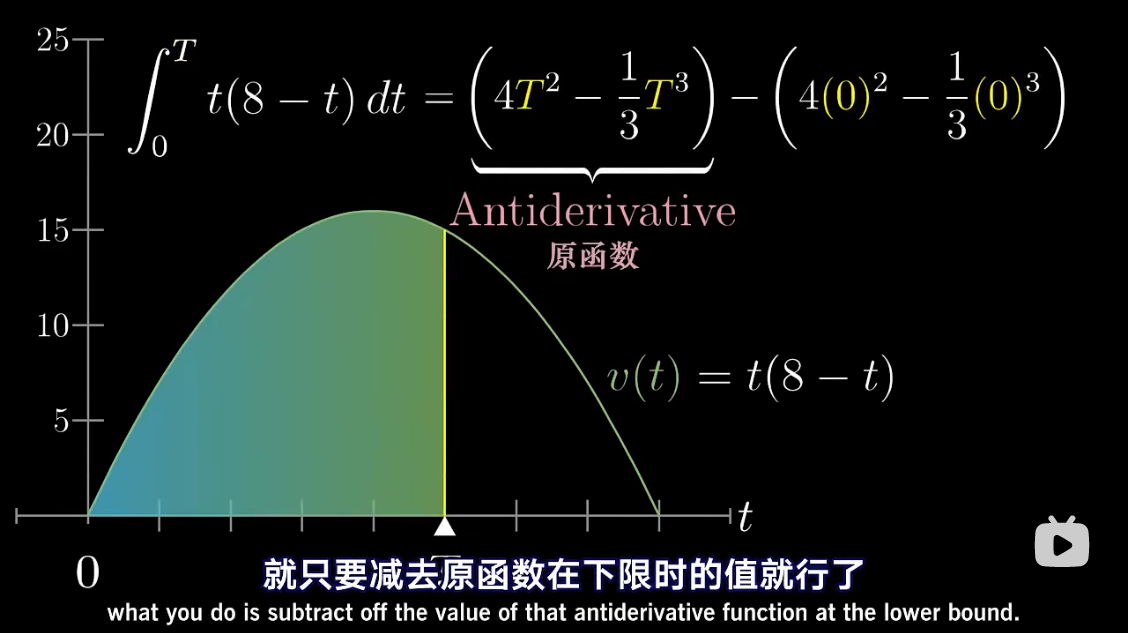
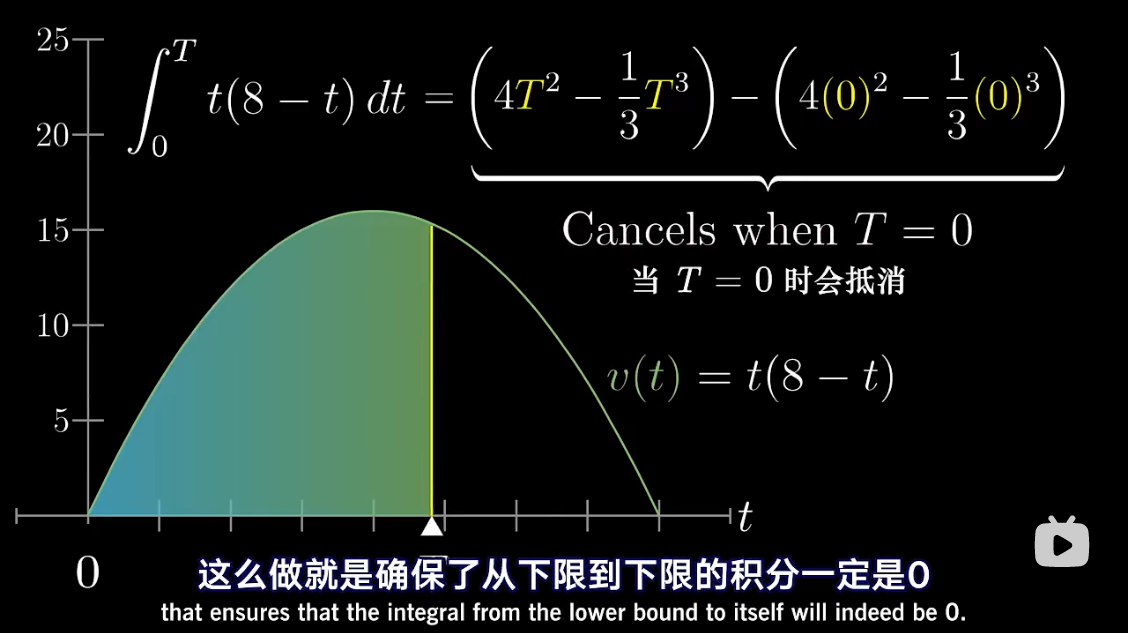
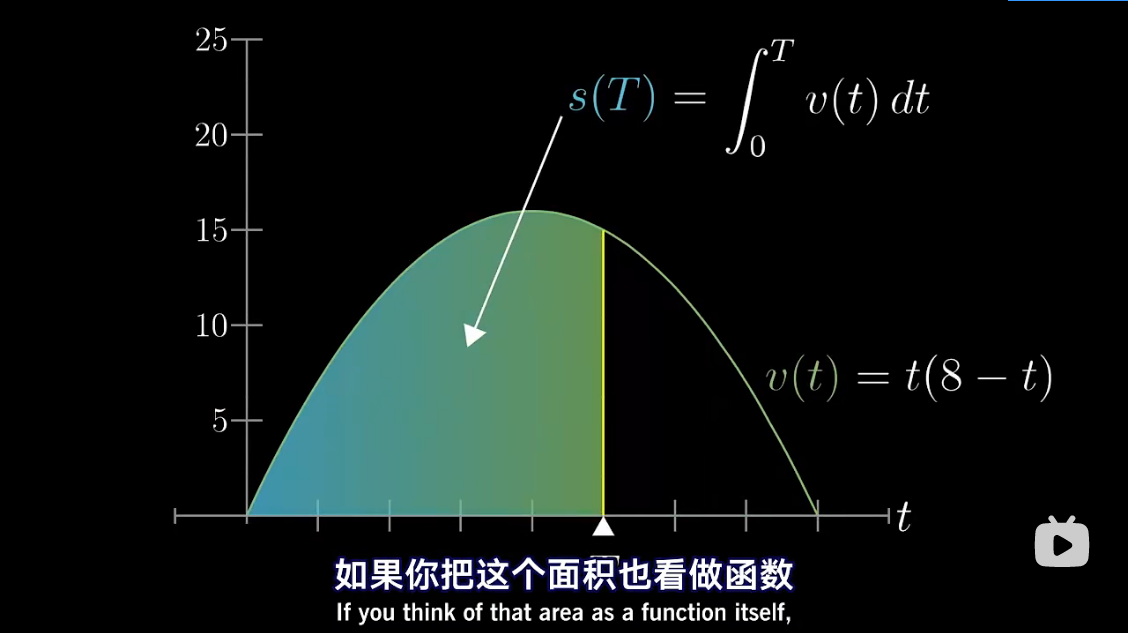
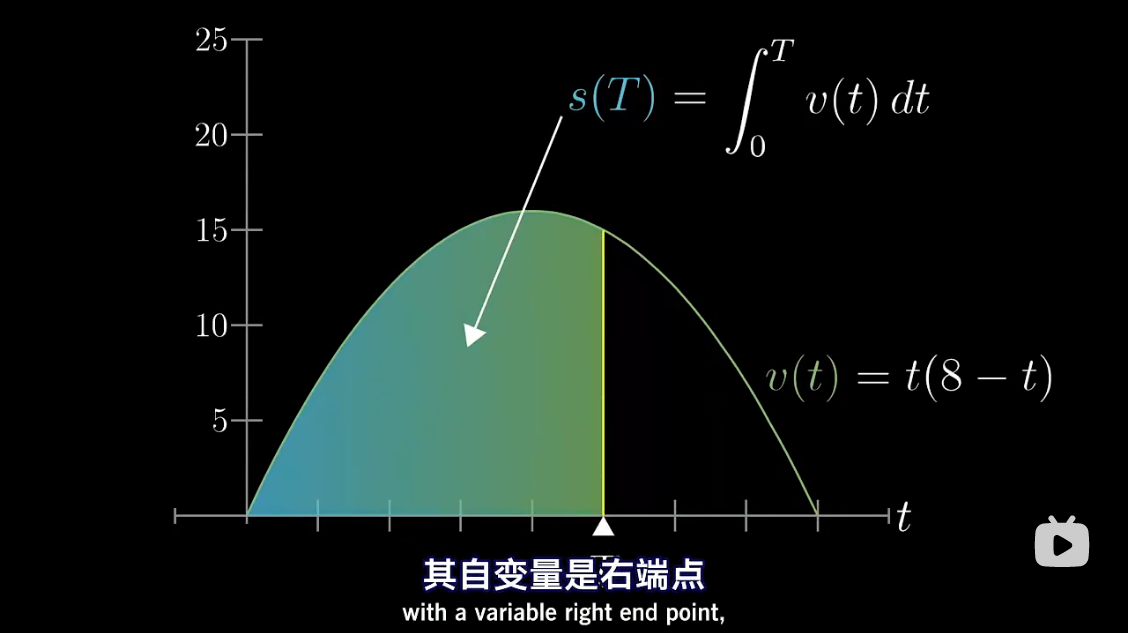
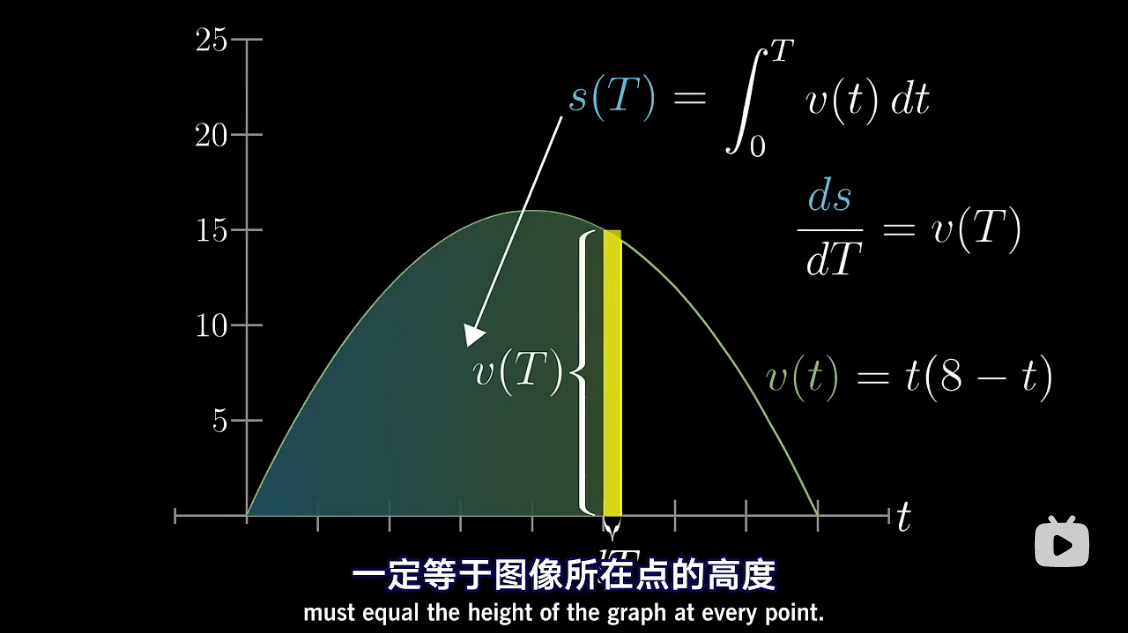
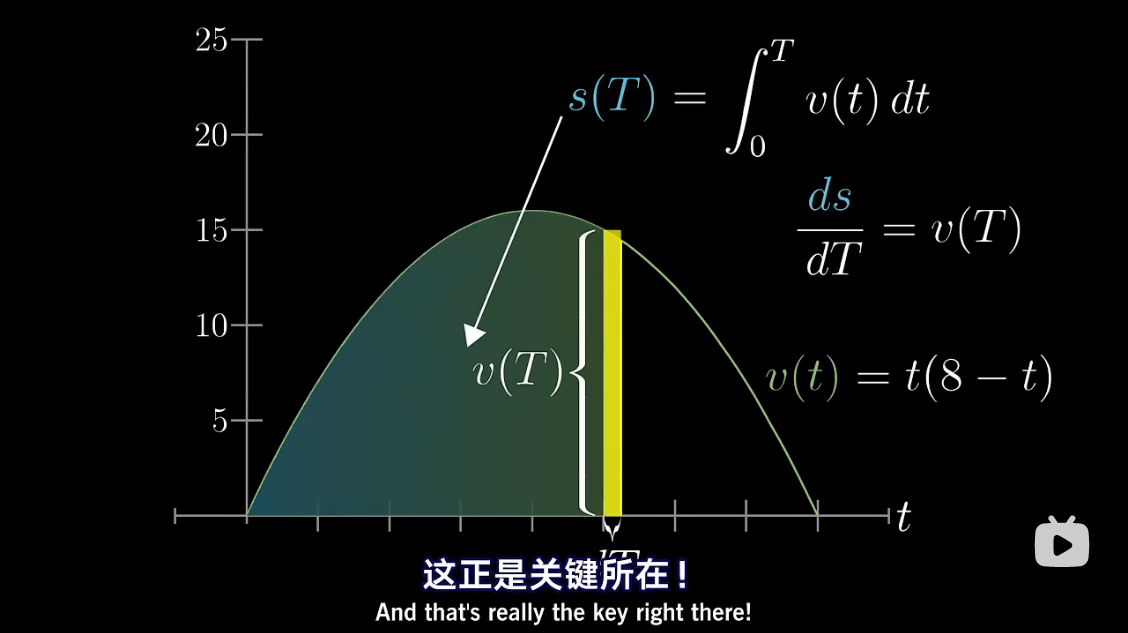
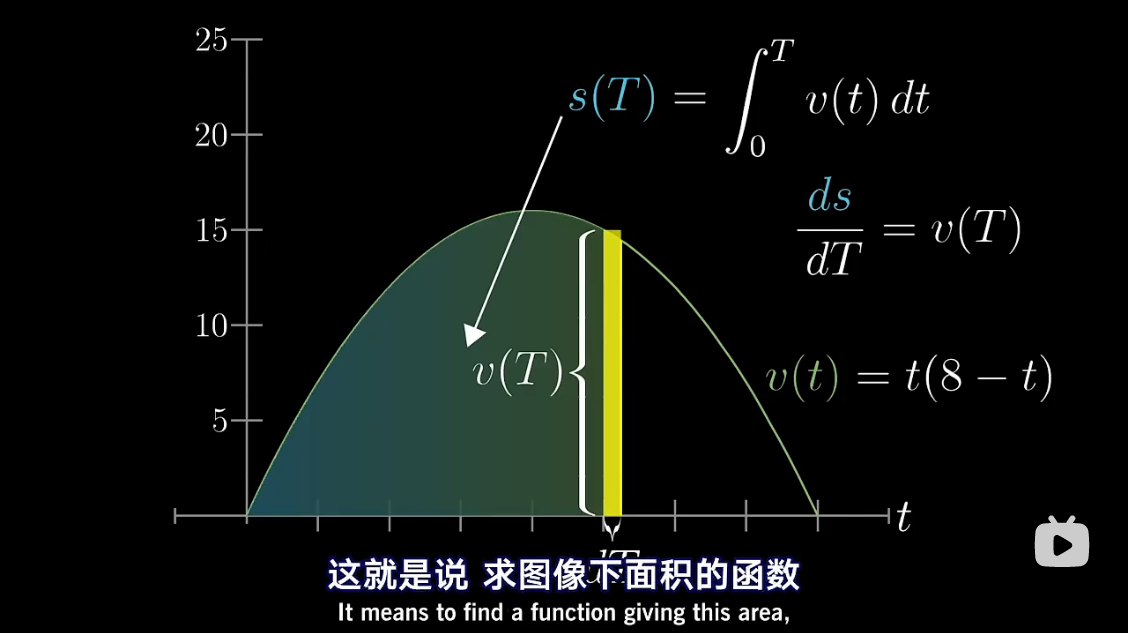
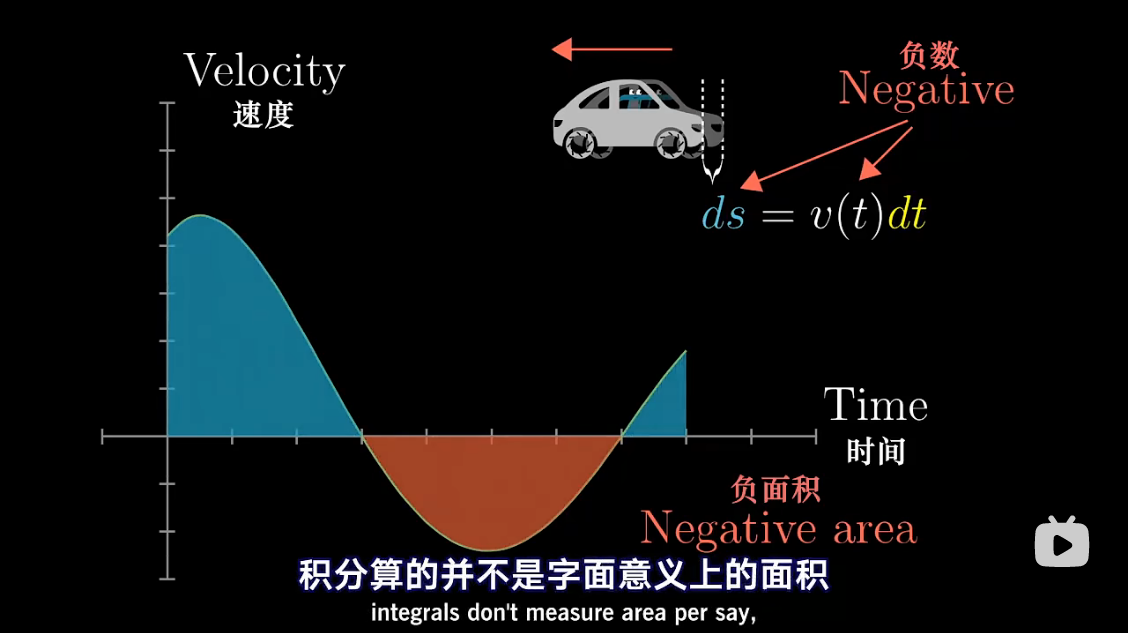
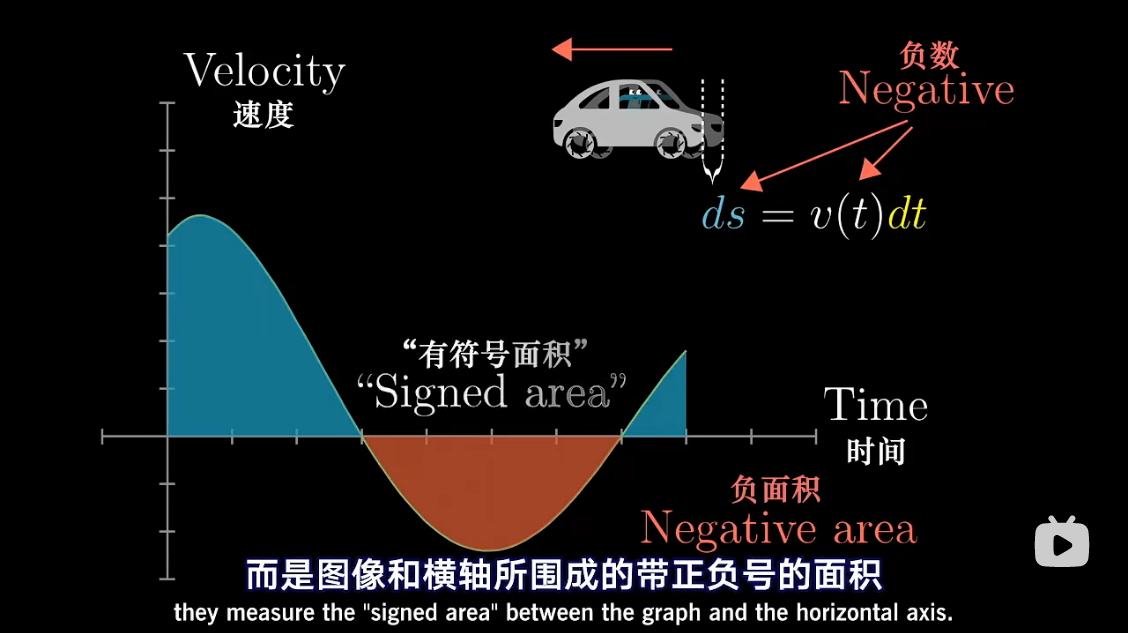
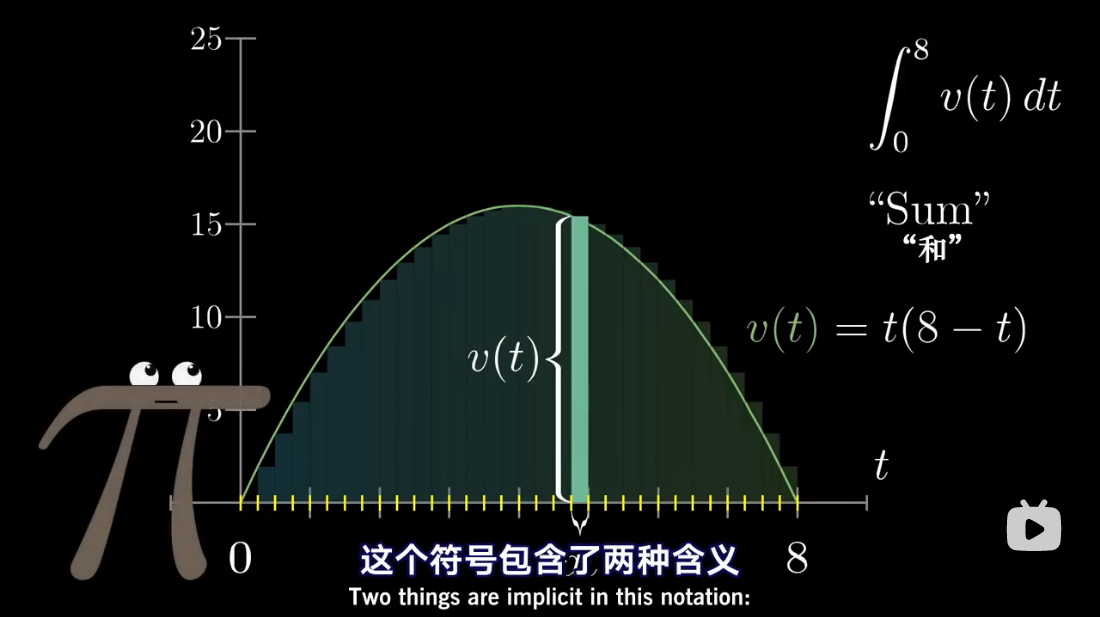
图解 antiderivative

 

---

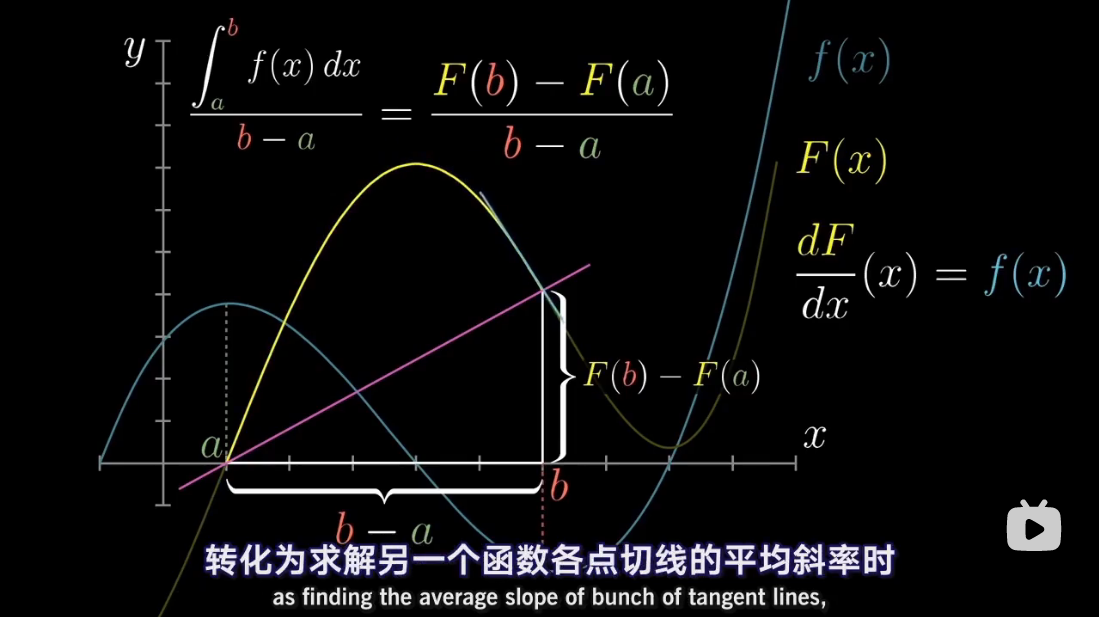
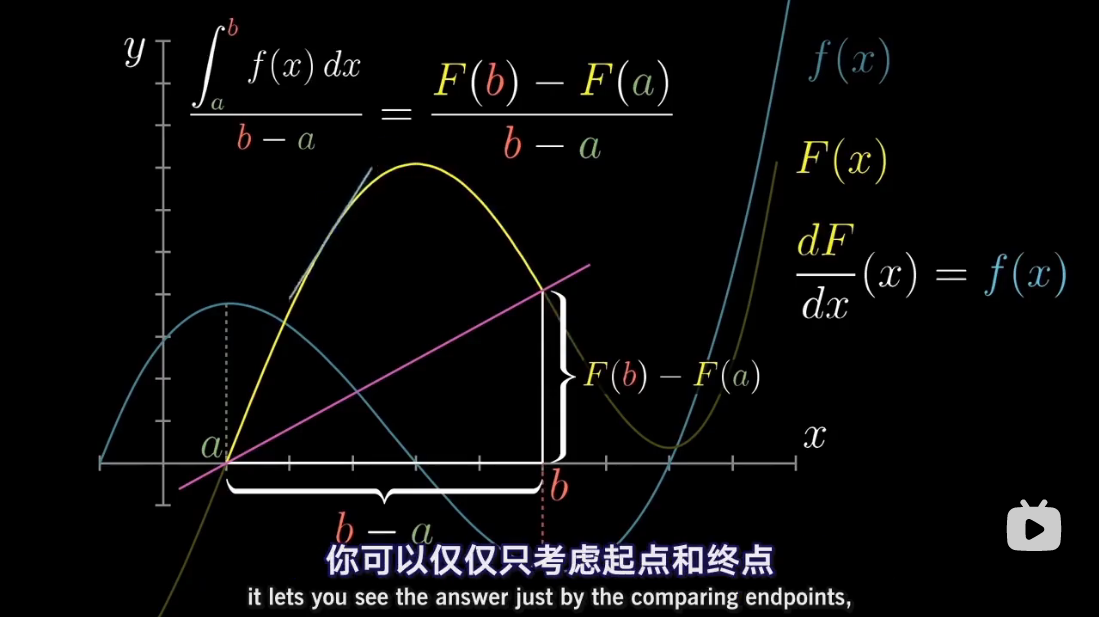
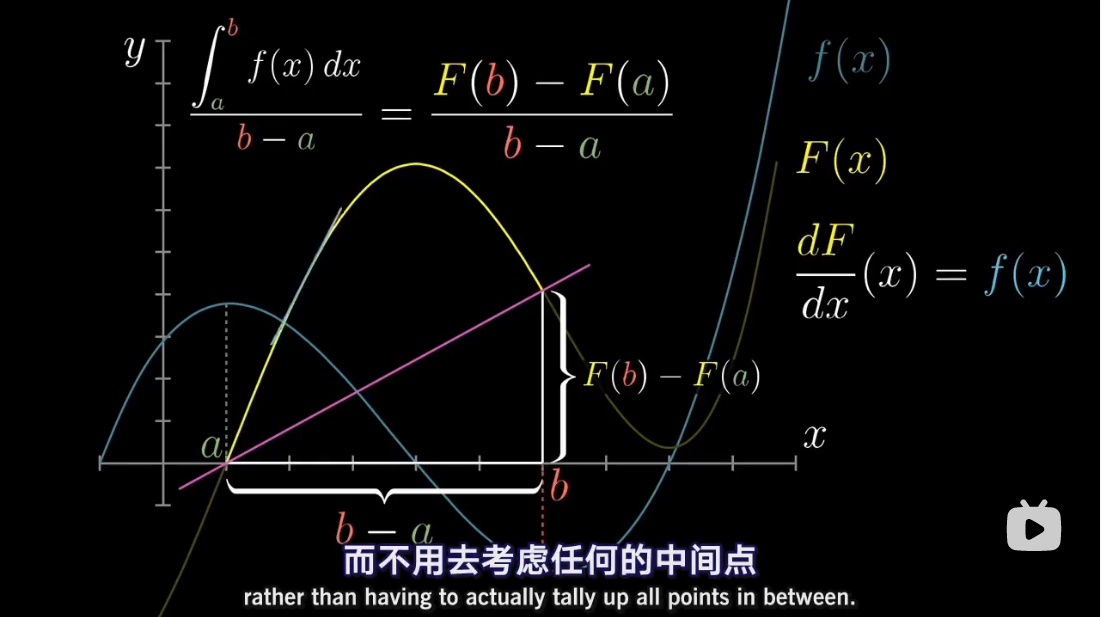
via：

• Antiderivative - Definition, Techniques, and Examples
  https://www.storyofmathematics.com/antiderivative/

• Antiderivative Rules - List, Formulas, Examples | What are Antidifferentiation Rules?
  https://www.cuemath.com/calculus/antiderivative-rules/

• Antiderivative Formula - Learn to Find the Antiderivative.
  https://www.cuemath.com/antiderivative-formula/

• Antiderivative of ln x - Formula, Proof, Examples, FAQs
  https://www.cuemath.com/calculus/antiderivative-of-lnx/

• lessonr.pdf - Derivatives and antiderivatives
  https://www.math.purdue.edu/~egbertn/sp2017/notes/lessonr.pdf