自动机理论 | 模型、应用及形式语言理论

原创已于 2025-11-28 13:00:34 修改 · 879 阅读

22 ·

CC 4.0 BY-SA版权

文章标签：

#自动机理论

于 2025-11-28 11:51:01 首次发布

computer science 专栏收录该内容

38 篇文章

订阅专栏

注：本文为 “自动机理论” 相关合辑。
中文引文，略作重排。
英文讨论，机翻未校。
未整理去重，如有内容异常，请看原文。

自动机、状态机及相关概念

一、基础概念

（一）自动机（Automaton）

自动机是有限状态机（Finite State Machine，FSM）的数学抽象模型，用于描述具有离散输入、输出和有限内部状态的动态系统的行为规律，是自动机理论的主要研究对象。

（二）状态机（State Machine）

状态机通常指有限状态机（Finite State Machine，FSM）的简称，是一种用于建模具有状态变化特性的对象或系统的工具。通过明确状态集合、状态转移规则及输入输出关系，刻画系统的动态行为。

（三）有限自动机（Finite Automata Machine，FAM）

有限自动机是计算机科学中的基础模型，在软件开发领域常被称作有限状态机（Finite State Machine，FSM），同时也是一种广泛应用的软件设计模式。其关键特征是系统仅包含有限个状态，且状态转移完全由输入和当前状态决定。

（四）有限状态机（Finite State Machine，FSM）

1. 形式化定义

一个有限状态机 $M$ 由六元组构成：
$(\Phi, O, S, \delta, f, \sigma_0)$
其中：

$\Phi$ ：有限输入符号集合；
$O$ ：有限输出符号集合；
$S$ ：有限状态集合；
$\delta$ ：状态转移函数， $\delta: S \times \Phi \to S$ ，描述当前状态与输入符号映射到下一状态的规则；
$f$ ：输出函数， $\times \Phi \to O$ （或 $\to O$ ，依类型而定），定义输出与状态、输入的关联；
$\sigma_0 \in S$ ：初始状态。

2. 分类及特征

根据输出与输入、系统状态的关系，有限状态机可分为 Moore 型和 Mealy 型两类，二者通过状态转移图直观区分（转移图为有向图，圆表示状态，有向曲线表示状态转移，指向初始状态的箭头标注起始点）。

（1）Mealy 型有限状态机

输出与系统状态和输入均相关。状态转移图中，有向曲线段标注输入和输出，以“/”分隔。

Mealy 型状态机

示例：图 1 所示 Mealy 型状态机含 1 位输入、1 位输出，两个状态 $A_1$ 和 $A_2$ ，初始状态为 $A_1$ 。
- 状态 $A_1$ 上自环曲线标注“1/0”，表示状态为 $A_1$ 且输入为 1 时，状态不变，输出为 0。
- $A_1$ 指向 $A_2$ 的箭头标注“0/1”，表示状态为 $A_1$ 且输入为 0 时，状态转为 $A_2$ ，输出为 1。
- 状态 $A_2$ 上自环曲线标注“1/1”，表示状态为 $A_2$ 且输入为 1 时，状态不变，输出为 1。
- $A_2$ 指向 $A_1$ 的箭头标注“0/0”，表示状态为 $A_2$ 且输入为 0 时，状态转为 $A_1$ ，输出为 0。
  复杂状态机的有向箭头可添加字符说明补充信息。

（2）Moore 型有限状态机

输出仅与系统状态相关，与输入信号无关，优势是实现输入与输出的分离。状态转移图中，输出值标注在状态后，以“/”分隔，输入信号标注在有向线段上。

Moore 型状态机

示例：图 2 所示 Moore 型状态机含 1 位输入、1 位输出，两个状态 $A_1$ 和 $A_2$ ，初始状态为 $A_1$ 。
- 状态标注“ $A_1/1$ ”表示处于 $A_1$ 时输出为 1，“ $A_2/0$ ”表示处于 $A_2$ 时输出为 0。
- 状态 $A_1$ 上自环曲线标注“1”，表示状态为 $A_1$ 且输入为 1 时，状态不变。
- $A_1$ 指向 $A_2$ 的箭头标注“0”，表示状态为 $A_1$ 且输入为 0 时，状态转为 $A_2$ 。
- 状态 $A_2$ 上自环曲线标注“0”，表示状态为 $A_2$ 且输入为 0 时，状态不变。
- $A_2$ 指向 $A_1$ 的箭头标注“1”，表示状态为 $A_2$ 且输入为 1 时，状态转为 $A_1$ 。
  对于输出取值为 ${0,1\}$ 的 Moore 型有限状态机，可称其为有限状态自动机，其转移图另有表示方式：用双圆环标注输出为 1 的状态，该状态称为接受状态。

接受状态表示

（五）有限状态自动机（Finite State Automaton，FSA / Finite State Machine，FSM）

1. 定义

有限状态自动机（Finite State Automaton，FSA）是一种抽象的计算模型，用于研究具有有限内存的计算过程及其对应的形式语言。它同时也是描述具有离散输入和输出的系统的数学模型。

2. 主要特征

有限状态集：系统具有有限个状态，每个状态对应不同的功能或处理逻辑。
输入字母表：输入字符串的字符构成字母表（Alphabet），所有输入串均为该字母表上的字符串。
状态转移：系统在任意状态下读入一个字符，根据当前状态和该字符通过状态转移函数（Transition Function）确定下一状态。
初始状态：存在唯一的初始状态（Start State）作为系统行为的起始点。
接受状态：存在若干终止状态（Accepting States），若输入串结束时系统处于终止状态，则表示该字符串被自动机接受。

3. 形式化定义

有限状态自动机（FA）由五元组构成：
$\Sigma, \delta, q_0, F)$
其中：

$Q$ ：非空有限的状态集合（State Set）， $\forall q \in Q$ ， $q$ 称为 $M$ 的一个状态。
$\Sigma$ ：非空有限的输入字母表（Input Alphabet）。
$\delta$ ：状态转移函数（Transition Function）， $\delta: Q \times \Sigma \to Q$ ，满足 $\delta(q,a)=p$ （ $\in Q$ ， $\in \Sigma$ ）。
$q_0 \in Q$ ：初始状态（Start State）。
$\subseteq Q$ ：接受状态集合（Accepting States）。

4. 工作原理

自动机从初始状态 $q_0$ 开始，逐一读入输入串（由 $\Sigma$ 中字符构成）的每个字符，根据当前状态、输入字符和转移函数 $\delta$ 确定下一步状态。当输入串结束时，若自动机处于 $F$ 中的某一状态，则接受该字符串；否则拒绝。

（六）确定性有限状态自动机（Deterministic Finite Automaton，DFA）

1. 形式化定义

确定性有限状态自动机（DFA）由五元组构成：
$\Sigma, \delta, q_0, F)$
其中：

$Q$ ：非空有限的状态集合。
$\Sigma$ ：非空有限的输入字母表。
$\delta$ ：确定性状态转移函数（Deterministic Transition Function）， $\delta: Q \times \Sigma \to Q$ ，满足 $\delta(q, \sigma)=p$ （ $\in Q$ ， $\sigma \in \Sigma$ ），对于每个状态和输入符号，存在唯一确定的下一状态。
$q_0 \in Q$ ：初始状态。
$\subseteq Q$ ：接受状态集合。

2. 特性

对于任何状态 $\in Q$ 和输入符号 $\in \Sigma$ ， $\delta(q,a)$ 必须存在且唯一。
同一状态下，不同输入符号可能导致不同的转移结果。
确定性意味着在任何时刻只有一条可能的转移路径。

（七）非确定性有限状态自动机（Non-Deterministic Finite Automaton，NFA）

1. 形式化定义

非确定性有限状态自动机（NFA）由五元组构成：
$\Sigma, \delta, q_0, F)$
其中：

$Q$ ：非空有限的状态集合。
$\Sigma$ ：非空有限的输入字母表。
$\delta$ ：非确定性状态转移函数（Non-Deterministic Transition Function）， $\delta: Q \times \Sigma \to 2^Q$ ，即映射到状态集的幂集，表示同一状态下接收同一输入时可能存在多个不确定的下一状态。
$q_0 \in Q$ ：初始状态。
$\subseteq Q$ ：接受状态集合。

2. 特性

对于状态 $\in Q$ 和输入符号 $\in \Sigma$ ， $\delta(q,a)$ 可以是空集、单一状态或多个状态的集合。
非确定性意味着在某些情况下存在多条可能的转移路径。
一个输入串被接受的条件是存在至少一条路径能够从初始状态到达接受状态。

3. 扩展定义（可选）

某些定义中，NFA 的转移函数可能扩展为 $\delta: Q \times \Sigma \cup \{\epsilon\} \to 2^Q$ ，其中 $\epsilon$ 表示空串转移（ $\epsilon$ -closure），但本定义中不包含此扩展。

二、概念间的关联与区别

（一）关联关系

术语等价性：有限自动机（FAM）与有限状态机（FSM）在软件开发领域表述等价，有限状态自动机（FSA）是 Moore 型有限状态机的特殊形式（输出取值为 ${0,1\}$ ）。
模型层级：自动机是有限状态机（FSM）的数学抽象模型，有限状态机是自动机理论在具体领域的应用体现。
相互转换：确定性有限状态自动机（DFA）与非确定性有限状态自动机（NFA）可相互转换，二者模型结构一致，仅状态转移函数存在差异。

（二）区别

自动机与状态机：自动机侧重数学理论层面的抽象描述，状态机侧重工程应用中的建模工具属性。
DFA 与 NFA：二者唯一区别在于状态转移函数：
- DFA 的转移函数为单值映射，每个（状态，输入）对对应唯一下一状态。
- NFA 的转移函数为多值映射，每个（状态，输入）对可能对应多个下一状态。
Moore 型与 Mealy 型 FSM：输出依赖关系不同：
- Moore 型输出仅依赖当前状态。
- Mealy 型输出依赖当前状态和输入。

三、应用领域

有限状态机（含有限自动机）作为一种通用建模工具，在多个学科和工程领域具有广泛应用：

计算机科学：用于计算机体系结构研究、逻辑操作分析、程序设计优化、计算复杂性理论研究，具体应用包括数字电路设计、游戏开发、单片机开发、状态机设计模式实现、基于事件转移的状态机工作流等。
语言学：作为语言识别器，用于各类形式语言的研究。
神经生理学：定义为神经网络的动态模型，用于研究神经生理活动、思维规律及人脑机制。
生物学：作为生命体生长发育模型，用于分析新陈代谢过程和遗传变异规律。
数学：用于定义可计算函数，支撑各类算法的研究与验证。

半自动机（转移系统）的规范定义与模型

一、定义与结构

1. 基本定义

半自动机（转移系统）是自动机理论中无输出函数的有限状态机，其核心模型仅包含状态集合、输入字母表和转移函数，专注于描述状态转移过程。

2. 模型要素

半自动机的标准模型由以下三个必备要素构成（部分文献会根据应用场景补充可选要素）：

状态集合（记为 $Q$ ）：
- 非空有限集，表示系统所有可能状态。
- 例如：交通信号灯的状态集合 $Q = \{红, 绿, 黄\}$ 。
输入字母表（记为 $\Sigma$ ）：
- 非空有限集，表示所有可能输入符号。
- 例如：控制信号灯切换的输入字母表 $\Sigma = \{触发\}$ 。
转移函数（记为 $\delta$ ）：
- 确定性半自动机： $\delta: Q \times \Sigma \to Q$
- 非确定性半自动机： $\delta: Q \times \Sigma \to 2^Q$
- 例如： $\delta(红, 触发) = 绿$ 表示系统从"红灯"状态接收"触发"输入后迁移至"绿灯"状态。
可选要素：
- 初始状态（ $q_0 \in Q$ ）
- 接受状态集合（ $\subseteq Q$ ）

二、与其他自动机的区别

与摩尔机（Moore Machine）的区别：
- 摩尔机包含输出函数 $\lambda: Q \to O$ ，输出仅依赖当前状态。
- 半自动机无输出函数。
与米利机（Mealy Machine）的区别：
- 米利机包含输出函数 $\lambda: Q \times \Sigma \to O$ ，输出依赖状态与输入。
- 半自动机无输出函数。
与确定有限状态自动机（DFA）的关系：
- DFA 是在半自动机基础上补充初始状态和接受状态后构成的扩展模型。
- 半自动机可视为 DFA 的简化形式，去除了接受状态和初始状态的约束。

三、应用场景

半自动机常用于以下场景：

系统状态流转的形式化建模
程序执行路径分析
离散事件系统的行为刻画
编译器的词法分析阶段
通信协议的状态流转
游戏 AI 的决策逻辑

四、参考文献

Hopcroft, J. E., Motwani, R., & Ullman, J. D. (2006). Introduction to Automata Theory, Languages, and Computation_.
联盟百科：半自动机是数学与计算机科学中的一类抽象计算模型。
- 半自动机 - 联盟百科
自动机理论-快懂百科
- 自动机理论-快懂百科

形式语言与自动机理论

philgao 发布于 2023-02-13 17:03・北京

概述

形式语言（Formal languages）和自动机理论（Theory of automata）是计算理论（Theory of computation）的一个重要分支，而计算理论本身则是计算机科学（Computer science）和数学的交叉领域。其发展得益于英国数学家阿兰·图灵（Alan Mathison Turing）为解决大卫·希尔伯特（David Hilbert）提出的数理逻辑中一阶逻辑的判定性问题而构想的图灵机（Turing machine）。尽管图灵机是一种纯理论的计算模型，但它意外地催生了计算理论这一新领域。该领域主要关注三个方面的问题：计算模型的选择（即形式语言和自动机理论）、可计算性理论（Computability theory）以及计算复杂性理论（Computational complexity theory）。它帮助我们理解计算机的真实世界模型，并为算法、硬件和软件的设计提供了理论基础。

自动机理论研究抽象的计算模型——自动机及其行为。20 世纪，数学家们开始开发能够模仿人类计算特征的机器，这些机器在理论上和实际应用中都能更快速、更可靠地完成计算任务。通过自动机，计算机科学家能够理解机器如何计算函数、解决问题，并将函数定义为可计算的或将问题描述为可判定的。在计算机科学中，自动机被用作计算机和计算过程的动态数学模型，用于研究计算机体系结构、逻辑操作、程序设计以及计算复杂性理论；在语言学中，自动机被用作语言识别器，用于研究各种形式语言；在神经生理学中，自动机被定义为神经网络的动态模型，用于研究神经生理活动和思维规律；在生物学中，自动机被用作生命体生长发育的模型，用于研究新陈代谢与遗传变异；在数学中，自动机被用来定义可计算函数，研究各种算法。

自动机理论是形式语言理论的基础，用于生成和识别不同的形式语言，二者密切相关。形式语言理论关注将语言表示为字母表上的操作集合。诺姆·乔姆斯基（Noam Chomsky）在 20 世纪 50 年代研究自然语言时，将自动机理论的思想扩展到形式语言领域，提出了形式语法的概念，并给出了语法的数学模型。形式语言研究语言的语法及其内部结构模式。随着编程语言 ALGOL 的语法被定义为上下文无关语法，语法在程序设计中的重要性逐渐显现，进而引发了语法导向编译和编译器设计的概念。此后，形式语言和自动机理论在计算机科学中得到了广泛应用，成为计算机科学研究不可或缺的一部分。语言学也因形式语言理论的发展而受益，自然语言的句法规律得到了更深入的理解。语言可以通过各种类型的自动机（如图灵机）来定义。一般来说，在字母表 $\Sigma$ 上运行的任何自动机或机器 $M$ 都可以产生一个有效的语言 $L$ 。例如，系统可以用有界的图灵机磁带表示，每个单元代表一个单词。当指令停止时，任何值为 1（或 ON）的单词都会被接受，并成为生成语言的一部分。形式语法系统是一种专门为语言生成而定义的自动机。与纯数学自动机类似，语法自动机只需要几个符号和几个生成规则，就可以生成各种复杂的语言。乔姆斯基的层次结构定义了四个嵌套的语言类（即正则语言、上下文无关语言、上下文有关语言和递归可枚举语言），其语法生成规则具有更严格的限制。

形式语言和自动机理论的应用范围已扩展到生物工程、自动控制系统、图像处理与模式识别等诸多领域。

自动机理论（Theory of automata）

“自动机（Automata）”一词来源于希腊语“αὐτόματα”，意为“自我表达”。自动机是一种抽象的自推进计算设备，它自动遵循预定的操作顺序。自动机起源于与“自动化（automation）”密切相关的“自动机（Automaton）”一词，表示执行特定过程的自动化设备。具有不同复杂性的实际或假设自动机已成为研究和实现具有可用于数学分析的结构的系统的不可或缺的工具。诺伯特·维纳（Norbert Wiener）和艾伦·M·图灵被视为该领域的先驱。电子数字计算机是通用自动机的最佳实例。自动机网络可以设计成模仿人类行为。

自动机的起源与发展

1936 年，英国数学家艾伦·马西森·图灵在《伦敦数学学会会刊》（Proceedings of the London Mathematical Society）上发表了一篇论文（《论可计算数及其在 Entscheidungs 问题中的应用》），构想了一种逻辑机器，其输出可用于定义可计算数。对于该机器，时间被认为是离散的，在给定时刻，其内部结构被简单地描述为一组有限状态之一。它通过扫描被划分为正方形的无界磁带来执行其功能，每个正方形要么包含有限数量的符号之一，要么是空白的。它一次只能扫描一个方块，如果处于任何内部状态（除了所谓的“被动”状态），它能够一次向前或向后移动一个方块、擦除一个符号、如果方块为空则打印一个新符号，并改变其自身的内部状态。计算出的数字由磁带上有限部分的符号（“程序”）和操作规则决定，其中包括在达到被动状态时停止。然后根据机器停止后磁带上剩余的符号解释输出编号。

20 世纪，数学家们开始开发能够模仿人类某些特征的机器，这些机器在理论上和实际应用中都能更快速、更可靠地完成计算任务。自 20 世纪中叶以来，自动机理论得到了广泛的改进，并在民用和军用机器中得到了实际应用。通过自动机，计算机科学家能够理解机器如何计算函数、解决问题，并将函数定义为可计算的或将问题描述为可判定的。

现代计算机的存储库可以存储大量（虽然有限）信息。最初的图灵机对存储库没有限制，因为无界磁带上的每个方块都可以容纳信息。在自动机理论的基本讨论中，图灵机仍然是一个标准的参考点，许多关于可计算性的数学定理已经在图灵机最初的框架内得到了证明。

自动机的构造（物理构造和逻辑构造）

自动机的部件由特定的材料和设备组成，如电线、晶体管、杠杆、继电器、齿轮等，其操作基于这些部件的机械和电子原理。然而，它们作为一系列离散状态的操作原理可以独立于其组件的性质或排列来理解。通过这种方式，可以抽象地将自动机视为一组物理上未指定的状态、输入、输出和操作规则，而自动机的研究则是对这些状态、输入和输出的研究。这种抽象模式产生的数学系统在某些方面类似于逻辑系统。因此，自动机可以被描述为逻辑定义的实体，其可以以机器的形式体现，术语“自动机”既指物理构造也指逻辑构造。

自动机定义与分类

自动机是机器的抽象模型，通过移动一系列状态或配置来对输入执行计算。在计算的每个状态，转换函数基于当前配置的有限部分确定下一配置。因此，一旦计算达到接受配置，它就接受该输入。

自动机一般可分为四大类，其中最通用和最强大的自动机是图灵机：

有限状态机（FSM Finite-state machine）
下推自动机（PDA Pushdown automata）
线性有界自动机（LBA Linear-bounded automata）
图灵机（Turing machine）

自动机本质上可以被理解为根据纸带的数量、长度和移动以及所使用的读写操作分类的图灵机。我们可以通过以下方式限制图灵机的能力：

若使用 TAPE 作为 STACK，则它将是“PDA”。
若使 TAPE 有限，则它将是“FSM”。
若 TAPE 大小等于输入大小，则为“LBA”。

上述 2 和 3 之间的主要区别在于：对于有限自动机，无论输入大小如何，TAPE 的大小都是固定的；而对于 LBA，TAPE 的大小会随输入大小变化：输入越大，TAPE 越大，输入越小，TAPE 就越小。

不同自动机之间的主要区别在于它们能够使用的存储空间有所差异：

有限状态自动机只能用状态来存储信息。
下推自动机除了使用状态以外，还可以用下推存储器（堆栈）。
线性有界自动机可以利用状态和输入/输出带本身，因为输入/输出带没有“先进后出”的限制。
图灵机等价于无约束文法。

自动机理论是计算机科学和数学的一个理论分支。发展自动机理论的主要动机是开发描述和分析离散系统动态行为的方法。所谓离散状态自动机有时用于强调内部状态的离散性质。主要类别是转换器（transducers）和接收器（acceptors）。

转换器（transducer）

在自动机理论中，转换器（transducer）是具有输入和输出的自动机。任何用于计算部分递归函数的图灵机都可以作为一个例子。最重要的转换器是有限转换器或顺序机，它可以被描述为具有输出的单向图灵机。在计算能力方面，它们是最弱的，而通用机器是最强的，另外还有中等能力的转换器。可以分为两种子类型，即 Moore 机（摩尔型有限状态机）和 Mealy 机（米利型有限状态机），其中：

若输出只和状态有关而与输入无关，则称为 Moore 状态机。
输出不仅和状态有关而且和输入有关系，则称为 Mealy 状态机。

接收器（acceptor）

接收器（acceptor）是一个没有输出的自动机，在特殊意义上，它识别或接受机器字母表上的单词。接受器的输入以通常的方式写在纸带上，但在计算结束时纸带是空白的，输入单词的接受由称为最终状态的特殊状态表示。自动机理论的一个基本结果是，每个递归可枚举集或部分递归函数的范围都是一个可接受的集。一般来说，接收器是双向无界的纸带自动机。语言学家诺姆·乔姆斯基（Noam Chomsky）在美国提出了生成语法理论，并结合这一理论对接收器进行了有益的分类。生成语法是一种通常与语言学相一致的分析系统。通过这种方式，语言可以被视为一组规则，数量有限，可以产生句子。在语言学或自动机理论的背景下，生成语法的使用是为了生成和划分一种语言的语法结构的整体，无论是自然的还是面向自动机的。可以分为以下四种子类型：

Recursively enumerable grammars and Turing acceptors
递归可枚举文法和图灵接受器
Finite-state grammars and finite-state acceptors
有限状态文法和有限状态接受器
Context-free grammars and pushdown acceptors
上下文无关文法和下推自动机接受器
Context-sensitive grammars and linear-bounded acceptors
上下文有关文法和线性有界自动机接受器

自动机的应用

自动机理论在计算理论、编译器生产、人工智能等领域非常有用。

有限自动机（FA）：编译器词法分析的设计、正则表达式识别、使用 Mealy 和 Moore 机器设计组合和时序电路、文本编辑器、拼写检查器、人工智能中的学习和决策的模型、解析文本以提取信息和结构数据。
下推自动机（PDA）：设计编译器的语法分析、实现堆栈、计算算术表达式、用于软件工程，验证和验证软件模型的正确性、在网络协议中使用，用于解析和验证传入的消息，并强制执行特定的消息格式、密码学中实现加密和解密的安全算法、字符串匹配和模式识别、XML 分析、自然语言处理如解析句子、识别词性和生成语法树、自动定理证明和形式验证、硬件和软件系统的验证。
线性有界自动机（LBA）：实现遗传编程、识别上下文相关语言、博弈论中用于建模和分析代理之间的交互。
图灵机（TM）：解决任何递归可枚举问题、理解复杂性理论、实现神经网络、机器人、人工智能、分析算法的时间和空间复杂性的理论模型、计算生物学中用于模拟和分析生物系统、人工智能中用作学习和决策的模型、研究经典计算和量子计算之间的关系、用于数字电路设计，用于模拟和验证数字电路的行为、用于人机交互，对人与计算机之间的交互进行建模和分析。

总之，自动机是用于表示和分析计算系统行为的数学模型。该理论涉及形式语言及其与自动机的关系的研究。自动机理论的基本概念是有限自动机，它是一种识别有限字母表上的字符串的简单机器。有限自动机可以被认为是有限状态机的数学模型，有限状态机是一种机器，它可以处于有限数量的状态之一，并根据其接收的输入在状态之间进行转换。自动机理论中的另一个重要概念是正则语言的概念，这是一种可以被有限自动机识别的形式语言。正则语言在形式语言的研究中很重要，有很多应用，包括编译器的设计和编程语言中正则表达式的实现。自动机理论的研究还包括下推自动机的概念，下推自动机是具有存储信息堆栈的自动机，这是通用计算机的数学模型。形式语言和自动机的理论被用于计算机科学的许多领域，包括编译器、算法以及计算机辅助设计和验证的算法。它也用于复杂性理论的研究，为算法及其复杂性的研究提供了基础。

有限状态机（FSM Finite-state machine）

用于计算的最简单的自动机是有限自动机。它只能计算非常原始的函数；因此，它不是一个适当的计算模型。此外，有限状态机无法概括计算阻碍了它的能力。第一批考虑有限状态机概念的人包括生物学家、心理学家、数学家、工程师和一些最早的计算机科学家。他们都有一个共同的兴趣：模拟人类的思维过程，无论是在大脑中还是在计算机中。沃伦·麦卡洛克和沃尔特·皮茨，两位神经生理学家，在 1943 年首次提出了有限自动机的描述。他们的论文题为“神经活动中固有的逻辑演算”，对神经网络理论、自动机理论、计算理论和控制论的研究做出了重大贡献。后来，两位计算机科学家 G.H.Mealy 和 E.F.Moore 在 1955 - 56 年发表的独立论文中将这一理论推广到更强大的机器上。有限状态机，Mealy 机和 Moore 机，因其工作而得名。虽然 Mealy 机器通过当前状态和输入确定其输出，但 Moore 机器的输出仅基于当前状态。

具有有限数量状态的自动机称为有限状态机（FSM finite state machine），也被称为有限自动机（finite automata）。

有限自动机的正式定义可以用 5 元组 $\Sigma, \delta, q_0, F)$ 表示，其中：

$Q$ 是一组有限状态。
$\Sigma$ 是一组有限的符号，称为自动机的字母表。
$\delta$ 是过渡函数。
$q_0$ 是初始状态（ $q_0 \in Q$ ）。
$F$ 是 $Q$ 的最终状态/状态的集合（ $\subseteq Q$ ）。

根据上述数学解释，可以说有限状态机包含有限数量的状态。每个状态都接受有限数量的输入，每个状态都有规则来描述机器对任何输入的动作，这些规则在状态转换映射函数中表示。同时，输入可能导致机器改变状态。对于每个输入符号，每个状态都有一个转换。此外，任何被非确定性有限自动机接受的 5 元组集合也被确定性有限自动机所接受。

有两种类型的有限自动机：

确定性有限自动机（DFA Deterministic Finite Automata）：在 DFA 中，对于每个输入字符，计算机只运行到一个状态。这里，计算的唯一性被称为确定性。DFA 不接受空移动。
非确定性有限自动机（NFA Non-deterministic Finite Automata）：NFA 可用于发送特定输入的任意数量的状态。它能够接受空移动。

可以根据有没有输出分为两类：

有输出的有限状态机：Moore Machine、Mealy Machine
无输出的有限状态机：DFA、NFA、 $\epsilon$ -NFA

由于内存量有限且恒定，FSM 的内部状态不具有进一步的结构。它们可以很容易地用状态图表示。

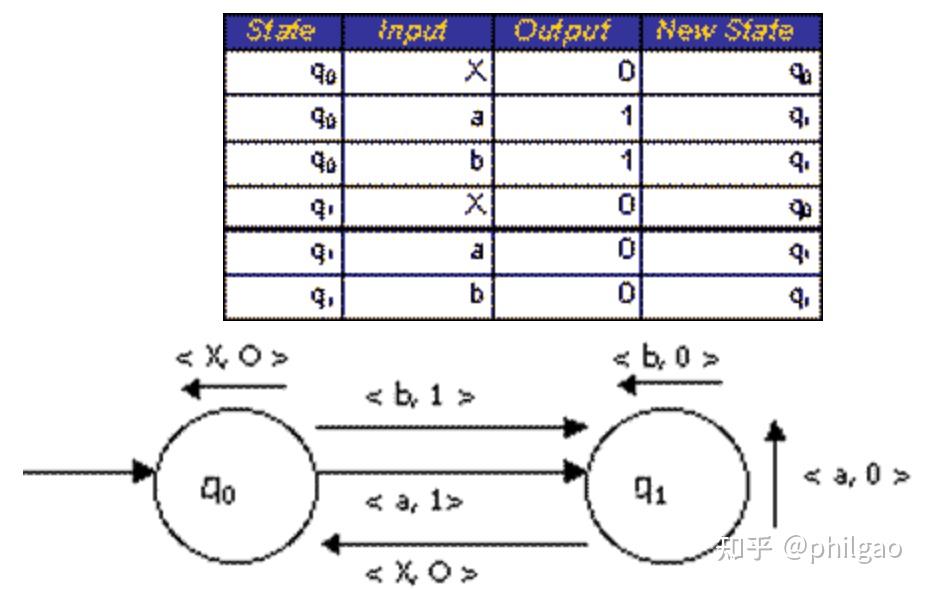
在这里插入图片描述

状态图说明了自动机的操作。状态由图的节点表示，过渡由箭头或分支表示，相应的输入和输出由符号表示。从左侧进入 $q_0$ 的箭头表示 $q_0$ 是机器的初始状态。不涉及状态更改的移动由单个节点两侧的箭头指示。这些箭头称为自循环。

存在几种类型的有限状态机，可分为三大类：

接受器（acceptors）：接受或不接受输入
识别器（recognizers）：识别输入或不识别输入
转换器（transducers）：从给定输入生成输出

有限状态机的应用可以在各种学科中找到。它们可以在具有有限单词数（标准情况）、无限单词数（Rabin 自动机、Büchi 自动机）、各种类型树的语言上操作，也可以在硬件电路中操作，其中输入、状态和输出是固定大小的位向量。

下推自动机（PDA Pushdown automata）

下推自动机是有限状态机，在所谓的堆栈中增加了额外的内存。新元素被推入堆栈。这些机器可以做的更多比有限状态机，但不如图灵机。下推自动机存在“确定”与“非确定”两种形式，两者并不等价（对于有限状态自动机两者是等价的）。下推自动机作为一个形式系统最早于 1961 年出现在 Oettinger 的论文中。它与上下文无关文法的等价性是由乔姆斯基于 1962 年发现的。

如果把下推自动机扩展，允许一个有限状态自动机存取两个栈，将得到一个能力更强的自动机，这个自动机与图灵机等价。

下推自动机有三个组件：

输入带
控制单元
具有无限大小的堆栈

PDA 可以正式描述为 7 元组 $\Sigma, \Gamma, \delta, q_0, Z, F)$ ，其中：

$Q$ 是有限数量的状态
$\Sigma$ 是输入字母表
$\Gamma$ 是堆栈符号
$\delta$ 是过渡函数： $\times (\Sigma \cup \{\epsilon\}) \times \Gamma \to Q \times \Gamma^*$
$q_0$ 是初始状态（ $q_0 \in Q$ ）
$Z$ 是初始栈顶符号（ $\in \Gamma$ ）
$F$ 是一组接受状态（ $\subseteq Q$ ）

线性有界自动机（LBA Linear-bounded automata）

线性有界自动机被认为是一种受限类型的图灵机。计算受到限制，在有限的有界区域内进行。可用作上下文有关语言的识别接受器。

1960 年，Myhill 引入了自动机模型，如今这种自动化模型被理解为确定性线性有界自动机。在此之后，另一位名叫 Landweber 的科学家对此进行了研究，并提出确定性 LBA 所接受的语言是持续的上下文敏感语言。

1964 年，黑田东彦专门为非确定性线性有界自动机引入了一种替代模型和许多通用模型，并确定了非确定性线性有限自动机所接受的语言正是上下文敏感语言。

线性有界自动机（LBA）类似于图灵机，具有以下一些特征：

具有非确定性逻辑的图灵机
具有多轨道的图灵机
带有限长度带的图灵机

LBA 可以正式描述为 8 元组 $\Sigma, \Gamma, \delta, q_0, B, F)$ ，其中：

$Q$ 是有限的过渡态集
$\Sigma$ 是输入字母表
$\Gamma$ 是磁带字母表
$\delta$ 是转换函数
$q_0$ 是初始状态
$B$ 是空白符号
$F$ 是一组有限的最终状态

图灵机（Turing machine）

1936 年，英国数学家艾伦·马西森·图灵在《伦敦数学学会会刊》（Proceedings of the London Mathematical Society）上发表了一篇论文（《论可计算数及其在 Entscheidungs 问题中的应用》），构想了一种逻辑机器，其输出可用于定义可计算数。对于该机器，时间被认为是离散的，在给定时刻，其内部结构被简单地描述为一组有限的状态之一。它通过扫描被划分为正方形的无界磁带来执行其功能，每个正方形要么以有限数量的符号之一的形式包含特定信息，要么是空白的。它一次只能扫描一个方块，如果处于任何内部状态（除了所谓的“被动”状态），它能够一次向前或向后移动一个方块、擦除一个符号、如果方块为空则打印一个新符号，并改变其自身的内部状态。计算出的数字由磁带上有限部分的符号（“程序”）和操作规则决定，其中包括在达到被动状态时停止。然后根据机器停止后磁带上剩余的符号解释输出编号。

图灵机由集合 $\Sigma, \Gamma, \delta, q_0, B, F)$ 正式定义，其中：

$Q$ 是有限状态集，其中一个状态 $q_0$ 是初始状态
$\Sigma$ 是输入符号的集合，且 $\Sigma \subseteq \Gamma$ 且 $\notin \Sigma$
$\Gamma$ 是允许带符号的有限集合
$\delta$ 是下一个移动函数，从 $\times \Gamma$ 到 $\times \Gamma \times \{L, R\}$ 的映射函数，其中 $L$ 和 $R$ 分别表示左和右方向
$q_0$ 是初始状态
$B$ 是 $\Gamma$ 中的空白符号
$\subseteq Q$ 是最终状态集

因此，图灵机和双向有限自动机（FSM）之间的主要区别在于图灵机能够改变磁带上的符号并模拟计算机的执行和存储。出于这个原因，可以说图灵机有能力对今天可以通过现代计算机计算的所有计算进行建模。

能被图灵机接受的字符串组成的语言称为递归可枚举语言。如果这个图灵机对于任何串都停机，则这个语言称为递归语言。

使用普通计算机是可以模拟图灵机的。尽管由于存储大小的限制，计算机实际上是状态数巨大的有限状态机，但是我们可以通过提醒人工更换硬盘来规避这一点。然而，普通计算机也可以用图灵机模拟，并且图灵机需要的步数和普通计算机相比只有多项式级别的区别。这件事比较显然，但较为复杂。我们用多个不同的带模拟计算机的不同部分，就可以用多带图灵机模拟普通计算机。于是普通计算机和图灵机的计算能力也是等同的。

形式语言（Formal languages）

自然语言处理的历史，在乔姆斯基（Noam Chomsky）之前所有关于自然语言处理的研究都是基于经验主义的，但由他在 20 世纪 50 年代发起，建立在阿克塞尔·图伊（Axel Thue）、艾伦·图灵（Alan Turing）和埃米尔·波斯特（Emil Post）的早期工作基础上，为语言理论提供了一个衡量标准，为描述的充分性设定了最低限度。建议对自然语言的经验领域进行一系列大规模的简化和抽象。特别是，这种方法完全忽略了意义。此外，与表达式使用有关的所有问题，如频率、上下文依赖性和处理复杂性都没有考虑在内。最后，假设对短字符串有效的模式以不受限制的方式应用于任意长度的字符串。至今日，不仅是语言学，理论计算机科学以及最近的分子生物学都表明，这些抽象概念被很好地选择了，保留了自然语言结构的基本方面。

乔姆斯基把语言定义为：按照一定规律构成的句子和符号串的有限或无限的集合。根据这个定义，无论哪一种语言都是句子和符号串的集合，当然自然语言也不例外，汉语、英语等所有自然语言，都是一个无限集合。构成这些集合的是句子、单词或其他符号。也可以把语言看成一个抽象的数学系统。无论把语言看作集合还是数学系统，我们都可以用数学的方法来进行刻画和描述。

无论哪种语言都是句子和符号串的集合，其描述的方法一般有以下三种：

穷举法：即把所有句子都枚举出来，显然适应性很窄。
文法（grammar）描述：为语言中的每个句子定义严格的构造规则，利用规则生成语言中合法的句子。
自动机（automata）法：通过对输入句子进行识别，从而判断哪些句子是属于语言的，哪些是属于语言的。

它们的区别在于：

文法是静态的、精确的描述语言及其结构。
自动机是动态的识别输入字符串是否属于语言的过程。
NLP 自然语言处理（Natural Language Processing）中的识别和分析算法大多兼取两者之长。

对于语言的研究，实际上包括 3 个方面。

如何表示或描述一个语言。若该语言是有穷语言，则可使用穷举法列举出语言中所包含的所有字符串；若该语言是无穷语言，则对该语言的表示，需要考虑语言的有穷描述。
如何判定一个给定的语言是否存在有穷描述。并不是所有的语言都存在有穷描述，即对于某些语言，并不存在有穷表示。
具有有穷表示的语言的结构以及结构的特性问题。

任何语言都是结构化的交流媒介，无论是口语或书面自然语言、手语或编码语言，还是正式的编程语言。语言有两个基本要素——语法（syntax）和语义（semantics）。在某些语言中，其含义可能会因第三个因素（称为使用上下文）而有所不同。

自然语言、形式语言与编程语言

自然语言（Natural Language）就是人类讲的语言，如汉语、英语。其不是人为设计（虽然有人试图强加一些规则）而是自然进化的。形式语言（Formal Language）是为了特定应用而人为设计的语言。如数学家用的数字和运算符号等。编程语言也是一种形式语言，是专门设计用来表达计算过程的形式语言。20 世纪 60 年代，美国人巴科斯（John Backus）和丹麦人诺尔（Peter Naur）在算法语言 ALGOL60 首次使用一种称为巴科斯 - 诺尔形式（BNF Backus - Naur form）的方法来描述程序设计语言的语法，极其类似于形式语言理论中的上下文无关文法。从此打开了形式语言广泛应用于描述程序设计语言的局面，使它发展成为理论计算机科学的一个重要分支。

形式语言的界限是明确的，而自然语言的界限往往不明确。因为自然语言有许多方言和习惯用法，而且处于不断发展之中。其次，自然语言不管如何庞大，它总是有限的。形式语言则以无限的语言为主要研究对象。例如，所有由 $n$ 个 $a$ 构成的字（ $\geq 1$ ）组成一个语言 $L_a = \{a, aa, aaa, \dots\}$ ，它就是无限的。因此，研究形式语言遇到的第一问题就是描述问题。描述的手段必须是严格的，而且必须能以有限的手段描述无限的语言。

形式语法（formal grammar）或文法的定义

语法是描述和分析语言的有力工具。它是一组规则，用来构造语言中的有效句子。下面是一个英语语法的简单例子：

在这里插入图片描述

使用上述规则或产生式（productions），我们可以导出如下简单句子：

在这里插入图片描述

下面是上图中第一个句子（This is a university）使用产生式的最左推导的例子：

在这里插入图片描述

除了几个合理的句子，我们还可以推导出“Computers run cheese”和“This am a lies”之类的这些没有语义意义（semantic sense）的句子，但它们语法正确。形式语法是语法工具，而不是语义工具。在语法分析阶段，我们验证结构，而不是意义。

形式语言（也称代数语言学）是用来精确的描述语言（人工和自然语言）及其结构的手段。它只研究语言的组成规则，不研究语言的含义。形式语言的研究始于 20 世纪初，50 年代中期将形式语言用于描述自然语言。

形式语法正式的定义是一个四元组（quadruple） $\Sigma, P, S)$ ，其中：

$N$ 是非终结符（non-terminal symbols）的有限集合；
$\Sigma$ 是终结符（terminal symbols）的有限集合；
$N$ 和 $\Sigma$ 不相交， $\cup \Sigma$ ，称为总词表；
$P$ 产生式（production rules）={α→β} 是一组重写规则的有限集合，其中 $\alpha, \beta$ 是由 $V$ 中元素构成的串，但是 $\alpha$ 中至少应含有一个非终结符号；
$\in N$ ，称为句子符或初始符（start symbol）。

与纯数学自动机一样，语法自动机只需要几个符号和几个生成规则就可以生成各种复杂的语言。如果两个语法 $G$ 和 $G^{'}$ 生成的语言 $L (G)$ 和 $L (G^{'})$ 是相同的，则它们是等价的。

句型与句子

文法 $\Sigma, P, S)$ 的句子形式（句型）通过下面的递归方式定义：

$S$ 是一个句子形式；
如果 $\gamma \beta \alpha$ 是一个句子形式，且 $\beta \to \delta$ 是 $P$ 中的产生式，那么 $\gamma \delta \alpha$ 也是一个句子形式。

句子是由初始符按照重写规则推导（Derivation）出来的句子形式，其中不含非终结符的句子形式称为 $G$ 生成的句子。

语言（Language）

由文法 $G$ 生成的语言是指 $G$ 生成的所有句子的集合，记作 $L (G)$ 。

$\{ x \mid x \in \Sigma, S \overset{*}{\underset{G}{\Rightarrow}} x \}$

/* 上下文无关文法的定义 */
start symbol = S                       /* 起始符号 */
non-terminals = {S}                    /* 非终结符集合 */
terminals = {a, b}                     /* 终结符集合 */

/* 产生式规则 */
production rules:
    S → aSb                            /* 规则1：生成形如 aSb 的字符串 */
    S → ba                             /* 规则2：生成字符串 ba */

/* 示例推导过程 */
S → aSb → abab                        /* 应用规则1，然后应用规则2 */
S → aSb → aaSbb → aababb              /* 应用规则1两次，然后应用规则2 */

/* 生成的语言 */
L = {abab, aababb, ...}               /* 该文法生成的语言包含所有形如 a^n b^n 的字符串，其中 n ≥ 1 */

可判定的语言（decidable languages）：如果有一个图灵机接受并停止每个输入字符串 $w$ ，那么该语言则被称为可判定或递归。每个可判定语言都是图灵可接受的。如果 $P$ 的所有 yes 实例的语言 $L$ 都是可判定的，则决策问题 $P$ 是可判定。

不可判定的语言（Undecidable Languages）：对于不可判定的语言，不存在接受该语言并对每个输入字符串 $w$ 做出决定的图灵机（尽管 TM 可以对某些输入字符串做出决定）。如果 $P$ 的所有 yes 实例的语言 $L$ 都不可判定，则决策问题 $P$ 被称为“不可判定”。无法解释的语言不是递归语言，但有时，它们可能是递归可枚举语言。

句子的推导（Derivation）

推导也被称为语法分析（parse），是一系列语法产生式或规则的应用，最终产生一个全部由终结符组成的字符串。如：语法 $G$ 有生成式 $\alpha \to \beta$ ，我们可以说 $x\alpha y$ 在 $G$ 中导出 $x\beta y$ 。对于同一个句子可以采用不同的推导方式，如最左推导时，我们总是用最左边的非终结符来替换（类似地也可定义最右推导）。下面是常见的句子推导方法：

最左推导（leftmost derivation）：每步推导只改写最左边的那个非终结符。
最右推导（rightmost derivation）：每步推导只改写最右边的那个非终结符。
规范推导：最右推导也称规范推导。

除了使用最左与最右推导来表示句子最终的推导结果，我们也可以使用分析树（parse tree）的形式来表示，如下面就是句子“This is a university”的一个分析树表示法：g

虽然分析树也包括了应用所有产生式，但它不会对产生式的顺序进行编码。对于一个无歧义（unambiguous）的语法，仅一个句子与分析树相对应。如果一个语法允许对某些句子生成多个分析树，则称其是具有歧义的（ambiguous）。

乔姆斯基层级（Chomsky hierarchy）

在乔姆斯基的语法理论中，文法被分为四种类型，分别是 3 型文法，2 型文法，1 型文法，0 型文法。又分别称为正则文法，上下文无关文法，上下文相关文法，和无约束文法。对于每一个级别，语法在规则上的限制性都会降低，但在自动化方面会更加复杂。每个级别也是后续级别的子集。

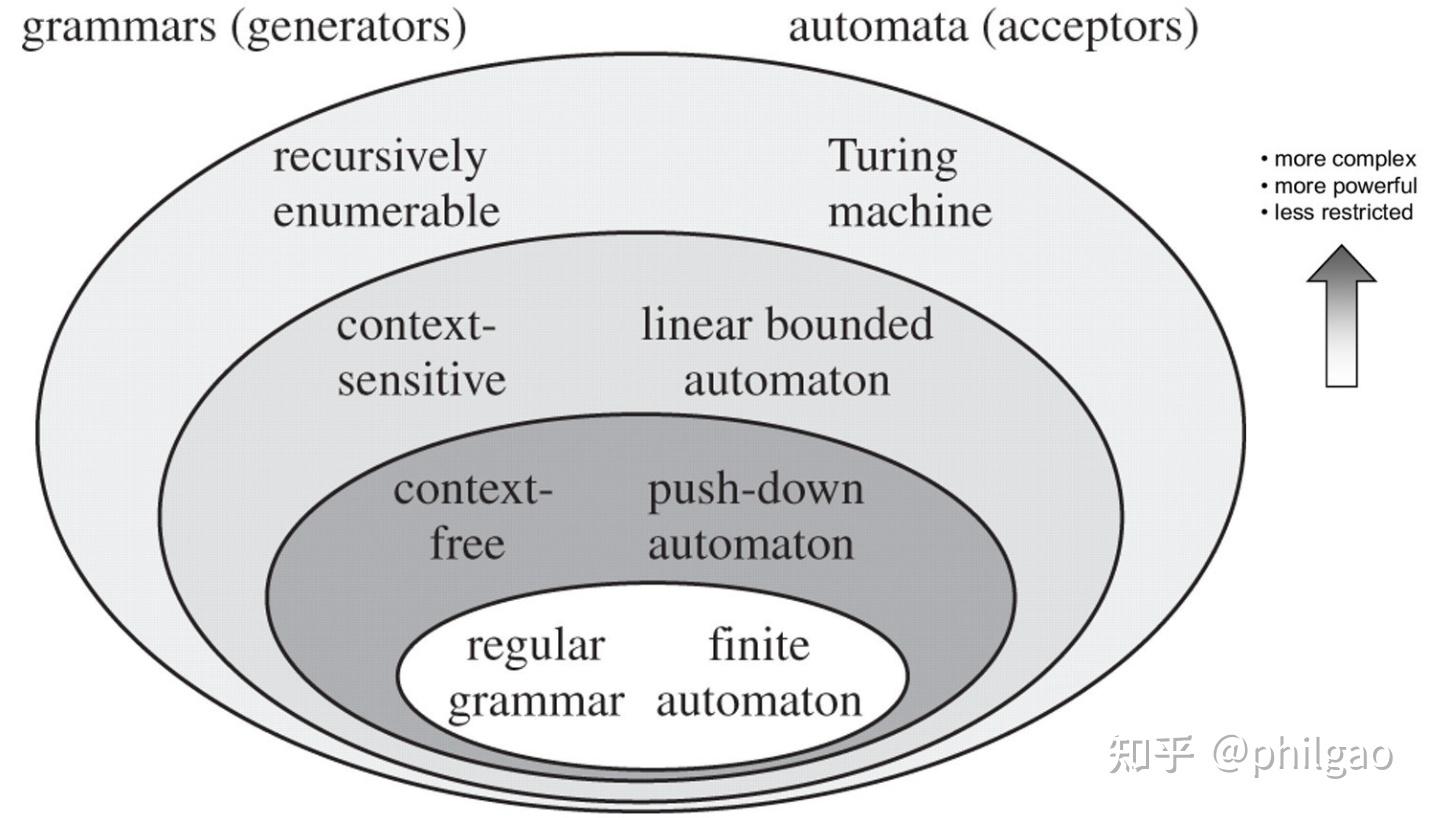
在这里插入图片描述

下表是乔姆斯基层次结构表示不同机器所接受的语言类别_：

Grammar type 语法类型	Grammar accepted 可接受语法	Language accepted 可接受语言	Automaton 自动机
0	unrestricted grammar 无限制语法	recursively enumerable language 递归可枚举语言	Turing Machine 图灵机
1	context-sensitive grammar 上下文相关语法	context-sensitive language 上下文相关语言	linear-bounded automata 线性有界自动机
2	Context-free grammar 上下文无关语法	Context-free language 上下文无关语言	Push down automata 下推自动机
3	regular grammar 正则语法	regular language 正则语言	finite state automaton 有限状态自动机

规则形式 _

TYPE	NAME	FORM OF RULES 规则形式
3	regular 正则的	$\to A\alpha \text{ or } A \to aA) \text{ and } A \to a \text{ for } A \in \mathcal{N} \text{ and } a \in \Sigma$
2	context free 上下文无关的	$\to \alpha \text{ where } A \in \mathcal{N} \text{ and } \alpha \in (\mathcal{N} \cup \Sigma)^*$
1	context sensitive 上下文相关的	$\alpha A B \to \alpha\gamma\beta \text{ where } A \in \mathcal{N} \text{ and } \alpha,\beta,\gamma \in (\mathcal{N} \cup \Sigma)^* \text{ and } \gamma \neq \varepsilon$
0	recursively enumerable 递归可枚举的	$\alpha \to \beta \text{ where } \alpha,\beta \in (\mathcal{N} \cup \Sigma)^* \text{ and } \alpha \neq \varepsilon$

随后的形式语言学研究表明，相对于认知科学（cognitive science）来说，这种四个层次有点过于粗糙，无法确定自然语言在这一领域的复杂程度。因此，提出了几个改进方案。这里特别重要的是扩展上下文无关语言（CFL）类的级别，即所谓的轻度上下文敏感语言（mildly context-sensitive languages），以及进一步将正则语言划分为子正则层次结构的级别（the sub-regular hierarchy），区分了正则语言类别中的几个复杂程度。

正则语言（Regular Languages）

正则文法（3 型文法）

文法规则只有（非终结符推出非终结符 + 终结符）或（非终结符推出终结符）这两种形式的文法。如果文法 $\Sigma, P, S)$ 的产生式 $P$ 中的规则满足如下形式： $\to Bx$ ，或 $\to x$ ，其中 $\in N$ ， $\in \Sigma$ ，则称该文法为正则文法（简写为 FSG）或称 3 型文法（左线性正则文法）。如果 $\to xB$ ，则该文法称为右线性正则文法。由这些语法生成的正则语言由有限自动机识别。

如： $\to wB$ 产生式右部至多只有一个非终结符，并且非终结符在同侧。

右线性（Right Linear）文法： $\to wB$ 或 $\to w$
左线性（Left Linear）文法： $\to Bw$ 或 $\to w$

是最具限制性的，它们必须在左手边和右手边具有单个非终结符，由单个非终结符或单个非终结符后接单个非终结符组成。

阿登定理（Arden’s Theorem）：主要是为了找到有限自动机的正则表达式。

正则语言的泵引理（Pumping Lemma）：泵引理是 1961 年由 Y. Bar - Hillel、M. Perles 和 E. Shamir 首次发表的。可以用来确定特定语言不在给定语言类中。但是它们不能被用来确定一个语言在给定类中，因为满足引理是类成员关系的必要条件，但不是充分条件。

上下文无关语言（Context-Free Languages）

上下文无关文法（2 型文法）

所有规则的左侧和推导结果不限于 $N$ 或 $\Sigma$ ，其实就是正则文法去掉限制。如果文法 $\Sigma, P, S)$ 的产生式 $P$ 中的规则满足如下形式： $\to \alpha$ ，其中 $\in N$ ， $\alpha \in (N \cup \Sigma)^*$ ，则称该文法为上下文无关文法（CFG）或称 2 型文法。由这些语法生成的上下文无关的语言由下推自动机识别。这是 NLP（Natural Language Processing）从业者非常感兴趣的一类语言。

上下文无关语言的歧义性：如果一个上下文无关语法 $G$ 对于某个字符串 $\in L(G)$ 有不止一个推导树，则称为有歧义性的语法。对于从该语法生成的某些字符串，存在多个最右边或最左边的推导。

上下文无关语言的泵引理：用于检查语法是否上下文无关。其实跟正则语言的泵引理本质是一样的，都是通过鸽笼原理（抽屉原理）来证明的。鄂登引理是另一种更强的上下文无关语言的泵引理。

上下文无关语言的闭包属性：在 Union、Concatenation、Kleene Star 的操作下会产生封闭。

上下文有关或敏感语言（Context-sensitive Languages）

上下文有关文法（1 型文法）

推导规则左右侧的不同之处体现在字串的中间，就是生活常识里的上下文相关了。如果文法 $\Sigma, P, S)$ 的产生式 $P$ 中的规则满足如下形式： $\alpha A \beta \to \alpha \gamma \beta$ ，其中 $\in N$ ， $\alpha, \beta, \gamma \in (N \cup \Sigma)^*$ ，且 $\gamma$ 至少包含一个字符，则称该文法为上下文有关文法（CSG）或称 1 型文法。由这些语法生成的上下文敏感的语言由线性有界自动机识别。是最高的可编程级别。

如：规则满足 $\alpha A \beta \to \alpha \gamma \beta$ ， $\alpha$ ， $\beta$ ， $\gamma$ 属于总词汇表，且 $\gamma$ 至少包含一个字符。

是上下文无关文法的特例（ $\alpha$ ， $\beta$ 为空）。
规则右端不小于规则左端。
规则左部不一定仅为一个非终结符，可以有上下文限制。

递归可枚举语言（recursively enumerable languages）

无约束文法（0 型文法）

如果文法 $\Sigma, P, S)$ 的产生式 $P$ 中的规则满足如下形式： $\alpha \to \beta$ ， $\alpha$ ， $\beta$ 是字符串， $\alpha$ 中至少包含 1 个非终结符且不能为空字符串，则称 $G$ 为无约束文法，或称 0 型文法。其生成的语言可被图灵机器识别。由于太通用和不受限制，从而无法描述编程或自然语言的语法。

背景知识（background knowledge）

字母表（Alphabet）

自动机理论中任何有限的符号集都被称为字母表。由字母 $\Sigma$ 表示的集合 ${a, b, c, d, e\}$ 称为字母集，而集合“a”，“b”，“c”，“d”，“e” 的字母称为符号。

字符串（String）

在自动机中，字符串是取自字母表集 $\Sigma$ 的有限符号序列。例如，字符串 $S =$ “adeaddadc” 在字母表集上有效 $\Sigma = \{a, b, c, d, e\}$ 。

字符串长度（Length of String）

字符串中存在的符号数称为字符串长度。对于字符串 $S =$ “adaada”，字符串的长度为 $∣ S ∣ = 6$ 。如果字符串的长度为 0，则称为空字符串。

Kleene Star/closure（ $\Sigma^*$ ）

它是符号集合 $\Sigma$ 上的一元运算符，它给出了集合 $\Sigma$ 上所有可能长度的所有可能字符串的无限集合，包括 $\lambda$ （空字符串）。例如，对于集合 $\Sigma = \{c, d\}$ ， $\Sigma^* = \{\lambda, c, d, cd, dc, cc, dd, \dots\}$ 。

Kleene plus（ $\Sigma^+$ ）

它是字母表集合中除 $\lambda$ （空字符串）之外的所有可能字符串的无限集合。对于集合 $\Sigma = \{a, d\}$ ， $\Sigma^+ = \{a, d, ad, da, aa, dd, \dots\}$ 。

语言（Language）

语言是某些字母集 $\Sigma$ 的 Kleene 星集 $\Sigma^*$ 的子集。语言可以是有限的，也可以是无限的。例如，如果一种语言在集合 $\Sigma = \{a, d\}$ 上取长度为 2 的所有可能字符串，则 $L = \{aa, ad, da, dd\}$ 。

集合

集合理论是计算机理论的重要基础，也是形式语言和自动机理论的基础。

集合关系

并、交、补、差、笛卡尔积、幂积、二元关系

笛卡尔积： $\times B$ ，即都分别对应的乘积。

如： $A = \{1, 2, 3\}$ ， $\{\text{长}, \text{短}\}$

则 $\times B = \{(1, \text{长}), (1, \text{短}), (2, \text{长}), (2, \text{短}), (3, \text{长}), (3, \text{短})\}$

幂积： $2^A$ ，即所有的子集。

如： $A = \{1, 2, 3\}$ ,

则 $2^A = \{\emptyset, \{1\}, \{2\}, \{3\}, \{1, 2\}, \{1, 3\}, \{2, 3\}, \{1, 2, 3\}\}$

二元关系：任意的 $\in A \times B$ ， $R$ 是 $A$ 到 $B$ 的二元关系

符号说明：

符号样式	LaTeX 代码	含义说明	使用场景
花体（𝒩）	`\mathcal{N}`	非终结符集合	形式语法、自动机理论
双线体/黑板粗体（ℕ）	`\mathbb{N}`	自然数集合（定义1：正整数与 0 的并集；定义2：仅正整数）	数学集合论、数论（“双线体”为视觉描述性别称）
普通斜体（N）	`N`（默认斜体）	一般变量或参数	代数方程（如未知数）、计数变量
粗体（𝐍）	`\mathbf{N}`	向量或矩阵名称；特定集合的缩写形式	线性代数（向量 𝐍）、部分教材中代指自然数集（非通用标准记法）
手写体（𝓝）	`\mathscr{N}`	特殊集合（如邻域集、符号集）	拓扑学（邻域集合 𝓝(x)）、符号逻辑

领域专用符号（如 𝒩、ℕ、𝓝）的含义由所属学科规范界定，使用时需遵循固定指代，不得随意替换；
普通样式符号（N、𝐍）的含义无统一预设，需结合具体上下文的定义或表述逻辑确定。

What are the conditions for a NFA for its equivalent DFA to be maximal in size?

非确定有限自动机（NFA）满足什么条件时，其等价确定有限自动机（DFA）的规模达到最大？

We know that DFAs are equivalent to NFAs in expressiveness power; there is also a known algorithm for converting NFAs to DFAs (unfortunately I do not know the inventor of that algorithm), which in worst case gives us $2^S$ states, if our NFA had $S$ states.
我们知道确定性有限自动机（DFA）与非确定有限自动机（NFA）在表达能力上是等价的；同时存在一种将 NFA 转换为 DFA 的已知算法（遗憾的是，我不清楚该算法的发明者）。若 NFA 有 $S$ 个状态，则该算法在最坏情况下会生成一个具有 $2^S$ 个状态的 DFA。

My question is: what is determining the worst case scenario?
我的问题是：什么因素决定了这种最坏情况？

Here’s a transcription of an algorithm in case of ambiguity:
为避免歧义，以下是该算法的详细描述：

Let $\Sigma, \delta, q_0, F)$ be a NFA. We construct a DFA $\Sigma, \delta', q'_0, F')$ where
设 $\Sigma, \delta, q_0, F)$ 为一个 NFA，我们构造对应的 DFA $\Sigma, \delta', q'_0, F')$ ，其中：

$\mathcal{P}(Q)$
$\{ S \in Q' \mid F \cap S \neq \emptyset \}$
$\delta'(S, a) = \bigcup_{s \in S} (\delta(s, a) \cup \delta^*(s, \varepsilon))$
$q'_0 = \{ q_0 \} \cup \delta^*(q_0, \varepsilon)$

where $\delta^*$ is the extended transition function of $A$ .
其中 $\delta^*$ 表示 $A$ 的扩展转移函数。

edited Mar 15, 2012 at 10:17
Raphael

asked Mar 8, 2012 at 10:20
Daniil

As comments state you could rescue this Q by asking for “minimal” NFA for a DFA (an open problem). I always thought this problem is closely connected to the P=?NP question in various ways & have some similar formulations that suggest that. It is similar in that you are asking about “compressible” vs “incompressible” DFAs where “incompressible” is worst case such that the minimal NFA is almost the size of the DFA. There is probably some theorem like, “most DFAs, taken at random, are incompressible [into NFAs]” as there are similar theorems in information theory regarding Kolmogorov complexity of strings etc.
正如评论中所指出的，你可以将问题修改为“求一个 DFA 对应的极小 NFA”（这是一个开放问题），从而使该问题更具研究价值。我一直认为这个问题在多个方面与 P=?NP 问题密切相关，并且有一些类似的表述支持这一观点。两者的相似之处在于，你都在探讨“可压缩”与“不可压缩”的 DFA——其中“不可压缩”指的是最坏情况，即极小 NFA 的规模几乎与原 DFA 相当。可能存在这样一个定理：“随机选取的大多数 DFA 是不可压缩的（即无法通过 NFA 减小规模）”，这与信息论中关于字符串柯尔莫哥洛夫复杂度的类似定理一致。

– vzn
Commented Mar 23, 2012 at 16:42

Answers

The algorithm you refer to is called the Powerset Construction, and was first published by Michael Rabin and Dana Scott in 1959.
你所提到的算法称为幂集构造法（Powerset Construction），由迈克尔·拉宾（Michael Rabin）和达纳·斯科特（Dana Scott）于 1959 年首次发表。

To answer your question as stated in the title, there is no maximal DFA for a regular language, since you can always take a DFA and add as many states as you want with transitions between them, but with no transitions between one of the original states and one of the new ones. Thus, the new states will not be reachable from the initial state $q_0$ , so the language accepted by the automaton will not change (since $\delta^*(q_0, w)$ will remain the same for all $\in \Sigma^*$ ).
针对你标题中的问题：正则语言不存在“最大规模”的 DFA。因为你可以对任意一个 DFA 进行如下操作：添加任意数量的新状态，并在这些新状态之间定义转移，但不允许原状态与新状态之间存在任何转移。这样一来，新状态从初始状态 $q_0$ 出发是不可达的，因此自动机接受的语言不会改变（因为对于所有 $\in \Sigma^*$ ， $\delta^*(q_0, w)$ 的结果保持不变）。

That said, it is clear that there can be no conditions on a NFA for its equivalent DFA to be maximal, since there is no unique equivalent DFA. In contrast, the minimal DFA is unique up to isomorphism.
由此可见，不存在任何条件能让 NFA 的等价 DFA 达到“最大规模”，因为等价 DFA 并不唯一。相反，极小 DFA 在同构意义下是唯一的。

A canonical example of a language accepted by a NFA with $n + 1$ states with equivalent DFA of $2^n$ states is
一个典型例子：某语言可由一个具有 $n + 1$ 个状态的 NFA 接受，其等价 DFA 则具有 $2^n$ 个状态，该语言为：

$\{ w \in \{0,1\}^* : |w| \geq n \text{ and the } n\text{-th symbol from the last one is } 1 \}$ .
$\{ w \in \{0,1\}^* : |w| \geq n \text{ 且从末尾数第 } n \text{ 个符号为 } 1 \}$ 。

A NFA for $L$ is $\langle Q, \{0,1\}, \delta, q_0, \{q_{n+1}\} \rangle$ , with $\delta(q_0, 0) = \{q_0\}$ , $\delta(q_0, 1) = \{q_0, q_1\}$ and $\delta(q_i, 0) = \delta(q_i, 1) = \{q_{i+1}\}$ for $\in \{1, \dots, n\}$ . The DFA resulting from applying the powerset construction to this NFA will have $2^n$ states, because you need to represent all $2^n$ words of length $n$ as suffixes of a word in $L$ .
接受 $L$ 的 NFA 定义为 $\langle Q, \{0,1\}, \delta, q_0, \{q_{n+1}\} \rangle$ ，其中转移函数满足： $\delta(q_0, 0) = \{q_0\}$ ， $\delta(q_0, 1) = \{q_0, q_1\}$ ，且对于 $\in \{1, \dots, n\}$ ，有 $\delta(q_i, 0) = \delta(q_i, 1) = \{q_{i+1}\}$ 。对该 NFA 应用幂集构造法得到的 DFA 将具有 $2^n$ 个状态，这是因为需要用这些状态表示长度为 $n$ 的所有 $2^n$ 种字符串（它们是 $L$ 中字符串的后缀）。

edited Mar 9, 2012 at 22:37
Gilles ‘SO- stop being evil’
answered Mar 8, 2012 at 11:05
Janoma

By the way, if you want the curly brackets to appear in the display math mode use { and }.
顺便说一句，如果你想在显示数学模式中显示花括号，需要使用 { 和 }。

– Zach Langley
Commented Mar 8, 2012 at 14:12

@ZachLangley I tried already, it doesn’t work :
@扎克·兰利我已经试过了，但没用 :

– Janoma
Commented Mar 8, 2012 at 14:21

It seems to be working for me in the preview. I can’t submit the edit though, because I’m only adding four characters and the minimum is six. You’re using two backslashes and it didn’t work?
在预览中，这种方式对我来说是有效的。但我无法提交编辑，因为我只添加了 4 个字符，而编辑的最小字符数要求是 6 个。你用的是两个反斜杠吗？还是没生效？

– Zach Langley
Commented Mar 8, 2012 at 14:33

@ZachLangley It works now, but two things: 1st, it didn’t work when I first posted the answer. 2nd, I think this is inconsistent with the behavior of LaTeX rendering in cstheory, but I might be wrong.
@扎克·兰利现在生效了，但有两点：第一，我第一次发布回答时它并没有生效；第二，我认为这与 cstheory 平台上的 LaTeX 渲染行为不一致，但我可能是错的。

– Janoma
Commented Mar 8, 2012 at 18:40

The resulting DFA is minimal? Could you speak a bit about how to prove that it is minimal?
得到的 DFA 是极小的吗？你能简要说明如何证明它是极小的吗？

– user834
Commented Jul 27, 2012 at 12:25

The worst-case of $2^S$ comes from the number of subsets of states of the NFA. To have the algorithm from Kleene’s theorem give an equivalent DFA with the worst-case number of states, there must be a way to get to every possible subset of states in the NFA. An example with two states over alphabet ${a, b\}$ has a transition from the initial state to the sole accepting state on symbol $a$ , a transition from the accepting state back to the initial on $b$ , and a transition from the accepting state back to itself on either an $a$ or a $b$ . The strings $\lambda$ , $a$ , $b$ , and $ab$ lead to subsets ${q_1\}$ , ${q_2\}$ , $\emptyset$ , and ${q_1, q_2\}$ , respectively, and these would need separate states in the DFA Kleene gives.
$2^S$ 这一最坏情况源于 NFA 状态集的子集数量。要使克林尼定理（Kleene’s theorem）中的算法生成具有最坏情况状态数的等价 DFA，必须存在一种方式能够到达 NFA 状态集的所有可能子集。例如，考虑一个字母表为 ${a, b\}$ 、具有两个状态的 NFA：初始状态在输入符号 $a$ 下转移到唯一的接受状态；接受状态在输入符号 $b$ 下转移回初始状态，在输入符号 $a$ 或 $b$ 下转移到自身。字符串 $\lambda$ 、 $a$ 、 $b$ 和 $ab$ 分别会到达子集 ${q_1\}$ 、 ${q_2\}$ 、 $\emptyset$ 和 ${q_1, q_2\}$ ，这些子集在克林尼定理生成的 DFA 中需要作为独立的状态存在。

edited Mar 8, 2012 at 13:39
answered Mar 8, 2012 at 12:47

via:

自动机，状态机，有限自动机，有限状态机，有限状态自动机，非确定下有限状态自动，确定性有限状态自动机的区别于联系-优快云博客 ThinerZQ 于 2015-07-24 21:27:01 发布
https://blog.youkuaiyun.com/c601097836/article/details/47040703
形式语言与自动机理论 - 知乎
https://zhuanlan.zhihu.com/p/604856636
formal languages - What are the conditions for a NFA for its equivalent DFA to be maximal in size?
https://cs.stackexchange.com/questions/130/what-are-the-conditions-for-a-nfa-for-its-equivalent-dfa-to-be-maximal-in-size