微积分 | 导数概念 / 定义 / 符号（一些讨论）

注：本文为 “微积分 | 导数” 相关讨论合辑。
英文引文，机翻未校。
如有内容异常，请看原文。

---

csdn 篇幅所限，另一篇

• 微积分 | 导数概念 / 定义 / 符号（一些久远的讨论）-优快云博客
  https://blog.youkuaiyun.com/u013669912/article/details/149746213

---

What is a Derivative?

什么是导数？

August 10, 2020 / By Dave Peterson

To start a series of posts on differentiation (one of the basic concepts studied in calculus), I’d like to look at a number of answers we’ve given to the basic question, What is a derivative? This includes questions about the meaning of the concept and its definition, as well as examples. Something all these questions have in common is that they come from students who have learned what the derivative is, formally, but they don’t feel they know what it really is. (We looked at the same topic from a single perspective earlier this year, in Derivative as Instantaneous Rate of Change.)
为了开启一系列关于微分（微积分中研究的基本概念之一）的文章，我想看看我们对“什么是导数？”这个基本问题给出的诸多答案。这包括关于该概念的含义、定义以及示例的问题。所有这些问题的共同点是，提问的学生虽然从形式上学习了导数是什么，但并不觉得自己真正理解导数的本质。（今年早些时候，我们从单一角度探讨过同一主题，参见《作为瞬时变化率的导数》。）

Derivatives, visually and numerically

导数的直观与数值理解

We’ll start with this question from 1998:
我们从1998年的这个问题开始：

What is a Derivative?
什么是导数？

What is the concise definition of a derivative? I kind of know the meaning, but I can’t see it visually. Do you have any ideas that will help?
导数的简明定义是什么？我略知其义，却难以直观领会。不知您有何方法能助我理解？

Rate of change

变化率

Doctor Pat answered:
帕特博士回答：

Max,
马克斯，

I’m not sure if I completely understand the question, so I will answer both sides of what you might have meant.
我不确定自己是否完全理解你的问题，所以我会从你可能想表达的两个方面来回答。

First, you need to think of a derivative as measuring the rate at which something changes as measured by something else. We do that a lot in life and never think of it as a derivative. For example, in a car, the speedometer is a measure of the change in position per unit of time. In this case we would write $\frac{dP}{dt}$ where $P$ stands for position along some path of travel (in miles) and $t$ stands for time (in hours). Of course the speedometer only works correctly when you are going forward. In airplanes they have a gauge that measures the same thing for elevation. It measures how fast you are going up (or down), which is important as you can imagine.
首先，你需要把导数理解为衡量某事物相对于另一事物的变化率的量。在生活中，我们经常做这样的事，却从未把它当作导数。例如，汽车里的速度表就是测量单位时间内位置变化的工具。在这种情况下，我们会写成 $\frac{dP}{dt}$，其中 $P$ 代表沿某条行驶路径的位置（单位为英里），$t$ 代表时间（单位为小时）。当然，只有向前行驶时，速度表的读数才准确。飞机上有一个仪表，用于测量海拔的变化率。可想而知，它能测量上升（或下降）的速度，这一点很重要。

The phrase “as measured by something else” is important. What Doctor Pat means, I think, is that it need not always be a rate in terms of time, though most examples we give tend to be; it can be a rate like “miles per gallon“, which is a rate of distance compared to fuel usage, or “liters per kilometer“, which is a rate of fuel usage compared to distance, or “cubic feet per foot of depth”. Whenever we have a function that calculates this from that, the derivative will be the rate at which this increases for each change in that.
“相对于另一事物”这一表述很重要。我认为，帕特博士的意思是，尽管我们给出的大多数例子都是与时间相关的速率，但变化率不一定总是“以时间为基准”；它可以是像“每加仑英里数”这样的比率（距离与燃油消耗量的比率），或者“每公里升数”（燃油消耗量与距离的比率），又或者“每英尺深度的立方英尺数”。只要我们有一个函数能根据“那个量”计算出“这个量”，导数就是“这个量”相对于“那个量”每单位变化的增长率。

When you see the stock market report on the TV in the evening, it measures the change in the aggregate stock index per unit of time. In this case the units are dollars per day.
当你在晚上看电视上的股市报道时，它会衡量股票综合指数每单位时间的变化。在这种情况下，单位是美元/天。

On a graph, the visual pattern is one of slope. If we measure the closing stock price from day to day we notice that the graph gets higher on days when the price change is positive, and lower when the stocks go down. The steeper the slope, the faster the change, and positive means I’m making money.
在图表上，视觉上的表现就是斜率。如果我们逐日测量股票收盘价，会发现当价格变化为正时，图表上升；当股票下跌时，图表下降。斜率越陡，变化越快；斜率为正意味着我在赚钱。

Here is an example of a stock index graph (Dow Jones, year-to-date):
以下是一个股票指数图表示例（道琼斯指数，年初至今）：

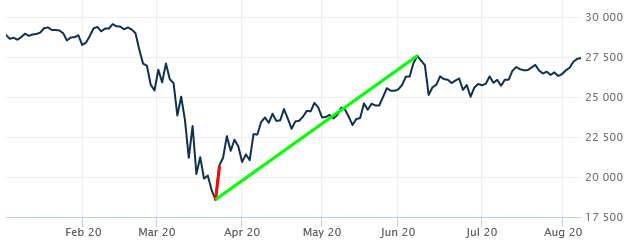
The red segment is one day’s change (March 23, $18,591.93 to March 24, $20,704.91) and its slope gives a daily rate of change of 2112.98 dollars per day; the green segment’s slope shows the average rate of change from March 23 to June 8, namely 90.71 dollars per day.
红色线段代表一天的变化（3月23日，18,591.93美元到3月24日，20,704.91美元），其斜率给出的日变化率为2112.98美元/天；绿色线段的斜率显示了从3月23日到6月8日的平均变化率，即90.71美元/天。

It’s worth noting that this graph is not smooth, but jagged, so there is no instantaneous rate of change (derivative); the one-day rate is the closest we can come.
值得注意的是，这个图表并非平滑的，而是锯齿状的，因此不存在瞬时变化率（导数）；单日变化率是我们能得到的最接近瞬时变化率的数值。

Slope

斜率

This makes sense in terms of how the derivative is defined. The basic part of the formula for the derivative is just the formula for slope. The instantaneous part is where the limit notation comes in. Let’s look at something simple like $y=x^2$.
这与导数的定义方式是相符的。导数公式的核心部分其实就是斜率公式。瞬时性的体现则涉及到极限符号。让我们来看一个简单的例子，比如 $y=x^2$。

If we wanted to find the derivative at $x=3$, we could look first at the graph for a clue. Is the curve going up or down? Imagine a tangent to the curve at $x=3$. The slope of the tangent line is the slope of the curve at that point, by definition.
如果我们想求 $x=3$ 处的导数，首先可以从图像中寻找线索。曲线在该点是上升还是下降？想象一下曲线在 $x=3$ 处的切线。根据定义，切线的斜率就是曲线在该点的斜率。

Here we see the graph of $y=x^2$, with the (dotted) tangent line at $(3,9)$ and a (dashed) secant line through that and another point on the curve (in this case, to the left):
下图是 $y=x^2$ 的图像，其中虚线是 $(3,9)$ 处的切线， dash 线是经过该点和曲线上另一点（此处为左侧一点）的割线：

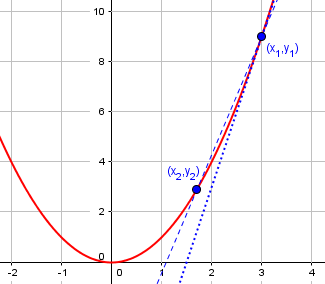
We find it numerically by taking two points, $x_1$ and $x_2$, and the associated $y$ values $y_1$ and $y_2$. In our case $x_1=3$ and $y_1=9$. If we pick $x_2$ to the right of $x_1$, then the slope between the two points would be given by:
我们可以通过取两个点 $x_1$ 和 $x_2$ 以及对应的 $y$ 值 $y_1$ 和 $y_2$，从数值上计算斜率。在我们的例子中，$x_1=3$，$y_1=9$。如果我们选取 $x_2$ 在 $x_1$ 的右侧，那么这两个点之间的斜率可由下式给出：

$$m=\frac{y_2-9}{x_2-3}$$

To find the “instantaneous” change, we just let $x_2$ get closer and closer to $3$. This is where the limit part comes in: as $x_2$ goes to $3$, the change in $x$ (which we call $dx$) goes toward zero.
为了求得“瞬时”变化率，我们只需让 $x_2$ 越来越接近 $3$。这就涉及到极限的概念：当 $x_2$ 趋近于 $3$ 时，$x$ 的变化量（我们称之为 $dx$）趋近于零。

So the derivative at $x=3$ is defined as
因此，$x=3$ 处的导数定义为

$$\underset{x\to 3}{\lim }\frac{x^2-9}{x-3}=\underset{x\to 3}{\lim }(x+3)=6$$

which is the slope of the tangent line at that point.
这就是该点处切线的斜率。

The derivative as a function

作为函数的导数

But there’s more to it than the derivative at a single point. Consider this question, from 2002:
但导数的意义不止于单个点的导数。来看2002年的这个问题：

Using Differentiation to Find Derivatives
用微分法求导数

I am a student in a high school Calculus math class. This is our first year of calculus.
我是一名高中生，正在上微积分课。这是我第一年学习微积分。

Recently our class has been working on differentiation and finding derivatives. However, we are having a difficult time understanding and grasping the concepts of derivatives. We would greatly appreciate it if you could simplify the whole idea of using differentiation to find derivatives. (It would be extremely helpful if you could possibly create for us a real life example or a practical application in which derivatives are used.)
最近我们班一直在学习微分法和求导数。但是，我们很难理解和掌握导数的概念。如果您能简化用微分法求导数这一整套概念，我们将非常感激。（如果您能为我们举一个导数应用的现实例子或实际应用场景，那将非常有帮助。）

This is a good place to point out an oddity in our terminology in English. The noun for what we are finding is “the derivative“, which basically means “a related function we have derived from the given function”. But the verb we use for that process is not “to derive”, but “to differentiate“, which comes from the “difference quotient” on which the derivative is based. The process is called “differentiation“. So, as Scott said, we “differentiate to find derivatives”!
这里可以提一下英语中术语的一个奇特之处。我们要求解的对象对应的名词是“derivative（导数）”，其基本含义是“从给定函数中推导（derive）出的一个相关函数”。但描述这一过程的动词却不是“to derive”，而是“to differentiate（求微分）”，这个词源于导数所基于的“difference quotient（差商）”。这个过程被称为“differentiation（微分法）”。所以，就像斯科特说的，我们“通过求微分（differentiate）来找到导数（derivatives）”！

Doctor Jerry replied:
杰瑞博士回复：

Hi Scott,
你好，斯科特，

We can’t compete with a textbook nor the presence of a teacher, who can interact with those listening to him, but I will say a few things in the hope that they will help.
我们无法与教科书相比，也无法替代能与听众互动的老师，但我会说几点，希望能有所帮助。

First, the idea of a limit is something that is a prerequisite for understanding the idea of a derivative. I’ll assume that you are familiar with the idea of limit.
首先，极限的概念是理解导数概念的前提。我假设你已经熟悉极限的概念。

With certain functions $f$ (whose graphs are “smooth”) we may associate a second function, which we may designate as $f^{\prime }$ or, preferred by some, $Df$. What is the value of $f^{\prime }(x)=(Df)(x)$? In terms of the graph of $f$, the value $f^{\prime }(x)$ is the slope of the tangent line to $f$ at the point $(x,f(x))$. Thus, for example, with the function $f(x)=x^2$ we associate the function $f^{\prime }(x)=2x$. If you graph $f$ you will see a parabola, opening upwards. Look now at the point $(2,f(2))=(2,2^2)=(2,4)$. The slope of the line tangent to the graph of $f$ at $(2,4)$ is $f^{\prime }(2)=2\cdot 2=4$. At the point $(3,9)$, the slope of the tangent to the graph of $f$ at $(3,9)$ is $f^{\prime }(3)=2\cdot 3=6$. And so on.
对于某些函数 $f$（其图像是“平滑的”），我们可以关联一个第二个函数，我们可以将其表示为 $f^{\prime }$，或者有些人更倾向于表示为 $Df$。$f^{\prime }(x)=(Df)(x)$ 的值是什么呢？从 $f$ 的图像来看，$f^{\prime }(x)$ 的值是 $f$ 在点 $(x,f(x))$ 处切线的斜率。例如，对于函数 $f(x)=x^2$，我们关联的函数是 $f^{\prime }(x)=2x$。如果你画出 $f$ 的图像，会看到一个开口向上的抛物线。看点 $(2,f(2))=(2,2^2)=(2,4)$，$f$ 的图像在 $(2,4)$ 处切线的斜率是 $f^{\prime }(2)=2\cdot 2=4$。在点 $(3,9)$ 处，$f$ 的图像在该点切线的斜率是 $f^{\prime }(3)=2\cdot 3=6$，依此类推。

We’ll look at some issues of notation next week. You are likely more familiar with the notation $f^{\prime }(x)$ than $(Df)(x)$; and you may also know it as $\frac{dy}{dx}$.
下周我们会讨论一些符号问题。你可能更熟悉 $f^{\prime }(x)$ 这种符号，而不是 $(Df)(x)$；你可能也知道它可以表示为 $\frac{dy}{dx}$。

Conveniently, Doctor Jerry has used exactly the same example as above. But whereas above we just considered the derivative at a single point, here we are using the full power of the derivative, which is a new function derived from the original, and defined in this way:
方便的是，杰瑞博士用了和上面完全相同的例子。但上面我们只考虑了单个点的导数，这里我们要发挥导数的全部作用——它是一个从原函数推导出来的新函数，其定义如下：

$$f^{\prime }(x)=\underset{h\to 0}{\lim }\frac{f(x+h)-f(x)}{h}=\underset{h\to 0}{\lim }\frac{(x+h{)}^2-x^2}{h}=\underset{h\to 0}{\lim }(2x+h)=2x$$

In particular, the derivative (slope) at $x=3$ is $f^{\prime }(3)=2(3)=6$ just as we saw above when we focused just on the one point.
特别是，$x=3$ 处的导数（斜率）是 $f^{\prime }(3)=2(3)=6$，这与我们上面只关注单个点时得到的结果一致。

So the process of differentiation (which in practice we would carry out using a simple formula that applies to any polynomial, rather than using limits) gives us a function whose value at any $x$ is the slope of the original function. That is what the derivative is.
因此，微分过程（在实际操作中，我们会使用适用于任何多项式的简单公式，而不是通过极限来进行）为我们得到一个新函数，该函数在任意 $x$ 处的值就是原函数在该点的斜率。这就是导数的本质。

An application: radioactive decay

一个应用：放射性衰变

That’s one interpretation of $f^{\prime }$; it gives the slopes of the tangent lines to the graph of $f$. There are many other interpretations; these may depend upon a physical interpretation of $x$ and $f(x)$. If, for example, $x$ is time and $f(x)$ is the AMOUNT of radium remaining at time $x$ (radium decays into something else; into, I think, radon, a gas), then $f(x)$ has the form
这是对 $f^{\prime }$ 的一种解释：它给出了 $f$ 的图像上各点切线的斜率。还有许多其他解释，这些解释可能取决于 $x$ 和 $f(x)$ 的物理意义。例如，如果 $x$ 是时间，$f(x)$ 是在时间 $x$ 时剩余的镭的量（镭会衰变成为其他物质，我认为会衰变成氡气），那么 $f(x)$ 的形式为

$f(x)=C\cdot e^{-k\cdot x}$,

where $C$ and $k$ are constants depending upon the amount of radium at time $0$ ($x=0$) and upon the physical characteristics of radium. We may assume, for example, that $f(x)$ gives the amount (in grams) of radium present at time $x$ (in years).
其中 $C$ 和 $k$ 是常数，$C$ 取决于时间 $0$（$x=0$）时镭的量，$k$ 取决于镭的物理特性。例如，我们可以假设 $f(x)$ 表示在时间 $x$（单位为年）时存在的镭的量（单位为克）。

It turns out that this function form can be obtained from a “differential equation”, an equation that describes how the derivative is related to the function itself; here we are taking it as a given.
事实证明，这种函数形式可以从一个“微分方程”中得到，微分方程描述了导数与函数本身的关系；这里我们直接采用这个函数形式。

When we know the function, we can differentiate it to find the rate of change:
当我们知道这个函数后，就可以通过求导来找到变化率：

$f^{\prime }(x)$ then gives the rate at which the radium is decaying, in grams per year.
那么 $f^{\prime }(x)$ 就表示镭的衰变率，单位是克/年。

You already know that the derivative of $f$ at $x$ is given by
你已经知道 $f$ 在 $x$ 处的导数由下式给出

$f^{\prime }(x)={\lim }_{h\to 0}\frac{f(x+h)-f(x)}{h}$.

Some prefer to write this in the equivalent form
有些人喜欢将其写成等价形式

$f^{\prime }(a)={\lim }_{x\to a}\frac{f(x)-f(a)}{x-a}$.

Graphically, the difference quotient $\frac{f(x)-f(a)}{x-a}$ may be interpreted as the slope of the line joining points $(a,f(a))$ and $(x,f(x))$ on the graph of $f$.
从图像上看，差商 $\frac{f(x)-f(a)}{x-a}$ 可以解释为 $f$ 的图像上连接点 $(a,f(a))$ 和 $(x,f(x))$ 的直线的斜率。

As $x$ approaches $a$, the slope of this line approaches the slope of the tangent line to the graph of $f$ at $(a,f(a))$, assuming that it exists.
假设切线存在，当 $x$ 趋近于 $a$ 时，这条直线的斜率趋近于 $f$ 的图像在 $(a,f(a))$ 处切线的斜率。

The “$a$” here is the same as the “$x_2$” in the first explanation. Observe how the two forms of the definition are related:
这里的“$a$”与第一种解释中的“$x_2$”是同一个概念。注意这两种定义形式之间的关系：

$f^{\prime }(x)={\lim }_{h\to 0}\frac{f(x+h)-f(x)}{h}$

$f^{\prime }(a)={\lim }_{x\to a}\frac{f(x)-f(a)}{x-a}$

The first finds the derivative at a fixed value $x$ by decreasing a difference $h$ to zero; the second finds the derivative at a fixed value $a$ by moving a point $x$ toward $a$, decreasing the distance $x-a$ to zero. The latter is the form we saw in the first answer above.
第一种形式通过让差值 $h$ 减小到零来求固定值 $x$ 处的导数；第二种形式通过让点 $x$ 向固定值 $a$ 移动，使距离 $x-a$ 减小到零来求 $a$ 处的导数。后者就是我们在上面第一个答案中看到的形式。

In the case of $f(x) = $ amount of radium at time $x$, the difference quotient
在 $f(x) = $ 时间 $x$ 时镭的量这一情况下，差商

$\frac{f(x)-f(a)}{x-a}$

is the change in the amount of radium between times $a$ and $x$, divided by the amount of time $x-a$ between these two times. This gives the approximate change in grams per year happening at time $a$. If $x$ is very near $a$, then the difference quotient will be very near the “instantaneous” rate of change of the radium at time $a$.
表示在时间 $a$ 到 $x$ 之间镭的量的变化，除以这两个时间点之间的时间间隔 $x-a$。这给出了在时间 $a$ 附近每年镭的量的近似变化（以克/年为单位）。如果 $x$ 非常接近 $a$，那么这个差商就会非常接近时间 $a$ 时镭的“瞬时”变化率。

That is, the limit of this difference quotient, for any given value of $x$, is $f^{\prime }(x)$. That seems like a lot of work; but here is the magic of calculus:
也就是说，对于任意给定的 $x$ 值，这个差商的极限就是 $f^{\prime }(x)$。这看起来步骤繁多，但这正是微积分的神奇之处：

You might be interested in the fact that in a few months you will be able to “differentiate” the expression
你可能会感兴趣的是，几个月后你就能“求导”下面这个表达式

$f(x)=C\cdot e^{-k\cdot x}$,

finding that
得到

$f^{\prime }(x)=(-k)\cdot C\cdot e^{-k\cdot x}$.

After understanding the IDEA of derivative, the actual calculation is relatively easy.
在理解了导数的概念之后，实际的计算就相对简单了。

Once you learn the quick methods for finding a derivative, you can forget how to calculate it as a limit, because that work has already been done for you. But it’s important not to forget the definition, because that is what the derivative means.
一旦你学会了求导数的快捷方法，就可以不用再通过极限来计算导数了，因为那些工作已经有人为你完成了。但重要的是不要忘记导数的定义，因为定义才体现了导数的本质。

Observe also how the derivative is related to the original function in this case: It is just $-k$ times the function value. This fact is the differential equation from which the original equation can be derived, because it describes the underlying fact about “exponential decay”:
还要注意，在这种情况下，导数与原函数的关系：它只是原函数值的 $-k$ 倍。这一事实就是可以推导出原方程的微分方程，因为它描述了“指数衰减”的基本特性：

$f^{\prime }(x)=-k\cdot f(x)$

. This says that the rate of change (e.g. the number of atoms per second that decay) is proportional to the current amount.
这表明变化率（例如，每秒衰变的原子数）与当前的量成正比。

Developing the definition

导数定义的推导

Now let’s dig just a little deeper, with a question from 1996:
现在让我们更深入一点，来看 1996 年的这个问题：

Derivatives
导数

I am taking calculus this year and I don’t understand the concept of the derivative. Could you explain it to me? It would be very helpful.
我今年在上微积分课，不太理解导数的概念。您能给我解释一下吗？这对我会很有帮助。

Doctor Daniel answered:
丹尼尔博士回答：

Hi Kandice,
你好，坎迪斯，

The concept of a derivative is really very important and I hope I can help explain it to you. Unfortunately, mathematicians use it so often that we sometimes assume that this idea, like many other important ones in math, is so obvious that it should be immediately clear. But it’s really not.
导数的概念确实非常重要，我希望能帮你解释清楚。不幸的是，数学家们经常使用它，以至于有时我们会认为，和数学中许多其他重要概念一样，导数的概念显而易见，应该能立刻被理解。但事实并非如此。

Let’s say you were given a function $f$, which is a function from real numbers to real numbers. (I’m hoping you’re pretty clear on the idea of functions here. If you’re not, please feel free to ask about that too; it’s another extremely important idea which people don’t always get.) Anyhow, we have this function $f:\mathbb{R}\to \mathbb{R}$. (That notation is just shorthand for $f$ maps from reals to reals.) Maybe, to put a concrete feel to it, $f$ is a function that maps the time, since an experiment began, to the amount of radioactive material in a source which is decaying. But the idea is general enough to just work for any function from $\mathbb{R}\to \mathbb{R}$.
假设给你一个函数 $f$，它是一个从实数集到实数集的函数。（我希望你对函数的概念有相当清晰的理解。如果没有，也请随时提问，函数是另一个人们并不总能理解的极其重要的概念。）总之，我们有这个函数 $f:\mathbb{R}\to \mathbb{R}$。（这个符号只是“$f$ 从实数集映射到实数集”的简写。）或许，为了更具体一些，可以把 $f$ 看作是一个函数，它将实验开始后的时间映射为正在衰变的放射源中放射性物质的量。但这个概念具有普遍性，适用于任何从 $\mathbb{R}\to \mathbb{R}$ 的函数。

You may not be familiar with the notation $f:\mathbb{R}\to \mathbb{R}$; it just means that the input of function $f$ is a real number, and the output is also a real number. We say that function $f$ “maps” the real numbers to the real numbers.
你可能不熟悉 $f:\mathbb{R}\to \mathbb{R}$ 这种符号；它只是表示函数 $f$ 的输入是一个实数，输出也是一个实数。我们说函数 $f$“将”实数集“映射到”实数集。

He chooses the same example as Doctor Jerry above, where the input is the time and the output is the amount of radium or whatever.
他选用了和上面杰瑞博士相同的例子，其中输入是时间，输出是镭或其他物质的量。

Now, suppose you want to find how fast the function is changing at any given moment. For example, you might be curious how fast the source is emitting radioactive particles. This would be measured in particles/sec, and it should be fairly easy to compute, all things considered. How would we try doing it?
现在，假设你想知道函数在任意给定时刻的变化有多快。例如，你可能想知道放射源释放放射性粒子的速度有多快。考虑到各种因素，这个速度的单位是粒子/秒，计算起来应该相当容易。我们该如何计算呢？

Well, let’s say we wanted to find the rate of change of the function at the time = 10 seconds. We could compute the amount of particles left in the sample after 10 seconds, $f(10)$, and the amount of particles left after 20 seconds, $f(20)$.
假设我们想求在时间为10秒时函数的变化率。我们可以计算10秒后样品中剩余的粒子量 $f(10)$，以及20秒后剩余的粒子量 $f(20)$。

$f(20)-f(10)$ is the amount of particles emitted in 10 seconds. If $f(x)$ is a straight line, then the rate of change at $x=10$ seconds will be roughly:
$f(20)-f(10)$ 是10秒内释放的粒子量。如果 $f(x)$ 是一条直线，那么在 $x=10$ 秒时的变化率大致为：

$$\frac{f(20)-f(10)}{20-10}$$

This is the slope of the line from $(20,f(20))$ to $(10,f(10))$. But suppose it’s not a line. Then the rate of change at 10 sec is probably closer to $f(11)-f(10)$, which is the slope of the line from $(11,f(11))$ to $(10,f(10))$. In fact, if we get closer and closer to 10, we’re computing the slope of a line that is closer and closer to what the function looks like closer and closer to when $x=10$. So, for example, $10\cdot (f(10.1)-f(10))$ is closer to our desired rate of change than $\frac{1}{10}\cdot (f(20)-f(10))$.
这是从点 $(20,f(20))$ 到点 $(10,f(10))$ 的直线的斜率。但假设 $f(x)$ 不是一条直线，那么10秒时的变化率可能更接近 $f(11)-f(10)$，这是从点 $(11,f(11))$ 到点 $(10,f(10))$ 的直线的斜率。事实上，当我们取的点越来越接近10时，我们计算出的直线的斜率就越来越接近函数在 $x=10$ 附近的变化情况。例如，$10\cdot (f(10.1)-f(10))$ 比 $\frac{1}{10}\cdot (f(20)-f(10))$ 更接近我们想要的变化率。

This is the average rate we’ve seen before, or the slope of the line joining two points on a curve.
这就是我们之前见过的平均变化率，或者说，是连接曲线上两点的直线的斜率。

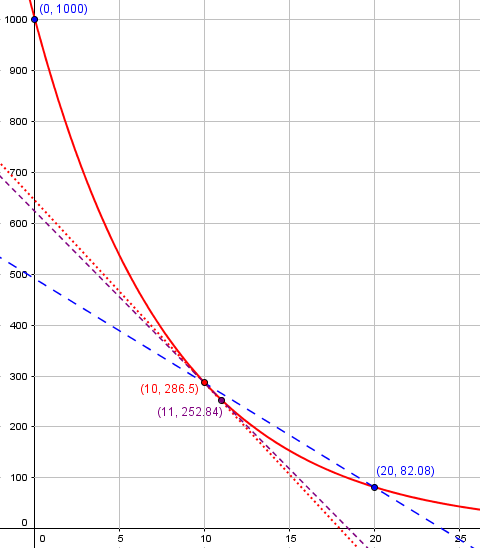
Here are two of those “secant lines”, through points at $x=10$ and $x=20$ or $x=11$, together with the actual tangent (dotted red):
下图是两条“割线”，一条经过 $x=10$ 和 $x=20$ 处的点，另一条经过 $x=10$ 和 $x=11$ 处的点，还有实际的切线（红色虚线）：

Remember that we’re really just computing the slope of lines that look a lot like our curve. What we want is the slope of the curve itself.
记住，我们实际上只是在计算那些与曲线非常相似的直线的斜率。我们想要的是曲线本身的斜率。

If you’re pretty clear on the definition of a limit, you should see the answer at this point. The slope of the curve (“the rate of change of the function $f$”, “the derivative of $f$”) at $x=10$ will be this limit:
如果你对极限的定义相当清楚，这时你应该能明白答案了。曲线在 $x=10$ 处的斜率（“函数 $f$ 的变化率”、“$f$ 的导数”）就是这个极限：

$$\underset{h\to 0}{\lim }\frac{f(10+h)-f(10)}{h}$$

The denominator and numerator are both approaching zero! In practice, however, the value of the numerator will include something with a power of $h$ which will cancel the $h$ on the denominator, and we’ll be fine.
分母和分子都在趋近于零！但在实际中，分子的值中会包含 $h$ 的幂次项，这能与分母中的 $h$ 相消，所以计算不会有问题。

In other words, if you had to calculate this limit directly, you would often find that the fraction could be simplified by canceling an $h$; that is not always true, and sometimes takes a lot of work!
换句话说，如果你必须直接计算这个极限，通常会发现可以通过消去 $h$ 来简化这个分数；但情况并非总是如此，有时简化过程会很繁琐！

This is the definition of the derivative of $f$ in general, rather than just at $x=10$:
这是函数 $f$ 的导数的一般定义，而不仅仅是 $x=10$ 处的导数：

$$f^{\prime }(x)=\underset{h\to 0}{\lim }\frac{f(x+h)-f(x)}{h}$$

What do we know that this must mean? Well, for starters, $f$ has to be a continuous function at the point we’re considering. Do you remember what continuity means? That means you could draw the graph of the function without ever lifting a pencil off the paper. In language of limits, that means
我们知道这一定意味着什么呢？首先，$f$ 在我们所考虑的点处必须是连续的。你还记得连续性的含义吗？连续性意味着你可以一笔画出函数的图像而不用提笔。用极限的语言来说，就是

$$\underset{h\to 0}{\lim }f(x+h)=f(x)$$

Otherwise, the numerator won’t be zero and the limit will be infinite. Another requirement is that the function doesn’t change directions suddenly as you get closer to $x$. Another (though it’s obvious) is that the function has to have a value at $x$; that is, $f(x)$ has to exist.
否则，分子就不会为零，极限就会是无穷大。另一个要求是，当趋近于 $x$ 时，函数不会突然改变方向。还有一个（虽然很明显）要求是，函数在 $x$ 处必须有定义，也就是说，$f(x)$ 必须存在。

These are conditions for a function to be “differentiable” at a given point.
这些是函数在某一点“可导”的条件。

If the derivative has a value at all points, then it’s clear that it’s also a function. So, for our function $f$, we can talk about the function $f^{\prime }$, which is its derivative, where $f^{\prime }(x)$ is the derivative of $f$ at the given point. You’ve probably learned formulas by now which help you compute these functions.
如果导数在所有点都有值，那么显然它也是一个函数。因此，对于我们的函数 $f$，我们可以谈论它的导函数 $f^{\prime }$，其中 $f^{\prime }(x)$ 是 $f$ 在给定点处的导数。到现在，你可能已经学习了一些有助于计算这些导函数的公式。

This is very important: Differentiation produces not a number but a function. In fact, as I see it, this is why the concept of functions was invented: to have a name for the thing that differentiation works on.
这一点非常重要：微分得到的不是一个数，而是一个*函数。事实上，在我看来，这就是函数概念被发明的原因：为微分所作用的对象命名。

That’s a very long answer to a very important question. The derivative of the function at a given point is the slope of the curve at that point. The way we compute it is by computing the slope of line segments which get closer and closer to the point itself, and eventually taking the limit of this process. It’s a function itself, and in practice, rather than computing the limit directly, we compute it using formulas which make our lives much easier.
对于一个非常重要的问题，这是一个相当长的答案。函数在某一点的导数就是曲线在该点的斜率。我们计算导数的方法是：计算越来越接近该点的线段的斜率，并最终取这个过程的极限。导数本身也是一个函数，在实际中，我们不会直接计算极限，而是使用能让我们的计算更简便的公式来求导。

---

What Derivative Notations Mean

导数符号的含义

August 17, 2020 / By Dave Peterson

Last week we looked at the meaning of the derivative. In doing so, we mostly used the notation “$f^{\prime }(x)$“, but mentioned another in passing. Here I want to look at our answers to several questions about the different notations you will see.
上周我们探讨了导数的含义。在讨论过程中，我们主要使用了“$f^{\prime }(x)$”这种符号，但也顺便提到了另一种符号。在这里，我想看看我们对几个关于导数符号问题的解答。

Several different notations

几种不同的符号

We’ll start with this question from 2013:
我们从2013年的这个问题开始：

Differences in Differentiation Notation?
微分符号的区别？

Hello, I am currently studying calculus, and am doing derivatives. I know how to take derivatives of various functions, but I am confused about the notation.
你好，我目前正在学习微积分，正在学导数部分。我知道如何求各种函数的导数，但对符号感到困惑。

I know that $\frac{d}{dx}(f(x))$ means “the derivative of function $f$.” But sometimes, when I’m reading the book, I see they write $\frac{dy}{dx}$, $\frac{d}{dy}$, or however they write it.
我知道 $\frac{d}{dx}(f(x))$ 表示“函数 $f$ 的导数”。但有时，我在看书时，会看到他们写 $\frac{dy}{dx}$、$\frac{d}{dy}$ 之类的符号。

I believe $\frac{dy}{dx}$ means “derivative of $y$ with respect to $x$,” or something similar to that, but I also get VERY confused when they say “with respect to $x$;” I don’t know what that means.
我认为 $\frac{dy}{dx}$ 表示“$y$ 对 $x$ 的导数”，或者类似的意思，但当他们说“关于 $x$”时，我非常困惑，不知道这是什么意思。

Can you please give me a general overview of the meanings of the different derivative notations?
你能给我大致介绍一下不同导数符号的含义吗？

Thanks!
谢谢！

The question is specifically about what is called Leibniz notation, after its inventor, one of the creators of calculus; but I will also mention a couple others.
这个问题专门涉及一种被称为莱布尼茨符号的符号，它以其发明者——微积分的创立者之一的名字命名；但我也会提到其他几种符号。

Leibniz notation: $\frac{dy}{dx}$

莱布尼茨符号：$\frac{dy}{dx}$

I answered:
我回答道：

Hi, Zanzabar.
你好，赞扎巴尔。

The basic idea is that we write $\frac{dy}{dx}$ to remind us that the derivative is defined as
基本思路是，我们用 $\frac{dy}{dx}$ 来提醒我们，导数的定义是

$$\underset{\Delta x\to 0}{\lim }\frac{\Delta y}{\Delta x}$$

That is, it is a slope: the ratio of a change in $y$ to a change in $x$. But we think of those changes as being very, very small – just looking at the limit.
也就是说，它是一个斜率：$y$ 的变化量与 $x$ 的变化量的比值。但我们认为这些变化量非常非常小——只关注极限情况。

Showing the notation as we couldn’t back then, this definition is
用我们现在的符号来表示（以前无法这样表示），这个定义是

$$\frac{dy}{dx}=\underset{\Delta x\to 0}{\lim }\frac{\Delta y}{\Delta x}$$

This is equivalent to the forms of the definition we discussed last week, where we called $\Delta x$ “$h$” and used $f(x)$ for $y$.
这与我们上周讨论的定义形式是等价的，上周我们将 $\Delta x$ 称为“$h$”，并用 $f(x)$ 表示 $y$。

When calculus was first invented, they actually thought of $dx$ and $dy$ as very tiny quantities, but that led to difficulties in logic – sometimes you’d be thinking of $dx$ as actually being zero, and sometimes not. (A philosopher complained that mathematicians were talking about “the ghosts of departed quantities,” and it was a valid complaint!) The idea of limits was created to avoid those problems; but we can still informally think of them that way.
在微积分刚被发明时，人们实际上将 $dx$ 和 $dy$ 视为非常小的量，但这带来了逻辑上的困难——有时你会认为 $dx$ 实际上是零，有时又不这么认为。（一位哲学家抱怨说，数学家们在谈论“逝去量的幽灵”，这是一个合理的抱怨！）极限概念的创立就是为了避免这些问题，但我们仍然可以非正式地那样看待它们。

So “d” can be thought of as meaning “a very small change in …,” and this …
所以“d”可以被理解为“……的一个非常小的变化”，而这个……

$$\frac{df(x)}{dx}$$

… means “the ratio of a very small change in the value of the function to the very small change in $x$ that caused it.” (Don’t tell a mathematician that I told you this … 😉
……表示“函数值的一个非常小的变化与引起该变化的 $x$ 的非常小的变化的比值”。（别告诉数学家这是我说的……；-）

I was exaggerating the disapproval of mathematicians. In fact, there is a field of mathematics today that has formally defined these concepts of “infinitesimals”, which Doctor Jordi discussed here:
我夸大了数学家们的反对态度。事实上，如今有一个数学领域已经正式定义了“无穷小量”这些概念，若尔迪博士在这里讨论过：

Nonstandard Analysis and the Hyperreals, by Jordi Gutierrez Hermoso
《非标准分析与超实数》，若尔迪·古铁雷斯·埃尔莫索 著

This approach is used at an introductory level in the textbook Elementary Calculus: An Infinitesimal Approach_, by H. Jerome Keisler. So the limit approach is not the only mathematically valid way to learn about derivatives.
这种方法在 H·杰罗姆·凯斯勒所著的《初等微积分：无穷小方法》这本教科书中被用于入门级教学。因此，极限方法并不是学习导数的唯一数学上有效的方法。

But we usually think of the notation as merely looking like a fraction.
但我们通常认为这种符号只是看起来像一个分数。

When we say “derivative with respect to $x$,” we mean that we are talking about the rate of change of the function value in relation to the change in $x$, as opposed to some other variable that might be floating around. (This becomes a lot more important when we are dealing with functions of more than one variable, but you won’t get to that for a while.) For example, I could tell you how fast the temperature is rising “with respect to time,” in order to emphasize that I am talking about how much the temperature is increasing per day, say, rather than how much hotter it is for every mile you drive south. The former would be a ratio of temperature to time; the latter, a ratio of temperature to distance. We usually know what that bottom variable is going to be from context, but sometimes it’s important to mention, and the notation makes it clear.
当我们说“关于 $x$ 的导数”时，意思是我们谈论的是函数值相对于 $x$ 的变化率，而不是相对于其他可能存在的变量的变化率。（当我们处理多变量函数时，这一点会变得重要得多，但你暂时还不会学到。）例如，我可以告诉你温度“相对于时间”上升的速度，目的是强调我说的是每天温度上升多少，而不是你向南每开一英里温度会升高多少。前者是温度与时间的比率，后者是温度与距离的比率。通常我们能从上下文知道分母的变量是什么，但有时明确提出来很重要，而这种符号能清楚地表示出来。

So “the derivative with respect to $x$” basically means “the derivative with $dx$ on the bottom of the notation.”
所以“关于 $x$ 的导数”基本上就是指“符号分母为 $dx$ 的导数”。

One place you will see multiple variables involved in one problem is when we use the chain rule:
在一个问题中涉及多个变量的情况之一是当我们使用链式法则时：

$$\frac{dy}{du}\cdot \frac{du}{dx}=\frac{dy}{dx}$$

There, it is very important which variable is used at each step.
在这种情况下，每一步使用哪个变量非常重要。

The more involved cases I referred to involve partial derivatives, a much later topic in calculus, where a different symbol $\frac{\partial z}{\partial x}$ is used for clarity. Here, $z$ might be a function of several variables, say $z=f(x,y)$, and we are treating $y$ temporarily as a constant.
我提到的更复杂的情况涉及偏导数，这是微积分中一个较晚才会学到的主题，为了清晰起见，会使用不同的符号 $\frac{\partial z}{\partial x}$。在这里，$z$ 可能是一个多变量函数，比如 $z=f(x,y)$，我们暂时将 $y$ 视为常数。

Lagrange notation: $f^{\prime }(x)$

拉格朗日符号：$f^{\prime }(x)$

I turned to the other common notation focusing on function notation, which many mathematicians today prefer:
我转而介绍另一种常见的、侧重于函数符号的符号，这是当今许多数学家更喜欢的符号：

The notation $f^{\prime }(x)$ is more formal, and avoids some of the dangerous implications of the $\frac{df}{dx}$ notation. It doesn’t suggest that the derivative actually IS a fraction (rather than the limit of a fraction); it just says we have a “derived function” – a new function that we obtained from another by this process.
符号 $f^{\prime }(x)$ 更正式，避免了 $\frac{df}{dx}$ 符号可能带来的一些误导性暗示。它不会让人觉得导数实际上是一个分数（而不是分数的极限）；它只是表明我们有一个“导出函数”——通过这个过程从另一个函数得到的新函数。

In one sense, this notation hides its meaning, making it less intuitive; any “derived function” could have been named this way. Its benefit is largely in not carrying any meaning that might distract you!
从某种意义上说，这种符号隐藏了其含义，使其不太直观；任何“导出函数”都可以用这种方式命名。它的好处主要在于不会携带任何可能分散你注意力的含义！

What makes this notation especially valuable is that it focuses attention on the function itself rather than on the variables. When we differentiate, we aren’t really doing anything to the variables, but only making a new function, the values of which turn out to be rates of change of the given function. On the other hand, it can hide what variable we are differentiating with respect to. (It’s the argument of the function, which isn’t always showing; and when more than one variable is in view, we have to modify the notation.)
这种符号的特别价值在于，它将注意力集中在函数本身而不是变量上。当我们求导时，实际上并不是对变量做什么操作，而只是得到一个新函数，这个新函数的值恰好是给定函数的变化率。另一方面，它可能会掩盖我们是对哪个变量求导。（求导所针对的变量是函数的自变量，但并不总是明确显示；当涉及多个变量时，我们就必须对符号进行修改。）

This notation, like the $\frac{d}{dx}$ notation, can be applied either to a named function, like $f^{\prime }$, or to a variable (thought of as a function), e.g. $y^{\prime }$.
这种符号和 $\frac{d}{dx}$ 符号一样，既可以应用于有名称的函数，如 $f^{\prime }$，也可以应用于变量（将变量视为函数），例如 $y^{\prime }$。

The modified notation used for functions of more than one variable looks like $f_x=\frac{\partial f(x,y)}{\partial x}$.
用于多变量函数的修改后的符号看起来像 $f_x=\frac{\partial f(x,y)}{\partial x}$。

Leibniz notation as an operator: $\frac{d}{dx}$

作为算子的莱布尼茨符号：$\frac{d}{dx}$

Now, when we write $\frac{d}{dx}$ separately, as in $\frac{d}{dx}f(x)$, we’re thinking of it as an operator – it tells us what we’re doing to the function $f$, and is essentially equivalent to putting the prime mark on it ($f^{\prime }$). The notation comes again from the analogy to fractions. Just as we can write …
现在，当我们将 $\frac{d}{dx}$ 单独写出，如 $\frac{d}{dx}f(x)$ 时，我们将其视为一个算子——它告诉我们我们正在对函数 $f$ 进行什么操作，本质上等同于在函数上加上撇号（$f^{\prime }$）。这种符号的由来再次与分数的类比有关。就像我们可以写……

$$\frac{2}{3}\cdot 6=\frac{2\cdot 6}{3}=4$$

… we can write
……我们可以写

$$\frac{d}{dx}f(x)=\frac{df(x)}{dx}=f^{\prime }(x)$$

It means “the derivative with respect to $x$ of …”.
它表示“……关于 $x$ 的导数”。

So just as
所以就像

$$\frac{2}{3}\cdot f(x)=\frac{2\cdot f(x)}{3},$$

we can write
我们可以写

$$\frac{d}{dx}\cdot f(x)=\frac{df(x)}{dx}.$$

It’s mere notation.
这仅仅是一种符号表示。

I then referred to the two pages we’ll be looking at below.
然后我提到了我们下面将要看到的两页内容。

Euler ($Df$) and Newton ($\dot{y}$) notations

欧拉符号（$Df$）和牛顿符号（$\dot{y}$）

I should mention here a couple other notations that are used in special contexts. One is $Df$, which was mentioned last week. The $D$ operator is essentially the same as $\frac{d}{dx}$. You can see an example of it in action here:
这里我应该提一下在特殊情况下使用的另外两种符号。一种是 $Df$，上周提到过。$D$ 算子本质上和 $\frac{d}{dx}$ 是一样的。你可以在这里看到它的一个应用示例：

Particular Solution of Differential Equation
微分方程的特解

Another notation is $\dot{x}=\frac{dx}{dt}$, which was used by Newton, and is still found particularly in physics. The dot specifically indicates differentiation with respect to time; otherwise, it is equivalent to the prime notation applied to a variable, like $y^{\prime }$. We don’t seem to have ever discussed it, except for a couple unarchived answers.
另一种符号是 $\dot{x}=\frac{dx}{dt}$，这是牛顿使用的符号，在物理学中尤其常见。点符号专门表示对时间求导；否则，它等同于应用于变量的撇号符号，如 $y^{\prime }$。除了几个未存档的答案外，我们似乎从未讨论过它。

Is $\frac{dy}{dx}$ a fraction? Yes and no …

$\frac{dy}{dx}$ 是分数吗？既是也不是……

A question from 2004, the first of the two I directed Zanzabar to, looked more closely at the $\frac{dy}{dx}$ notation:
2004 年的一个问题（我给赞扎巴尔推荐的两个问题中的第一个）更深入地探讨了 $\frac{dy}{dx}$ 符号：

Can $\frac{dy}{dx}$ Be Treated as a Fraction?
$\frac{dy}{dx}$ 可以被当作分数对待吗？

When I learned about derivatives, I learned that $\frac{dy}{dx}$ was a notation that implied “derivative of $y$ with respect to $x$.” I understood that. But I am confused about whether or not the notation $\frac{dy}{dx}$ can be treated as a fraction, giving individual meanings to $dy$ and $dx$.
当我学习导数时，我知道 $\frac{dy}{dx}$ 是一个符号，表示“$y$ 对 $x$ 的导数”。这一点我理解。但我困惑的是，$\frac{dy}{dx}$ 这种符号是否可以被当作分数对待，从而赋予 $dy$ 和 $dx$ 各自的含义。

For example, in integration by substitution:
例如，在换元积分法中：

integrate ($\sin (3x+5)dx$)
求 $\int \sin (3x+5)dx$

$u=3x+5$

$\frac{du}{dx}=3$

$dx=\frac{du}{3}$

That is the part that confuses me. How can the $dx$ be solved for? What exactly is “$dx$”?
这正是让我困惑的地方。怎么能解出 $dx$ 呢？“$dx$”到底是什么？

I understand that $\frac{dy}{dx}$ is a limit, and that it is a slope. But the idea of it being simply a notation doesn’t help me understand how you can multiply out the bottom. Any help would be appreciated…
我知道 $\frac{dy}{dx}$ 是一个极限，也是一个斜率。但仅仅将其视为一种符号，无法帮助我理解为什么可以将分母乘过去。希望能得到您的帮助……

This separate use of $dx$ and $dy$ is particularly common in integration, which is the inverse of differentiation, but is also used in other ways. Is it really legal to break $\frac{dy}{dx}$ apart like this?
$dx$ 和 $dy$ 的这种单独使用在积分（微分的逆运算）中尤为常见，但也用于其他方面。像这样将 $\frac{dy}{dx}$ 拆开真的合理吗？

This topic was previously discussed in less depth, in the post Why Do People Treat $\frac{dy}{dx}$ as a Fraction?, where I quoted an unarchived answer from 2015, and gave links to some of the pages we’re looking at here.
这个主题之前在《为什么人们把 $\frac{dy}{dx}$ 当作分数对待？》一文中有过较浅层次的讨论，在那篇文章中，我引用了 2015 年一个未存档的答案，并给出了我们在这里所看的一些页面的链接。

No …

不是……

Doctor Vogler answered:
沃格勒博士回答：

Hi Amit,
你好，阿米特，

Thanks for writing to Dr Math. The easy answer to your question is that your definition for $\frac{dy}{dx}$ is correct; it means the derivative of $y$ with respect to $x$, and $dy$ and $dx$ are meaningless when written alone, so that
感谢你给数学博士写信。你的问题的简单答案是，你对 $\frac{dy}{dx}$ 的定义是正确的；它表示 $y$ 对 $x$ 的导数，而 $dy$ 和 $dx$ 单独写出来是没有意义的，所以

$dx=\frac{du}{3}$

is not a meaningful expression but should be written
不是一个有意义的表达式，而应该写成

$\frac{dx}{du}=\frac{1}{3}$.

This follows the formal definition of $\frac{dy}{dx}$, which represents a single operator on a function, not an actual fraction. But certain things you can do with a derivative look an awful lot like what we can do with fractions:
这符合 $\frac{dy}{dx}$ 的正式定义，它表示对函数的一个单一算子，而不是一个实际的分数。但对导数进行的某些操作，看起来非常像我们对分数进行的操作：

And when certain nice things happen that look like fractions, such as:
当某些看起来像分数的奇妙现象出现时，例如：

$$\frac{dy}{dz}=\frac{1}{\frac{dz}{dy}}$$

and
以及

$$\frac{dz}{dx}=\frac{dz}{dy}\cdot \frac{dy}{dx}$$

then this is actually just the Chain Rule at work. And the reason that
那么这实际上只是链式法则在起作用。而

$\int f(g(x))g^{\prime }(x)dx=\int f(u)du$

is not that
并不是因为

$u=g(x)$

implies
意味着

$du=g^{\prime }(x)dx$

but rather the Chain Rule again.
而是再次因为链式法则。

The chain rule, and the related concept of substitution in an integral “just happen” to look like you can juggle $dx$ and $dy$ and $du$, called differentials, as if they were numbers themselves. And the rules for substitution in an integral are proved by the chain rule, not by treating differentials as real entities.
链式法则以及积分中相关的换元概念，“恰好”看起来像你可以像处理数字一样摆弄 $dx$、$dy$ 和 $du$（称为微分）。积分中的换元法则是由链式法则证明的，而不是通过将微分视为真实实体来证明的。

… But, yes, in fact

……但实际上，是的

All of that is true, except that I should qualify the “not a meaningful expression.” You see, something is only meaningless until somebody gives it a formal meaning. Then you hope that the meaning they gave it has useful properties (such as, that it relates to derivatives…). In fact, this has been done, and there is a good deal of mathematics that has gone into the theory of differentials, and it fits into integrals, and putting the differential “$dx$” at the end of every integral also makes sense according to this theory, and so on. One math doctor alluded to some of this on Differentials.
所有这些都是事实，但我应该对“不是一个有意义的表达式”进行限定。你看，某事物只有在有人赋予它正式意义之前才是无意义的。然后你会希望他们赋予的意义具有有用的性质（例如，与导数相关……）。事实上，人们已经做到了这一点，并且有大量的数学知识投入到了微分理论中，微分理论与积分相契合，根据这一理论，在每个积分的末尾加上微分“$dx$”也是有意义的，等等。

You can also get books that discuss this in more detail. But the fact is that most people who use calculus don’t really need all of the theory of differentials, and the Chain Rule indeed suffices to verify most facts that you would get from treating $\frac{dy}{dx}$ as a fraction. The reason you can treat it as a fraction is that $\frac{dy}{dx}$ is the limit of a fraction, and so most of the operations you would do to the fraction you can do before you take the limit. In other words, before the limit is taken, it is a fraction, so you can treat it as one. But then you take the limit and it becomes a derivative.
你也可以找到更详细讨论这个问题的书籍。但事实是，大多数使用微积分的人并不真正需要全部的微分理论，链式法则确实足以验证大多数将 $\frac{dy}{dx}$ 当作分数对待时得到的结论。你可以将其当作分数对待的原因是，$\frac{dy}{dx}$ 是一个分数的极限，因此你对分数进行的大多数操作，都可以在取极限之前进行。换句话说，在取极限之前，它就是一个分数，所以你可以将其当作分数对待。但当你取极限后，它就变成了导数。

We can say that the derivative “inherits” some (not all) of the behavior of fractions from the fraction (difference quotient) that is at the heart of its definition. That fraction is the motivation for the notation, and the notation makes it easy to remember things like the chain rule, but you have to remember that in spite of all this, it isn’t really a fraction, and you can only treat it as a fraction where there is a theorem that says you can.
我们可以说，导数从其定义核心的分数（差商）中“继承”了一些（并非全部）分数的性质。那个分数是这种符号的设计动机，而且这种符号让人们很容易记住像链式法则这样的内容，但你必须记住，尽管如此，它并不真的是一个分数，只有在有定理表明可以将其当作分数对待的情况下，你才能这样做。

One place where we actually write differentials on their own, besides integration, is in estimation, which ties in with the theory of differentials:
除了积分之外，我们实际上单独使用微分的一个地方是在估计中，这与微分理论相关：

Finally, there is also the theory of estimating with derivatives, where I always say to think of
最后，还有用导数进行估计的理论，在这个理论中，我总是说可以这样想：

$dx=$ change in $x$

$dy=$ change in $y$

$x=$ unchanged value of $x$

$y=$ unchanged value of $y$

For example, to estimate $(1.98{)}^6$, we use
例如，要估计 $(1.98{)}^6$，我们使用

$y=x^6$

$dy=6x^{5}dx$

$x=2$

$dx=-0.02$

(so that $x+dx=1.98$), and therefore
（这样 $x+dx=1.98$），因此

$y=2^6=64$

$dy=6x^{5}dx=6\cdot 32\cdot (-0.02)=-3.84$

which implies that
这意味着

$y+dy=64-3.84=60.16$,

which is, in fact, a pretty close approximation to $(1.98{)}^6$. And this is essentially treating $\frac{dy}{dx}$ as a fraction before we’ve taken the limit, since $dx$ doesn’t go all the way to zero but only to $-0.02$.
实际上，这与 $(1.98{)}^6$ 的值非常接近。这本质上是在取极限之前将 $\frac{dy}{dx}$ 当作分数对待，因为 $dx$ 并没有完全趋近于零，而只是到 $-0.02$。

Does this help you to understand how differentials are a fraction in some sense but not in others? If you have any questions about this or need more help, please write back and show me what you have been able to do, and I will try to offer further suggestions.
这是否帮助你理解了微分在某种意义上是分数，而在其他意义上不是分数呢？如果你对此有任何疑问或需要更多帮助，请回信告诉我你目前的理解情况，我会尽力提供进一步的建议。

What’s squared in the second derivative?

二阶导数中的平方代表什么？

The second page I recommended was this, also from 2004:
我推荐的第二页内容也来自 2004 年：

Meaning of Second Derivative Notation
二阶导数符号的含义

What does the second derivative notation, $\frac{d^{2}y}{d{x}^2}$, really mean?
二阶导数符号 $\frac{d^{2}y}{d{x}^2}$ 真正的含义是什么？

I understand that the notation in the numerator means the 2nd derivative of $y$, but I fail to understand the notation in the denominator. Isn’t it supposed to mean with respect to $x$? Why is there an $x^2$ in the notation?
我明白分子的符号表示 $y$ 的二阶导数，但我不理解分母的符号。它不是应该表示“关于 $x$”吗？为什么符号中会有 $x^2$ 呢？

We haven’t until now shown any second derivatives, which look like this:
到目前为止，我们还没有展示过二阶导数，其形式如下：

$f^{\prime \prime }(x)=D^{2}y=\frac{d^{2}y}{d{x}^2}$

In Newton’s notation,
在牛顿符号中，

$\frac{d^{2}x}{d{t}^2}=\ddot{x}$

I answered this one:
我回答了这个问题：

Hi, Jamie.
你好，杰米。

I don’t think this is explained nearly as often as it should be! There is no $x^2$ in this notation, and in fact no multiplication (i.e., it is not $d{x}^2$ as you say). It is
我认为这个问题并没有得到应有的频繁解释！这个符号中没有 $x^2$，实际上也没有乘法（也就是说，它不像你说的那样是 $d{x}^2$）。它是

$\frac{d^{2}y}{d{x}^2}$

and the “d” represents the “differential operator”, which evidently has higher precedence than exponentiation. That is, “dx” as a whole is thought of as a quantity (think of it as a small change in $x$), and the denominator is “$(dx{)}^2$”.
其中“d”代表“微分算子”，显然它的优先级高于指数运算。也就是说，“dx”整体被视为一个量（可以认为是 $x$ 的一个小变化），而分母是“$(dx{)}^2$”。

Having written a lot on the order of operations, I’m sensitive to the fact that if $d{x}^2$ were a multiplication, it would mean $d(x^2)$. Instead, you have to think of $d$ as an operator that “binds tightly to” the variable, making $dx$ a single unit. The second derivative notation comes from once again imagining that the derivative is really a fraction:
由于写过很多关于运算顺序的内容，我意识到如果 $d{x}^2$ 是乘法，它应该表示 $d(x^2)$。相反，你必须将 $d$ 视为一个与变量“紧密结合”的算子，使 $dx$ 成为一个单一单元。二阶导数的符号再次源于将导数想象成一个分数：

But here is where it comes from: the second derivative is just the derivative of the derivative, or
但它的由来是这样的：二阶导数就是导数的导数，即

$\frac{d}{dx}\left(\frac{dy}{dx}\right)=\frac{d(dy)}{(dx{)}^2}=\frac{d^{2}y}{d{x}^2}$

You might read it as “the second derivative of $y$, with respect to $x$ TWICE”; that last word is the reason for the “$d{x}^2$”. When you have functions of more than one variable you can see things like
你可以将其读作“$y$ 对 $x$ 的二阶导数”；最后一个“阶”字就是“$d{x}^2$”的由来。当涉及多变量函数时，你会看到类似这样的符号

$\frac{d^{2}z}{dxdy}$

(though a modified “d” is used to avoid some confusion); this means you are taking one derivative with respect to $x$ and another with respect to $y$:
（尽管为了避免一些混淆会使用一个修改过的“d”）；这表示你先对 $x$ 求一次导，再对 $y$ 求一次导：

$\frac{d}{dx}\left(\frac{dz}{dy}\right)$

These last things, partial derivatives, look like
这些最后的符号，偏导数，看起来像

$\frac{{\partial }^{2}z}{\partial x\partial y}=\frac{\partial }{\partial x}\left(\frac{\partial z}{\partial y}\right)$

I closed with a reference to the same page Doctor Vogler had mentioned:
最后我引用了沃格勒博士提到的同一页内容：

This notation is based on analogies to fractions, and it can be dangerous to imagine that the $dx$ and $dy$ and $d$ alone actually stand for numbers; but the notation works very well in making many formulas memorable. See this page for more on differentials:
这种符号基于与分数的类比，将 $dx$、$dy$ 和单独的 $d$ 想象成实际代表数字是有风险的；但这种符号能很好地帮助人们记住许多公式。

Another view of the second derivative

二阶导数的另一种理解

Let’s look at one more question about this, from 2009:
让我们再看一个2009年关于这个问题的提问：

Differential Notation
微分符号

Why is the second derivative written as $\frac{d^{2}y}{d{x}^2}$?
为什么二阶导数要写成 $\frac{d^{2}y}{d{x}^2}$ 呢？

Doctor Vogler replied, with thoughts similar to mine:
沃格勒博士的回答与我的想法相似：

Hi Jordan,
你好，乔丹，

Thanks for writing to Dr. Math. It seems mysterious how the numerator repeats the $d$ but the denominator repeats the $dx$, but it makes sense if you think about it the right way.
感谢你给数学博士写信。分子重复“d”而分母重复“dx”，这看起来很奇怪，但如果从正确的角度去理解，就说得通了。

You are familiar with the notation
你熟悉这个符号

$\frac{dy}{dx}$

to mean “the derivative of $y$ with respect to $x$”. Sometimes, when you want to use a formula instead of a variable, you can put that in the place of $y$, as in
表示“$y$ 对 $x$ 的导数”。有时，当你想用一个公式而不是一个变量时，可以用公式代替 $y$，例如

$\frac{d(\cos x)}{dx}$

or, more conveniently (especially for complicated formulas),
或者，更方便地（尤其是对于复杂公式）

$\frac{d}{dx}(\cos x)$.

As we saw earlier, we can put the variable or function either within the fractional notation, or outside of it.
正如我们之前看到的，我们既可以将变量或函数放在分数符号内部，也可以放在外部。

So then if that is the derivative of $\cos x$, then what is its derivative? Naturally, it would be
那么如果这是 $\cos x$ 的导数，它的导数又是什么呢？自然是

$\frac{d}{dx}\left(\frac{d}{dx}(\cos x)\right)$.

Does that make sense? And when you write it this way, it is natural that one would abbreviate this by using the “squaring” notation on the $d$ in the numerator and the $dx$ in the denominator, as in
这说得通吗？当你这样写时，很自然地会在分子的“d”和分母的“dx”上使用“平方”符号来缩写，就像这样

$\frac{d^2}{d{x}^2}(\cos x)$.

Of course, you’re not really squaring, because it’s not multiplication; but it’s a convenient notation, especially when the 2 becomes 12 or an unspecified $n$. Similarly, the derivative of $\frac{dy}{dx}$ would be
当然，你并不是真的在平方，因为这不是乘法；但这是一种方便的符号，尤其是当数字2变成12或未指定的 $n$ 时。同样，$\frac{dy}{dx}$ 的导数是

$\frac{d}{dx}\left(\frac{dy}{dx}\right)$

which is why you get $\frac{d^{2}y}{d{x}^2}$.
这就是为什么会有 $\frac{d^{2}y}{d{x}^2}$ 这种写法。

He also comments on the order of operations issue:
他还对运算顺序问题发表了看法：

I should like to point out that we are NOT squaring the $x$ in the denominator, like $d/d(x^2)$, but are squaring the $dx$. It might have been better if we wrote $(dx{)}^2$ instead of $d{x}^2$, but that is not the notation in common usage by mathematicians, who instead treat the “$dx$” as a single piece.
我想指出的是，我们不是对分母中的 $x$ 进行平方，像 $d/d(x^2)$ 那样，而是对 $dx$ 进行平方。如果我们写成 $(dx{)}^2$ 而不是 $d{x}^2$ 可能会更好，但这不是数学家们常用的符号，他们将“$dx$”视为一个整体。

---

What Do $dx$ and $dy$ Mean?

$dx$ 和 $dy$ 是什么意思？

August 24, 2020 / By Dave Peterson

We’ve looked at the meaning of the derivative, and of its various notations, including $\frac{dy}{dx}$. This leads to the next question: What does $dx$ or $dy$ mean on its own? This was touched on last time, but there’s a lot more to say that I couldn’t fit there. We’ll look at more advanced approaches to differentials in themselves, then at two perspectives on what they mean in integrals.
我们已经探讨了导数的含义以及它的各种符号，包括 $\frac{dy}{dx}$。这就引出了下一个问题：$dx$ 或 $dy$ 单独出现时是什么意思？上次我们简单提到了这一点，但还有很多内容没来得及说。我们将先看看对微分本身更深入的理解，然后从两个角度探讨它们在积分中的含义。

Differentials as functions

作为函数的微分

We’ll start with the page two of us referred to in our answers last time, which comes from 1998:
我们从上次回答中提到的那页内容开始，它来自 1998 年：

Differentials
微分

I have to reach this conclusion:
我必须得出这个结论：

If you can get the differentials of a function, you can differentiate it, but if you can differentiate it, you can not necessarily get its differentials.
如果能得到一个函数的微分，就能对它求导，但如果能对它求导，不一定能得到它的微分。

Please help.
请帮忙。

As we’ve already seen, differentials can be discussed from several different perspectives. This question, lacking clear context, doesn’t indicate what kind of function is in view, or what approach to differentials is being taken. What does it mean here to “get a function’s differentials”? Doctor Jerry answered by suggesting one possible context, giving a definition that is quite different from what we’ve seen so far, where differentials were just infinitesimal numbers:
正如我们已经看到的，微分可以从多个不同角度来讨论。这个问题缺乏明确的背景，没有说明所涉及的函数类型，也没有说明采用的是哪种微分方法。在这里，“得到一个函数的微分”是什么意思呢？杰瑞博士通过提出一种可能的背景来回答，给出了一个与我们目前所看到的截然不同的定义——在之前的定义中，微分只是无穷小量：

Hi Maria,
你好，玛丽亚，

The standard definition of the differential of a real-valued function $f$ of a real variable is:
实变量的实值函数 $f$ 的微分的标准定义是：

At a given point $x$, the differential $d{f}_x$
在给定点 $x$ 处，$f$ 的微分 $d{f}_x$

($df$ sub $x$; usually the $x$ is omitted) of $f$
（$df$ 下标 $x$；通常省略 $x$）

is the linear function defined on $\mathbb{R}$ by:
是定义在 $\mathbb{R}$ 上的线性函数，定义为：

$d{f}_x(h)=f^{\prime }(x)\cdot h$

Everyday usage of the differential often suppresses the fact that the differential is a linear function. For example, if $y=f(x)=x^2$, then we write:
在日常使用中，微分常常掩盖了它是线性函数这一事实。例如，如果 $y=f(x)=x^2$，那么我们会写成：

$dy=df=2x\cdot dx$

where $dx$ is used instead of $h$. This is for good reason. The finite numbers $dy$ and $dx$ appearing in $dy=2x\cdot dx$ can be manipulated to obtain:
其中 $dx$ 用来代替 $h$。这是有充分理由的。在 $dy=2x\cdot dx$ 中出现的有限数 $dy$ 和 $dx$ 可以通过运算得到：

$\frac{dy}{dx}=2x$

I feel that I haven’t replied directly to your question. I think that this is because I don’t fully understand your question.
我觉得我没有直接回答你的问题。我想这是因为我没有完全理解你的问题。

Please write again if my answer has not helped.
如果我的回答没有帮助，请再次来信。

This definition takes the differential of a function to be itself a function, namely the function whose value is the vertical change $\Delta y$ along the tangent line for a given horizontal change ($h$ or $\Delta x$ or $dx$). In this way, we don’t have to think of $dy$ as a number-that-is-not-really-a-number (an infinitesimal), yet we get the action of multiplying the derivative by any number $dx$.
这个定义将函数的微分本身视为一个函数，即对于给定的水平变化（$h$ 或 $\Delta x$ 或 $dx$），其值是沿切线的垂直变化 $\Delta y$ 的函数。通过这种方式，我们不必将 $dy$ 视为一个并非真正数字的数（无穷小量），但我们可以实现将导数乘以任何数 $dx$ 的运算。

In his example, the differential of $f(x)=x^2$ at $x=3$ is $df(h)=d{f}_3(h)=f^{\prime }(3)\cdot h=6h$. From this perspective, the usual way of writing the differential as if it were a number is just a shortcut. Retaining the variable $x$, we could say, fully, $d{f}_x(dx)=2x\cdot dx$, or briefly, just $dy=2x\cdot dx$. For a very slightly different version of this definition, see here.
在他的例子中，$f(x)=x^2$ 在 $x=3$ 处的微分是 $df(h)=d{f}_3(h)=f^{\prime }(3)\cdot h=6h$。从这个角度来看，通常将微分写成仿佛是一个数的形式，只是一种简化写法。保留变量 $x$，我们可以完整地写成 $d{f}_x(dx)=2x\cdot dx$，或者简单地写成 $dy=2x\cdot dx$。关于这个定义的一个略有不同的版本，请参见这里。

Maria asked for more, giving a little more context but still not quite making it clear what level she is at:
玛丽亚请求进一步解释，提供了更多背景信息，但仍未完全说清楚她的理解程度：

Thanks for your answer. I know that the question is a little bit confusing, and at the beginning I thought it was a problem of the translation from English of the Math books. Your answer helped a little, so I am going to try to rephrase it.
感谢你的回答。我知道这个问题有点令人困惑，一开始我以为是数学书从英文翻译过来时出现的问题。你的回答有所帮助，所以我会试着重新表述一下。

What is the difference between finding the derivatives of a function ($\frac{dy}{dx}$), and finding its differentials ($dy,dx$)?
求一个函数的导数（$\frac{dy}{dx}$）和求它的微分（$dy,dx$）有什么区别？

In the books I’ve seen they define differentials supposing that $f(x)$ is differentiable.
在我看过的书中，它们在定义微分时都假设 $f(x)$ 是可导的。

My teacher gave a hint to reach this conclusion: if you can find the differentials of $f$, then $f$ is differentiable, but if $f$ is differentiable you can’t necessarily find its differentials.
我的老师给了一个得出这个结论的提示：如果能找到 $f$ 的微分，那么 $f$ 是可导的，但如果 $f$ 是可导的，不一定能找到它的微分。

That is why I can prove this, starting with a function that is differentiable.
这就是为什么我可以从一个可导函数开始来证明这一点。

It is still unclear what “the derivatives of a function” means; perhaps she doesn’t intend a plural.
“函数的导数”是什么意思仍然不清楚；也许她并不是指复数形式的“多个导数”。

Doctor Jerry started his answer by restating the previous definition:
杰瑞博士在回答时，首先重申了之前的定义：

Hi Maria,
你好，玛丽亚，

Suppose $f(x)=x^2$. To find the derivative of $f$ we use the definition of derivative: $f^{\prime }(x)$ is the limit as $h\to 0$ of the quotient
假设 $f(x)=x^2$。为了求 $f$ 的导数，我们使用导数的定义：$f^{\prime }(x)$ 是当 $h\to 0$ 时，商

$\frac{f(x+h)-f(x)}{h}$

的极限。

For this function, $f^{\prime }(x)=2x$.
对于这个函数，$f^{\prime }(x)=2x$。

Okay, this much is clear; there is no possible ambiguity.
好的，这一点很清楚，没有任何歧义。

The differential of $f$ at $x$ is defined to be the linear function $df$, which is defined on all of $\mathbb{R}$ by:
$f$ 在 $x$ 处的微分被定义为线性函数 $df$，它在整个 $\mathbb{R}$ 上的定义是：

$df(h)=f^{\prime }(x)\cdot h$

Often, the notation $df(h)$ is shortened to $df$ or, if $y=f(x)$, then we write $dy$ instead of $df$. Then the above definition is:
通常，$df(h)$ 这个符号会被简化为 $df$，或者如果 $y=f(x)$，我们会用 $dy$ 代替 $df$。那么上面的定义就是：

$dy=f^{\prime }(x)\cdot dx$ or
或

$\frac{dy}{dx}=f^{\prime }(x)$

Unless you are studying differential geometry, in which $dx$ is interpreted slightly differently, $dx$ is not the differential of a function. It is a variable, the same as $h$.
除非你正在学习微分几何（在微分几何中，$dx$ 的解释略有不同），否则 $dx$ 并不是某个函数的微分。它是一个变量，和 $h$ 一样。

I’m going to omit the rest of the answer, because I don’t think the question and its context were ever clarified, so it isn’t clear what answer is needed.
我将省略答案的其余部分，因为我认为这个问题及其背景始终没有得到澄清，所以不清楚需要什么样的答案。

If you want to dig deeper …

如果你想更深入地了解……

Doctor Jerry mentioned differential geometry in passing, as a place where differentials are defined more deeply. We have only occasionally gone into that territory; I want to just quote the conclusion to an unarchived answer to a question about differentials, by Doctor Fenton in 2009, in case you are interested:
杰瑞博士顺便提到了微分几何，在那里微分有更深入的定义。我们只是偶尔涉足那个领域；如果你感兴趣，我想引用芬顿博士在 2009 年对一个关于微分的问题的未存档回答的结论：

There is also a more sophisticated viewpoint in which what is integrated is not a function $f(x)$, but rather what is called a “differential form”. This viewpoint involves a lot of complicated mathematical structure and is more commonly seen in calculus of functions of several variables (see, for example, Differential_form)
还有一种更复杂的观点，认为被积分的不是函数 $f(x)$​，而是所谓的“微分形式”。这种观点涉及许多复杂的数学结构，在多变量函数微积分中更常见（例如，参 Differential_form)

but it can also be used in one-dimensional calculus as well (e.g. in David Bressoud’s book Second Year Calculus).
但它也可以用于一维微积分（例如，在大卫·布雷苏德的《第二年微积分》一书中）。

So, the easiest viewpoint is the purely formal one, in which you do useful but basically meaningless computations ($du=g^{\prime }(x)dx$ which does the bookkeeping), but there is also a more complicated viewpoint in which the computations are not meaningless, but they require you to learn more abstract mathematics. For example, the one-dimensional differential form $dx$ becomes a mapping from intervals on the real line to $\mathbb{R}$, and
所以，最简单的观点是纯形式的观点，在这种观点中，你进行有用但基本上无意义的计算（$du=g^{\prime }(x)dx$ 起到记录的作用），但还有一种更复杂的观点，在这种观点中，这些计算并非无意义，但它们要求你学习更多抽象的数学知识。例如，一维微分形式 $dx$ 成为从实线上的区间到 $\mathbb{R}$ 的映射，并且

$dx([a,b])=b-a$,

while the differential form $3x^{2}dx$ (to use one of Bressoud’s examples) is the mapping which takes the interval $[a,b]$ to
而微分形式 $3x^{2}dx$（用布雷苏德的一个例子）是将区间 $[a,b]$ 映射到

${\int }_a^{b}3x^{2}dx=\frac{b^3}{3}-\frac{a^3}{3}$.

This becomes the viewpoint used in modern differential geometry.
这成为现代微分几何中使用的观点。

Differentials in definite integral notation

定积分符号中的微分

Last week we talked about the use of differentials within symbols for the derivative. Let’s look at a couple questions about their use in integration. First, we have this, from 2002:
上周我们讨论了微分在导数符号中的使用。让我们来看几个关于它们在积分中使用的问题。首先是这个2002年的问题：

The Meaning of ‘$dx$’ in an Integral

积分中“$dx$”的含义

No matter how many times it’s explained to me, and even though I’ve taken several advanced math courses (diff eq, linear algebra, etc), nobody has ever given me a satisfactory explanation for the meaning of the notation in which an integral has $dx$ appended to the end if $x$ is the variable which we are integrating with respect to. In physics, for example, $dx$ seems to mean a very small amount of $x$, and then we use it in an integral to integrate whatever physical quantity is being discussed. I just don’t understand.
无论向我解释多少次，即使我已经修过几门高级数学课程（微分方程、线性代数等），也没有人能给我一个令人满意的解释，来说明当 $x$ 是我们要积分的变量时，积分符号末尾加上 $dx$ 这种符号的含义。例如，在物理学中，$dx$ 似乎表示 $x$ 的一个非常小的量，然后我们在积分中用它来对所讨论的物理量进行积分。我就是不明白。

Or, when a differential is defined, all of a sudden the $dx$ has a meaning, but then when an integral is being evaluated, the teacher says, “Oh, the $dx$ is just a formality.”
或者，当定义微分时，$dx$ 突然有了意义，但当计算积分时，老师会说：“哦，$dx$ 只是一种形式。”

So, sometimes it’s a formality, sometimes a vital concept, sometimes a physical quantity, sometimes a derivative: What is it?
所以，它有时是一种形式，有时是一个重要的概念，有时是一个物理量，有时是一个导数：它到底是什么？

When we write $\int f(x)dx$, we read it as “the integral [or antiderivative] of $f(x)$ with respect to $x$,” assigning no meaning to “$dx$” other than telling us what variable we care about. (In fact, sometimes the $dx$ can just be omitted entirely, when the variable is clear!) This is not very different from its use in a derivative, where it also means “with respect to $x$“. What does it mean here?
当我们写 $\int f(x)dx$ 时，我们将其读作“$f(x)$ 关于 $x$ 的积分（或原函数）”，除了告诉我们所关注的变量外，“$dx$”没有其他含义。（事实上，有时当变量明确时，$dx$ 完全可以省略！）这与它在导数中的使用没有太大区别，在导数中它也表示“关于 $x$”。在这里它是什么意思呢？

Doctor Jeremiah took the question, focusing on the idea of a definite integral:
耶利米博士回答了这个问题，重点讲解了定积分的概念：

Hi Nosson,
你好，诺森，

Think about it this way:
可以这样想：

An integral gives you the area between the horizontal axis and the curve. Most of the time this is the $x$ axis.
积分给你的是水平轴和曲线之间的面积。大多数时候，水平轴就是 $x$ 轴。

                       y

                       |                    |
                     --|--              ----|---- f(x)
                   /   |   \          /     |
                  /    |     --------       |
        |        /     |                    |
   -----|-------       |                    |
        |              |                    |
        |              |                    |
--------|--------------+--------------------|----- x
        a                                   b

And the area enclosed is:
所围成的面积是：

$Area={\int }_a^{b}f(x)dx$

This is a definition of the definite integral, in a broad sense; what follows defines how it can be calculated in principle (and therefore, how it is formally defined):
从广义上讲，这是定积分的一个定义；接下来定义了原则上如何计算它（因此，它的正式定义是怎样的）：

But say you didn’t want to use an integral to measure the area between the $x$ axis and the curve. Instead you just calculate the average value of the graph between $a$ and $b$ and draw a straight flat line $y=avg(x)$ (the average value of $x$ in that range).
但假设你不想用积分来测量 $x$ 轴和曲线之间的面积。相反，你只需计算图像在 $a$ 到 $b$ 之间的平均值，并画一条水平直线 $y=avg(x)$（该范围内 $x$ 的平均值）。

Now you have a graph like this:
现在你有了这样一个图像：

                       y

                       |                    |
                     - | -              - - | - - f(x)
        |          /   |   \          /     |
   -----|-----------------------------------|---- avg(x)
        |        /     |                    |
   - - -|- - - -       |                    |
        |              |                    |
        |              |                    |
--------|--------------+--------------------|----- x
        a                                   b

And the area enclosed is a rectangle:
所围成的面积是一个矩形：

Area = $avg(x)\cdot w$
where $w$ is the width of the section
其中 $w$ 是该部分的宽度

The height is $avg(x)$ and the width is $w=b-a$ or in English, “the width of a slice of the $x$ axis going from $a$ to $b$.”
高度是 $avg(x)$，宽度是 $w=b-a$，或者用通俗的话说，“从 $a$ 到 $b$ 的 $x$ 轴切片的宽度”。

His width $w$ would often be called $\Delta x$; we’ll see that later.
他所说的宽度 $w$ 通常会被称为 $\Delta x$；我们稍后会看到。

But say you need a more accurate area. You could break the graph up into smaller sections and make rectangles out of them. Say you make 4 equal sections:
但假设你需要更精确的面积。你可以把图像分成更小的部分，并用它们做出矩形。假设你分成4个相等的部分：

                       y

                       |                    |
                  |----|---|        |-------|---- f(x)
                  |    |   |        |       |
                  |    |   |--------|       |
        |         |    |   |        |       |
   -----|---------|    |   |        |       |
        |         |    |   |        |       |
        |         |    |   |        |       |
--------|---------|----+---|--------|-------|----- x
        a                                   b

And the area is:
面积是：

Area = section 1 + section 2 + section 3 + section 4
   = $avg(x,1)\cdot w+avg(x,2)\cdot w+avg(x,3)\cdot w+avg(x,4)\cdot w$

where $w$ is the width of each section. The sections are all the same size, so in this case $w=(b-a)/4$ or in English, “the width of a thin slice of the $x$ axis going from $a$ to $b$.”
其中 $w$ 是每个部分的宽度。这些部分大小相同，所以在这种情况下，$w=(b-a)/4$，或者用通俗的话说，“从 $a$ 到 $b$ 的 $x$ 轴薄片的宽度”。

His width $w$ would often be called $\Delta x$; we’ll see that later.
他所说的宽度 $w$ 通常会被称为 $\Delta x$；我们稍后会看到。

But say you need a more accurate area. You could break the graph up into smaller sections and make rectangles out of them. Say you make 4 equal sections:
但假设你需要更精确的面积。你可以把图像分成更小的部分，并用它们做出矩形。假设你分成4个相等的部分：

And the area is:
面积是：

${\sum }_{n=1}^{4}avg(x,n)\cdot w$

But it’s still not accurate enough. Let’s use an infinite number of sections. Now our area becomes a summation of an infinite number of sections. Since it’s an infinite sum, we will use the integral sign instead of the summation sign:
但这仍然不够精确。让我们用无穷多个部分。现在我们的面积变成了无穷多个部分的总和。由于这是一个无穷和，我们将使用积分符号而不是求和符号：

$Area=\int avg(x)\cdot w$

where $avg(x)$ for an infinitely thin section will be equal to $f(x)$ in that section, and $w$ will be “the width of an infinitely thin section of the $x$ axis.”
其中，对于无限薄的部分，$avg(x)$ 将等于该部分中的 $f(x)$，而 $w$ 将是“$x$ 轴上无限薄部分的宽度”。

So instead of $avg(x)$ we can write $f(x)$, because they are the same if the average is taken over an infinitely small width.
所以我们可以用 $f(x)$ 代替 $avg(x)$，因为如果在无限小的宽度上取平均值，它们是相同的。

Again, a lot of details are being omitted to keep things intuitive.
同样，为了保持直观性，省略了很多细节。

And we can rename the $w$ variable to anything we want. The width of a section is the difference between the right side and the left side. The difference between two points is often called the delta of those values. So the difference of two $x$ values (like $a$ and $b$) would be called delta-$x$. But that is too long to use in an equation, so when we have an infinitely small delta, it is shortened to $dx$.
我们可以把 $w$ 变量重命名为任何我们想要的名称。一个部分的宽度是右侧和左侧之间的差值。两个点之间的差值通常被称为这些值的增量。所以两个 $x$ 值（如 $a$ 和 $b$）之间的差值会被称为 delta-$x$（$\Delta x$）。但在方程中使用这个名称太长了，所以当我们有一个无限小的增量时，它被简写为 $dx$。

If we replace $avg(x)$ and $w$ with these equivalent things:
如果我们用这些等价的东西代替 $avg(x)$ 和 $w$：

$Area=\int f(x)dx$

So, as in the infinitesimal approach to the derivative, $dx$ is thought of (informally) as a very small change in $x$.
所以，就像导数的无穷小方法中那样，$dx$（非正式地）被认为是 $x$ 的一个非常小的变化。

So what the equation says is:
所以这个方程的意思是：

Area equals the sum of an infinite number of rectangles that are $f(x)$ high and $dx$ wide (where $dx$ is an infinitely small distance).
面积等于无穷多个矩形的总和，这些矩形的高为 $f(x)$，宽为 $dx$（其中 $dx$ 是一个无限小的距离）。

So you need the $dx$ because otherwise you aren’t summing up rectangles and your answer wouldn’t be total area.
所以你需要 $dx$，因为否则你就不是在求和矩形的面积，你的答案也就不会是总面积。

$dx$ literally means “an infinitely small width of $x$”.
$dx$ 字面意思是“$x$ 的一个无限小的宽度”。

This, of course, applies specifically to the definite integral. From this perspective, we can think of the indefinite integral as inheriting the same notation via the Fundamental Theorem of Calculus, which ties the two together.
当然，这特别适用于定积分。从这个角度来看，我们可以认为不定积分通过将两者联系在一起的微积分基本定理，继承了相同的符号。

The differential doesn’t have to be at the end!

微分不一定非要在末尾！

One consequence of teaching students that the differential in an integral means only “… with respect to $x$” can be seen in the following question, from 2003, about a relatively unusual variation in the notation:
教学生积分中的微分只表示“……关于 $x$”会导致一种结果，从 2003 年的这个问题中可以看出，这个问题涉及一种相对不常见的符号变化：

Integral Notation - Missing Integrands
积分符号——缺失的被积函数

I have seen some integral notation used that I am not familiar with. It looks like this:
我见过一些我不熟悉的积分符号。它看起来像这样：

$\int dxf(x)+...$

There does not seem to be an integrand (i.e. a function being integrated). I’m not sure if $f(x)$ is to be integrated. I have two theories, but I can’t see the point in writing the expression as it is if either of my theories is correct.
似乎没有被积函数（即正在被积分的函数）。我不确定 $f(x)$ 是否要被积分。我有两种推测，但如果我的任何一种推测是正确的，我都不明白为什么要这样写这个表达式。

My theories about what this might mean:
我对它可能的含义的推测：

1. The above notation is the same as writing:
   上面的符号与下面的写法相同：

   $\int 1\cdot dx\cdot f(x)+...$ (note the explicit 1 here)
   $\int 1\cdot dx\cdot f(x)+...$（注意这里明确的1）

   =

   $(x+C)\cdot f(x)+...$ (where $C$ is a constant of integration)
   $(x+C)\cdot f(x)+...$（其中 $C$ 是积分常数）

2. The rest of the expression is to be integrated with respect to $x$.
   表达式的其余部分要关于 $x$ 积分。

If (1) is correct, then what was the point of writing the integral - why wasn’t $(x+C)$ just written instead? If (2) is correct, then how does one know when to “stop integrating” (i.e. if there is some term to be added on to the expression that is not to be integrated, how is it distinguished?).
如果（1）是正确的，那么写积分的意义是什么——为什么不直接写 $(x+C)$ 呢？如果（2）是正确的，那么如何知道什么时候“停止积分”（即，如果表达式中有一些项不需要被积分，如何区分它们？）。

I have seen this recently in multi-variate calculus, i.e. when $x$ is in ${\mathbb{R}}^n$ rather than $\mathbb{R}$: does this situation justify the use of the integral notation somehow?
我最近在多元微积分中见过这种情况，即当 $x$ 在 ${\mathbb{R}}^n$ 中而不是在 $\mathbb{R}$ 中时：这种情况在某种程度上证明了这种积分符号的使用是合理的吗？

Chris’s first guess is that the $dx$ closes off the integral, so that what follows is to be multiplied; the second (which is correct) is that it doesn’t matter where the $dx$ is placed.
克里斯的第一个猜测是，$dx$ 标志着积分的结束，因此后面的内容要被相乘；第二个猜测（正确的）是，$dx$ 放在哪里并不重要。

He is right that this notation is particularly common in calculus with more than one variable. One might write, for example,
他说得对，这种符号在多变量微积分中特别常见。例如，有人可能会写

${\int }_0^{b}dy{\int }_0^{a}dxf(x,y)$

or
或者

${\int }_0^{b}dy{\int }_0^{a}f(x,y)dx$

rather than
而不是

${\int }_0^b{\int }_0^{a}f(x,y)dxdy$

to indicate that we are to integrate first with respect to $x$, and then integrate the result with respect to $y$. One benefit is that it makes it easier to see which limits go with which variable.
以表明我们要先对 $x$ 积分，然后对结果对 $y$ 积分。这样做的一个好处是，更容易看出哪个极限对应哪个变量。

I answered:
我回答道：

Hi, Chris.
你好，克里斯，

It is common to learn about integration in such a way that the “dx” seems to be a marker for the end of the integral, as if the “long S” were a left parenthesis and the “dx” were the right parenthesis. But it doesn’t work that way. In fact, what you are integrating is the product of a function and $dx$; and multiplication is commutative! So these mean the same thing:
人们学习积分时，通常会觉得“dx”似乎是积分结束的标志，就好像那个“长S”是左括号，“dx”是右括号。但事实并非如此。实际上，你要积分的是一个函数和 $dx$ 的乘积；而乘法是可交换的！所以这些表示同样的意思：

$\int f(x)dx$ and $\int dxf(x)$

If you then add something, you must use parentheses if it is to be part of the integral:
如果你接着添加一些东西，如果这些东西是积分的一部分，就必须使用括号：

$\int dxf(x)+g(x)=\left[\int f(x)dx\right]+g(x)$

is the sum of an integral and a function, while
是一个积分和一个函数的和，而

$\int dx(f(x)+g(x))=\int (f(x)+g(x))dx$

is the integral of the sum of two functions.
是两个函数之和的积分。

That is, presumably the integral has higher precedence than addition, so you “stop integrating” at the first plus sign. But even then, I’m not positive that this rule I just made up is always followed; let me know if you think it doesn’t fit the practice in your text, and show me an example.
也就是说，大概积分的优先级高于加法，所以你在第一个加号处“停止积分”。但即便如此，我也不能肯定我刚刚制定的这个规则总是被遵守；如果你认为它不符合你课本中的做法，请告诉我，并给我举个例子。

Seeing the differential as part of a product is necessary in order to understand the notation. This can be done whether you think of $dx$ as a mere notation, so that the “product” is as illusory as the “quotient” in a derivative, or you think explicitly about the Riemann sum.
为了理解这个符号，有必要将微分视为乘积的一部分。无论你将 $dx$ 视为一种纯粹的符号（因此“乘积”就像导数中的“商”一样是虚幻的），还是明确地考虑黎曼和，都可以这样理解。

I don’t see my ideas about parentheses followed universally; it is not uncommon to see $\int x^2-2x+3dx$ rather than $\int (x^2-2x+3)dx$. This is probably due to the common use of the differential to terminate the integrand, and the fact that it would be meaningless to take the $dx$ as associated only with the last term, despite the usual order of operations. This laxity may carry over into integrals where $dx$ is written first, though the ambiguity is much greater there. Too often, as in some other aspects of order of operations, you ultimately just have to recognize what interpretation makes sense in context.
我发现我关于括号的想法并没有被普遍遵循；常见的是 $\int x^2-2x+3dx$ 而不是 $\int (x^2-2x+3)dx$。这可能是因为通常用微分来标记被积函数的结束，而且尽管有通常的运算顺序，但将 $dx$ 仅与最后一项关联是没有意义的。这种不严谨可能会延续到 $dx$ 写在前面的积分中，尽管那里的歧义要大得多。很多时候，就像在运算顺序的其他一些方面一样，你最终只需要识别哪种解释在上下文中是合理的。

In writing this, it has occurred to me that my reference to commutativity is not quite valid, specifically when it comes to definite integrals. The following are not the same:
在写这篇文章时，我突然想到，我提到的交换性并不完全正确，特别是对于定积分。以下内容 不 相同：

${\int }_0^b{\int }_0^{a}f(x,y)dxdy\ne {\int }_0^b{\int }_0^{a}f(x,y)dydx$

That’s because the order of the differentials determines the meaning of the limits of integration. Everything about calculus notation is a little slippery.
那是因为微分的顺序决定了积分限的含义。关于微积分符号的一切都有点难以捉摸。

Chris replied,
克里斯回复道，

Doctor Peterson,
彼得森博士，

Thank you for your quick and helpful reply.
感谢您快速而有帮助的回复。

I was indeed taught that integration begins with the “long S” and ends with the (for example) $dx$.
我确实被教导说，积分从“长S”开始，以（例如）$dx$ 结束。

I have, however, seen the following notation:
然而，我见过以下符号：

$\int \frac{dx}{f(x)+g(x)}$

and assumed it was a convenient notation rather than being a justifiable mathematical expression.
并认为这是一种方便的符号，而不是一个合理的数学表达式。

Perhaps I need to go and look at calculus from first principles again to see why this is the case.
也许我需要重新从基本原理出发学习微积分，看看为什么会这样。

That is both convenient notation and justifiable! Again, we are thinking of the $dx$ as being multiplied by a fraction, and therefore equivalent to part of the numerator.
这种写法既方便又合理！同样，我们可以把 $dx$ 看作是与一个分数相乘，因此它相当于分子的一部分。

A particularly good example of the usefulness of the differential in an indefinite integral arises in the substitution method, where we can replace the $dx$ with an expression that we actually multiply.
微分在不定积分中的实用性有一个特别好的例子，就是在换元法中，我们可以用一个实际相乘的表达式来替换 $dx$。

---

via：

• What is a Derivative? – The Math Doctors
  https://www.themathdoctors.org/what-is-a-derivative/
• What Derivative Notations Mean – The Math Doctors
  https://www.themathdoctors.org/what-derivative-notations-mean/
• What Do dx and dy Mean? – The Math Doctors
  https://www.themathdoctors.org/what-do-dx-and-dy-mean/