注:本文为 “滤波器 | 数学 / 电路 / 场” 相关文章《上中下》合辑。
图片清晰度受限于原文原状。
滤波器往事 —— 数学、电路和场
原创 但以理 瑞宏之声 2025 年 01 月 23 日 13:02 浙江
滤波器概念的提出
首先从这个射频工程师熟悉的方程开始,这个被评为人类最美十大方程之首的方程到底出自谁手,中间的大胡子还是右边的型男?

图一、a) 麦克斯韦方程,b) 麦克斯韦,c)亥维赛德
也许绝大多数同学都会说,肯定是中间的麦克斯韦啊,这还用问么,这位可比肩牛顿和爱因斯坦的物理学家在前人基础上提出了著名的麦克斯韦方程,尤其是位移电流的提出,引出了电磁波动方程,将电学、磁学、光学联系在了一起,为今天的信息时代打下了理论基础。诚然,麦克斯韦的伟大无需多言,但今天我们内容的主角却是右边这位 ——Oliver Heaviside(奥利弗・亥维赛德,1850~1925)英国数学家和物理学家,他未上大学,自学了电磁学并自创了矢量微积分学,基于对这两者的精通他将麦克斯韦原始的二十多个方程简化为了上述四个方程,对称、简洁、深刻 使其被誉为上帝写下的诗歌,也使得今天的我们能轻易写出这组方程(否则大厂射频工程师面试的时候估计 90% 以上的同学都写不出麦克斯韦方程组了)。亥维赛德生活的年代正是有线电话刚好兴起的时代,他后来成为了一名电报员,期间他提出了著名的电报员方程,给了电压和电流信号在电缆上随空间 / 时间变化的传播方程,进而提出了损耗常数、相位常数、趋肤效应、特性阻抗、反射、负载等一系列概念,他是传输线理论的奠基人。在当电报员工作期间他意识到在电缆上周期性引入线圈可以抑制某些通话噪声并于 1887 年发表了文章,这其实就是最早的低通滤波器,亥维赛德没有意识到这一发现将对大西洋对岸的美国电话电报公司(AT&T)带来深远的影响,更在后来兴起的无线通信中发挥了无可替代的作用。
先简单介绍一下啥是滤波器,我们知道无论是有线通信还是无线通信都是基于电磁波,如图二本质都是对无线电波段的利用。
无线电波的频率(波段)划分与应用 img
| 频率范围 | 波长范围 | 符号 | 频段 | 波段 | 用途 |
|---|---|---|---|---|---|
| 3 H z ∼ 30 K H z 3Hz \sim 30KHz 3Hz∼30KHz | 1 0 8 m ∼ 1 0 1 m 10^{8}m \sim 10^{1}m 108m∼101m | VLF | 甚低频 | 长波 | 音频、电话、数据终端、长距离导航时标 |
| 30 ∼ 300 K H Z 30 \sim 300KHZ 30∼300KHZ | 1 0 4 m ∼ 1 0 3 m 10^{4}m \sim 10^{3}m 104m∼103m | LF | 低频 | 长波 | 导航、信标、电力线通信 |
| 300 K H z ∼ 3 M H z 300KHz \sim 3MHz 300KHz∼3MHz | 1 0 3 m ∼ 1 0 2 m 10^{3}m \sim 10^{2}m 103m∼102m | MF | 中频 | 中波 | 调幅广播,移动陆地通信、业余无线电 |
| 3 ∼ 30 M H z 3 \sim 30MHz 3∼30MHz | 1 0 2 m ∼ 1 0 1 m 10^{2}m \sim 10^{1}m 102m∼101m | HF | 高频 | 短波 | 移动无线电话、短波广播、定点军用通信 |
| 30 ∼ 300 M H z 30 \sim 300MHz 30∼300MHz | 1 0 1 m ∼ 1 0 0 m 10^{1}m \sim 10^{0}m 101m∼100m | VHF | 甚高频 | 米波 | 电视、调频广播、空中管制车辆通信、航 |
| 300 M H z ∼ 3 G H z 300MHz \sim 3GHz 300MHz∼3GHz | 1 0 2 c m ∼ 1 0 1 c m 10^{2}cm \sim 10^{1}cm 102cm∼101cm | UHF | 特高频 | 分米波 | 电视、空间遥测、雷达导航、点对点通信、移动通信 |
| 3 ∼ 30 G H z 3 \sim 30GHz 3∼30GHz | 1 0 1 c m ∼ 1 0 0 c m 10^{1}cm \sim 10^{0}cm 101cm∼100cm | SHF | 超高频 | 厘米波 | 微波接力、卫星和空间通信、雷达 |
| 30 ∼ 300 G H z 30 \sim 300GHz 30∼300GHz | 1 0 1 m m ∼ 1 0 0 m m 10^{1}mm \sim 10^{0}mm 101mm∼100mm | EHF | 极高频 | 毫米波 | 雷达、微波接力、射电天文学 |
图二、无线电波波段划分与应用
图三是我国无线电频谱的划分图,可以看到这零零碎碎的划分,本质就是为了更好的利用无线频谱这一不可再生资源,如何利用呢,就是使用本文主角 —— 滤波器。滤波器顾名思义就是滤除掉不需要的电磁波的器件,不难想象一个理想的滤波器的样子应该如图四蓝色曲线所示(又叫 “砖块” 滤波器),在需要的频谱内(即通带)信号可以畅通的通过,在不需要频谱外(即阻带)信号完全抑制掉,本文试着讲讲这一百多年来人们是如何在追求这一目标上不断前行的,即黄色曲线的演进(图四)。
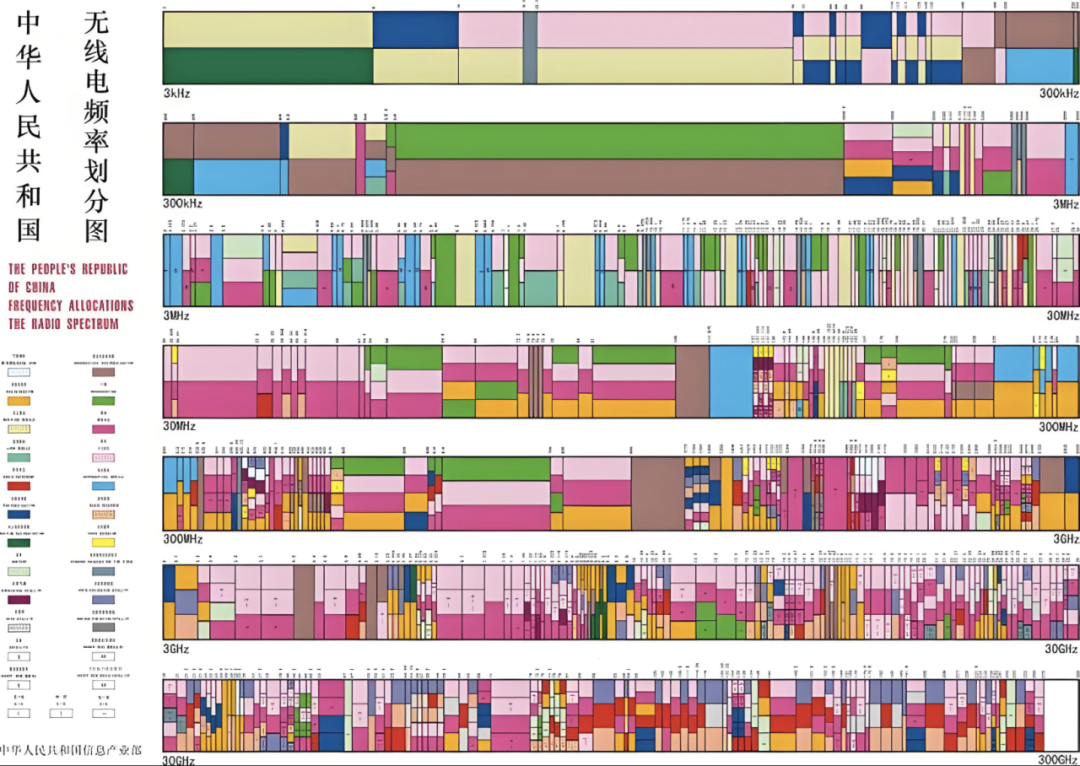
图三、中国无线电频谱划分
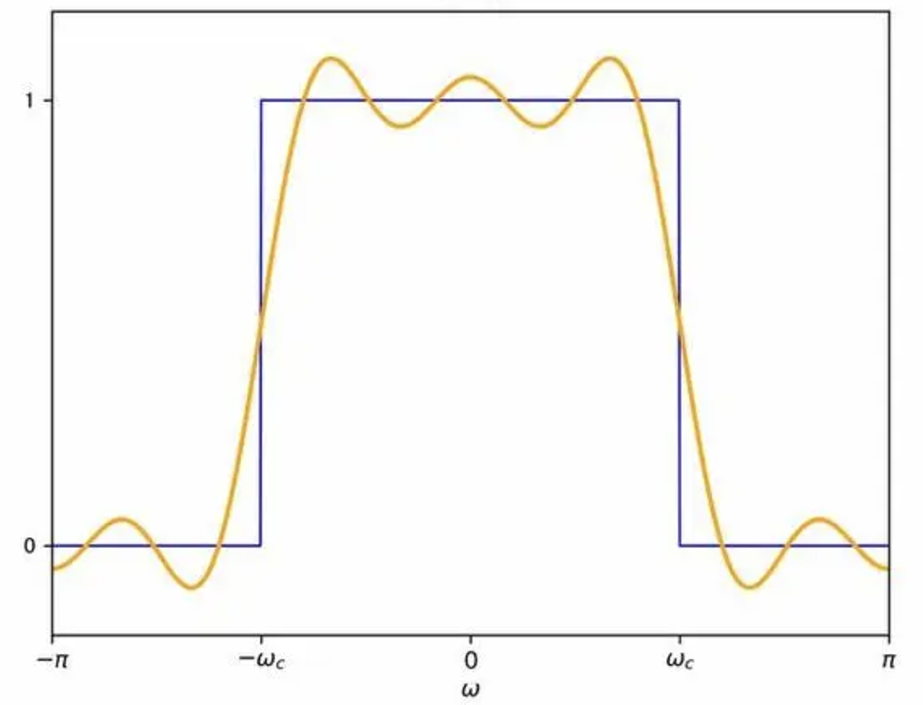
图四、理想滤波器曲线(蓝)VS 实际滤波器曲线(黄)
第一款滤波器诞生
继续回到 100 多年以前,时间来到 20 世纪的第一个 10 年,接下来重点介绍的是 AT&T 公司这个电信巨头及其下属的贝尔实验室,他们将引领接下来几十年滤波器领域的创新,第一位出场的重量级人物是 G.A.Campbell (1870 ~1954) 。

图五、a)Campbell,b)Pupin
Campbell 1891 年本科毕业于麻省理工,1893 年硕士毕业于哈佛,然后去欧洲先后师从两位数学大神克莱因和庞加莱学习数学,跟随物理大神玻尔兹曼学习电学, 1897 年 Campbell 回到美国加入 AT&T,他一边工作一边攻读博士,并于 1901 年从哈佛获得博士学位,Campbell 是最早意识到亥维赛德工作价值的人之一,其博士研究方向即为传输线加载线圈的研究,扎实的数学功底以及工作上的需要使得他成为第一个精准设计滤波器的人,他的第一项研究成果就是在电缆上精确计算间隔和插入电感量使得电缆可以在某个频率响应截止从而抑制掉某些干扰提升了信号质量增加了传输距离,1900 年 5 月波士顿郊外的一条线缆第一次增加了加载线圈用于提升通话质量这可能是世界上第一款滤波器应用。这个技术发明很快出现了争议,哥伦比亚大学的 M.Pupin 教授(1858~1935)声称 1900 年就获得了电缆加载线圈的专利(图六)。
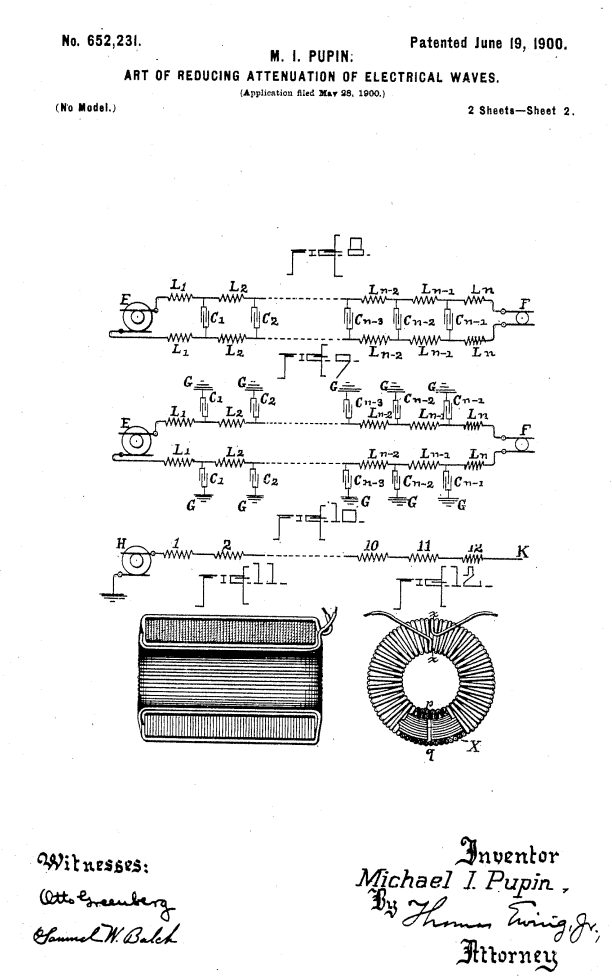
图六、Pupin 1900 年申请的加载线圈专利
Campbell 反驳到他更早就在 AT&T 内部进行过该 idea 的演示,只是 AT&T 内部管理问题导致了专利申请滞后,双方进行了非常复杂的法律争辩,最终 AT&T 考虑到继续争辩下去所有专利都有可能被亥维赛德于 1887 年发表的论文给无效掉,因此他们搁置了争议购买了 Pupin 的专利,在 17 年时间内共付给 Pupin 45 万美金的专利费(想想在 1910 年代那是多大一笔钱),AT&T 的决策是英明的,基于线圈加载的滤波器理念他们后续又开发了合路器,实现了一根线缆承载多路通话的功能,大大降低了电缆的铺设开销(尤其是后来的跨海电缆),据统计 AT&T 因为新兴的滤波器技术截止 1925 年就一共节约了 2 亿美金电缆开销,也许 AT&T 觉得过于对该技术的鼻祖亥维赛德有所亏欠,提出要给予他一定补偿,但亥维赛德拒绝了,他只要求大家承认是他第一个提出该理论的人。再说说 Pupin 他的一生也颇具传奇色彩,他出生于塞尔维亚,早年颠沛流离,移民到美国后一边做体力劳动营生一边学习,五年后考上哥伦比亚大学,1883 年大学毕业后他跑去英国剑桥大学找麦克斯韦学习电磁学,但去了后发现麦克斯韦已经去世,整个剑桥居然没有人可以教授这门课,于是他又到德国师从亥姆霍兹学习电磁学,回到哥伦比亚大学后他一直教授这门课,为电磁学理论早期传播做出了巨大贡献,他是 NASA 主要创始人之一,还参与了美国数学学会,美国物理学会的创建,担任过美国电气工程师协会、美国无线电研究所和美国科学促进会的主席或者副主席,连他的自传《从移民到发明家》都获得了普利策奖。
Campbell 的工作仍在继续,在 1910~1920 年之间,他将滤波器电路的发展推向了第一个高峰,他提出了滤波器里面最经典的梯形(ladder)拓扑结构(图七 a),该电路拓扑是当今 SAW、BAW、LTCC、LC 等滤波器用得最多的结构,Campbell 基于该拓扑完成了低通滤波器的精确设计,仅通过增加 “梯子” 的长度就可以获得更好的滤波效果,接下来基于频率变换可以设计出任意截止频率的低通滤波器;完成低通滤波器研究后通过互补性变换(电容和电感互换转换)Campbell 将低通滤波器可变换为高通、带通、带阻等不同形式,并给出了其对应的电路结构(图七 b),该工作发表于《Physical Theory of the Electric Wave-Filter》,可以说该论文是滤波器电路理论第一篇集大成者,里面的滤波器各种拓扑结构以及低通到高通、带通、带阻的变换依然是微波专业本科及研究生必学知识。除 ladder 结构外,Campbell 还提出了晶格型(lattice)滤波器拓扑结构(图七 c),该类结构后来在电磁场滤波器中应用较少但在声波类 SAW、BAW 滤波器上应用较多。
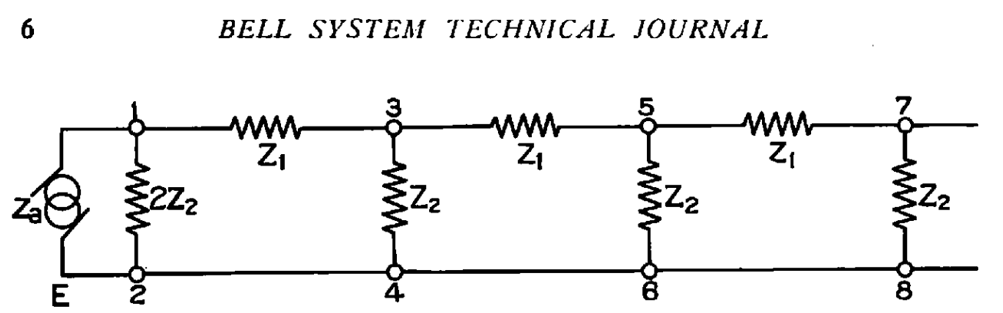
a) 梯形滤波器电路拓扑
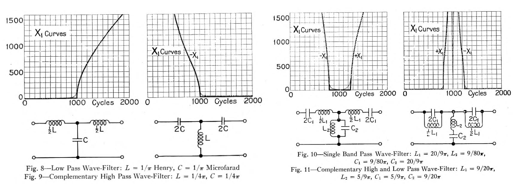
b) 低通、高通、带通、带阻对应的 ladder 电路拓扑结构
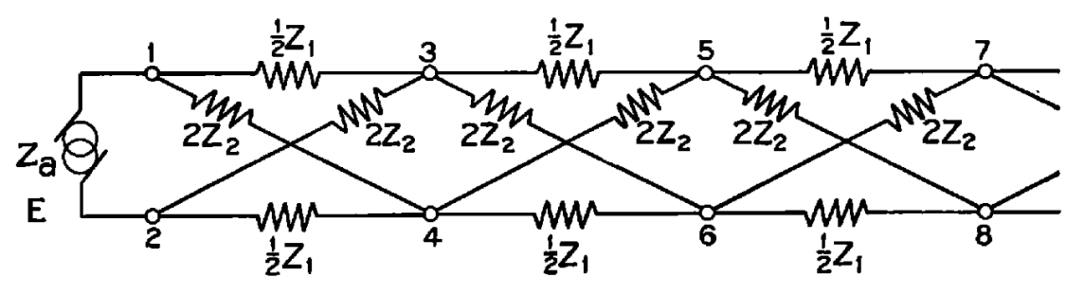
c) 晶格型滤波器电路拓扑
图七、Campbell 论文里面的各种滤波电路
Campbell 的理论已经非常完善,但细心的射频工程师就会发现,他的滤波器都是标准切比雪夫 / 巴特沃斯结构,其频率远端滤波能力很好,但滤波器最最看重的频率近端滤波能力还不行,解决该问题的人是 Campbell 在贝尔实验室的同事 O.J. Zobel(1887~1970),Zobel 博士毕业于威斯康星大学,早年曾进行热力学方面的研究工作, 1916 年加入 AT&T 进行传输线研究工作,此时 Campbell 已经完成滤波器的电路设计大多数工作,Zobel 在其基础上提出了新的拓扑结构(图八)。
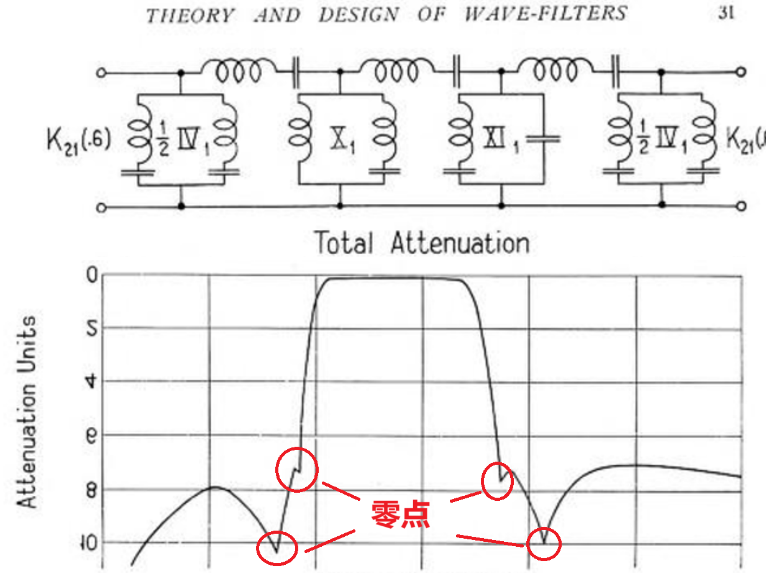
图八、Zobel 增加近端零点后的滤波器电路拓扑
注意该结构的 4 个并联支路在标准谐振回路基础上引入了额外的电容或者电感,这样一来滤波曲线上会出现近端零点,从而大大改善频率近端的滤波能力,但该结构也有缺点就是频率远端滤波能力不强,为了解决该问题,Zobel 将他的拓扑结构和 Campbell 的结合起来,得到了近端和远端都有不错滤波器能力的电路拓扑,且他还解决了两者级联带来的匹配问题,至此,滤波器电路拓扑基本完成,后续的所有滤波电路拓扑理论上都是在这两者工作上的变种(在数学上等价,可以相互推导),因为其强大的滤波器设计能力,AT&T 将频分复用技术(FDM)发挥到了极致(早期国际电信联盟制定的语音通信带宽为 300Hz~3400Hz,信道间隔为 4000Hz,也就是极限情况下过渡带只有 600Hz,需要非常陡峭的滤波能力)使得一根电缆上可以实现多路电话信号传输,大大降低铺设成本,可以说滤波器理论的发明为早期电话的普及做出了巨大贡献。除了滤波器工作以外,Zobel 在阻抗匹配研究上也有巨大贡献,因为一个好的阻抗匹配网络本质就是一个滤波器,Zobel 提出的恒阻匹配网络(也叫 Zobel 网络)如今在滤波器设计上已经逐渐被其他设计方法所取代,但依然还用在音响设计上。Zobel 还有一个巨大贡献就是,他是最早意识到通信当中的噪声是无法消除的工程师之一,最早提出 “白噪声” 这一概念,这一工作也为后来香农的信息论提供了参考。
滤波器和数学函数的正式结合
滤波器的定义很多,可能大多数人最先接触到的滤波器名字就是切比雪夫滤波器、巴特沃斯滤波器、椭圆函数滤波器,很显然这些都和数学函数相关,前面的内容滤波器主要是和电路相关比如低通、高通、带通、带阻,是什么原因让滤波器和数学函数联系在了一起?接下来要介绍第一位大咖是 R.M. Foster(1896~1998),Foster 1917 年毕业于哈佛大学数学系,然后加入贝尔实验室,没错这一节内容依然是贝尔实验室主导,Foster 和 Campbell、Zobel 成为了同事,那个时候滤波器已经形成了一套精准的设计流程,但对工程师经验要求非常高,首先要根据滤波器通带和阻带信息得到初步的电路拓扑结构和初值,然后根据其响应和规格进行对比,通常要进行很多轮迭代和阻抗匹配调整才能得到较为满意的滤波曲线,这一过程类似于现在的优化算法,只不过不是基于计算机而是基于工程师的经验和数学能力。Foster 在其 1924 年发表的论文《A reactance theorem》中提出了全新的方式,首先根据电路拓扑写出其随频率变化的函数表达式,然后工程师根据需要指定通带和阻带频率位置(主要是指定频率响应的极点和零点),将其带入函数表达式中可以一步步求出该滤波电路拓扑下各个电感和电容元件的值,即完成了滤波器设计,Foster 的工作开启了滤波器网络综合的大门,没错,你熟知的 “网络” 这个词最先来源于滤波器设计,后来因特网兴起后让位于了后者这个更宏大的产业。鉴于网络综合这一概念太过重要,后续会反复提起,先解释一下滤波器设计两条路径 —— 优化和网络综合。
我们以图九千手观音这个舞蹈为例来说明两种思路的差异,设计目的:一条漂亮的滤波曲线,对应这里就是最终呈现的这个惊艳舞姿,每一个演员对应一个电路元件,编排导演就对应设计师。优化法导演大概会是这样的一个过程, “大家先站成一排,第一排姑娘的把手放在胸前,第二排的姑娘把手微微张开,第三排的姑娘把手张开得比第二排得多一点,第四排的姑娘把手张开更多一点…… 哎,第二排姑娘咋回事呢,手打开太多了,收一点,第三排姑娘咋回事不是让你收,你还要打开多一点…… 目前很好,大家保持住,听我节拍,1 至 5 排缩手,6 至 10 排手打直,怎么回事,8 排做反了,重新来一编…… 一个月后,经过大家反复的辛苦排练我们越来越流畅了,终于可以上台表演了”;如果是网络综合导演的思路应该会是这样一个过程,“我先给大家编个号,小美 1 号站第一排,静静 2 号站第二排,大漂亮 3 号站第三排……,下面我分解每一个人的动作,1 号首先将双手放到胸前,膝盖弯曲 20 度,2 号双手打开呈 30 度角,3 号双手打开 40 度角…… 当我喊节拍 1 的时候 1~5 号把手缩回来,6~10 号把手伸直,当我喊节拍 2 的时候 1~5 号伸手,6~10 号把手缩回来…… OK,动作要领分解到这里,各位领取角度计然后回家对着镜子按要领进行练习,明天我们第一次合练…… 一周后,我们已经非常流畅了,可以上台表演了”。

图九、千手观音舞蹈图(图片来源于网络)
两者的本质区别就是综合预先要对最终结果有一个清晰定量的认识并且要能将该结果分解成每个个体的指标,在滤波器设计中这需要非常深厚的数学功底。可以说综合相比优化优势巨大,唯一问题就是数学推导非常复杂,但这一问题在计算机引入后,通过编程实现后代价几乎为 0,因此网络综合法在滤波器设计中越来越受欢迎(当然这是后话)。
Foster 的工作很快启发了另外一个滤波器界里程碑式的人物 ——Wilhelm Cauer (威廉▪考尔 1900~1945)德国人,毕业于柏林工业大学,早年研究广义相对论,后来他加入了 AT&T 在德国的分公司开始接触滤波器设计,他和 Campbell,Zobel 和 Foster 都有书信往来,考尔很快意识到 Foster 的工作具有重大意义,在 1926 年至 1931 年期间他在这一领域继续深入研究,很快他抓住该工作的两个关键点,第一要找到一个函数可以无限逼近 “砖块” 滤波器即通带损耗极限小,阻带抑制极限大,两者之间过度极限快;第二该函数要能被无源器件的阻抗网络来实现,最后考尔选择了切比雪夫逼近,最开始考尔选择的是通带内和通带外都带有波纹的切比雪夫函数,该函数也被成为椭圆函数,基于该函数进行网络综合得到的滤波器就被称为椭圆函数滤波器或者叫考尔滤波器,后来可以证明椭圆函数是切比雪夫函数的一种特殊形式,可以通过简化退化成我们熟知的切比雪夫函数,因此可以说切比雪夫和椭圆函数滤波器都是考尔最先发明出来的,更重要的是考尔开启了一个滤波器设计的新范式,通过一条优美的函数曲线去逼近滤波模版要求,然后基于特定拓扑结构通过精准的解析法逐个求出电路元器件的值。大家还记得学习微波工程中关于低通原型值的表格吧,里面的数据完全是天马行空毫无规律可言(图十),这些值就来自于考尔的研究工作。
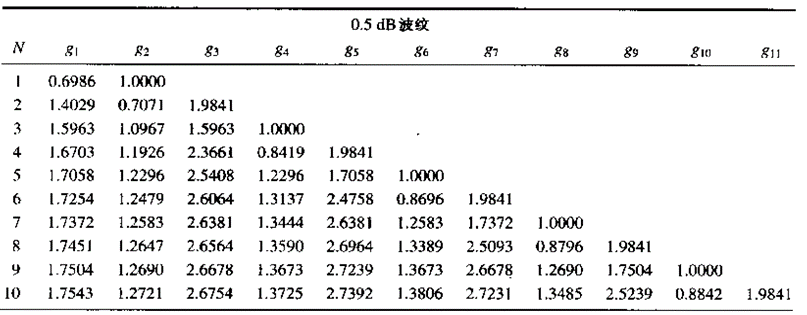
图十、0.5db 带内波纹的切比雪夫滤波器低通原型值,摘自《现代滤波器结构与设计》
同样值得一提的是英国物理学家 S.Butterworth(斯蒂芬。巴特沃斯 1885~1958)他在 1930 年代也独立发明了巴特沃斯滤波器,其大致思路和考尔一样,但他选取的逼近函数不是切比雪夫函数而是频率 s 的 n 次幂函数(n 为滤波器阶数),相比考尔的椭圆函数巴特沃斯函数的滚降要差许多,因此当前应用越来越少。相比于 Foster,考尔正式引入了切比雪夫函数作为逼近,而不是通过工程师经验来随意规定极点和零点来作为逼近(你可以理解为这种方法得到最佳逼近的几率非常非常小),其次就是考尔的工作中允许了电阻的存在,可以模拟出滤波器的损耗,而 Foster 理论里面只有电容和电感是无法模拟出滤波器损耗。即便如此考尔的工作依然存在两个问题,首先虽然考尔采用切比雪夫函数综合法得到了一些电容、电感值,但数学上依然没严格证明所有切比雪夫函数都一定可以被实际电容、电感实现,该工作后来被 S.Schelkunoff(谢昆诺夫 1897~1992)和 S.Darlington(达林顿,1906~1997)在 1940 年左右所证明,特别感谢 Darlington 在 1984 年发表了一篇回忆滤波器的历史的论文,本文很多素材也来自于他的回忆;其次考尔一开始选定的电路拓扑并不是 ladder 结构,而是需要引入一种阻抗变换器,这个在实际实现中非常麻烦,该问题一直到 1950 年才解决。考尔的工作是滤波器历史上的里程碑,从考尔的工作以后滤波器设计变得精确、优美,从此滤波器的设计有了坚实的数学根基。滤波器这些大咖基本都很长寿,Foster 更是超过 100 岁,但考尔却很不幸,他只活了 44 岁,由于他有一位远亲犹太祖先使得他在二战中首先被纳粹德国打压,郁不得志,1945 年苏联攻占柏林后他却被苏联士兵杀害,这样一位天才式的人物在时代洪流下的命运也是那么的无足轻重。
图十一、a) Foster,b) Cauer,c) Darlington
至此,滤波器技术这颗大树的树根和树干已经发展起来了,接下来就是各种开枝散叶。
电磁场滤波器的发展
● 滤波器和电磁场相结合,分布式器件替代集总元器件
二次世界大战期间,由于磁控管和雷达的广泛应用,频率来到了几十 MHz 到几千 MHz,功率可达到千瓦甚至更高级别,传统的电容、电感元器件因为功率问题和寄生效应原因越来越难以应对精准的大功率微波电路设计,滤波器发展也从集总器件逐步转变为分布式器件,这期间滤波器研究的中心从贝尔实验室转移到了麻省理工辐射实验室(RL)和哈佛大学无线电研究实验室(RRL)。
鉴于二战中雷达发挥出的巨大潜力,为雷达配套的高频微波理论研究被提到了很高优先级,大量优秀的科学家投入到了这个工作,最有代表性的产出是来自麻省理工辐射实验室 Montgomery, C. G.; Dicke, R. H.; Purcell, E. M. 等合著的《Principles of Microwave Circuits》,本书对各类传输线例如同轴线、矩形波导、圆波导的场模式以及电路参数进行了详细的研究;阐述了 Z 矩阵、Y 矩阵、S 矩阵的意义及其串联、并联、级联的计算;腔体谐振器、波导耦合器、魔 T 的设计和计算等等,可以说今天我们微波工程教材里面的大多数内容都在这本书中包含了,如图十二 b 是 Purcell, E. M. 整理的 TE21 模电场和磁场分布图。
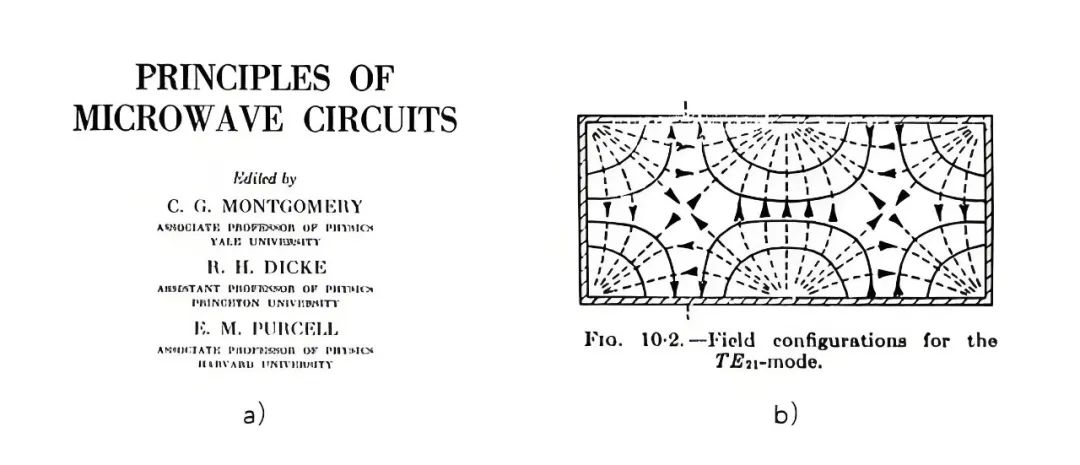
图十二、a)《Principles of Microwave Circuits》封面,b)TE21 模电场和磁场分布图
特别值得一提的是 Purcell, E. M.(珀塞尔),他在哈佛大学获得博士学位,在麻省理工辐射实验室工作期间做了大量关于微波理论的开创性研究,后来他回到哈佛大学开始研究核磁共振,并因此获得 1952 年诺贝尔物理学奖,除此之外他还是射电天文学开创者之一,最早银河系悬臂就是他观测得到的,不得不佩服早期微波科学家扎实的物理和数学基础,可以支撑他们横跨多个领域的研究。

图十三、a) Purcell,b)Bethe,c)Bethe
提出的谐振腔之间的耦合系数计算公式
除 Purcell 外,另外一个早年微波界传奇人物是 Hans Bethe(1906~2005),德裔美国人,毕业于慕尼黑大学,后加入康奈尔大学任教,他曾经也加入麻省理工辐射实验室工作在此期间提出了著名的小孔耦合理论,至今腔体类滤波器的耦合系数计算以及定向耦合器设计就是基于他的公式推导出来的,Bethe 在离开辐射实验室后加入了曼哈顿计划并为核物理研究做出了卓越贡献例如计算铀 235 的临界质量(同时他的一生都在为约束核武器发展而奔走呼吁),他发现了恒星发光原理,并因恒星核合成理论方面的研究获得了 1967 年诺贝尔物理学奖。
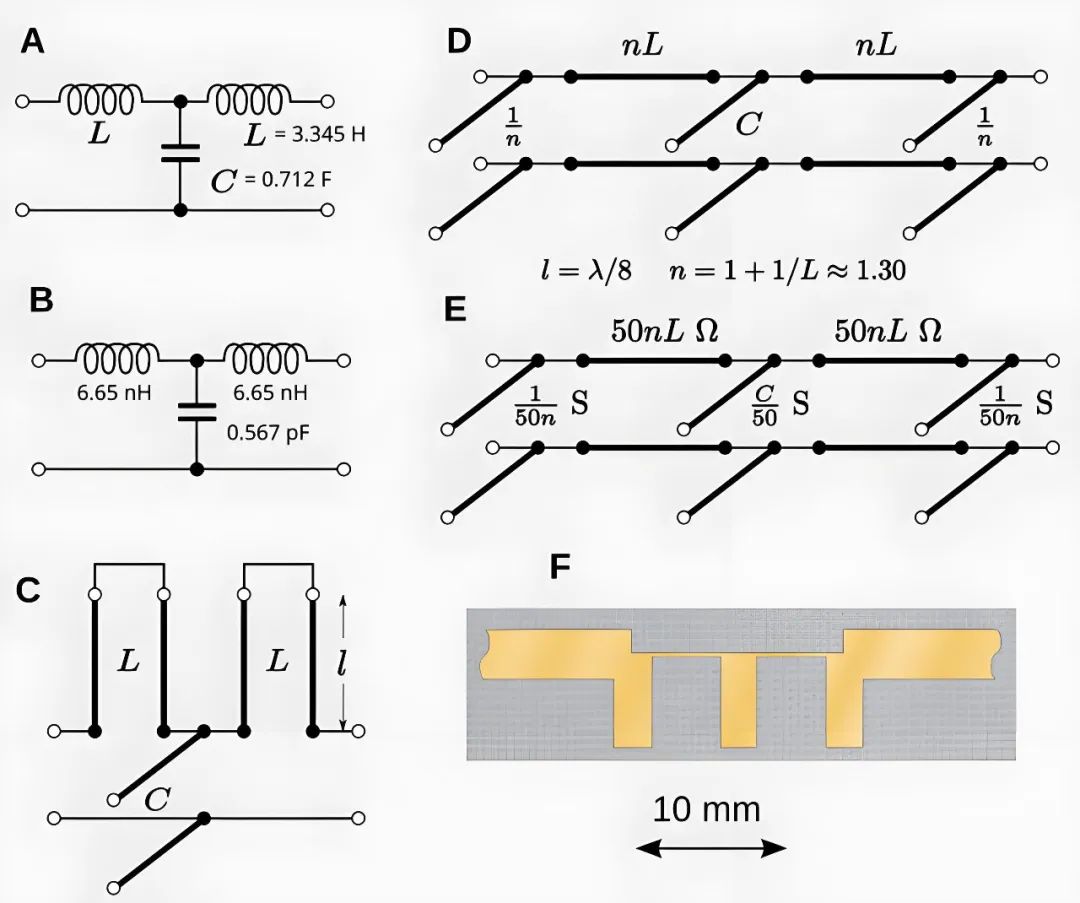
有了上面的微波传输线基础理论的研究后,P.I. Richards (1923–1978,博士毕业于哈佛大学并任职于哈佛大学无线电研究实验室) 和 K. Kuroda 系统地总结了如何基于电容电感集总器件经过一些列变换得到分布式器件的值,基本过程如下图:
图十四、Richards 变换和 Kuroda 法则(图片来源于网络)
step A 利用考尔或巴特沃斯的工作得到标准三阶滤波器归一化的电容电感值,step B 利用频率变换将电容电感归一化值变为实际工作频率下对应的绝对值,step C 是 Richards 想到的通过引入一段 1/8 波长短路线和开路先来分别等效串联电感和并联电容,step D 是 Kuroda 想到的通过引入 1/4 波长变压器可以将不好实现的串联电感转变为并联电容,setp E 是基于 50ohm 阻抗系统对传输线进行阻抗缩放,step F 即是得到最终的分布式元件具体尺寸从而完成从集总器件到分布式器件的设计(本例是一个微带结构,同理也可以用于波导、同轴结构或者带状线结构)。整个这个过程就是现代微波课程中经常出现的 Richards 变换和 Kuroda 法则。
致此电磁场滤波器发展已初具一门学科的雏形了,有了数学和电路理论基础,有了各种物理实现形式,一般电子工程本科阶段也就学习到这个深度,但如果你只会这些你设计的滤波器在当今社会是不会有竞争力的,因为滤波器接下来的发展越来越妙到毫颠。
● 耦合矩阵以前的滤波器发展
因为受高功率的影响,电磁场滤波器中发展最快的是波导滤波器以及腔体滤波器,首先还是麻省理工辐射实验室在 1948 年出版的《Microwave Transmission Circuits》中详细介绍了波导和同轴腔谐振器及滤波器设计方法,作者是 G. L. Ragan,R. M. Fano and A. W. Lawson. 本书前面几章对各种传输线例如同轴线、波导、脊波导进行详细阐述,同时也对调谐器、功分器、开关等微波器件进行了介绍,最后两章系统的介绍了滤波器的电路理论及设计,首先是低通和高通滤波器的设计,主要就是用微波元器件来实现电容或电感如图十五。
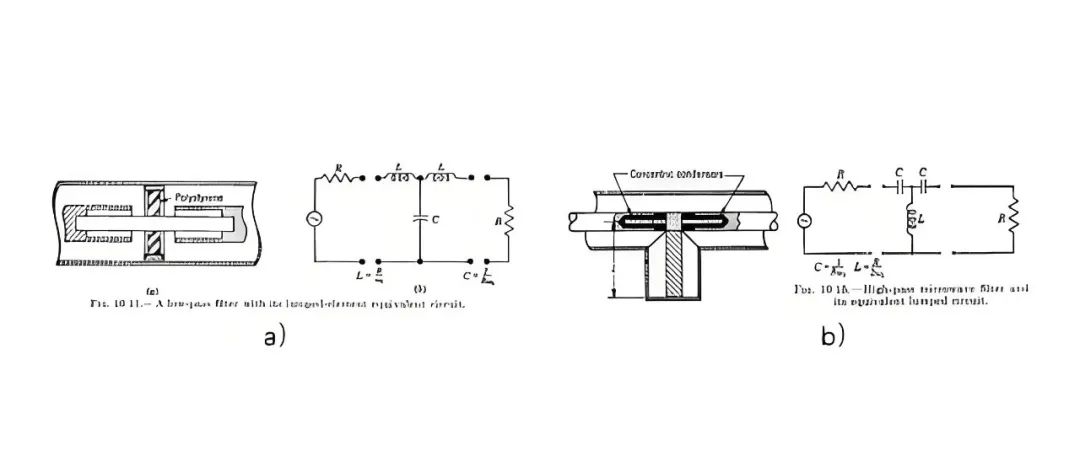
图十五、a)低通滤波器实现形式及对应电路 b)高通滤波器实现形式及对应电路
其次介绍了各种同轴和波导谐振器及其馈电的设计(图十六 a,b,c),然后通过 1/4 波长阻抗变换器将各个谐振器连接起来构成整个滤波器(图十六 d)。
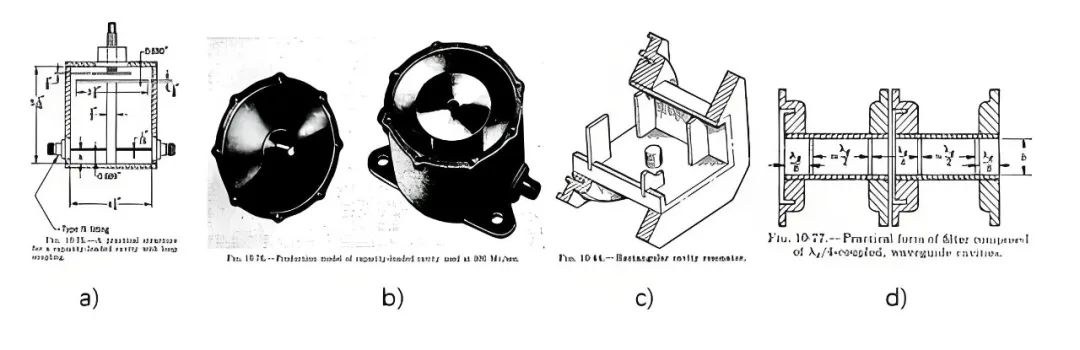
图十六、a) 同轴谐振器极其馈电示意图,b)同轴谐振器实物,c) 波导谐振器,d) 波导谐振器通过 1/4 波长阻抗变换器连接成的滤波器
简单介绍一下作 R.M.Fano(1917~2016),意大利裔美籍科学家,麻省理工博士毕业并在辐射实验室工作,他的前期工作主要是滤波器和阻抗匹配网络设计,其博士毕业论文就是 “任意阻抗宽带匹配的理论限制” 这也为日后他和 H.W.Bode 一起提出 “Bode-Fano 约束条件” 打下了基础,这一条件用滤波器的思维就很容易理解,如果输入 / 输出固定的情况下,一个滤波器带宽越宽往往他的驻波就越难以做小,也即是一个匹配网络的宽度和深度乘积为一个定值。Fano 的职业生涯横跨三个领域,他因滤波器领域的贡献被评为 IEEE fellow,但后期他的工作主要在信息论和计算机领域,他和 Bode 除了在微波工程有合作外,还一起与香农合作为信息论的开创做出了大量开拓性的工作。
顺便也介绍一下 H.W.Bode(1905~1982),荷兰裔美籍科学家,硕士毕业后在贝尔实验室工作并在哥伦比亚大学完成博士学业,早年间研究滤波器,其中声学场滤波器里面的 Bode Q 的计算公式就是他 1940 年左右提出的,后期他转而研究控制理论,提出了 Bode plot(波特图)。二战爆发后,他第一次尝试将无线通信、计算机和反馈控制系统结合到一起的发明了自动防空控制系统,通过雷达提供有关敌机位置的数据,然后将其反馈给高射炮伺服系统,实现自动击落敌机,二战结束后他又与导弹之父冯布劳恩一起参与了导弹以及反弹道导弹的控制系统的设计。
接上面,因为 1/4 波长阻抗变换器的引入,导致整个滤波器系统增加了额外尺寸开销, Fano 在 Microwave Transrmssion Circuits 这本书中提到直接耦合的滤波器(图十七),可以看到直接耦合滤波器没有了 1/4 波长阻抗变换器取而代之的是一个 “耦合窗膜片”,这样整个滤波器的尺寸会得到显著减小,但 Fano 并没有在书中给出精准的设计公式,该情况一直到 1957 年 S.B.Cohn 在他发表的经典论文 “Direct-Coupled-Resonator Filters” 中通过引入一个特殊的 T 型或者 Pi 型网络替代 1/4 波长变换器并给出了两者的换算公式,才算完成了这种日后用得最多的滤波器结构形式的精确设计方法,同时该结构也能实现更宽的带宽(超过 20%)。本文很多内容也来自 Cohn 在 1984 年发表的关于回忆微波滤波器发展历史的论文。
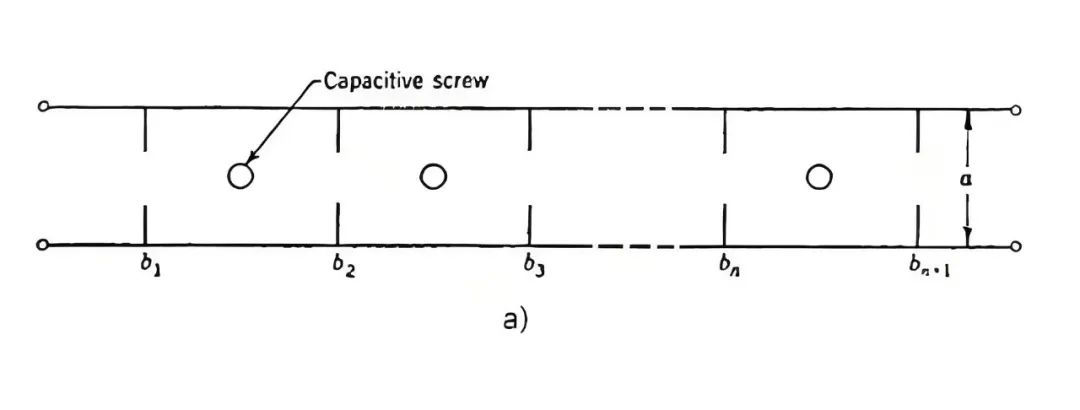
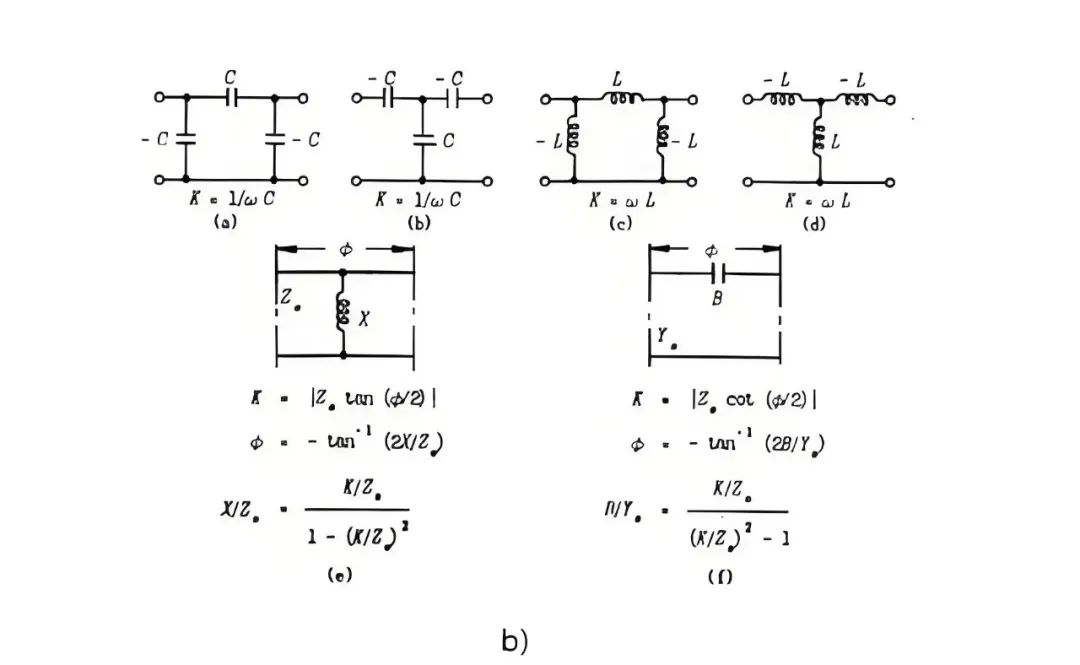
图十七、a) 直接耦合滤波器,b)” 耦合窗膜片” 等效电路图
在 Cohn 的论文之后,L. Young 围绕这种结构的进行了更深入的一些研究,包括进一步拓展带宽等,G. L. Matthaei 基于该理论完成了梳状结构和交指结构的带状线滤波器设计,后来该方法也被用于微带结构,至今微波仿真 EDA 工具中集成的微带 / 带状线滤波器设计工具包就是基于他的论文计算的。1964 年 G. L. Matthaei,L. Young 和 E. M. T. Jones 发表了滤波器历史上第一部集大成者巨著 《Microwave Filters, Impedance-Matching Networks and Coupling Structures》,该书中文译名叫《现代滤波器结构及设计》一般是微波工程滤波器方向研究生的入门教材,说是入门但要完全读懂里面公式其实需要很好的电路、数学和电磁场功底。因为书皮是黑色的,因此这本书在滤波器界也被称为 “Black Bible”,2014 年欧洲微波周在该书问世 50 周年之际会议专门给了一个议题纪念该书的出版问世,很多大咖纷纷表达了 Black Bible 对自己工作的帮助和启发,Matthaei 老爷子当时已经 90 多岁高龄还视频连线讲述了这本书的创作背景。该书系统总结了前人在滤波器电路、数学和各种电磁场结构的工作,在给定指标要求下,可以一步步通过查表的方法得到一个相当靠谱的结构参数,在那个没有计算机和仿真软件的年代,本书极大的降低了设计门槛,为滤波器的发展做出了巨大贡献。

图十八、a) Matthaei,b)“Black Bible” 封面
● 耦合矩阵的诞生以及电磁场滤波器设计方法的成熟
还是要先从 Microwave Transrmssion Circuits 这本 1940 年的书说起,书中第十章中提到一种非常前沿的设计,在圆波导中利用 TE111 的一对简并模设计出了第一个一腔双模滤波器(图十九),首先圆波导相比矩形波导有更好的 Q 值优势,其次一腔双模相比于单模有差不多一倍的体积优势,两者的结合使得这种圆波导双模滤波器成为后续卫星通信里面滤波器的首选方案并一直沿用到今天,而笔者看来该类滤波器一个更大的价值是间接催生了后续在电磁场滤波器中占据统治地位的耦合矩阵设计方法论。
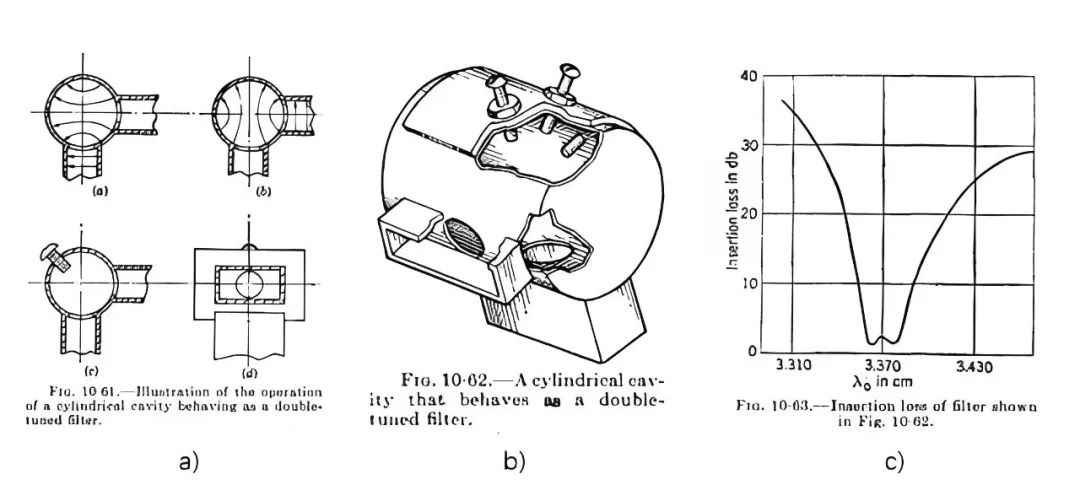
图十九、a) TE111 双模电场分布及耦合调谐、馈电示意图,b) 双模滤波器实物,c) 双模滤波器响应曲线
在进入耦合矩阵方法论之前先继续看一下一腔双模、多模滤波器的进展,本文写了这么多接下来我们终于可以看到第一位中国人的名字 —— 林为干院士(1919~2015),林院士本科毕业于西南联大,博士毕业于加州伯克利,他的博士论文《Microwave Filters Employing a Single Cavity Excited in More Than One Mode》中对上面提到的双模滤波器进一步拓展到了一腔三模、一腔五模(图二十),即便在有强大计算机和仿真工具的今天这也是一件极其复杂的设计,论文得到了答辩委员会的高度评价,被认为是微波技术研究中的重大突破,根据答辩委员会提出的建议,林院士对论文进行完善后寄到《应用物理》杂志,该杂志在 1951 年 8 月号的首页上发表了该论文,引起了很大反响。除滤波器外,林院士先后还发表《微波网络》、《微波理论和技术》、《电磁场工程》、《电磁场理论》4 书共 380 余万字,为国内的微波事业做出了突出贡献因此他也被尊称为 “中国微波之父”。
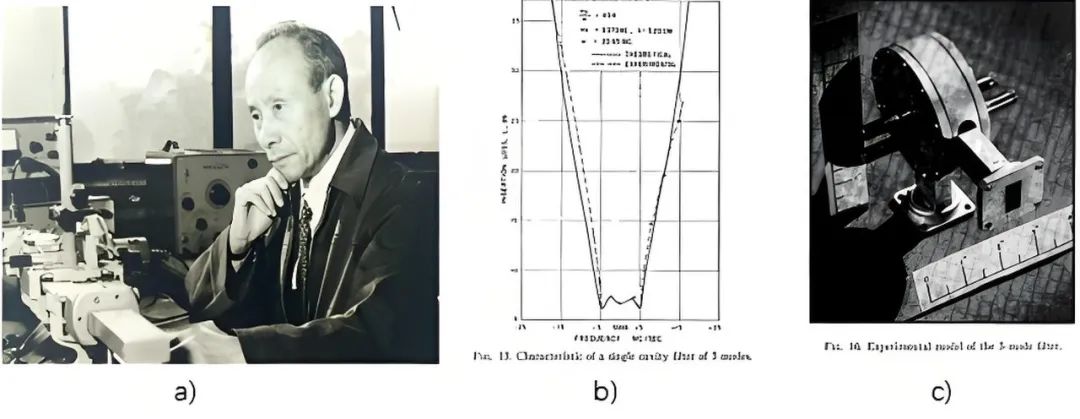
图二十、a) 林为干院士,b) 一腔五模滤波器频率响应图,c) 一腔五膜滤波器实物
时间来到上世纪 70 年代,因为卫星通信的兴起,要求滤波器小型化轻量化的同时还要具备低损耗、大功率特性,满足这些条件的最佳选择就是上面提到的圆波导双模滤波器。由于高滚降的要求,此时的微波滤波器拓扑结构相比早期滤波器有了一个明显的不一样,早期微波滤波器拓扑主要是一种一维结构,一连串谐振器顺序排列,但由于近端抑制要求越来越高,滤波器需要用到一种 cross coupling(交叉耦合)的结构来提升滚降速度,这时滤波器拓扑就由一维变为了二维,以图二十一的 4 阶滤波器为例,S 代表输入端口,L 代表输出端口,1、2、3、4 代表四个谐振器,之前的拓扑结构主要以图二十一 a 为主,输入 —— 各谐振器 —— 输出,通过主耦合(黑色线)一维排列,而交叉耦合(红色线)引入后,原来的一维结构就变为二维结构了,如图二十一 b,c,d,e 所示。这个时候考尔当时的逐级提取电路综合法处理起来就会非常的麻烦,二维结构,似乎很容易想到该矩阵出手了(回头看总觉得所有的进步都是顺理成章,但如果自己处于那个节点估计也是手足无措)。
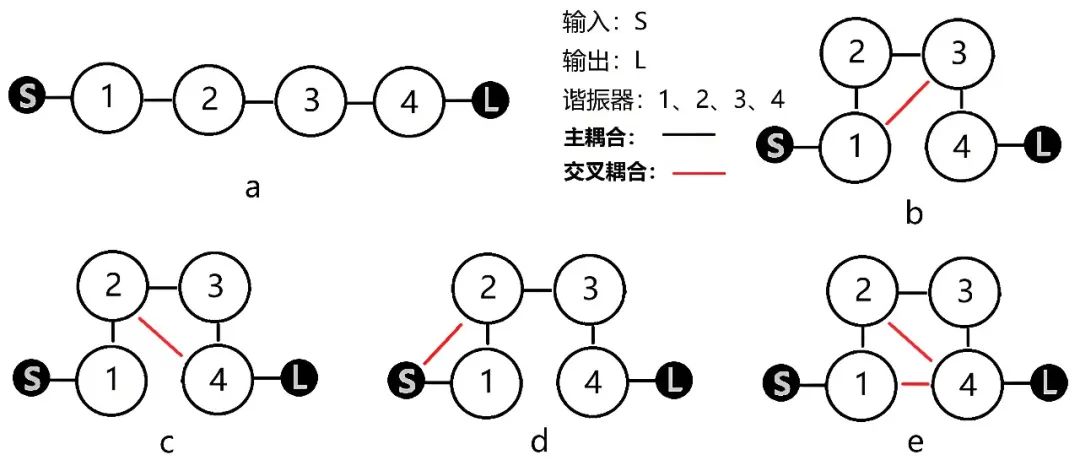
图二十一、a) 无交差耦合四阶滤波器,b) 带交叉耦合四阶滤波器
A.E.Atia,1962 年本科毕业于埃及 Ain Shams University 大学,1969 年博士毕业于加州伯克利大学后加入了通信卫星的先驱 COMSAT 公司,一直从事各种微波技术开发,1972 年在他发表的论文《narrow band waveguide filter》中系统的描述了用矩阵形式来表征这种复杂的谐振器之间的耦合形式,矩阵中的每个元素都是通过一系列数学和电路公式处理得到,同时又可以对应到实际滤波器的每个关键物理结构。通过这一套理论 Atia 设计了一个圆波导双模 8 阶 4 个零点的滤波器,曲线的优美程度、设计和实测的精准吻合度已经和今天的滤波器没啥大的差别了,在那个年底堪称艺术品。
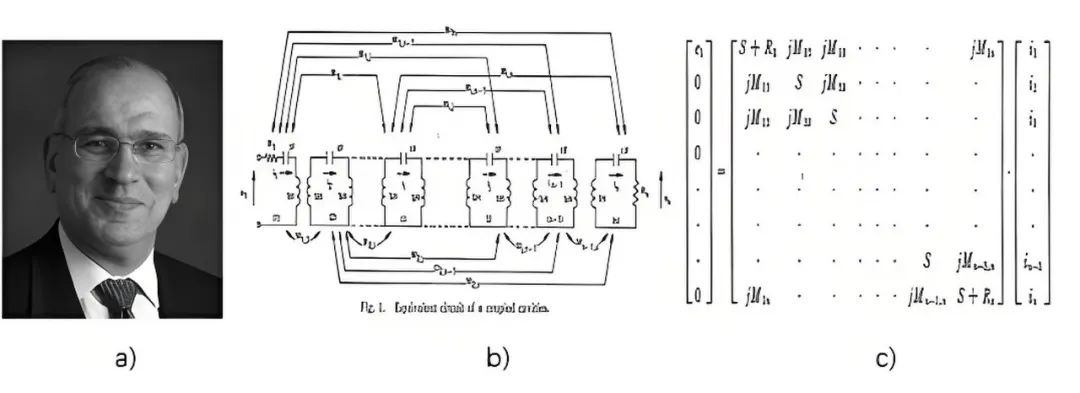
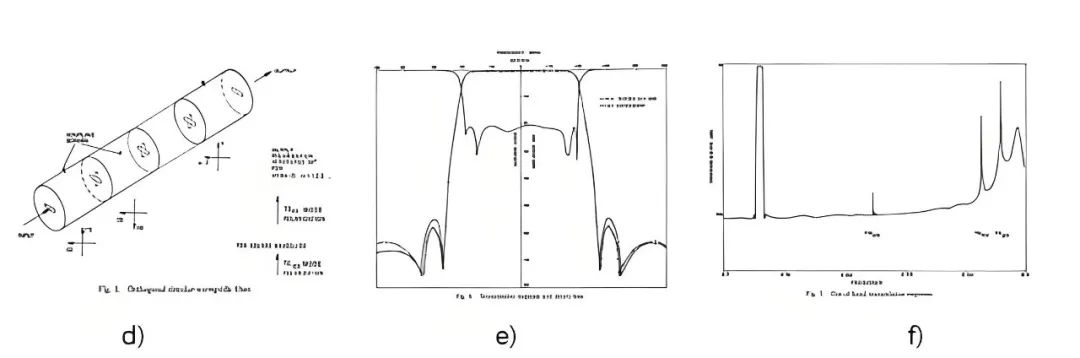
图二十二、a) Atia,b) 耦合矩阵电路示意图,c) 耦合矩阵,d) 圆波导双模滤波器,e) 8 阶 4 零点双模滤波器仿真实测对比图,f) 滤波器宽带响应曲线
Atia 虽然在 70 年代就系统的提出了耦合矩阵理论,但由于那个时候计算机尚未普及,过程复杂导致一般工程师很难掌握,加之需要到卫星通信那么高要求的场景太少,这套理论一直未获得足够发展和推广,他的爆发还需要下一个时代节点。
时间来到 2000 年左右,因为移动通信的兴起,相比卫星通信更需要海量高功率、高抑制、低损耗、小体积、低成本的滤波器,那个年代的加拿大滤波器巨头公司 COMDEV 引领了这一波技术浪潮,同轴腔体滤波器结合耦合矩阵理论成为了最佳解决方案,其首席科学家 Richard J. Cameron,于 1999 年和 2003 年先后发表了 2 篇文章《General coupling matrix synthesis methods for Chebyshev filtering functions》《Advanced coupling matrix synthesis techniques for microwave filters》在 Atia 的基础上进一步完善了耦合矩阵理论,前一篇给出了从切比雪夫函数到多项式再到耦合矩阵的方法,Atia 文章中缺失了切比雪夫函数到多项式的分解过程;后一篇文章将滤波器零点数扩展到了 N 阶 N 零点,Atia 的文章中最多支持 N 阶 N-2 零点(虽然电磁场滤波器很少会用到 N 阶 N 零点的情况,但声学场滤波器就必须是 N 阶 N 零点),同时 Cameron 的两篇文章中还给出了更为详尽的矩阵变换的方法;还是以图二十一 b、c、d 为例,假如要实现相同的滤波曲线,如果用传统方法,针对不同拓扑 b、c、d 要分别进行一套独立的电路提取过程,但基于耦合矩阵理论就方便多了,前面的过程都一样,得到耦合矩阵后保持其本征值不变,通过矩阵变换就可以实现从 b 变到 c 或 d,用计算机编程计算整个过程不到 1 秒钟。通过耦合矩阵,b、c、d 这三种在之前看来完全不同的滤波器设计最后实现了数学上的等价。
2005 年意大利米兰理工大学教授 Giuseppe Macchiarella 在其发表的论文《An Analytical Technique for the Synthesis of Cascaded N-Tuplets Cross-Coupled Resonators Microwave Filters Using Matrix Rotations》中对耦合矩阵理论补充上了最后一环,他提出了一条针对滤波器常用拓扑更容易实现的矩阵变换路径,结合计算机编程,完美闭环了耦合矩阵整套理论,使得其使用门槛再次大大降低。耦合矩阵理论首先在波导滤波器和腔体滤波器中开始应用,笔者 2006 年参加工作时国内一些年轻工程师刚开始采用该方法,但一些资深工程师还是习惯原有优化设计法,经过近 20 年发展现在该方法已经从腔体滤波器逐步扩散到各类介质、微带、LTCC 等形式的电磁场滤波器中,基本统治了电磁场滤波器设计方法(带宽 30% 以内基本都 OK)。

图二十三、a) Cameron,b) Macchiarella
最后简单总结一下电磁场滤波器的发展历程,1. Foster 提出网络综合法;2. 考尔引入切比雪夫函数;3.Purcell、Fano、Cohn、Matthaei 对各种微波元件、谐振器和滤波器的研究;4.Atia 提出耦合矩阵理论;5. Cameron 和 Macchiarella 完善耦合矩阵理论。如图二十四所示,当前电磁场滤波器主流的设计方法是 首先根据客户规格得到满足需求的切比雪夫函数,然后再从网络综合法得到电路元件的值再进一步得到耦合矩阵,最后通常场仿真工具将耦合矩阵映射到实际的物理结构,最终形成了一个优美、精确、高效的一套设计方法论。
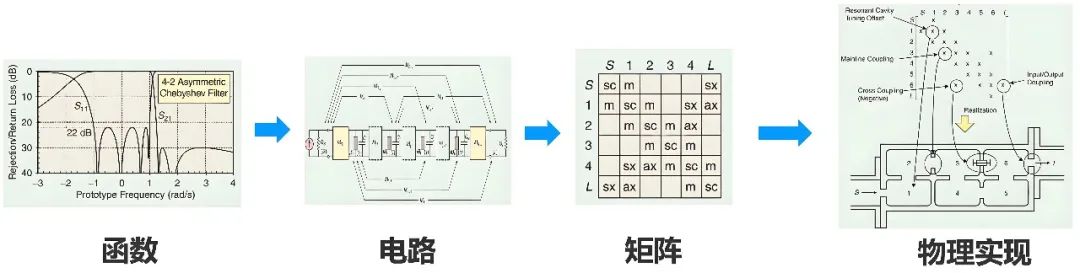
图二十四、当前基于耦合矩阵理论的电磁场滤波器设计流程
暴力优化的低效性
也许有些工程师会说不需要知道网络综合和耦合矩阵这一套数学和电路理论,只需要在仿真工具中搭好物理结构,然后采用暴力优化的方法也可以设计出滤波器。诚然,对于指标要求较低、滤波器阶数少且抑制宽松的情况,暴力优化很快也能得到不错的结果。但对一些阶数多且近端抑制高的滤波器来说,暴力优化相对于上述那套理论实际上要低效得多。例如,移动通信基站 band28F 频段需要 12 阶 + 5 零点的滤波器,用暴力优化的办法几乎不可避免地会陷入局部最优。
AI 设计滤波器的挑战
作者也经常被问道为何不用万能的 AI 来设计滤波器。当下这是一个值得认真对待的话题。个人理解可以从以下两点讨论:
-
参数离散化与计算复杂度
波器是模拟系统,首先要对其进行离散变为数字系统。以中等难度的移动通信 B3 频段发射通道滤波器为例,影响性能较大的参数大致有 20 个左右。凭借工程师经验,每个参数变化区间可以锁定在 5 毫米以内。假如以回波影响 2db@20db 这一敏感度来限定,那么每个参数的变化大致要控制在 5 微米以内,也就是每一个参数需要离散 1000 段。那最终的参数组合是 100020=1060 次方,这已经是一个天文数字。如果是一个四工器,这个数字会更高,达到 10^100 次方。
-
训练等待时间和资源消耗
每变一个参数,滤波器的影响如何得到?也就是训练的等待时间。假如是仿真,每次变化至少要 20 分钟计算时间;如果是实物调试,虽然可以在一秒钟内完成,但如何设计一套系统确保每个参数都可以调谐且精度控制在 5 微米以内是一个巨大挑战。即便成功,投入产出比会让人大跌眼镜:大概需要用一个 AlphaGo 量级的资源,设计出一个单价约 500 块钱的东西。
AI 与滤波器设计的差距
其次,AI 是否真的适用于滤波器设计呢?笔者用神经网络优化过滤波器,但发现其效率甚至不如普通的梯度法。这可能是因为:
-
滤波器结构特性
滤波器是一种窄带多谐振结构(其他射频器件基本都是宽带少谐振结构),意味着它极其敏感且局部最优非常多。结构上一点很小的误差就会导致性能大幅恶化,这也解释了为何高性能电磁场滤波器都需要手工调试。
-
AI 算法的优势与局限
AI 类算法的优势是不需要问题连续、可导甚至不需要明确的数学模型。但它的判断基于模糊逻辑,单个来看非常低效,必须依赖摩尔定律带来的规模优势才能发挥魔力。而梯度法恰好相反,如果一个问题背后有电路模型,它会非常聪明且快速地找到答案,消耗资源也极少。
算法选择的哲学
因此没有万能的算法,只有特定模型最合适的算法。AI 不是 “行不行” 的问题,而是 “划不划算” 的问题。Deepseek 着实惊艳,但笔者认为 AI 要渗透到社会的每个角落真正成为第四次工业革命还需要大幅提升其能耗比才行。
-
能耗对比:AlphaGo vs 李世石
AlphaDog 计算能耗几百万瓦,而李世石的大脑仅消耗 20 瓦。这可能就是为何地球几十亿年来自然进化出的是碳基生命而不是硅基生命吧。
工程领域的 AI 应用
因此对于具体工程领域来说,工程师对 AI 的应用一定是深刻理解本领域问题的各个环节:
-
在一些没有精确数学模型而大量依赖人的经验判断的环节中,也许 AI 是合适的。
-
但切不可 “万事皆可 AI”,工程师语言一定是定量分析而不是定性结论。正如罗胖所说,“一具体就深刻”。
声学场滤波器的发展
● 石英晶体滤波器
笔者最先接触到的声学场滤波器是在 2010 年 Avago 的一款 FBAR 双工器,当时其尺寸面积仅为 2.5mm*2.0mm,测试其性能后发现损耗居然只有 1db 多一点,反推其 Q 值大概有 1000 的样子,这令笔者非常惊讶,小尺寸的滤波器也有比如 LTCC,小型化的陶瓷滤波器等,但既要尺寸小又要 Q 值好在传统电磁场思维模式下是不行的,后来了解其原理,原来它是利用逆压电效应将电磁波转换为了声波,利用声波谐振来滤波最后再转换成电磁波,由于声速相比于电磁波的速度低 5 个数量级,当两者激励频率一致时,声波的波长要相比电磁波低 5 个数量级,所有的谐振器都是基于波长相关的,因此声波类谐振器 / 滤波器就要比同频率电磁场谐振器 / 滤波器小 5 个数量级。
笔者一直好奇到底是谁想出了这天才般的 idea,查了 SAW/BAW 的历史发现这些技术好像在上世纪 60 年代一下就冒出来了,中间总觉得少了一些环节,后来不断顺着论文的参考文献捋,发现这些滤波器里面提到的 BVD 模型和 Mason 模型的其提出者 Van-Dyke 和 W.P.Mason 主要都是研究石英晶体滤波器的,也许答案就在这里面。
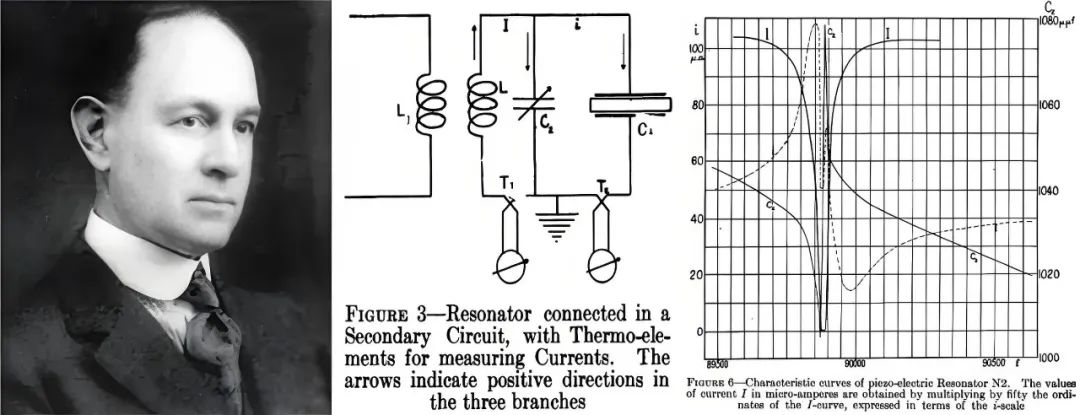
首先第一位出场的大咖是 W.G.Cady (1874~1974),美国物理学家和电气工程师,本科毕业于布朗大学,1900 年博士毕业于柏林大学,1902 年加入美国卫斯理大学任教,早期他主要从事无线电探测器方面的工作,一次世界大战期间他与美国海军实验室合作研究压电产生的高频声波来探测潜艇,这让他对压电晶体产生了浓厚的兴趣,他注意到连接到变频电子振荡器的石英晶体在特定的频率下会强烈振动,但在其他频率下它根本不会振动后,这激发了他将其应用于射频的想法,1921 年他在《物理评论》杂志上发表了文章《THE PIEZO-ELECTRIC RESONATOR》,首次提出用石英晶体作为振荡器和窄带高选择性滤波器,很快他还基于该谐振器申请了频率标准器和频率稳定器的专利并在 IRE(Institute of Radio Engineers,也是今天大名鼎鼎的 IEEE 的前身)发表了关于石英晶体频率控制电路的论文。于是乎一种完全不同于电容 + 电感组合的新型谐振器被提出来了,深深影响了后来射频电路和滤波器的发展,如果说瑞利是声学场滤波器的麦克斯韦的话,那么 Cady 就是声学场滤波器的 Heaviside。
a) b) c)
图二十五、a)Cady b) 石英晶体振荡器 c) 石英晶体振荡器频率 / 电流响应曲线
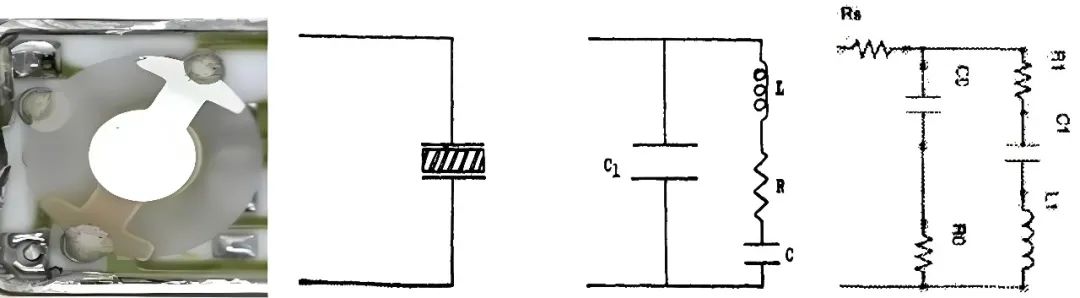
在 Cady 发现石英晶体谐振器后,他在卫斯理大学的同事 Van-Dyke 于 1928 年发表论文《THE PIEZO-ELECTRIC RESONATOR AND ITS EQUIVALENT NETWORK》给出了其电路模型,也就是声学滤波器最常用的 BVD 模型(Butterworth Van-Dyke 模型,Butterworth 到底对该模型做出的贡献是啥笔者尚未找到),可以看出其电路符号是一个三明治形状(至今所有的声学场电路符号都是沿用于此),这来自于早年石英晶体采用圆盘加上下电极的制作方式,Van-Dyke 给的等效电路模型中串联支路代表声学谐振点,并联电容支路代表石英晶体的平板电容效应。该模型用了 70 多年后于 2000 年被修正为 MBVD 模型,引入了下图最右边 Rs 和 R0 以便更精准的模拟声学谐振器的 Q 值。
a) b) c) d)
图二十六、a) 三明治石英晶体谐振器(图片来源于网络),b) 石英晶体谐振器电路示意图,c) 石英晶体谐振器等效电路 BVD 模型,d) 声学谐振器 MBVD 电路模型
作为滤波器基本单元的谐振器有了,接下来介绍的大咖就是真正将石英晶体谐振器利用起来完成了各种滤波器设计的人,W.P.Mason (1900~1986) 1928 年毕业于哥伦比亚大学获物理学博士学位,同时他也是一位贝尔实验室工程师,从 1925 年到 1965 年一共在贝尔实验室工作了 40 年,从前面的内容我们可以知道,上世纪 20 年代的贝尔实验室里面滤波器大牛云集,Campbell 给出了各种滤波器的电路拓扑,Zobel 在其基础上增加了零点,Foster 将网络综合的概念引入到滤波器设计中。Mason 将这些理论都用到了石英晶体滤波器设计中,尤其是 Zobel 的方法(在图八中,第三个并联谐振器就和石英晶体谐振器电路模型一样)。
当时贝尔实验室工程师已经意识到电感线圈的 Q 值不够,1929 年 Mason 采用石英晶体谐振器取代 LC 谐振器实现了 108KHz 的滤波器,因为石英晶体谐振器的带宽只有 0.1% 左右,因此 Mason 选择的电路拓扑是 Campbell 的 lattice 结构,该结构相比常用的 ladder 结构带宽更宽。可即便如此,最开始 Mason 能实现的带宽也仅仅在 0.4% 的样子,后来 Mason 尝试在石英晶体谐振器基础上引入外部电感后(该方法至今仍然是声波类滤波器拓宽带宽的有效方法),带宽可以进一步拓宽到 6%(但电感引入会影响石英晶体谐振器 Q 值),Mason 的设计方法差不多统治了石英晶体滤波器 20 年。
除石英晶体滤波器外,Mason 对滤波器电路理论发展也做出了贡献,他是最早采用 A,B,C,D 参数计算滤波器级联阻抗的人,他提出的 Mason 模型也是后来 BAW/FBAR 滤波器常用的设计基础。除在石英晶体滤波器电路方面的研究外,Mason 对于石英晶体的不同切型也做了大量研究,在频率为 100KHz 的应用中主要采用 X 切提升带宽,后来随着频率升高到 30MHz,这个时候主要采用 AT 切。
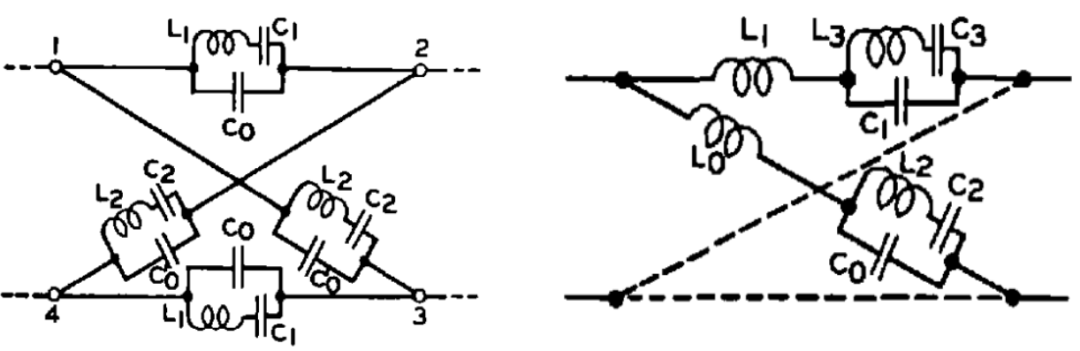
a) b)
图二十七、a) 基于 lattice 拓扑的石英晶体滤波器电路模型,b) 通过串联电感来改善带宽的电路模型
如图二十八,石英晶体滤波器早年主要是基于单个分离谐振器进行拼接制作,整体电路复杂,尺寸大,后来被 Monolithic 晶体滤波器取代(这点很像分离谐振器陶瓷滤波器被 Monoblock 陶瓷滤波器取代,因为制作更简单体积也更小),并在上世纪 60 年代时广泛应用于收音机里面。

a) b)
图二十八、a) 石英晶体滤波器,b)Monolithic 石英晶体滤波器 (图片来源于网络)
石英晶体滤波器优点非常多,Q 值高,温度稳定性好,价格便宜,因此是低频窄带滤波器的最佳方案,但其缺点也很明显首先就是带宽太窄通常小于 1%,到了 GHz 级别后带宽更是不到 0.1%,因此对于 GHz 级的应用来说,还需要寻找更合适的方案。
● SAW(Surface Acousitic Wave)滤波器
如果说石英晶体滤波器是所有声学场滤波器的始祖的话,你会觉得同为三明治结构 BAW 滤波器也许更像它的直系子孙,而 SAW 无论如何也不像,笔者也一直好奇为何会有人想到跳过平板而用叉指电极来激励声表面波呢。
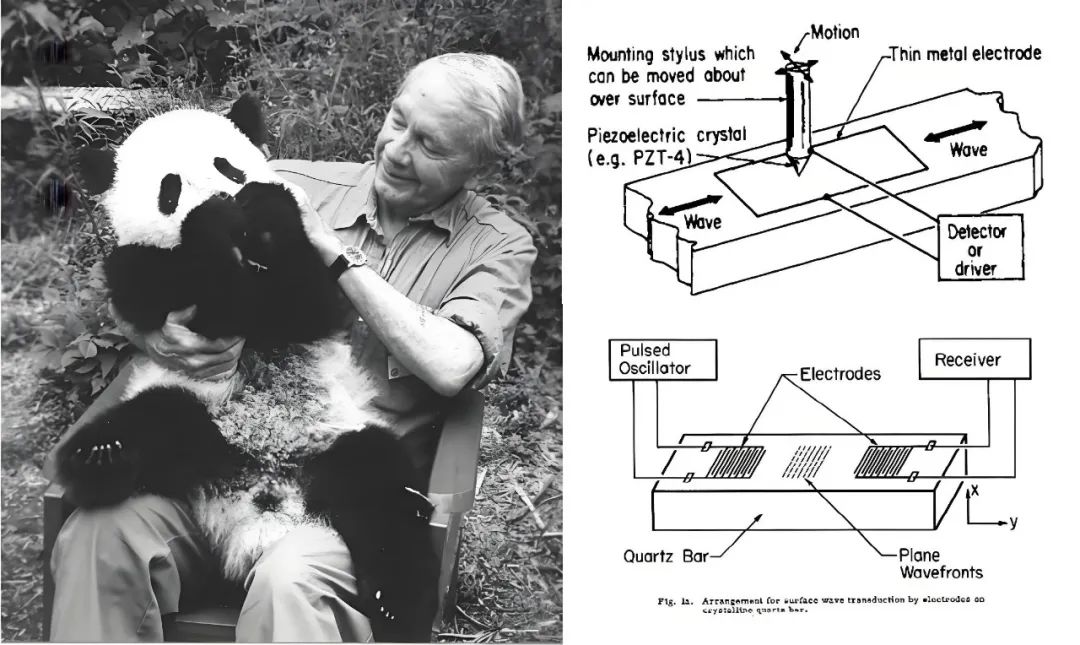
R.M.White (1930~2020), 1956 年博士毕业于哈佛大学应用物理专业,读书期间他曾在贝尔实验室射频部门实习,毕业后加入通用电气公司的微波部门,博士期间他的论文主要是声波的传播研究,学习和工作经历使他横跨声波和电磁学两个领域,1962 年他返回加州大学伯克利分校电气工程系任教,1965 年他在《应用物理》杂志上发表了《DIRECT PIEZOELECTRIC COUPLING TO SURFACE ELASTIC WAVES》第一次提出了在石英晶体上用叉指电极换能器(IDT)来激励声波,从而拉开了 SAW 滤波器设计的序幕。
2007 年针对他的一次采访可以看出他的灵感来源:“至于表面波,当我参与其中时,我试图解决的一个问题是任期合同问题 [笑]。我最初试图制造表面声波放大器,即放大压电半导体中表面声波的设备,因为人们已经证明可以对体波进行放大。因此,为了做到这一点,我必须想出一种产生表面波的方法。当时人们使用的方法非常笨拙:将金楔放在表面上进行机械运动。我突然想到 —— 我认为这是因为我曾在通用电气公司从事过行波管研究,行波管由周期性结构和间隔电极组成 —— 放大器就像一个行波管。你发出波并刺激电子,它们可以相互馈送能量。因此,从这一点开始,叉指换能器的想法似乎非常自然,因为你已经建立了一个结构,其中激发电场具有合适的频率,与压电结构的声波谐振频率相吻合。1962 年,我们还刚刚在伯克利建立了一个微加工实验室。因此,在那里制造这些电极结构是可行的。这就是一切的起源。”
a) b)
图二十九、a) White b) 传统机械方式激励声波和 IDT 激励声波
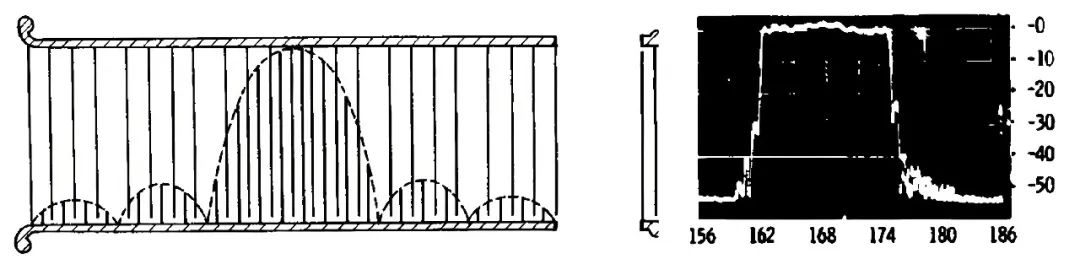
SAW IDT 被发明后首先应用场景是作为时延线,相比用传输线绕圈的方式,SAW IDT 只需要在芯片大小就可以实现很大的时延。70 年代 SAW 开始大量应用于电视中频滤波器,压电材料也开始由石英逐步转换到 ZnO,LiTaO3 和 LiNbO3,这个时候设计方法主要是脉冲函数法,一般通过对 IDT 进行周期加权和变迹加权来实现想要的波形(图三十),这时期 SAW 滤波器设计和电磁场滤波器设计有很多共通之处,”Black Bible” 作者 G. L. Matthaei 还用电磁场滤波器中经典的横向滤波器(transversal filter)概念来解释和设计 SAW 滤波器,得到了很好的响应曲线。
a) b)
图三十、a) 周期加权 SAW 滤波器 b) SAW 滤波器响应曲线
到了 80 年代 SAW 滤波器开始追求低损耗,并在 90 年代开始逐步取代介质滤波器应用于移动通信中,这个过程中需要釆用单相单向换能器(SPUDT)或耦合谐振滤波器(CRF)原先的脉冲函数设计法已经不能满足设计需求,取而代之的就是 COM 理论(Coupling of Modes), COM 理论最早是贝尔实验室 J.R.Pierce(1910~2002,其传奇程度个人觉得比前面那些大咖还要传奇,以后有机会再细说) 在 1954 年提出,用于模拟波导滤波器、行波管等微波元件的理论。
在 70 年代末该理论被引入到声学谐振器领域,1989 年 B.P. Abbott 在其博士论文中对其进行了全面的修正和优化使其对于基于瑞利波的 SAW 有很高的模拟精度,后续 Pleskky 和 Hashimoto 教授又做了大量工作使其可以用于 LiTaO3 衬底 SH 波的 SAW,90 年代后基于 COM 模拟谐振器 + 遗传算法 / 模拟退火算法优化滤波器的组合设计模式逐步成为主流,直至今天也依然是大多数 SAW 滤波器公司的主流设计方法。
除设计方法的进步外,在材料以及工艺方面 SAW 滤波器一样进步明显。在材料方面,1997 年 Hashimoto 教授发表论文表明采用 42° LiTaO3 相比 36° LiTaO3 SAW 滤波器插损可提升 0.5db。在工艺方面,由于 LiTaO3 和 LiNbO3 衬底的 SAW 温漂系数较大(40~70ppm),这使得其在近端抑制要求高的场景应用大为受限。
在降低 SAW 的温漂上,人们尝试了两种不同的方法,1995 年,Hickernell 等人发表论文表明溅射厚度在 015–0.3λ 范围内的 SiO2 层可使 36° LiTaO3 和 64° LiNbO3 SAW 器件的温漂几乎降为 0,这也成为后来溅射路线 TCSAW(Temperature Compensation SAW)的开端。1997 年 K. Onishi 等人发表论文,通过 LiTaO3/LiNbO3 压电衬底键合到低温漂的玻璃基片上可以大幅提升 SAW 温漂,这也成为后来键合路线 TCSAW 的开端。
TCSAW 发明后在 sub 1GHz 以下其性能已经可以比拟 FBAR 滤波器了,2016 年村田公司 Takai 等人发表论文《Investigations on design technologies for SAW quadplexer with narrow duplex gap》里面的 IHP SAW 滤波器(现在更多被称为 Thin Film SAW,TFSAW)拥有 3500 超高 Q 值和 8ppm 超低温漂系数,该技术使得 SAW 可以在 sub 3GHz 以下性能比拟 FBAR,同时成本更具竞争力,当前 4 种主要的 SAW 滤波器如图三十一所示。
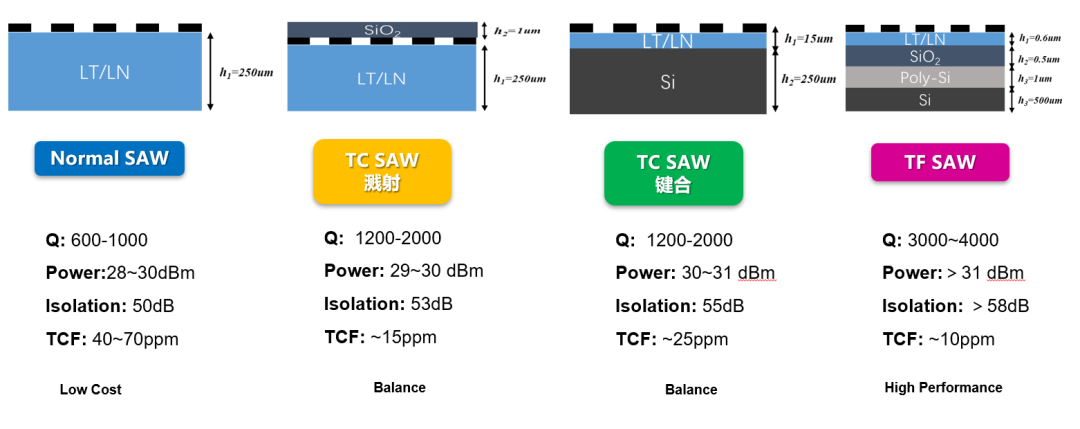
图三十一、4 种主要的 SAW 滤波器对比
● BAW(Bulk Acousitic Wave)滤波器
前面提到 BAW 滤波器更像石英晶体滤波器的直系子孙,其诞生主要是为了解决石英晶体滤波器的高频化和小型化。
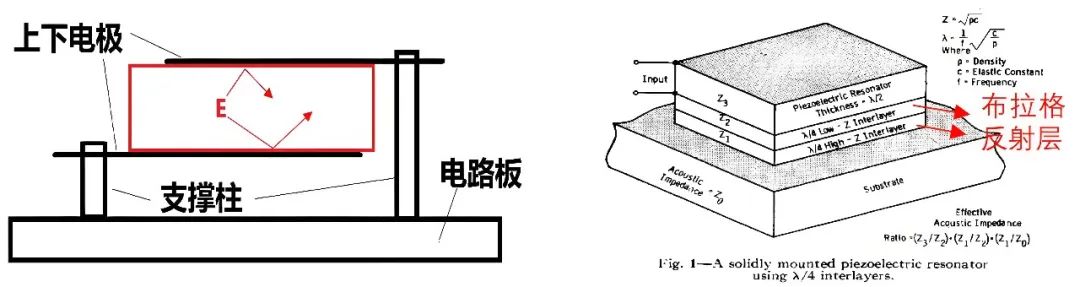
上世纪 60 年代随着集成电路的兴起,人们迫切需要找到一种高 Q、小型化且易于集成的谐振元器件,介质谐振器有很高的 Q 但体积太大不利于集成,因此一开始人们将目标放在了石英晶体谐振器的小型化上,如图三十二 a 所示,石英晶体需要上下电极都悬空以便声波能量能够在固体 / 空气表面形成全反射从而将能量全部束缚在晶体内(红色区域内),当频率低,石英晶体较大时这个是没问题的,但如果频率来到 GHz 级别,石英体厚度大约为 um 级别时,如下结构显然就不可行了,如何在 um 级别尺寸上实现全反射结构就是接下来几十年 BAW 技术发展的主线。
1964 年 W.E.NEWELL 提出了一种完全新型的构思,如图三十二 b,整个谐振器安装在一个衬底上,但为了防止能量从下电极泄露到衬底,引入了一种声学隔离层,即通过 1/4 波长高 / 低声阻抗交替的结构(布拉格反射层)来实现能量全反射进而达到和悬空一样的能量束缚效果,但受加工条件的影响,NEWELL 的构思要到 90 年代才得以实现。
a) b)
图三十二、a) 石英晶体谐振器能量支撑束缚示意图 b) 布拉格反射层能量束缚示意图
与此同时,图三十二 a 的结构人们也没有放弃,1980 年南加州大学 K.M. Lakin 教授在他论文《UHF COMPOSITE BULK WAVE RESONATORS》中提出了一种两面悬空的薄膜体声波结构如图三十三所示,电极采用铝,压电薄膜材料采用 ZnO 材料,谐振器制备在硅衬底上,然后将下电极下方的硅衬底再蚀刻掉,形成两面悬空的结构,确保能量束缚在压电薄膜中,从而获得了在 500MHz 左右 9000 的 Q 值(耦合系数仅 0.3%),同年 T. W. Grudkowsk 也提出了类似结构,这就是最早的 FBAR(Film Bulk Acousitic wave Resonator)结构。
1992 年 Lakin 教授在他的论文《THIN FILM BULK ACOUSTIC WAVE FILTERS FOR GPS》中提出基于 AlN 压电材料的 FBAR 滤波器同时在该论文中还系统的阐述了 FBAR ladder 滤波器设计过程,首先是基于谐振单元的 BVD 模型通过 ABCD 矩阵建立与 S 参数的联系,根据设计需求对谐振单元 BVD 模型进行调整(频率、静态电容等),然后通过数值算法(论文中为有限差分,当前多为有限元算法)计算 FBAR 谐振器各种杂波情况,进而对 BVD 模型的响应曲线进行修正,最后得到的滤波器响应曲线(如图三十四)已经非常准确,受限于当时的材料和加工工艺,其插损偏大。这套流程基本也是后来大多数公司的 FBAR 设计流程,近年来还引入了电磁场模型进一步提升了仿真精度。
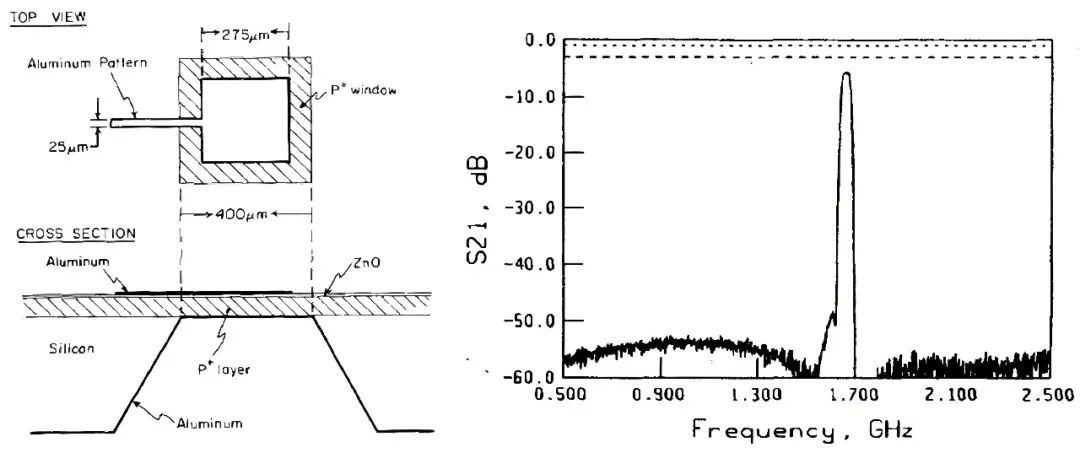
图三十三、两面悬空 FBAR 谐振器示意图
图三十四、基于 AlN 的 FBAR 滤波器响应曲线
1994 年 NEWELL 的思路终于等来了具体的实现方案,R. J. Weber 申请了一项专利如图三十五,详细描述了如何通过半导体加工工艺实现布拉格反射层,其中 36、37 为电极材料,35 为压电材料,整个 40 结构就是布拉格反射层,20 是硅衬底。
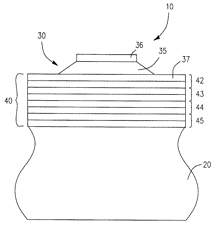
图三十五、基于布拉格反射层的 BAW SMR 结构
1995 年 Lakin 教授在他论文《Development of miniature filters for wireless applications》系统的梳理了 BAW 谐振器的各种实现结构,如图三十六所示,其中 a 结构也被称为板凳结构 FBAR,该结构后来被 d 结构取代,也就是大名鼎鼎的浴盆结构 FBAR,走该结构路线的公司主要是 AVAGO(现博通);b 结构就是 air gap FBAR 后来又被称为蒙古包结构,走该技术路线的公司主要是太阳诱电;c 结构就是 BAW SMR,走该技术路线的公司主要有 Qorvo 和 Epcos(现高通),总之为了实现上下电极间的能量束缚,人们在半导体加工工艺方面想尽了办法,这也是为何 BAW 的工艺比 SAW 要复杂得多。
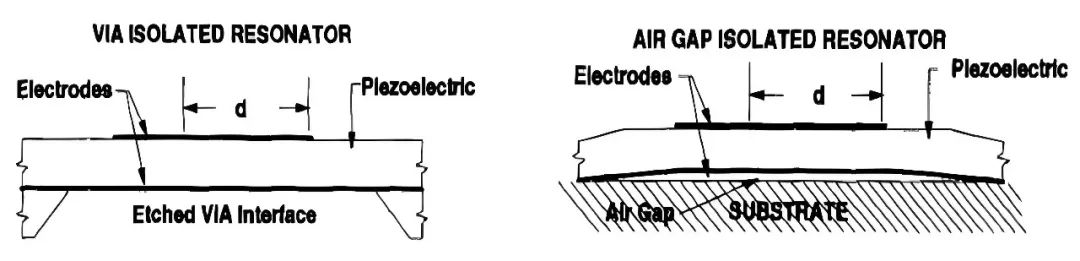
图三十六、a) “板凳” 结构 FBAR b)“蒙古包” 结构 FBAR
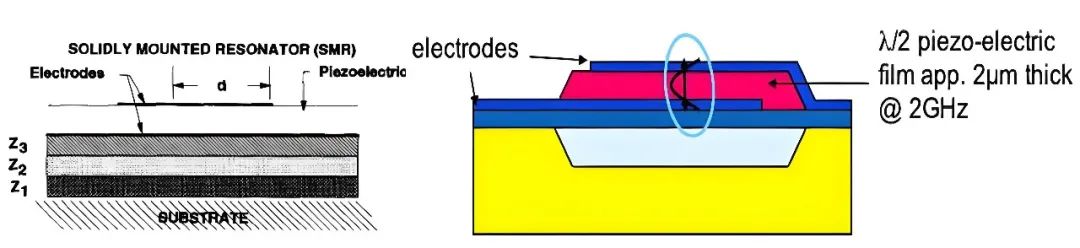
图三十六、c) BAW SMR d) “浴盆” 结构 FBAR
到此 BAW 滤波器的主要结构都已明确,但这不代表用这些结构就能做出性能优异的滤波器了,除核心结构外,BAW 谐振器还有以下几个难点,杂波抑制、电极材料、频率调节、压电材料调节等问题。
首先看杂波抑制,BAW 谐振器在振动的上下边界进行能量束缚同时还要考虑尽可能消除能量沿压电薄膜的横向泄露,这方面主要有三个方面的优化,如图三十七 a 所示的对压电薄膜进行截断,图三十七 b 和 c 所示的方式在 A.link 等 2005 年发表的论文《Suppression of Spurious Modes in Mirror-Type Thin Film BAW Resonators Using an Appropriate Shape of the Active Area》中有详细的对比,最后结论是 b 质量加载的方式结合 c 中(e)形状电极的谐振器对杂波的抑制最好,从而使谐振器 Q 值也最高,围绕这几个方向也是 BAW 专利布局的必争之地,AVAGO 布局最早相对优势最大。
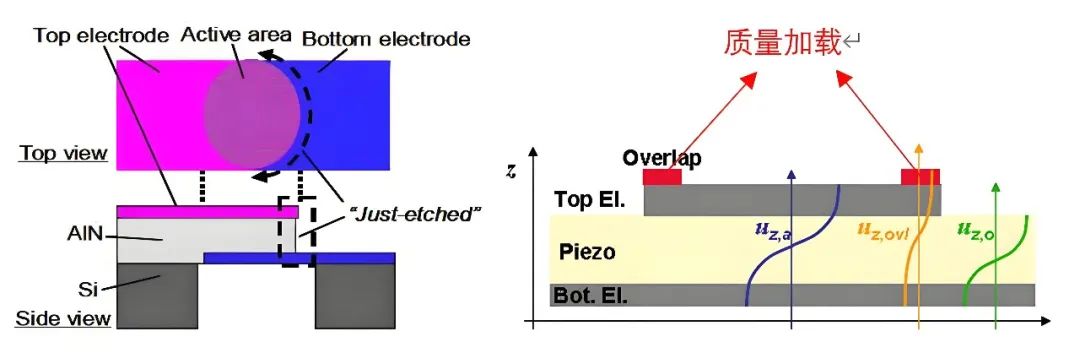
图三十七、a) 压电薄膜截断 b)电极边缘质量加载
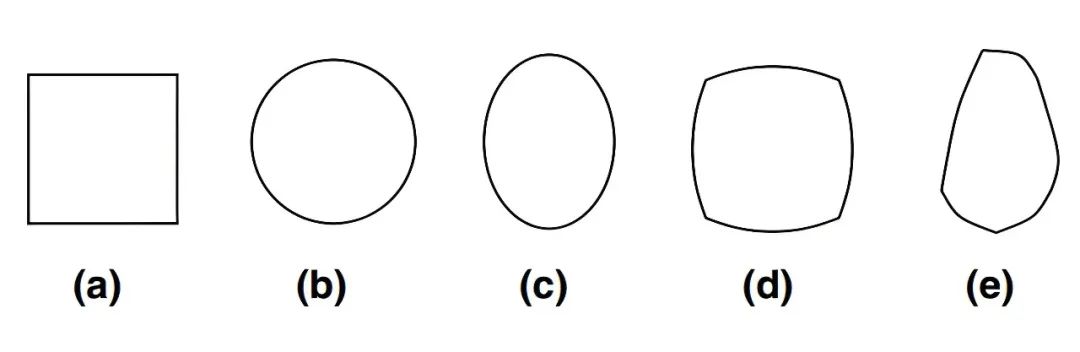
图三十七、c) 电极形状优化
其次是电极材料,对于一个理想的 BAW 电极要具备以下几个特征,低电阻率、低弹性损耗和高声阻抗,一些公司采用的是叠层材料电极比如钨和铝的叠层,前者具备低弹性损耗和高声阻抗,后者由较低电阻率,AVAGO 采用的是钼电极,太阳诱电采用的是稀有元素钌电极。
接下来是频率调节,假如一个 BAW 滤波器有 10 个谐振器,由于工艺原因人们在沉积压电薄膜时只能有一个厚度,那么意味着起初这是个谐振器都是一个谐振频率,熟悉声学滤波器设计的朋友知道,如果所有谐振器频率一样,是无法构成一个滤波器的,那么必然要对每个谐振器进行细微差异化调整,这个工作就是频率调节。
1998 年 Hasnain Lukdawala 在他论文《SIMPLE POST-PROCESSING TECHNIQUE TO TUNE RESONANT FREQUENCY OF FILM BULK ACOUSTIC RESONATORS AND STACKED CRYSTAL FILTERS》中提到一种频率调整方式就是在电极材料上先沉积一层质量加载层(论文中为氮化硅)使整个谐振器频率低偏,然后再用反应离子蚀刻(RIE)的方法 “打磨” 掉部分氮化硅从而使频率升高(图三十八),通过控制氮化硅 “打磨” 量就可以精准控制频率的微调。无论是沉积相同膜厚最后进行 “打磨” 微调还是利用光罩沉积不同膜厚,都需要面临复杂的频率调整工序,以一个滤波器为例,通常需要 4~5 种不同的频率调整工序,如果是双工器不同谐振频率会更多,需要用到的频率调整工序也会响应大幅增加,这就是为何 BAW 滤波器 / 双工器的光刻次数要远多于 SAW 的原因。
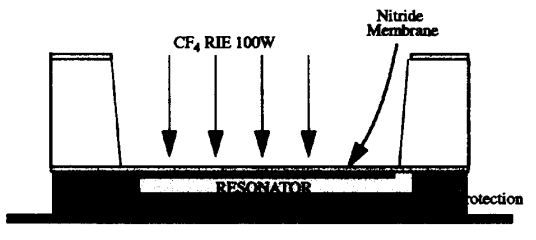
图三十八、RIE 修频示意图
最后一点就是压电薄膜材料,起初压电薄膜材料是 ZnO,后续很快被 AlN 取代,因为后者的温漂系数、损耗因子和声速都优于前者,同时还有一个更重要的原因就是 AlN 工艺很容易与 CMOS 工艺兼容,因此目前 AlN 是 BAW 滤波器用得最广泛的材料,随着 5G 高频段的到来,需要滤波器频率更高、带宽更大,单晶 AlN 薄膜拥有更优的损耗因子和导热系数因而更适合高频应用,AlN 参杂镁、锆、钪等元素可以进一步拓宽带宽,但代价是 Q 值会恶化。
相比于 SAW,BAW 技术因为工艺复杂度原因投入到实际应用中较晚,1999 年安捷伦公司(后来的 AVAGO)R.Ruby 制作了一款各方面性能都非常不错的 FBAR PCS 频段双工器(图三十九)并成功应用于三洋手机(图四十),从 1993 年开始研究到 2001 年成功应用于手机,Ruby 及其团队对 FBAR 产业化做出了卓越贡献。在 2016 年村田 IHP SAW(现 TFSAW)问世以前 FBAR 一直代表着声学场滤波器的最高性能水平,当前在 Sub 3GHz 以下 TFSAW 各方面性能均可比拟 FBAR 滤波器了,考虑到成本因素,未来 FBAR 技术更大的舒适空间将会在 3~7GHz。
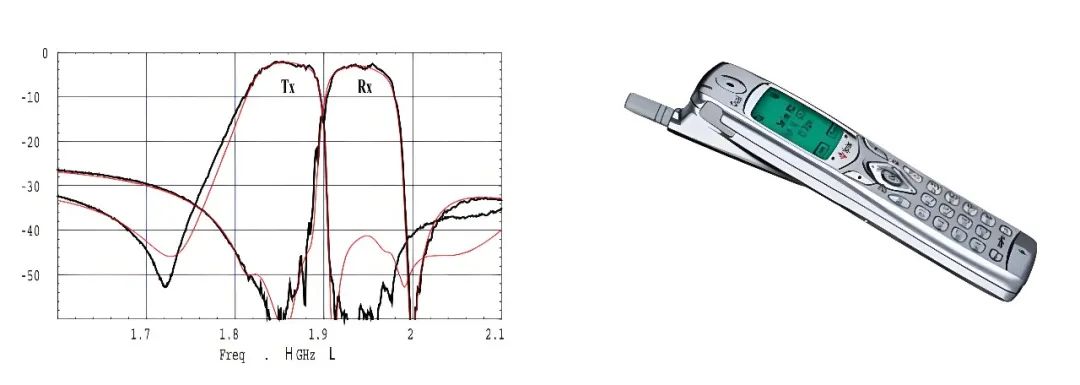
图三十九、Avago FBAR PCS 双工器响应曲线
图四十、第一款采用 FBAR 双工器的手机
● 总结
滤波器第一波技术高潮源于有线电话的兴起,这个期间诞生了滤波器电路理论和数学理论,同时石英晶体滤波器作为一种特殊的实现方式开启了声学场滤波器的一波发展;第二波技术高潮是二战后雷达和高频应用的出现催生了各种形式电磁场滤波器的蓬勃发展;第三波技术高潮是卫星通信的兴起催生了耦合矩阵理论以及高性能波导滤波器,同时电视机的普及让 SAW 逐步取代石英滤波器,声学场滤波器频率从几十 KHz 级别进步到几百 MHz 级别;第四波技术高潮是移动通信的兴起,电磁场腔体滤波器和介质滤波器在基站侧取得了巨大的成功,声学场方面各种 SAW 和 BAW 滤波器在手机侧百花齐放。
为什么我们要花这么多精力去梳理这些古老的历史,我们觉得有以下三个方面的原因,首先梳理出来我们今天习以为常的技术的来源和演进过程,搞清楚了过去更能帮助看清未来;其次是讲讲面对新的需求时我们领域前辈们技术创新思路是如何开展的,这些思路也许对今天仍然有启发;最后本文第一次尝试将所有滤波器技术当作一个整体来看,如今滤波器的 “形” 太多种多样了,但滤波器的 “神” 永远是那条数学曲线,如何使其 “形神兼备” 就是工程师的工作。
当下无线通信依然在蓬勃发展,滤波器在整个射频技术中仍然是创新比较活跃的领域,未来滤波器的创新的核心字眼一定是 “融合” 二字,首先滤波器要贴近系统和放大器、天线、开关等领域进行融合;其次滤波器自身各个细分方向也需要融合,电磁场滤波器可以和声学场滤波器进行融合,声学场滤波器可以更好的和滤波器数学及电路理论融合;最后是滤波器电磁场 / 声学场和材料、工艺的融合并驱动数学和电路的进步。图四十一是整个滤波器技术的一个梳理,树冠层面是各种实现形式的滤波器,其中蓝色部分是国内技术做得比较好的方向,黄色部分是国内还有一定差距的方向,红色是国内技术还有较大差距的方向,其中红色和黄色都是和半导体工艺强相关的领域;树干层面是更基础的电路理论以及设计方法论;树根层面是最基础的物理和数学理论。当前国内的创新主要还集中在树冠层面,相信未来我们也会有更多树干、树根层面的创新,因为需求和市场在我们一方。
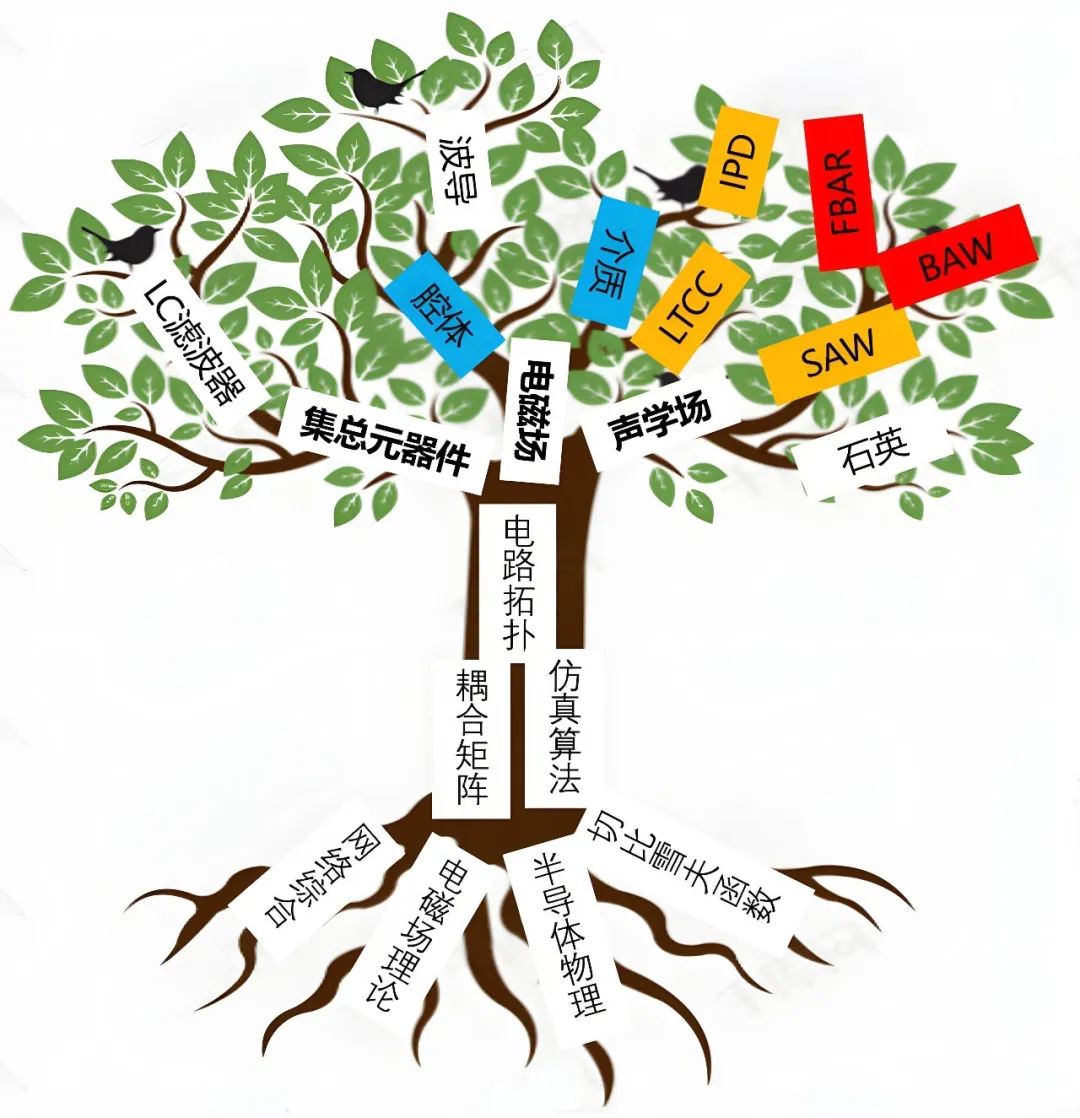
图四十一、滤波器技术树
滤波器技术发展简表:
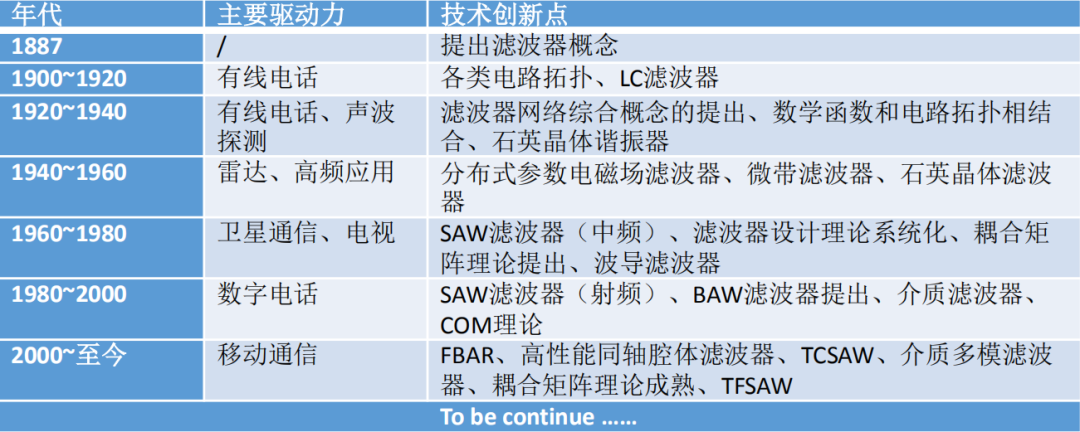
● 参考文献
-
Campbell, George Ashley, “Physical Theory of the Electric Wave-Filter”. The Bell System Technical Journal. I (1922.11).
-
Zobel, O J, “Theory and Design of Uniform and Composite Electric Wave Filters”,The Bell System Technical Journal, Vol. 2 (1923), pp. 1–46.
-
Foster, R M, “A reactance theorem”, Bell System Technical Journal, Vol. 3, pp259–267, 1924.
-
E. Cauer, W. Mathis, and R. Pauli, “Life and Work of Wilhelm Cauer (1900 – 1945)”, Proceedings of the Fourteenth International Symposium of Mathematical Theory of Networks and Systems (MTNS2000), Perpignan, June 2000.
-
S. Darlington, “A history of network synthesis and filter theory for circuits composed of resistors, inductors, and capacitors”, IEEE Transactions on Circuits and Systems, Vol.31,1984
-
Montgomery. C. G., Dicke. R. H., Purcell. E. M., “PRINCIPLES OF MICROWAVE CIRCUITS”, NEW YORK:McGRAW- HILL BOOK COMPANY, INC
-
H. A. Bethe, “Theory of Diffraction by Small Holes”, Phys. Rev. 66, 163, 1944
-
Paul I. Richards, “Resistor-transmission-line circuits”, Proceedings of the IRE, vol. 36, iss. 2, pp. 217–220, 1948.
-
G. L. Ragan,R. M. Fano and A. W. Lawson,“The Theory of Microwave Filters” and “The Design of Microwave Filters”, chapters 9 and 10 of Microwave Transmission Circuits, vol. 9 in the Radiation Laboratory Series 1948.
-
Levy, Ralph; Cohn, Seymour B., “A history of microwave filter research, design, and development”, IEEE Transactions on Microwave Theory and Techniques, vol. 32, iss. 9, pp. 1055–1067, September 1984.
-
S. B. Cohn, “Direct-coupled-resonator filters; Proc. IRE, vol. 45,pp. 187-96, Feb. 1957.
-
G. L. Matthaei, L. Young, and E. M. T, Jones, Microwave Filters, Impedance-Matching Networks and Coupling Structures. New York:McGraw-Hill,ch.5.
-
Wei‐gan Lin, “Microwave Filters Employing a Single Cavity Excited in More than One Mode”, J. Appl. Phys. 22, 989–1001, 1951
-
A. E. Atia and A. E. Williams, “Narrow-bandpass waveguide filters,”IEEE Trans. Microwave Theory Tech., vol. MTT-20, pp. 258–265, Apr.1972.
-
R. J. Cameron, “General coupling matrix synthesis methods for Chebyshev filtering functions,” IEEE Trans. Microwave Theory Tech., vol. 47,pp. 433–442, Apr. 1999.
-
R. J. Cameron, “Advanced coupling matrix synthesis techniques for microwave filters”, IEEE Trans. Microw. Theory Techn., vol. 51, no. 1, pp. 1-10, Jan. 2003.
-
S. Tamiazzo and G. Macchiarella, “An analytical technique for the synthesis of cascaded N-tuplets cross-coupled resonators microwave filters using matrix rotations”, IEEE Trans. Microw. Theory Techn., vol. 53, no. 5, pp. 1693-1698, May 2005.
-
W.G.Cady"Thepiezoelectricresonator," Physical Review A, vol. 17, pages 531-533,1921
-
K.S. Van Dyke, “The Piezo-Electric Resonator and Its Equivalent Network”, Proceedings of the Institute of Radio Engineers,Vol: 16, Issue: 6,pp:742~762, June 1928
-
Mason,WarrenP.,“Thepropagationcharacteristics of sound tubes and acoustic filters”, Physical Review, vol. 31, no. 2, pp. 283–295, February 1928.
-
R.M.White and F. W. Voltmer, “Direct piezoelectric coupling to surface elastic waves,” Appl. Phys. Lett., vol. 7, no. 12, pp. 314–316,Dec. 1965.
-
B.P. Abbott;C.S. Hartmann;D.C. Malocha,”A coupling-of-modes analysis of chirped transducers containing reflective electrode geometries”Proceedings., IEEE Ultrasonics Symposium,1989.
-
C.C.W.Ruppel, “Acoustic wave filter technology—A review”, IEEE Trans. Ultrason. Ferroelectr. Freq. Control, vol. 64, no. 9, pp. 1390-1400, Sep. 2017.
-
W.E.Newell,“Tuned integrated circuits—A state-of-the-art survey,” Proc. IEEE, vol. 52, no. 12, pp. 1603–1608, Dec. 1964.
-
K.M. Lakin and J. S. Wang, “UHF composite bulk wave resonators,” in Proc. IEEE Ultrason. Symp., Nov. 1980, pp. 834–837.
-
K. M. Lakin, G. R. Kline, and K. T. McCarron, “Development of miniature filters for wireless applications,” in IEEE MTT-S Int. Microw.Symp. Dig., May 1995, pp. 883–886.
-
R. Ruby, P. Bradley, J. D. Larson, III, and Y. Oshmyansky, “PCS 1900 MHz duplexer using thin film bulk acoustic resonators (FBARs),”Electron. Lett., vol. 35, no. 10, pp. 794–795, May 1999.
-
A. Link et al., “Suppression of spurious modes in mirror-type thin film BAW resonators using an appropriate shape of the active area,” in Proc.IEEE Ultrason. Symp., Sep. 2005, pp. 1179–1182.
-
T. Takai et al., “Investigations on design technologies for SAW quadplexer with narrow duplex gap,” in IEEE MTT-S Int. Microw. Symp.Dig., May 2016, pp. 1–4.
-
H. Lakdawala and E. S. Kim, “Simple post-processing technique to tune resonant frequency of film bulk acoustic resonators and stacked crystal filters,” in Proc. IEEE Freq. Control Symp., May 1998,pp. 831–835.
via:
-
滤波器往事 —— 数学、电路和场(上)原创 但以理 瑞宏之声 2025 年 01 月 23 日 13:02 浙江
https://mp.weixin.qq.com/s/FvzEdVf3_4zMY_KZ30sctg -
滤波器往事 —— 数学、电路和场(中)原创 但以理 瑞宏之声 2025 年 02 月 06 日 13:25 浙江
https://mp.weixin.qq.com/s/-2UFQ1Y4qYOxcBYpQoOoHw -
滤波器往事 —— 数学、电路和场(下)原创 但以理 瑞宏之声 2025 年 02 月 13 日 14:26 浙江
https://mp.weixin.qq.com/s/4P42f-47STKGOW6lN-b_aQ





















 5407
5407










