傅里叶变换 | 原理 / 性质

注：本文为 “傅里叶变换 | 原理 / 性质” 相关合集。
略作重排，未整理去重。
图片清晰度限于引文原状.
如有内容异常，请看原文。

---

傅里叶变换原理

作者 Heinrich

引言

本文的主旨在于，在不借助任何数学公式的前提下，帮助读者对傅里叶分析形成直观理解。

傅里叶分析不仅是一种数学工具，更是一种能彻底转变个人既有世界观的思维模式。然而，傅里叶分析的公式形式较为复杂，导致许多大一新生初次接触时便陷入困惑，进而对其产生抵触情绪。

事实上，傅里叶分析本是内容有趣的知识，但在大学课程中却成为让学生望而却步的“杀手课程”，这很大程度上源于教材编写者在内容呈现上过于严肃。正因如此，笔者一直致力于撰写一篇能通俗阐释傅里叶分析的趣味性文章，力求让高中生也能理解。无论读者从事何种职业，本文都保证其能够读懂，并体验到通过傅里叶分析认知世界全新维度时的愉悦感。对于已有一定基础的读者，建议阅读时不要仅浏览未知内容，对已掌握的部分也应仔细研读，如此方能获得新的感悟。

需要说明的是，学习本身并非易事，笔者撰写本文的目的，是为读者营造更轻松、更有趣的学习体验。但请务必避免将本文收藏或保存地址后，计划“日后有时间再读”——这类情况屡见不鲜，最终往往导致文章被长期搁置。建议读者静下心来耐心阅读，相比传统课本，本文的阅读过程会更为轻松愉悦。

另外，本文统一以“正弦波”（Sine Wave）指代简谐波，无论是 cos 函数还是 sin 函数对应的波形，均在此范畴内。

一、什么是频域

从个体诞生开始，人们感知的世界便以时间为主轴，呈现动态演进的特征。例如股票价格的波动轨迹、人类身高的增长变化、汽车行驶的路径等，都随时间推移而改变。这种以时间维度为参照体系，观察动态世界现象的研究方式，在学术领域被定义为时域分析。通常情况下，人们会习惯性地认为，世间万事万物都持续处于随时间变化的动态过程中，不存在绝对静止的状态。

但如果提出一种截然不同的观察视角——通过该视角会发现世界实则有永恒不变的一面，这一观点或许会令人诧异。但这并非臆想，这个“静止”的世界在学术范畴内被称作频域。

我们先举一个公式上并非严谨恰当，但意义上极为贴切的例子，帮助理解频域：

在你的认知中，一段音乐是什么样的？

上图呈现的，是我们对音乐最普遍的理解——一段随时间变化的震动波形（时域视角）。但对于熟悉乐器的人来说，音乐更直观的理解或许是这样的：

看到这里，其实频域的概念已基本清晰：上图是音乐在时域的呈现，下图则是音乐在频域的呈现。由此可见，频域这一概念对大家而言并不陌生，只是此前未曾明确意识到它的存在。

现在我们可以回过头，重新理解一开始那句看似“痴人说梦”的话：世界是永恒的。

将上述两图进一步简化，对比会更明显：

• 时域视角：

  
  在时域中，我们看到钢琴的琴弦随时间上下摆动，轨迹如同股票走势般动态变化；

• 频域视角：
  在频域中，不存在“变化”，只有一个个永恒固定的音符 ♪ 。

所以，你眼中看似落叶纷飞、变化无常的世界，本质上或许只是“上帝怀中一份早已谱好的乐章”——这并非鸡汤文，而是有严谨数学依据的结论：傅里叶分析告诉我们，任何周期函数，都可以看作是不同振幅、不同相位的正弦波叠加而成。结合前文的音乐例子，这一结论可理解为：通过对钢琴不同琴键、以不同力度、在不同时间点的敲击，能组合出任何一首乐曲（即“不同正弦波叠加出复杂周期信号”）。

而贯穿时域与频域的方法之一，便是我们常说的傅里叶分析。傅里叶分析主要分为傅里叶级数（Fourier Series）和傅里叶变换（Fourier Transformation）两类，接下来我们将从更简单的傅里叶级数开始谈起。

二、傅里叶级数（Fourier Series）的频谱

通过具体案例结合图像，能更直观地理解傅里叶级数的频谱概念。若说“用正弦波叠加出带 90 度角的矩形波”，多数人可能会像最初的我一样表示怀疑，但看完下图后，这一结论会变得清晰：

• 第一幅图：单一正弦波 $\cos (x)$（可形象理解为“郁闷的正弦波”）；
• 第二幅图：两个正弦波叠加，表达式为 $\cos (x)+a\cdot \cos (3x)$（可形象理解为“2 个卖萌的正弦波”）；
• 第三幅图：四个正弦波叠加；
• 第四幅图：十个正弦波叠加。

随着叠加的正弦波数量逐渐增加，最终波形会越来越接近标准矩形波。这背后的原理是：所有正弦波的上升部分会让原本缓慢递增的曲线逐渐变陡，而下降部分则会抵消曲线上升到最高点后的继续增长趋势，使其保持水平，最终形成矩形。但需注意，要叠加出“标准 90 度角的矩形波”，需要无穷多个正弦波——这也体现了傅里叶级数的无限性特征。

事实上，不仅是矩形波，任何可想象的波形都能通过正弦波叠加得到。这是未接触过傅里叶分析的人在直觉上的第一个难点，但接受这一设定后，后续的频域分析会变得更易理解。

从“频率分量”视角看正弦波叠加

仍以“正弦波累加成矩形波”为例，换个角度观察这一过程：

图中最前方的黑色曲线，是所有正弦波叠加后的总和（即逐渐接近矩形波的波形）；后方按不同颜色排列的曲线，是构成矩形波的各个正弦波“分量”。这些分量按频率从低到高、从前到后排列，且每个分量的振幅各不相同。

细心观察会发现，每两个正弦波分量之间还有一条直线——这并非分割线，而是“振幅为 0 的正弦波”，意味着组成特定波形（如矩形波）时，部分频率的正弦波是无需参与叠加的。这里的“不同频率的正弦波”，我们称之为频率分量。

频域的基本组成单元

要理解频谱，需先明确频域的“基本单元”，这类似时域中“1 秒”作为时间基本单位的逻辑：

1. 频域的“1”（基础频率分量）
   若将第一个频率最低的分量视为频域的“1”，则频域的基本单元便由此确立。具体而言，若以角频率为 ${\omega }_0$ 的正弦波 $\cos ({\omega }_{0}t)$ 作为基础波形，那么频域的基本单元就是 ${\omega }_0$。

2. 频域的“0”（直流分量）
   有“1”必有“0”，频域的“0”对应的是 $cos(0t)$——这是一个周期无限长的正弦波，在图像上表现为一条水平直线，因此在频域中，“0 频率”也被称为直流分量。在傅里叶级数的叠加中，直流分量仅影响整个波形相对于数轴的上下平移，不会改变波形本身的形状。

3. 频域基本单元的几何意义
   回顾初中知识：正弦波是“圆周运动在一条直线上的投影”。基于这一原理，频域的基本单元（特定频率的正弦波），也可理解为“一个始终在旋转的圆”，其在直线上的投影即为对应的正弦波。

   相关动态演示如下：
   
   

矩形波在频域中的形态（频谱）

明确频域基本单元后，我们来观察矩形波在频域中的“模样”——这便是我们常说的频谱：

首先看矩形波在频域中的原始呈现：

这一图像较为抽象，教科书常在此处留白，易让读者困惑。实际上，频域图像（频谱）的直观形式如下：

更清晰的频谱图：

从频谱图中可明显发现：偶数项频率分量的振幅均为 0，这与前文提到的“振幅为 0 的正弦波”完全对应。

频谱的动态演示：

需说明的是，我在学习傅里叶变换时，维基百科尚未收录此类动态频谱图，当时便已构思过类似的表达方法；后续内容中，还会补充维基未涉及的另一重要概念——相位谱。

傅里叶级数的深层启示：“世界是静止的”

回顾前文提到的“世界是静止的”，这一说法看似抽象，结合傅里叶级数可得到更具象的理解：

我们眼中“混乱的表象”（如时间轴上不规则的曲线），本质是无穷多个规则正弦波在时域上的叠加；而正弦波又是“旋转的圆在直线上的投影”。若用一个比喻来概括：

我们所见的世界，如同皮影戏的幕布——幕布前的“小人”（对应时域中的不规则现象）看似运动无规律，难以预测下一步轨迹；但幕布后，有无数个“齿轮”（对应频域中的正弦波/旋转圆）始终按固定规律旋转，永不停歇。这种“表象混乱、本质规律”的特征，正是傅里叶级数带给我们的深刻启示。

三、傅里叶级数（Fourier Series）的相位谱

上一章的关键词是“从侧面看”，本章的关键词则是“从下面看”。

在正式展开前，先解答一个常见问题：傅里叶分析究竟有什么用途？这部分内容相对枯燥，已了解的读者可直接跳至下一条分割线。

傅里叶分析的用途

首先介绍一个最直接的用途。无论是听广播还是看电视，“频道”都是大家熟悉的概念——“频道”本质是“频率的通道”，不同频道会将不同频率作为传输载体，实现信息传递。大家可以尝试以下操作，直观感受时域与频域的差异：

1. 先在纸上画一个 $\sin (x)$ 的曲线，无需精准，只需体现大致形态，这一过程并不困难；
2. 接着尝试绘制 $\sin (3x)+\sin (5x)$ 的图形，此时不仅难以保证精准，甚至可能无法判断曲线的升降趋势；
3. 即便给出 $\sin (3x)+\sin (5x)$ 的曲线，但不告知其表达式，要从中单独分离出 $\sin (5x)$ 的部分，在时域中基本无法实现。

但在频域中，这类问题会变得非常简单——信号的频率成分仅以几条竖线的形式呈现，分离特定频率成分的操作一目了然。

由此可见，许多在时域中难以完成的数学操作，在频域中却能轻松实现，这正是傅里叶变换的价值之一。尤其在工程领域，从信号中去除特定频率成分的“滤波”操作，是信号处理的概念，而这一过程只有在频域中才能高效完成。

再介绍一个更重要但稍复杂的用途——求解微分方程。微分方程在各行业应用广泛，但其求解过程十分繁琐，除基础的加减乘除运算外，还需处理微分与积分。而傅里叶变换可将时域中的微分、积分运算，转化为频域中的乘法、除法运算，大幅降低求解难度。

傅里叶分析的其他重要用途，将在后续内容中逐步补充。

相位谱的概念

通过时域到频域的变换，我们得到的“频谱”（本质是振幅谱）仅反映了各正弦波的振幅信息，并未包含时域信号的全部特征。基础正弦波的表达式为 $A\cdot \sin (\omega t+\theta )$，其中振幅 $A$、角频率 $\omega$、相位 $\theta$ 缺一不可——相位 $\theta$ 决定了波在时域中的位置，因此频域分析仅靠振幅谱远远不够，还需引入“相位谱”。

那么相位谱具体如何体现？为避免图像杂乱，我们以 7 个正弦波叠加的信号为例进行说明：

1. 相位的标记与投影
   由于正弦波具有周期性，需通过特定标记确定其在时域中的位置。下图中，红色圆点代表各正弦波距离频率轴最近的波峰；为清晰展示波峰位置，将红色圆点向下方平面投影，得到的粉色圆点即为波峰位置的投影标记（需注意：投影点仅反映波峰与频率轴的距离，并非直接对应相位）。
   
   

2. 时间差与相位差的换算
   需明确一个关键概念：时间差不等于相位差。若将正弦波的一个完整周期视为 $2\pi$（或 360 度），则相位差是“时间差在一个周期中所占的比例”。具体换算公式为：
   相位差 = （时间差 / 周期）× $2\pi$

3. 相位谱的生成与特征
   在完整的立体频域图中，将投影得到的“时间差”依次除以对应频率的“周期”，再通过上述公式换算，即可得到下方的“相位谱”。这也印证了本章关键词——“频谱（振幅谱）从侧面看，相位谱从下面看”。

   观察相位谱可发现，其相位值仅为 0 或 $\pi$。这是因为 $\cos (t+\pi )=-\cos (t)$，相位为 $\pi$ 的波本质是原波“上下翻转”后的形态；对于周期方波的傅里叶级数而言，这种相位谱已属于简单类型。

   此外，由于 $\cos (t+2\pi )=\cos (t)$，相位差具有周期性——$\pi$、$3\pi$、$5\pi$ 等均为相同相位。为避免歧义，通常定义相位谱的值域为 $(-\pi ,\pi ]$，因此图中所有非 0 相位差均统一表示为 $\pi$。

时域与频域的对应

最后，通过一张集合图，完整呈现时域信号、振幅谱与相位谱的对应关系：

四、傅里叶变换（$FourierTransformation$）

通过前文对频域及傅里叶级数的介绍，大家已建立基础认知。此前提及的“钢琴琴谱”示例，虽能直观传递概念，但在数学表达上存在偏差，其关键问题在于傅里叶级数与实际非周期信号的适配性差异——傅里叶级数的本质是将周期信号分解为无限个离散的正弦波，而现实世界中多数信号（如自然现象、时间序列等）并非周期性存在。

在数字信号处理领域，时域与频域的信号特征存在鲜明对应关系，可概括为：

• 往昔发生的事件（如连续的时间过程），对应时域中连续非周期信号；
• 人们对事件的回忆（如片段化的记忆提取），则类似频域中周期离散信号。

需要明确的是，目前不存在能直接将“连续非周期信号”转化为“周期离散信号”的数学工具。不同信号分析工具的时域 - 频域对应关系需精准区分：

• 傅里叶级数：处理时域周期连续信号，输出频域非周期离散信号（可回顾第一章示意图辅助理解）；
• 傅里叶变换：重要功能是将时域非周期连续信号，转换为频域非周期连续信号。

二者的信号特征对应关系可通过下图直观区分：

从另一个角度理解，傅里叶变换可视为对“周期无限大的信号”进行的傅里叶分析——当信号周期趋近于无穷时，原傅里叶级数中的离散频率会逐渐密集，最终形成连续的频率分布。

此前“钢琴琴谱”的比喻虽形象，但需注意：琴谱对应的是时间上离散的频率点，并非傅里叶变换所描述的连续频谱，只是在传递“信号可分解为频率成分”的概念上具有参考价值。

离散谱与连续谱的对比

傅里叶变换与傅里叶级数的差异之一，在于频域输出从“离散谱”变为“连续谱”。为清晰区分二者，可通过图像对比理解：

1. 离散谱（傅里叶级数）：
   以傅里叶级数常用的频谱图为例，从高频方向观察，其频率成分呈离散分布，各频率点间存在明显间隔，图像如下：
   

2. 连续谱（傅里叶变换）：
   想象离散谱中各频率点逐渐靠近、间隔不断缩小，直至完全衔接形成连续分布，最终呈现如“波涛起伏的大海”般的连续形态，图像如下：
   

（注：为更清晰展示连续谱的波动特征，上图选用了优化视觉效果的参数，非严格计算参数。）

从数学运算层面看，离散谱的信号合成采用“求和符号”（对离散频率成分叠加），而连续谱的信号合成则需采用“积分符号”（对连续频率区间累积），这是二者在计算逻辑上的区别。

要进一步理解傅里叶变换的深层价值，需引入一个关键数学工具——欧拉公式，其将为后续更复杂的信号分析提供基础。

五、宇宙耍帅第一公式：欧拉公式

虚数单位 $i$ 是高中数学的基础概念，其定义为“$-1$ 的平方根”（即 $i^2=-1$），但多数人对其物理意义的理解较为浅显。通过以下分析可揭示其作用：

首先观察数轴上的线段变换：

• 长度为 1 的红色线段，乘以 3 后长度变为 3（蓝色线段），仅发生“缩放”；
• 乘以 $-1$ 后，线段绕原点旋转 180 度（绿色线段），发生“旋转”。

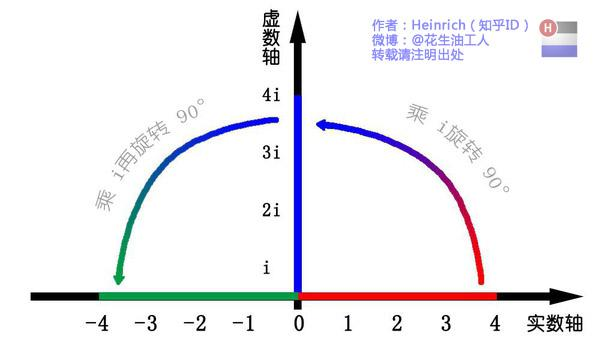
由于“乘 $-1$”等价于“连续乘两次 $i$”（$i\cdot i=-1$），可推导出：乘一次 $i$ 对应线段绕原点旋转 90 度。

基于这一特性，可建立“虚数轴”（与实数轴垂直），实数轴与虚数轴共同构成“复平面”（复数的几何表示空间）。至此，虚数 $i$ 的物理意义明确——实现平面内的旋转操作。

欧拉公式的形式与意义

欧拉公式的表达式为：
$$e^{ix}=\cos x+i\sin x$$

该公式的数学价值远超傅里叶分析领域，被称为“宇宙耍帅第一公式”，原因在于其特殊形式——当 $x=\pi$ 时，公式可简化为：
$$e^{i\pi }+1=0$$

此式巧妙融合了数学领域的五大常数：自然底数 $e$、圆周率 $\pi$、虚数单位 $i$、自然数 1 与 0，形式简洁且内涵深刻，常被用于展现数学的内在美感。

欧拉公式的几何意义

从图像角度解读，欧拉公式描述的是复平面内的圆周运动：

• 随着参数 $x$（可理解为时间或角度）的变化，复指数 $e^{ix}$ 对应的点在复平面上以原点为圆心、半径为 1 做圆周运动；
• 若将该圆周运动沿时间轴展开，轨迹会形成一条螺旋线；
• 螺旋线在“实数轴”上的投影，即为基础余弦函数 $\cos x$；
• 螺旋线在“虚数轴”上的投影，即为基础正弦函数 $\sin x$。

其几何形态可通过下图直观观察：

欧拉公式的关键价值在于，将原本独立的正弦波、余弦波统一为简洁的复指数形式，为傅里叶变换中“用复指数表示正弦信号”提供了理论支撑，也为后续复杂信号（如电磁波）的分析奠定了基础。关于复数的更深层次理解，可参考相关专业资料进一步拓展。

复数的物理意义

复数最直观的物理意义在于其可表示旋转。以具体运算为例：

• 算式 $4\cdot i\cdot i=-4$ 对应的几何意义，是实数“4”在数轴上完成 180 度旋转，最终指向“-4”；
• 而 $4\cdot i$ 则表示“4”在数轴上旋转90度，其结果对应复平面中虚轴上的 $4i$。

指数形式下的复数特征

首先观察实数指数函数 $e^t$ 的图像，其呈现为单调递增的曲线，如下所示：

当在指数部分引入虚数单位 $i$，即形成复指数函数 $e^{it}$ 时，函数图像会转变为螺旋线，形态与电磁场的分布特征高度相似，具体图像如下：

复数对二维信息的保留作用

复数的另一重要物理意义，在于其运算过程中能完整保留二维信息，这与实数运算存在显著差异：

• 以实数加法 $3+5=8$ 为例，运算结果“8”无法反向追溯原始加数“3”和“5”——原始的二维维度信息（两个独立数值）被覆盖，存在无数种分解可能；
• 而复数运算 $3+5i$ 则不同，其结果始终可清晰拆解为实部“3”与虚部“5”，原始二维信息完全保留，如同复平面中对坐标的精准记录。

复数在电磁场描述中的应用

基于“旋转特性”与“二维信息保留”两大优势，复数成为描述电场与磁场的理想工具，具体体现在三方面：

1. 信息不损失：电场强度与磁场强度可分别对应复数的实部与虚部进行叠加运算，二者的独立信息不会因运算而丢失；
2. 满足垂直关系：电场与磁场在空间中呈90度垂直分布，这一特性与复数实轴、虚轴的垂直关系天然契合；
3. 便捷实现旋转：若需使电场或磁场在空间中旋转90度，仅需将对应复数乘以虚数单位 $i$ 即可完成，运算逻辑简洁直观。

相关物理模型示意图如下：

复数在正弦波（电磁波）变换中的应用

（受@physixfan 答案启发补充）在频域中，正弦波可视为构成其他波动的“基础元素”（类似自然数中的“1”），基于基础元素的倍数叠加可实现线性运算（如 $5=1\times 5$ 或 $5=2+3$）。但实数域无法通过线性运算完成正弦波的相位与振幅协同变换（如将 $2\sin (\omega t)$ 变为 $4\sin \left(\omega t+\frac{\pi }{6}\right)$），而复数可通过以下方式解决这一问题：

1. 正弦波的复数表示：依据欧拉公式，任意正弦波可表示为复指数形式在实轴上的投影。例如，两个不同相位、振幅的正弦波，可分别对应复指数 $A\cdot e^{i{\theta }_1}$ 与 $B\cdot e^{i{\theta }_2}$（其中 $A$、$B$ 为振幅，${\theta }_1$、${\theta }_2$ 为相位）；
2. 线性变换的实现：若需将 $A\cdot e^{i{\theta }_1}$（对应 $2\sin (\omega t)$）变换为 $B\cdot e^{i{\theta }_2}$（对应 $4\sin \left(\omega t+\frac{\pi }{6}\right)$），仅需两步操作：
   • 振幅调整：将复数乘以系数“2”，使振幅从“2”放大至“4”；
   • 相位调整：将相位 ${\theta }_1$ 增加 $\frac{\pi }{6}$（即30度），使其与 ${\theta }_2$ 一致；
3. 投影回实轴：将变换后的复指数重新投影至实轴，即可得到目标正弦波。

这一特性对电磁波分析极具价值——电磁波本质为正弦波，若需调整其时间延迟/提前、空间前移/后移，仅需通过复指数乘法改变相位，即可高效完成变换。

六、指数形式的傅里叶变换

借助欧拉公式可知：正弦波的叠加，亦可理解为螺旋线的叠加在实数空间的投影。若要以形象案例理解螺旋线的叠加，可参考以下内容：

光波

高中阶段已学习，自然光是由不同颜色的光叠加而成，其中最具代表性的实验为牛顿的三棱镜实验：

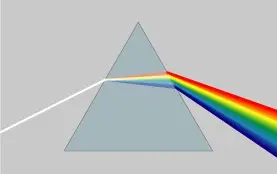
事实上，我们很早就接触过光的频谱，只是尚未深入了解频谱的重要意义。需要注意的是，傅里叶变换得到的频谱与可见光频谱存在差异——前者并非频率范围有限的叠加，而是涵盖从 0 到无穷大所有频率的组合。

对于正弦波，可通过以下两种方式理解：

1. 前文已提及的螺旋线在实轴上的投影；
2. 借助欧拉公式的形式理解，相关公式如下：

$e^{it}=\cos (t)+i\sin (t)$

$e^{-it}=\cos (t)-i\sin (t)$

将上述两式相加后除以 2，可得：

$\cos (t)=\frac{e^{it}+e^{-it}}{2}$

该式的物理意义可解读为：$e^{it}$ 可视为一条逆时针旋转的螺旋线，$e^{-it}$ 则为一条顺时针旋转的螺旋线；而 $\cos (t)$ 是这两条旋转方向相反的螺旋线叠加结果的一半，原因在于两条螺旋线的虚数部分会相互抵消。

以光波为例，类似极化方向不同的两束光波，其磁场部分抵消、电场部分加倍的现象。在此定义中，逆时针旋转的螺旋线对应正频率，顺时针旋转的螺旋线对应负频率（需注意此处并非复频率）。

前文已介绍连续的傅里叶变换频谱，接下来可进一步想象连续螺旋线的形态，具体如图所示：

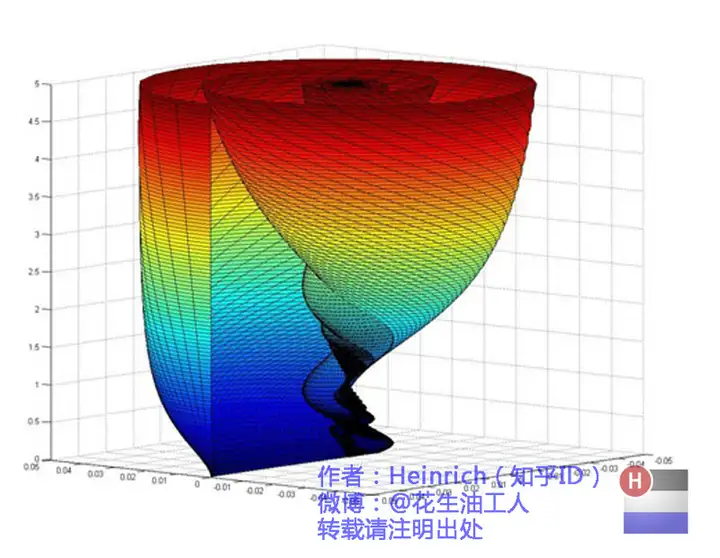
观察上图后，可思考该图形在时域中的形态，答案如下：

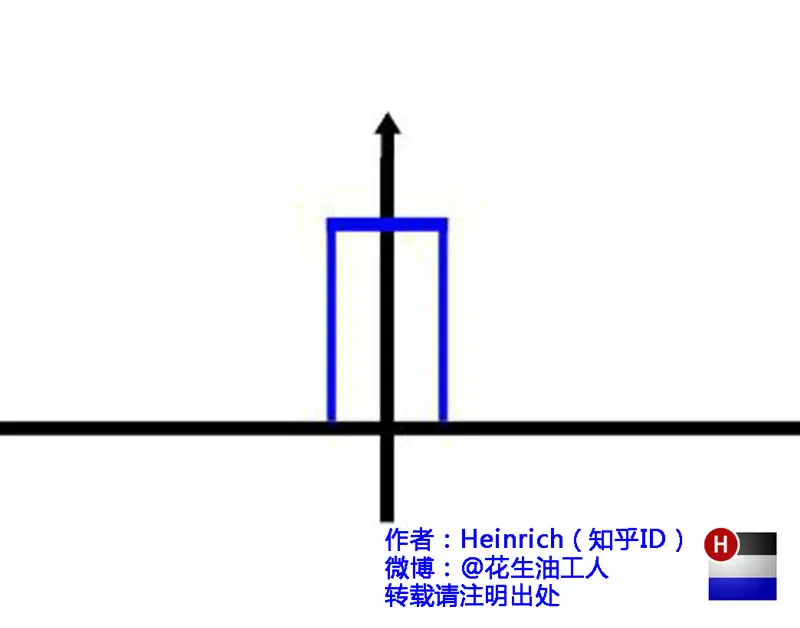
上述对比体现了数学的特殊性——常将简单问题通过抽象形式呈现。需要说明的是，为便于观察，上图中仅展示了正频率部分，负频率部分未予呈现。

仔细观察可发现，海螺图中的每一条螺旋线均清晰可见，且每条螺旋线具有不同的振幅（旋转半径）、频率（旋转周期）与相位；将所有螺旋线整合至同一平面，便形成了该海螺图。

至此，关于傅里叶变换与傅里叶级数的形象化理解已介绍完毕，最后通过下图进行总结：

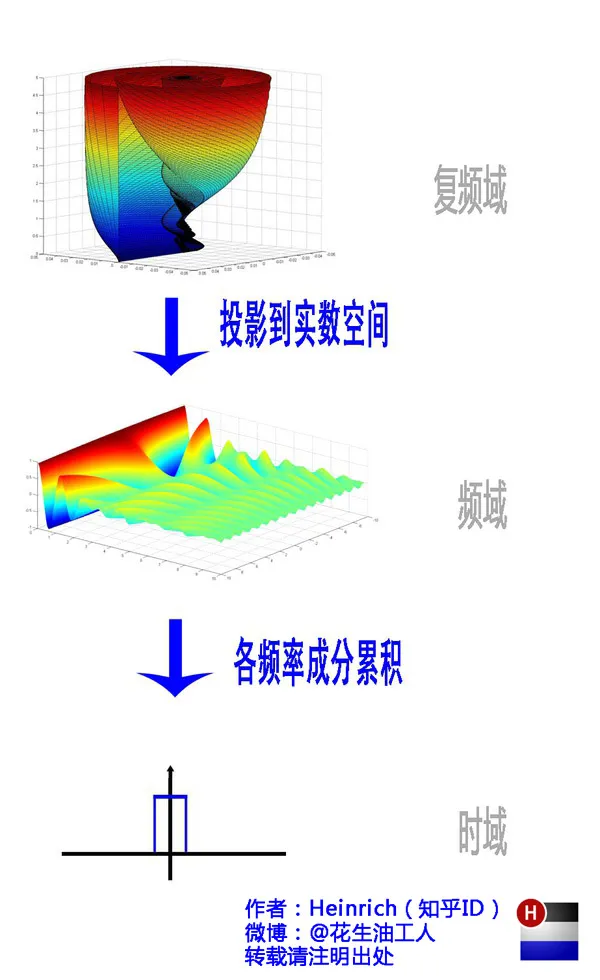
以上便是傅里叶相关内容的全部讲解。

信号与系统是多数工科专业的基础课程，尤其对通信专业而言至关重要。笔者对相关公式逐一分析，力求为每个公式提供直观理解。需明确的是，这种学习方法对数学研究者而言存在局限性——随着概念抽象程度提升与维度增加，图像或模型理解法将逐渐失效，但对于工科学生而言，此类理解已能满足基础需求。

客观而言，数学工具对工科生与理科生的意义存在本质差异：工科生只需理解原理、掌握应用方法及查询技巧即可。然而，当前多数高校将重要数学课程交由数学系教师授课，导致教学过程中出现偏差——数学教师侧重推导与证明，学生却始终困惑“学习该内容的实际用途”。

缺乏明确目标的教育是彻底的失败。学生在开始学习数学工具时，往往不清楚其作用与现实意义，而教材中仅呈现晦涩的概念（部分概念定语长达二十余字）与复杂公式，难以激发学习兴趣。

笔者有幸在学习过程中遇到大连海事大学的吴楠老师，其课程设计围绕两条线索展开：一条自上而下，先阐述课程意义与将面临的问题，让学生明确所学知识在现实中的应用场景；另一条自下而上，从基础内容逐步延伸，梳理知识体系，最终与前一条线索中的问题形成完美衔接。

本文仅介绍了傅里叶分析的一种新颖理解方式，而非系统的学习方法。在学习过程中，仍需扎实掌握公式与概念——学习并无捷径。但笔者希望通过本文，能让读者在漫长的学习道路上感受到更多乐趣。

作 者：韩 昊 知 乎：Heinrich 谨以此文献给大连海事大学的吴楠老师，柳晓鸣老师，王新年老师以及张晶泊老师。
谨以此文献给大连海事大学的吴楠老师，柳晓鸣老师，王新年老师以及张晶泊老师。

Heinrich 编辑于 2014-05-26 03:14

---

我所理解的快速傅里叶变换（FFT）

沈子恒 于 2016-10-22 18:01:58 发布

1. 历史放在最前头

首先 FFT 是离散傅立叶变换 (DFT) 的快速算法，那么说到 FFT，我们自然要先讲清楚傅立叶变换。先来看看傅立叶变换是从哪里来的？

傅立叶是一位法国数学家和物理学家的名字，英语原名是 Jean Baptiste Joseph Fourier (1768-1830), Fourier 对热传递很感兴趣，于 1807 年在法国科学学会上发表了一篇论文，运用正弦曲线来描述温度分布，论文里有个在当时颇具争议性的命题：任何连续周期信号可以由一组适当的正弦曲线组合而成。当时审查这个论文的人，其中有两位是历史上著名的数学家拉格朗日 (Joseph Louis Lagrange, 1736-1813) 和拉普拉斯 (Pierre Simon de Laplace, 1749-1827)，当拉普拉斯和其他审查者投票通过并要发表这个论文时，拉格朗日坚决反对，在近 50 年的时间里，拉格朗日坚持认为傅立叶的方法无法表示带有棱角的信号，如在方波中出现非连续变化斜率。法国科学学会屈服于拉格朗日的权威，拒绝了傅立叶的工作，幸运的是，傅立叶还有其它事情可忙，他参加了政治运动，随拿破仑远征埃及，法国大革命后因为怕被推上断头台而一直在逃难。直到拉格朗日死后 15 年这个论文才被发表出来。

谁是对的呢？拉格朗日是对的：正弦曲线无法组合成一个带有棱角的信号。但是，我们可以用正弦曲线来非常逼近地表示它，逼近到两种表示方法不存在能量差别，基于此，傅立叶是对的。

2. 傅里叶变换的意义：

为什么我们要用正弦曲线来代替原来的曲线呢？如果我们也还可以用方波或三角波来代替，分解信号的方法是无穷的，但分解信号的目的是为了更加简单地处理原来的信号。用正余弦来表示原信号会更加简单，* 因为正余弦拥有其他信号所不具备的性质：正弦曲线保真度。一个正弦曲线信号输入后，输出的仍是正弦曲线，只有幅度和相位可能发生变化，但是频率和波的形状仍是一样的，且只有正弦曲线才拥有这样的性质，正因如此我们才不用方波或三角波来表示。*

傅立叶变换的物理意义在哪里？

傅立叶原理表明：任何连续测量的时序或信号，都可以表示为不同频率的正弦波信号的无限叠加。而根据该原理创立的傅立叶变换算法利用直接测量到的原始信号，以累加方式来计算该信号中不同正弦波信号的频率、振幅和相位。当然这是从数学的角度去看傅立叶变换。

那么从物理的角度去看待傅立叶变换，它其实是帮助我们改变传统的时间域分析信号的方法转到从频率域分析问题的思维，下面的一幅立体图形可以帮助我们更好得理解这种角度的转换：

所以，最前面的时域信号在经过傅立叶变换的分解之后，变为了不同正弦波信号的叠加，我们再去分析这些正弦波的频率，可以将一个信号变换到频域。有些信号在时域上是很难看出什么特征的，但是如果变换到频域之后，就很容易看出特征了。这就是很多信号分析采用 FFT 变换的原因。另外，FFT 可以将一个信号的频谱提取出来，这在频谱分析方面也是经常用的。

傅立叶变换提供给我们这种换一个角度看问题的工具，看问题的角度不同了，问题也许就迎刃而解！

3. FFT 是怎样完成的？

首先，按照被变换的输入信号类型不同，傅立叶变换可以分为 4 种类型：

1、非周期性连续信号傅立叶变换（Fourier Transform）
2、周期性连续信号傅立叶级数 (Fourier Series)
3、非周期性离散信号离散时域傅立叶变换（Discrete Time Fourier Transform）
4、 周期性离散信号离散傅立叶变换 (Discrete Fourier Transform)

下面是四种原信号图例：

这里我们要讨论是离散信号，对于连续信号我们不作讨论，因为计算机只能处理离散的数值信号，最终目的是运用计算机来处理信号的，所以对于离散信号的变换只有离散傅立叶变换（DFT）才能被适用。对于计算机来说只有离散的和有限长度的数据才能被处理，对于其它的变换类型只有在数学演算中才能用到，在计算机面前只能用 DFT 方法，我们要讨论的 FFT 也只不过是 DFT 的一种快速的算法。

DFT 的运算过程是这样的：.

$X\left(k\right)=\frac{1}{N}\sum _{n=0}^{N-1}X\left(n\right)e^{-j\pi nt/N}$

可见，在计算机上进行的离散傅里叶变换（DFT），使用的输入值是数字示波器经过模数转换器（ADC）后采集到的采样值，也就是时域的信号值。输入采样点的数量决定了转换的计算规模。变换后的频谱输出包含同样数量的采样点，但是其中有一半的值是冗余的，通常不会显示在频谱中。因此，真正有用的信息是 $\frac{N}{2}+1$ 个点。-

FFT 的过程大大简化了在计算机中进行 DFT 的过程，简单来说，如果原来计算 DFT 的复杂度是 $N\ast N$ 次运算（$N$ 代表输入采样点的数量），进行 FFT 的运算复杂度是 $N\lg 10N$，因此，计算一个 1,000 采样点的 DFT，使用 FFT 算法只需要计算约 3,000 次，而常规的 DFT 算法需要计算 1,000,000 次！-=

典型的时域 2 分裂算法图示如下：

4. 变换前后信号的对应关系

以一个实际的信号为例来说明：

示波器采样得到的数字信号，就可以做 FFT 变换了。$N$ 个采样点，经过 FFT 之后，就可以得到 $N$ 个点的 FFT 结果。为了方便进行 FFT 运算，通常 $N$ 取 2 的整数次方。

假设采样频率为 $F_s$，信号频率 $F$，采样点数为 $N$。那么 FFT 之后结果就是一个为 $N$ 点的复数。每一个点就对应着一个频率点。这个点的模值，就是该频率值下的幅度特性。具体跟原始信号的幅度有什么关系呢？

假设原始信号的峰值为 $A$，那么 FFT 的结果的每个点（除了第一个点直流分量之外）的模值应该是 $A$ 除以 $N$，而不是 $A$ 的 $N/2$ 倍。而第一个点就是直流分量，它的模值是直流分量的 $N$ 倍。而每个点的相位，就是在该频率下的信号的相位。

第一个点表示直流分量（即 0Hz），而最后一个点 $N$ 表示负频率 $-F_s/2$，而不是 $F_s$。这中间被 $N-1$ 个点平均分成 $N$ 等份，每个点的频率依次增加。例如某点 $n$ 所表示的频率为：$F_n=(n-1)\cdot F_s/N$。由上面的公式可以看出，$F_n$ 所能分辨到的最小频率为 $F_s/N$。

如果采样频率 $F_s$ 为 1024Hz，采样点数为 1024 点，则可以分辨到 1Hz。1024Hz 的采样率采样 1024 点，刚好是 1 秒，也就是说，采样 1 秒时间的信号并做 FFT，则结果可以分析到 1Hz。如果采样 2 秒时间的信号并做 FFT，则结果可以分析到 0.5Hz。如果要提高频率分辨率，则必须增加采样点数，也即延长采样时间。频率分辨率和采样时间是倒数关系。-=

下面这幅图更能够清晰地表示这种对应关系：

变换之后的频谱的宽度（Frequency Span）与原始信号也存在一定的对应关系。根据 Nyquist 采样定理，FFT 之后的频谱宽度（Frequency Span）最大只能是原始信号采样率的 1/2，如果原始信号采样率是 4GS/s，那么 FFT 之后的频宽最多只能是 2GHz。时域信号采样周期（Sample Period）的倒数，即采样率（Sample Rate）乘上一个固定的系数即是变换之后频谱的宽度，即 Frequency Span = K*（1/ΔT），其中 ΔT 为采样周期，K 值取决于我们在进行 FFT 之前是否对原始信号进行降采样（抽点），因为这样可以降低 FFT 的运算量。如下图所示：

可见，更高的频谱分辨率要求有更长的采样时间，更宽的频谱分布需要提高对于原始信号的采样率，当然我们希望频谱更宽，分辨率更精确，那么示波器的长存储就是必要的！它能提供您在高采样率下采集更长时间信号的能力！

5. 几种典型周期函数的频谱图

频谱泄露：

所谓频谱泄露，就是信号频谱中各谱线之间相互干扰，使测量的结果偏离实际值，同时在真实谱线的两侧的其它频率点上出现一些幅值较小的假谱。产生频谱泄露的主要原因是采样频率和原始信号频率不同步，造成周期的采样信号的相位在始端和终端不连续。简单来说就是因为计算机的 FFT 运算能力有限，只能处理有限点数的 FFT，所以在截取时域的周期信号时，没有能够截取整数倍的周期。信号分析时不可能取无限大的样本。只要有截断不同步就会有泄露。如下图所示：

上图的信号频率为 2.1 MHz，采集时间内没有截取整数倍周期的信号，FFT 运算之后谱线的泄露现象严重，可以看到能量较低的谱线很容易被临近的能量较高的谱线的泄露给淹没住。

因此，避免频谱泄露的方法除了尽量使采集速率与信号频率同步之外，还可以采用适当的窗函数。

不同的窗函数对频谱谱线的影响不同，基本形状可以参看下图：

可以看到，不同的窗函数的主瓣宽度和旁瓣的衰减速度都不一样，所以对于不同信号的频谱应该使用适当的窗函数进行处理。

矩形窗 (Rectangular)：加矩形窗等于不加窗，因为在截取时域信号时本身就是采用矩形截取，所以矩形窗适用于瞬态变化的信号，只要采集的时间足够长，信号宽度基本可以覆盖整个有效的瞬态部分。

汉宁窗 (Von Hann)：如果测试信号有多个频率分量，频谱表现的十分复杂，且测试的目的更多关注频率点而非能量的大小。在这种情况下，需要选择一个主瓣够窄的窗函数，汉宁窗是一个很好的选择。

flattop 窗：如果测试的目的更多的关注某周期信号频率点的能量值，比如，更关心其 EUpeak,EUpeak-peak,EUrms，那么其幅度的准确性则更加的重要，可以选择一个主瓣稍宽的窗，flattop 窗在这样的情况下经常被使用。

6. 总结

FFT 是离散傅立叶变换的快速算法，可以将一个信号变换到频域。有些信号在时域上是很难看出什么特征的，但是如果变换到频域之后，就很容易看出特征了。这就是很多信号分析采用 FFT 变换的原因。另外，FFT 可以将一个信号的频谱提取出来，这在频谱分析方面也是经常用的。

虽然很多人都知道 FFT 是什么，可以用来做什么，怎么去做，但是却不知道 FFT 之后的结果是什意思、如何决定要使用多少点来做 FFT。

现在我就根据实际经验来说说 FFT 结果的具体物理意义。一个模拟信号，经过 ADC 采样之后，就变成了数字信号。采样定理告诉我们，采样频率要大于信号最高频率的两倍，这些我就不在此罗嗦了。

采样得到的数字信号，就可以做 FFT 变换了。$N$ 个采样点，经过 FFT 之后，就可以得到 $N$ 个点的 FFT 结果。为了方便进行 FFT 运算，通常 $N$ 取 2 的整数次方（参见 FFT 原理）。FFT 运算量：$N{\log }_{2}N$（2 为对数的底）。

假设采样频率为 $F_s$，信号频率 $F$，采样点数为 $N$。那么 FFT 之后结果就是一个为 $N$ 点的复数。每一个点就对应着一个频率点。这个点的模值，就是该频率值下的幅度特性。具体跟原始信号的幅度有什么关系呢？假设原始信号的峰值为 $A$，那么 FFT 的结果的每个点（除了第一个点直流分量之外）的模值就是 $A$ 的 $N/2$ 倍。而第一个点就是直流分量，它的模值就是直流分量的 $N$ 倍。而每个点的相位呢，就是在该频率下的信号的相位。第一个点表示直流分量（即 0Hz），而最后一个点 $N$ 的再下一个点（实际上这个点是不存在的，这里是假设的第 $N+1$ 个点，也可以看做是将第一个点分做两半分，另一半移到最后）则表示采样频率 $F_s$，这中间被 $N-1$ 个点平均分成 $N$ 等份，每个点的频率依次增加。例如某点 $n$ 所表示的频率为：$F_n=(n-1)\cdot F_s/N$。由上面的公式可以看出，$F_n$ 所能分辨到频率 $F_0=F_s/N$。假设频率分辨率 $F_0=F_s/N$ 限定，采样频率 $F_s$ 也给定，也已知信号最高频率 $F_h$，那么由采样定理：$F_s\ge 2F_h$ 得到：$N=F_s/F_0=2F_h/F_0$，即采样点必须满足这样一个关系式。

如果采样频率 $F_s$ 为 1024 Hz，采样点数为 1024 点，则可以分辨到 1 Hz。1024Hz 的采样率采样 1024 点，刚好是 1 秒，也就是说，采样 1 秒时间的信号并做 FFT，则结果可以分析到 1 Hz，如果采样 2 秒时间的信号并做 FFT，相应的采样点也为原来 2 倍，则结果可以分析到 0.5Hz。如果要提高频率分辨力，则必须增加采样点数，也即延长采样时间，所以频率分辨率和采样时间是倒数关系，就是说，要想分辨出频率间隔越小的频率（频率分辨率越高），采样时间越长越好。-=

---

信号与系统以及数字信号处理

一、卷积、傅里叶变换与拉普拉斯变换的概念及应用

1. 引子：信号与系统学习的问题

在工科电子类专业的信号相关课程学习中，普遍存在“重公式背诵、轻概念理解”的现象。学习者虽能通过推导公式、计算积分应付考试，但毕业时仍未掌握知识的逻辑，尤其对“卷积为何存在”“变换有何用途”等本质问题缺乏认知。

探讨信号与系统的工具时，需先明确“工具的用途”而非“工具的形式”。例如“卷积有什么用”，若仅回答“为后续章节学习铺垫”，则脱离工程应用本质。本节将通过电子系统测试的典型场景，结合数学工具的工程价值，逐步阐释卷积、傅里叶变换与拉普拉斯变换的意义。

2. 卷积的定义与工程应用：有限长信号的响应求解

2.1 场景设定：线性时不变系统的测试需求

考虑一款单输入 - 单输出线性时不变（LTI）电子设备，其特性满足：对任意有限持续时间的输入信号，输出信号的持续时间同样有限，符合因果系统与稳定系统的基本假设，即系统不会对未来输入产生响应，且输入能量有限时输出能量也有限。工程测试中，需确定该设备对多种输入信号的输出响应。

2.2 初始测试与效率瓶颈

首先对设备进行基础测试：输入信号为 $x_1(t)=\sin (t)$，持续时间限定为 $t<1\text{s}$，$t\ge 1\text{s}$ 时 $x_1(t)=0$，通过信号发生器输入信号，示波器记录输出波形 $y_1(t)$，完成单次物理测试。

若需进一步测试数千种不同形式的有限长输入信号，如指数衰减信号 $x_2(t)=t\cdot e^{-t}$、矩形脉冲信号 $x_3(t)=\text{rect}(t/0.5)$ 等，且均有明确数学表达式与有限持续时间，若对每种信号逐一进行物理测试，将面临测试周期长、人力成本高的效率瓶颈。此时需一种通过数学计算推导输出的方法，替代重复的物理测试。

2.3 单位冲激响应与卷积原理

2.3.1 单位冲激信号的物理意义

定义“单位冲激信号” $\delta (t)$，其数学特性为：

• 时域特性：仅在 $t=0$ 时刻有非零值，满足 $\delta (t)=0$（$t\ne 0$）；
• 能量特性：总能量为 $1\text{J}$，即 ${\int }_{-\infty }^{+\infty }\delta (t)dt=1$；
• 抽样特性：对任意连续信号 $f(t)$，满足 $f(t)\cdot \delta (t-t_0)=f(t_0)\cdot \delta (t-t_0)$，即冲激信号可“提取”信号在特定时刻的取值。

对上述电子设备输入单位冲激信号 $\delta (t)$，记录此时的输出信号 $h(t)$，称为设备的“单位冲激响应”。$h(t)$ 是描述 LTI 系统特性的物理量，一旦通过单次测试获取 $h(t)$，即可通过数学运算推导任意输入信号的输出，无需重复物理测试。

2.3.2 输入信号的冲激分解

对任意有限长输入信号 $x(t)$，设其持续时间为 $t\in [0,T]$，$T$ 为有限值，可从数学上分解为无穷多个“冲激元”的叠加，即：

$$x(t)={\int }_0^{T}x(\tau )\cdot \delta (t-\tau )d\tau$$

其中，$\tau$ 为积分变量，代表冲激元的延迟时刻，$x(\tau )\cdot \delta (t-\tau )d\tau$ 是 $t=\tau$ 时刻的冲激元，其幅度为 $x(\tau )d\tau$，延迟时间为 $\tau$。该分解的本质是：将连续信号“离散化”为无数个幅度微小的冲激信号，便于利用 LTI 系统的线性特性求解输出。

2.3.3 卷积运算的定义与输出推导

根据 LTI 系统的两个性质：

• 线性性：若输入 $x_1(t)$ 对应输出 $y_1(t)$，输入 $x_2(t)$ 对应输出 $y_2(t)$，则输入 $a\cdot x_1(t)+b\cdot x_2(t)$ 对应输出 $a\cdot y_1(t)+b\cdot y_2(t)$（$a,b$ 为常数）；
• 时不变性：若输入 $x(t)$ 对应输出 $y(t)$，则输入 $x(t-\tau )$（延迟 $\tau$ 时刻）对应输出 $y(t-\tau )$。

结合上述性质，冲激元 $x(\tau )\cdot \delta (t-\tau )d\tau$ 对应的输出为 $x(\tau )\cdot h(t-\tau )d\tau$，$h(t-\tau )$ 是单位冲激响应的延迟形式。将所有冲激元的输出叠加，即对 $\tau$ 积分，得到输入 $x(t)$ 对应的输出 $y(t)$，该积分运算即为“卷积”，数学表达式为：

$$y(t)=x(t)\ast h(t)={\int }_0^{T}x(\tau )\cdot h(t-\tau )d\tau$$

其中，“$\ast$”为卷积运算符。从物理意义上，卷积的本质是“输入信号的冲激分解 + 系统响应的线性叠加”，其价值在于：将“多输入信号的输出求解”转化为“单次冲激响应测试 + 数学积分计算”，大幅提升工程测试效率。

3. 傅里叶变换的定义与工程应用：无限长信号的响应求解

3.1 新场景的挑战：无限长周期输入信号

若待测试的输入信号为无限长周期信号，如工频干扰信号 $x(t)=\sin (2\pi \cdot 50t)+\sin (2\pi \cdot 150t)$，周期 $T=0.02\text{s}$，$t\in [-\infty ,+\infty ]$，则前文的卷积方法无法直接应用。该信号持续时间无限，卷积积分 ${\int }_{-\infty }^{+\infty }x(\tau )h(t-\tau )d\tau$ 可能发散，且信号波形无简单封闭表达式，直接积分计算难度极大。

此时需引入“域变换”思想：将时间域中难以处理的无限长、复杂波形信号，映射到“频率域”（另一数学域），在频率域中完成简化计算后，再映射回时间域，得到输出响应。傅里叶变换正是实现这一“时频映射”的工具。

3.2 傅里叶变换的原理

3.2.1 信号的频率域分解

任何周期信号均可通过傅里叶级数分解为一系列不同频率的简谐分量（正弦/余弦信号）的叠加。对于周期为 $T$ 的信号 $x(t)$，其傅里叶级数展开式为：

$$x(t)=\sum _{n=-\infty }^{+\infty }{C}_n\cdot e^{jn{\omega }_{0}t}$$

其中：

• ${\omega }_0=2\pi /T$ 为基波角频率（单位：$\text{rad/s}$）；
• $n$ 为整数（$n=0,\pm 1,\pm 2,\dots$），代表谐波次数，$n{\omega }_0$ 为第 $n$ 次谐波的角频率；
• $C_n$ 为第 $n$ 次谐波的复振幅，反映该频率分量的幅度与相位，计算式为 $C_n=\frac{1}{T}{\int }_{-T/2}^{T/2}x(t)\cdot e^{-jn{\omega }_{0}t}dt$。

对于非周期但满足“绝对可积”条件（${\int }_{-\infty }^{+\infty }|x(t)|dt<\infty$）的无限长信号，可将其视为“周期 $T\to \infty$ 的周期信号”。此时基波角频率 ${\omega }_0\to 0$，离散谐波频率 $n{\omega }_0$ 变为连续频率 $\omega$，傅里叶级数过渡为傅里叶变换，其定义式为：

$$X(j\omega )={\int }_{-\infty }^{+\infty }x(t)\cdot e^{-j\omega t}dt$$

其中，$X(j\omega )$ 称为信号 $x(t)$ 的“傅里叶变换”（频率域表示），可分解为幅度谱 $|X(j\omega )|$（反映各频率分量的幅度大小）与相位谱 $\arg [X(j\omega )]$（反映各频率分量的相位偏移），二者共同描述信号的频率特性。

3.2.2 卷积定理：时频域的运算映射

LTI 系统在频率域的特性可通过“频率响应” $H(j\omega )$ 描述，$H(j\omega )$ 是系统单位冲激响应 $h(t)$ 的傅里叶变换，即：

$$H(j\omega )={\int }_{-\infty }^{+\infty }h(t)\cdot e^{-j\omega t}dt$$

$H(j\omega )$ 的物理意义是：系统对不同频率简谐分量的幅度放大倍数与相位调整量，幅度谱 $|H(j\omega )|$ 表示放大倍数，相位谱 $\arg [H(j\omega )]$ 表示相位调整量。

信号与系统中的卷积定理指出：时间域中输入信号与单位冲激响应的卷积，对应频率域中输入信号傅里叶变换与系统频率响应的乘积，即：

$$\mathcal{F}\left[x(t)\ast h(t)\right]=X(j\omega )\cdot H(j\omega )$$

该定理将时间域中复杂的卷积积分，转化为频率域中简单的代数乘法，彻底解决了无限长信号的输出求解难题。

3.2.3 无限长信号的输出求解步骤

针对无限长周期输入信号 $x(t)$，其输出响应 $y(t)$ 的求解步骤如下：

1. 计算输入信号的傅里叶变换 $X(j\omega )$：对周期信号，可通过傅里叶级数得到离散频谱 $C_n$，再转化为连续频谱的冲激序列形式 $X(j\omega )=2\pi {\sum }_{n=-\infty }^{+\infty }{C}_n\cdot \delta (\omega -n{\omega }_0)$；
2. 获取系统的频率响应 $H(j\omega )$：由单位冲激响应 $h(t)$ 经傅里叶变换得到，或通过扫频仪等设备直接测量；
3. 计算输出信号的频率域表示 $Y(j\omega )$：根据卷积定理，$Y(j\omega )=X(j\omega )\cdot H(j\omega )$；
4. 傅里叶逆变换求时域输出：通过逆变换将 $Y(j\omega )$ 映射回时间域，即 $y(t)=\frac{1}{2\pi }{\int }_{-\infty }^{+\infty }Y(j\omega )\cdot e^{j\omega t}d\omega$。

通过上述步骤，时间域中无限长、复杂的信号响应问题，在频率域中转化为有限步骤的代数运算，大幅降低计算难度，且频率域的频谱分布更规整（如周期信号的频谱为离散冲激，易于分析），是工程中处理无限长信号的方法。

4. 拉普拉斯变换的引入：非绝对可积信号的扩展

当电子设备的输出信号为无限长非周期且不满足绝对可积的信号，如指数增长信号 $y(t)=e^{0.5t}$（$t\ge 0$）时，傅里叶变换会因积分发散而不存在（如 ${\int }_0^{+\infty }{e}^{0.5t}dt$ 趋于无穷大）。此时需引入拉普拉斯变换，通过扩展“频率”的定义（引入复频率），解决非绝对可积信号的分析问题。

拉普拉斯变换的思想是：给信号 $x(t)$ 乘以一个“衰减因子” $e^{-\sigma t}$（$\sigma$ 为实常数），使原本不满足绝对可积的信号（如 $e^{0.5t}$）变为可积信号（即 $e^{0.5t}\cdot e^{-\sigma t}=e^{-(\sigma -0.5)t}$，当 $\sigma >0.5$ 时，信号随时间衰减至 0），再对衰减后的信号进行傅里叶变换。

其定义式（工程中常用单边拉普拉斯变换，因实际信号多为因果信号，即 $t<0$ 时 $x(t)=0$）为：

$$X(s)={\int }_0^{+\infty }x(t)\cdot e^{-st}dt$$

其中，$s=\sigma +j\omega$ 为复频率（$\sigma$ 为实部，$j\omega$ 为虚部），$\sigma$ 的取值范围称为“收敛域”，仅当 $s$ 落在收敛域内时，拉普拉斯变换才存在。

拉普拉斯变换的价值在于：

• 扩展了变换的适用范围，可分析傅里叶变换无法处理的非绝对可积信号（如指数增长信号、不稳定系统的响应）；
• 将时域中的微分方程（描述系统输入输出关系）转化为复频域中的代数方程，简化不稳定系统（如含正反馈的电路）的分析与设计；
• 当 $\sigma =0$ 时，$s=j\omega$，拉普拉斯变换退化为傅里叶变换，即 $X(j\omega )=X(s){|}_{\sigma =0}$，体现了两种变换的统一性。

5. 信号与系统学习的启示

5.1 学习困境的根源

学习者未能掌握信号与系统知识，并非能力不足，更多源于教材与教学方式的局限。多数教材过度侧重数学推导（如微积分运算、公式证明），却未说明推导的工程目的；教师若仅照本宣科、复述 PPT，未从“问题驱动”角度解释“为何需要该工具”，则易导致学习者陷入“知其然，而不知其所以然”的误区。

例如谷歌经典面试题“用 3 句话向老太太解释数据库”，其考察“对概念本质的理解”。若无法剥离细节、提炼逻辑，仅专注公式背诵与计算，将难以将理论转化为工程能力。

5.2 概念的补充阐释

5.2.1 频率的物理本质

频率是描述信号“周期性变化快慢”的物理量，源于对简谐振动的抽象。任何含周期性变化的信息（如音频信号的音调高低、光的颜色、电子震荡的周期）均具有频率特性，其数学模型可通过“圆周运动的投影”直观理解：

在 $x\text{-}y$ 平面内，一个质点以原点为中心、半径为 1 做匀速圆周运动（角速度为 $\omega$），若将 $x$ 轴视为时间轴，那么该圆周运动在 $y$ 轴上的投影，就是 $\sin (\omega t)$ 的波形。圆周运动速度越快（$\omega$ 越大），$\sin (\omega t)$ 的波形越密集，对应频率越高。

工程中频率的缩放模式分为两类：

• 频率缩放（音调变化）：如老式磁带快放时，音频信号的频率加倍（$\sin (t)$ 变为 $\sin (nt)$，$n>1$），导致音调升高；
• 时域抽样（速度变化）：如 CD 快放时，通过丢弃部分时域采样点实现“速度加快”，但信号的频率未变，因此音调不变。

5.2.2 傅里叶变换中负数/复数的意义

傅里叶变换结果 $X(j\omega )$ 中的负数与复数部分，是数学计算的必然结果，不具有直接物理意义，仅为保证“时频映射完整性”而存在：

• 负数频率：源于复指数形式 $e^{j\omega t}=\cos (\omega t)+j\sin (\omega t)$，负数频率 $\omega <0$ 与正数频率 $\omega >0$ 共同对应实信号的正弦/余弦分量，二者的幅度谱呈偶对称（$|X(j\omega )|=|X(j(-\omega ))|$），相位谱呈奇对称（$\arg [X(j\omega )]=-\arg [X(j(-\omega ))]$），实际分析中仅需关注 $\omega \ge 0$ 的部分；
• 复数部分：用于同时描述信号的幅度与相位信息，通过“取模”可得到幅度谱（物理可测量），“取实部/虚部”可还原时域实信号，复数本身不直接对应物理量。

5.2.3 信号与系统课程的主旨

信号与系统课程的目标是：建立“信号 - 系统 - 传输介质”的数学模型，解决“如何设计信号、如何分析系统、如何匹配介质”的工程问题，具体体现在：

1. 传输介质的频率特性分析：不同介质（如以太网线、光纤、空气）对不同频率信号的传输能力不同（如网线适合基带信号，光纤适合高频信号），需建立介质的频率响应模型，判断信号传输后的失真程度；
2. 信号设计与传输速率优化：已知介质频率特性后，设计适配的信号形式（如调制信号），结合香农定理实现理论最大传输速率；
3. 跨领域应用延伸：除通信物理层外，还可结合香农信息理论用于声音/图像处理（如滤波去噪）、模式识别（如特征提取）、智能控制（如系统稳定性调节）等领域。

从学科关联角度看：计算机专业课程构建“数据表达的逻辑模型”（如数据结构解决逻辑编码与纠错），而信号与系统构建“物理层的数学模型”——若接收端信号波形混乱（如失真严重），则无法判断信号代表“1”还是“0”，逻辑纠错也失去意义。在工业控制中，数模转换（如温度、压力等物理量转数字信号）的前提，正是基于信号理论设计的数学转换模型。

5.2.4 系统设计的逻辑与分类

系统设计的关键是构建系统函数（连续系统为 $H(s)$ 或 $H(j\omega )$，离散系统为 $H(z)$），该函数直接描述输入与输出的映射关系，无需关注中间物理实现（如电路拓扑、元器件参数），这也是“信号与系统”课程与“电子电路”课程的本质区别。

设计系统函数的前提是：将输入信号 $x(t)$ 与输出信号 $y(t)$ 均用数学函数表示（如 $x(t)=\sin ({\omega }_{0}t)$、$y(t)=A\sin ({\omega }_{0}t+\phi )$），通过分析信号的分解与系统的响应规律，确定系统函数的形式。

复杂信号的分析依赖“分解 - 叠加”逻辑：将复杂信号（如方波、三角波）分解为若干简单信号（如正弦信号）的叠加，利用 LTI 系统的线性性分别求解各简单信号的输出，再叠加得到总输出。分解过程涉及的微积分运算（如傅里叶级数求和、傅里叶变换积分）是实现工具，课程重点是理解“为何分解”“如何通过分解简化分析”的逻辑，而非单纯计算。

系统的分类可从两个维度划分：

1. 按功能分类：
   • 基础功能：调制解调（信号抽样与重构）、信号叠加、滤波（频率选择）、功率放大、相位调整、时钟同步、负反馈锁相环；
   • 复杂功能：由多个子系统组成的集成系统（可绘制系统流程图，逻辑与编程流程图一致，符号层面无本质区别）；
   • 离散功能：数字信号处理（如离散滤波、傅里叶变换的离散实现），为后续课程内容。
2. 按系统特性分类：
   • 无状态系统：输出仅由当前输入决定（如电阻的 $V=IR$）；
   • 有限状态机：输出由当前输入与有限个历史状态决定（如触发器电路）；
   • 线性系统：满足叠加性与齐次性，物理层中多数连续系统属于线性时不变（LTI）系统。

5.2.5 教材选择的建议

信号与系统的基础是“符号系统”，其理论框架基于集合论（如信号的集合定义、系统的映射关系），微积分仅为实现该框架的运算工具。若缺乏集合论构建的系统框架，微积分运算将失去意义——学习者甚至无法明确运算目的。

从“问题驱动”与“认知逻辑”角度，推荐加州大学伯克利分校 Edward A. Lee 与 Pravin Varaiya 合著的《信号与系统》。该书遵循“先定义概念（如信号、系统的集合论定义）→ 提出工程问题（如如何分析信号响应）→ 引入数学工具（如卷积、变换）→ 验证工具有效性”的逻辑，符合人类“从本质到应用”的认知习惯，避免单纯罗列公式与推导。

国内多数教材的局限在于：过度侧重数学推导的细节呈现（如傅里叶变换的积分证明、卷积的计算步骤），未说明“推导该公式的目的”“该工具解决什么工程问题”；仅从方法论层面罗列知识点，未从认识论角度解释“为何需要这些知识点”，导致内容本末倒置，增加学习难度。

二、到底什么是频率？什么是系统？

本节将进一步展开讲解傅里叶变换 $F$。需注意，傅里叶变换中的 $F$ 可代表频率（frequency）概念，也可涵盖其他概念——它本质是一种概念模型，旨在解决特定计算问题（如时间域无限长输入信号的输出求解）。

若将傅里叶变换视为一个 C 语言函数，信号的输入输出问题视为 IO 问题，那么任何难以直接求解的 $x\to y$ 问题，均可通过 $x\to f(x)\to f^{-1}(x)\to y$ 的流程间接求解。

1. 到底什么是频率？

一个基本假设是：任何信息都具有频率特性，例如音频信号的音调高低、光的频谱、电子震荡的周期等。基于这些特性，我们抽象出“简谐振动”的概念，其数学名称即为频率。

想象在 $x\text{-}y$ 平面内，一个原子以原点为中心、半径为 1 做匀速圆周运动；若将 $x$ 轴视为时间轴，那么该圆周运动在 $y$ 轴上的投影，就是 $\sin (t)$ 的波形。这一原理对中学生而言也易于理解。

不同频率模型对应不同的圆周运动速度：圆周运动速度越快，$\sin (t)$ 的波形越密集。频率的缩放主要有以下两种模式：

• (a) 老式收音机以磁带为音乐介质，快放时会感觉歌声音调变高、音色怪异。这是因为“圆周运动”速度加倍，每个声音分量对应的 $\sin (t)$ 波形变为 $\sin (nt)$。
• (b) 在 CD 或计算机上快放或慢放音频时，仅会感觉歌手演唱速度变快或变慢，音调不会升高。原因是快放时采用时域采样法，丢弃部分波形，但承载信息的输出波形宽度不变；慢放时则相反，通过填充时域信号实现波形拉长。

2. 傅里叶变换得到的结果有负数/复数部分，有什么物理意义吗？

解释：傅里叶变换是一种数学工具，其结果中的负数与复数部分不具有直接物理意义，仅为保证计算完整性而存在。

3. 信号与系统这门课的基本主旨是什么？

对通信与电子类专业学生而言，多数工作涉及设计 OSI 七层模型中的物理层技术。该技术的难点在于：需明确传输介质的电气特性——不同传输介质对不同频率段的信号处理能力不同。例如，以太网线处理基带信号，广域网光纤传输高频调制信号，移动通信中 2G 与 3G 需满足不同载频特性。

那么，如何判断空气、电线、光纤等介质在传输一定距离后，能否基本保持输入信号的频率特性？这就需要建立介质的频率响应数学模型。同时，已知介质频率特性后，如何设计传输信号以实现理论上的最大传输速率？——这正是“信号与系统”课程带领学习者探索的关键领域。

当然，信号与系统的应用不止于此。结合香农信息理论，它还可用于信息处理（声音、图像）、模式识别、智能控制等领域。若说计算机专业课程构建的是数据表达的逻辑模型，那么信号与系统则建立了更底层、具有物理意义的数学模型。数据结构知识可解决逻辑信息的编码与纠错问题，而信号知识能帮助设计码流的物理载体（若接收的信号波形混乱，将无法判断信号代表“1”还是“0”，逻辑纠错也会失去意义）。在工业控制领域，计算机应用的前提是各类数模转换，要将温度、电阻、压力、速度等物理现象产生的连续模拟信号，通过特定设备转换为有意义的数字信号，首先需设计可行的数学转换模型。

4. 如何设计系统？

系统设计的关键是构建物理层面的系统函数（包括连续或离散状态），系统需具备输入与输出功能，而中间处理过程与具体物理实现（如电子电路设计）相关，并非本课程重点。“信号与系统”的本质，是根据特定需求设计系统函数。设计系统函数的前提，是将输入与输出均用函数（如 $\sin (t)$）表示。

分析复杂信号时，可将其分解为若干简单信号的叠加，分解过程涉及大量微积分运算，但这些具体数学运算并非课程——课程重点是理解分解逻辑与系统设计思路。

系统有哪些种类？

• (a) 按功能分类：包括调制解调（信号抽样与重构）、叠加、滤波、功放、相位调整、信号时钟同步、负反馈锁相环，以及由若干子系统组成的复杂系统（可绘制系统流程图，其逻辑与编程中的流程图相似，在符号层面无本质区别）；此外，还包括离散状态的数字信号处理（后续课程内容）。
• (b) 按系统类别划分：包括无状态系统、有限状态机、线性系统等。其中，物理层的连续系统函数属于复杂线性系统。

5. 最好的教材？

符号系统的基础是集合论，而非微积分。若缺乏集合论构建的系统框架，微积分运算将失去意义——学习者甚至无法明确运算目的。

从计算机视角学习“信号与系统”，推荐教材之一是加州大学伯克利分校（UC Berkeley）Edward A. Lee 与 Pravin Varaiya 合著的《信号与系统》。该书遵循“先定义概念（如信号、系统的集合论定义）→ 提出工程问题（如如何分析信号响应）→ 引入数学工具（如卷积、变换）→ 验证工具有效性”的逻辑，符合人类认知习惯。

国内多数教材的局限在于：过度侧重数学推导的细节呈现（如傅里叶变换的积分证明、卷积的计算步骤），未说明“推导该公式的目的”“该工具解决什么工程问题”；仅从方法论层面罗列知识点，未从认识论角度解释“为何需要这些知识点”，导致内容本末倒置，增加学习难度。

三、抽样定理是干什么的？

1. 举个例子

以打电话为例：电话机发出的信号为脉冲调幅（PAM）信号，电话线路中传输的并非话音本身，而是话音经信道编码转换后的脉冲序列，接收端需通过解码恢复语音波形。

那么，如何将连续的语音信号转换为一系列脉冲，才能保证传输基本不失真？最直接的思路是抽样：每隔 $M$ 毫秒对话音信号采样一次，记录电信号振幅，将振幅转换为脉冲编码后传输；接收端再按特定规则重构语音波形。

由此产生两个问题：每隔 $M$ 毫秒采样一次，$M$ 需小到何种程度才算足够？接收端如何从脉冲序列中恢复语音波形？

针对第一个问题：语音信号属于时间频率信号（其傅里叶变换对应时间频率），可将其分解为若干不同频率的单音混合体（周期函数可通过傅里叶级数展开，非周期区间函数可视为周期延拓后的周期信号展开，效果一致）。对于信号中的最高频率分量，若抽样方式能保证该分量的信息不丢失，那么所有低频分量的信息也能通过抽样保存。

若人类语音的高频上限为 3000 Hz，那么最高频率分量可近似为 $\sin (3000t)$。要通过抽样保存该 $\sin$ 函数的信息，需保证每个周期内至少采样两次（波峰与波谷各一次），即抽样频率为最高频率分量的 2 倍（奈奎斯特抽样定理）。此时，抽样信号与原始模拟连续信号一一对应、完全等价，可通过抽样信号无损恢复原始信号。

针对第二个问题：接收端如何从脉冲序列（梳状波形）恢复模拟连续信号？首先需明确，频率域中的脉冲序列已包含原始信号的全部信息，但原始信息仅存在于特定频率以下。

假设输入脉冲信号为 $I$，通过设备 $X$ 后输出原始语音信号 $O$，则三者满足时域卷积关系 $I\ast X=O$（$\ast$ 表示卷积）。由于时域特性分析较复杂，可转换至频率域：根据傅里叶变换的性质，时域卷积对应频率域乘法，即 $F(I)\times F(X)=F(O)$。

由此可明确设备 $X$ 的频率特性：$F(X)$ 需为理想低通滤波器（频率域图形呈矩形），其对应的时域波形为钟形函数（因包含时间轴负半轴部分，实际中无法完全实现）。通过此类信号处理设备，可从输入脉冲序列中恢复出接近理想的原始语音信号。

实际应用中，抽样频率通常略高于奈奎斯特频率——对于 3 kHz 的语音信号，标准抽样频率设定为 8 kHz，以预留一定冗余，避免因实际设备误差导致信号失真。

2. 再举一个例子

数字图像的分辨率也与抽样定理密切相关：抽样密度越高，图像分辨率越高，画面越清晰。若抽样频率不足，会出现“混叠”现象——例如网络上常见的一幅视觉错觉图：近视者戴眼镜时看到的是爱因斯坦头像，摘下眼镜后却看到梦露头像。

这一现象的本质是：摘下眼镜后，人眼分辨率降低（等效于抽样频率不足），图像中的高频分量失真并混入低频分量，导致视觉感知出现偏差。此处需注意，图像的傅里叶变换对应的是“空间频率”，而非时间频率，但其原理与时间域的抽样定理一致。

或许有人会问：为何不直接在信道中传输原始语音模拟信号？原因在于模拟信号抗干扰能力弱、无纠错机制，而抽样后的数字脉冲信号具有更强的抗干扰性与可纠错性，能显著提升传输可靠性。

需特别说明的是，并非所有信号都能通过理想抽样保存信息——例如时域存在跳变的方波信号，其频率域带宽为无穷大。若用有限带宽的抽样信号表示方波，等效于仅取傅里叶级数的部分和；在恢复原始信号时，方波的不可导点（跳变处）会出现“吉布斯现象”，即波形边缘产生高频振荡毛刺，无法完全复现原始方波的陡峭跳变。

3. 为什么傅里叶想出了这么一个级数来？

傅里叶级数的诞生，源于西方哲学与科学中的思想——正交分析方法。

例如研究一个立体物体的形状时，我们会建立 $x$、$y$、$z$ 三个互相正交的坐标轴：任意一个轴在其他轴上的投影均为 0，通过物体在三个轴上的投影（即三视图），可完整还原其立体形态。同理，信号的分解与分析也可借鉴这一思路：将复杂信号分解为若干互相正交的三角函数分量的无限和，这正是傅里叶的重要贡献。

正交性的关键意义在于：各分量之间相互独立、无干扰，可通过分别计算每个分量的系数，再叠加得到原始信号，大幅简化了复杂信号的分析难度。

四、傅里叶变换的复数 小波入门

一、复数：一种“概念工具”，而非客观存在

从本质上讲，“复数”是人类为解决数学问题构建的概念模型，而非现实世界中客观存在的物理量。

什么是“概念”？以一张纸为例：我们通常认为纸有两个面，“面”就是人类对纸的形态特征的主观认知——如同“大”与“小”的概念，仅对人的意识有意义，对客观存在的纸本身无意义（这一哲学观点可参考康德《纯粹理性批判》中对“先天认知形式”的论述）。若将纸条一端旋转 180 度后与另一端粘连，形成“莫比乌斯圈”，此时“纸有两个面”的概念便不再成立——这说明概念是人类对客观世界的加工与抽象，而非客观世界的本质属性。

复数的概念源于数学运算的需求：如何求解满足 $x^2=-1$ 的数？在实数轴上，任何实数的平方均非负数（$(-1)\times (-1)=1$），因此需扩展数的定义，构建一个包含实数与“虚数”的新数域——复数域。

在复数域中，实数的运算法则可视为复数运算的特例。例如 $1\times (-1)=-1$，可理解为“方向的反转”：将复数看作平面上的向量，$-1$ 相当于向量绕原点旋转 180 度（即“向后转”）；那么 $(-1)\times (-1)=1$，就是“向后转两次回到原位”。

而 $x^2=-1$ 的求解，可通过“旋转 90 度”实现：将向量绕原点逆时针旋转 90 度（对应虚数单位 $i$），旋转两次后恰好得到 $-1$（即 $i^2=-1$）。由于这种旋转需要两个维度描述（实轴与虚轴），复数域必须用平面（复平面）表示，而非直线（实数轴）。

由此可推导出复数乘法的特性：两个复数相乘，结果的模（绝对值）等于两复数模的乘积，结果的辐角（旋转角度）等于两复数辐角的和（即棣莫弗定理）。需注意的是，这一特性并非复数域“天然具有”，而是人类为满足 $x^2=-1$ 的求解需求，在构建复数域时刻意设计的运算规则——是“认知决定性质”，而非“性质决定认知”。

二、复数与傅里叶变换的关联

由于三角函数可视为复平面上圆周运动的投影（如 $\sin (t)$ 是单位圆上点在虚轴的投影，$\cos (t)$ 是在实轴的投影），复数域天然地将三角函数与指数运算（乘法）统一起来——通过欧拉公式 $e^{j\omega t}=\cos (\omega t)+j\sin (\omega t)$，可将实数域的三角函数分解转化为复数域的指数形式。

基于这一统一，我们可从实数域的傅里叶级数（形如 $\sum [A_n\cos (n{\omega }_{0}t)+B_n\sin (n{\omega }_{0}t)]$），推导出形式更简洁的复数域傅里叶级数（形如 $\sum C_n{e}^{jn{\omega }_{0}t}$）。尽管复数本身无直接物理意义，但复数域的傅里叶级数与实数域的级数一一对应，只需通过“取模”或“取实部”等操作，即可将复数结果映射回具有物理意义的实数信号。

傅里叶变换公式的本质

傅里叶变换的核心是解决非周期信号的频率分析问题，其公式可从复数域傅里叶级数推导而来：

1. 对于周期信号，傅里叶级数将其分解为离散频率分量的叠加（频率间隔为基频 ${\omega }_0=2\pi /T$，$T$ 为周期）；
2. 对于非周期信号，可将其视为“周期 $T\to \infty$ 的周期信号”：此时基频 ${\omega }_0\to 0$，离散频率分量逐渐密集，最终变为连续频率；同时，每个频率分量的振幅 $C_n\to 0$（否则总能量会无穷大）；
3. 为使连续频率的“振幅”具有实际意义，需将 $C_n$ 乘以 $T$（即除以 ${\omega }_0$），此时离散的级数求和 $\sum C_n{e}^{jn{\omega }_{0}t}$ 便转化为连续的积分——这就是傅里叶变换的由来。

需注意两个关键概念的变化：

• 周期信号的傅里叶级数：对应离散频率点，每个点有确定的振幅（能量）；
• 非周期信号的傅里叶变换：对应连续频率域，单个频率点的振幅为无穷小（能量为 0），需通过“频率区间内的积分”描述能量分布（即“频谱密度”）。

此外，傅里叶变换公式中的 $\sqrt{2\pi }$ 仅为“归一化系数”——目的是保证正变换与反变换的一致性（即信号经变换再逆变换后，能完全恢复原始形态）。系数的具体分配可灵活调整（如正变换除以 $2\pi$、反变换不除，或两者均除以 $\sqrt{2\pi }$），不影响变换的逻辑。

至于变换结果中的“负数部分”，本质是复平面上的方向（辐角）对应——可理解为三角函数的相位信息，忽略相位仅看振幅，即可得到实数域的频率特性（如信号的幅频特性曲线）。

三、从傅里叶变换到小波变换

傅里叶变换虽强大，但存在明显局限性：

1. 仅能分析信号的“全局频率特性”，无法定位频率分量在时间域的分布（例如无法判断一个突变信号的突变发生在何时）；
2. 对非平稳信号（频率随时间变化的信号，如语音、地震波）的分析能力较弱；
3. 需满足狄利克雷条件（如信号绝对可积），对某些奇异信号（如冲激信号的导数）不适用。

为解决这些问题，“小波变换”应运而生。

1. 小波的思想：“时频局部化”

傅里叶变换使用的基函数是“无限长的三角函数”（如 $\sin (\omega t)$、$e^{j\omega t}$），覆盖整个时间域；而小波变换使用的基函数是“有限长的小波函数”——通过对一个“母小波”（如 Haar 小波、Daubechies 小波）进行尺度缩放（对应频率调整）与时间平移（对应时间定位），生成一组正交基函数，从而实现对信号“局部时频特征”的分析。

例如分析一段语音信号时：

• 对母小波进行“大尺度缩放”（拉伸），可得到低频小波基，用于捕捉语音中的慢变分量（如元音）；
• 对母小波进行“小尺度缩放”（压缩），可得到高频小波基，用于捕捉语音中的快变分量（如辅音的爆破音）；
• 通过时间平移，可精确定位这些分量在语音中的出现时刻。

2. 小波变换的优势与应用

与傅里叶变换相比，小波变换的优势在于时频分辨率的灵活调整：

• 分析低频信号时，可采用“宽时间窗、窄频率窗”，兼顾时间分辨率与频率精度；
• 分析高频信号时，可采用“窄时间窗、宽频率窗”，优先保证时间定位精度。

这种特性恰好满足海森堡测不准原理的约束（时频分辨率无法同时达到最优），在实际应用中表现出更强的适应性。

小波变换的典型应用包括：

• 图像压缩（如 JPEG 2000 标准）：通过保留图像的低频轮廓与关键高频细节，在高压缩比下仍保持较好画质；
• 信号去噪：利用小波基对噪声（通常为高频）与有效信号（通常为低频）的分离能力，滤除噪声；
• 故障诊断：通过分析机械振动信号的小波变换结果，定位故障发生的时间与频率特征（如轴承磨损的高频冲击信号）。

3. 小波与傅里叶的关系

小波变换可视为傅里叶变换的“扩展”而非“替代”：

• 当小波基函数取极限（尺度趋近于无穷大，时间窗覆盖整个时间域）时，小波变换可退化为傅里叶变换；
• 傅里叶变换是“全局时频分析”工具，适用于平稳信号；小波变换是“局部时频分析”工具，适用于非平稳信号，二者互补。

从计算复杂度来看，小波变换的运算量通常为 $O(N)$（$N$ 为信号长度），低于快速傅里叶变换（FFT）的 $O(N\log N)$，更适合实时信号处理场景。

四、从连续变换到离散变换：拉普拉斯与 Z 变换的延伸

傅里叶变换与小波变换的讨论集中在“连续信号”领域，但工程实践中更多面对的是“离散信号”（如计算机采样后的数字信号）。为解决离散信号的分析与系统设计问题，拉普拉斯变换与 Z 变换应运而生，二者可视为傅里叶变换在复频域的扩展与离散化。

1. 拉普拉斯变换：傅里叶变换的“复频域升级”

傅里叶变换的应用存在一个关键限制：要求信号满足“绝对可积”条件（即 ${\int }_{-\infty }^{+\infty }|f(t)|dt<\infty$），否则变换结果会出现无穷大，无法有效分析。例如指数增长信号 $f(t)=e^{at}$（$a>0$），其傅里叶变换不存在，但在工程中这类信号（如电容充电过程、人口增长模型）却十分常见。

拉普拉斯变换通过引入“复频率” $s=\sigma +j\omega$（$\sigma$ 为实部，$j\omega$ 为虚部），解决了这一问题。其思想是：给信号 $f(t)$ 乘以一个“衰减因子” $e^{-\sigma t}$，使原本不满足绝对可积的信号（如 $e^{at}$）变为可积信号（即 $e^{at}\cdot e^{-\sigma t}=e^{-(\sigma -a)t}$，当 $\sigma >a$ 时，信号随时间衰减至 0），再对衰减后的信号进行傅里叶变换。

其定义式（工程中常用单边拉普拉斯变换，因实际信号多为因果信号，即 $t<0$ 时 $x(t)=0$）为：

$$X(s)={\int }_0^{+\infty }x(t)\cdot e^{-st}dt$$

其中，$s=\sigma +j\omega$ 为复频率（$\sigma$ 为实部，$j\omega$ 为虚部），$\sigma$ 的取值范围称为“收敛域”，仅当 $s$ 落在收敛域内时，拉普拉斯变换才存在。

拉普拉斯变换的价值在于：

• 扩展了变换的适用范围，可分析傅里叶变换无法处理的非绝对可积信号（如指数增长信号、不稳定系统的响应）；
• 将时域中的微分方程（描述系统输入输出关系）转化为复频域中的代数方程，简化不稳定系统（如含正反馈的电路）的分析与设计；
• 当 $\sigma =0$ 时，$s=j\omega$，拉普拉斯变换退化为傅里叶变换，即 $X(j\omega )=X(s){|}_{\sigma =0}$，体现了两种变换的统一性。

在系统设计中，拉普拉斯变换的关键价值在于：将时域中的微分方程（描述系统输入输出关系）转化为复频域中的代数方程，大幅简化求解过程。例如，RLC 电路的时域微分方程经拉普拉斯变换后，可直接通过代数运算得到系统函数 $H(s)=F(s)/X(s)$（输出与输入的拉普拉斯变换之比），再通过分析 $H(s)$ 的极点、零点分布，即可判断系统的稳定性与频率响应。

2. Z 变换：离散信号的“拉普拉斯变换”

拉普拉斯变换针对的是连续信号，而 Z 变换是离散信号的“复频域分析工具”，可视为拉普拉斯变换在离散域的对应形式。其思路是：对离散信号 $x(n)$（$n$ 为整数，代表采样时刻）进行“离散化复频域映射”，将时域中的差分方程转化为 Z 域中的代数方程，方便离散系统（如数字滤波器、单片机控制电路）的分析与设计。

Z 变换的定义式为：

$$Z[x(n)]=X(z)=\sum _{n=-\infty }^{+\infty }x(n)z^{-n}$$

其中 $z=r{e}^{j\theta }$ 为复变量（$r$ 为模，$\theta$ 为辐角），称为“Z 域变量”。

其与傅里叶变换、拉普拉斯变换的关联可通过“抽样信号”建立：

• 若连续信号 $f(t)$ 经周期抽样（抽样周期为 $T$）得到离散信号 $x(n)=f(nT)$，则 $x(n)$ 的 Z 变换与 $f(t)$ 的拉普拉斯变换满足 $X(z)=L[f(t)\cdot {\sum }_{n=0}^{\infty }\delta (t-nT)]{|}_{s=\frac{1}{T}\ln z}$，即 Z 变换是拉普拉斯变换经“$z=e^{sT}$”映射后的离散形式；
• 当 $r=1$ 时，$z=e^{j\theta }$，此时 Z 变换退化为离散傅里叶变换（DFT），即 $X(e^{j\theta })=Z[x(n)]{|}_{r=1}$，其中 $\theta =\omega T$ 称为“数字角频率”，对应连续域中的角频率 $\omega$。

在数字系统中，Z 变换的关键应用包括：

• 分析离散系统的稳定性：通过判断系统函数 $H(z)=X(z)/Y(z)$ 的极点是否全部落在 Z 域的单位圆内（$|z|<1$），若极点在单位圆外，则系统不稳定；
• 设计数字滤波器：通过调整 $H(z)$ 的零点、极点位置，实现低通、高通、带通等滤波功能，例如 FIR（有限长单位脉冲响应）滤波器、IIR（无限长单位脉冲响应）滤波器的设计均基于 Z 变换；
• 信号的离散域处理：如语音信号的降噪、图像的边缘检测，可通过 Z 变换将信号映射到 Z 域，进行频谱调整后再通过逆 Z 变换还原为时域离散信号。

需特别说明的是，离散傅里叶变换（DFT）虽能分析离散信号的频率特性，但计算复杂度为 $O(N^2)$（$N$ 为信号长度），在 $N$ 较大时难以实时处理。而快速傅里叶变换（FFT）通过“分治法”将 DFT 的计算复杂度降至 $O(N\log N)$，本质是利用了 Z 变换在单位圆上的对称性与周期性，是工程中分析离散信号频率特性的工具（如示波器的频谱分析功能、音频处理软件的均衡器）。

五、总结：信号分析工具的“进化逻辑”

从傅里叶变换到小波变换，从拉普拉斯变换到 Z 变换，信号与系统领域的数学工具始终遵循“问题驱动”的进化逻辑——每一种变换的诞生，都是为了解决前一种工具无法覆盖的场景：

1. 傅里叶变换：解决“平稳信号的全局频率分析”问题，是信号频域分析的基础，但无法处理非平稳信号与无限能量信号；
2. 拉普拉斯变换：扩展傅里叶变换至“复频域”，解决不稳定系统与非绝对可积信号的分析问题，是连续系统设计的工具；
3. Z 变换：将拉普拉斯变换离散化，解决“离散信号与数字系统”的分析设计问题，为数字信号处理奠定基础；
4. 小波变换：突破傅里叶变换的“全局时频局限”，实现“非平稳信号的局部时频分析”，适用于语音、图像、故障诊断等需要定位时频特征的场景。

这些工具并非“替代关系”，而是“互补关系”——在实际工程中，需根据信号类型（连续/离散、平稳/非平稳）与系统需求（稳定性分析、滤波设计、时频定位）选择合适的工具。例如：

• 分析电网的工频谐波（平稳信号），可使用傅里叶变换；
• 设计汽车发动机的振动故障诊断系统（非平稳信号，需定位故障发生时间），需使用小波变换；
• 设计手机基带芯片中的数字滤波器（离散系统），需使用 Z 变换与 FFT；
• 分析含正反馈的振荡电路（不稳定连续系统），需使用拉普拉斯变换。

理解这些工具的“设计逻辑”与“适用场景”，远比背诵公式与推导过程更重要——正如前文所述，工科学习的重点是“理解工具的用途、掌握工具的使用”，而非陷入纯数学的细节泥沼。只有明确“为什么用”，才能真正掌握“怎么用”，进而将这些理论工具转化为解决实际工程问题的能力。

重编自：http://blog.renren.com/GetEntry.do?id=871736090&owner=905902345 (原文链接已沉寂.)

---

Fourier series & synthesis

by Izaak Neutelings

Posted on 10. July 2023

Some basic examples of Fourier series, synthesis and series of sines, cosines, rectangle, sawtooth, triangle functions, as well as a 3D figure to breakdown synthesis into the time and frequency domain.

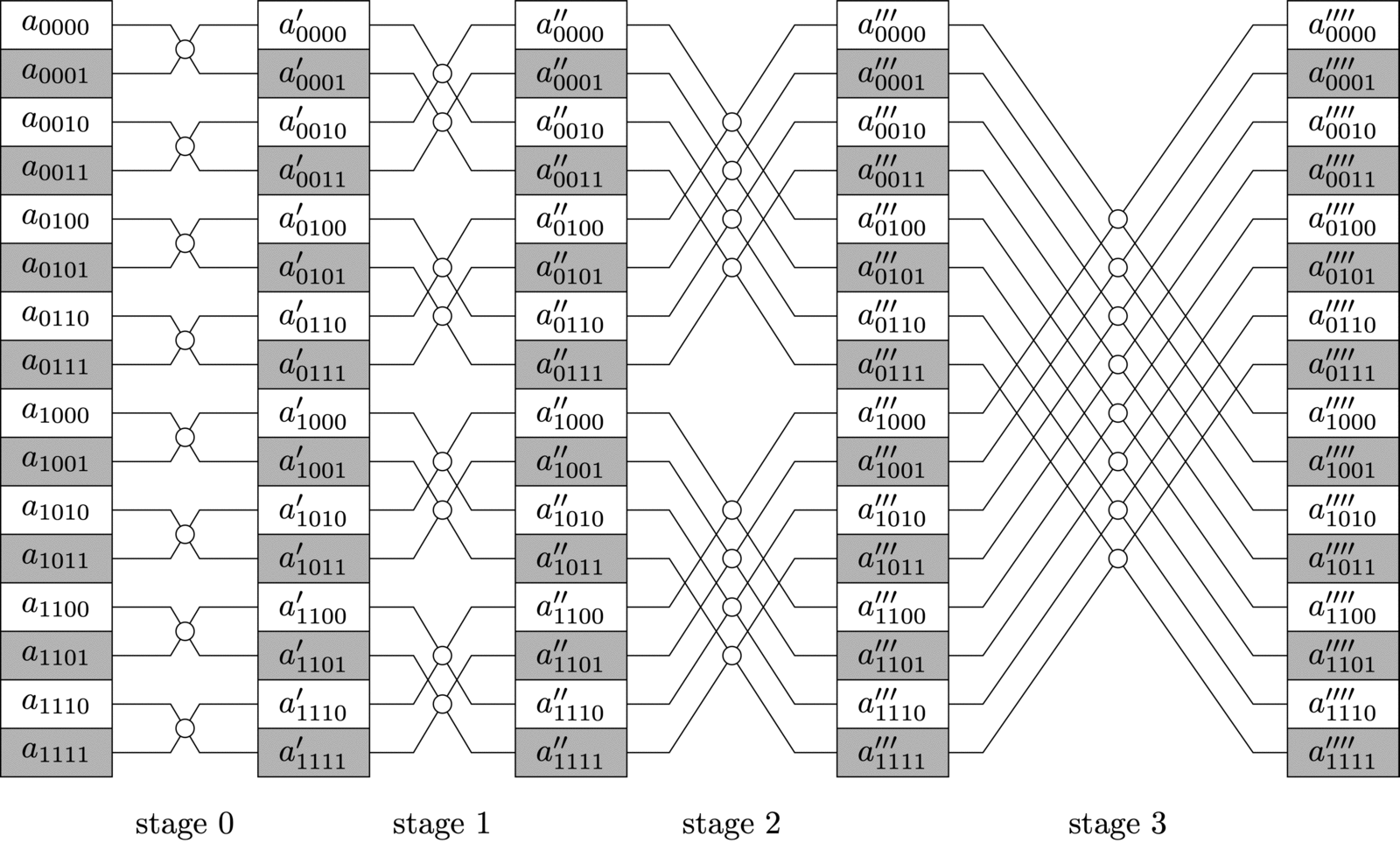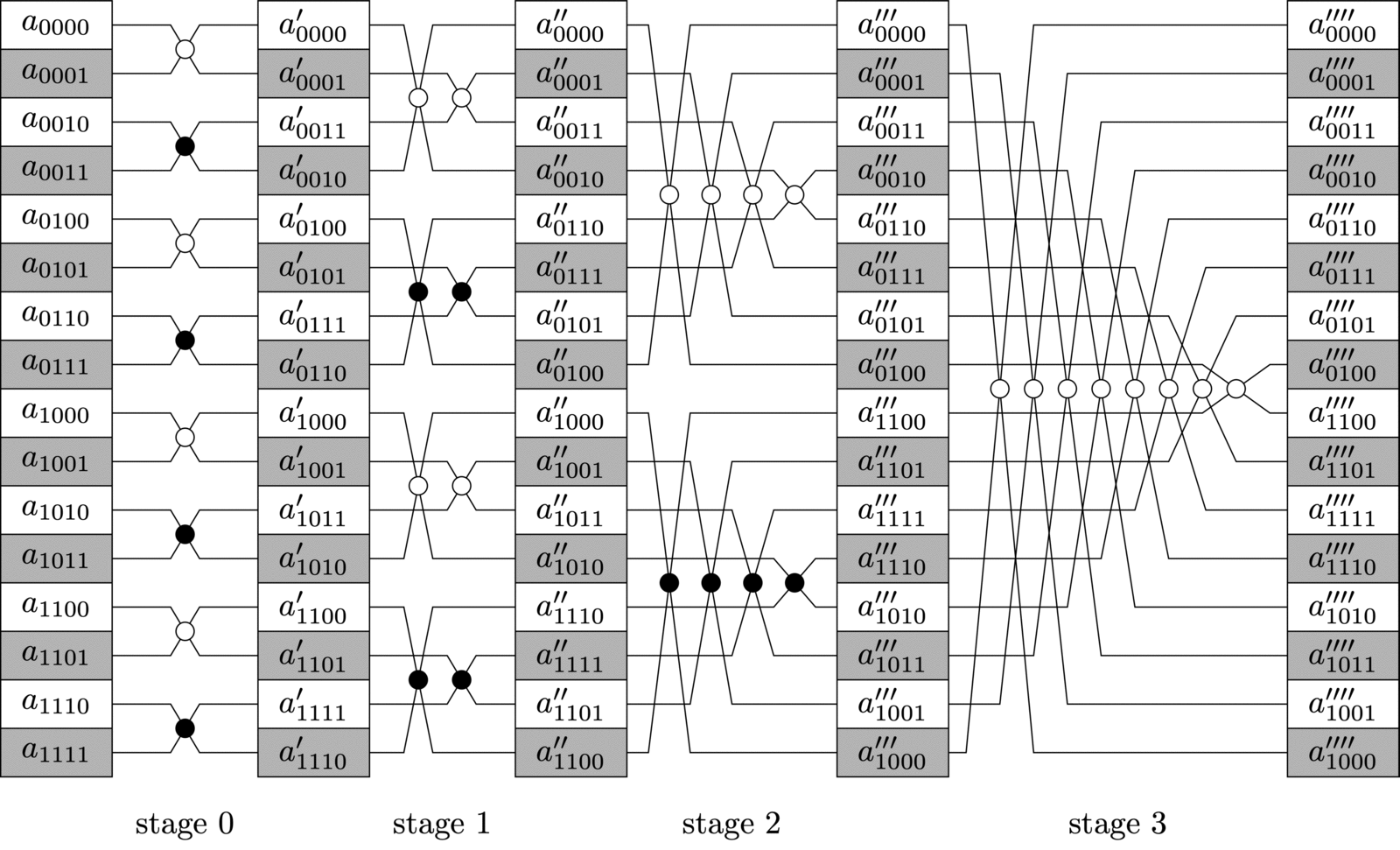
Fast Fourier Transform

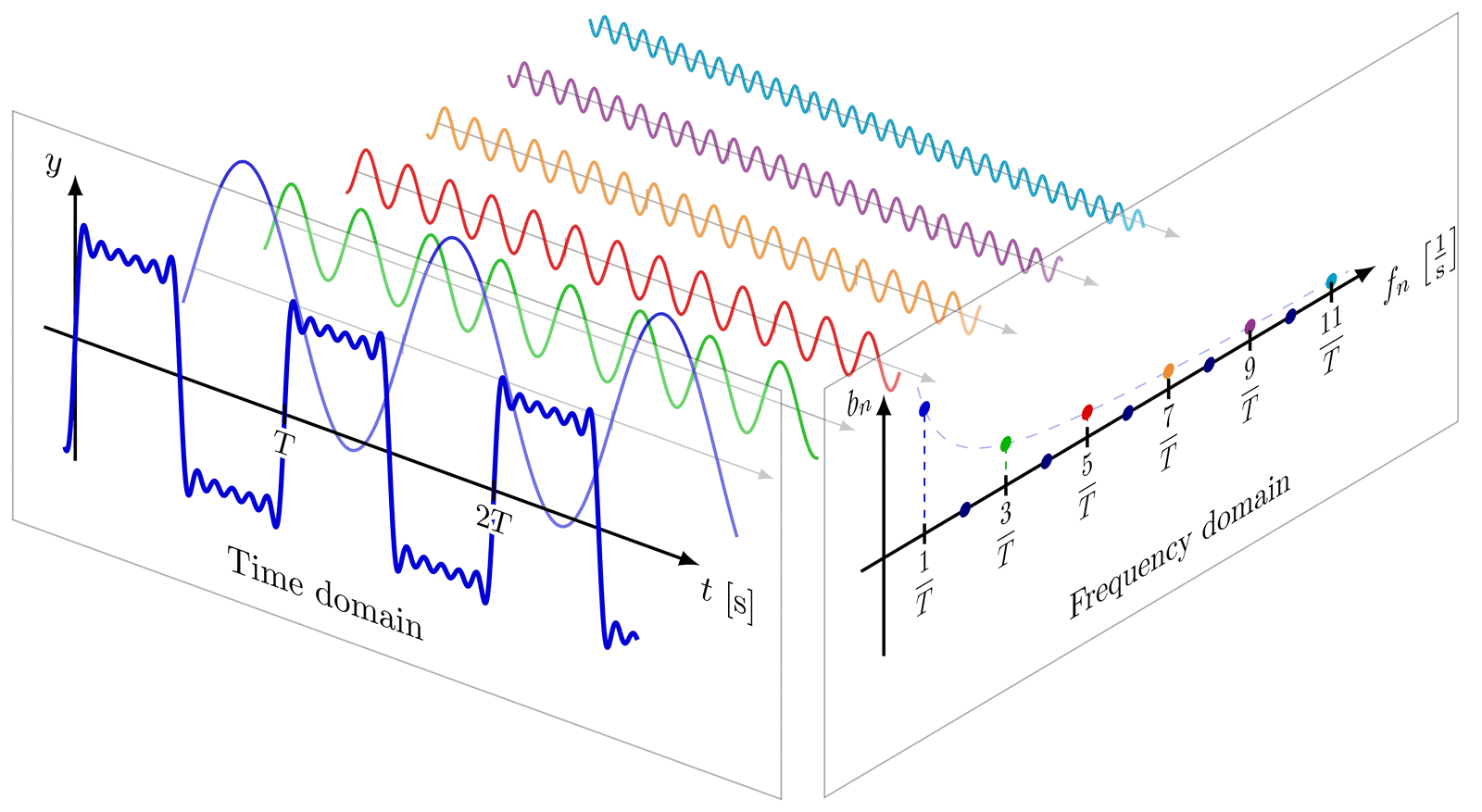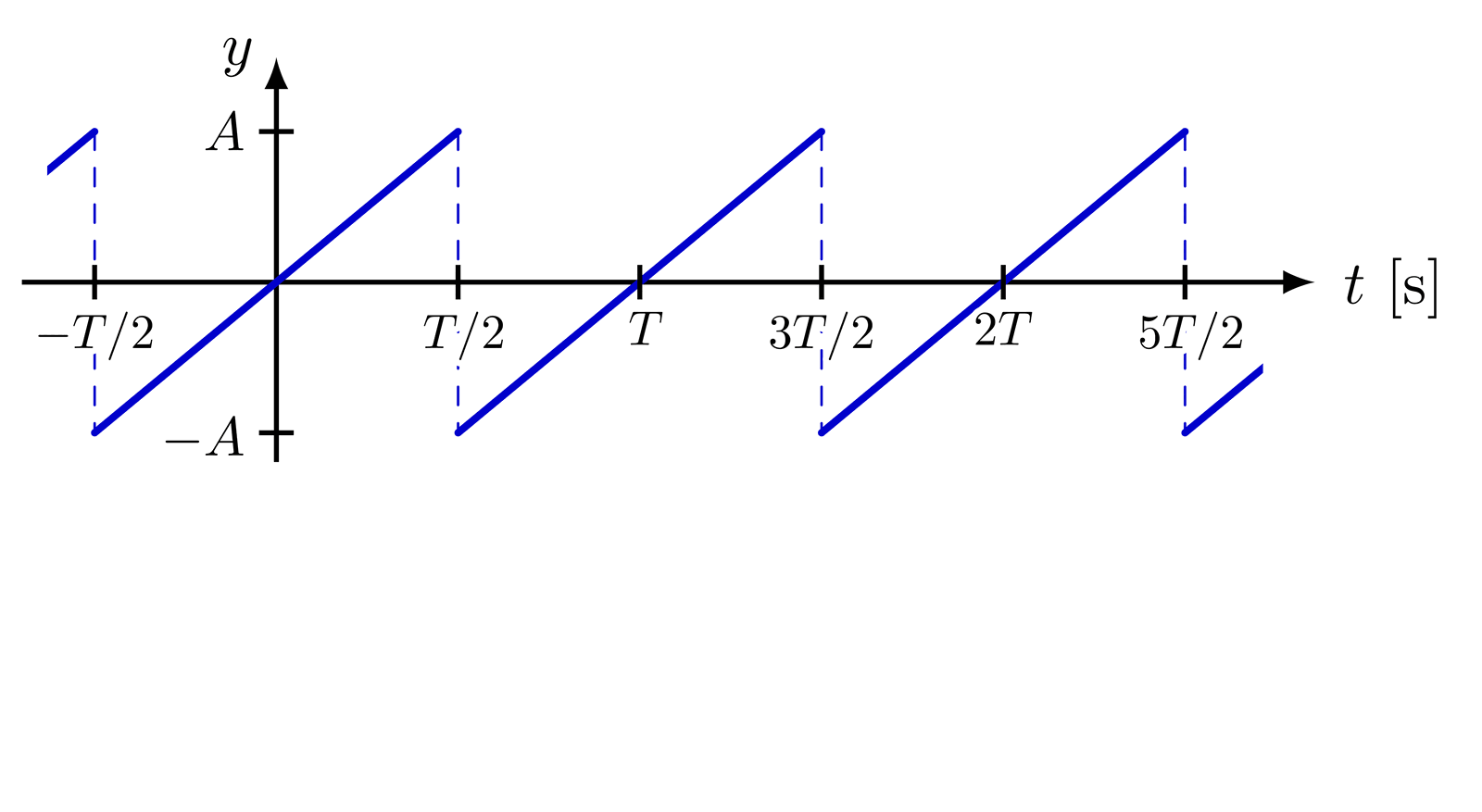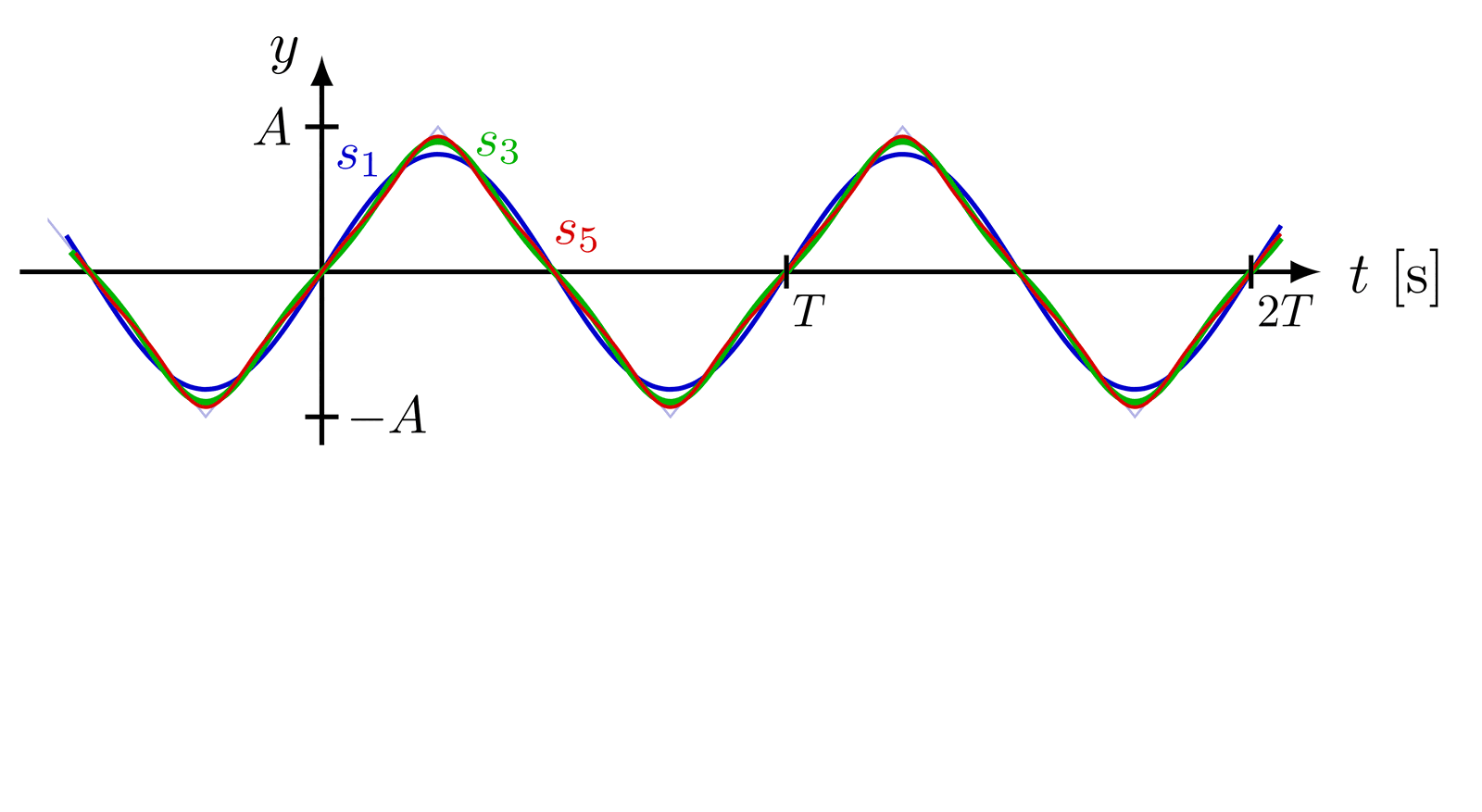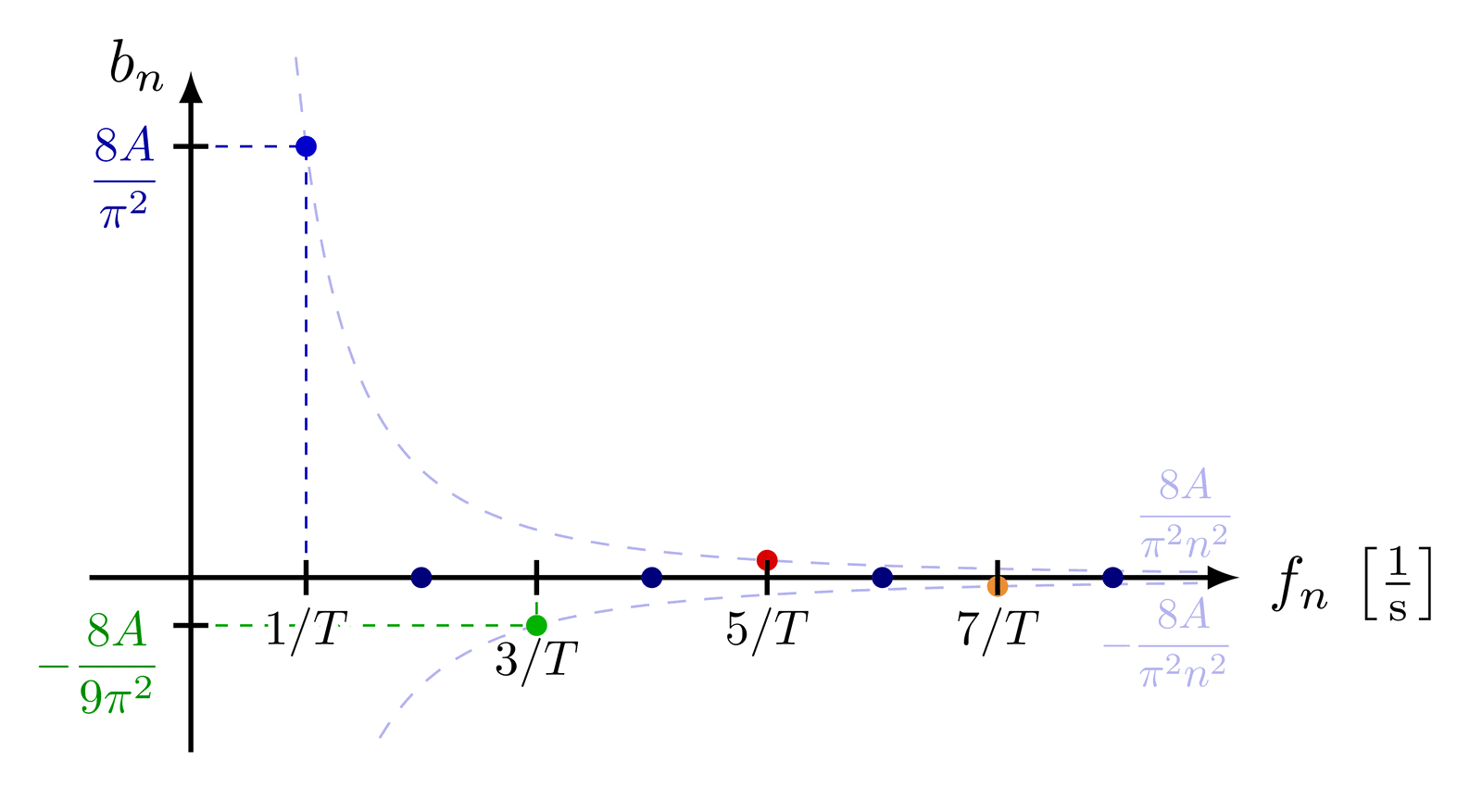
Fourier series & synthesis

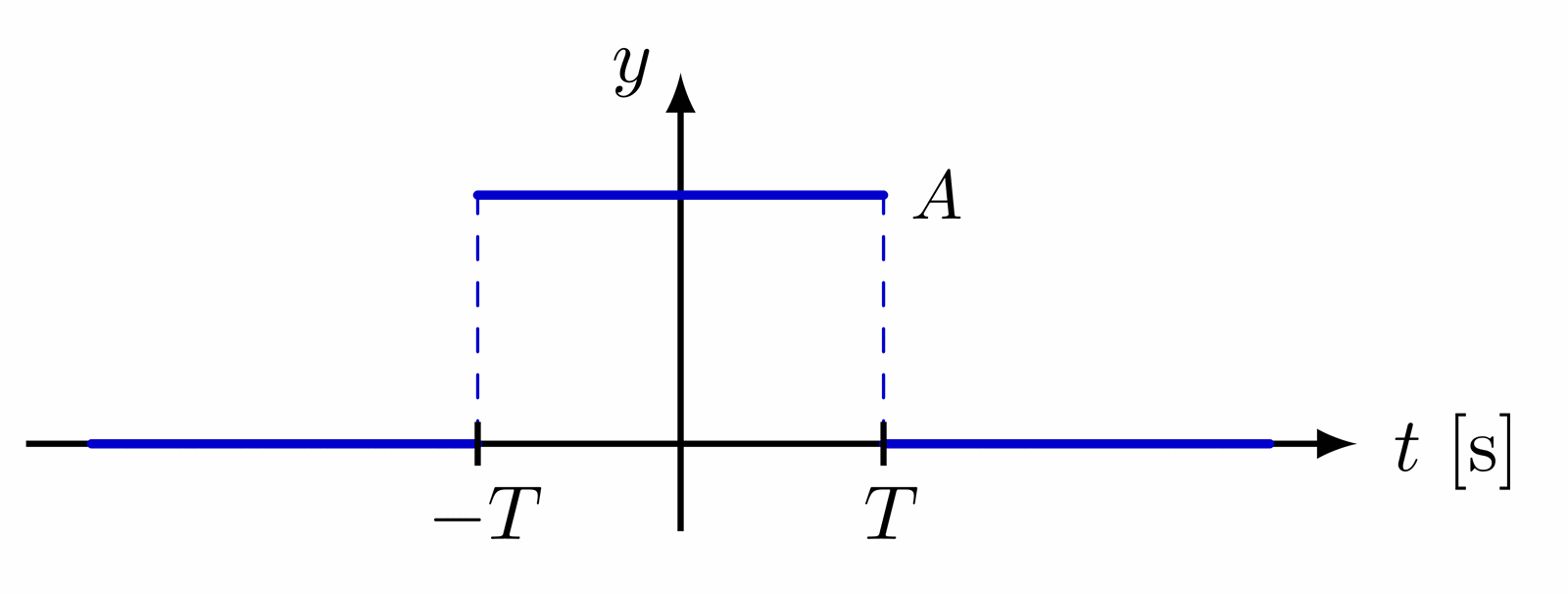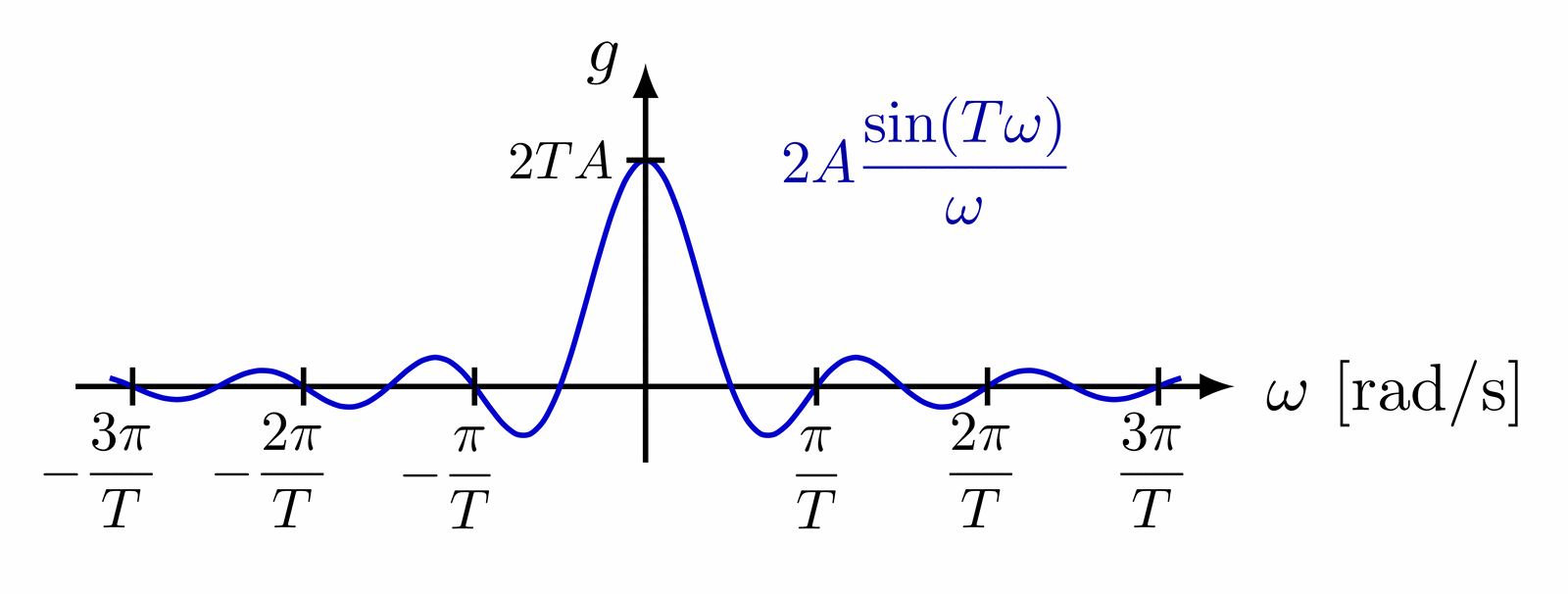
Fourier transform

---

via:

• 傅里叶分析之掐死教程（完整版）作者：韩 昊 微博：@花生油工人 更新于 2014.06.06 - 知 乎：Heinrich
  https://zhuanlan.zhihu.com/p/19763358

• 我所理解的快速傅里叶变换（FFT）_快速傅里叶变换原理 - 优快云 博客 沈子恒 于 2016-10-22 18:01:58 发布
  https://blog.youkuaiyun.com/shenziheng1/article/details/52891807

• Fourier series & synthesis – TikZ.net
  https://tikz.net/fourier_series/

• fourier analysis – TikZ.net
  https://tikz.net/tag/fourier-analysis/

• PHY111, Physik I HS2020 | Physik-Institut | UZH
  https://www.physik.uzh.ch/de/lehre/PHY111/HS2020.html#Lecture_information