豆瓣9.5，几十万人读过的顶级微积分入门神作，读者评价读完神清气爽！

转载 于 2025-09-26 16:00:00 发布 · 228 阅读 · 0 ·
CC 4.0 BY-SA版权
原文链接：https://mp.weixin.qq.com/s?__biz=MjM5Njc0MjIwMA==&mid=2649838182&idx=1&sn=20e4bce0e1da541346fe3c07980e7e2a&chksm=bf8573034b7ace1eaa37a8d693d86458799592d5259220fed596abeda11a65be5bee0819a8b7&scene=126&sessionid=0

对于大多数学生来说，微积分或许是他们曾经上过的倍感迷茫且最受挫折的一门课程了。

对于理科和工科的大学生来说，微积分的学习将贯穿他们大部分专业课程。

它奠定了我们对变量变化规律的理解，对于解决实际问题有重要作用。掌握微积分，你就掌握了理解和描述许多专业知识的工具！

因此一本好的微积分教材对于学生学习而言举足轻重！而图灵出版的这本《普林斯顿微积分读本》堪称国内最好入门微积分的教材了，累计畅销30余万册，豆瓣更有上千人持续9年打出9.5的高分！每次高校线下展示备受欢迎！激励过很多想要学习却不知从何入门的学生！

来源 | 《普林斯顿微积分读本（修订版）》

作者 | 【美】阿德里安·班纳

译者 | 杨爽 赵晓婷 高璞

01

经典神作怎么用？

本书旨在帮助你学习单变量微积分的主要概念,同时也致力于教会你求解问题的技巧.无论你是第一次接触微积分,还是为了准备一次测验,或是已经学过微积分还想再温习一遍,我都希望本书能够对你有所帮助.

写作本书的灵感来自我在普林斯顿大学的学生们.他们在过去的几年里发现,与课堂授课、作业讲解以及他们的教科书一样,本书的初稿是很有帮助的学习指南.以下是他们在学习过程中提出的一些你可能也想问的问题.

这本书为什么这么厚？

我是假设你真的想要掌握这门课程,而不只是想囫囵吞枣,一知半解,所以你已经准备好投入一些时间和精力,去阅读并理解这些详尽的阐述.

阅读之前，我需要知道些什么？

你需要了解一些基本的代数知识,并且要知道如何求解简单的方程式.本书的前两章涵盖了你所需要的大部分的微积分预备知识.

啊!下周就要期末考试了,我还什么都不知道呢!从哪里开始啊？接下来的几页就会介绍如何使用本书来备考.

例题的求解过程在哪里？我所看到的只是大量的文字与少量的公式.

首先,看一个求解过程并不能教会你应该怎样思考.所以我通常试图给出一种“内心独白”,即当你尝试求解问题的时候,脑海中应该经历怎样的思考过程.最后,你想到了求解问题的所有知识点,但仍然需要用正确的方式把它们全部写出来.我的建议是,先看懂并理解问题的求解方法,然后再返回来尝试自己解答.

定理的证明哪儿去了？

本书中的大部分定理都以某种方式被验证了.在附录A 中可以找到更多正式的证明过程.

主题没有次序!我该怎么办呢？

学习微积分没有什么标准次序.我选择的顺序是有效的,但你可能还得通过搜索目录来查找你需要的主题,其余的可以先忽略.我也可能遗漏了一些主题.为什么不尝试给我发送电子邮件呢?地址是adrian calclifesaver.com.你一定想不到,我可能会为你写一个附加章节(也为下一版写,如果有的话!).

你使用的一些方法和我学到的不一样.到底谁的正确,我的任课老师的还是你的？希望我们都没错!如果还有疑问,就请教你的任课老师什么是对的吧.

页边空白处怎么没有微积分的历史和有趣的史实呢？本书中有一点微积分历史内容,但不在这里过多分散我们的注意力.如果你想记下这些历史内容,就请阅读一本关于微积分历史的书吧（《微积分的历程程：从牛顿到勒贝格》）,那才更有趣,而且比零零散散的几句话更值得关注.

我们学校可以用这本书作为教材吗？

这本书配有很好的习题集,可以作为一 本教材,也可以用作一本学习指南.你的任课老师也会发现这本书很有助于备课,特别是在问题求解的技巧方面.

这些录像是什么？在网站www.calclifesaver.com 上, 你可以找到我过去复习课的录像,其中涉及了很多(但不是全部)本书的章节和例题.

本书官方授权中文视频课程现已上线,由B站知名知识区UP主、山东财经大学副教授宋浩领衔,高校名师团队倾情讲授.本课程提炼了书中的重点和精华,提供了国内相应的定义和方法,使学生更容易理解和接受,并引导学生拓展思考.课程风格深入浅出、循循善诱,能帮助广大学生克服对微积分的恐惧,在考试中获得高分.

02

如何使用这本书备考？

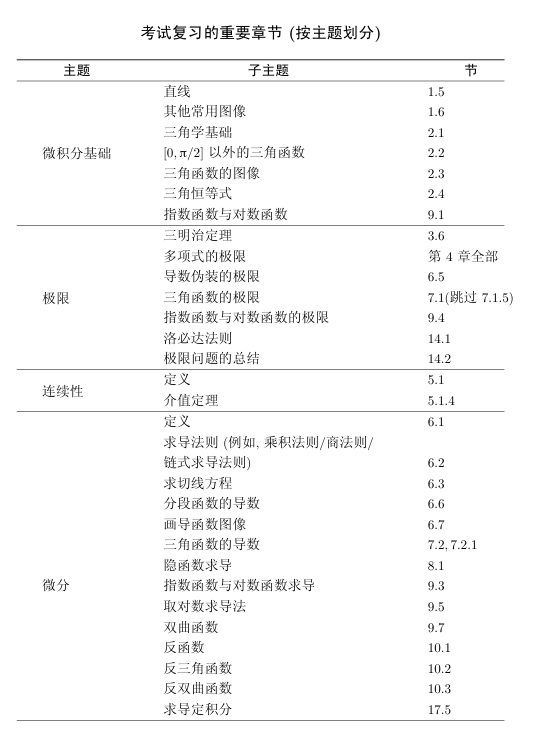
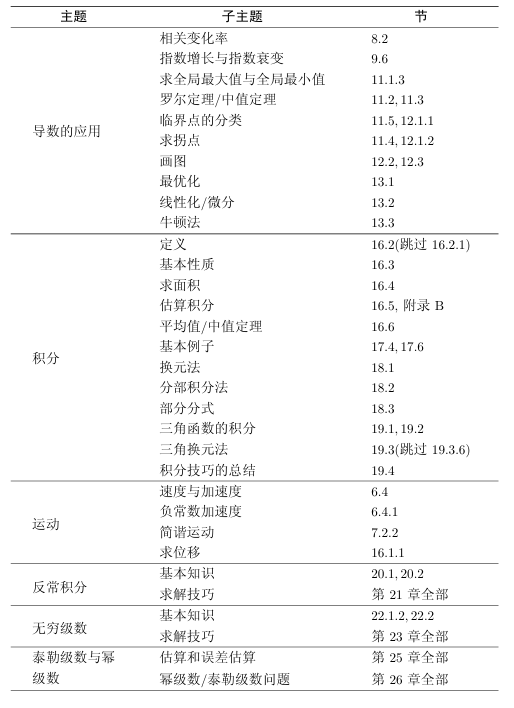
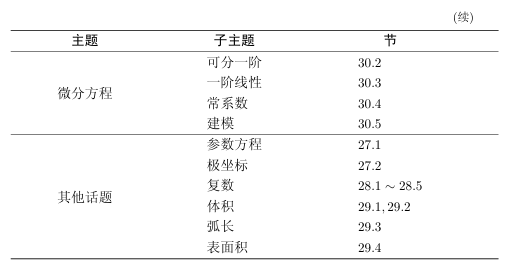
如果你快要参加考试了,那么发挥本书效用的机会就来了.我很同情你的处境,因为你没有时间阅读整本书的内容!但是你不用担心,后面的那张表会标出本书的主要章节,来帮助你备考.此外,纵观整本书,下列图标会出现在书中页边空白处,让你快速识别什么是重要内容.

  • 把你自己总结的所有重要的知识点和公式都写出来,以便记忆.虽说数学不是死记硬背,但也有一些关键的公式和方法,最好是你能自己写得出来.好记性不如烂笔头嘛!通常来说,做总结足以巩固和加强你对所学知识的理解.这也是我没有在每一章的结尾部分做要点总结的主要原因.如果你自己去做,那将会更有价值.

  • 尝试自己做一些类似的考试题,比如你们学校以前的期末试题,并在恰当的条件下进行测验.这将意味着遵守不间断,不吃饭,不看书,不打手机,不发电子邮件,不发信息等诸如此类的考试规则.完成之后,再看看你是否可以得到一套标准答案来评阅试卷,或请人帮你评阅.

01

图片

《普林斯顿微积分读本（修订版）》

作者：【美】阿德里安·班纳

译者：杨爽 赵晓婷 高璞

本书阐述了求解微积分的技巧，详细讲解了微积分基础、极限、连续、微分、导数的应用、积分、无穷级数、泰勒级数与幂级数等内容，旨在教会读者如何思考问题从而找到解题所需的知识点，着重训练大家自己解题的能力。

本书适用于大学低年级学生、高中高年级学生、想学习微积分的数学爱好者以及广大数学教师。本书既可用作为教材、习题集，也可作为学习指南，同时还有利于教师备课。

turingbooks
关注
博客
现代数学思考方法发生了什么转变？这本书刷新了很多人的认知！
12-01 15
作者着眼于数学思考方法的发展，将数学划分为古代数学、中世纪数学、近代数学、现代数学，以生动的讲述方法清晰呈现了数学的发展脉络，并结合日常经验讲述了诸多数学概念与思想的来源与发展。与绘画中的这种风格极为相似的，是前文提到过的以希尔伯特的《几何基础》为起点的现代数学的思考方法，也就是关于结构的思考方法。现代数学则如我刚才所言，是关于结构的，即构成式的。然而，由于结构的思考方法在20世纪之后才逐渐发展，因此对于“这种思考方法是万能的吗”“可以把数学简单地称为‘结构的科学’吗”这类问题，人们仍然存在一定的疑虑。
博客
这一场线下的 AI 碰撞，你准备好了吗？
11-29 32
AI Maker Summit 由 AI 创业者阿颖——“AI 产品阿颖”公众号主理人、聚创稻壳 CEO，倾力打造，这里汇聚了一群热爱动手、热爱探索、热爱新技术的人——工程师、产品经理、AI 创作者等等。每一场分享都由一线实操嘉宾呈现，他们带来新鲜的思考、新鲜的经验和新鲜的判断，一切都是最鲜活的前沿。一年的最后，停下忙碌和日复一日的脚步，给自己和团队一次呼吸“新鲜”AI 空气的机会，重新审视自己。你会听到别人怎么判断趋势，怎么踩坑，怎么验证想法，也会看到不同领域的人在同一张桌子上碰出新的方向。
博客
硅谷大佬上手 Gemini 3，直言：“回不去了。” 普通人现在到底该学什么？
11-29 32
他称谷歌的进展可能会给公司带来短期的经济压力，但强调 OpenAI 在快速追赶。9 周实战，带你从 0 到 1 打造自己的智能 Agent，从基础原理到工具调用，从协作系统到项目落地，每周直播 + 社群陪跑，明星导师李博杰亲自授课，干货密度拉满，让你快速构建 Agent，从零到一。这不是他的态度转变的问题，而是整个行业正在发生的一个非常明显的趋势，大模型的迭代速度，已经快到连巨头都喘不过气。在这场快得几乎让人来不及眨眼的竞速里，巨头们都在拼命往前跑，而我们普通人能做的，就是尽量别停在原地。
博客
如何找到未来的风口行业？麦肯锡分析师独家深度实操分享
11-28 90
不过，如果你按着他们的框架，愣是梳理出了一个行业的商业模式、产业链、市场规模、竞争格局等等，对于大多人来说，可能还是不知道怎么用。“在家快速搞定一顿饭”这个需求，一开始满足这个需求的是干粮，接着是方便面，后来有了电话外卖，这些年又诞生了外卖平台和预制菜。只有整个行业的竞争格局比较好的时候，也就是横向竞争没那么激烈、纵向你又有议价权的时候，整个行业才能比较好的赚钱。“时光机理论”，背后也是类似的逻辑。类比一下就是，真正实用的，应该是「树状」的知识体系，而不少课程给到我们的，只是一团团「云状」的知识。
博客
豆瓣9.5分！这才是全球史上所有顶尖大学数学教材中使用率最高的一本神作！
11-27 78
这种反复的、情境化的训练，培养了学生的思维模式，使学生在面对复杂陌生的情景时，能超越机械计算，学会像数学家一样思考。在哈佛大学的牵头下，集结数学教授与物理学、工程学、计算机科学、经济学等领域的专家，共同设计了一套强调“自然理解”和“跨学科应用”的“哈佛教材”，几乎摒弃了传统教科书对形式化推导的追求。斯图尔特作为波利亚的学生，不仅亲承大师教诲，更是将他的“四步解题法”（理解题目、思考计划、实施计划、回顾反思）扩展和深化，设计了自己的“解题的基本原则”，创造性地嵌入到微积分的知识体系中，成为了本书的独特标志。
博客
这一场直播非常关键！！
11-27 45
一句话：看完这场直播，你就能判断 —— Agent 这条路，你到底要不要跟上。Agent 到底是什么？和工作流 /ChatGPT 有啥本质区别？为什么今年所有大厂、SaaS、ToB 公司都在做 Agent？想提升效率、想升职加薪、想做副业但不知道怎么用 AI 的人。天天用 ChatGPT 但不知道怎么“让它自动干活”的人。普通人能不能做出一个自己的 Agent？从零构建 Agent 的核心步骤是什么？被 AI 吓到但还没开始学的人。
博客
你应该写一个 Agent ！
11-27 39
你输入的每一句话、保存的每个输出、描述的每个工具、工具的每次输出，都会消耗 Token（也就是说：它们都占据了你用来假装和无状态黑盒对话的字符串数组的空间）。我从没认真对待过那种说法：要让我和 LLM 说“你是个勤勉尽责的助手，若我让你专心递黄油，你就会心甘情愿地只做这件事，绝不会想着把我血液里的铁元素提炼出来做回形针”。MCP 只是帮你把一个单上下文窗口的简单编程 Agent “拉壮丁”去做客服查询，最多帮你省了几十行代码，却让你丧失了对 Agent 架构的掌控力。我只是想让你明白其中的道理。
博客
信息论之父香农的开山之作《通信的数学理论》中文版正式发布！
11-26 64
1948 年，香农发表了著名论文《通信的数学理论》（A mathematical theory of communication），首次提出“信息熵”的概念，从此，一切抽象的信息都可被数学化度量，这篇论文也被视为信息论的开山之作。更令人惊讶的是，无论信息的内容是什么，莎士比亚的诗、贝多芬的交响曲，还是黑泽明的电影，最有效的传输方式都是先把它们转化为比特。这本书不像科幻小说那样刺激，但读懂它，你会明白我们生活的这个世界，本质上是一场宏大的信息传递，而香农，就是第一个揭示这场游戏规则的人。
博客
B 站 500 万人都在学的 Python 数据分析全流程，直播解锁实战技巧！
11-23 55
想象一下，用 Python 抓取销售数据，分析广告投放，再生成漂亮的可视化图表，不仅有成就感，还特别有趣。在直播里，你不仅可以看到书里讲的方法如何在真实场景中操作，还能边看边动手实践。书里从环境搭建、数据采集，到数据清洗、分析和可视化，每一步都循序渐进，贴近真实场景。无论你是零基础的新手，还是想提升数据分析能力的朋友，这次直播都是一次难得的机会。如果把这个时代的声音调大，你会听到一个越来越清晰的节奏：数据、数据、还是数据。看完书，你不仅能学会工具，更能理解数据思维，知道如何用数据解决问题。
博客
2025年了，Strang在1976年出版的《斯特朗线性代数》，仍然是最好的数学教材！
11-22 112
教授反对传统教学“从定义到定理”的僵化模式，而是主张“从直观到抽象”的自然过程，以具体问题为出发点，以自然理解为核心，以实际应用为落脚点，引导读者“自己发现”数学概念。因此，他从不急于抛出抽象定义和推导，转而采用一种近乎“讲故事”的形式，用口语化的叙事风格、略带风趣的方式解释复杂的数学思想。此外，本书在编排上的另一大特点是，提早引入线性变换这一教学难点，并不拘一格地将其融入到各个主题中：先随着矩阵一起，介绍相对容易接受的伸缩、旋转、反射、投影，而把更一般的线性变换（特别是相似变换）放到后面。
博客
写代码时我只怕 bug，做管理后我怕所有人！
11-21 49
本书之所以有价值，不是因为它告诉你如何去成为一个伟大的领导者，而是它把技术管理的真实逻辑告诉你，让你第一次意识到原来你遇到的问题，不是你一个人的问题。而当你终于看懂这些隐秘的动机与反应，你会突然意识到原来团队不是被技术难倒的，而是被我们彼此之间那些说不出口的情绪、需求和期待绊住了脚。”“是不是我升得太快了？技术管理者是一个孤独的岗位，没有前辈带，没有师傅教，遇到问题又不能对下讲，向上讲也不一定有人能懂。它告诉你如何建立信任，做清晰沟通，给反馈，管冲突，理优先级，带节奏，带团队文化，甚至是带自己。
博客
豆瓣评分 9.0，改变无数人编程认知的那本书，十年后重磅升级！
11-20 74
那时没有这么多视频教程，也没有现成的代码片段，学编程就是在一行行枯燥的代码里摸索，看不懂就翻回去，敲不对就从头再试。被誉为“C语言圣经”，是日本最具影响力的 C 语言入门教程之一，自出版以来不断重印、修订，紧贴当下开发环境和规范。全书共 13 章，包含 243 个可运行的示例程序与 245 张精心设计的图表，能够帮读者高效学习 C 语言，全面提升编程能力。多年之后回望，我们才明白《明解 C 语言》解决的不只是语法难点，而是第一次接触编程的人普遍拥有的不安与困惑。它既是时代的起点，也是个人程序人生的开端。
博客
不信这个书单治不了你的数学恐惧症 | 图灵2025年最全数学书单
11-19 212
本书从古希腊几何学时代讲起，涵盖代数、微积分、集合、数论、拓扑、逻辑等几乎全部数学分支中的证明故事，讲述了证明的演变及其在数学中的重要作用和启发意义。全书从分析的源头——数系的结构和集合论开始，然后引向分析基础，再进入幂级数、多元微分学和傅里叶分析，最后介绍勒贝格积分，几乎完全是以具体的实直线和欧几里得空间为背景，完美结合了严格性和直观性。小故事，小游戏，学中玩，玩中学。这本书涵盖了线性代数的核心知识和方法，也融入了丰富的应用案例，并在具体的计算和抽象的论述之间找到平衡，弥补了传统线性代数课程的不足。
博客
B 站 500 万人都在学的神级数据分析课，终于出版了！
11-18 103
没有判断力，再好的代码你也不敢用。Requests、Selenium、BeautifulSoup、lxml ，可能之前你只听过名字，但你会在这本书中真实体验到：“原来数据可以让我自己拿，不用求别人。这本书实战导向，作者按现实常用的任务来编写，与其说教你代码，不如说教你如何把遇到的问题都解决掉。比如你明明知道竞争对手的视频火了，但你想分析一下评论、投放、关键词到底在哪儿发力，唯一的办法是用手一点点往下翻。更现实一点，你可能只是想做一个选题、一篇论文、一份汇报，但数据总是乱的、脏的、缺的，你只能对着屏幕叹气。
博客
他一生贫困与苦难，留下不到一页纸的定律，但改写了数学、物理科学史进程！
11-17 97
作者着眼于数学思考方法的发展，将数学划分为古代数学、中世纪数学、近代数学、现代数学，以生动的讲述方法清晰呈现了数学的发展脉络，并结合日常经验讲述了诸多数学概念与思想的来源与发展。第三定律描述的是行星轨道的大小与其公转时间之间的关系，具体内容是“行星绕太阳公转周期的平方和它们的椭圆轨道的半长轴的立方成正比”。用微分表达的行星瞬间运动情况，也与牛顿的万有引力定律相合，即太阳和火星互相被引力吸引，这种引力的大小与二者距离的平方成反比。这个火星与太阳之间形成的“雨刮器”，其扫过的面积在相等的时间内总是相等的。
博客
豆瓣评分 9.4，为什么很多人都在推荐这本书？几页就能让你看懂！
11-16 76
在本书中，你将学习如何规划和编写大模型的各个组成部分、为大模型训练准备适当的数据集、进行通用语料库的预训练，以及定制特定任务的微调。我原本以为这本书要么会过度简化、要么会高度抽象，甚至可能出现那种你先接受这个公式就好的玄乎讲法，但它其实很踏实，从最基础的模块开始讲起，一步步带你把模型搭出来。豆瓣评分 9.4，全网疯传的大模型教程，由畅销书作家塞巴斯蒂安•拉施卡撰写，通过清晰的文字、图表和实例，逐步指导读者创建自己的大模型。相反，如果你想要非常深入的理论推导，这本书不是论文风那种深度，完全能够理解。
博客
新书上市 | 跪了！看了人大附中名师给孩子划的数学知识点，才明白什么叫降维打击……
11-15 86
此外，在撰写工作中，我得到了出版社戴老师、魏老师的鼓励与帮助，他们提出的建议和意见为本书增色不少，在此一并谢过。的你，通过本书，可以了解高中数学的知识脉络，明确高中数学的知识板块，构建高中数学的知识框架，可以让它陪着你开始“学”数学；的你，通过本书，可以丰富课本学习的知识维度，形成逻辑清晰的知识网络，理顺螺旋上升的知识链条，可以让它陪着你深入“习”数学；的你，通过本书，可以归纳考试要求的知识清单，填补习题背后的知识漏洞，重温方法技巧的知识基础，可以让它陪着你继续“懂”数学。
博客
MIT教授Gilbert Strang的线性代数课为何被称为“天花板课程”？
11-14 126
.....直到今天，我仍然记得并使用他的矩阵乘法的列图和行图（AB 的每一列都是 A 的列的线性组合）--这在其他地方很少教授，但确实有帮助。他的一生充满了对数学的热爱、对知识的渴望和对后辈的关爱，成为我们永远的楷模。"数学系主任 Michel Goemans 教授表示："他对数学教学产生了巨大的影响，通过他的课程讲座向麻省理工学院的数万名学生，通过他的教科书向其他学术机构的无数学生，以及通过他的在线讲座和数字媒体向全球的数百万人。"我喜欢学生，想帮助他们，"他在 2019 年的一次采访中说。
博客
数学圈公认的两本高数高分入门神作，内容循序渐进，秒杀市面上绝大多数教材！
11-14 136
教授反对传统教学“从定义到定理”的僵化模式，而是主张“从直观到抽象”的自然过程，以具体问题为出发点，以自然理解为核心，以实际应用为落脚点，引导读者“自己发现”数学概念。他的写作风格是教科书中的一股清流，注重数学概念的直观理解，而不仅仅是数学推导，避免对定义、定理、证明的枯燥罗列。此外，本书在编排上的另一大特点是，提早引入线性变换这一教学难点，并不拘一格地将其融入到各个主题中：先随着矩阵一起，介绍相对容易接受的伸缩、旋转、反射、投影，而把更一般的线性变换（特别是相似变换）放到后面。（p710练习67）
博客
一份线性代数的自救指南！
11-12 119
按照现行的国际标准，线性代数是通过公理化来表述的。本书为线性代数入门的科普读物，书中以“如何理解线性代数”“如何理解矩阵的基础概念与计算方法”为线索，用漫画故事生动呈现了线性代数初学者的学习历程。本书内容循序渐进，结构严谨，从直观描述开始，逐步引入形式描述，注重从几何角度引导读者理解线性代数的本质，是帮助读者学习线性代数、加深对线性代数理解的数学教材。通俗易懂，非常适合自学。这本书涵盖了线性代数的核心知识和方法，也融入了丰富的应用案例，并在具体的计算和抽象的论述之间找到平衡，弥补了传统线性代数课程的不足。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值