基于三维混沌映射的高效图像加密算法
引言
随着科学技术的快速发展,数字信息已在我们的日常生活中广泛传播。图像作为重要的数字源之一,已成为人们之间共享信息的一种常见且直接的方式。因此,大量图像通过计算机或手机在网络上传输。然而,由于存在未授权访问、读取和篡改等问题,图像的安全性已成为我们所有人面临的紧迫问题。为解决这一问题,可采用密码学技术来抵御非法攻击者,从而保护图像内容[1, 2]。
由于混沌系统(映射)具有非线性、遍历性以及对参数和初始条件的高敏感性等优异特性,基于混沌的图像加密算法近年来受到了广泛关注。例如,提出了一种二维 Logistic‐ICMIC级联映射并将其应用于图像加密方案中。通过同时采用比特级混淆与扩散,经过一些比较后结果显示具有更高的安全性、更低的计算量和更小的时间复杂度。在一项研究中,借助生物DNA序列操作和细胞神经网络提出了一种新的图像加密方案,其中设计了比特替换、密钥流生成和扩散过程。为了使密钥流依赖于明文图像,提出了一种反馈结构,解决了“传统置换操作只能打乱图像像素位置”的问题。
然而,当前一些基于混沌的方法是将加密算法分为置换和扩散两个阶段,并使用双混沌系统(映射)或设置两组密钥。例如,在[9]中,分段线性混沌映射被使用了两次,并采用两组独立的密钥;随后引入了一种新的扩散策略,并对像素比特位进行置换。在[10],中,切线延迟椭圆反射腔映射和斜帐篷映射均被用于加密算法中,其中一个用于置换操作,另一个用于扩散操作。为了解决这些问题,我们提出一种仅使用一个混沌映射和一组密钥的新图像加密算法。由于高维混沌系统(映射)能够表现出复杂的混沌行为,本文所提出的算法采用了三维混沌映射[11] 。本文其余部分组织如下:首先,详细描述所提出的图像密码系统;然后,进行仿真及相关安全分析;最后,对我们方法做出一些结论。
2. 所提出的图像密码系统
2.1 三维混沌映射
一种三维交织逻辑映射(ILM)[11]定义如下
$$
\begin{cases}
x_{i+1} = \left( k_1 y_i x_i z_i \mu_1 \right) \mod 1 \
y_{i+1} = \left[ \frac{k_2}{y_i + z_i} + x_i \mu_2 \right] \mod 1 \
z_{i+1} = \left[ x_i y_i + k_3 z_i \mu_3 \right] \mod 1
\end{cases}
\quad (1)
$$
其中 $0 < \mu_1 \leq 3.999$,$k_1 > 33$,$k_2 > 37$,$k_3 > 35$,$\mu_2,\mu_3$ 是固定的。那么,上述 ILM 将表现出超混沌行为。更多内容可参考文献 [11]。
2.2 加密过程
通常,有意义的自然图像中相邻像素之间具有很强的相关性。为了降低这种相关性,我们采用置换方法来打乱像素位置,即对所有像素进行交换。假设明文图像的大小为 $P \in \mathbb{R}^{m \times n}$。在算法中通过设置随机的密钥作为ILM的初始条件。为了使生成的密钥流依赖于明文图像,计算一个因子
$$
s = \sum_{i,j} P(i,j)^2 \quad (2)
$$
其中 $s$ 是一个整数。然后,它被设计并转换为一个小数
$$
u = f(s) \quad (3)
$$
其中 $f(s)$ 是一个通过迭代的循环操作使 $s/10$ 小于10的函数。接下来,密钥通过以下方式更新
$$
\begin{cases}
x_0 = (x_0 + 0.1 / 3 + u) \mod 1 \
y_0 = (y_0 + 0.2 / 5 + u) \mod 1 \
z_0 = (z_0 + 0.3 / 7 + u) \mod 1
\end{cases}
\quad (4)
$$
其中 $\mod$ 是模函数。然后,通过迭代对ILM进行若干轮迭代,得到 ${x_0,x_1,x_2,\dots}$、${y_0,y_1,y_2,\dots}$ 和 ${z_0,z_1,z_2,\dots}$。这里,${x_0,x_1,x_2,\dots}$ 和 ${y_0,y_1,y_2,\dots}$ 用于第一次置乱,而 $W={x_t,x_{t+1},\dots,x_{t+m}}$、$V={y_t,y_{t+1},\dots,y_{t+n}}$ 和 ${z_0,z_1,z_2,\dots}$ 用于第二次置乱。需要注意的是,$x_0,y_0,z_0$ 会根据明文图像自动更新。因此,在通信过程中,发送方和接收方无需记录或保存它们。
置乱加密。选择两组集合 $X={x_{t+1},x_{t+2},\dots,x_{t+m}}$ 和 $Y={y_{t+1},y_{t+2},\dots,y_{t+n}}$,其中 $t$ 是为避免有害影响而设置的一个数。对这两组集合进行排序函数操作,并获得索引 ${h_1,h_2,\dots,h_m}$ 和 ${l_1,l_2,\dots,l_n}$。然后,根据 $H$ 对明文图像的行进行交换(即将第 $i$-th 行移动到第 $h_i$-th 行)以及根据 $L$ 对列进行交换(即将第 $i$-th 列移动到第 $l_i$-th 列)。由此,通过第一次置乱得到置换后的图像 $A$。再次选择两组集合 $W={w_{t+1},w_{t+2},\dots,w_{t+m}}$ 和 $V={v_{t+1},v_{t+2},\dots,v_{t+n}}$,并将所有元素转换为灰度层级由
$$
W = \left[ W \times 10^{14} \right] \mod n, \quad V = \left[ V \times 10^{14} \right] \mod m
$$
根据图像大小对置换后的图像分别进行行和列的循环置换,得到新图像 $B$。因此,在第二次置乱后,置换加密完成。
扩散加密。为了抵御统计攻击,通常在置换之后采用扩散来改变明文图像中的灰度分布。通过使用密钥 $x_0$、$y_0$ 和 $z_0$ 迭代 ILM,可以获得三个序列,即 ${x_0,x_1,x_2,\dots}$、${y_0,y_1,y_2,\dots}$、${z_0,z_1,z_2,\dots}$。然后将它们排列为 ${x_0,y_0,x_1,y_1,\dots}$ 和 ${x_0,z_0,x_1,z_1,\dots}$。丢弃前几次迭代以避免有害影响后,选取部分元素形成两个长度为 $mn$ 的随机集合,即
$$
S_1 = {x_{r+1},y_{r+1},x_{r+2},y_{r+2},\dots,x_{r+mn},y_{r+mn}}
$$
$$
S_2 = {x_{r+1},z_{r+1},x_{r+2},z_{r+2},\dots,x_{r+mn},z_{r+mn}}
$$
为了匹配图像大小,$S_1$ 和 $S_2$ 按从上到下、从左到右的顺序被重新排列为矩阵 $D \in \mathbb{R}^{m \times n}$ 和 $F \in \mathbb{R}^{m \times n}$。在所提出的算法中,扩散加密设计如下:
$$
\begin{cases}
D_i = \left[ 10^{14} \times d_i \right] \mod 256 \
F_i = \left[ 10^{14} \times f_i \right] \mod 256 \
k_e = \left[ 3k_1 + 5k_2 + 10^{14} \times z_0 \right] \mod 256 \
C_i = (B_i + D_i + F_i + k_e) \mod 256
\end{cases}
\quad (5)
$$
其中 $i=1,2,\dots,m$。$C_i$、$B_i$、$D_i$、$F_i$ 分别表示行。$e$ 是一个元素全为1的向量。因此,可得到密文图像 $C$。
2.3 所提出算法的流程图
我们提出了一种新的图像加密算法,该算法采用一个混沌系统和一组密钥。所提出的图像加密方案的示意图如图1所示。
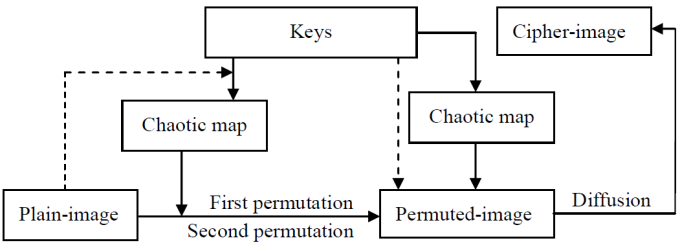
2.4 解密过程
由于我们的方法中设计的置换‐扩散结构是对称密码,因此解密过程可以通过加密过程的逆操作来实现。要从密文图像恢复出明文图像,首先以逆序进行扩散,然后对逆向循环操作执行置换,最后对所有列和行进行逆向交换。
3. 仿真
在本节中,为了验证所提出算法的有效性,随机选取了一些图像(灰度和彩色)进行测试,如图2所示。仿真在Windows 7系统的PC上使用MATLAB R2011b进行。从这些结果可以看出,与明文图像相比,密文图像没有泄露任何有用信息。
 Lena的明文图像,(b) Lena的密文图像,(c) Cameraman的明文图像,(d) Cameraman的密文图像,(e) Rice的明文图像,(f) Rice的密文图像,(g) Building的明文图像,(h) Building的密文图像,(i) Lake的明文图像,(j) Lake的密文图像,(k) Tree的明文图像,(l) Tree的密文图像)
Lena的明文图像,(b) Lena的密文图像,(c) Cameraman的明文图像,(d) Cameraman的密文图像,(e) Rice的明文图像,(f) Rice的密文图像,(g) Building的明文图像,(h) Building的密文图像,(i) Lake的明文图像,(j) Lake的密文图像,(k) Tree的明文图像,(l) Tree的密文图像)
4. 安全分析
4.1 密钥空间
密钥空间是密钥的组合。在我们的方法中,使用了ILM中的三个初始条件 $x_0$、$y_0$ 和 $z_0$,而不考虑其他控制参数。因此,如果精度设置为 $10^{-14}$,则密钥空间大小可达 $10^{42}$。这样,穷举攻击将变得不可能。
4.2 直方图
图像的直方图显示了消息的统计信息,尤其是可以在其中观察到像素值的分布。为了使统计攻击不可行,理想的图像密码系统应使密文图像中的灰度分布均匀。图3显示了使用我们方法前后Lena、Boat和Baboon的直方图。因此,攻击者很难对所提出的算法发起统计攻击。
 Lena的明文图像,(b) Lena的密文图像,(c) Boat的明文图像,(d) Boat的密文图像,(e) Baboon的明文图像,(f) Baboon的密文图像)
Lena的明文图像,(b) Lena的密文图像,(c) Boat的明文图像,(d) Boat的密文图像,(e) Baboon的明文图像,(f) Baboon的密文图像)
4.3 信息熵
信息熵 [12] 通常用于测试接收到的图像/消息的随机性,其定义为
$$
E(m) = \sum_{i=0}^{L-1} p(m_i) \log_2 \frac{1}{p(m_i)} \quad (6)
$$
其中 $L = 2^k$,对于灰度图像 $k = 8$。表1列出了部分测试图像的结果。显然,密文图像的信息熵值接近理论值8。
| 测试图像 | 明文图像 | 密文图像 |
|---|---|---|
| Lena | 7.4532 | 7.9974 |
| Peppers | 7.5715 | 7.9993 |
| Baboon | 7.3579 | 7.9994 |
4.4 明文图像的敏感性
像素变化率(NPCR)和归一化平均变化强度(UACI)是两种有效工具 [13],用于衡量对明文图像任何改变的敏感性,其计算方式如下
$$
\text{NPCR} = \frac{\sum_{i,j} D(i,j)}{m \times n} \times 100\% \quad (7)
$$
$$
\text{UACI} = \frac{\sum_{i,j} |C’(i,j) - C(i,j)|}{m \times n \times 255} \times 100\% \quad (8)
$$
其中
$$
D(i,j) =
\begin{cases}
0, & \text{if } C’(i,j) = C(i,j) \
1, & \text{otherwise}
\end{cases}
\quad (9)
$$
其中 $C’$ 和 $C$ 是两个密文图像。通过随机改变位置(203,176)处的一位,彩色图像Lena的结果列于表2和表3中。从中可知,所有NPCR值均超过99.5%。因此,所提出的算法对明文图像具有高敏感性,能够有效抵抗差分攻击。
| 通道 | UACI | NPCR |
|---|---|---|
| R | 33.3494 | 99.6384 |
| G | 33.2799 | 99.5544 |
| B | 32.1391 | 99.5513 |
| 通道 | UACI | NPCR |
|---|---|---|
| Lena | 33.1534 | 99.5880 |
| Boat | 33.1481 | 99.5838 |
| Peppers | 33.4113 | 99.6151 |
5. 结论
本文提出了一种基于三维混沌映射的图像加密算法。结合传统的置换‐扩散加密结构,我们的方法采用了双重置换。然后,进一步进行扩散操作以重写明文图像的灰度分布。幸运的是,我们仅使用一个混沌映射和一组密钥即可实现高安全性。为了验证我们算法的性能,展示了密钥空间、直方图、信息熵和敏感性分析结果。





















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








