深蓝学院运动规划作业ch6 飞行走廊硬约束轨迹优化

Tipriest_

已于 2024-11-25 16:00:35 修改

阅读量1.1k

点赞数 20

分类专栏：机器人轨迹规划文章标签： matlab 数学建模几何学

于 2024-11-14 23:29:08 首次发布

本文链接：https://blog.youkuaiyun.com/titan__/article/details/143780424

版权

机器人轨迹规划专栏收录该内容

3 篇文章

订阅专栏

一. 问题构建：

在minimum_snap的基础上，飞行走廊考虑了环境中的障碍物约束问题，在将可通行区域限制为走廊环境后，为原本的轨迹优化问题增加了不等式约束，同时取消了原来优化后的轨迹必须经过路径中间的n-2个waypoint的约束限制，使得生成的轨迹和时间分配可以更自由，下面来看一下新的问题的表达形式：

(1) 问题定义形式：

飞行走廊约束下的minimum_snap问题经过转化之后将会变成了一个具有不等式约束的QP问题，问题的表达形式为:

$\begin{array}{cc}\min&c^TQ_0c\\s.t.&A_{eq}C=b_{eq}\\&A_{ie}C\leq b_{ie}\\&c_{j\in\Omega_{j,j}=1,2,3,\ldots,m}\end{array}$

对比一下无约束时候的minimum_snap问题的表达形式，

可以发现在飞行走廊情况下问题的定义形式主要出现了以下区别：

a. 原来的多项式系数 $p$ 变成了替换为了贝塞尔曲线的控制点 $c$ 。

b. 新增了不等式约束。

同时，通过对于飞行走廊概念的理解可以发现有如下的区别：

c. 对于给定的n个控制点waypoint，ch5的轨迹优化会有n-1段轨迹，是每个控制点之间的轨迹，但是飞行走廊具有n段轨迹(如上图中的5段轨迹所示)。

(2) 贝塞尔曲线性质

出于贝塞尔曲线的以下四个优秀性质，在飞行走廊进行轨迹生成的时候，使用了Bernstein基底的贝塞尔曲线，贝塞尔曲线的定义式如下

$B_j(t) = c_j^0 b_n^0(t) + c_j^1 b_n^1(t) + \cdots + c_j^n b_n^n(t) = \sum_{i=0}^n c_j^i b_n^i(t)$

$b_n^i(t) = \binom{n}{i} \cdot t^i \cdot (1 - t)^{n - i}$

贝塞尔曲线主要具有以下的四个性质：

第一点：贝塞尔曲线一定经过控制该段贝塞尔曲线生成的第一个和第n+1个控制点，并且一定不经过其他控制带你，n为生成的贝塞尔曲线的阶数，上述贝塞尔曲线的定义式中的 $c_j$ 为贝塞尔曲线的控制点。

第二点：控制点若构成一个凸包区域，则由这些控制点生成的贝塞尔曲线一定在这些凸包区域内。

第三点：贝塞尔曲线具有Hodo性质，贝塞尔曲线的导数的控制点由贝塞尔曲线的控制点决定。

第四点：一段贝塞尔曲线的时间长度必须为[0, 1]。

知道了贝塞尔曲线的控制点，就可以通过Bernstein基底获得对应的多项式表达式，也可以直接预先计算好，知道贝塞尔曲线的控制点，可以根据如下的变换矩阵得到多项式表达式的各个系数：

例如，当阶次为6阶时，多项式的各个系数为：

所以理论上，现在我们已经可以得到新的能量函数Q为

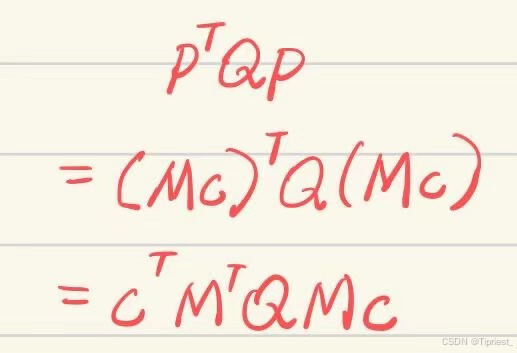
但是，由于贝塞尔曲线性质4的存在，事情并没有这么简单，我们还需要引入一个时间缩放因子s。

(3) 能量函数Q0：

通过对minimum_snap的重新推导发现，时间归一到[0,1]进行缩放之后，原来的T(k)项现在变成1不需要考虑，多出来了s的时间缩放项进行处理。因此再计算Q的每一个值的时候，最终每一项需要乘上s^-(2k-3)，

我们用Q0矩阵代表考虑了时间缩放因子和M变换矩阵之后的Q矩阵，对给定的5阶，四个点的情况求其 $Q_0$ 矩阵，因为 $Q_0 = M^{T}QM$ ，首先求Q矩阵为

$M$ 矩阵为:

$Q_0$ 矩阵为：

这里有一个地方要注意一下，目前的假设条件并不能保证 $Q_0$ 一定为正定的，因此使用matlab函数

获得与 $Q_0$ 最接近的正定矩阵。

(4) 约束项1 $A_{eq}c=b_{eq}$

根据贝塞尔曲线的性质，仍然应该有整条轨迹的起点和终点的位置及各阶导数满足约束条件，每两段轨迹之间的连续性约束也仍然需要满足，相比于ch5只是少了每个轨迹中间点之间的位置约束，最终得到的 $A_{eq}$ 与 $b_q$ 分别为:

(5) 约束项2 $A_{ie}c\leq b_{ie}$

对于n个waypoint，飞行走廊会有n段轨迹，每一段会有(n_order+1)个控制点，每一段的控制点都应该在这一段的飞行走廊的矩形凸包内部，下一段的控制点都应该在下一个飞行走廊的矩形凸包内部，由于连续性约束，上一段的最后一个控制点和下一段的第一个控制点是一个控制点，所以隐性地有：两端轨迹之间的交点处于两段轨迹所在的矩形凸包相交的区域内，因此在位置上需要施加的约束共有n*(n_order+1)个

对于速度项，就像是多项式在求导后会降一阶一样，每一段轨迹的速度会有n_order个控制点，因此在速度上需要施加的约束共有n*(n_order)个

同理，在加速度上需要施加的约束共有n*(n_order-1)个

但是，上面提到的施加约束的是一个大于和一个小于约束，所以将大于约束转换为小于约束之后，最后的约束还要整体乘以二，

因此，对于给定的5阶，四个点的情况共有120个约束需要满足

a. 需要满足的最大最小位置约束