深蓝学院 运动规划作业ch8 MPC用于跟踪控制

一、介绍

(1) 模型预测控制基本组成：

• 模型：包括系统模型和问题模型
• 预测：包括状态空间，输入空间，参数空间
• 控制：求解最优控制策略的过程
  • 简单说明一下状态空间，输入空间，参数空间及三者之间的关系
  • 
  • 
  • 
  • 

(2) 模型预测控制的优化目标：

模型预测控制的优化目标包括running cost 和 final cost，其中最后的障碍物约束往往是非凸的，因此需要单独进行处理

(3) 输入量的参数化方法：

使用各种方法对于原输入量的还原效果：

(4) 优化方法：

基于搜索，凸优化和非凸优化的优化方法：

(5) MPC控制一般流程:

但是，对于一个如四旋翼的控制系统，保证系统稳定不发散的情况需要上千Hz的控制频率，这种级别的控制频率在环路中需要对系统的二次规划或者其他规划问题进行每秒钟上千次的求解太吃算力了，所以据此出现了Tube based MPC

(6) Tube based MPC

Tube based MPC 可以以低频率求解优化问题，使得系统需要的计算量较小，但是又可以以较高的频率对扰动和模型的不确定性进行反应 Assiociate controller可以使我们的real state在x*周围一定范围内，只要real_state保持在x*一定范围内，我们的控制就算成功了

(7) MPC常用软件

二、线性模型预测控制

(1) 系统模型

使用一个三阶积分器的质点模型作为系统模型进行预测控制，首先将模型进行离散化，

将离散后的模型转换为预测模型

预测模型计算(预测接下来的20个时间点)：

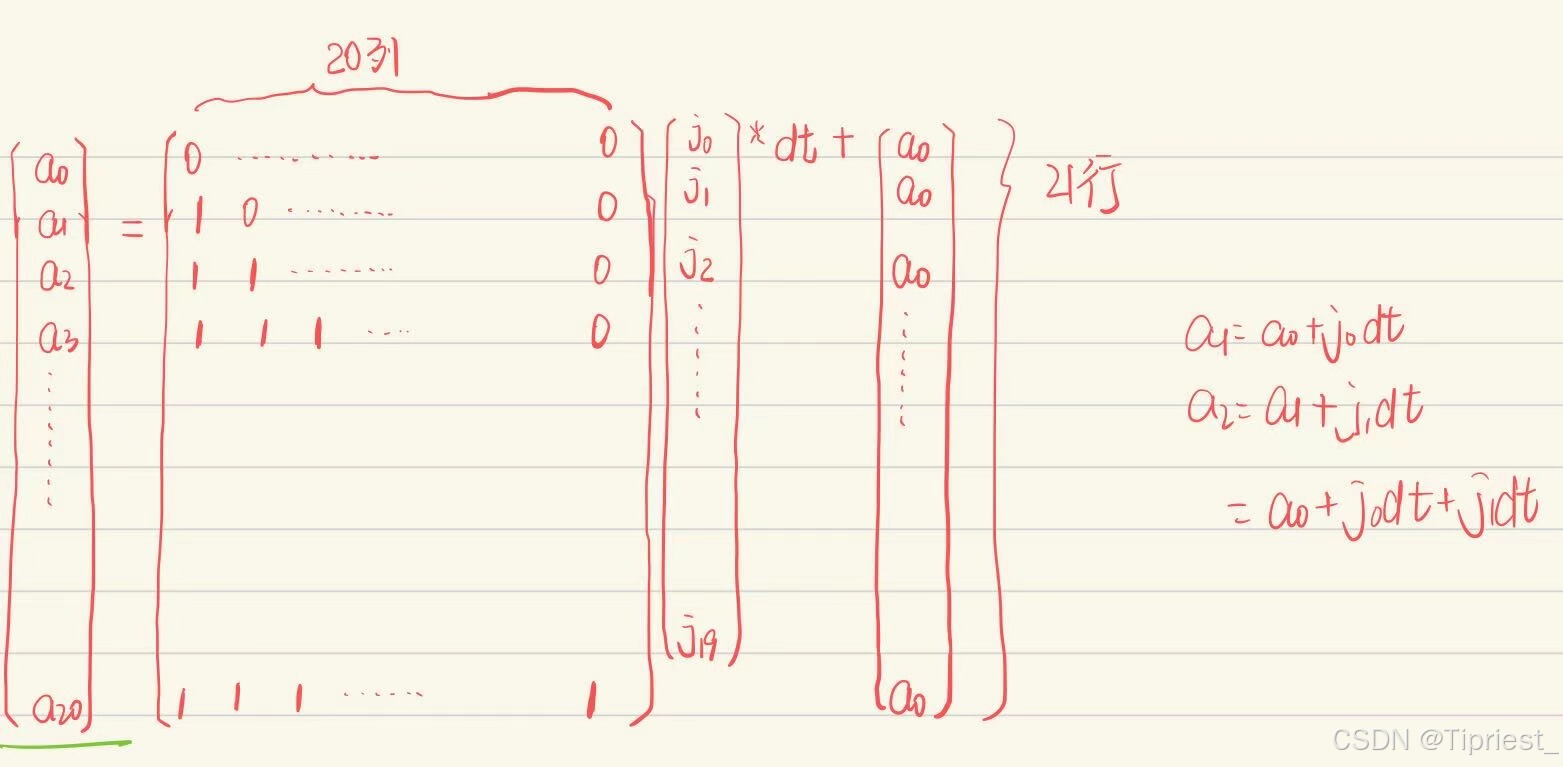
我是通过这样的方法计算了各个变量接下来的预测矩阵，课程中给出了通过解析式直接计算各个预测矩阵的系数的方法：

(2) 问题模型

(3) 使用matlab求解器求解：

(4) 不同权重下求解结果:

(5) 对速度和加速度项施加约束

但是这种硬约束的施加缺少考虑，比如由于某种意外情况导致系统的某一个状态，比如速度违反了硬约束，这种情况往往就会无法求解，因此在施加软硬约束时，需要进行一些更聪明的选择，这个暂且按下不提，对于现在题目中的情况，有一种基于软约束的更好的解决方案。

可以看到结果满足我们的要求，违反了约束限制的状态量首先减小到了可接受范围，然后其他的约束项开始生效。

(6) 软硬约束变量施加选择:        

对于状态量施加软约束，对于控制量施加硬约束往往会是一个聪明的选择。

(7) 线性MPC的限制

总是需要一个线性或者可以近似线性化的模型，

障碍物限制往往是非凸的

三、非线性模型预测控制

四、作业

(1) 问题定义

(2) 推导

这个下面的求解暂时还没有加速度和加速度约束

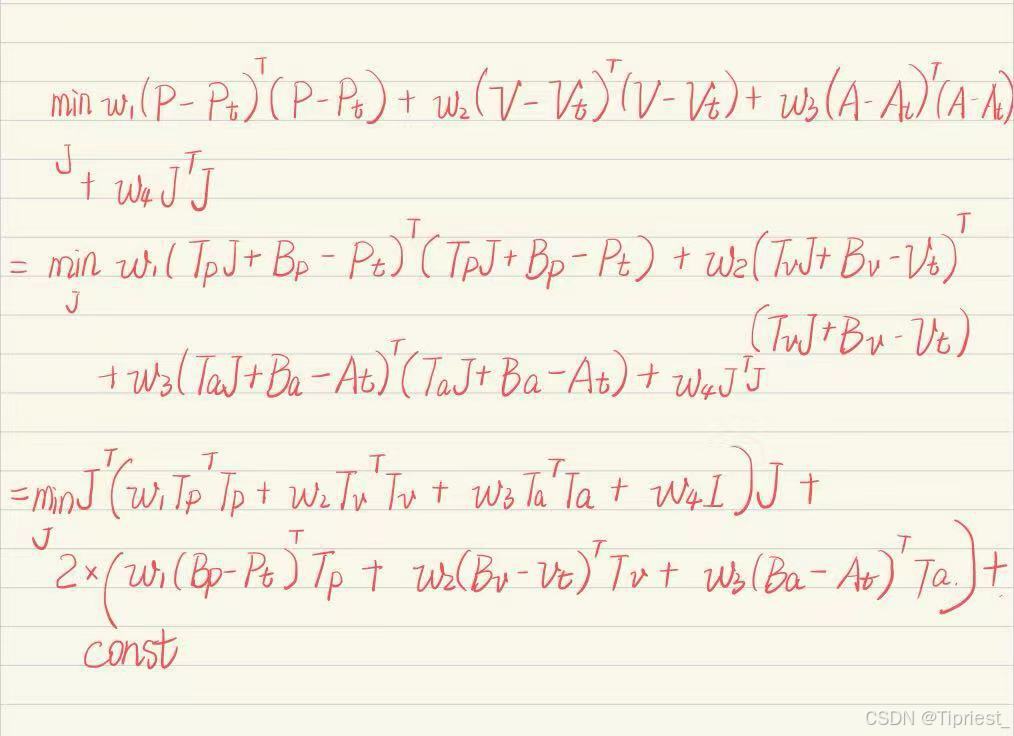
(3) 跟踪结果:

(4) 代码:

Lessons/[深蓝]运动规划/ch8 MPC at master · Tipriest/Lessons · GitHubContribute to Tipriest/Lessons development by creating an account on GitHub.https://github.com/Tipriest/Lessons/tree/master/%5B%E6%B7%B1%E8%93%9D%5D%E8%BF%90%E5%8A%A8%E8%A7%84%E5%88%92/ch8%20MPC

五、参考资料：

移动机器人运动规划-深蓝学院 - 专注人工智能与自动驾驶的学习平台https://www.shenlanxueyuan.com/course/575