深蓝学院 运动规划作业ch5 轨迹平滑优化

一. minimum_snap求解：

(1) 问题定义

minimum_snap问题经过转化问题之后变成了一个有约束QP问题，问题的表达形式为:

(2) 能量函数Q

其中的每一段Q的表达形式如下：

对给定的5阶，四个点的情况求其Q矩阵，Q矩阵的形式如下所示：

(3) 约束项

后面的约束项分为两部分，第一部分为各阶导数约束(包含了起始点和终点的各阶导数约束，和中间点的位置约束)

第二部分为每两端之间的连续性约束，第一段和第二段之间的表达形式分别如下所示

第一部分约束如上所示：这个还是上面的5阶，4个点的情况，从上倒下每一个绿块分别代表起始点，终止点，第二个，第三个点

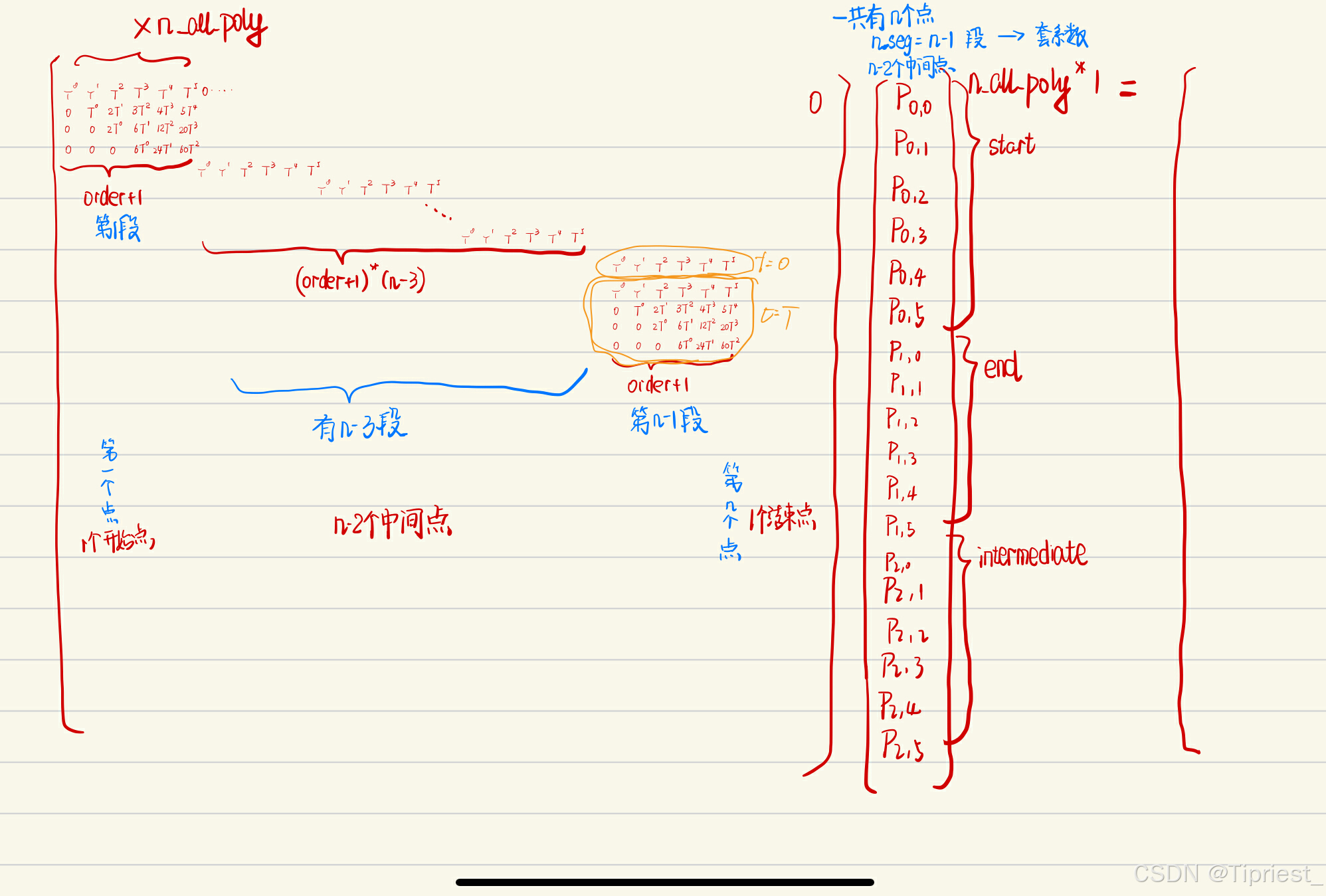
有一点对于第一部分约束的写写画画

第二部分约束如上所示：每两端之间的连续性约束的表达形式如下所示，黄色的是第一段和第二段之间的连续性约束，红色的是第二段和第三段之间的连续性约束

(4) 规划结果

最后结果如下所示:

(5) 时间分配

关于是否对每一段时间进行计算规划出的轨迹的对比，第一张图片的每一段时间都是1,第二段是有一个总的时间，每一段时间是根据两个路径点之间的路径进行分配的，效果很明显要优于第一种情况。

(6)代码

Lessons/[深蓝]运动规划/ch5 轨迹生成/matlab/minimum_snap求解 at master · Tipriest/Lessons · GitHubContribute to Tipriest/Lessons development by creating an account on GitHub.https://github.com/Tipriest/Lessons/tree/master/%5B%E6%B7%B1%E8%93%9D%5D%E8%BF%90%E5%8A%A8%E8%A7%84%E5%88%92/ch5%20%E8%BD%A8%E8%BF%B9%E7%94%9F%E6%88%90/matlab/minimum_snap%E6%B1%82%E8%A7%A3

二. minimum_snap闭式求解：

(1) 问题定义

因为minimum_snap的约束为等式约束，所以可以将等式约束带入到能量矩阵J中，具体的带入是通过两部分巧妙地将每一段的导数连续性约束和每两端之间的连续性约束代入

(2) 多项式系数转换矩阵M

将每一段多项式的系数映射为具有物理意义的每一段轨迹的起点和终点的位置，速度，加速度，jerk等等，具体由多少取决于多项式的阶数，(n_order+1)/2个，这样做有两个好处：

系数具有物理意义，具有数值稳定性

可以便于一会将已经知道的各点的位置以及起点和终点的位置及各阶导数代入到系数项中完成一个等式约束的代入

最后对于一个5阶多项式，有4个点的情况，转换矩阵M为如下所示的情况。

(3) 选择矩阵

选择矩阵将上一步转换好的d更新为约束点与自由点，约束点是指已经指定了参数的那些点，比如起始点和结束点的位置及各阶导数，比如各个中间节点的位置，其他不确定的点则称为自由点。以下面的这张图为例，红色的方框代表了一个有3个节点，2段的轨迹，具有黄色方框所圈出来的9个约束点和3个自由点。

除了筛选出确定的约束点和不确定的自由点之外，选择矩阵同时将连续性约束进行了融入，原本的d矩阵具有线段数量 n_seg*(n_order+1)个参数(每个线段的起始点和结束点及其各阶导数)，在连续性约束条件下，n_seg个线段其实有n_seg-1套共享的边界参数，因此有(n_seg-1)*(n_order+1)/2个参数是可以被省略的，因此在经过矩阵暗含连续性约束的选择之后，最后的d矩阵去除了冗余项，对于一个7阶多项式，有4个点的情况，情况应如下图所示：

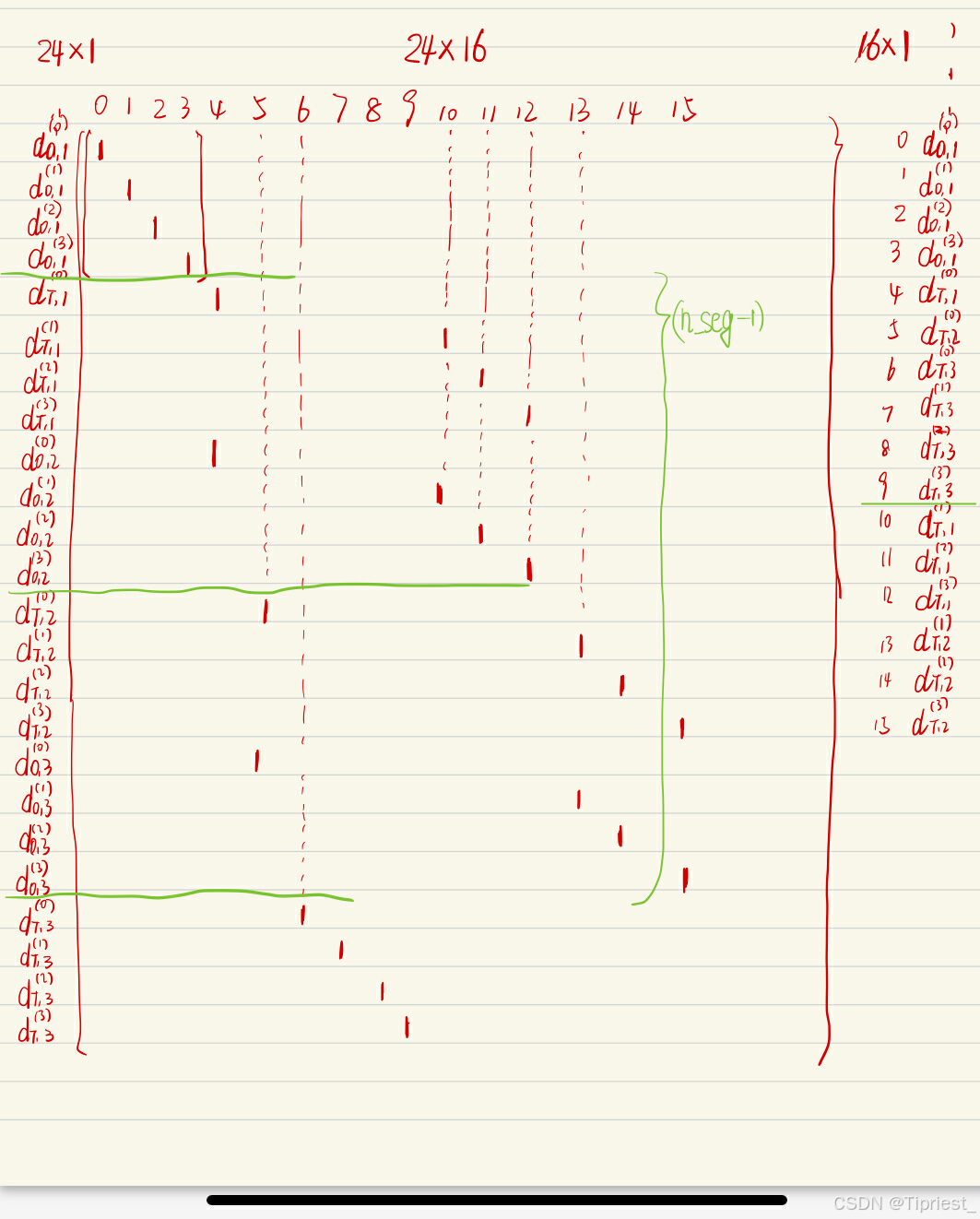
在matlab中的结果:

(4)无约束等价形式

在通过选择矩阵将连续性约束条件代入之后，可以得到原能量矩阵J变换为如下形式，注意是约束点，也就意味着是已知的。

对该式进行求解可以得到：

因此最后可以得到相应的规划结果：

(5) 代码:

https://github.com/Tipriest/Lessons/tree/master/%5B%E6%B7%B1%E8%93%9D%5D%E8%BF%90%E5%8A%A8%E8%A7%84%E5%88%92/ch5%20%E8%BD%A8%E8%BF%B9%E7%94%9F%E6%88%90/matlab/minimum_snap%E9%97%AD%E5%BC%8F%E6%B1%82%E8%A7%A3https://github.com/Tipriest/Lessons/tree/master/%5B%E6%B7%B1%E8%93%9D%5D%E8%BF%90%E5%8A%A8%E8%A7%84%E5%88%92/ch5%20%E8%BD%A8%E8%BF%B9%E7%94%9F%E6%88%90/matlab/minimum_snap%E9%97%AD%E5%BC%8F%E6%B1%82%E8%A7%A3

(6) ROS效果: